Autonomous Aerial Refueling Ground Test Demonstration—A Sensor-in-the-Loop, Non-Tracking Method
Abstract
:1. Introduction
2. Method
2.1. 3D Flash LIDAR Camera

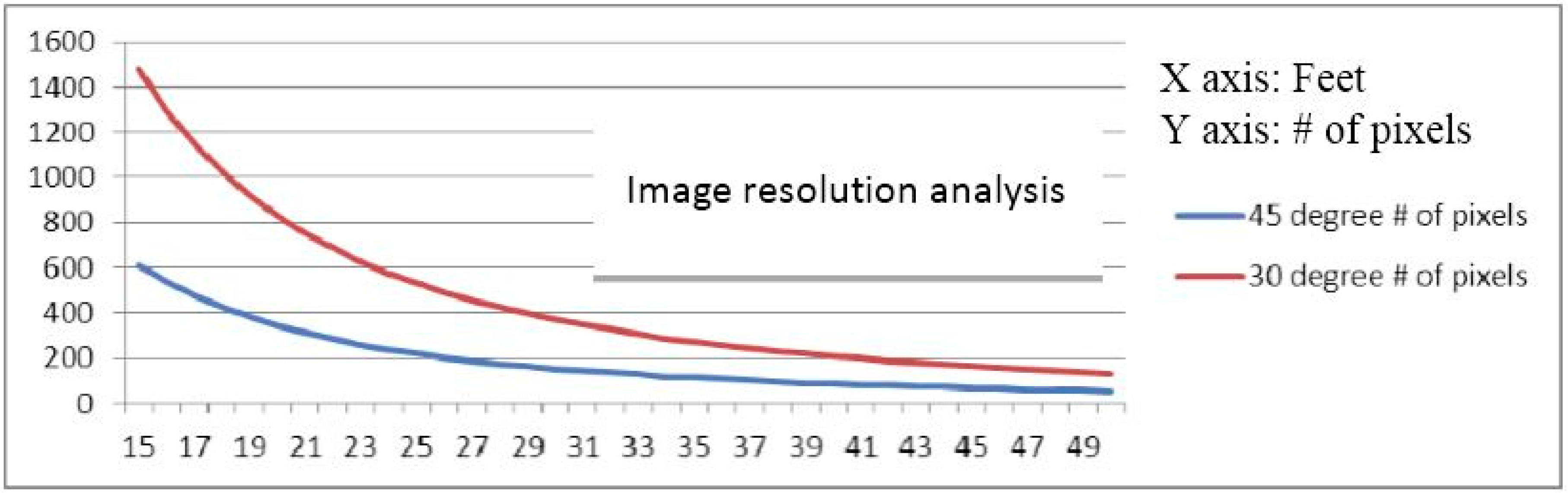


2.2. MA-3 Drogue

2.3. Range Calculation
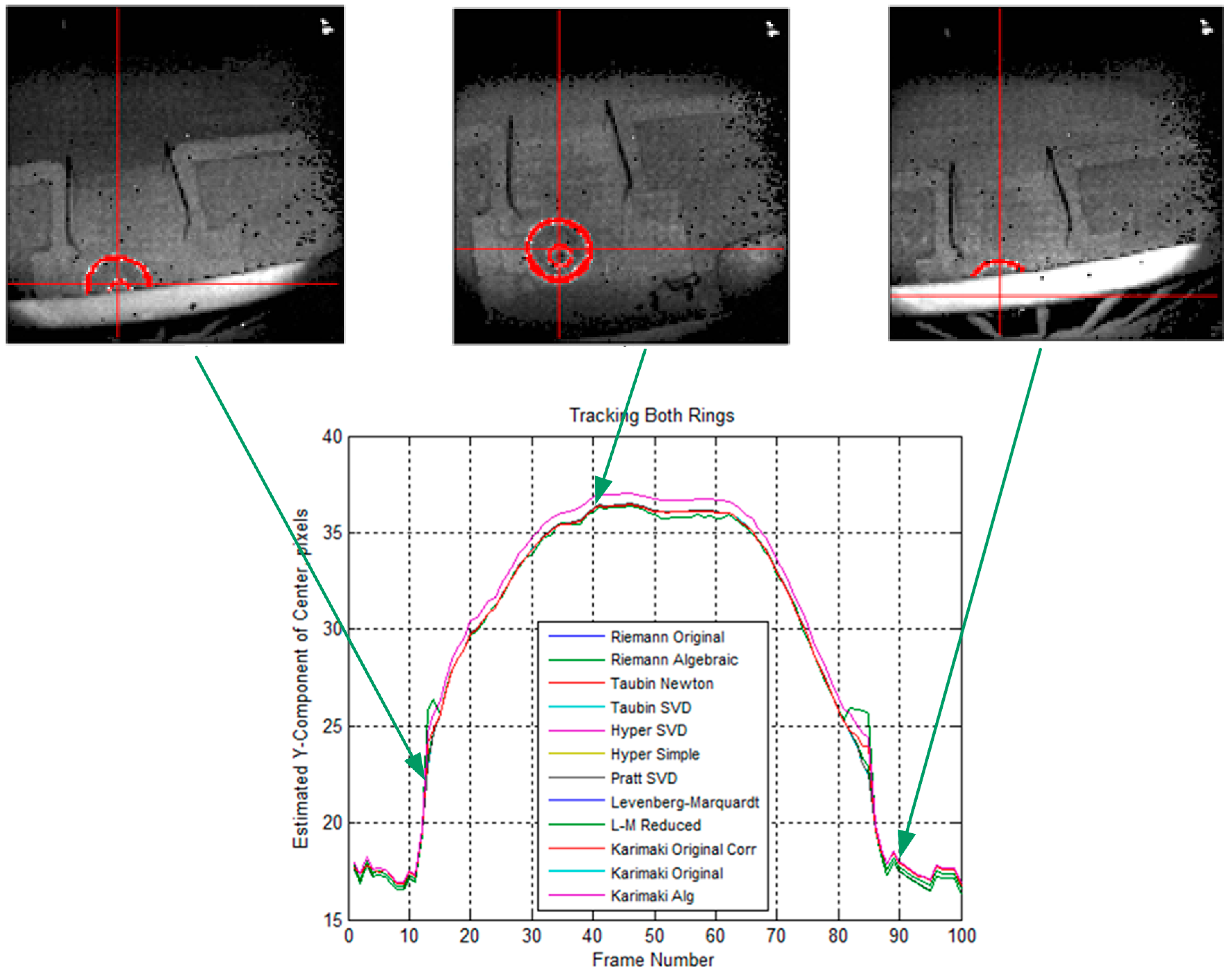
2.4. Drogue Center Estimation
| Item | How We Can Use This Information |
|---|---|
| Single object tracking | Cross over issue is not considered |
| Single camera | Information handling is simplified |
| Simple background | Only have probe, drogue, hose, and tanker |
| Plane movement | Drogue randomly moves in horizontal/vertical directions |
| Known object of interest | Highly reflective materials. Camera setting can be simplified |
| Bounded field of view | Use automatic target detection and recognition for each frame instead of tracking which will fail if the target is outside the FOV. |


3. Ground Test Evaluation
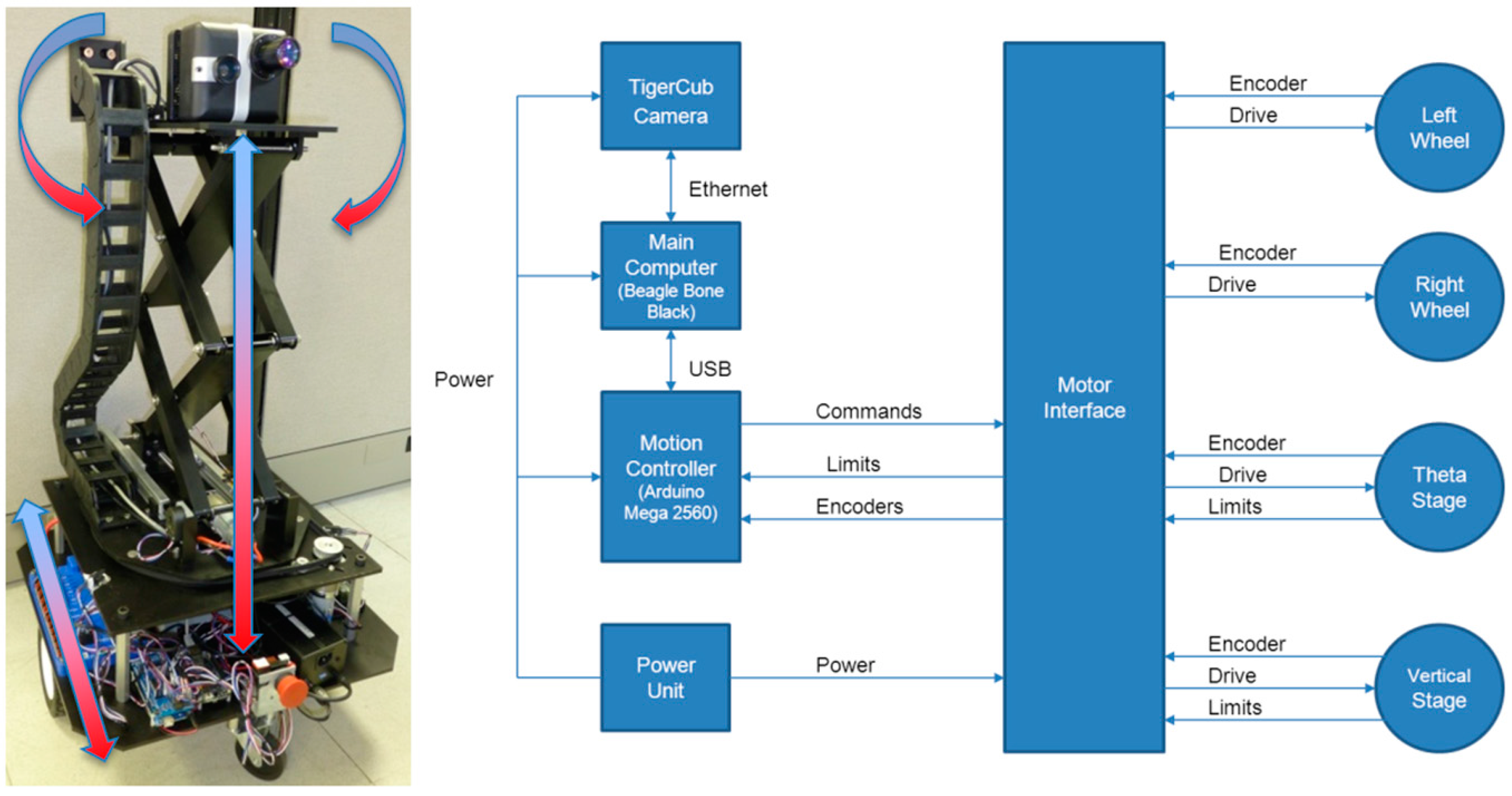
3.1. Robot Design and Fabrication


3.2. Control Electronics
3.3. Full Size Drogue Mock-up

3.4. Pseudo Codes Implemented on the Ground Robot
- Loop Until Distance < Distance_Threshold
- Input one 128 × 128 3D Flash LIDAR image A
- Final_list_count = 0; //initialize
- Distance = 0; //initialize
- Final_list = { }; //initialize
- For each pixel p with quadruplets information—(x, y, range, intensity) in A {
- if (the intensity of p > (range associated) minimum intensity threshold){
- Add p(x, y, 1/range) into Final_list
- Final_list_count++;
- Distance + = p’s range;
- }
- } End For
- if (Final_list_count < 10) continue;
- Distance = Distance/Final_list_count;
- Estimated_Center = Taubin_Circle_Fit (Final_list)
- Ground_Robot_Motion (Estimated_Center, Distance)
- End loop
3.5. Perform Ground Test Autonomously



3.6. Evaluation and Discussion


4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mao, W.; Eke, F.O. A Survey of the Dynamics and Control of Aircraft during Aerial Refueling. Nonlinear Dyn. Syst. Theory 2008, 8, 375–388. [Google Scholar]
- Tomas, P.R.; Bhandari, U.; Bullock, S.; Richardson, T.S.; du Bois, J. Advanced in Air to Air Refuelling. Prog. Aerosp. Sci. 2014, 71, 14–35. [Google Scholar] [CrossRef]
- Nalepka, J.P.; Hinchman, J.L. Automated Aerial Refueling: Extending the Effectiveness of Unmanned Air Vehicles. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, San Francisco, CA, USA, 15–18 August 2005; pp. 240–247.
- Capt. Beau Duarte, the manager for the Navy’s Unmanned Carrier Aviation Program, in the Release. Available online: http://www.cnn.com/2015/04/22/politics/navy-aircraft-makes-history/index.html (accessed on 23 April 2015).
- Latimer-Needham, C.H. Apparatus for Aircraft-Refueling in Flight and Aircraft-Towing. U.S. Patent 2,716,527, 30 August 1955. [Google Scholar]
- Leisy, C.J. Aircraft Interconnecting Mechanism. U.S. Patent 2,663,523, 22 December 1953. [Google Scholar]
- Williamson, W.R.; Abdel-Hafez, M.F.; Rhee, I.; Song, E.J.; Wolfe, J.D.; Cooper, D.F.; Chichka, D.; Speyer, J.L. An Instrumentation System Applied to Formation Flight. IEEE Trans. Control Syst. Technol. 2007, 15, 75–85. [Google Scholar] [CrossRef]
- Williamson, W.R.; Glenn, G.J.; Dang, V.T.; Speyer, J.L.; Stecko, S.M.; Takacs, J.M. Sensors Fusion Applied to Autonomous Aerial Refueling. J. Guid. Control Dyn. 2009, 32, 262–275. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, G.J. Understanding GPS: Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Khanafseh, S.M.; Pervan, B. Autonomous Airborne Refueling of Unmanned Air Vehicles Using the Global Position System. J. Aircr. 2007, 44, 1670–1682. [Google Scholar] [CrossRef]
- Brown, A.; Nguyen, D.; Felker, P.; Colby, G.; Allen, F. Precision Navigation for UAS critical operations. In Proceeding of the ION GNSS, Portland, OR, USA, 20–23 September 2011.
- Monteiro, L.S.; Moore, T.; Hill, C. What Is the Accuracy of DGPS? J. Navig. 2005, 58, 207–225. [Google Scholar] [CrossRef]
- Hansen, J.L.; Murray, J.E.; Campos, N.V. The NASA Dryden AAR Project: A Flight Test Approach to an Aerial Refueling System. In Proceeding of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 2004–2009.
- Vachon, M.J.; Ray, R.J.; Calianno, C. Calculated Drag of an Aerial Refueling Assembly through Airplane Performance Analysis. In Proceeding of the 42nd AIAA Aerospace Sciences and Exhibit, Reno, NV, USA, 5–8 January 2004.
- Campoy, P.; Correa, J.; Mondragon, I.; Martinez, C.; Olivares, M.; Mejias, L.; Artieda, J. Computer Vision Onboard UAVs for Civilian Tasks. J. Intell. Robot. Syst. 2009, 54, 105–135. [Google Scholar] [CrossRef] [Green Version]
- Conte, G.; Doherty, P. Vision-based Unmanned Aerial Vehicle Navigation Using Geo-referenced Information. EURASIP J. Adv. Signal Process. 2009. [Google Scholar] [CrossRef]
- Luington, B.; Johnson, E.N.; Vachtsevanos, G.J. Vision Based Navigation and Target Tracking for Unmanned Aerial Vehicles. Intell. Syst. Control Autom. Sci. Eng. 2007, 33, 245–266. [Google Scholar]
- Madison, R.; Andrews, G.; DeBitetto, P.; Rasmussen, S.; Bottkol, M. Vision-aided navigation for small UAVs in GPS-challenged Environments. In Proceeding of the AIAA InfoTech at Aerospace Conference, Rohnert Park, CA, USA, 7–10 May 2007; pp. 318–325.
- Ollero, A.; Ferruz, F.; Caballero, F.; Hurtado, S.; Merino, L. Motion Compensation and Object Detection for Autonomous Helicopter Visual Navigation in the COMETS Systems. In Proceeding of the IEEE International Conference on Robotics and Autonomous, New Orleans, LA, USA, 26 April–1 May 2004; pp. 19–24.
- Vendra, S.; Campa, G.; Napolitano, M.R.; Mammarella, M.; Fravolini, M.L.; Perhinschi, M.G. Addressing Corner Detection Issues for Machine Vision Based UAV Aerial Refueling. Mach. Vis. Appl. 2007, 18, 261–273. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. Combined Corner and Edge Detector. In Proceedings of the 4th Alvery Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151.
- Kimmett, J.; Valasek, J.; Junkings, J.L. Autonomous Aerial Refueling Utilizing a Vision Based Navigation System. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibition, Monterey, CA, USA, 5–8 August 2002.
- Nobel, A. Finding Corners. Image Vis. Comput. 1988, 6, 121–128. [Google Scholar] [CrossRef]
- Smith, S.M.; Bradly, J. M SUSAN—A New Approach to Low Level Image Processing. Int. J. Comput. Vis. 1997, 23, 45–78. [Google Scholar] [CrossRef]
- Doebbler, J.; Spaeth, T.; Valasek, J.; Monda, M.J.; Schaub, H. Boom and Receptacle Autonomous Air Refueling using Visual Snake Optical Sensor. J. Guid. Control Dyn. 2007, 30, 1753–1769. [Google Scholar] [CrossRef]
- Herrnberger, M.; Sachs, G.; Holzapfel, F.; Tostmann, W.; Weixler, E. Simulation Analysis of Autonomous Aerial Refueling Procedures. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibition, San Francisco, CA, USA, 15–18 August 2005.
- Fravolini, M.L.; Ficola, A.; Campa, G.; Napolitano, M.R.; Seanor, B. Modeling and Control Issues for Autonomous Aerial Refueling for UAVs using a Probe-Drogue Refueling System. Aerosp. Sci. Technol. 2004, 8, 611–618. [Google Scholar] [CrossRef]
- Pollini, L.; Campa, G.; Giulietti, F.; Innocenti, M. Virtual Simulation Setup for UAVs Aerial Refueling. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Austin, TX, USA, 11–14 August 2003.
- Pollini, L.; Mati, R.; Innocenti, M. Experimental Evaluation of Vision Algorithms for Formation Flight and Aerial Refueling. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Providence, RI, USA, 16–19 August 2004.
- Mati, R.; Pollini, L.; Lunghi, A.; Innocenti, M.; Campa, G. Vision Based Autonomous Probe and Drogue Refueling. In Proceedings of the 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006.
- Junkins, J.L.; Schaub, H.; Hughes, D. Noncontact Position and Orientation Measurement System and Method. U.S. Patent 6,266,142 B1, 24 July 2001. [Google Scholar]
- Kimmett, J.; Valasek, J.; Junkins, J.L. Vision Based Controller for Autonomous Aerial Refueling. In Proceedings of the 2002 IEEE International Conference on Control Applications, Glasgow, Scotland, 17–20 September 2002.
- Tandale, M.D.; Bowers, R.; Valasek, J. Trajectory Tracking Controller for Vision-Based Probe and Drogue Autonomous Aerial Refueling. J. Guid. Control Dyn. 2006, 4, 846–857. [Google Scholar] [CrossRef]
- Valasek, J.; Gunman, K.; Kimmett, J.; Tandale, M.; Junkins, L.; Hughes, D. Vision-based Sensor and Navigation System for Autonomous Air Refueling. In Proceeding of the 1st AIAA Unmanned Aerospace Vehicles, Systems, Technologies, and Operations Conference and Exhibition, Vancouver, BC, Canada, 20–23 May 2002.
- Pollini, L.; Innocenti, M.; Mati, R. Vision Algorithms for Formation Flight and Aerial Refueling with Optimal Marker Labeling. In Proceeding of the AIAA Modeling and Simulation Technologies Conference and Exhibition, San Francisco, CA, USA, 15–18 August 2005.
- Lu, C.P.; Hager, G.D.; Mjolsness, E. Fast and Globally Convergent Pose Estimation from Video Images. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 610–622. [Google Scholar] [CrossRef]
- Martinez, C.; Richardson, T.; Thomas, P.; du Bois, J.L.; Campoy, P. A Vision-based Strategy for Autonomous Aerial Refueling Tasks. Robot. Auton. Syst. 2013, 61, 876–895. [Google Scholar] [CrossRef]
- Irani, M.; Anandan, P. About Direct Methods. Lect. Notes Comput. Sci. 2000, 1833, 267–277. [Google Scholar]
- Bergen, J.R.; Anandan, P.; Hanna, K.J.; Hingorani, R. Hierarchical Model-Based Motion Estimation. Lect. Notes Comput. Sci. 1992, 588, 237–252. [Google Scholar]
- Thomas, P.; Bullock, S.; Bhandari, U.; du Bois, J.L.; Richardson, T. Control Methodologies for Relative Motion Reproduction in a Robotic Hybrid Test Simulation of Aerial Refueling. In Proceeding of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012.
- Christopher Longuet-Higgins, H. A computer algorithm for reconstructing a scene from two projections. Nature 1981, 293, 133–135. [Google Scholar] [CrossRef]
- Hartley, R. In Defense of the Eight-Point Algorithm. IEEE Trans. Pattern Recogn. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Malis, E.; Chaumette, F.; Boudet, S. 2 ½D Visual Servoing with Respect to Unknown Objects Through a New Estimation Scheme of Camera Displacement. Int. J. Comput. Vis. 2000, 37, 79–97. [Google Scholar] [CrossRef]
- Lots, J.F.; Lane, D.M.; Trucco, E. Application of a 2 ½D Visual Servoing to Underwater Vehicle Station-keeping. In Proceeding of the IEEE OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000.
- Stettner, R. High Resolution Position Sensitive Detector. U.S. Patent 5,099,128, 24 March 1992. [Google Scholar]
- Stettner, R. Compact 3D Flash Lidar Video Cameras and Applications. Proc. SPIE 2010, 7684. [Google Scholar] [CrossRef]
- Chen, C.; Stettner, R. Drogue Tracking Using 3D Flash LIDAR for Autonomous Aerial Refueling. Proc. SPIE 2011, 8037. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts Propagating with Curvature-dependent Speed: Algorithms Based on Hamilton-Jacobi Formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bonin-Font, F.; Ortiz, A.; Oliver, G. Visual Navigation for Mobile Robots: A Survey. J. Intell. Robot. Syst. 2008, 53, 263–296. [Google Scholar] [CrossRef]
- Kendoul, F. Survey of Advances in Guidance, Navigation, and Control of Unmanned Rotorcraft Systems. J. Field Robot. 2012, 29, 315–378. [Google Scholar] [CrossRef]
- Cai, G.; Dias, J.; Seneviratne, L. A Survey of Small-Scale Unmanned Aerial Vehicles: Recent Advances and Future Development Trends. Unmanned Syst. 2014, 2, 1–25. [Google Scholar]
- OpenCV. Available online: http://opencv.org (accessed on 23 April 2015).
- Rusu, R.B.; Cousins, S. 3D is Here: Point Cloud Library. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 9–13.
- Robot Operating System (ROS). Available online: http://www.ros.org (accessed on 23 April 2015).
- Chernov, N. Circular and Linear Regression: Fitting Circles and Lines by Least Squares, 1st ed.; Chapman & Hall/CRC Monographs on Statistics & Applied Probability Series; CRC Press: London, UK, 2010. [Google Scholar]
- Chernov, N. Matlabe Codes for Circle Fitting Algorithms. Available online: http://people.cas.uab.edu/~mosya/cl/MATLABcircle.html (accessed on 23 April 2015).
- Coope, I.D. Circle Fitting by Linear and Nonlinear Least Squares. J. Optim. Theory Appl. 1993, 76, 381–388. [Google Scholar] [CrossRef]
- Gander, W.; Golub, G.H.; Strebel, R. Least squares fitting of circles and ellipses. Bull. Belg. Math. Soc. 1996, 3, 63–84. [Google Scholar]
- Karimaki, V. Effective Circle Fitting for Particle Trajectories. Nuclear Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1991, 305, 187–191. [Google Scholar] [CrossRef]
- Kasa, I. A Curve Fitting Procedure and Its Error Analysis. IEEE Trans. Instrum. Measur. 1976, 25, 8–14. [Google Scholar] [CrossRef]
- Nievergelt, Y. Hyperspheres and hyperplanes fitted seamlessly by algebraic constrained total least-squares. Linear Algebra Appl. 2001, 331, 43–59. [Google Scholar] [CrossRef]
- Pratt, V. Direct Least-Squares Fitting of Algebraic Surfaces. Comput. Graph. 1987, 21, 145–152. [Google Scholar] [CrossRef]
- Taubin, G. Estimation of Planar Curves, Surfaces and Non-planar Space Curves Defined by Implicit Equations, with Applications to Edge and Range Image Segmentation. IEEE Transit. Pattern Anal. Mach. Intell. 1991, 13, 1115–1138. [Google Scholar] [CrossRef]
- Matlab: The Language Technical Computing. Available online: http://www.mathworks.com/products/matlab/ (accessed on 23 April 2015).
- Gill, P.R.; Murray, W.; Wright, M.H. The Levenberg-Marquardt Method. Practical Optimization; Academic Press: London, UK, 1981; pp. 136–137. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Application to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Dibley, R.P.; Allen, M.J.; Nabaa, N. Autonomous Airborne Refueling Demonstration Phase I Flight-Test Results. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-I.; Koseluk, R.; Buchanan, C.; Duerner, A.; Jeppesen, B.; Laux, H. Autonomous Aerial Refueling Ground Test Demonstration—A Sensor-in-the-Loop, Non-Tracking Method. Sensors 2015, 15, 10948-10972. https://doi.org/10.3390/s150510948
Chen C-I, Koseluk R, Buchanan C, Duerner A, Jeppesen B, Laux H. Autonomous Aerial Refueling Ground Test Demonstration—A Sensor-in-the-Loop, Non-Tracking Method. Sensors. 2015; 15(5):10948-10972. https://doi.org/10.3390/s150510948
Chicago/Turabian StyleChen, Chao-I, Robert Koseluk, Chase Buchanan, Andrew Duerner, Brian Jeppesen, and Hunter Laux. 2015. "Autonomous Aerial Refueling Ground Test Demonstration—A Sensor-in-the-Loop, Non-Tracking Method" Sensors 15, no. 5: 10948-10972. https://doi.org/10.3390/s150510948
APA StyleChen, C.-I., Koseluk, R., Buchanan, C., Duerner, A., Jeppesen, B., & Laux, H. (2015). Autonomous Aerial Refueling Ground Test Demonstration—A Sensor-in-the-Loop, Non-Tracking Method. Sensors, 15(5), 10948-10972. https://doi.org/10.3390/s150510948





