A Model-Based 3D Template Matching Technique for Pose Acquisition of an Uncooperative Space Object
Abstract
:1. Introduction
2. Template Matching for Pose Acquisition
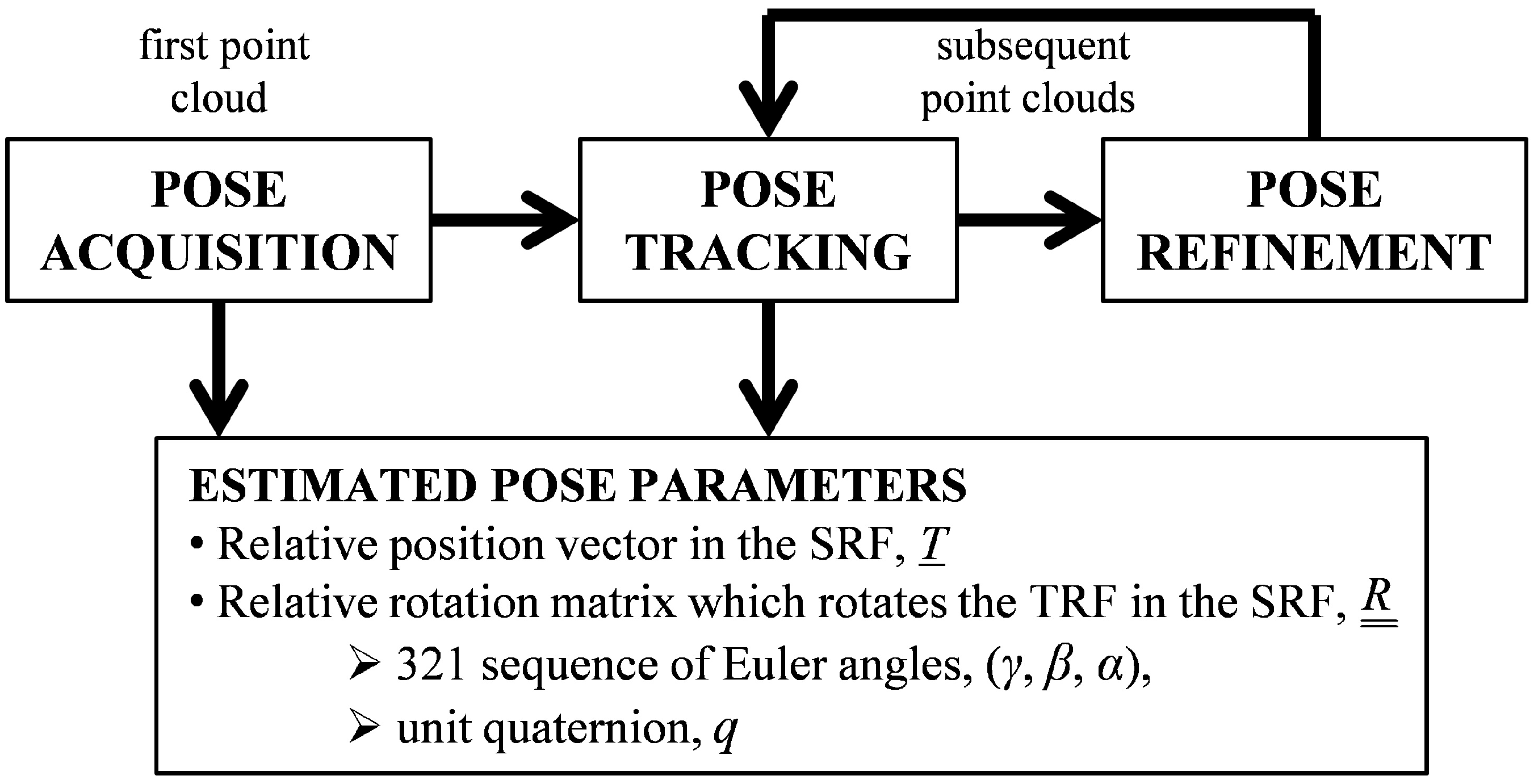
2.1. 3D On-Line Template Matching

2.2. On-Line Fast Template Matching
3. Simulation Environment
3.1. Target Selection and Modeling

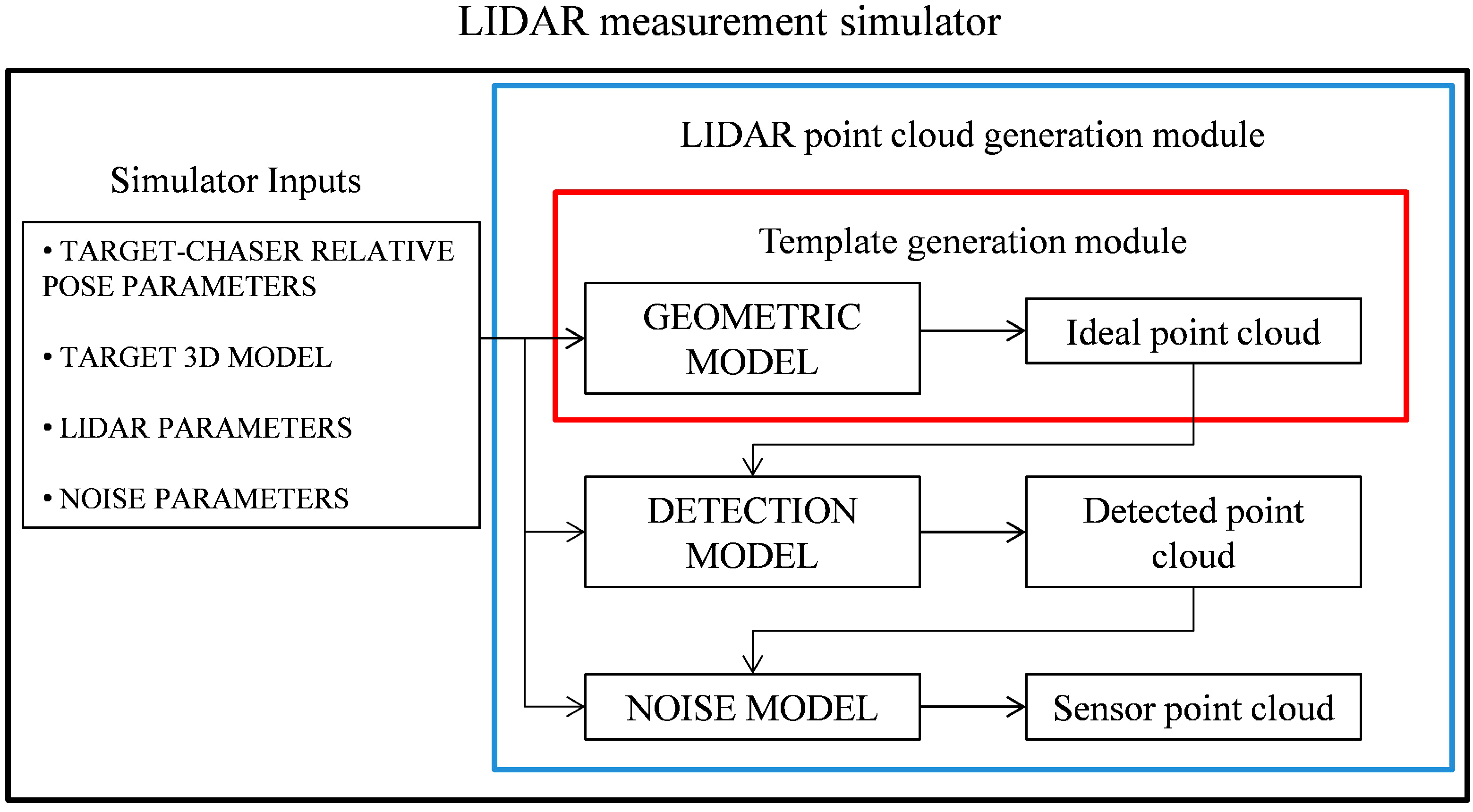
3.2. LIDAR Measurement Simulator
3.3. Relative Dynamics Simulator
4. TM Performance Analysis
4.1. Sensor Parameters
4.2. TM Success Criterion
| LIDAR Transmitter Parameters | LIDAR Detector (InGaAs PAD) Parameters | ||
|---|---|---|---|
| λ, laser wavelength | 1540 nm | η, quantum efficiency | 0.7247 |
| PwTRAN, average laser pulse power | 1 mW | GAPD, gain | 10 |
| τW, pulse width | 1 ns | Ca, capacitance | 1.5 pF |
| PRF, pulse repetition frequency | 10 kHz | Temp, operating temperature | 273.15 K |
| dθ, beam divergence | 0.02° | iD, dark current mean intensity | 150 nA |
| LIDAR Aperture Parameters | Measurement Noise Parameters | ||
| D, aperture diameter | 2.5 cm | σRANGE, range uncertainty | 25 mm |
| LIDAR Optical Band-Pass Filter Parameters | σLOS, pointing uncertainty | 0.0007° | |
| Δλ, filter bandwidth | 24 nm | PO, outliers probability | 5%–7% |
| τO, filter transmittance | 0.3898 | ||
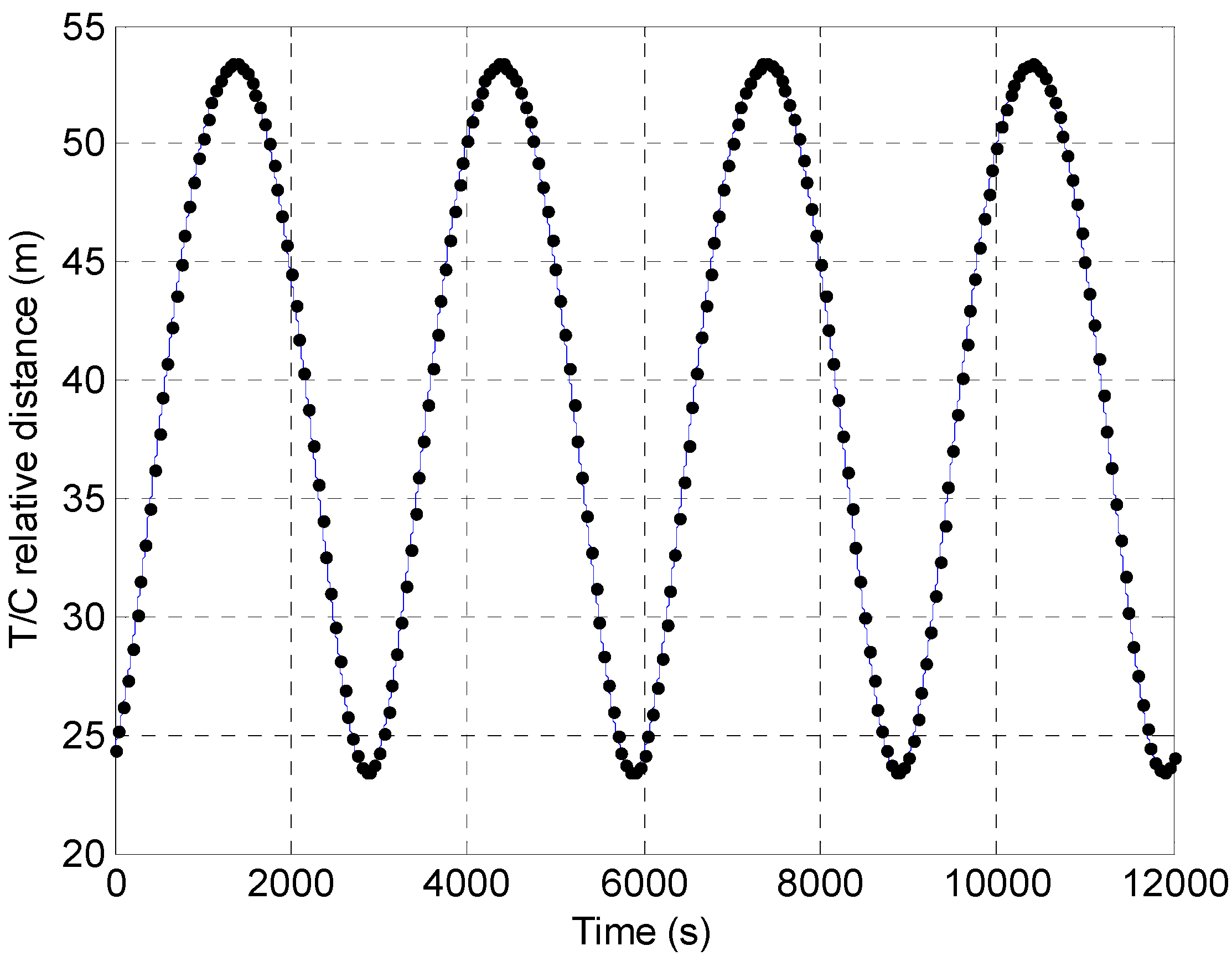
4.3. Simulation Scenarios
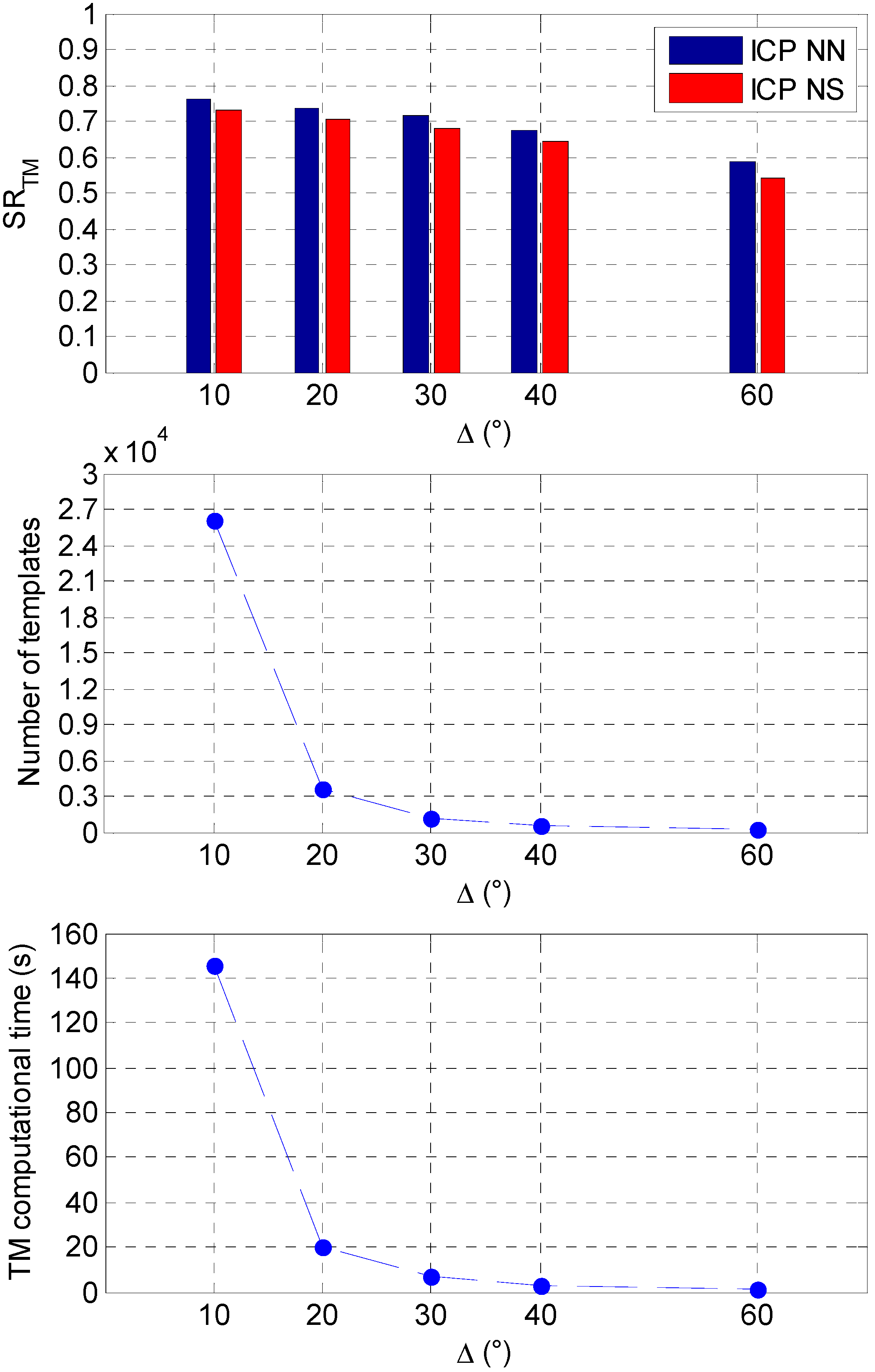
4.4. Simulation Results
| Average Attitude Estimation Error | ||||||
|---|---|---|---|---|---|---|
| Δ (°) | 10 | 20 | 30 | 40 | 60 | |
| Successful pose estimates | 184 | 177 | 173 | 163 | 142 | |
| Euler angles | α (°) | 9.73 | 14.04 | 13.83 | 39.83 | 56.88 |
| β (°) | 6.17 | 6.88 | 8.15 | 14.50 | 18.97 | |
| γ (°) | 21.40 | 22.70 | 37.45 | 47.62 | 78.45 | |
| Relative Position Vector Components | Average Position Estimation Error | |||||
|---|---|---|---|---|---|---|
| Δ = 10° | Δ = 20° | Δ = 30° | Δ = 40° | Δ = 60° | ||
| On-line TM success | TX (m) | 2.809 | 2.697 | 2.689 | 2.772 | 2.853 |
| TY (m) | 1.324 | 1.268 | 1.251 | 1.343 | 1.369 | |
| TZ (m) | 1.924 | 1.936 | 1.868 | 1.808 | 1.868 | |
| On-line TM failure | TX (m) | 4.021 | 4.198 | 4.130 | 3.773 | 3.443 |
| TY (m) | 1.588 | 1.714 | 1.732 | 1.478 | 1.412 | |
| TZ (m) | 4.698 | 4.360 | 4.390 | 4.192 | 3.601 | |
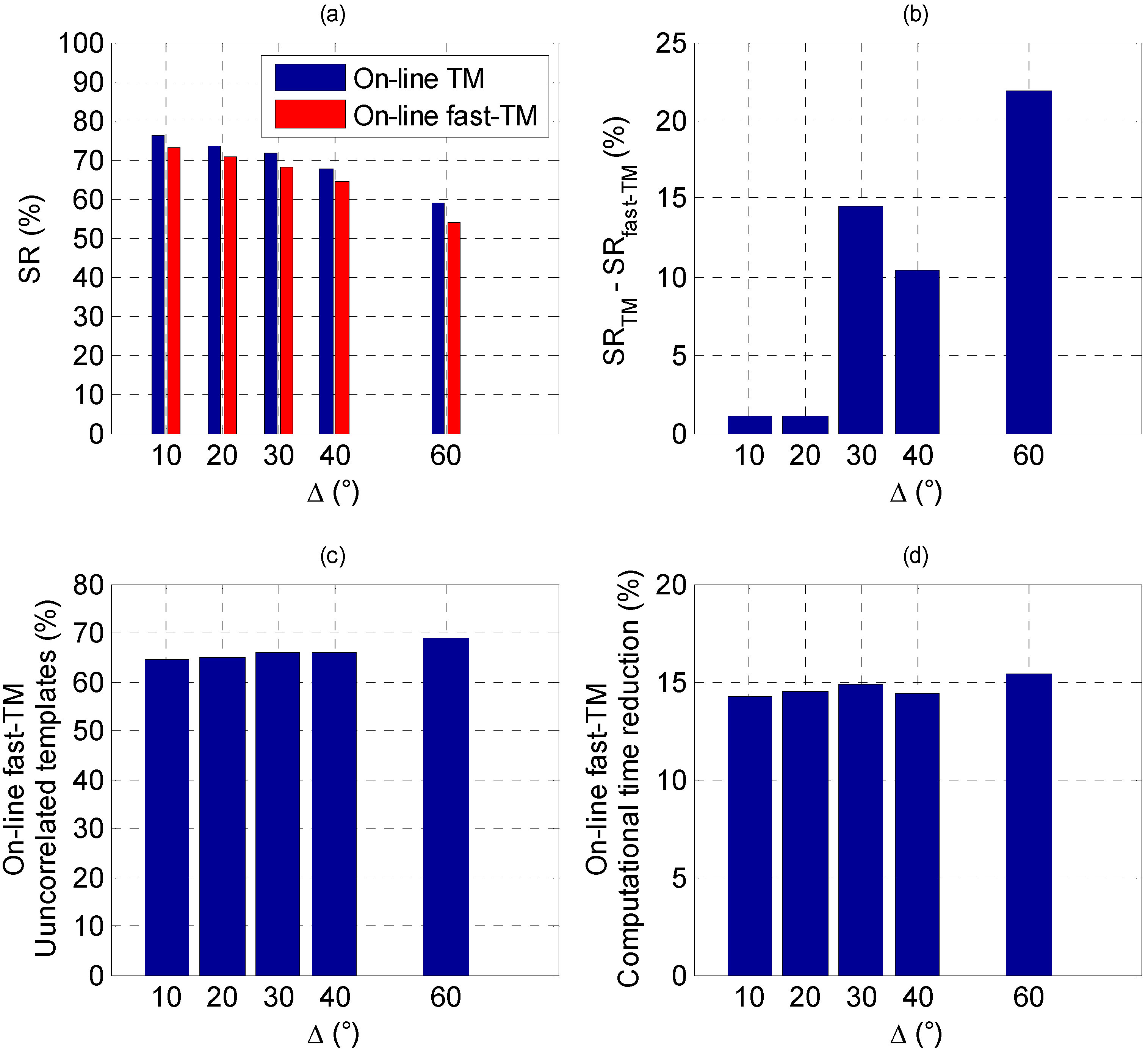
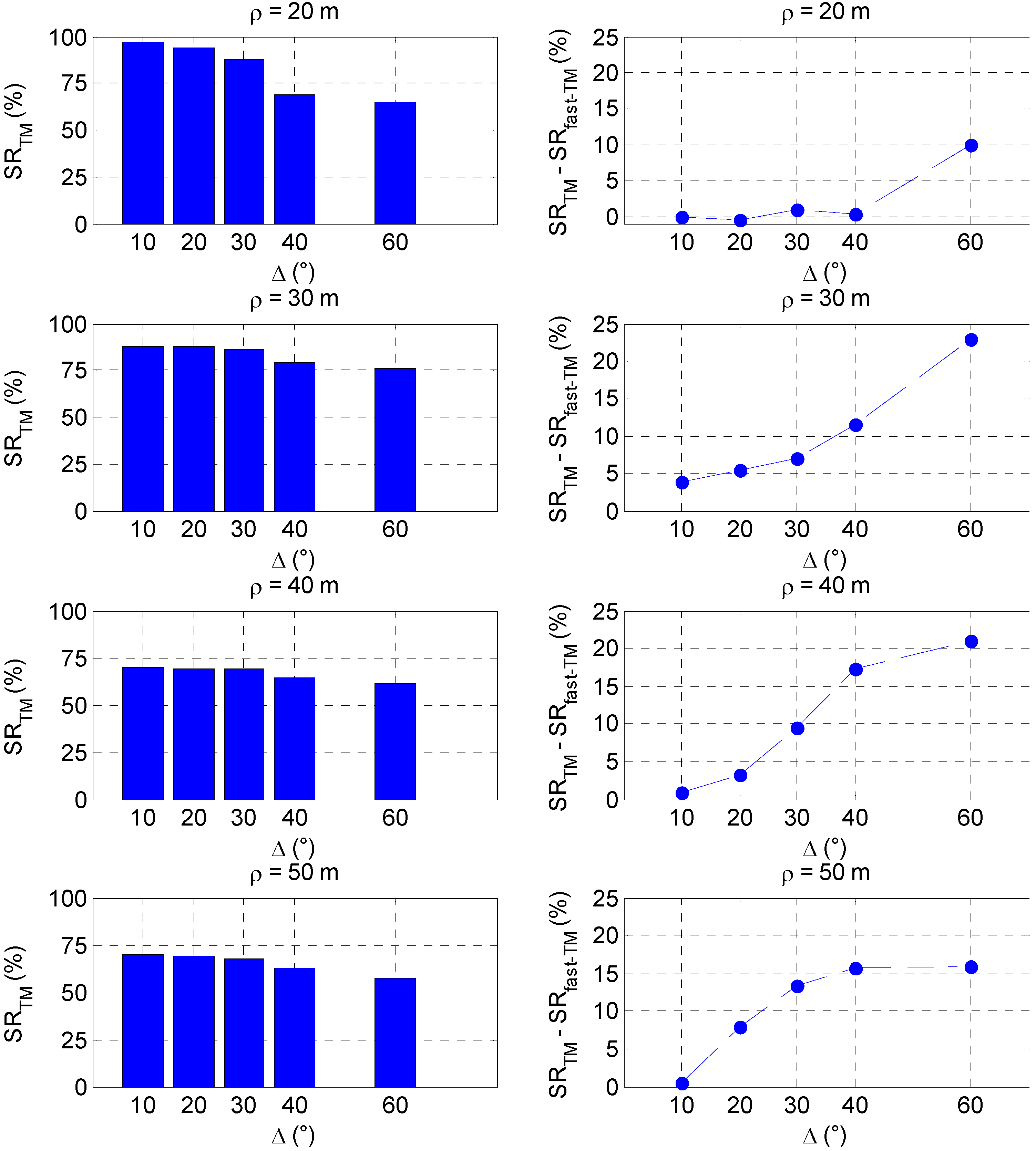
4.5. TM Failure Detection Approach
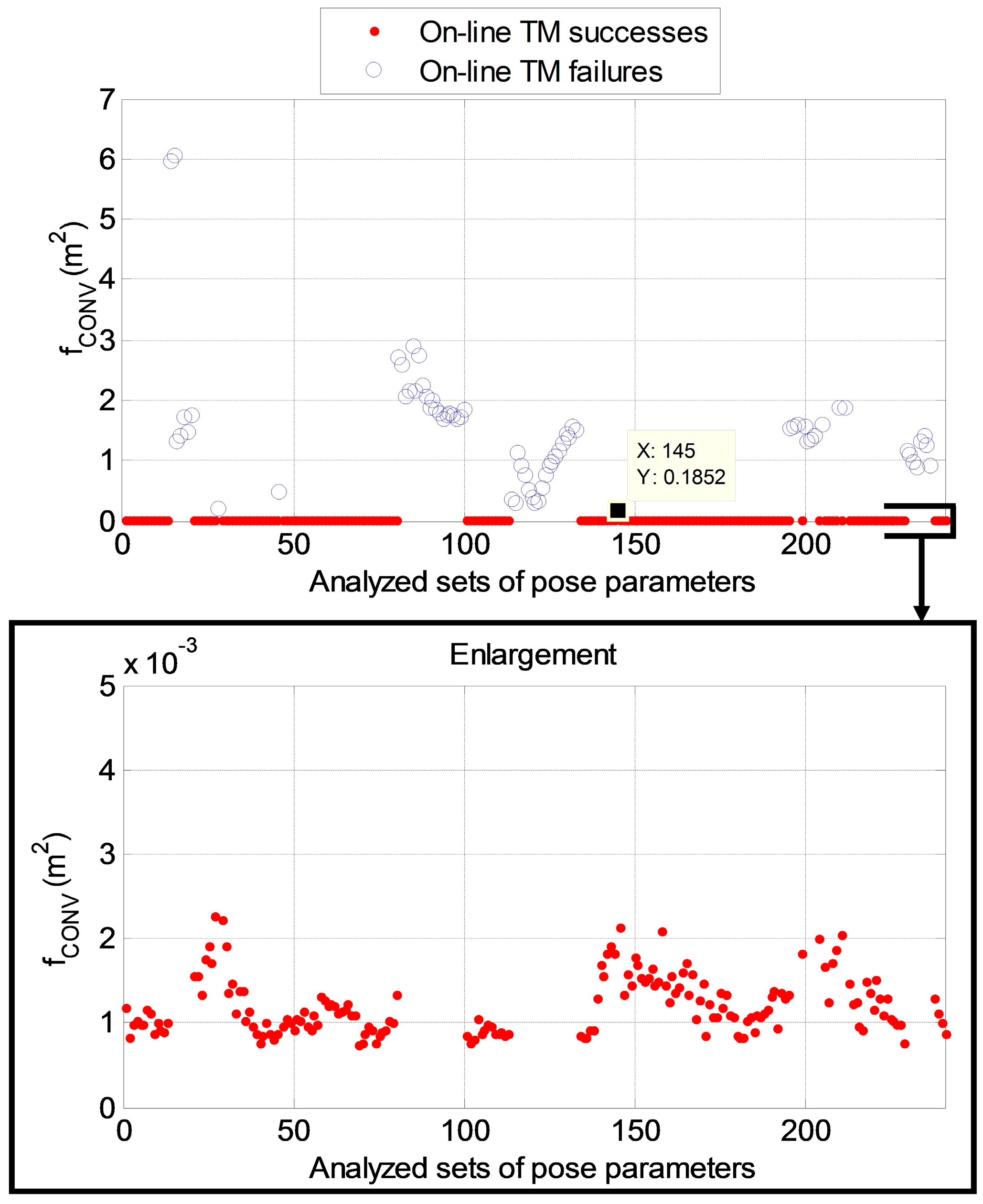
| fCONV (m2) | |||||
|---|---|---|---|---|---|
| Δ(°) | TM Failure: Minimum Value | TM Failure: Mean Value | TM Success: Maximum Value | TM Success: Mean Value | |
| On-line TM | 10 | 0.1882 | 1.4620 | 0.0023 | 0.0012 |
| 20 | 0.1882 | 1.4738 | 0.0023 | 0.0012 | |
| 30 | 0.1852 | 1.5309 | 0.0023 | 0.0012 | |
| 40 | 0.1539 | 1.3478 | 0.0026 | 0.0012 | |
| 60 | 0.1254 | 1.6681 | 0.0029 | 0.0013 | |
| On-line fast-TM | 10 | 0.3086 | 1.5513 | 0.0023 | 0.0012 |
| 20 | 0.3513 | 1.6901 | 0.1702 | 0.0022 | |
| 30 | 0.1254 | 1.4034 | 0.0023 | 0.0012 | |
| 40 | 0.1539 | 1.4273 | 0.0027 | 0.0013 | |
| 60 | 0.1254 | 1.7980 | 0.0026 | 0.0012 | |

4. Conclusions
Author Contributions
Conflicts of Interest
References
- Murphy-Chutorian, E.; Trivedi, M.M. Head pose estimation in computer vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 607–626. [Google Scholar] [CrossRef] [PubMed]
- Erol, A.; Bebis, G.; Nicolescu, M.; Boyle, R.D.; Twombly, X. Vision-based hand pose estimation: A review. Comput. Vis. Image Underst. 2007, 108, 52–73. [Google Scholar] [CrossRef]
- Zhu, M.; Derpanis, K.G.; Yang, Y.; Brahmbhatt, S.; Zhang, M.; Phillips, C.; Lecce, M.; Daniilidis, K. Single Image 3D Object Detection and Pose Estimation for Grasping. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA 2014), Hong Kong, China, 31 May–7 June 2014.
- Ulrich, M.; Wiedemann, C.; Steger, C. CAD-based recognition of 3D objects in monocular images. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation (ICRA 2009), Kobe, Japan, 12–17 May 2009; Volume 9, pp. 1191–1198.
- Bonnal, C.; Ruault, J.M.; Desjean, M.C. Active debris removal: Recent progress and current trends. Acta Astronaut. 2013, 85, 51–60. [Google Scholar] [CrossRef]
- Clerc, X.; Retat, I. Astrium Vision on Space Debris Removal. In Proceeding of the 63rd International Astronautical Congress (IAC 2012), Napoli, Italy, 1–5 October 2012.
- Tatsch, A.; Fitz-Coy, N.; Gladun, S. On-orbit servicing: A brief survey. In Proceedings of the 2006 Performance Metrics for Intelligent Systems (PerMIS’06) Workshop, Gaithersburg, MD, USA, 21–23 August 2006.
- Doignon, C. An Introduction to Model-Based Pose Estimation and 3-D Tracking Techniques. In Scene Reconstruction, Pose Estimation and Tracking, 1st ed.; Stolkin, R, Ed.; InTech: Morn Hill, Winchester, UK, 2007; pp. 359–382. [Google Scholar]
- Reinbacher, C.; Ruther, M.; Bischof, H. Pose Estimation of Known Objects by Efficient Silhouette Matching. In Proceedings of the IEEE 20th International Conference on Pattern Recognition (ICPR 2010), Istanbul, Turkey, 23–26 August 2010; pp. 1080–1083.
- Petit, A.; Marchand, E.; Kanani, K. Vision-Based Detection and Tracking for Space Navigation in a Rendezvous Context. In Proceedings of the 11th International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS 2011), Torino, Italy, 4–6 September 2011.
- Ruel, S.; Luu, T.; Anctil, M.; Gagnon, S. Target localization from 3D data for on-orbit autonomous rendezvous and docking. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008.
- Greenspan, M.; Jasiobedzki, P. Pose determination of a free-flying satellite. In Proceedings of the 2002 International Conference on Imaging Science, Systems, and Technology (CISST’2002), Las Vegas, NV, USA, 24–27 June 2002.
- Christian, J.A.; Cryan, S. A Survey of LIDAR Technology and Its Use in Spacecraft Relative Navigation. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Honolulu, HI, USA, 18–21 August 2008.
- De Luca, L.T.; Bernelli, F.; Maggi, F.; Tadini, P.; Pardini, C.; Anselmo, L.; Grassi, M.; Pavarin, D.; Francesconi, A.; Branz, F.; et al. Active space debris removal by a hybrid propulsion module. Acta Astronaut. 2013, 91, 20–33. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. Uncooperative pose estimation with a LIDAR-based system. Acta Astronaut. 2014. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Dawoud, N.N.; Samir, B.B.; Janier, J. Fast Template Matching Method Based Optimized Sum of Absolute Difference Algorithm for Face Localization. Int. J. Comput. Appl. 2011, 18, 30–34. [Google Scholar]
- Briechle, K.; Hanebeck, U.D. Template matching using fast normalized cross correlation. Proc. SPIE 2001, 4387. [Google Scholar] [CrossRef]
- Gavrila, D.M.; Philomin, V. Real-time object detection using distance transforms. In Proceedings of the IEEE International Conference on Intelligent Vehicles, Stuttgart, Germany, 28–30 October 1998; pp. 274–279.
- Desnos, Y.L.; Buck, C.; Guijarro, J.; Suchail, J.L.; Torresand, R.; Attema, E. ASAR-Envisat’s advanced synthetic aperture radar. ESA Bull. 2000, 102, 91–100. [Google Scholar]
- ENVISAT Mission & System Summary. Available online: https://earth.esa.int/support-docs/pdf/mis_sys.pdf (accessed on 22 December 2014).
- Gilmore, D.G. Spacecraft Thermal Control Handbook; The Aerospace Press: El Segundo, CA, USA, 2002. [Google Scholar]
- Blais, F. Review of 20 Years of Range Sensor Development. J. Electron. Imaging 2004, 13, 231–240. [Google Scholar] [CrossRef]
- Euliss, X.G.; Christiansen, A.; Athale, R. Analysis of laser-ranging technology for sense and avoid operation of unmanned aircraft systems: The tradeoff between resolution and power. Proc. SPIE 2008, 6962. [Google Scholar] [CrossRef]
- Richmond, R.D.; Cain, S.E. Direct Detection LADAR Systems; SPIE Press: Bellingham, WA, USA, 2010. [Google Scholar]
- Goodman, J.W. Statistical Optics; Wiley-Interscience: New York, NY, USA, 1985. [Google Scholar]
- Reference Solar Spectral Irradiance: ASTM G-173. Available online: http://rredc.nrel.gov/solar/spectra/am1.5/ASTMG173/ASTMG173.html (accessed on 22 December 2014).
- Ansalone, L. A Search Algorithm for Stochastic Optimization in Initial Orbit Determination. PhD Thesis, University of Rome “La Sapienza”, 2014. [Google Scholar]
- Fasano, G.; D’Errico, M. Modeling Orbital Relative Motion to Enable Formation Design from Application Requirements. Celestial Mech. Dyn. Astron. 2009, 105, 113–139. [Google Scholar] [CrossRef]
- Liebe, C.C.; Abramovici, A.; Bartman, R.K.; Bunker, R.L.; Chapsky, J.; Chu, C.C.; Clouse, D.; Dillon, J.W.; Hausmann, B.; Hemmati, H.; et al. Laser Radar for Spacecraft Guidance Applications. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 8–15 March 2003.
- Laurin, D.G.; Beraldin, J.A.; Blais, F.; Rioux, M.; Cournoyer, L. A three dimensional tracking and imaging laser scanner for space operations. Proc. SPIE 1999, 3707. [Google Scholar] [CrossRef]
- Samson, C.; English, C.; Deslauriers, A.; Christie, I.; Blais, F. Imaging and Tracking Elements of the International Space Station Using a 3D Auto-Synchronized Scanner. Proc. SPIE-Int. Soc. Opt. Eng 2002. [Google Scholar] [CrossRef]
- Hamamatsu InGaAs APD G8931–20 Datasheet. Available online: http://www.hamamatsu.com/resources/pdf/ssd/g8931–20_kapd1019e03.pdf (accessed on 22 December 2014).
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceeding of the 3rd IEEE International Conference on 3D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152.
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. DAR-based autonomous pose determination of a large space debris. In Proceeding of the 65th International Astronautical Congress (IAC 2014), Toronto, ON, Canada, 29 September–3 October 2014.
- Gaylor, D.E.; Barbee, B.W. Algorithms for safe spacecraft proximity operations. In Proceedings of the 17th AAS/AIAA Space Flight Mechanics Meeting, Sedona, AZ, USA, 28 January–1 February 2007; Volume 127.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A Model-Based 3D Template Matching Technique for Pose Acquisition of an Uncooperative Space Object. Sensors 2015, 15, 6360-6382. https://doi.org/10.3390/s150306360
Opromolla R, Fasano G, Rufino G, Grassi M. A Model-Based 3D Template Matching Technique for Pose Acquisition of an Uncooperative Space Object. Sensors. 2015; 15(3):6360-6382. https://doi.org/10.3390/s150306360
Chicago/Turabian StyleOpromolla, Roberto, Giancarmine Fasano, Giancarlo Rufino, and Michele Grassi. 2015. "A Model-Based 3D Template Matching Technique for Pose Acquisition of an Uncooperative Space Object" Sensors 15, no. 3: 6360-6382. https://doi.org/10.3390/s150306360
APA StyleOpromolla, R., Fasano, G., Rufino, G., & Grassi, M. (2015). A Model-Based 3D Template Matching Technique for Pose Acquisition of an Uncooperative Space Object. Sensors, 15(3), 6360-6382. https://doi.org/10.3390/s150306360








