The Optimization Based Dynamic and Cyclic Working Strategies for Rechargeable Wireless Sensor Networks with Multiple Base Stations and Wireless Energy Transfer Devices
Abstract
:1. Introduction
2. The Description and the Preliminary Modeling of the Problem
2.1. Problem Description
| Symbols | Definitions |
|---|---|
| D | The area in which a wireless sensor network is deployed |
| S | The service station |
| The set of all base stations | |
| One base station | |
| The number of all sensor stations | |
| The set of all sensor nodes | |
| One sensor node | |
| The set of all wireless energy transfer devices | |
| One wireless energy transfer device | |
| The cardinality of a set | |
| One sub network | |
| The set of sensor nodes, base station and wireless energy transfer device of | |
| The initial battery energy of a wireless sensor node | |
| The minimum energy required to keep sensor nodes functioning properly | |
| The maximum value of the sensor node in normal replenishing cycles | |
| The minimum value of the sensor node in normal replenishing cycles | |
| The path along which the wireless energy transfer device travels | |
| The time duration spent on charging the sensor node along the travelling path | |
| The sojourn time | |
| The data generating rate of the sensor node | |
| The sending data rate from the sensor node to the sensor node at time | |
| The receiving data rate of the sensor node from the sensor node at time | |
| The sending data rate from the sensor node to the base station sensor node at time | |
| The sending data rate from the sensor node to the wireless energy transfer device sensor node at time | |
| The sending data rate from the sensor node to the sensor node in phase | |
| The receiving data rate of the sensor node from the sensor node in phase | |
| The sending data rate from the sensor node to the base station sensor node in phase | |
| The sending data rate from the sensor node to the wireless energy transfer device sensor node in phase | |
| Indicator functions | |
| The remaining energy of the sensor node at time | |
| The power of sensor node at time | |
| The power of sensor node in phase | |
| The power factors | |
| The replenishing power | |
| The travelling velocity of wireless energy transfer devices | |
| The length of the normal replenishing cycle | |
| The time duration spent on travelling along | |
| The total length of the travelling path | |
| The service station | |
| The sensor node along the travelling path | |
| The distance between two successive points along the travelling path | |
| The time instance at which the wireless energy transfer device arrives at the sensor node in normal replenishing cycles | |
| The index set of phases | |
| The time interval relating to | |
| The objective value yield by the solution to the optimization problem, OPT-i | |
| The data routing scheme in phase m in the normal replenishing cycles | |
| The length of the pre-normal replenishing stage | |
| The time at which the wireless energy transfer device arrorives at the sensor node in pre-normal replenishing stage | |
| The data routing scheme in phase in the pre-normal replenishing stage | |
| The initial energy of the sensor node at the beginning of each normal replenishing cycle | |
| The replenishing power used be wireless energy transfer devices in the pre-normal replenishing stage when charging the sensor node |
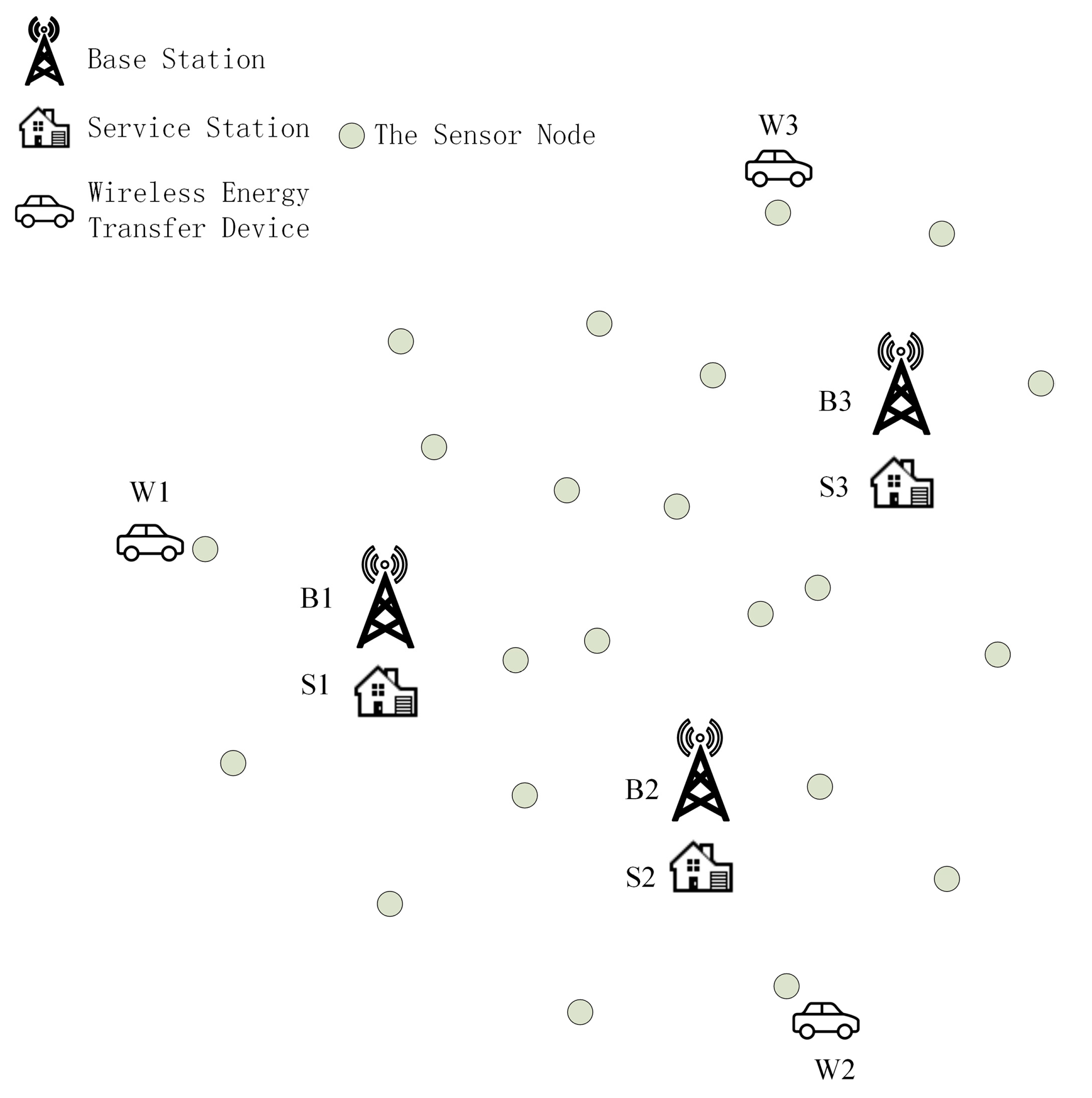
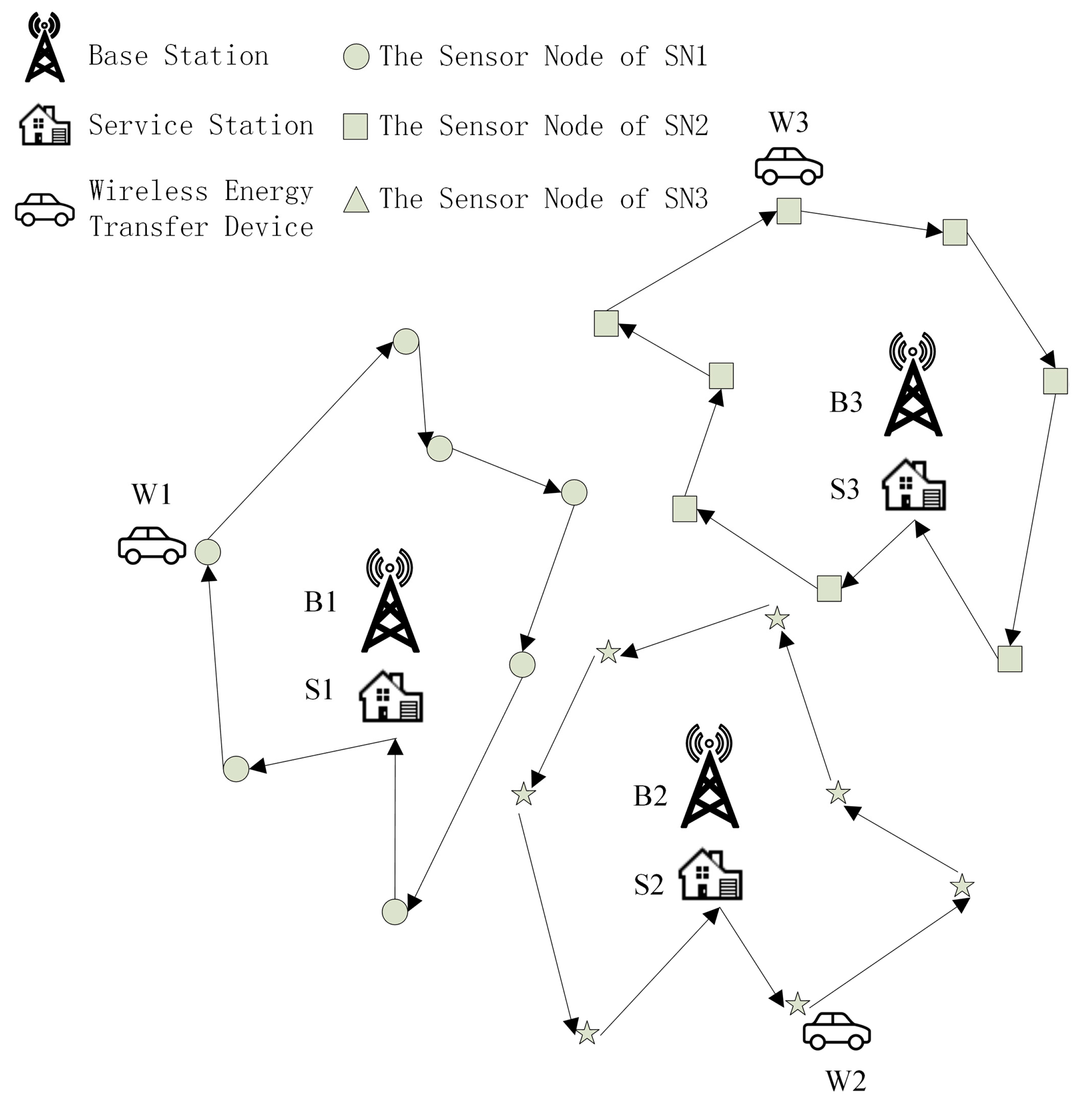
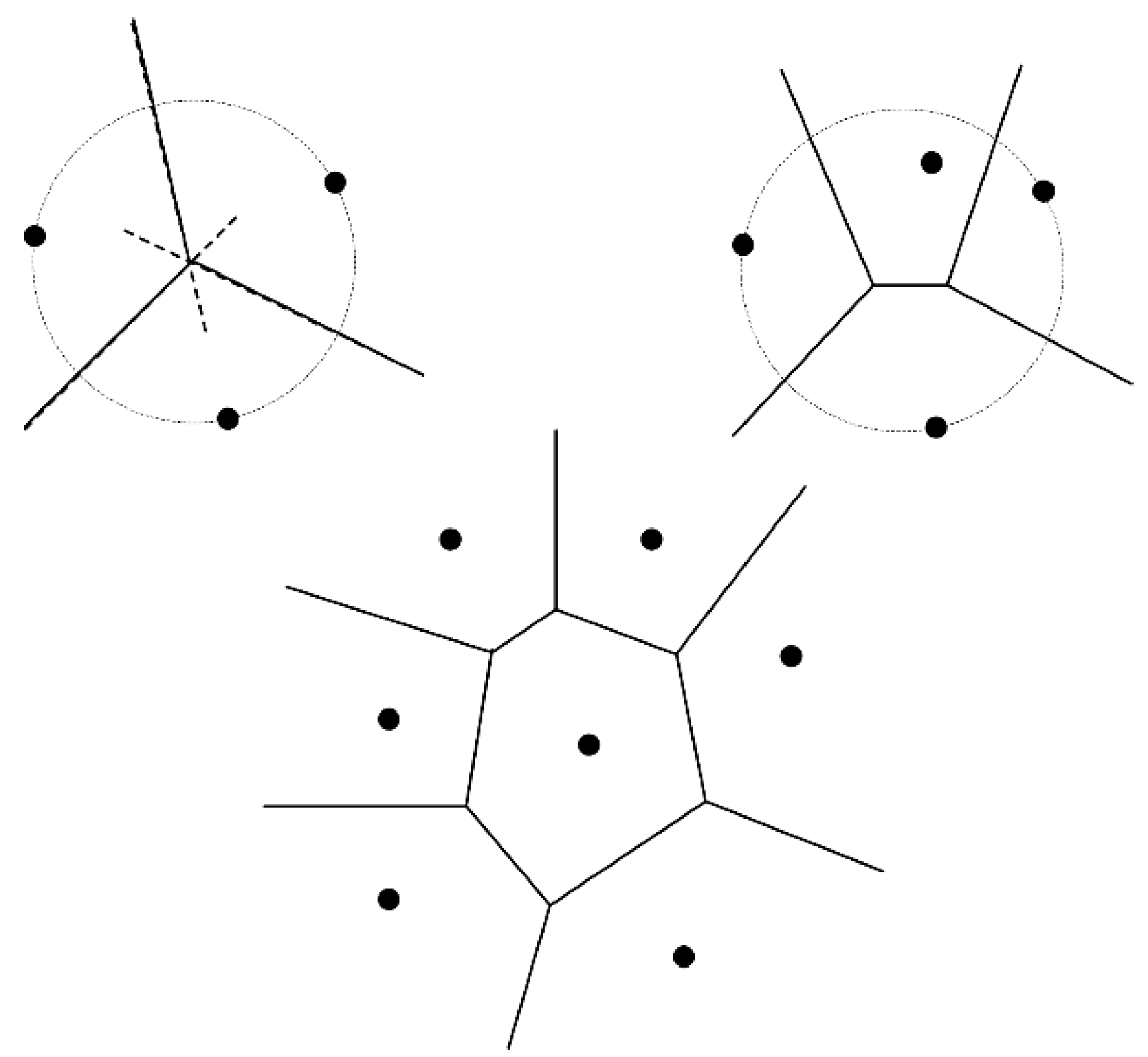
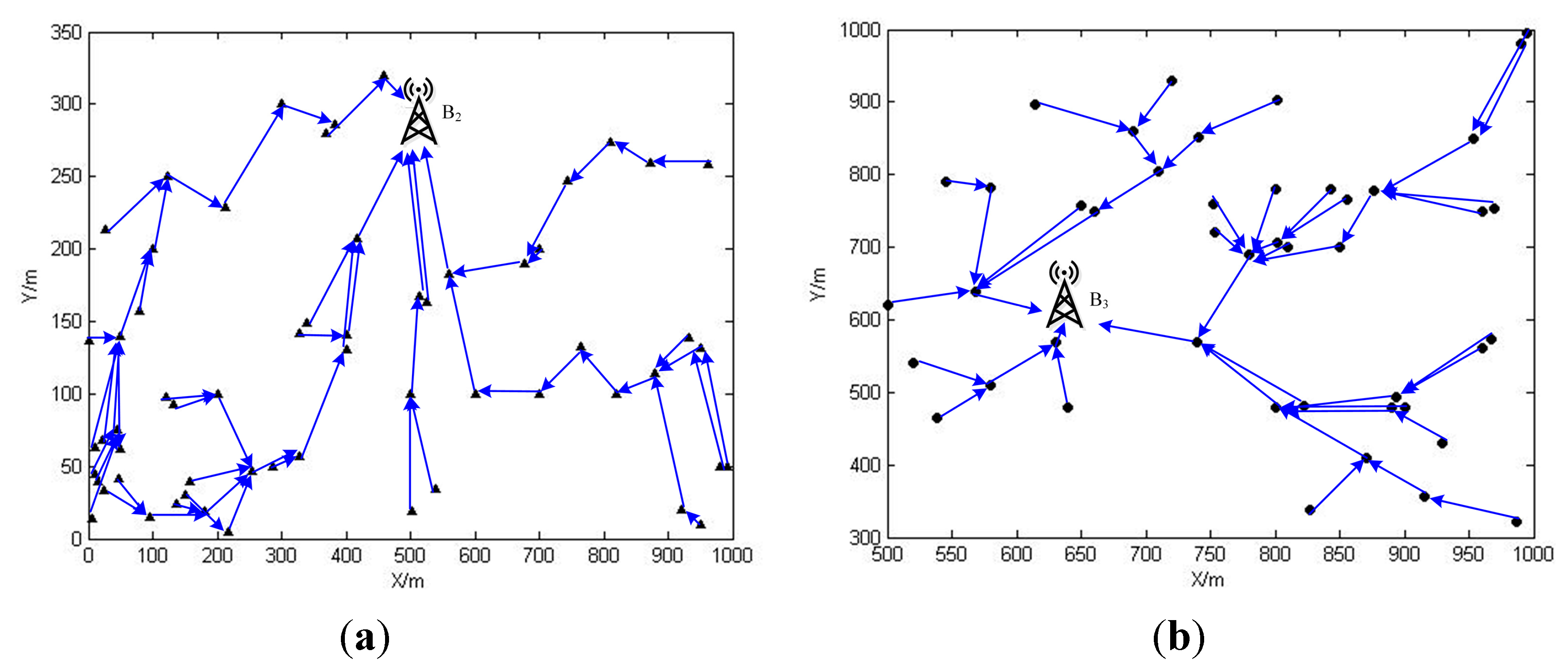
2.2. Subnet Partition Using Voronoi Diagram
- (I)
- ;
- (II)
- ;
- (III)
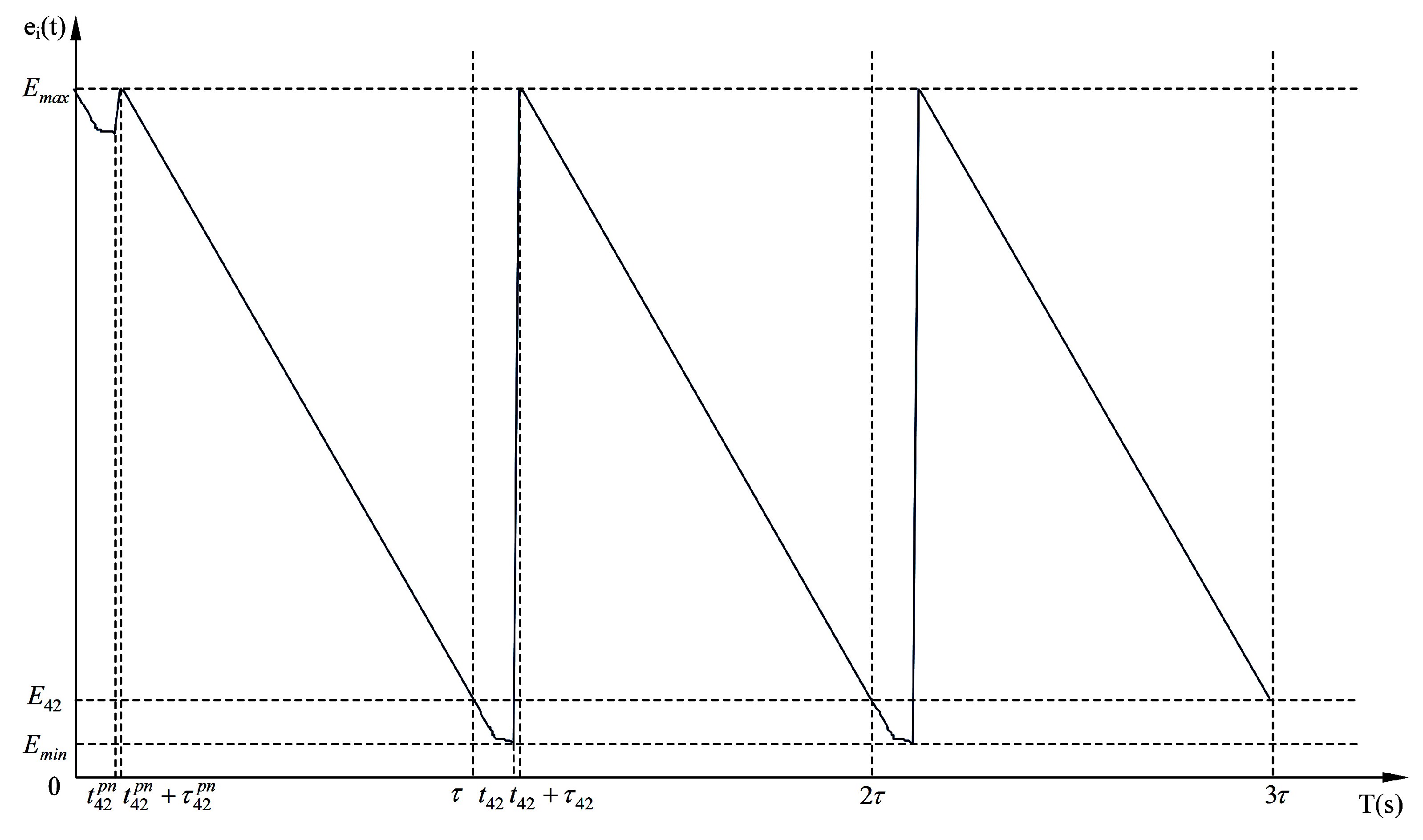
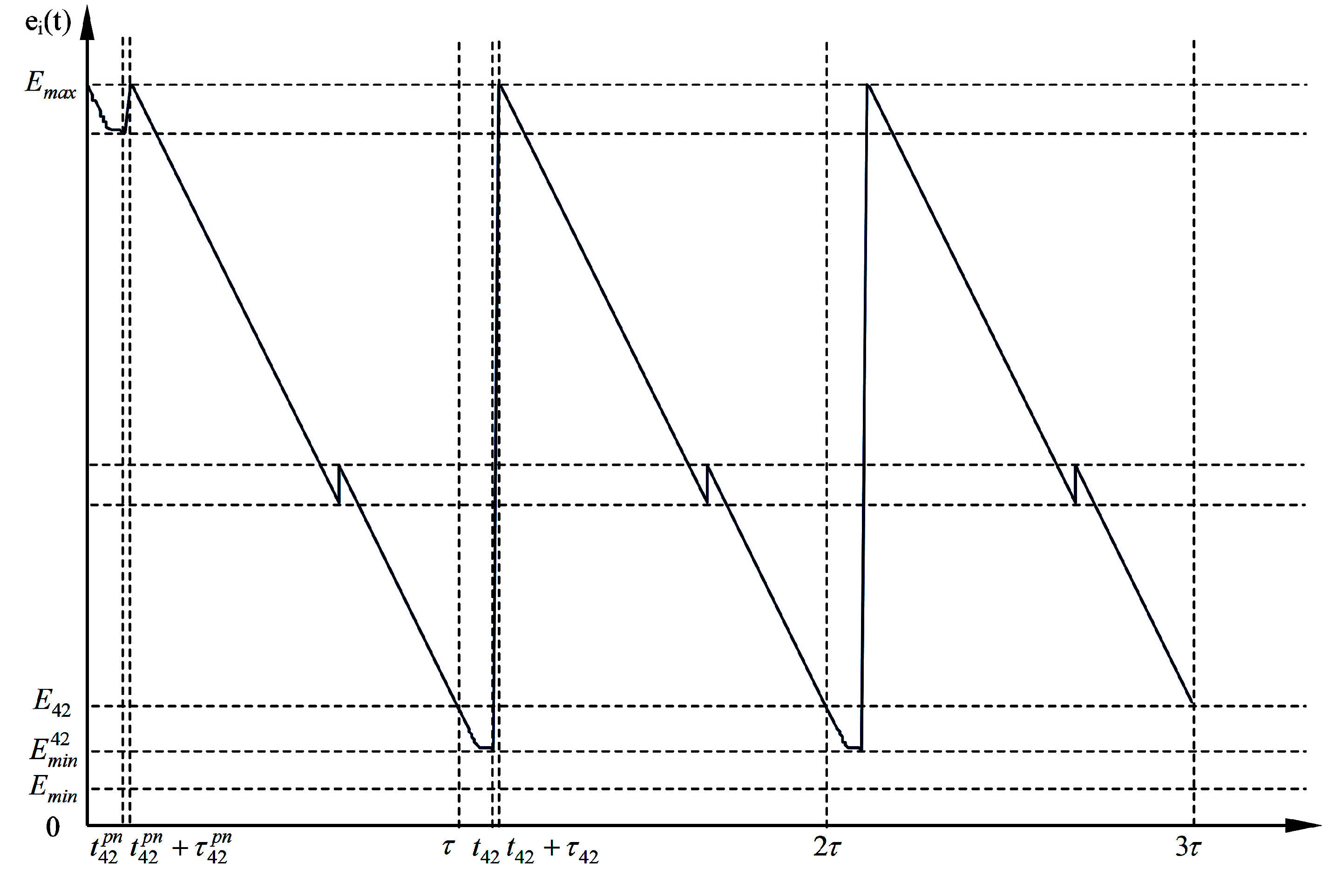
2.3. The Modeling of Normal Replenishing Cycles
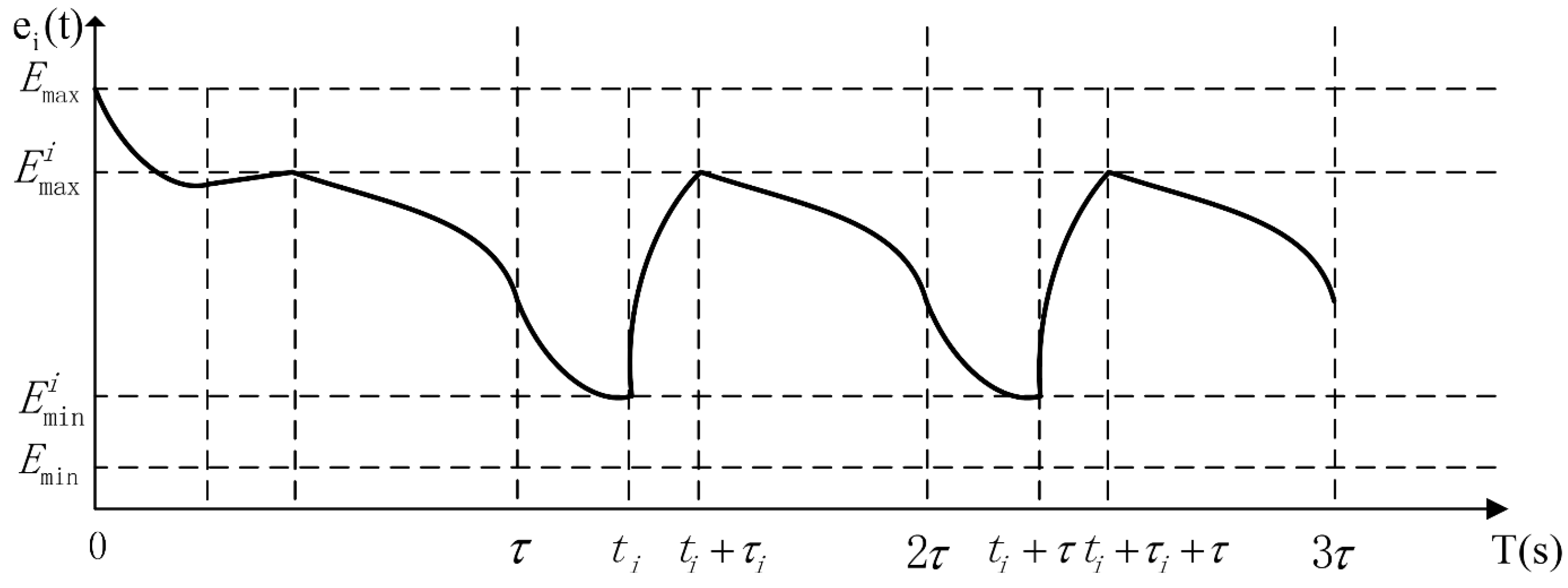
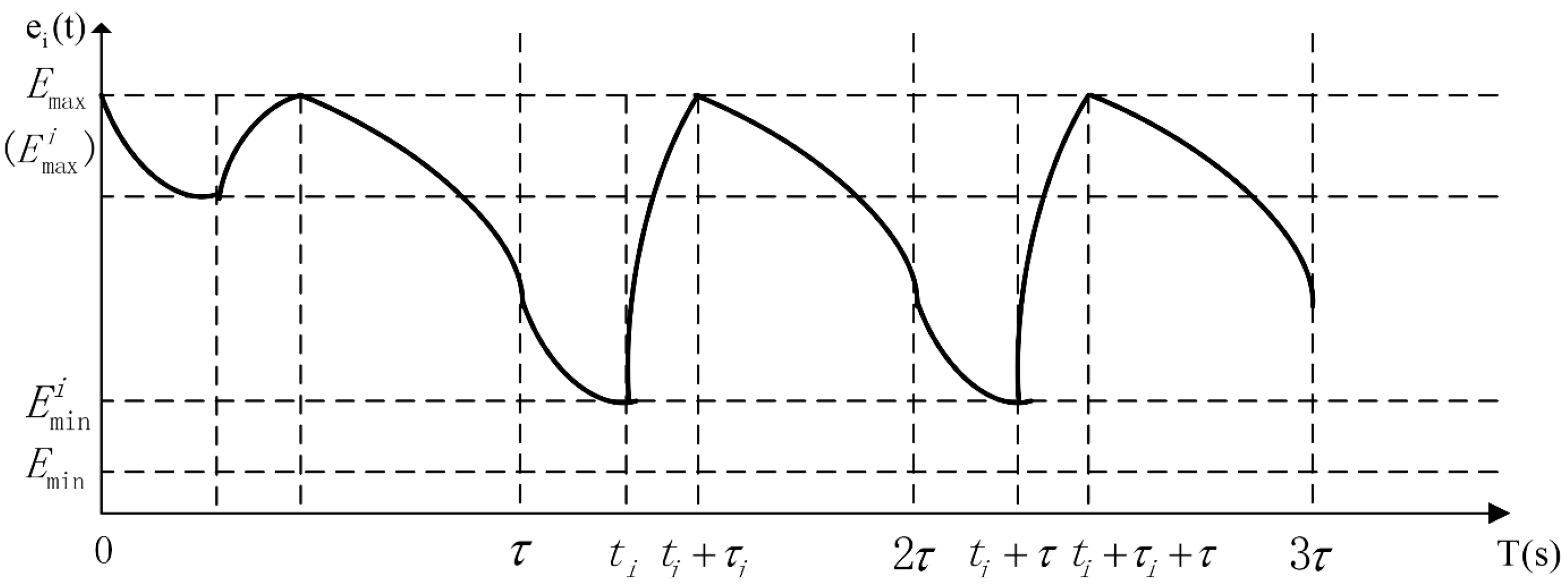
3. Modeling the Normal Replenishing Cycle from a Multi-Phased Aspect
3.1. The Analysis of Working Phases of a Wireless Energy Transfer Device
3.2. The Discrete Model with Respect to Multiple Phases
3.3. The Equal Optimality of OPT-3 and OPT-2
4. The Analysis of OPT-3 and Its Linearization
4.1. Two Necessary Conditions for the Optimality of OPT-3
4.2. The Linearization of OPT-3
5. The Pre-Normal Replenishing Stage
- (I)
- ;
- (II)
- ;
- (III)
- .
6. The Simulation and Numerical Analysis
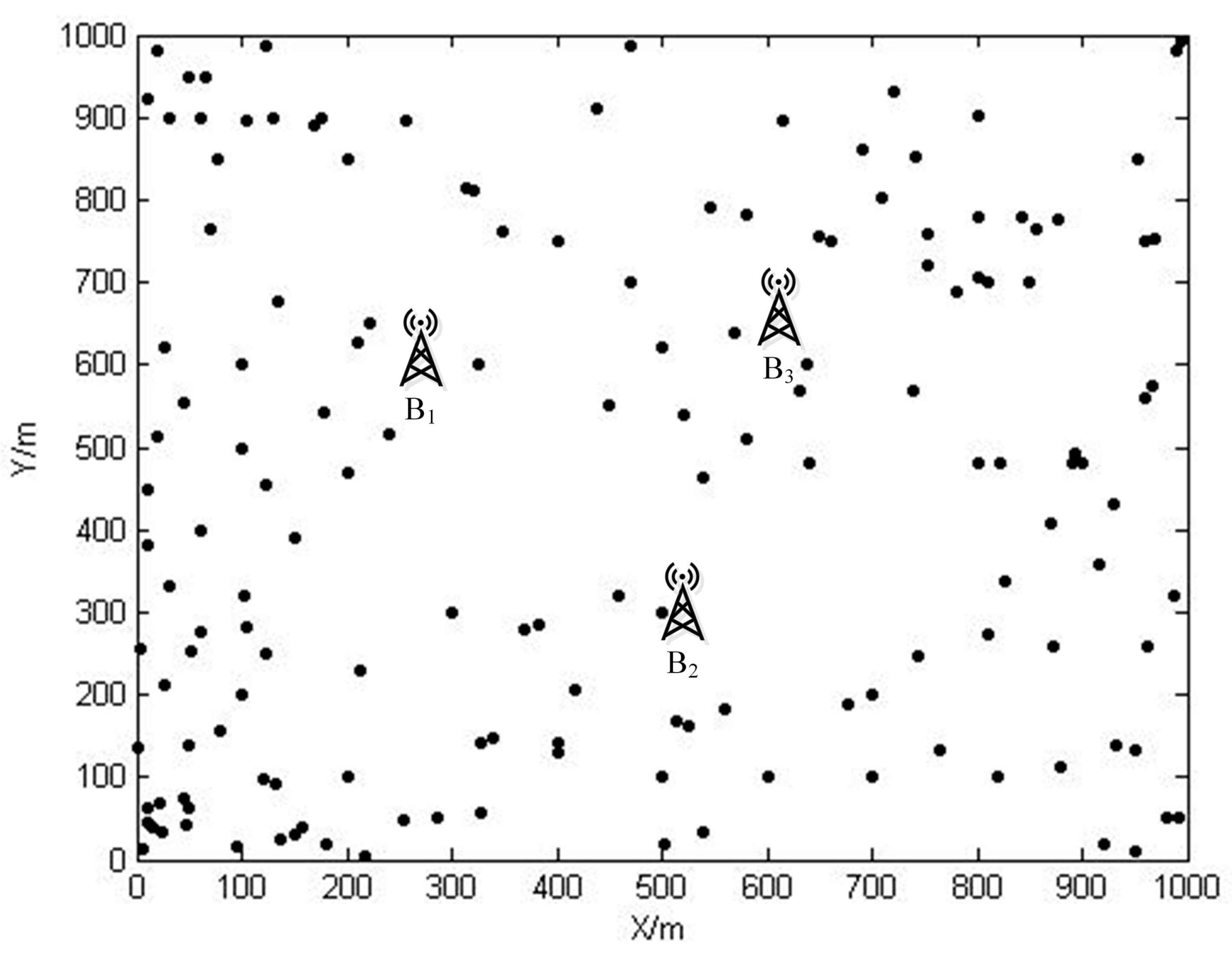
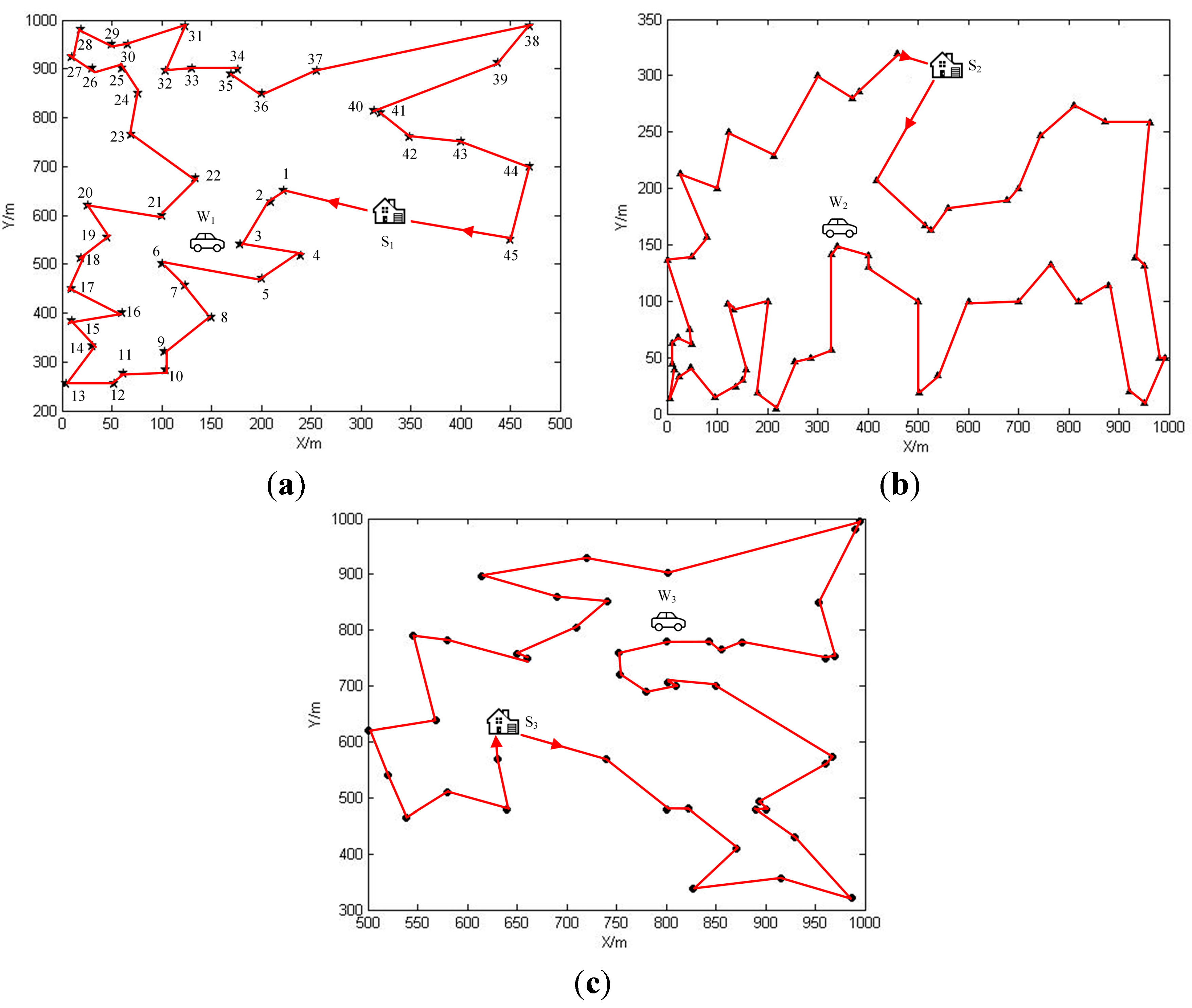
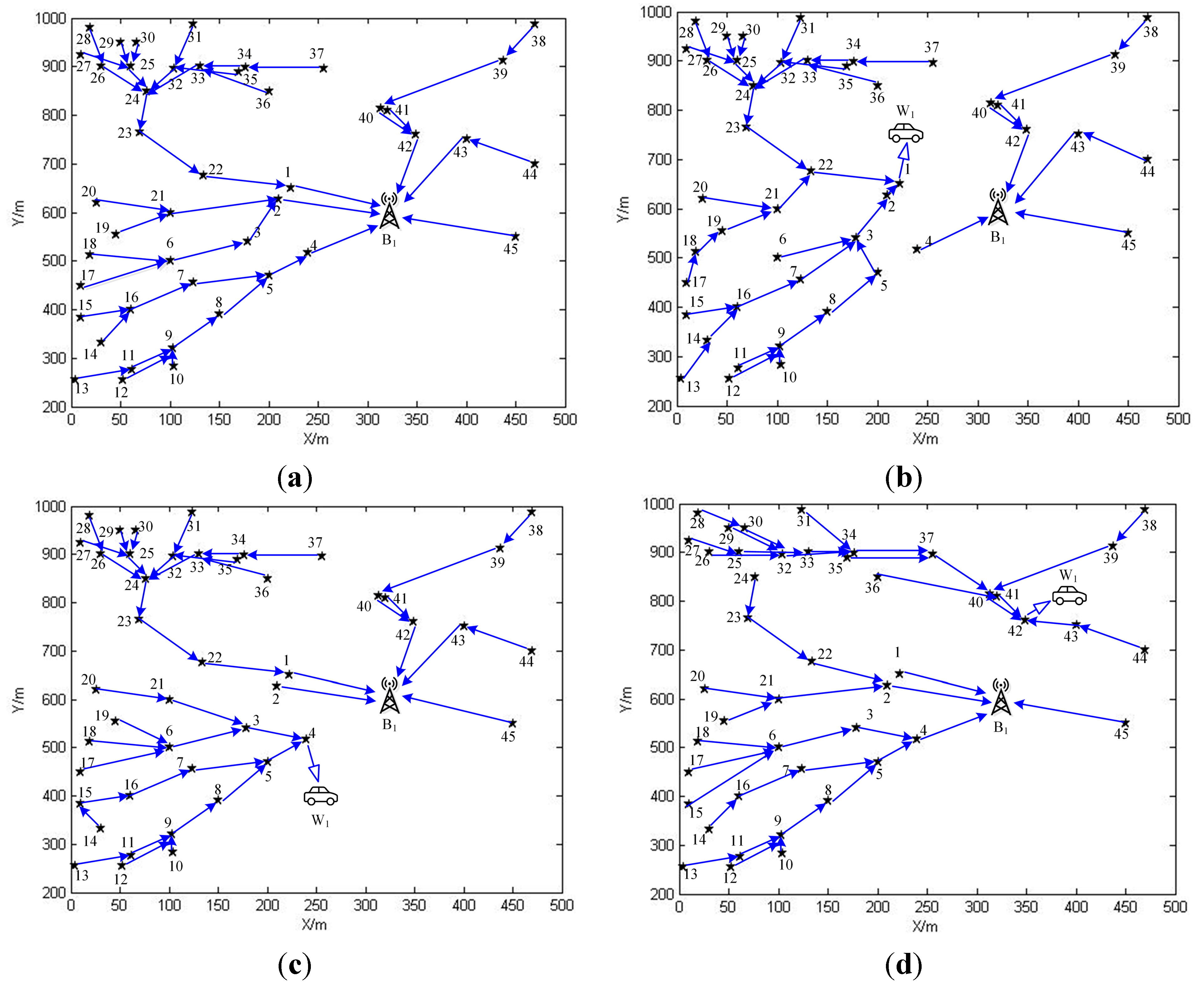
6.1. The Simulation Scenarios
6.2. Simulation Results and Numerical Analysis
| Node No. | Coordinates | Ri(Kbits/s) | Node No. | Coordinates | Ri(Kbits/s) | Node No. | Coordinates | Ri(Kbits/s) |
|---|---|---|---|---|---|---|---|---|
| 1 | 222 650 | 12 | 51 | 700 200 | 15 | 101 | 213 229 | 14 |
| 2 | 210 627 | 14 | 52 | 744 247 | 16 | 102 | 300 300 | 15 |
| 3 | 179 541 | 15 | 53 | 810 274 | 16 | 103 | 370 280 | 15 |
| 4 | 240 517 | 15 | 54 | 872 259 | 15 | 104 | 383 286 | 12 |
| 5 | 200 470 | 15 | 55 | 963 258 | 19 | 105 | 459 320 | 12 |
| 6 | 100 500 | 15 | 56 | 933 139 | 11 | 106 | 740 570 | 14 |
| 7 | 123 456 | 16 | 57 | 950 132 | 16 | 107 | 800 480 | 16 |
| 8 | 150 390 | 16 | 58 | 980 50 | 15 | 108 | 822 482 | 11 |
| 9 | 103 320 | 11 | 59 | 992 50 | 11 | 109 | 871 409 | 16 |
| 10 | 104 282 | 19 | 60 | 950 10 | 14 | 110 | 827 338 | 15 |
| 11 | 62 277 | 19 | 61 | 920 20 | 14 | 111 | 915 357 | 16 |
| 12 | 52 254 | 12 | 62 | 879 114 | 16 | 112 | 987 321 | 14 |
| 13 | 4 255 | 14 | 63 | 820 100 | 15 | 113 | 929 430 | 15 |
| 14 | 30 333 | 12 | 64 | 765 133 | 16 | 114 | 890 480 | 15 |
| 15 | 10 383 | 15 | 65 | 700 100 | 14 | 115 | 900 480 | 11 |
| 16 | 60 400 | 19 | 66 | 600 100 | 15 | 116 | 894 494 | 16 |
| 17 | 10 450 | 16 | 67 | 539 34 | 16 | 117 | 960 560 | 16 |
| 18 | 19 512 | 11 | 68 | 502 19 | 19 | 118 | 967 574 | 12 |
| 19 | 45 555 | 11 | 69 | 500 100 | 14 | 119 | 850 700 | 15 |
| 20 | 26 620 | 11 | 70 | 400 130 | 19 | 120 | 802 706 | 11 |
| 21 | 100 600 | 15 | 71 | 400 141 | 12 | 121 | 810 700 | 15 |
| 22 | 134 676 | 12 | 72 | 340 149 | 12 | 122 | 780 690 | 15 |
| 23 | 70 764 | 14 | 73 | 327 142 | 14 | 123 | 754 720 | 11 |
| 24 | 77 850 | 12 | 74 | 327 57 | 11 | 124 | 752 760 | 12 |
| 25 | 60 900 | 16 | 75 | 287 50 | 14 | 125 | 800 780 | 14 |
| 26 | 30 900 | 14 | 76 | 254 47 | 12 | 126 | 843 780 | 11 |
| 27 | 10 923 | 16 | 77 | 217 5 | 16 | 127 | 856 766 | 11 |
| 28 | 19 980 | 15 | 78 | 180 19 | 15 | 128 | 877 777 | 15 |
| 29 | 50 950 | 14 | 79 | 200 100 | 15 | 129 | 960 750 | 19 |
| 30 | 66 950 | 11 | 80 | 133 93 | 12 | 130 | 970 754 | 11 |
| 31 | 123 988 | 19 | 81 | 120 98 | 11 | 131 | 953 850 | 11 |
| 32 | 104 897 | 14 | 82 | 157 39 | 12 | 132 | 990 980 | 16 |
| 33 | 130 900 | 16 | 83 | 150 30 | 14 | 133 | 995 994 | 11 |
| 34 | 176 899 | 12 | 84 | 136 24 | 12 | 134 | 802 902 | 14 |
| 35 | 170 890 | 15 | 85 | 95 15 | 14 | 135 | 720 930 | 14 |
| 36 | 200 850 | 19 | 86 | 47 41 | 11 | 136 | 614 897 | 15 |
| 37 | 256 897 | 16 | 87 | 24 33 | 15 | 137 | 690 860 | 12 |
| 38 | 470 988 | 15 | 88 | 5 14 | 12 | 138 | 741 852 | 16 |
| 39 | 437 912 | 19 | 89 | 15 39 | 12 | 139 | 710 804 | 11 |
| 40 | 313 814 | 12 | 90 | 10 45 | 12 | 140 | 650 757 | 12 |
| 41 | 320 810 | 14 | 91 | 10 63 | 11 | 141 | 660 750 | 15 |
| 42 | 349 761 | 16 | 92 | 22 68 | 16 | 142 | 580 783 | 15 |
| 43 | 400 750 | 16 | 93 | 50 62 | 11 | 143 | 545 790 | 16 |
| 44 | 470 700 | 14 | 94 | 44 75 | 12 | 144 | 568 638 | 14 |
| 45 | 450 550 | 14 | 95 | 2 137 | 15 | 145 | 500 620 | 14 |
| 46 | 418 207 | 19 | 96 | 50 140 | 14 | 146 | 520 540 | 14 |
| 47 | 513 167 | 12 | 97 | 80 157 | 16 | 147 | 539 464 | 14 |
| 48 | 525 163 | 14 | 98 | 27 213 | 14 | 148 | 580 510 | 16 |
| 49 | 559 183 | 15 | 99 | 100 200 | 15 | 149 | 640 480 | 12 |
| 50 | 678 190 | 12 | 100 | 123 250 | 12 | 150 | 630 570 | 15 |

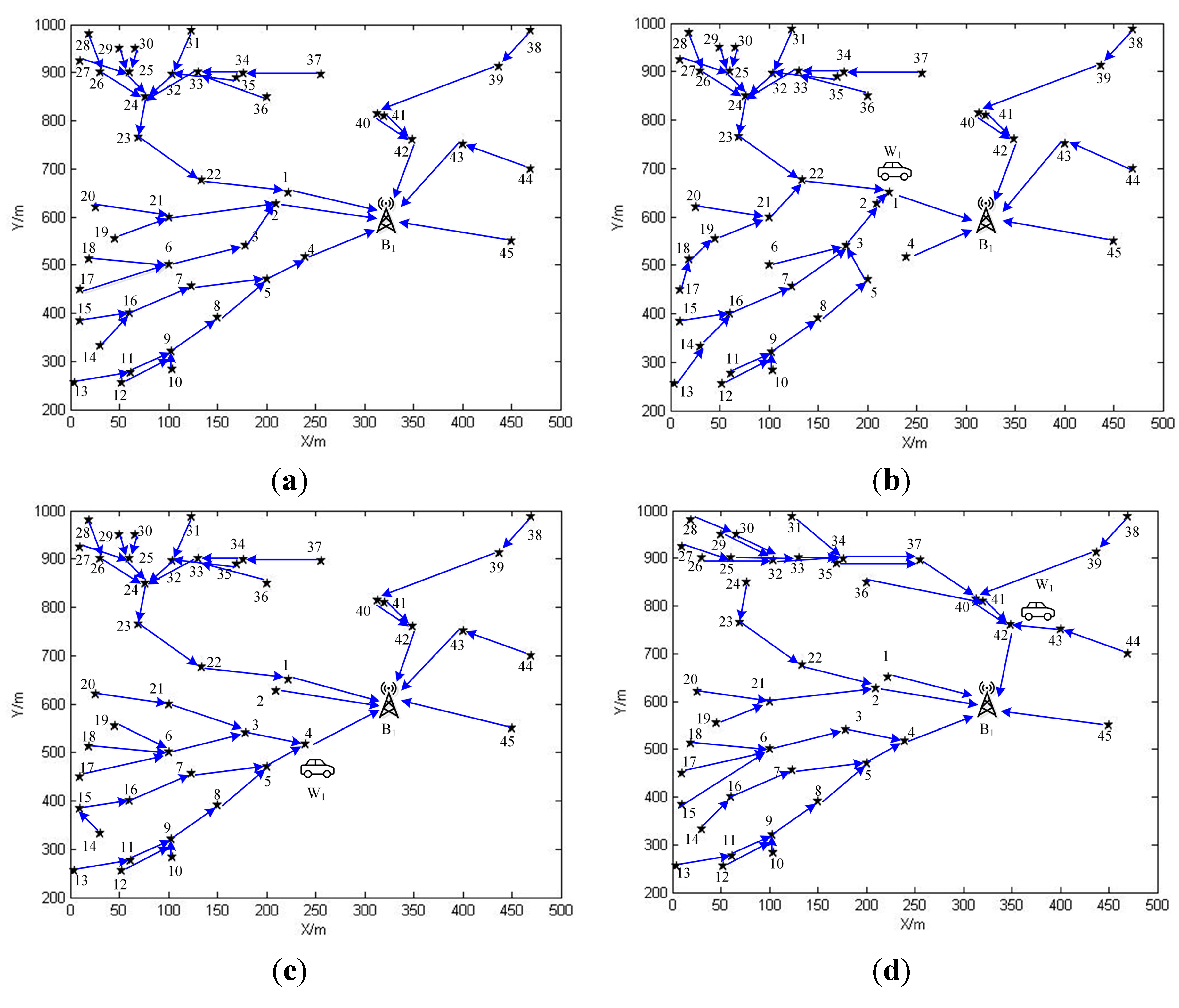
| Node No. | Coordinates | Ri(Kbits/s) | Arrival Time(s) | Charging Time(s) | Remaining Battery Energy (kJ) |
|---|---|---|---|---|---|
| 1 | 222 650 | 12 | 143,383.35 | 2073.44 | 0.58 |
| 2 | 210 627 | 14 | 145,461.98 | 874.59 | 6.50 |
| 3 | 179 541 | 15 | 146,354.85 | 252.28 | 9.65 |
| 4 | 240 517 | 15 | 146,620.24 | 2063.12 | 0.54 |
| 5 | 200 470 | 15 | 148,695.70 | 535.50 | 8.67 |
| 6 | 100 500 | 15 | 149,252.08 | 198.43 | 9.83 |
| 7 | 123 456 | 16 | 149,460.44 | 247.30 | 9.58 |
| 8 | 150 390 | 16 | 149,722.01 | 498.50 | 8.31 |
| 9 | 103 320 | 11 | 150,237.37 | 336.27 | 9.06 |
| 10 | 104 282 | 19 | 150,581.24 | 28.91 | 10.66 |
| 11 | 62 277 | 19 | 150,618.61 | 81.19 | 10.37 |
| 12 | 52 254 | 12 | 150,704.82 | 38.97 | 10.61 |
| 13 | 4 255 | 14 | 150,753.39 | 28.54 | 10.66 |
| 14 | 30 333 | 12 | 150,798.37 | 34.47 | 10.65 |
| 15 | 10 383 | 15 | 150,843.61 | 28.89 | 10.67 |
| 16 | 60 400 | 19 | 150,883.06 | 192.9 | 9.82 |
| 17 | 10 450 | 16 | 151,090.11 | 91.98 | 10.34 |
| 18 | 19 512 | 11 | 151,194.62 | 39.55 | 10.63 |
| 19 | 45 555 | 11 | 151,244.22 | 35.19 | 10.67 |
| 20 | 26 620 | 11 | 151,292.95 | 30.14 | 10.66 |
| 21 | 100 600 | 15 | 151,338.42 | 315.94 | 8.31 |
| 22 | 134 676 | 12 | 151,671.01 | 1230.68 | 4.14 |
| 23 | 70 764 | 14 | 152,923.46 | 1716.06 | 2.05 |
| 24 | 77 850 | 12 | 154,656.77 | 990.56 | 5.83 |
| 25 | 60 900 | 16 | 155,657.89 | 156.12 | 10.10 |
| 26 | 30 900 | 14 | 155,820.01 | 86.10 | 10.28 |
| 27 | 10 923 | 16 | 155,912.21 | 28.58 | 10.66 |
| 28 | 19 980 | 15 | 155,952.33 | 44.98 | 10.56 |
| 29 | 50 950 | 14 | 156,005.94 | 24.18 | 10.68 |
| 30 | 66 950 | 11 | 156,031.32 | 20.83 | 10.71 |
| 31 | 123 988 | 19 | 156,067.56 | 81.21 | 10.39 |
| 32 | 104 897 | 14 | 156,167.36 | 136.82 | 10.25 |
| 33 | 130 900 | 16 | 156,309.41 | 231.85 | 9.65 |
| 34 | 176 899 | 12 | 156,550.46 | 91.06 | 10.44 |
| 35 | 170 890 | 15 | 156,643.69 | 33.19 | 10.63 |
| 36 | 200 850 | 19 | 156,686.88 | 68.46 | 10.47 |
| 37 | 256 897 | 16 | 156,769.96 | 87.65 | 10.57 |
| 38 | 470 988 | 15 | 156,904.12 | 47.87 | 10.56 |
| 39 | 437 912 | 19 | 156,968.56 | 857.96 | 6.53 |
| 40 | 313 814 | 12 | 157,858.13 | 174.13 | 10.10 |
| 41 | 320 810 | 14 | 158,033.26 | 31.57 | 10.66 |
| 42 | 349 761 | 16 | 158,077.36 | 2064.68 | 0.54 |
| 43 | 400 750 | 16 | 160,152.47 | 910.50 | 6.13 |
| 44 | 470 700 | 14 | 161,080.17 | 49.66 | 10.56 |
| 45 | 450 550 | 14 | 161,160.10 | 186.72 | 9.86 |
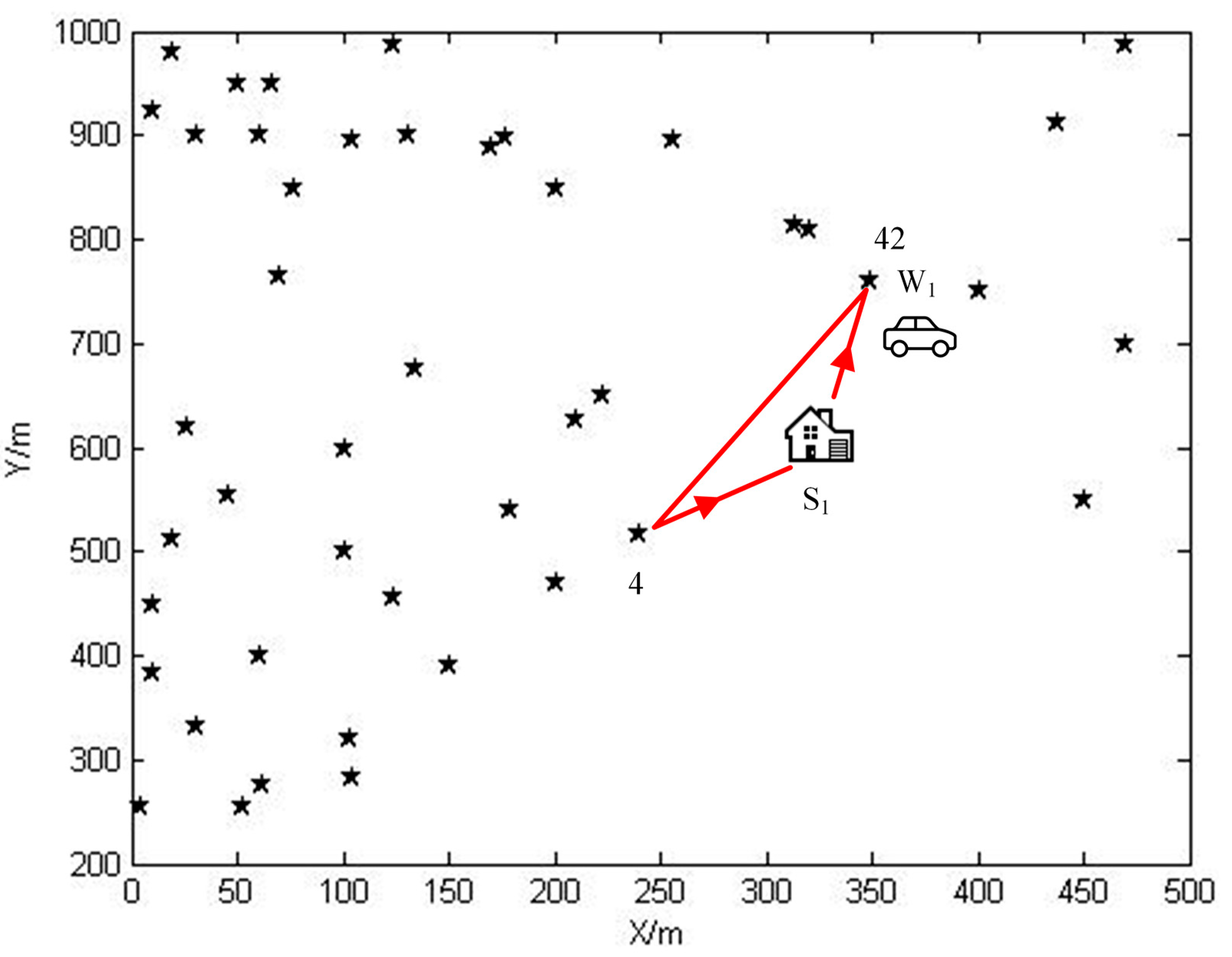
| Phase No. | Power of 42nd Node (W) | Phase No. | Power of 42nd Node (W) |
|---|---|---|---|
| 0 | 0.0759 | 23 | 0.0011 |
| 1 | 0.0759 | 24 | 0.0047 |
| 2 | 0.0759 | 25 | 0.0047 |
| 3 | 0.0759 | 26 | 0.0047 |
| 4 | 0.0759 | 27 | 0.0047 |
| 5 | 0.0759 | 28 | 0.0047 |
| 6 | 0.0759 | 29 | 0.0047 |
| 7 | 0.0759 | 30 | 0.0047 |
| 8 | 0.0759 | 31 | 0.0047 |
| 9 | 0.0759 | 32 | 0.0047 |
| 10 | 0.0759 | 33 | 0.0047 |
| 11 | 0.0759 | 34 | 0.0047 |
| 12 | 0.0759 | 35 | 0.0047 |
| 13 | 0.0759 | 36 | 0.0047 |
| 14 | 0.0759 | 37 | 0.0047 |
| 15 | 0.0759 | 38 | 0.0295 |
| 16 | 0.0759 | 39 | 0.0154 |
| 17 | 0.0759 | 40 | 0.0047 |
| 18 | 0.0759 | 41 | 0.0047 |
| 19 | 0.0759 | 42 | 0.0307 |
| 20 | 0.0759 | 43 | 0.0267 |
| 21 | 0.0759 | 44 | 0.0204 |
| 22 | 0.0154 | 45 | 0.0759 |
7. Conclusions
Acknowledgments
Author Contributions
Appendix
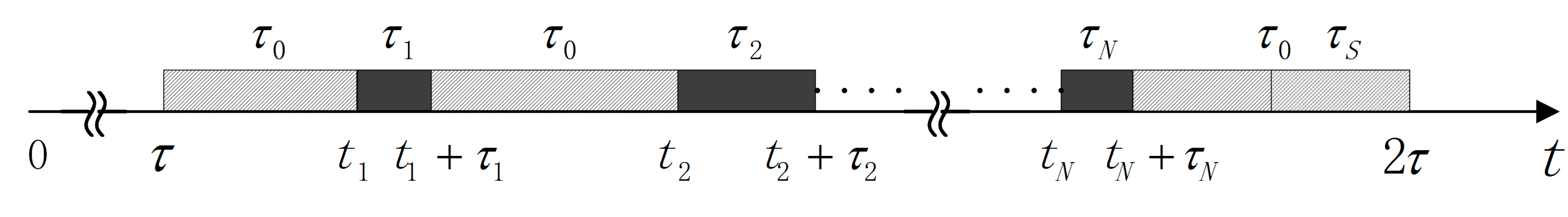
- (I)
- ;
- (II)
- ;
- (III)
- .
- (I)
- holds.
- (II)
- holds since:
- (III)
- holds since:
Conflicts of Interest
References
- Joel, W.B.; Chris, G.; Boleslaw, S. In-network outlier detection in wireless sensor networks. Knowl. Inf. Syst. 2013, 34, 23–54. [Google Scholar] [CrossRef]
- Amaldi, E.; Capone, M. Design of wireless sensor networks for mobile target detection. IEEE/ACM Trans. Netw. 2012, 20, 784–797. [Google Scholar] [CrossRef]
- Dervis, K.; Selcuk, O. Cluster based wireless sensor network routing using artificial bee colony algorithm. Wirel. Netw. 2012, 18, 847–860. [Google Scholar] [CrossRef]
- Selcuk, O.; Ozturk, C. A comparative study on differential evolution based routing implementations for wireless sensor networks. In Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Trabzon, Turkey, 2–4 July 2012; pp. 1–5.
- Nicolas, G.; Nathalie, M. Greedy routing recovery using controlled mobility in wireless sensor networks. In Proceedings of the Ad-hoc, Mobile, and Wireless Network, Wroclaw, Poland, 8-10 July 2013; Volume 7960, pp. 209–220.
- Zhao, Y.Z.; Miao, C.; Zhang, J.B. A survey and projection on medium access control protocols for wireless sensor networks. ACM Comput. Surv. 2012, 45, 7:1–7:37. [Google Scholar] [CrossRef]
- Jang, B.; Lim, J.B. An asynchronous scheduled MAC protocol for wireless sensor networks. Comput. Netw. 2013, 57, 85–98. [Google Scholar] [CrossRef]
- Pei, H.; Li, X. The evolution of MAC protocols in wireless sensor networks: A survey. IEEE Commun. Surv. Tutor. 2012, 15, 101–120. [Google Scholar]
- Chen, L.Y.; Li, M.; Liu, K.; Liu, Z.L.; Zhang, J.Y.; Peng, T.; Liu, Y.; Xu, Y.J.; Luo, Q.; He, T. Distributed range-free localisation algorithm for wireless sensor networks. Electron. Lett. 2014, 50, 894–896. [Google Scholar] [CrossRef]
- Chen, C.P.; Mukhopadhyay, S.C.; Chuang, C.L.; Lin, T.S.; Liao, M.S.; Wang, Y.C.; Jiang, J.A. A hybrid memetic framework for coverage optimization in wireless sensor networks. IEEE Trans. Cybern. 2014, PP, 1. [Google Scholar]
- Mukhopadhyay, S.C. Wearable sensors for human activity monitoring: A review. IEEE Sens. J. 2015, 15, 1321–1330. [Google Scholar] [CrossRef]
- Murthy, J.K.; Kumar, S. Energy efficient scheduling in cross layer optimized cluster wireless sensor networks. Int. J. Comput. Sci. Commun. 2012, 3, 149–153. [Google Scholar]
- Gandelli, A.; Mussetta, M.; Pirinoli, P.; Zich, R.E. Optimization of integrated antennas for wireless sensor networks. Proc. SPIE 2005, 5649, 9–15. [Google Scholar]
- Antonio, P.; Grimaccia, F.; Mussetta, M. Architecture and methods for innovative heterogeneous wireless sensor network applications. Remote Sens. 2012, 4, 1146–1161. [Google Scholar] [CrossRef]
- Shigeta, R.; Sasaki, T. Ambient RF energy harvesting sensor device with capacitor-leakage-aware duty cycle control. IEEE Sens. J. 2013, 13, 2973–2983. [Google Scholar] [CrossRef]
- Yang, S.S.; Yang, X.Y. Distributed networking in autonomic solar powered wireless sensor networks. IEEE J. Sel. Areas Commun. 2013, 31, 750–761. [Google Scholar] [CrossRef]
- Li, H.J.; Jaggi, N. Relay scheduling for cooperative communications in sensor networks with energy harvesting. IEEE Trans. Wirel. Commun. 2011, 10, 2918–2928. [Google Scholar] [CrossRef]
- Sugihara, R.; Gupta, R.K. Optimal speed control of mobile node for data collection in sensor networks. IEEE Trans. Mob. Comput. 2010, 9, 127–139. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, Y. An optimization based distributed algorithm for mobile data gathering in wireless sensor networks. In Proceedings of the 2010 IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–5.
- Zhao, M.; Ming, M. Efficient data gathering with mobile collectors and space-division multiple access technique in wireless sensor networks. IEEE Trans. Comput. 2011, 60, 400–417. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.X.; Zhang, C.; Xun, L.; Hui, S.Y.R. A methodology for making a three-coil wireless power transfer system more energy efficient than a two-coil counterpart for extended transfer distance. IEEE Trans. Power Electron. 2015, 30, 933–942. [Google Scholar] [CrossRef]
- Tang, S.C.; McDannold, N.J. Power loss analysis and comparison of segmented and unsegmented energy coupling coils for wireless energy transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 215–225. [Google Scholar] [CrossRef]
- Salas, M.; Focke, O.; Herrmann, A.S.; Lang, W. Wireless power transmission for structural health monitoring of fiber-reinforced-composite materials. IEEE Sens. J. 2014, 14, 2171–2176. [Google Scholar] [CrossRef]
- Thoen, B.; Wielandt, S.; de Baere, J.; Goemaere, J.-P.; de Strycker, L.; Stevens, N. Design of an inductively coupled wireless power system for moving receivers. In Proceedings of the 2014 IEEE Wireless Power Transfer Conference (WPTC), Jeju, Korea, 8–9 May 2014; pp. 48–51.
- Li, S.; Mi, C.C. Wireless power transfer for electric vehicle applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 4–17. [Google Scholar] [CrossRef]
- RamRakhyani, A.K.; Lazzi, G. Interference-free wireless power transfer system for biomedical implants using multi-coil approach. Electron. Lett. 2014, 50, 853–855. [Google Scholar] [CrossRef]
- Laskovski, A.N.; Dissanayake, T.; Yuce, M.R. Wireless Power Technology for Biomedical Implants. Biomedical Engineering. Available online: http://www.intechopen.com/books/biomedical-engineering/wireless-power-technology-for-biomedical-implants (accessed on 13 March 2015).
- Kilinc, E.G.; Conus, G.; Weber, C.; Kawkabani, B.; Maloberti, F.; Dehollain, C. A System for wireless power transfer of micro-systems in-vivo implantable in freely moving animals. IEEE Sens. J. 2014, 14, 522–531. [Google Scholar] [CrossRef]
- Russell, D.; McCormick, D.; Taberner, A.; Nielsen, P.; Hu, P.; Budgett, D.; Lim, M.; Malpas, S. Wireless power delivery system for mouse telemeter. In Proceedings of the Biomedical Circuits and Systems Conference (BioCAS 2009), Beijing, China, 26–28 November 2009; pp. 273–276.
- Badr, B.M.; Somogyi-Gsizmazia, R.; Delaney, K.R.; Dechev, N. Wireless power transfer for telemetric devices with variable orientation, for small rodent behavior monitoring. IEEE Sens. J. 2015, 15, 2144–2156. [Google Scholar] [CrossRef]
- Chen, X.L.; Umenei, A.E.; Baarman, D.W.; Chavannes, N.; De Santis, V.; Mosig, J.R.; Kuster, N. Human exposure to close-range resonant wireless power transfer systems as a function of design parameters. IEEE Trans. Electromagn. Compat. 2014, 56, 1027–1034. [Google Scholar] [CrossRef]
- Hong, S.; Cho, I.; Choi, H.; Pack, J. Numerical analysis of human exposure to electromagnetic fields from wireless power transfer systems. In Proceedings of the Wireless Power Transfer Conference (WPTC), Jeju, Korea, 8–9 May 2014; pp. 216–219.
- Park, S. Preliminary study of wireless power transmission for biomedical devices inside a human body. In Proceedings of the Microwave Conference Proceedings (APMC), Koganei, Japan, 5–8 November 2013; pp. 800–802.
- Oruganti, S.K.; Heo, S.H.; Ma, H.; Bien, F. Wireless energy transfer: Touch/Proximity/Hover sensing for large contoured displays and industrial applications. IEEE Sens. J. 2015, 15, 2062–2068. [Google Scholar] [CrossRef]
- Oruganti, S.K.; Heo, S.H.; Ma, H.; Bien, F. Wireless energy transfer-based transceiver systems for power and/or high-data rate transmission through thick metal walls sing sheet-like waveguides. Electron. Lett. 2014, 50, 886–888. [Google Scholar] [CrossRef]
- Xie, L.; Shi, Y. On renewable sensor networks with energy transfer: The multi-node case. In Proceedings of the IEEE SECON, Seoul, Korea, 18–21 June 2012; pp. 10–18.
- Khripkov, A.; Hong, W.; Pavlov, K. Integrated resonant structure for simultaneous wireless power transfer and data telemetry. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1659–1662. [Google Scholar] [CrossRef]
- Shi, L.; Han, J.; Han, D.; Ding, X.; Wei, Z. The dynamic routing algorithm for renewable wireless sensor networks with wireless power transfer. Comput. Netw. 2014, 74, 34–52. [Google Scholar] [CrossRef]
- Heinzklman, W. Application-specific Protocol Architectures for Wireless Networks. Ph.D. Dissertation, Department of Electrical Engineering and Computer Science, MIT (Massachusetts Institute of Technology), Cambridge, MA, USA, June 2000. [Google Scholar]
- Concorde [EB/OL]. Available online: http://www.math.uwaterloo.ca/tsp/concorde/index.html (accessed on 28 September 2013).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Han, J.; Shi, L. The Optimization Based Dynamic and Cyclic Working Strategies for Rechargeable Wireless Sensor Networks with Multiple Base Stations and Wireless Energy Transfer Devices. Sensors 2015, 15, 6270-6305. https://doi.org/10.3390/s150306270
Ding X, Han J, Shi L. The Optimization Based Dynamic and Cyclic Working Strategies for Rechargeable Wireless Sensor Networks with Multiple Base Stations and Wireless Energy Transfer Devices. Sensors. 2015; 15(3):6270-6305. https://doi.org/10.3390/s150306270
Chicago/Turabian StyleDing, Xu, Jianghong Han, and Lei Shi. 2015. "The Optimization Based Dynamic and Cyclic Working Strategies for Rechargeable Wireless Sensor Networks with Multiple Base Stations and Wireless Energy Transfer Devices" Sensors 15, no. 3: 6270-6305. https://doi.org/10.3390/s150306270
APA StyleDing, X., Han, J., & Shi, L. (2015). The Optimization Based Dynamic and Cyclic Working Strategies for Rechargeable Wireless Sensor Networks with Multiple Base Stations and Wireless Energy Transfer Devices. Sensors, 15(3), 6270-6305. https://doi.org/10.3390/s150306270





