In-Network Processing of an Iceberg Join Query in Wireless Sensor Networks Based on 2-Way Fragment Semijoins
Abstract
:1. Introduction

- We consider a logical fragmentation of join operand relations based on the aggregate counts of the joining attribute values, proposing a 2-way fragment semijoin operation using a Bloom filter as a synopsis of the joining attribute values. In the backward reduction of the 2-way fragment semijoin, the false positives inherent with the Bloom filter are efficiently handled.
- We take advantage of the Highest Count First strategy with which efficient reduction of the join operand relation (called Low Count Cut) occurs, developing a dynamic programming algorithm that generates the optimal sequence of 2-way fragment semijoins. The Highest Count First strategy is shown to be more effective in filtering non-joinable tuples than the transmissions of the value ranges widely used in WSNs.
- Through implementation and a set of detailed experiments, we show that our approach considerably outperforms the previous one.
2. Problem Statement
3. Background
3.1. Semijoin and 2-Way Semijoin
3.2. Bloom Filter
3.3. SRJA

- Optimization 1: Before the above process begins, the tuples whose value of count exceeds α is sent separately for checking their joinability because they are likely to be qualified for the query.
- Optimization 2: The tuples whose value of A belongs to a sparse range are also separately sent. Eliminating a sparse range would make the synopsis more selective.
- Optimization 3: For a range to be tagged as DIVIDE, the maxcount of the opposite range (opp_maxcount) is also sent when the tagged synopses are sent back. When the range is divided into subranges, the tuples which turn out not to be qualified for the query (countmaxcount) are deleted.
- NAÏVE: The external join where all the tuples of and are sent to the base station.
- SIJ: The synopsis join of [2] extended for iceberg joins where and are sent to and fully reduced there.
4. Overview of Our Approach
| Notation | Description |
|---|---|
| , | and when i = 0; and when i = 1 |
| α | Iceberg threshold |
| The coordinator sensor node in the region for (i = 0, 1) | |
| The sensor node located at the midpoint between and . | |
| A | The joining attribute |
| The domain of A | |
| ||A|| | The size of a value of A |
| , | 2-way fragment semijoin operator |
| A logical fragment of defined as (i = 0, 1) | |
| The initial maximum value of the attribute count in (i = 0, 1) | |
| The current highest value of the attribute count in (i = 0, 1) | |
| The current lowest value of the attribute count in (i = 0, 1) | |
| The current state of after reduced by a sequence of fragment semijoins (i = 0, 1) | |
| A logical fragment of defined as (i = 0, 1) | |
| A fragment semijoin for which is the reducer relation | |
| Given and , the optimal sequence of fragment semijoins that fully reduces and provided that the first semijoin is (i = 0, 1) | |
| The cost of | |
| The cost of | |
| The value of attribute count in with which (Equation (2)) is minimized (i = 0, 1). Let n = . Then, the following sequence of fragment semijoins is the prefix of : . | |
| The Bloom filter sent for | |
| The size of | |
| The optimal number of hash functions used for | |
| The cost of handling false positives with in executing |
4.1. 2-Way Fragment Semijoin
4.2. Low Count Cut (LCC)
4.3. Highest Count First (HCF)
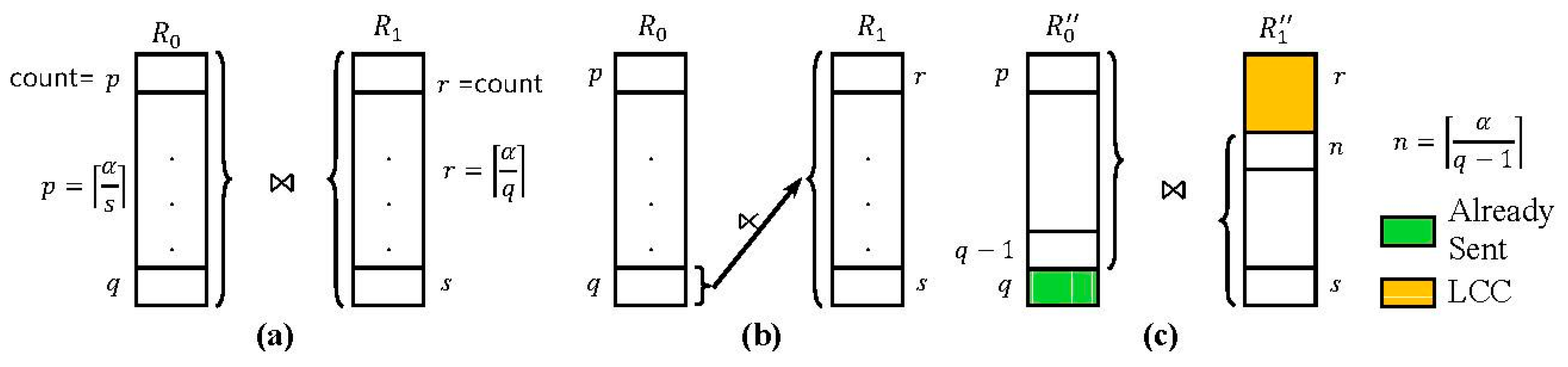
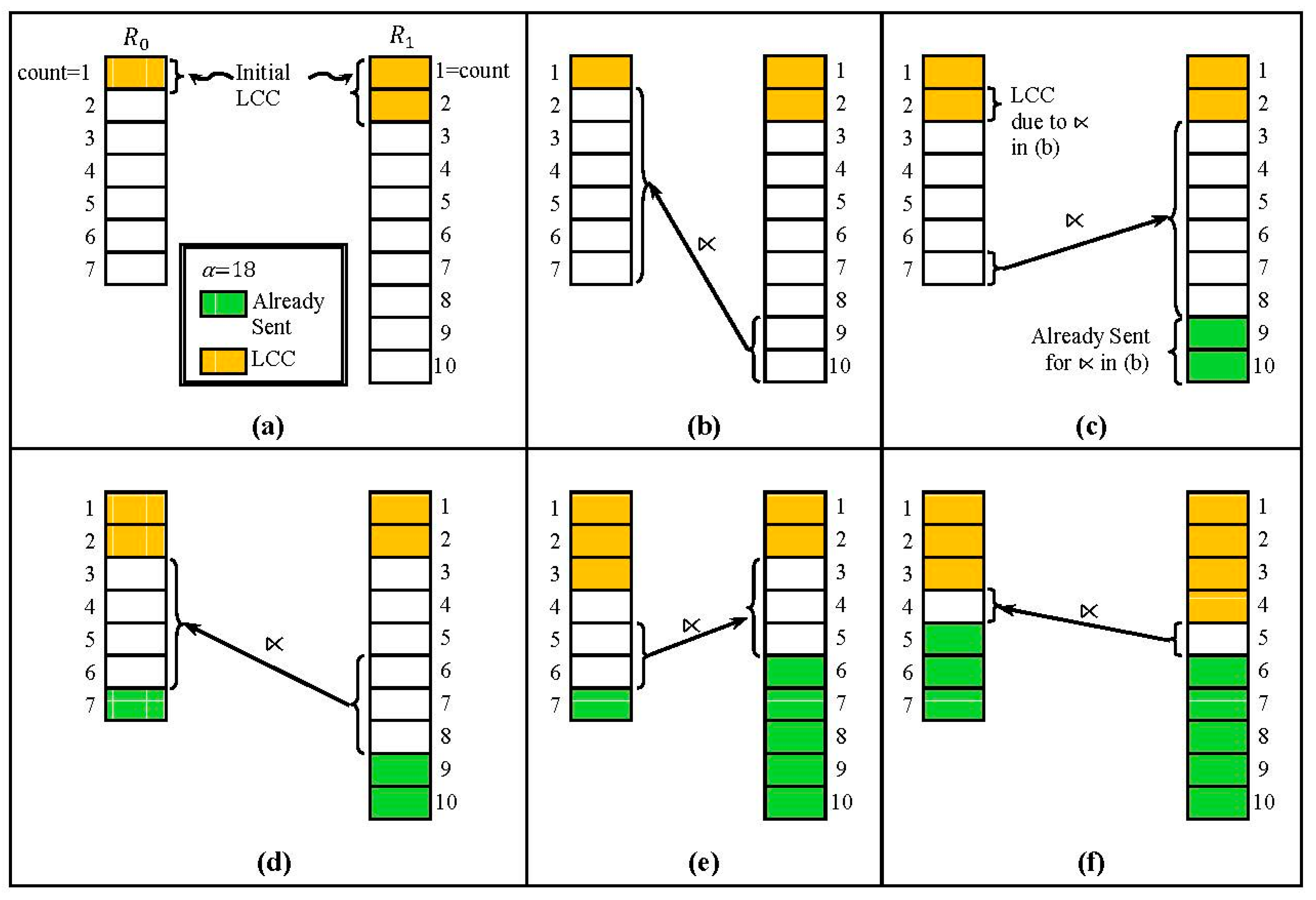
4.4. Fragment Semijoin Sequence
5. Optimal Sequence of Fragment Semijoins
5.1. Formulation of Optimization Problem
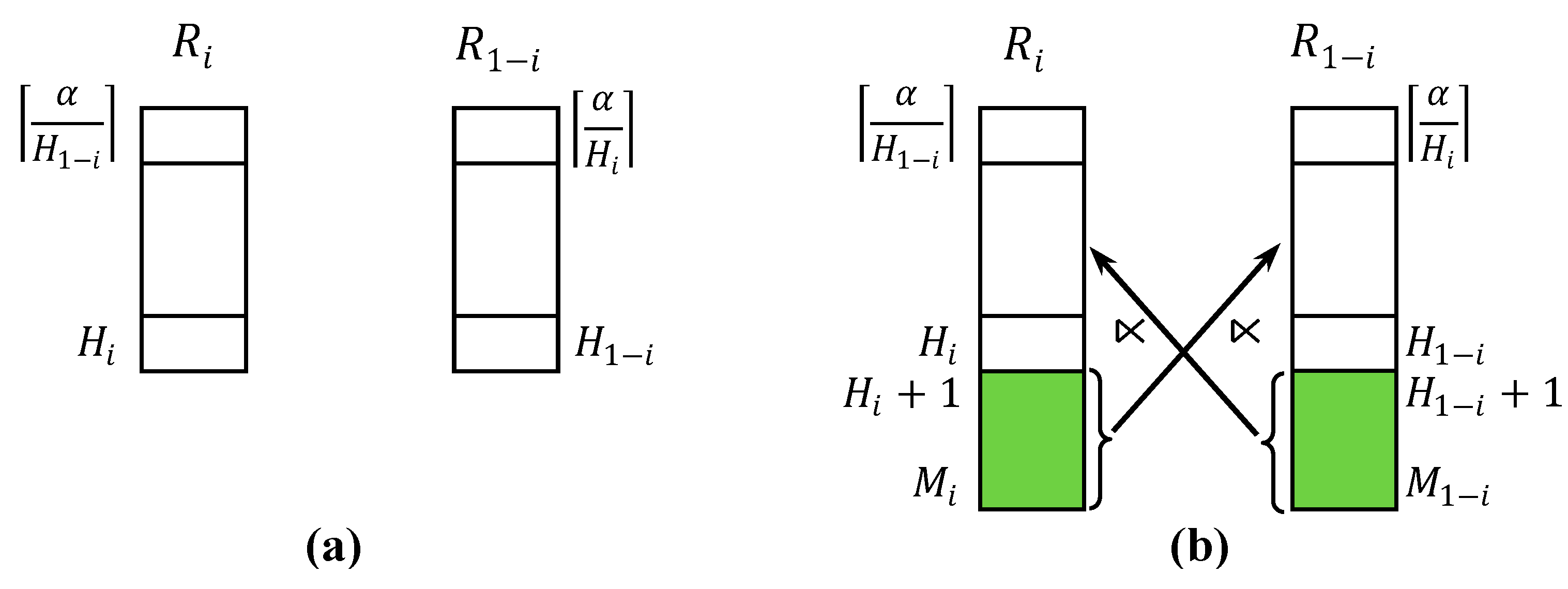
5.2. Cost of 2-Way Fragment Semijoin
5.2.1. Size of Bloom Filter
5.2.2. Cost of Handling False Positives
5.2.3. Optimal Number of Hash Functions.
5.3. Dynamic Programming Algorithm


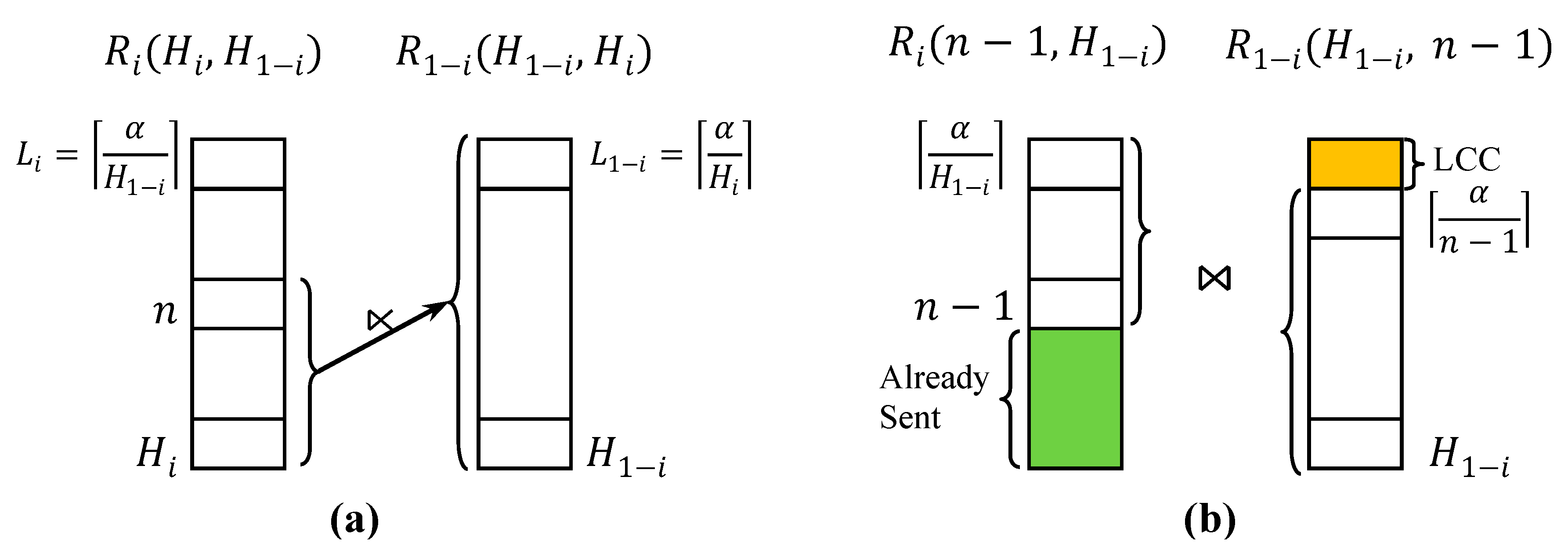
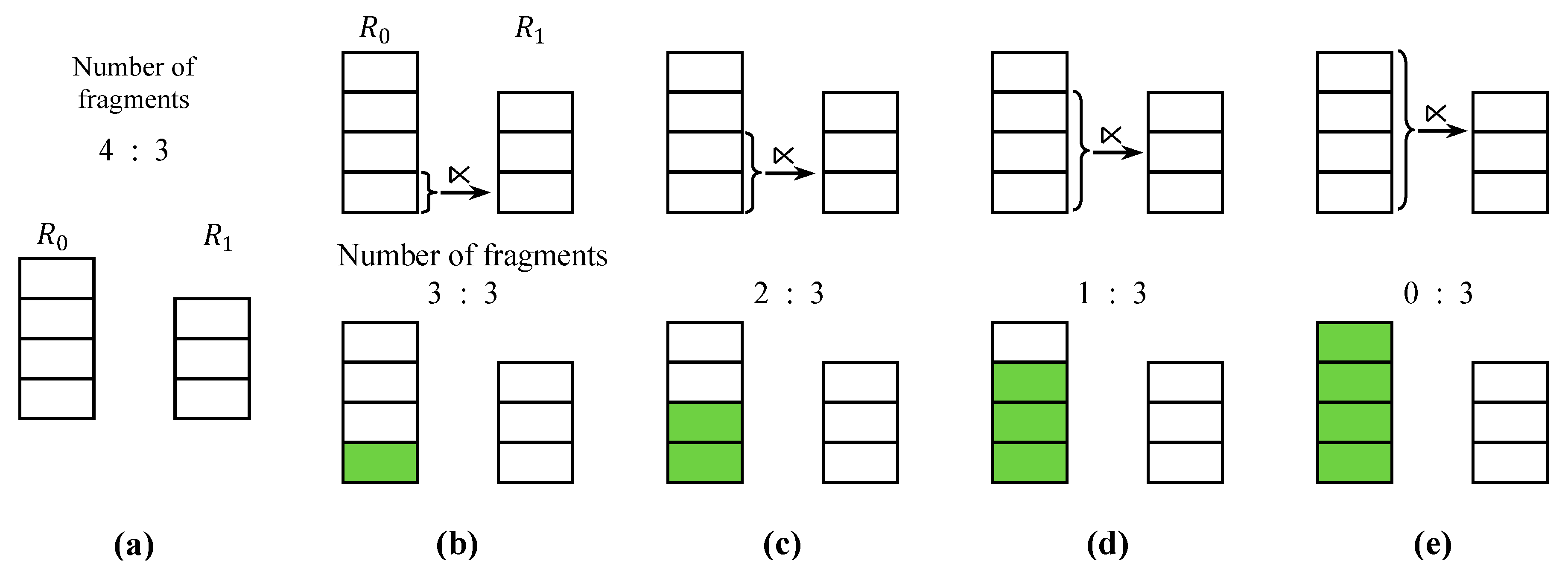
5.4. Post Optimization
5.5. Query Optimization and Processing

6. Performance Evaluation of Our Scheme and SRJA
6.1. Parameters
| Parameter | Value |
|---|---|
| Size of a region (nn nodes) | n = 5, 10, 15 |
| The distance between and | 30 hops |
| The range of joining attribute values | 1..10,000 |
| The range of count | 1..15 |
| Epoch (i.e., sampling interval) | 10, 20, 30, 40, 50, 60 s(default: 30 s) |
| Query window size | 3 h |
| Iceberg threshold () | 50, 100, 150, 200 |
6.2. Experimental Results
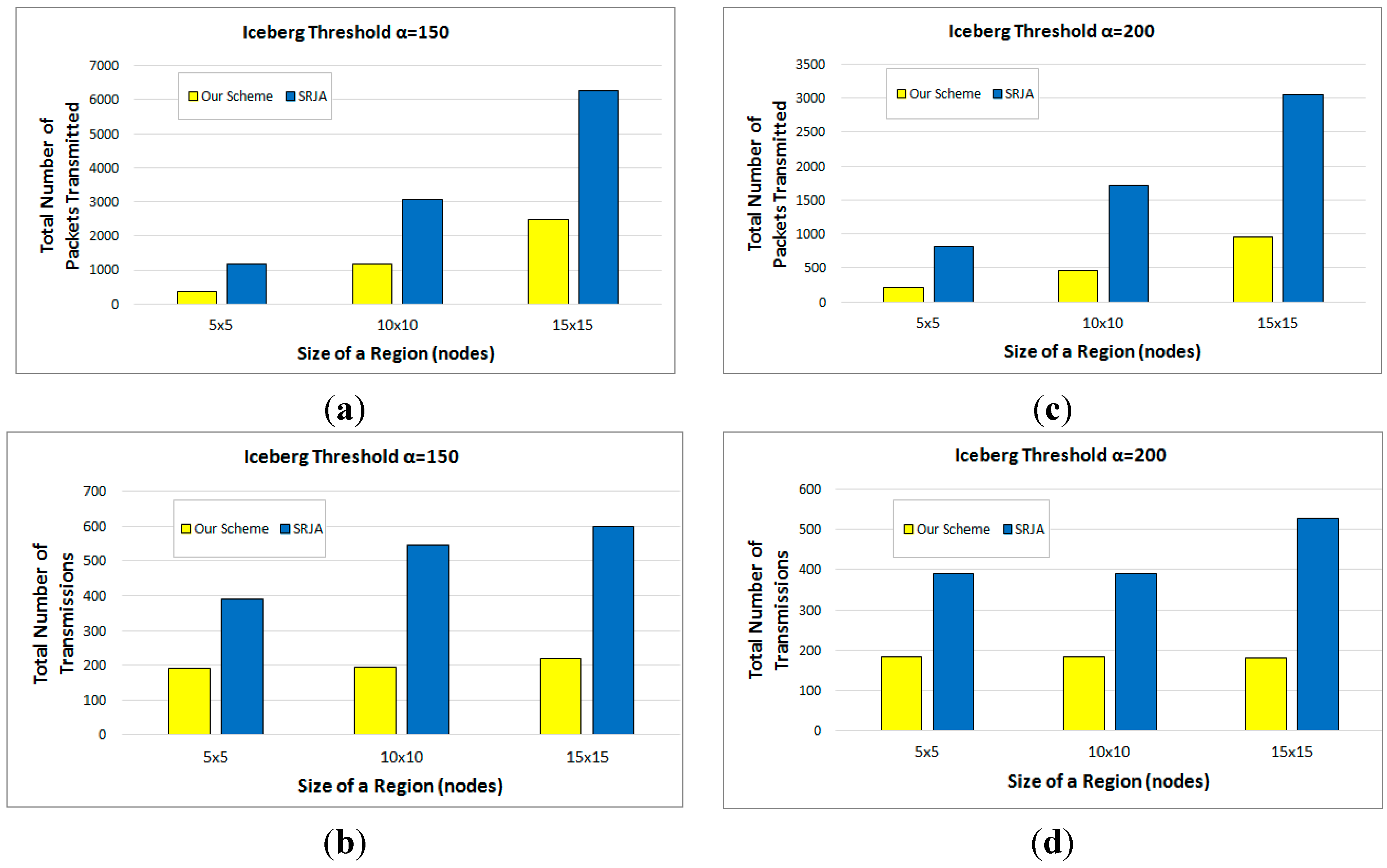
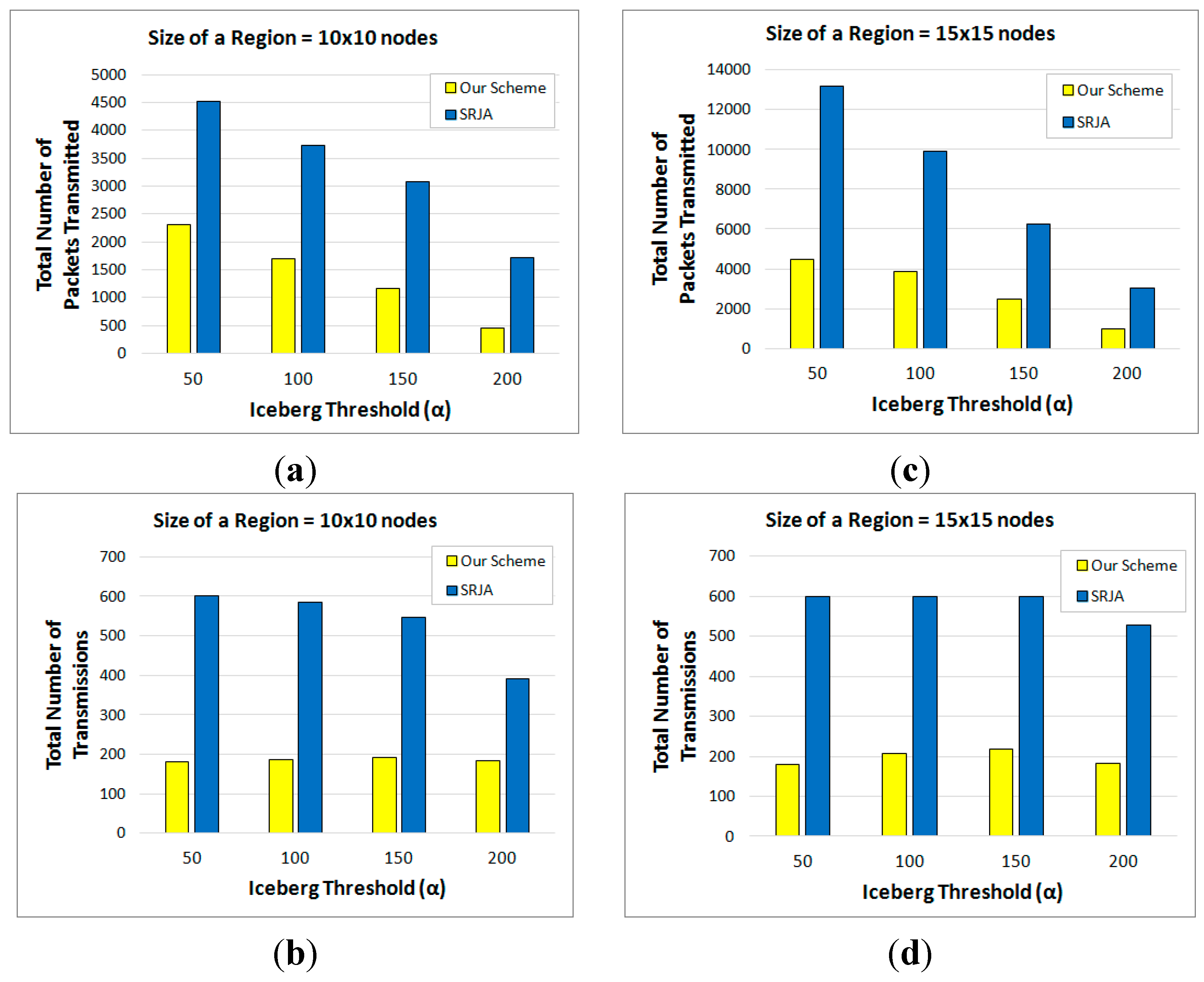
- In SRJA, the histogram-based value ranges are sent as a synopsis of the joining attribute values. In our scheme, a Bloom filter constructed from a count-based fragment is sent as a synopsis of the joining attribute values. The Bloom filter is more compact than the value ranges. Besides, the false positives are efficiently handled in the backward reduction phase of the 2-way fragment semijoins in our scheme.
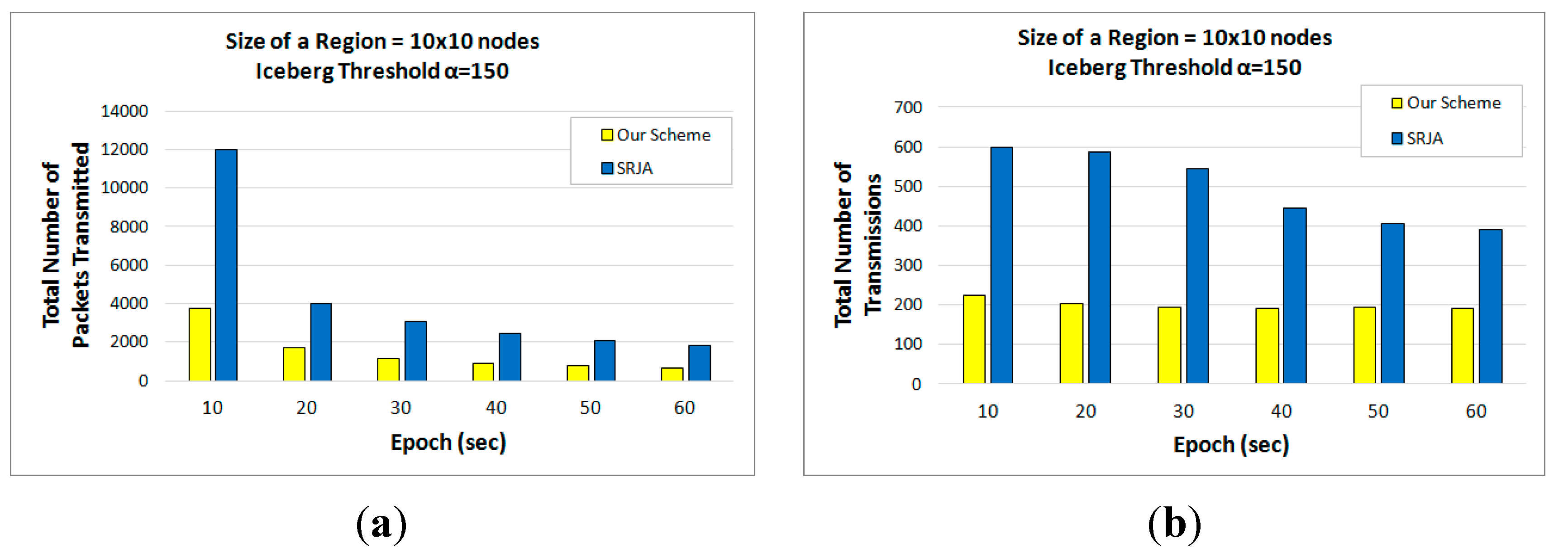
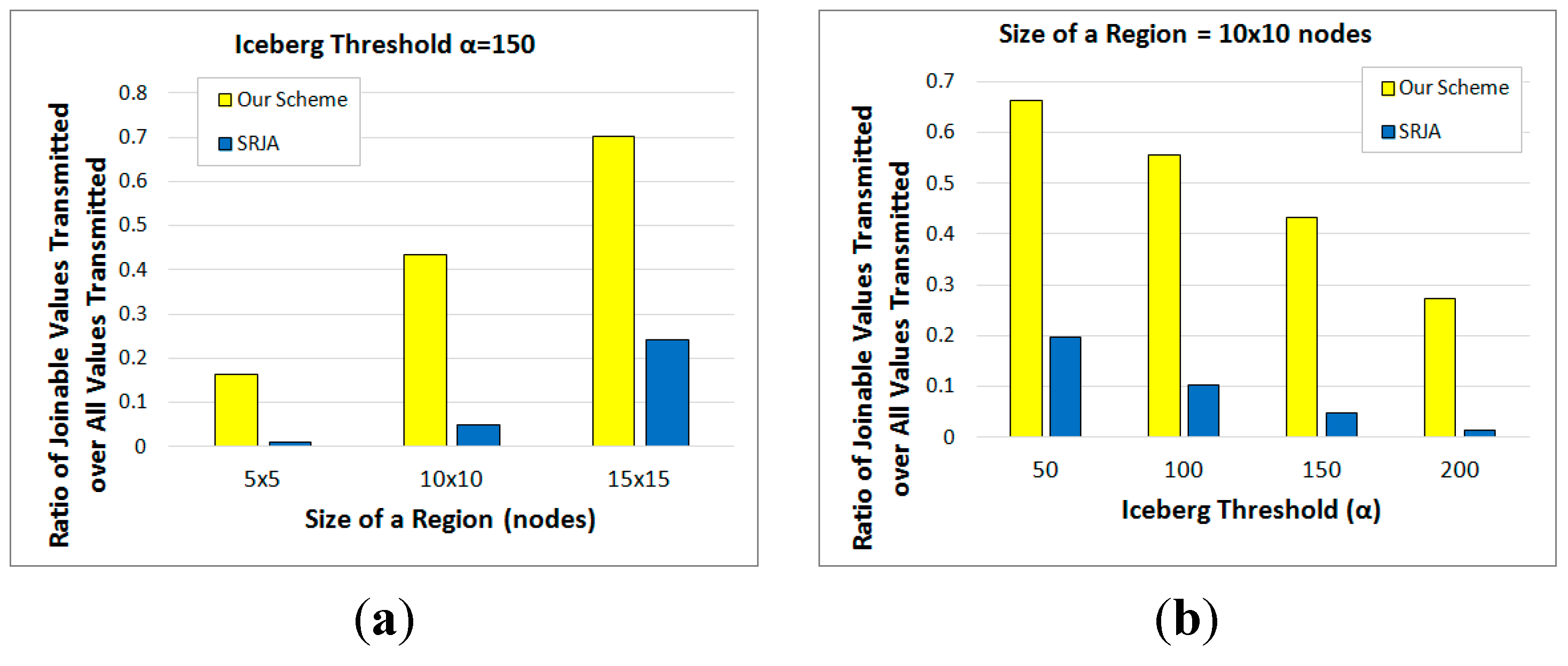
6.3. Analytical Comparison of the Total Number of Transmissions
6.3.1. SRJA
6.3.2. Our Scheme
7. Related Work
8. Conclusions
Conflicts of Interest
References
- Madden, S.; Franklin, M.; Hellerstein, J.; Hong, W. TinyDB: An Acquisitional Query Processing System for Sensor Networks. ACM Trans. Database Syst. 2005, 1, 122–173. [Google Scholar] [CrossRef]
- Yu, H.; Lim, E.; Zhang, J. On In-Network Synopsis Join Processing for Sensor Networks. In Proceedings of the 7th International Conference on Mobile Data Management, Nara, Japan, 9–13 May 2006; pp. 32–39.
- Kang, H. In-network processing of joins in wireless sensor networks. Sensors 2013, 13, 3358–3393. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Guibas, L. Wireless Sensor Networks: An Information Processing Approach; Morgan Kaufmann: San Francisco, CA, USA, 2004. [Google Scholar]
- Stattner, E.; Vidot, N.; Hunel, P.; Collard, M. Wireless Sensor Network for Habitat Monitoring: A Counting Heuristic. In Proceedings of the 37th Annual IEEE Conference on Local Computer Networks Workshops, Clearwater, FL, USA, 22–25 October 2012; pp. 753–760.
- Lai, Y.; Lin, Z.; Gao, X. SRJA: Iceberg Join Processing in Wireless Sensor Networks. In Proceedings of the International Workshop on Database Technology and Applications, Wuhan, China, 27–28 November 2010; pp. 1–4.
- Shou, Y.; Mamoulis, N.; Cao, H.; Papadias, D.; Cheung, D. Evaluation of Iceberg Distance Joins. In Proceedings of the 8th International Symposium on Advances in Spatial and Temporal Databases, Santorini Island, Greece, 24–27 July 2003; pp. 270–288.
- Cohen, S.; Matias, Y. Spectral Bloom Filters. In Proceedings of the ACM SIGMOD International Conference on Management of Data, San Diego, CA, USA, 9–12 June 2003; pp. 241–252.
- Arasu, A.; Babu, S.; Widom, J. The CQL continuous query language: Semantic foundations and query execution. VLDB J. 2006, 2, 121–142. [Google Scholar] [CrossRef]
- Bloom, B. Space/time trade-offs in hash coding with allowable errors. Comm. ACM 1970, 7, 422–426. [Google Scholar] [CrossRef]
- Kang, H.; Roussopoulos, N. Using 2-way Semijoins in Distributed Query Processing. In Proceedings of the 3rd IEEE International Conference on Data Engineering, Los Angeles, CA, USA, 3–5 February 1987; pp. 644–651.
- Roussopoulos, N.; Kang, H. A pipeline n-way join algorithm based on the 2-way semijoin program. IEEE Trans. Knowl. Data Eng. 1991, 4, 486–495. [Google Scholar] [CrossRef]
- Bernstein, P.A.; Chiu, D.W. Using semi-joins to solve relational queries. J. ACM 1981, 1, 25–40. [Google Scholar] [CrossRef]
- Özsu, M.T.; Valduriez, P. Principles of Distributed Database Systems, 3rd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Li, Z.; Ross, K.A. RERF Join: An Alternative to Two-way Semijoin and Bloomjoin. In Proceedings of the 4th International Conference on Information and Knowledge Management, Baltimore, MD, USA, 28 November–2 December 1995; pp. 137–144.
- Andrei, B.; Mitzenmacher, M. Network applications of Bloom filters: A survey. Internet Math. 2004, 4, 485–509. [Google Scholar]
- Mullin, J.K. Optimal semijoins for distributed database systems. IEEE Trans. Softw. Eng. 1990, 5, 558–560. [Google Scholar] [CrossRef]
- Abadi, D.; Madden, S.; Lindner, W. REED: Robust, Efficient Filtering and Event Detection in sensor networks. In Proceedings of the 31st International Conference on very Large Data Bases, Trondheim, Norway, 30 August–2 September 2005; pp. 769–780.
- Lai, Y.; Chen, Y.; Chen, H. PEJA: Progressive energy-efficient join processing for sensor networks. J. Comput. Sci. Technol. 2008, 6, 957–972. [Google Scholar] [CrossRef]
- Pandit, A.; Gupta, H. Communication-Efficient Implementation of Range-Join in Sensor Networks. In Proceedings of 11th International Conference on Database Systems for Advanced Applications, Singapore, 12–15 April 2006; pp. 859–869.
- Chowdhary, V.; Gupta, H. Communication-efficient Implementation of Join in Sensor Networks. In Proceedings of the 10th International Conference on Database Systems for Advanced Applications, Beijing, China, 17–20 April 2005; pp. 447–460.
- Coman, A.; Nascimento, M. Distributed Algorithm for Joins in Sensor Networks. In Proceedings of the 19th International Conference on Scientific and Statistical Database Management, Banff, Canada, 9–11 July 2007.
- Coman, A.; Nascimento, M.; Sander, J. On Join Location in Sensor Networks. In Proceedings of the 8th International Conference on Mobile Data Management, Mannheim, Germany, 7–11 May 2007; pp. 190–197.
- Min, J.; Yang, H.; Chung, C. Cost based in-network join strategy in tree routing sensor networks. Inf. Sci. 2011, 16, 3443–3458. [Google Scholar] [CrossRef]
- Mihaylov, S.; Jacob, M.; Ives, Z.; Guha, S. Dynamic Join Optimization in Multi-Hop Wireless Sensor Networks. In Proceedings of the 36th International Conference on very Large Data Bases, Singapore, 13–17 September 2010; pp. 1279–1290.
- Mihaylov, S.; Jacob, M.; Ives, Z.; Guha, S. A Substrate for In-Network Sensor Data Integration. In Proceedings of the 5th Workshop on Data Management for Sensor Networks, Auckland, New Zealand, 24 August 2008; pp. 35–41.
- Stern, M.; Buchmann, E.; Böhm, K. Towards Efficient Processing of General-Purpose Joins in Sensor Networks. In Proceedings of the 25th IEEE International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009; pp. 126–137.
- Stern, M.; Böhm, K.; Buchmann, E. Processing Continuous Join Queries in Sensor Networks: A Filtering Approach. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Indianapolis, IN, USA, 6–11 June 2010; pp. 267–278.
- Yang, X.; Lim, H.; Özsu, M.; Tan, K. In-Network Execution of Monitoring Queries in Sensor Networks. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Beijing, China, 12–14 June 2007; pp. 521–532.
- Mo, S.; Fan, Y.; Li, Y.; Wang, X. Multi-Attribute Join Query Processing in Sensor Networks. J. Netw. 2014, 10, 2702–2712. [Google Scholar]
- Min, J.; Kim, J.; Shim, K. TWINS: Efficient time-windowed in-network joins for sensor networks. Inf. Sci. 2014, 1, 87–109. [Google Scholar] [CrossRef]
- Fang, M.; Shivakumar, N.; Garcia-Molina, H.; Motwani, R.; Ullman, J.D. Computing Iceberg Queries Efficiently. In Proceedings of the 24th International Conference on Very Large Data Bases, New York, NY, USA, 24–27 August 1998; pp. 299–310.
- Zhao, H.; Lall, A.; Ogihara, M.; Xu, J. Global Iceberg Detection over Distributed Data Streams. In Proceedings of the 26th International Conference on Data Engineering, Long Beach, CA, USA, 1–6 March 2010; pp. 557–568.
- Manjhi, A.; Shkapenyuk, V.; Dhamdhere, K.; Olston, C. Finding (Recently) Frequent Items in Distributed Data Streams. In Proceedings of the 21st International Conference on Data Engineering, Tokyo, Japan, 5–8 April 2005; pp. 767–778.
- Zhao, Q.; Ogihara, M.; Wang, H.; Xu, J. Finding Global Icebergs over Distributed Data Sets. In Proceedings of the 25th ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, Chicago, IL, USA, 26–28 June 2006; pp. 298–307.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H. In-Network Processing of an Iceberg Join Query in Wireless Sensor Networks Based on 2-Way Fragment Semijoins. Sensors 2015, 15, 6105-6132. https://doi.org/10.3390/s150306105
Kang H. In-Network Processing of an Iceberg Join Query in Wireless Sensor Networks Based on 2-Way Fragment Semijoins. Sensors. 2015; 15(3):6105-6132. https://doi.org/10.3390/s150306105
Chicago/Turabian StyleKang, Hyunchul. 2015. "In-Network Processing of an Iceberg Join Query in Wireless Sensor Networks Based on 2-Way Fragment Semijoins" Sensors 15, no. 3: 6105-6132. https://doi.org/10.3390/s150306105
APA StyleKang, H. (2015). In-Network Processing of an Iceberg Join Query in Wireless Sensor Networks Based on 2-Way Fragment Semijoins. Sensors, 15(3), 6105-6132. https://doi.org/10.3390/s150306105





