Distributed Efficient Similarity Search Mechanism in Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Work
| Mechanisms | Schemes | ||||
|---|---|---|---|---|---|
| Range Query | Bit Code Mapping | MDA [9] | |||
| Tree Structure | Multiply Rooted Hierarchical Index | DIFS [10] | |||
| Binary Tree | DIM [12] | ||||
| Dimension (attribute) | Range Query vs. Point Query | Load Balancing | Data Aggregation | ||
| Similarity Searching | Single | Both | Yes | No | SSA [6] |
| Multi | Range | Yes | No | SDS [7] | |
3. Basic System Operation
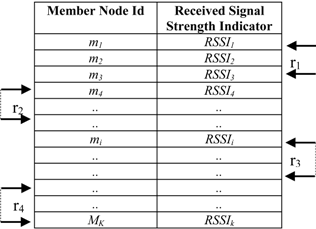
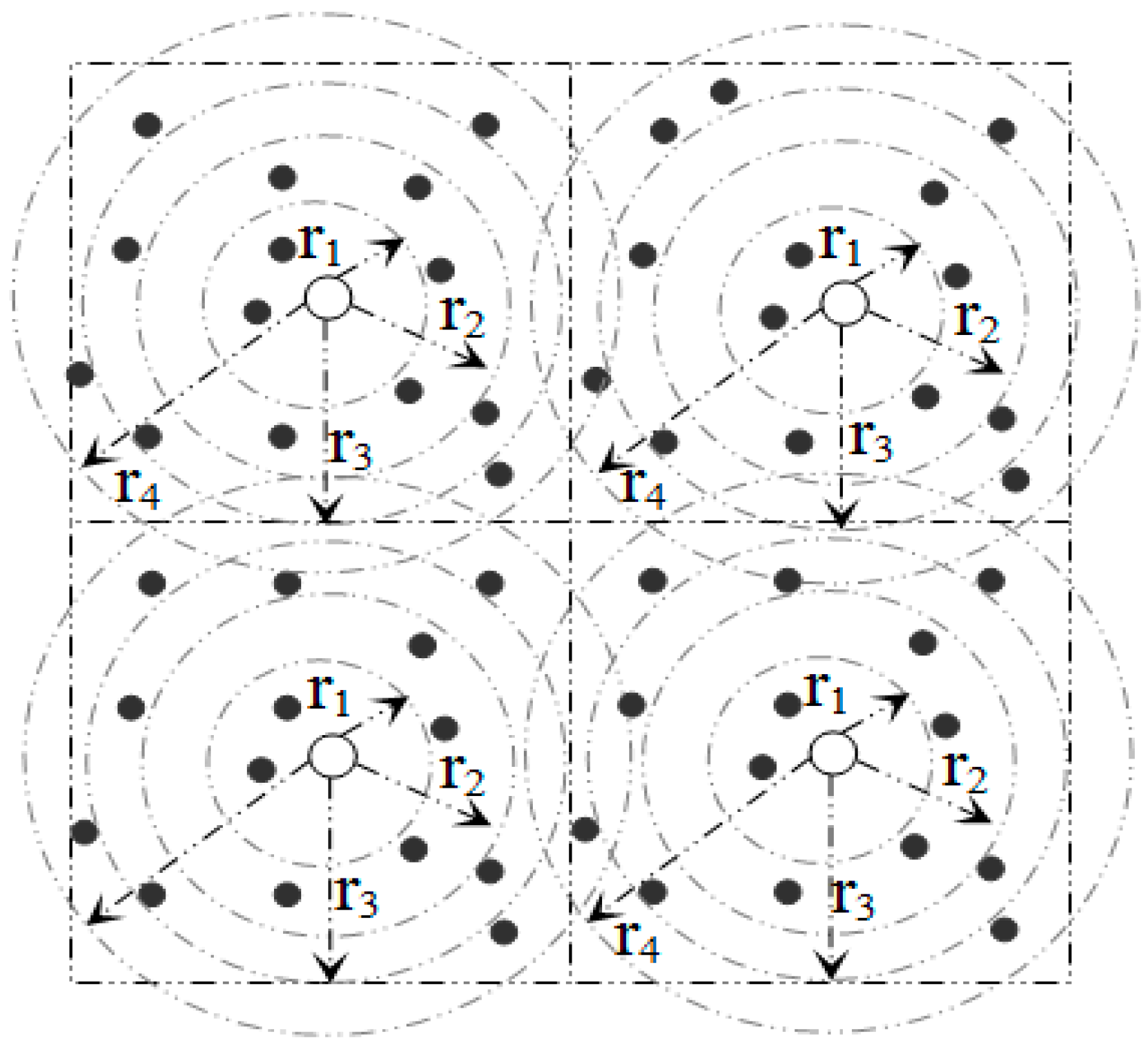
3.1. Network Architecture
3.2. Metric-Based Searching
d(a, b) = 0 if a = b (identity)
d(a, b) = d(b, a) (symmetry)
d(a, c) ≤ d(a, b) + d(b, c) (triangle inequality)
X = {a ϵ I|d(q, a) ≤ r}
3.3. Data Processing and Mapping
| Member Node | First Attribute | Second Attribute | Third Attribute |
|---|---|---|---|
| 1 | v11 | v12 | v13 |
| 2 | v21 | v22 | v23 |
| 3 | v31 | v32 | v33 |
| After applying Equations (6) and (7) | |||
| max (v11, v21, v31) | max (v12, v22, v32) | max (v13, v23, v33) | |
| min (v11, v21, v31) | min (v12, v22, v32) | min (v13, v23, v33) | |
| avg (v11, v21, v31) | avg (v12, v22, v32) | avg (v13, v23, v33) | |
| Attribute | Weight |
|---|---|
| A1 | W1 |
| A2 | W2 |
| .... | .... |
| Al | wl |
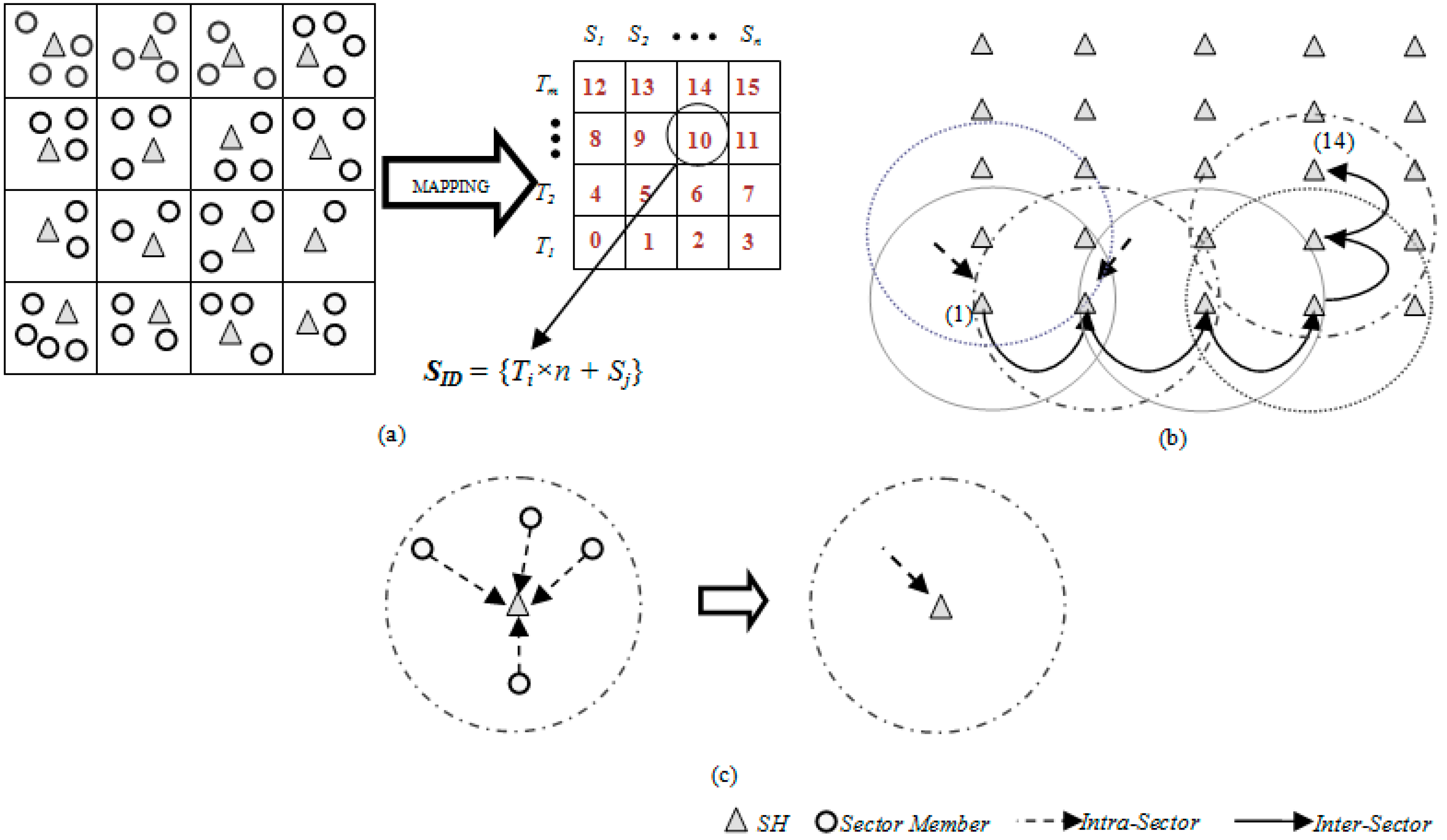
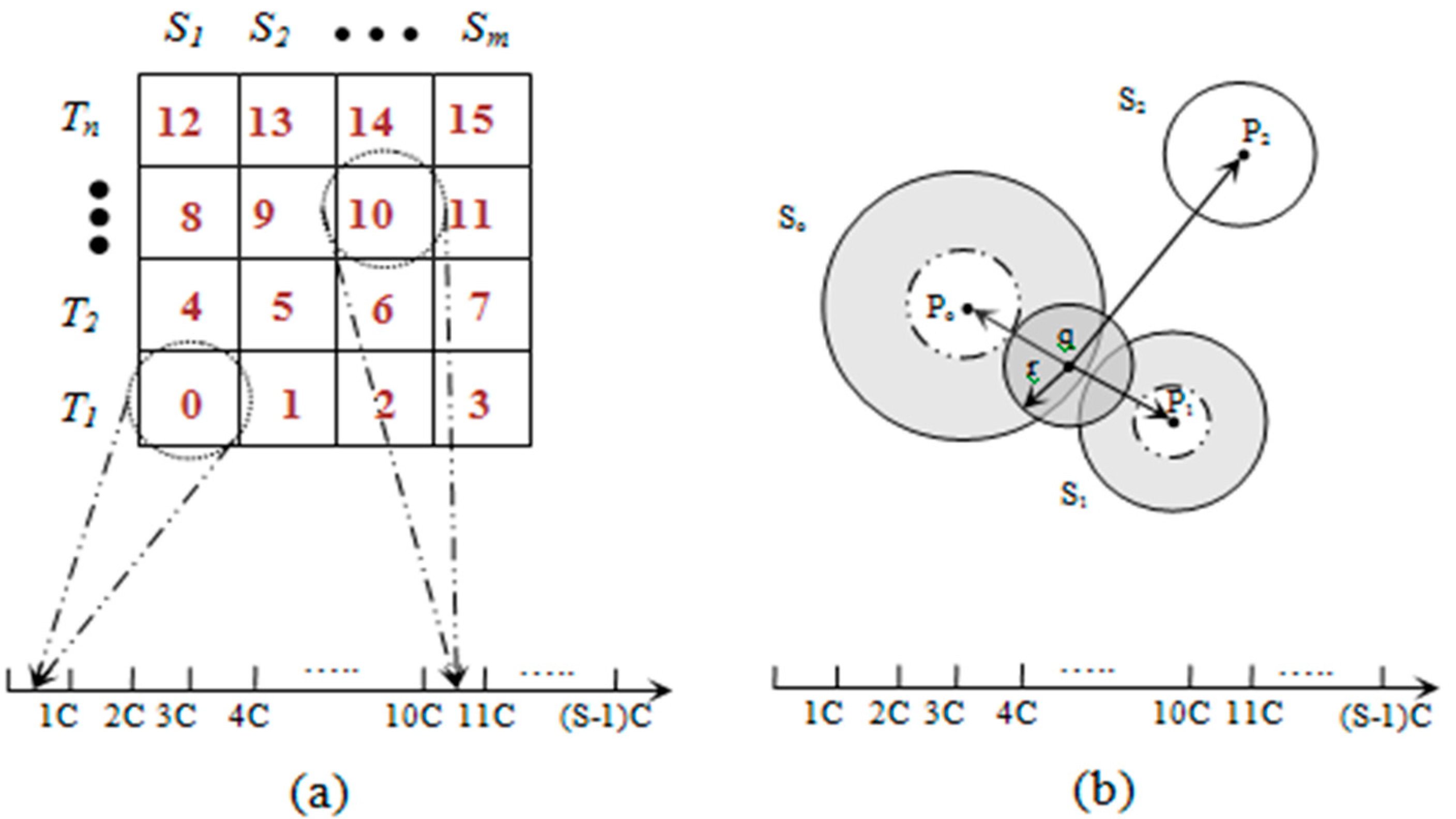
3.3.1. Pivot Point Generation
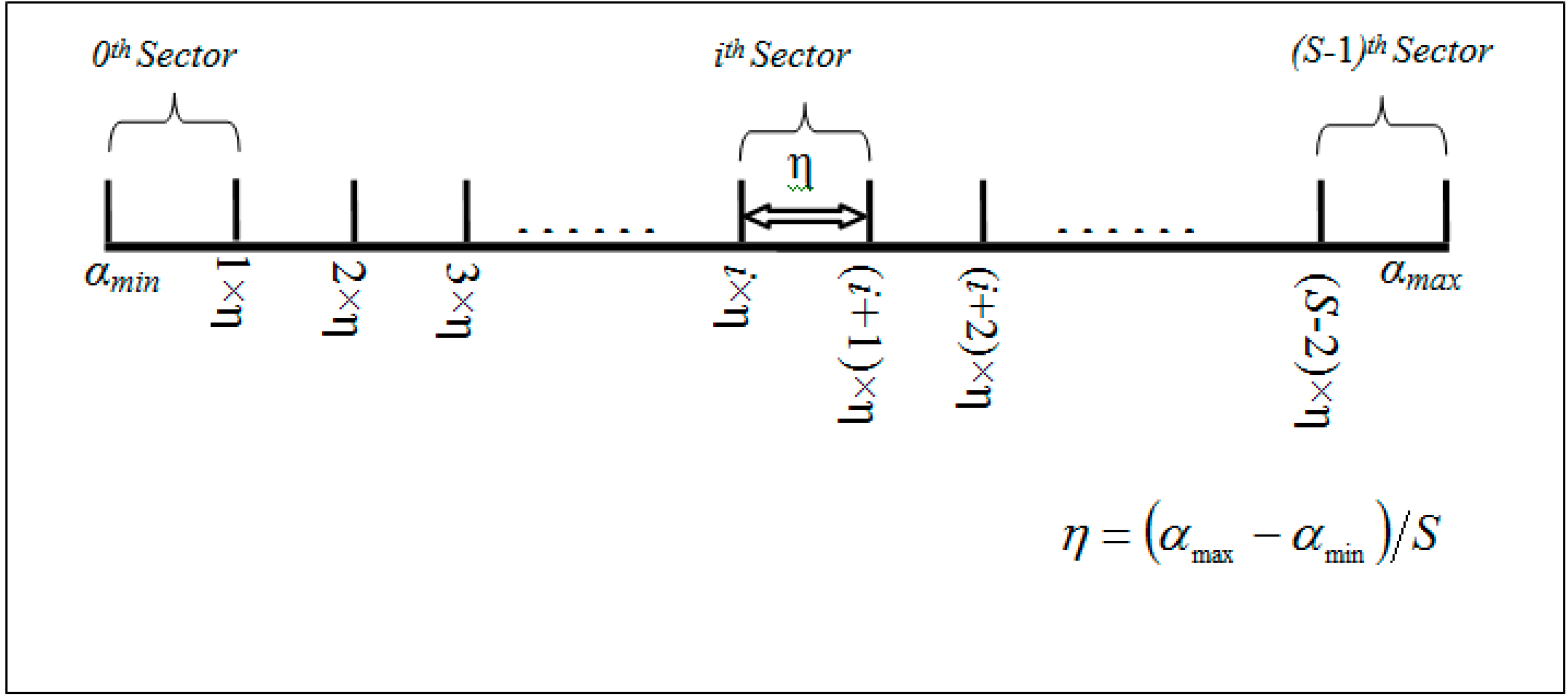
3.3.2. Mapping
3.4. SBD Routing
| Algorithm 1. Pivot Point Generation Algorithm (implemented at each SH node). |
Input: attrRangeTable (containing minimum, maximum, average and theta of each attribute), W (weights to different attributes based on their importance in the event description). Output: P (derived pivot point for each sector) 1: mapRec.minRange ← 0; mapRec.maxRange ← 0 2: m ← lengthof(attrRangeTable) 3: for each i from 1 to m do 4: mapRec.minRange ← mapRec.minRange + (attrRangeTable[i].min/attrRangeTable[i].max) × W[i] 5: mapRec.maxRange ← mapRec.maxRange + (attrRangeTable[i].max/attrRangeTable[i].max) × W[i] 6: mapRec.com ← mapRec.com + (attrRangeTable[i].avg)/attrRangeTable[i].max) × W[i] 7: mapRec.theta ← mapRec.theta + (attrRangeTable.theta)/attrRangeTable[i].max) × W[i] 8: i ← i + 1 9: end for 10: comLowerLimit ← mapRec.com − mapRec.theta 11: comUpperLimit ← mapRec.com + mapRec.theta 12: // S is the total number of sectors 13: η ← (comUpperLimit − comLowerLimit)/(S − 1) 14: for each j from 0 to S do 15: if j = 0 16: then P[j] ← mapRec.minRange 17: else if j = S 18: then P[j] ← mapRec.maxRange 19: else 20: P[j] ← comLowerLimit + j × η 21: end if 22: j ← j + 1 23: end for |
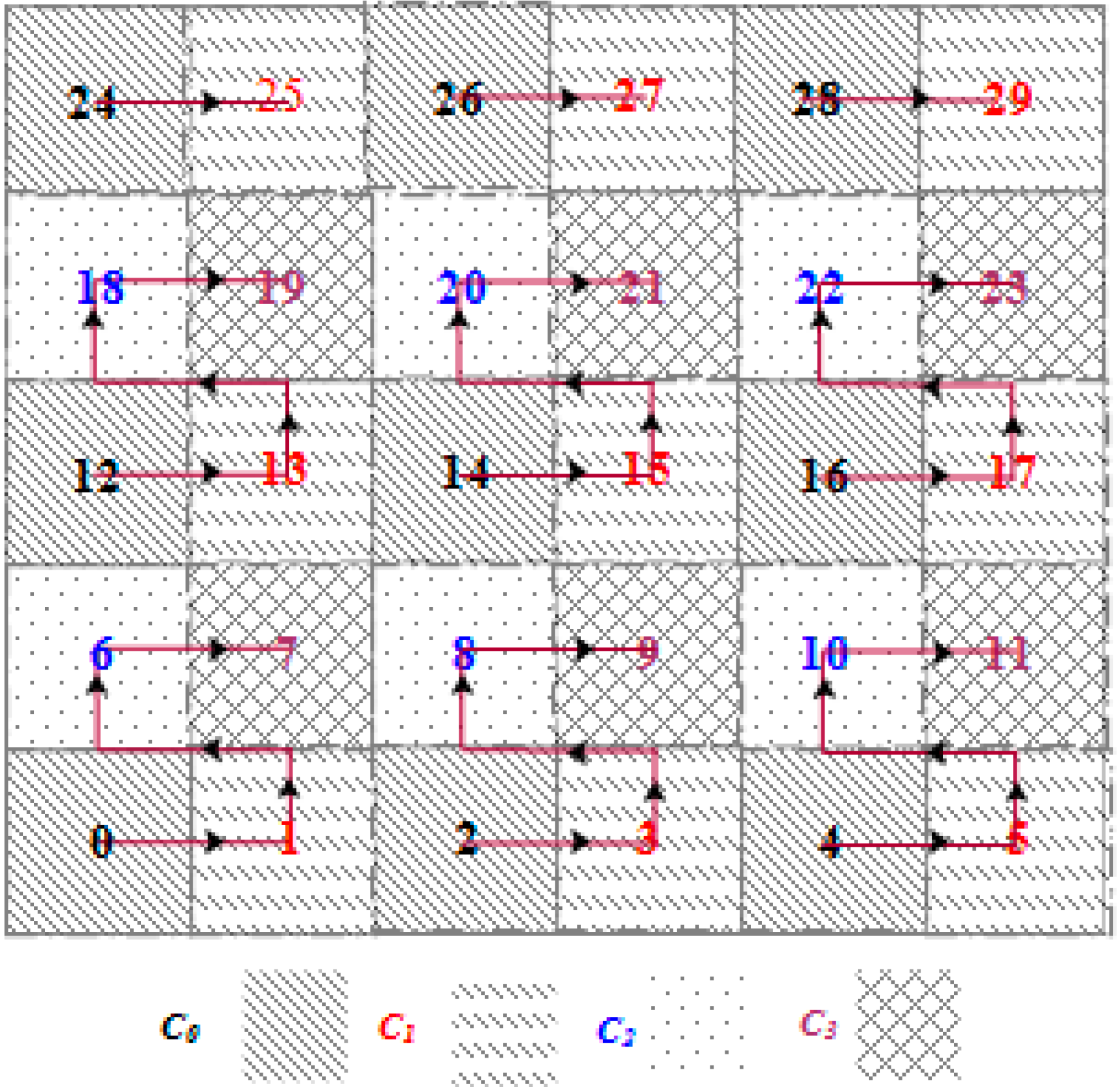
| Algorithm 2. Conflict free TDMA frame slot assignment GCA (implemented at each SH node). |
Input: HD = 2 (circular hop distance between two sectors), m, n (total number of tracks (or rows) and sectors (or columns) in the grid, respectively) Output: Conflict-free time-slot (Ci) with frame length L = 4 × epoch (length of the slot assigned to a sector) 1: for each j from 1 to m do 2: for each i from (j − 1) × n to (j × n − 1) do 3: if i < n × j 4: then SHi ← C0 5: end if 6: if i +1 < n × j 7: then SHi+1 ← C1 8: end if 9: if i + n < m × n 10: then SHi+n ← C2 11: end if 12: if i + n + 1 < m × n 13: then SHi+n+1 ← C3 14: end if 15: i = i + HD 16: end for 17: j = j + HD 16: end for |
| Algorithm 3. Head_Selection (), implemented in member nodes, selects the closest SH based on the rank calculated using Equation (22). |
Input: rank, SHInfo 1: sort SHInfo in descending order based on rank 2: create network layer packet joinCntrlPacket 3: SHD ← pop top element from SHInfo.SHS 4: set SELF_NET_ADDR as source, SHD as destination and Packet Type = 4 to joinCntrlPacket 5: //Unicast joining request to the closest head node. 6: toMacLayer (joinCntrlPacket, SHD) |
| Algorithm 4. Search_Next_Hop (SHi), implemented at each sector head node. |
Input: Target SHi, where SHi ∈ [1...S], m- number of tracks (rows) and n- number of sectors per track (columns) Output: Next Hop SHk, where SHk ∈ [1...S], 1: //Finding the row and column position of //destination sector head and current head in the //grid 2: destCol ← SHi%n; 3: destRow ← SHi/n; 4: curCol ← nextHopCol ← (SELF_NET_ADDR)%n 5: curRow ← nextHopRow ← (SELF_NET_ADDR)/n 6: SHk ← −1 7: //Moving the packet to the same column where //destination sector lies 8: if curCol < destcol 9: /*Move toward right */ 10: then nextHopCol ← nextHopCol + 1 11: else if curCol > destcol 12: /*Move toward left */ 13: then nextHopCol ← nextHopCol − 1 14: //It is in same column so move toward up or down 15: else if curCol = destCol 16: then if curRow < destRow 17: /*Move vertically up*/ 18: then nextHopRow ← nextHopRow + 1 19: else if curRow > destRow 20: /*Move vertically down*/ 21: then nextHopRow ← nextHopRow − 1 22: end if 23: end if 24: /*convert to sector number*/ 25: SHk ← nextHopRow × n + nextHopCol 26: Return SHk |
Alternate Route
- (a)
- The last relay SHR forwards the packet one hop up or down along sector path.
- (b)
- SBD returns to its normal mode of operation.
- (a)
- The last relay SHR forwards the packet one hop left or right along the track path
- (I)
- The recipient SHR forwards the packet up or down along sector path
- (b)
- SBD returns to its normal mode of operation.
- (0) →(1) → (2) → (3) → (8) → (13) → (18) → (23)
(7) → (8) → (13) → (18) → (23)
(1)→ (6) → (7) → (8)→(13) → (18) → (23)
(11) → (12) → (13) → (18) → (23) and so on.

3.5. Insertion
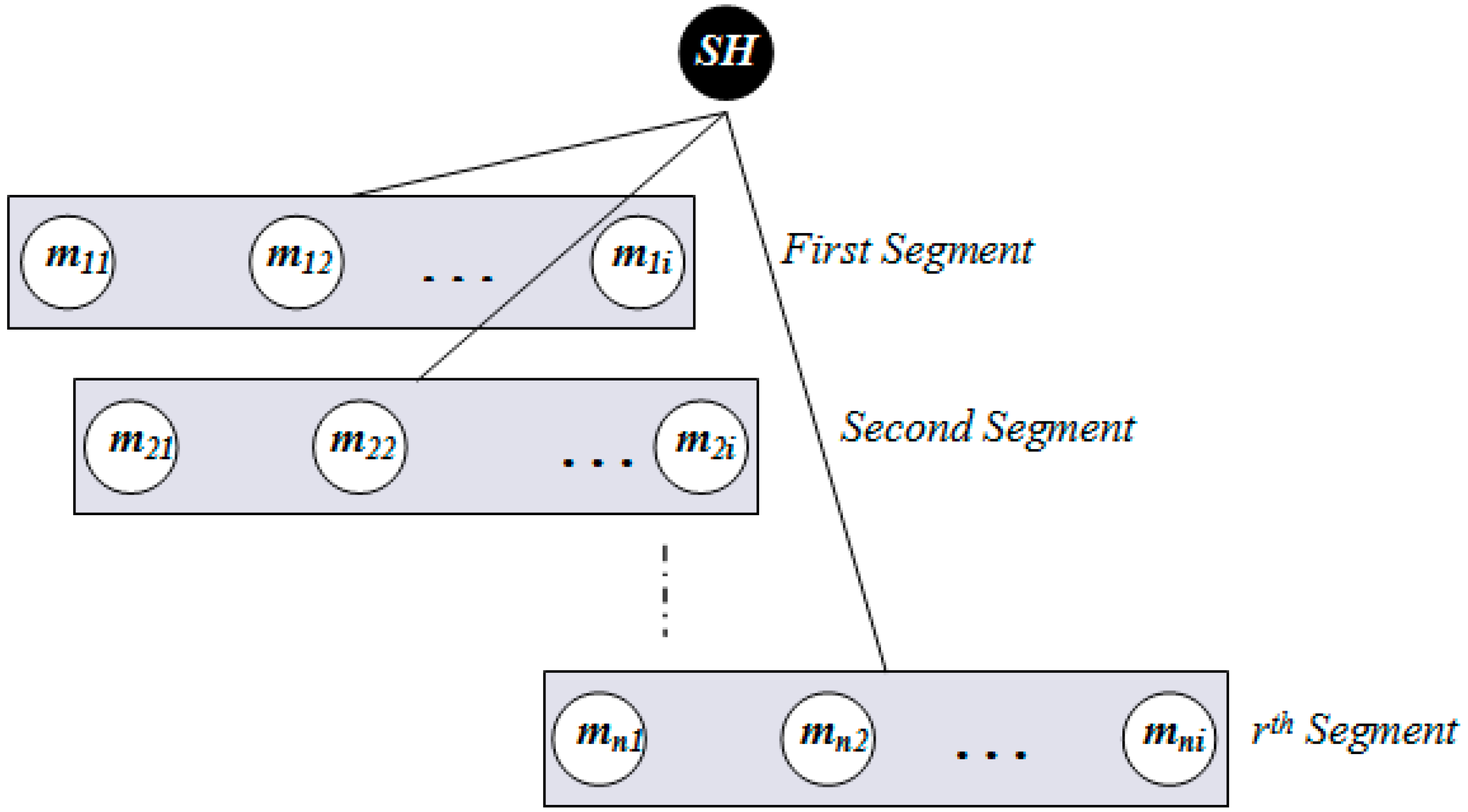
| Algorithm 5. Search_Target_Node (segment[i]), implemented at each SH node. |
Input: segment[i] (a data structure containing member node ID and tally to count the number of packets stored in the corresponding member node) Output: return the target Member Node ID. 1: sort segment[i] in ascending order based on segment[i].tally 2: segment[i].tally ← segment[i].tally + 1 3: memberNodeId ← segment[i].ID 4: return memberNodeId |
3.6. Querying
3.6.1. Range Query
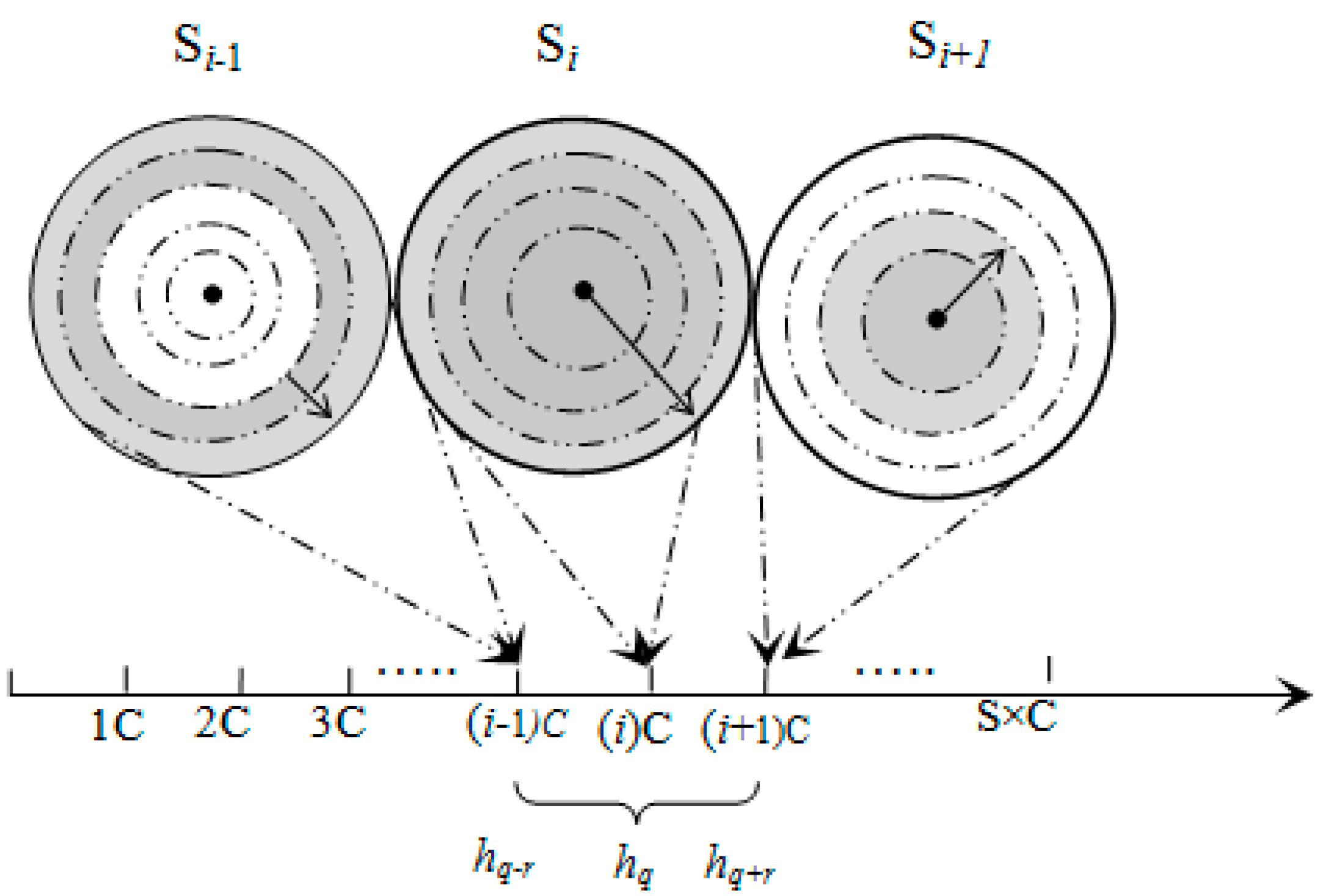
3.6.2. K-Nearest Neighbor Query
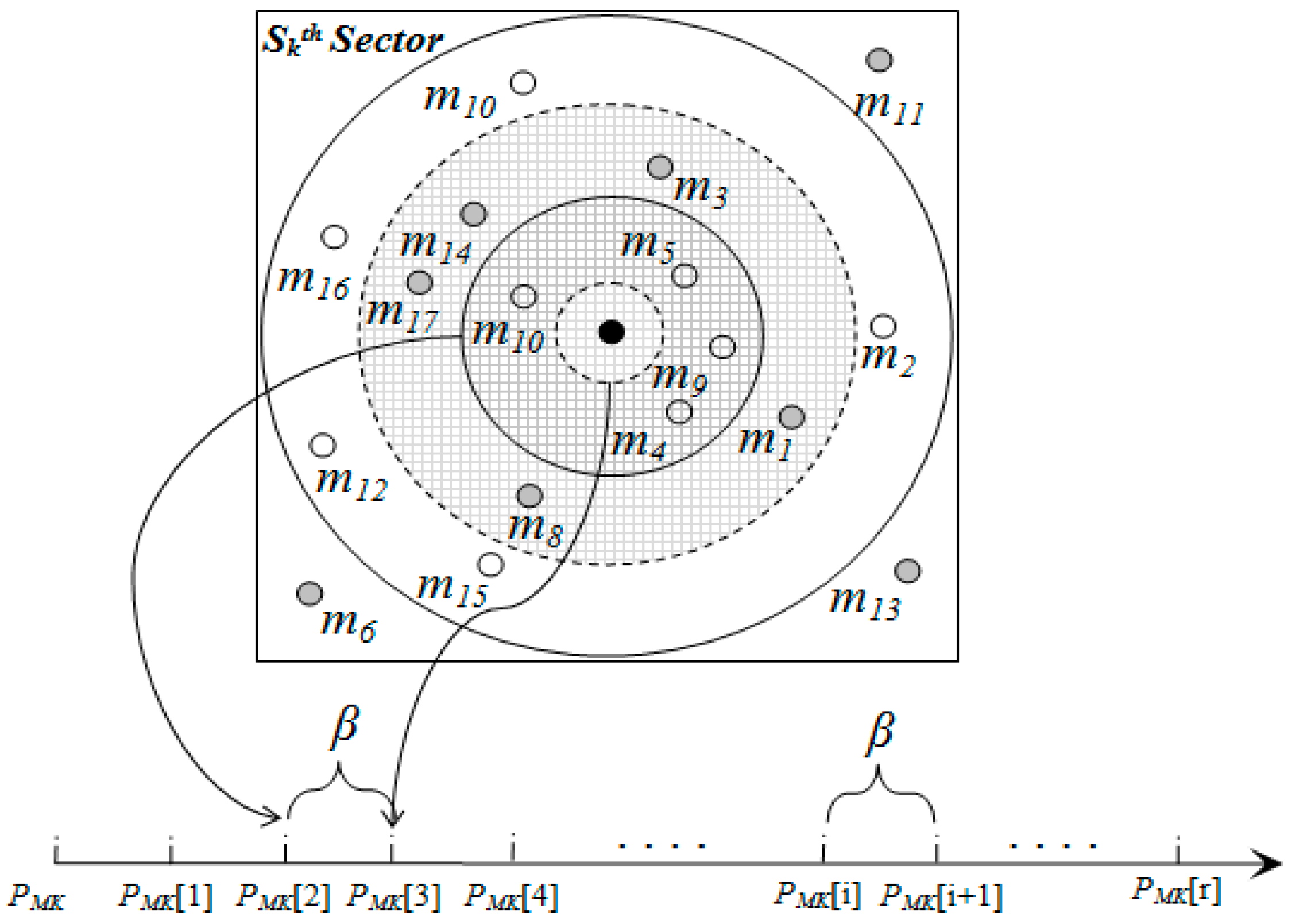
4. DCSMSS Analysis
4.1. SBD Analysis
| Notations | Description |
|---|---|
| Clu | Cost of local update |
| α | Local update rate |
| Cru | Cost of remote update |
| λ | Remote update rate |
| Cqr | Cost of query request and response |
| η | Query rate |
| Si | ith sector number |
| ti | ith track number (row) |
| si | ith sector number (column) |
| Cru,to,so,n | Cost of remote update from S0 to S1, S2, …, Sn |
| Ctx,SH | Transmission cost between two SH |
5. Performance Evaluation
| Parameter | Setting |
|---|---|
| Field Size | 60 × 60 m2, 90 × 90 m2, 120 × 120 m2, 150 × 150 m2 |
| Number of Nodes (n) | 80 (3600 m2), 180 (8100 m2), 320 (14,400 m2), 500 (22,500 m2) |
| Member Node Density (fm) | 1 node/56.25 m2 |
| Sector Head Node (SH) Density (fSH) | 1 node/225 m2 |
| Radio Range (member node) | ~8 m |
| Radio Range (SH) | ~20 m |
| Transmission Power | 0 dBm (SH), –5 dBm (membernode) |
| Power Consumption in Sending and Receiving Messages | 57.42 mW (SH), 46.2 mW (member node) |
| Power Consumption Per Sensing | 0.02 mJoule |
| Data Rate, Modulation Type, Bits Per Symbol, Bandwidth, Noise Bandwidth, Noise Floor, Sensitivity | 250 Kbps, PSK, 4, 20 MHz, 194 MHz, -100 dBm, -95 dBm |
| pathLossExponent | 2.4 |
| Initial Average Path Loss (PL(d0)) | 55 |
| Reference Distance (d0) | 1.0 m |
| Gaussian Zero-Mean Random Variable (Xα) | 4.0 |
| MAC Protocol, Maximum Transimission Retries | SMAC [16], 2 |
| SMAC Acknowledgment, Synchronization, RTS, CTS Packet Size | 11, 11, 13, 13 bytes |
5.1. SBD Performance
5.1.1. Energy Consumption
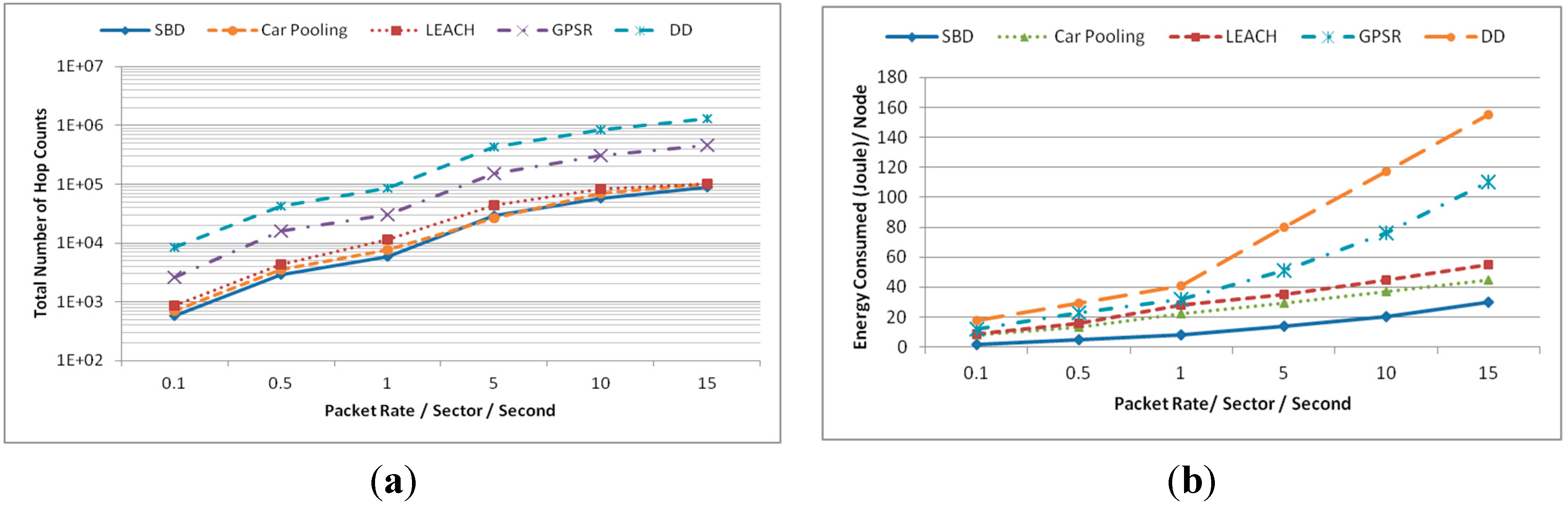
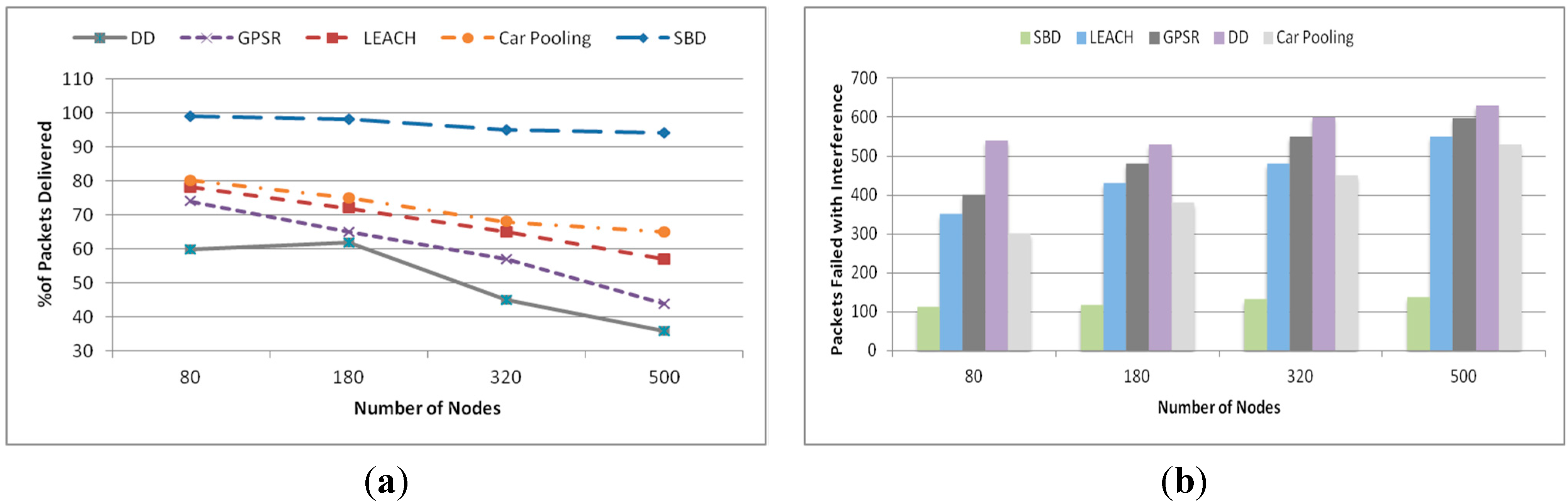
5.1.2. Latency
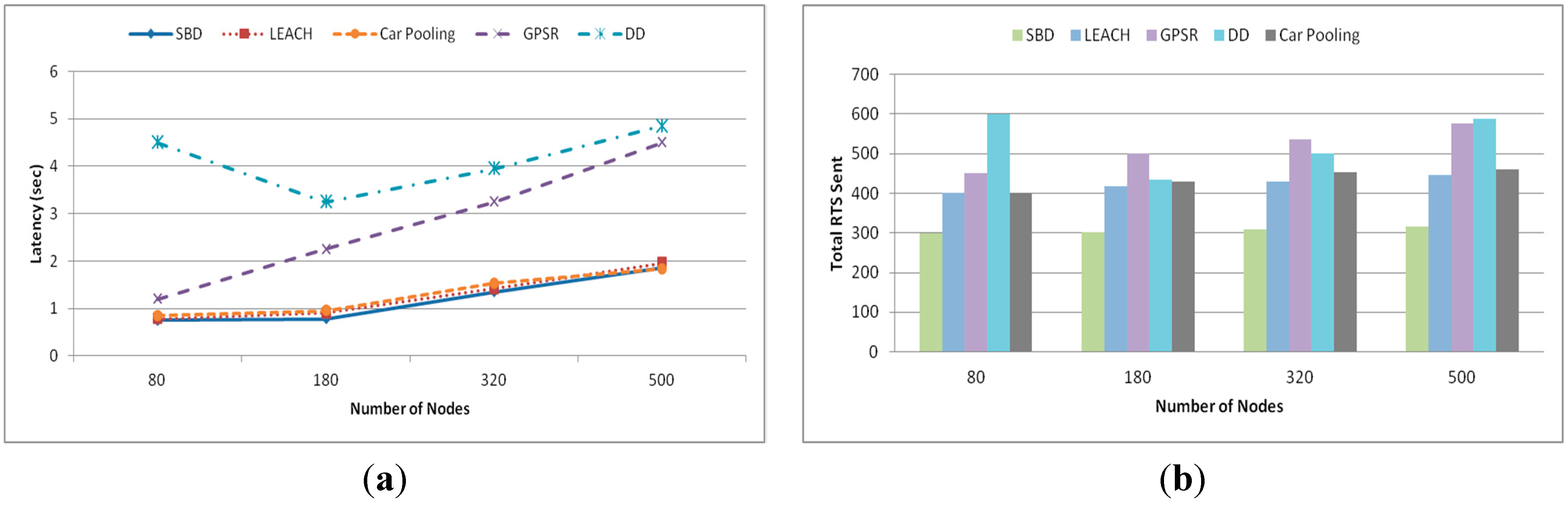
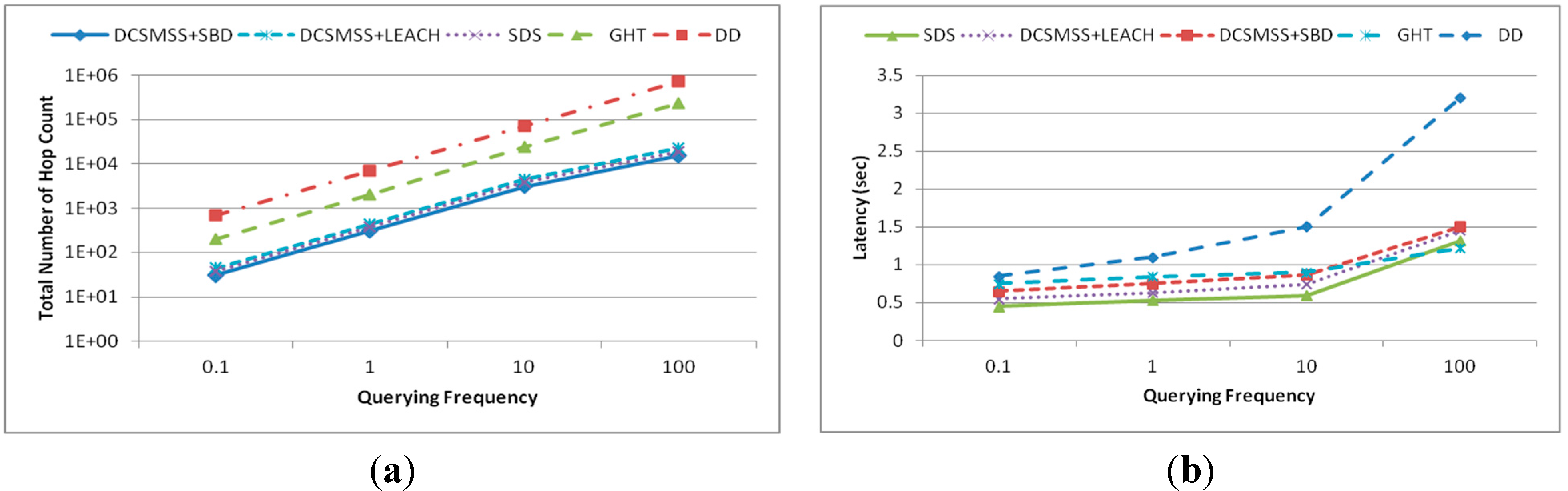
5.2. Querying Performance
5.2.1. Point Query

5.2.2. Range Query
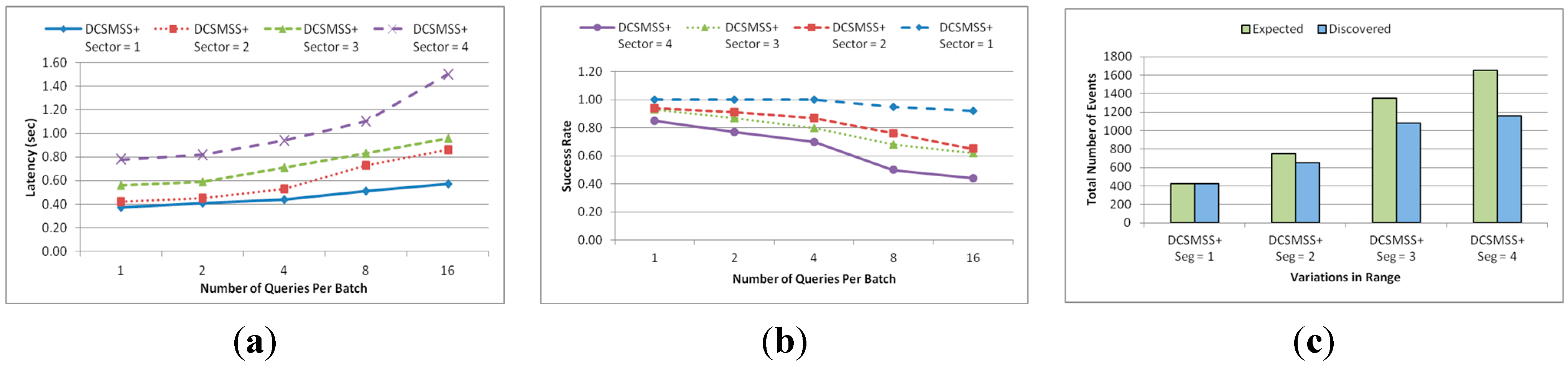
5.2.3. KNN Query
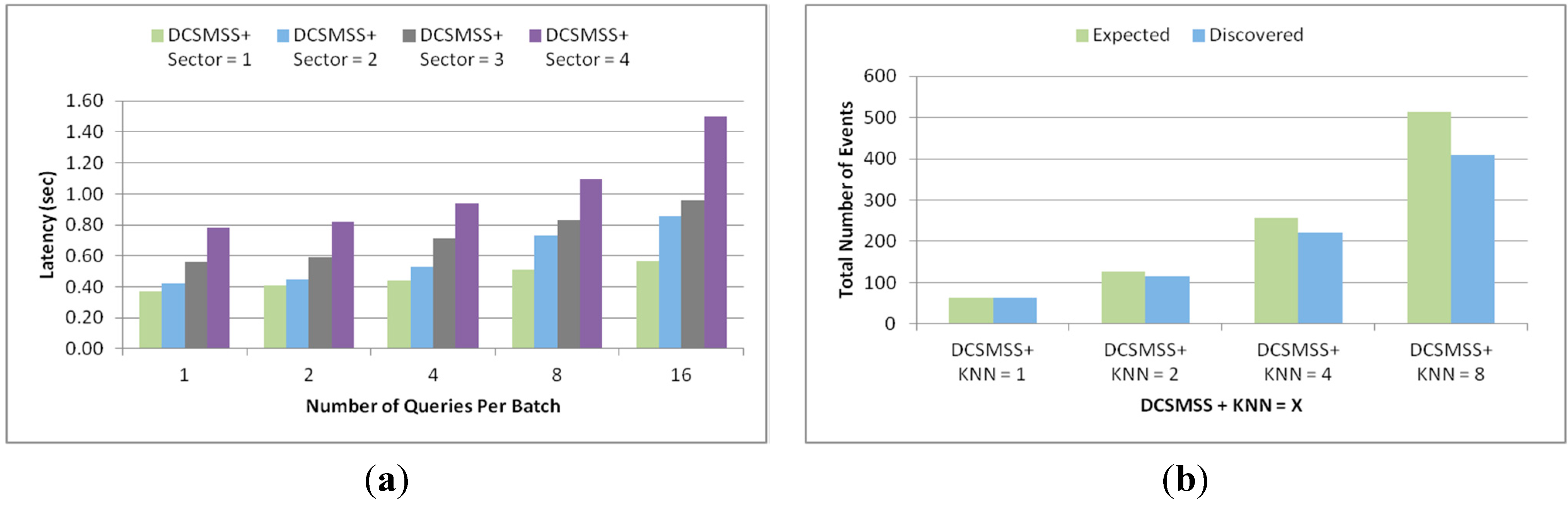
5.2.4. Similarity Searching
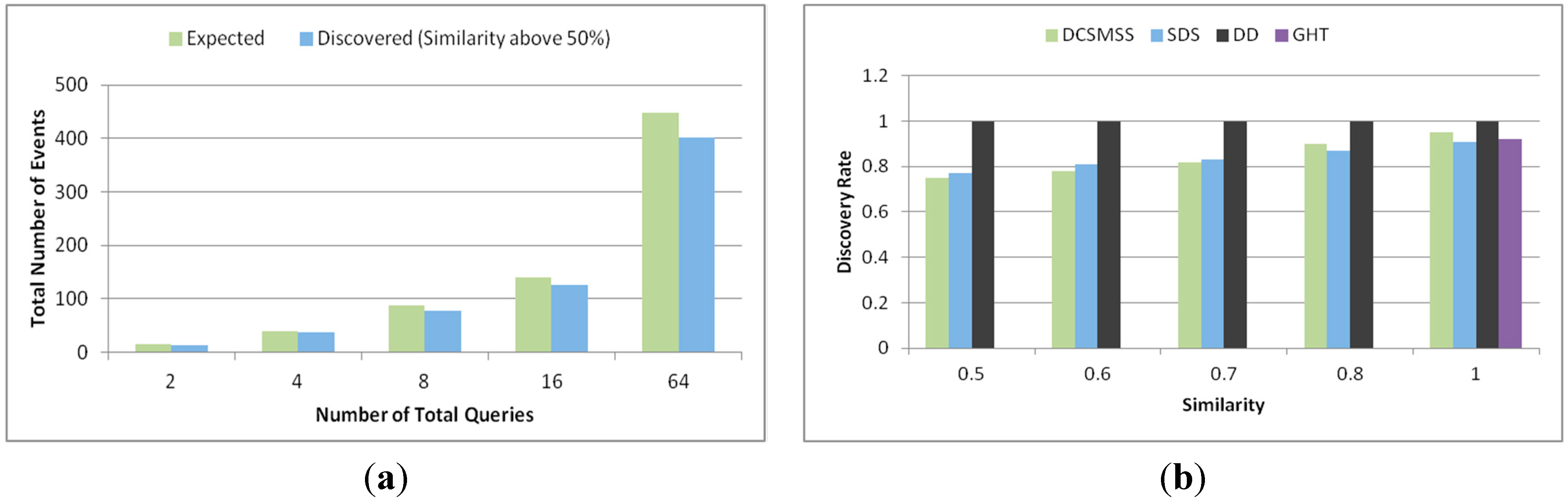
5.2.5. Scalability
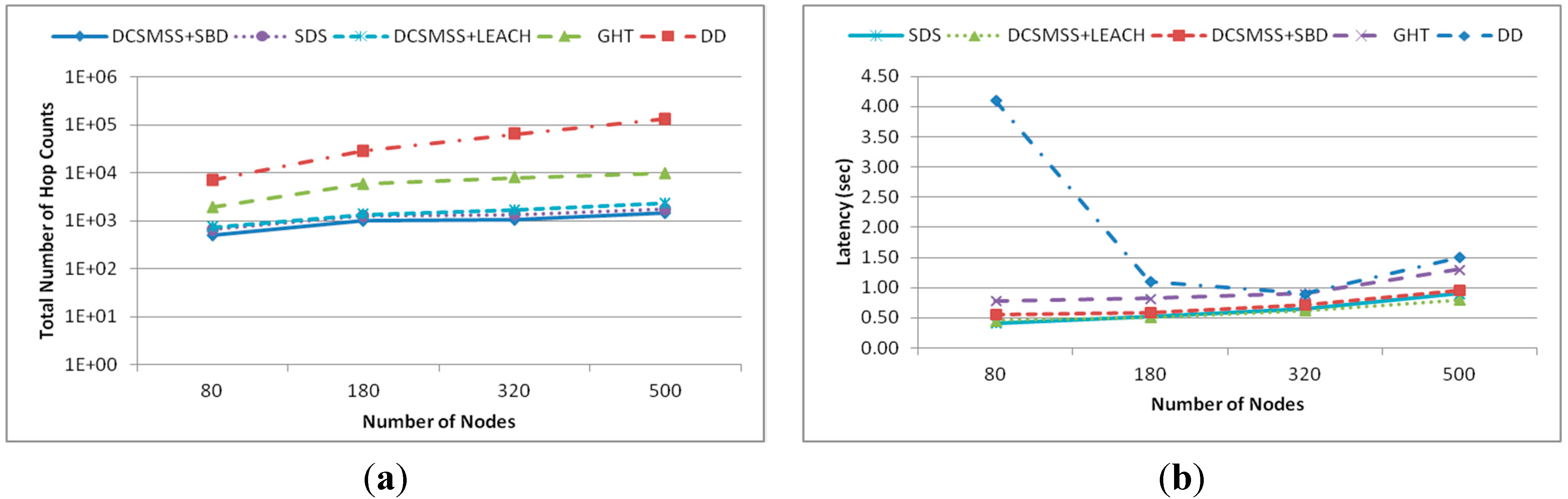
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ahmed, K.; Gregory, M.A. Techniques and Challenges of Data Centric Storage Scheme in Wireless Sensor Network. J. Sens. Actuator Netw. 2012, 1, 59–85. [Google Scholar] [CrossRef]
- Ahmed, K.; Gregory, M.A. Wireless Sensor Network Data Centric Storage Routing using Castalia. In Proceedings of the Australasian Telecommunication Networks and Applications Conference, Brisbane, Australia, 7–9 November 2012; pp. 1–8.
- Jagadish, H.V.; Ooi, B.C.; Tan, K.L.; Yu, C.; Zhang, R. iDistance: An adaptive B+-tree based indexing method for nearest neighbor search. ACM Trans. Database Syst. 2005, 30, 364–397. [Google Scholar] [CrossRef]
- Ahmed, K.; Gregory, M.A. Optimized TDMA based distance routing for Data Centric Storage. In Proceedings of the 2012 IEEE 3rd International Conference on Networked Embedded Systems for Every Application (NESEA), Liverpool, UK, 13–14 December 2012; pp. 1–7.
- Rumín, Á.C.; Pascual, M.U.; Ortega, R.R.; López, D.L. Data Centric Storage Technologies: Analysis and Enhancement. Sensors 2010, 10, 3023–3056. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.C.; Su, I.F.; Lee, C. An efficient mechanism for processing similarity search queries in sensor networks. Inf. Sci. 2011, 181, 284–307. [Google Scholar] [CrossRef]
- Shen, H.; Zhao, L.; Li, Z. A Distributed Spatial-Temporal Similarity Data Storage Scheme in Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2011, 10, 982–996. [Google Scholar] [CrossRef]
- Shen, H.; Li, T.; Schweiger, T. An Efficient Similarity Searching Scheme Based on Locality Sensitive Hashing. In Proceedings of the 3rd International Conference on Digital Telecommunications (ICDT), Bucharest, Romania, 29 June–5 July 2008.
- Liao, W.H.; Chen, C.C. Data storage and range query mechanism for multi-dimensional attributes in wireless sensor networks. IET Commun. 2010, 4, 1799–1808. [Google Scholar] [CrossRef]
- Greenstein, B.; Estrin, D.; Govindan, R.; Ratnasamy, S.; Shenker, S. DIFS: A distributed index for features in sensor networks. In Proceedings of the 2003 IEEE International Workshop on Sensor Network Protocols and Applications, Anchorage, AK, USA, 11 May 2003; pp. 163–173.
- Li, X.; Kim, Y.J.; Govindan, R.; Hong, W. Multi-dimensional range queries in sensor networks. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003; pp. 63–75.
- Ye, F.; Zhong, G.; Lu, S.; Zhang, L. Gradient broadcast: A robust data delivery protocol for large scale sensor networks. Wirel. Netw. 2005, 11, 285–298. [Google Scholar] [CrossRef]
- Bahillo, A.; Mazuelas, S.; Lorenzo, R.; Fernández, P.; Prieto, J.; Durán, R.; Abril, E. Hybrid RSS-RTT localization scheme for indoor wireless networks. EURASIP J. Adv. Signal Process. 2010, 2010, 17. [Google Scholar] [CrossRef]
- Hashemi, H. The indoor radio propagation channel. IEEE Proc. 1993, 81, 943–968. [Google Scholar] [CrossRef]
- Adler, S.; Pfeiffer, S.; Will, H.; Hillebrandt, T.; Schiller, J. Measuring the distance between wireless sensor nodes with standard hardware. In Proceedings of the 2012 9th Workshop on Positioning Navigation and Communication (WPNC), Dresden, Germany, 15–16 March 2012; pp. 114–119.
- Wei, Y.; Heidemann, J.; Estrin, D. An energy-efficient MAC protocol for wireless sensor networks. In Proceedings of the Twenty-First Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, 23–27 June 2002; pp. 1567–1576.
- Instruments, T. (2012, July) CC2530 Second Generation System-on-Chip Solution for 2.4 GHz IEEE 802.15.4/RF4CE/ZigBee. Available online: http://www.ti.com/product/cc2530 (accessed on 10 December 2014).
- Handy, M.J.; Haase, M.; Timmermann, D. Low energy adaptive clustering hierarchy with deterministic cluster-head selection. In Proceedings of 4th International Workshop on Mobile and Wireless Communications Network, Stockholm, Sweden, 9–11 September 2002; pp. 368–372.
- Karp, B.; Kung, H.T. GPSR: Greedy perimeter stateless routing for wireless networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 243–254.
- Intanagonwiwat, C.; Govindan, R.; Estrin, D. Directed diffusion: A scalable and robust communication paradigm for sensor networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 56–67.
- Ratnasamy, S.; Karp, B.; Yin, L.; Yu, F.; Estrin, D.; Govindan, R.; Shenker, S. GHT: A geographic hash table for data-centric storage. In Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications, Atlanta, GA, USA, 28 September 2002.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, K.; Gregory, M.A. Distributed Efficient Similarity Search Mechanism in Wireless Sensor Networks. Sensors 2015, 15, 5474-5503. https://doi.org/10.3390/s150305474
Ahmed K, Gregory MA. Distributed Efficient Similarity Search Mechanism in Wireless Sensor Networks. Sensors. 2015; 15(3):5474-5503. https://doi.org/10.3390/s150305474
Chicago/Turabian StyleAhmed, Khandakar, and Mark A. Gregory. 2015. "Distributed Efficient Similarity Search Mechanism in Wireless Sensor Networks" Sensors 15, no. 3: 5474-5503. https://doi.org/10.3390/s150305474
APA StyleAhmed, K., & Gregory, M. A. (2015). Distributed Efficient Similarity Search Mechanism in Wireless Sensor Networks. Sensors, 15(3), 5474-5503. https://doi.org/10.3390/s150305474