An Analog Circuit Approximation of the Discrete Wavelet Transform for Ultra Low Power Signal Processing in Wearable Sensor Nodes
Abstract
:1. Introduction

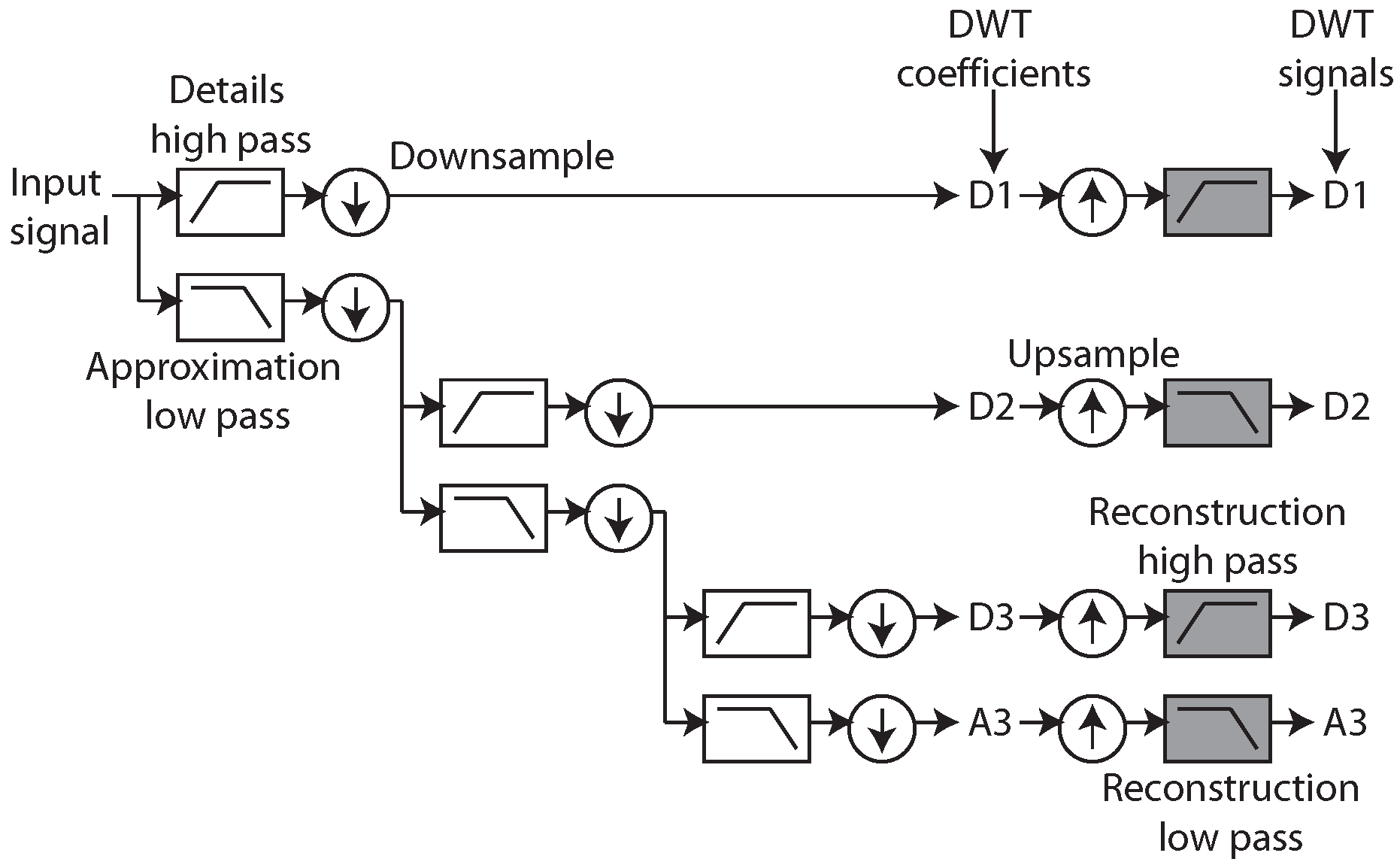
2. The Analog Discrete Wavelet Transform
2.1. Overview
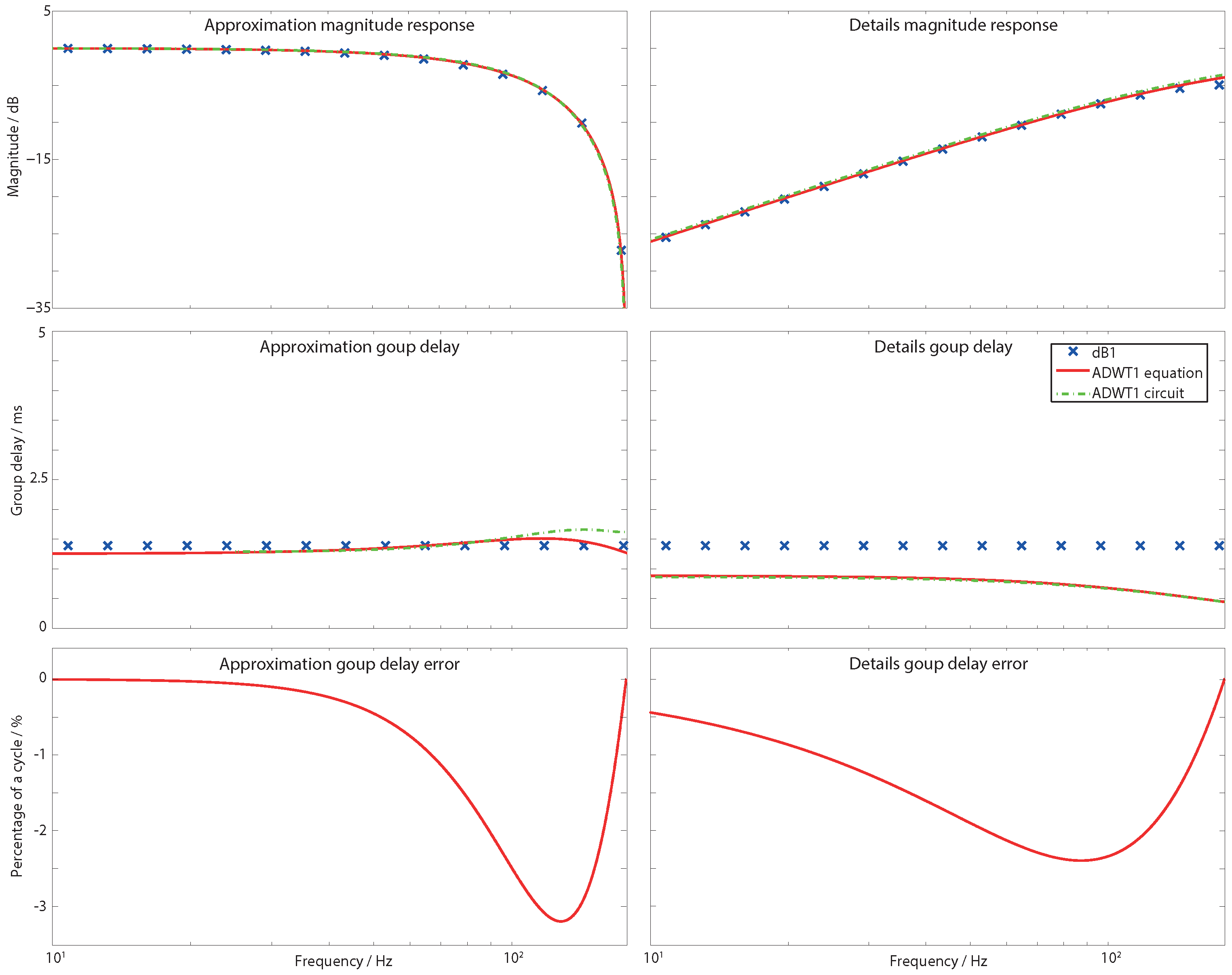
2.2. ADWT Estimation: Magnitude Response
| Mother Wavelet | Filter | Coefficients |
|---|---|---|
| dB1 | A1 | |
| D1 | ||
| dB4 | A4 | |
| D4 |
| Filter | s Domain Transfer Function |
|---|---|
| A1 | |
| D1 | |
| A4 | |
| D4 |
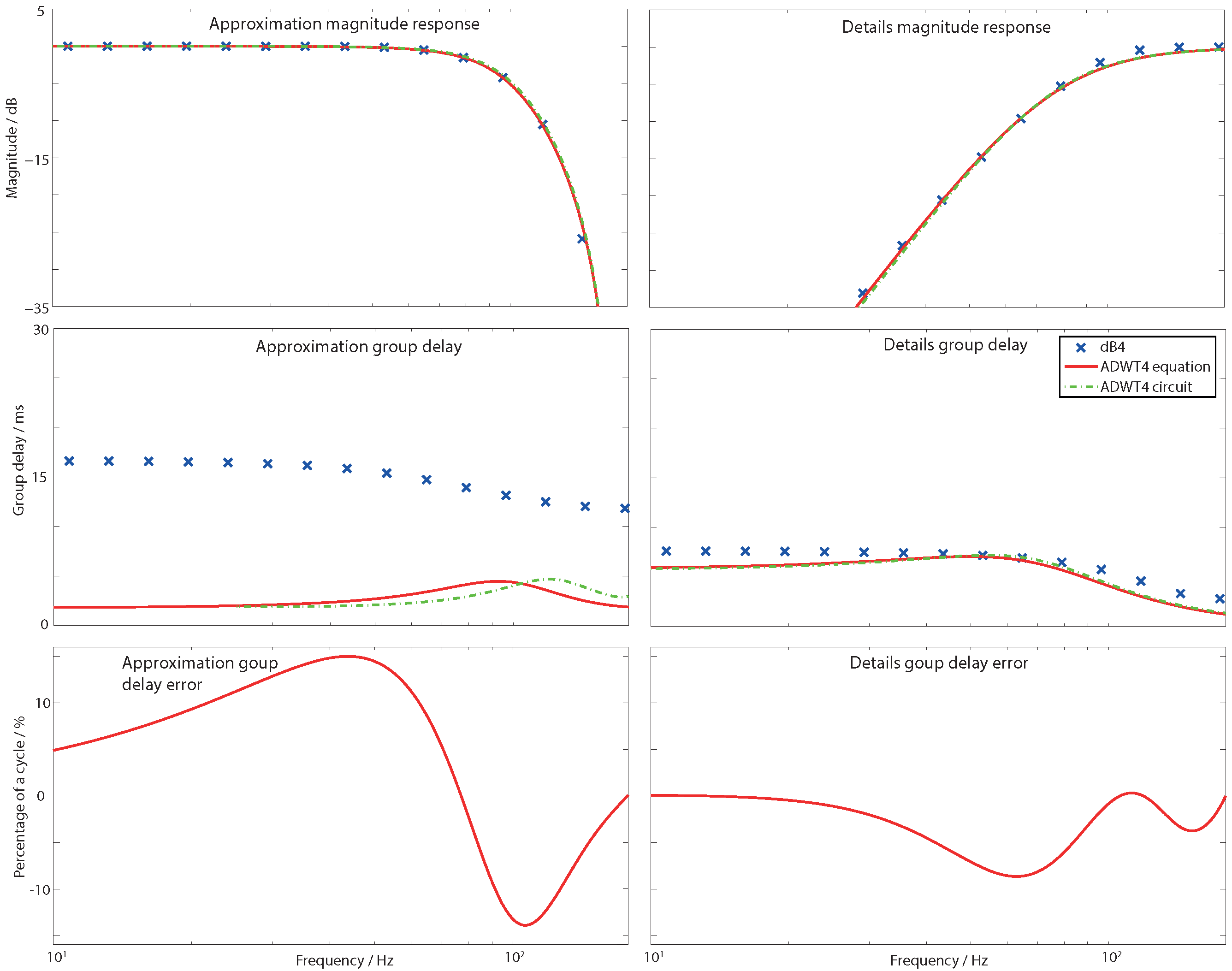
2.3. ADWT Estimation: Group Delay Response
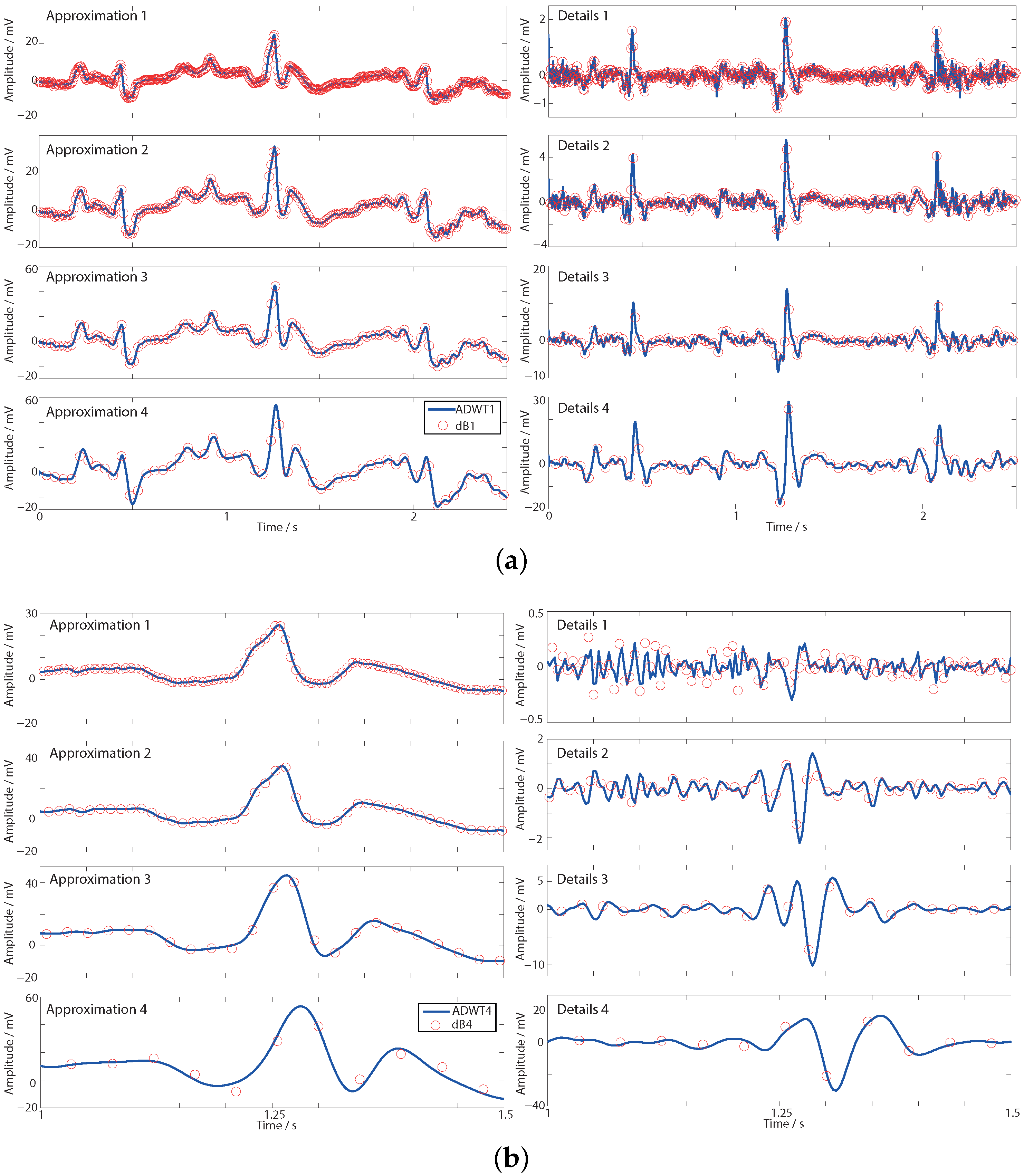
2.4. Reconstruction
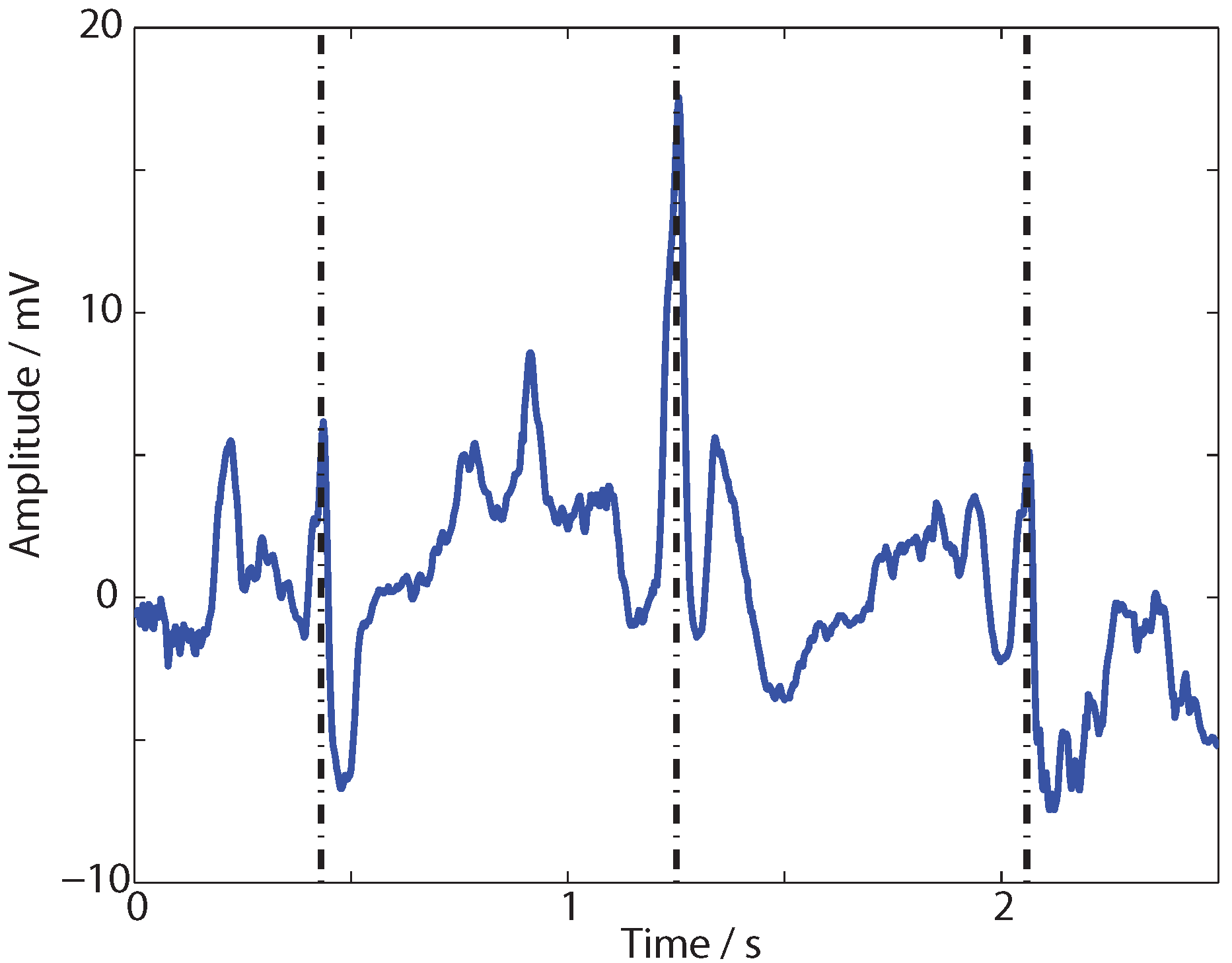
3. Application Performance
- Details, level 2: 12.5–25 Hz.
- Details, level 3: 6.25–12.5 Hz.
- Details, level 4: 3.125–6.25 Hz.
- Approximations, level 4: 0–3.125 Hz.
| Training Features; | Wake | Sleep | ||
|---|---|---|---|---|
| Test Features | Sensitivity / % | Selectivity / % | Sensitivity / % | Selectivity / % |
| dB1 | ||||
| DWT; DWT | 95.8 | 98.5 | 97.2 | 92.4 |
| DWT; ADWT | 95.2 | 98.7 | 97.6 | 91.5 |
| dB4 | ||||
| DWT ; DWT | 98.1 | 94.7 | 89.0 | 96.0 |
| DWT ; ADWT | 98.0 | 94.2 | 87.7 | 96.0 |
4. Fully Custom Circuit Implementation
4.1. Design
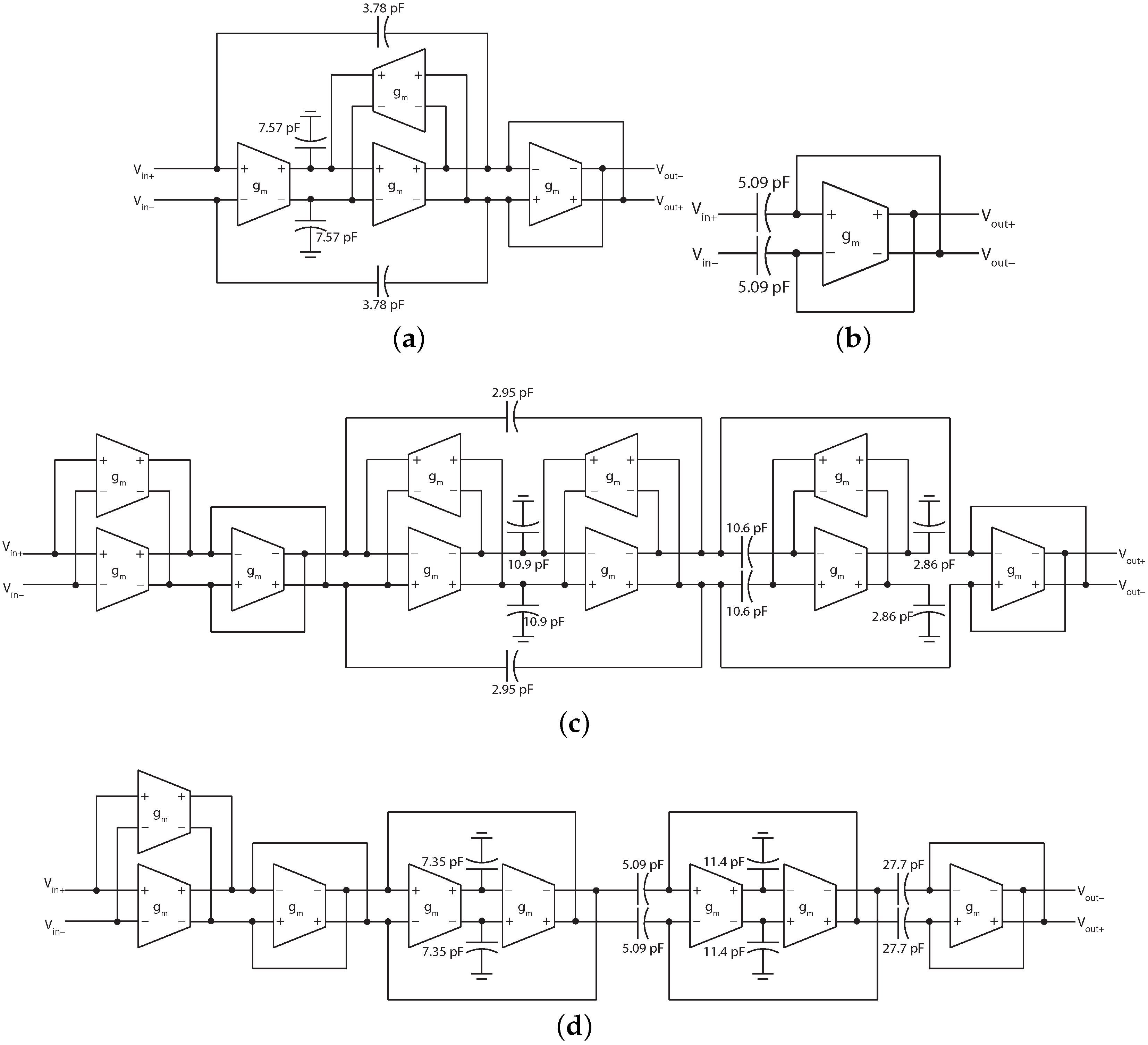

| Transistor | W/L/μm |
|---|---|
| M1, M2 | 12/1 |
| M3, M4 | 4/1 |
| M5, M6 | 25/5 |
| M7–M10, M19–M22 | 30/5 |
| M11, M12 | 14/20 |
| M13, M14 | 7.1/20 |
| M15, M16, M23, M24 | 2.9/20 |
| M17, M18 | 16/5 |
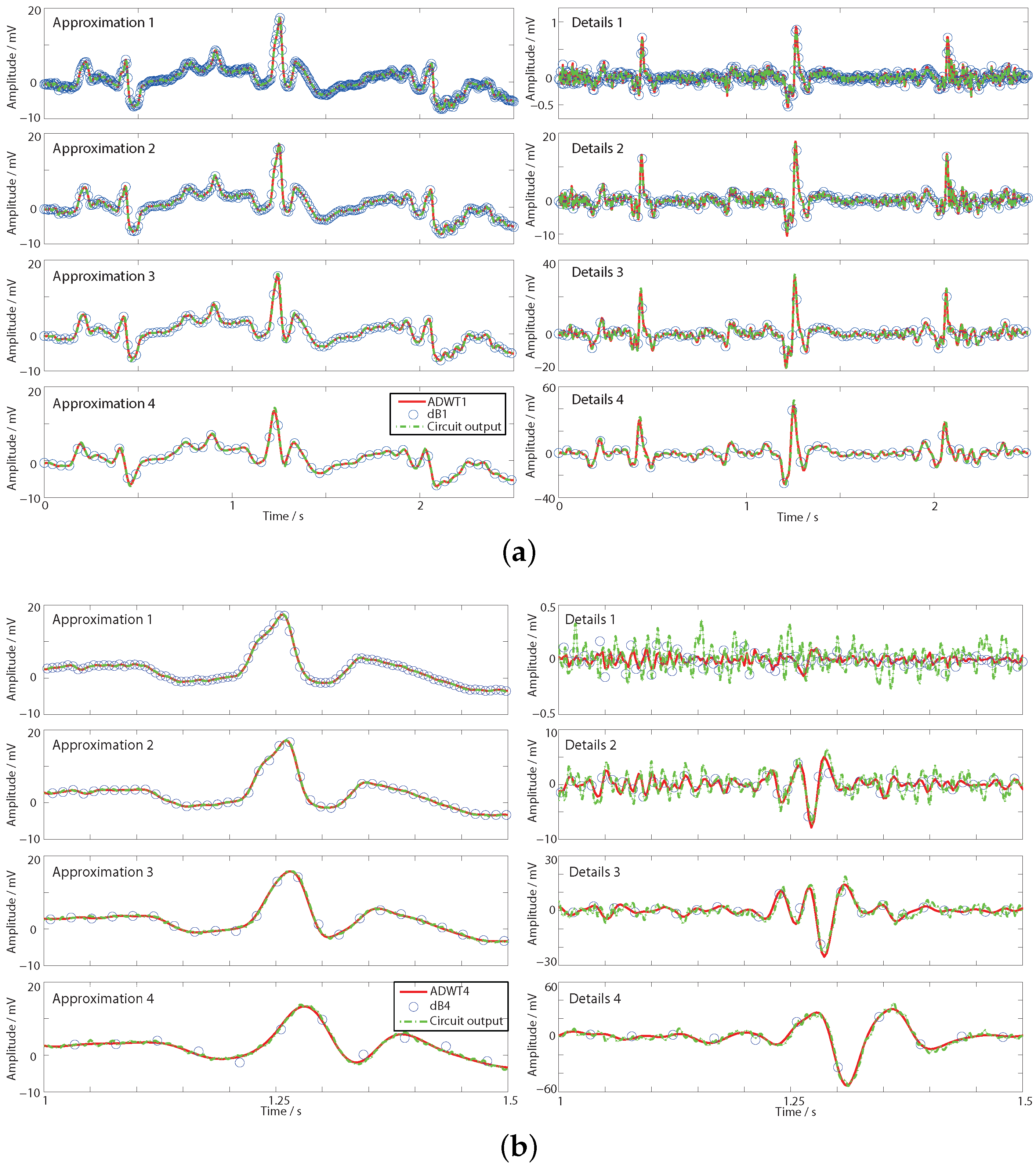
4.2. Simulation Results
| Parameter | A1 | D1 | A4 | D4 |
|---|---|---|---|---|
| CMOS process | 0.18 μm, triple well, 6 metal layers, single poly, MIM capacitors available | |||
| Supply voltage | 1.3 V | |||
| Bias current | 512 pA | |||
| Area | 0.12 mm | 0.42 mm | ||
| Power consumption | 16.7 nW | 7.2 nW | 35.8 nW | 29.4 nW |
| Signal input range | 100 mV | 100 mV | 100 mV | 100 mV |
| THD (100 mVpp, 10 or 180 Hz input) | –55.7 dB | –56.5 dB | –52.5 dB | –44.5 dB |
| Input referred noise (0.16m–3 dB point–1k Hz) | 100 μV | 70 μV | 93 μV | 219 μV |
| Dynamic range | 51 dB | 54 dB | 52 dB | 44 dB |
| Tuning range | 2–720 Hz | 2–720 Hz | 2–720 Hz | 2–720 Hz |
| Ref. | Year | Mother Wavelet | Levels | Channels | Process/μm | Analysis Frequency/Hz | V | Input Range | Power/W | Area/mm |
|---|---|---|---|---|---|---|---|---|---|---|
| [26] | 2007 | sym4 | 4 | 32 | 0.18 | 12.5 k | 1.3 | 10 bit | 76 μ | 0.22 |
| [27] | 2007 | sym4 | 4 | 32 | 0.13 | 12.5 k | – | 10 bit | 50 μ | 0.69 |
| [28] | 2007 | dB4 | 3 | 1 | 0.18 | 12.5 M | 1.8 | 16 bit | 26 m | 0.55 |
| [17] | 2010 | dB6 | 7 | 1 | 0.35 | 69.4 M | 3.3 | 8 bit | 154 m | 0.06 |
| [29] | 2011 | dB3 | 2 | 20 | 0.07 | 5 k | 0.6 | 8 bit | 10 μ | 0.21 |
| [30] | 2011 | Custom | 8 | – | 0.18 | 500 | 1 | 9 bit | 29 μ | 3 |
| [31] | 2012 | Quadratic spline | 3 | 1 | 0.35 | 150 | 1.8 | 10 bit | 830 n | 1.11 |
| [32] | 2014 | sym4 e | 4 | 32 | 0.13 | 13k | 1.2 | 10 bit | 800 μ | 1.21 |
| [33] | 2014 | Custom | 4 | – | 0.18 | 125 | 0.5 | 9 bit | 435 n | – |
| [34] | 2015 | dB4 | 3 | 1 | 0.18 | 180 | 0.5 | 16 bit | 26 μ | 0.53 |
| This work | 2015 | ADWT1 (dB1) | 4 | 1 | 0.18 | 180 | 1.3 | 51 dB | 37 n | 0.48 |
| This work | 2015 | ADWT4 (dB4) | 4 | 1 | 0.18 | 180 | 1.3 | 44 dB | 114 n | 1.68 |
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bachmann, C.; Ashouei, M.; Pop, V.; Vidojkovic, M.; Groot, H.; Gyselinckx, B. Low-power wireless sensor nodes for ubiquitous long-term biomedical signal monitoring. IEEE Commun. Mag. 2012, 50, 20–27. [Google Scholar] [CrossRef]
- Frantz, G.; Henkel, J.; Rabaey, J.; Schneider, T.; Wolf, M.; Batur, U. Ultra-Low Power Signal Processing [DSP Forum]. IEEE Signal Processing Mag. 2010, 27, 149–154. [Google Scholar] [CrossRef]
- Miyashita, D.; Yamaki, R.; Hashiyoshi, K.; Kobayashi, H.; Kousai, S.; Oowaki, Y.; Unekawa, Y. An LDPC Decoder with Time-Domain Analog and Digital Mixed-Signal Processing. IEEE J. Solid State Circuits 2014, 49, 73–83. [Google Scholar] [CrossRef]
- Sarpeshkar, R. Analog Versus Digital: Extrapolating from Electronics to Neurobiology. Neural Comput. 1998, 10, 1601–1638. [Google Scholar] [CrossRef] [PubMed]
- Haddad, S.A.P.; Serdijn, W.A. Ultra Low-Power Biomedical Signal Processing: An Analog Wavelet Filter Approach for Pacemakers; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Sarpeshkar, R. Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-Inspired Systems; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Calhoun, B.H.; Brooks, D. Can Subthreshold and Near-Threshold Circuits Go Mainstream? IEEE Micro 2010, 30, 80–85. [Google Scholar] [CrossRef]
- Tarassenko, L. Interview with Lionel Tarassenko. Electron. Lett. 2011, 47. [Google Scholar] [CrossRef]
- Sarpeshkar, R. Universal Principles for Ultra Low Power and Energy Efficient Design. IEEE Trans. Circuits Syst. II 2012, 59, 193–198. [Google Scholar] [CrossRef]
- Schlottmann, C.R.; Shapero, S.; Nease, S.; Hasler, P. A Digitally Enhanced Dynamically Reconfigurable Analog Platform for Low-Power Signal Processing. IEEE J. Solid State Circuits 2012, 47, 2174–2184. [Google Scholar] [CrossRef]
- Xu, J.; Busze, B.; van Hoof, C.; Makinwa, K.A.A.; Yazicioglu, R.F. A 15-Channel Digital Active Electrode System for Multi-Parameter Biopotential Measurement. IEEE J. Solid State Circuits 2015, 50, 2090–2100. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way, 3rd ed.; Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Addison, P.S.; Walker, J.; Guido, R.C. Time–frequency analysis of biosignals. IEEE Eng. Med. Biol. Mag. 2009, 28, 14–29. [Google Scholar] [CrossRef] [PubMed]
- Haddad, S.A.P.; Bagga, S.; Serdijn, W.A. Log-domain wavelet bases. IEEE Trans. Circuits Syst. I 2005, 52, 2023–2032. [Google Scholar] [CrossRef]
- Karel, J.M.H.; Haddad, S.A.P.; Hiseni, S.; Westra, R.L.; Serdijn, W.A.; Peeters, R.L.M. Implementing Wavelets in Continuous-Time Analog Circuits with Dynamic Range Optimization. IEEE Trans. Circuits Syst. I 2012, 59, 229–242. [Google Scholar] [CrossRef]
- Li, H.; He, Y.; Yichuang, S. Detection of Cardiac Signal Characteristic Point Using Log-Domain Wavelet Transform Circuits. Circuits Syst. Sig. Proc. 2008, 27, 683–698. [Google Scholar]
- Zhao, W.; Sun, Y.; He, Y. Minimum component high frequency Gm-C wavelet filters based on Maclaurin series and multiple loop feedback. Electron. Lett. 2010, 46, 34–36. [Google Scholar] [CrossRef]
- Gurrola-Navarro, M.A.; Espinosa-Flores-Verdad, G. Analogue wavelet transform with single biquad stage per scale. Electron. Lett. 2010, 46, 616–618. [Google Scholar] [CrossRef]
- Casson, A.J.; Rodriguez-Villegas, E. A 60 pW gm C Continuous Wavelet Transform Circuit for Portable EEG Systems. IEEE J. Solid State Circuits 2011, 46, 1406–1415. [Google Scholar] [CrossRef]
- Casson, A.J.; Rodriguez-Villegas, E. Nanowatt multi-scale continuous wavelet transform chip. Electron. Lett. 2014, 50, 153–154. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A. A review of wavelets in biomedical applications. IEEE Proc. 1996, 84, 626–638. [Google Scholar] [CrossRef]
- Addison, P.S. The little wave with the big future. Phys. World 2004, 13, 35–39. [Google Scholar] [CrossRef]
- Logesparan, L.; Casson, A.J.; Rodriguez-Villegas, E. Optimal features for online seizure detection. Med. Biol. Eng. Comput. 2012, 50, 659–669. [Google Scholar] [CrossRef] [PubMed]
- Gajic, D.; Djurovic, Z.; Gligorijevic, J.; di Gennaro, S.; Savic-Gajic, I. Detection of epileptiform activity in EEG signals based on time-frequency and non-linear analysis. Front. Comput. Neurosci. 2015, 19. [Google Scholar] [CrossRef] [PubMed]
- Faust, O.; Acharya, U.R.; Adeli, H.; Adelig, A. Wavelet-based EEG processing for computer-aided seizure detection and epilepsy diagnosis. Seizure 2015, 26, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Kamboh, A.M.; Raetz, M.; Oweiss, K.G.; Mason, A. Area-Power Efficient VLSI Implementation of Multichannel DWT for Data Compression in Implantable Neuroprosthetics. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 128–135. [Google Scholar] [CrossRef] [PubMed]
- Oweiss, K.G.; Mason, A.; Suhail, Y.; Kamboh, A.M.; Thomson, K.E. A Scalable Wavelet Transform VLSI Architecture for Real-Time Signal Processing in High-Density Intra-Cortical Implants. IEEE Trans. Circuits Syst. I 2007, 54, 1266–1278. [Google Scholar] [CrossRef]
- Wang, C.; Gan, W.S. Efficient VLSI Architecture for Lifting-Based Discrete Wavelet Packet Transform. IEEE Trans. Circuits Syst. II 2007, 54, 422–426. [Google Scholar] [CrossRef]
- Narasimhan, S.; Chiel, H.J.; Bhunia, S. Ultra-Low-Power and Robust Digital-Signal-Processing Hardware for Implantable Neural Interface Microsystems. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 169–178. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zheng, Y.; Phyu, M.W.; Zhao, B.; Je, M.; Yuan, X. Multiple Functional ECG Signal is Processing for Wearable Applications of Long-Term Cardiac Monitoring. IEEE Trans. Biomed. Eng. 2011, 58, 380–389. [Google Scholar] [PubMed]
- Ieong, C.I.; Mak, P.I.; Lam, C.P.; Dong, C.; Vai, M.I.; Mak, P.U.; Pun, S.H.; Wan, F.; Martins, R.P. A 0.83-μW QRS Detection Processor Using Quadratic Spline Wavelet Transform for Wireless ECG Acquisition in 0.35-μm CMOS. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Kamboh, A.M.; Mason, A.J. A configurable realtime DWT-based neural data compression and communication VLSI system for wireless implants. J. Neurosci. Methods 2014, 227, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhou, J.; Yang, Y.; Wang, B.; Lan, J.; Wang, C.; Luo, J.; Goh, W.L.; Kim, T.T.H.; Je, M. A 457 nW Near-Threshold Cognitive Multi-Functional ECG Processor for Long-Term Cardiac Monitoring. IEEE J. Solid State Circuits 2014, 49, 2422–2434. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, J.; Liao, L.; Lan, J.; Luo, J.; Liu, X.; Je, M. Near-Threshold Energy- and Area-Efficient Reconfigurable DWPT/DWT Processor for Healthcare-Monitoring Applications. IEEE Trans. Circuits Syst. II 2015, 62, 70–74. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, D.J.; Workman, M.L. Digital Control of Dynamic Systems, 3rd ed.; Addison-Wesley: Boston, UK, 1997. [Google Scholar]
- Herley, C.; Vetterli, M. Wavelets and recursive filter banks. IEEE Trans. Signal Process. 1993, 41, 2536–2556. [Google Scholar] [CrossRef]
- Moody, G.B.; Muldrow, W.; Mark, R.G. A noise stress test for arrhythmia detectors. Comput. Cardiol. 1984, 11, 381–384. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Casson, A.J.; Rodriguez-Villegas, E. An Inverse Filter Realisation of a Single Scale Inverse Continuous Wavelet Transform. In Proceedings of the IEEE International Symposium on Circuits and Systems, 2008. ISCAS 2008, Seattle, WA, USA, 18–21 May 2008; pp. 904–907.
- Kemp, B.; Zwinderman, A.H.; Tuk, B.; Kamphuisen, H.A.C.; Oberye, J.J.L. Analysis of a sleep-dependent neuronal feedback loop: The slow-wave microcontinuity of the EEG. IEEE Trans. Biomed. Eng. 2000, 47, 1185–1194. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Krystal, A.D.; Edinger, J.D.; Wohlgemuth, W.K.; Marsh, G.R. NREM Sleep EEG Frequency Spectral Correlates of Sleep Complaints in Primary Insomnia Subtypes. Sleep 2002, 25, 626–636. [Google Scholar]
- Whitham, E.M.; Pope, K.J.; Fitzgibbon, S.P.; Lewis, T.; Clark, C.R.; Loveless, S.; Broberg, M.; Wallace, A.; DeLosAngeles, D.; Lillie, P.; et al. Scalp electrical recording during paralysis: Quantitative evidence that EEG frequencies above 20 Hz are contaminated by EMG. Clin. Neurophysiol. 2007, 118, 1877–1888. [Google Scholar] [CrossRef] [PubMed]
- Casson, A.J.; Luna, E.; Rodriguez-Villegas, E. Performance metrics for the accurate characterisation of interictal spike detection algorithms. J. Neurosci. Methods 2009, 177, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Veeravalli, A.; Sanchez-Sinencio, E.; Silva-Martinez, J. Transconductance amplifier structures with very small transconductances: A comparative design approach. IEEE J. Solid State Circuits 2002, 37, 770–775. [Google Scholar] [CrossRef]
- Stefanovic, D.; Kayal, M. Structured Analog CMOS Design; Springer: Berlin, Germany, 2008. [Google Scholar]
- Chen, G.; Rodriguez-Villegas, E.; Casson, A.J. Wearable Algorithms: An Overview of a Truly Multi-Disciplinary Problem. In Wearable Sensors; Sazonov, E., Neuman, M.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 353–382. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casson, A.J. An Analog Circuit Approximation of the Discrete Wavelet Transform for Ultra Low Power Signal Processing in Wearable Sensor Nodes. Sensors 2015, 15, 31914-31929. https://doi.org/10.3390/s151229897
Casson AJ. An Analog Circuit Approximation of the Discrete Wavelet Transform for Ultra Low Power Signal Processing in Wearable Sensor Nodes. Sensors. 2015; 15(12):31914-31929. https://doi.org/10.3390/s151229897
Chicago/Turabian StyleCasson, Alexander J. 2015. "An Analog Circuit Approximation of the Discrete Wavelet Transform for Ultra Low Power Signal Processing in Wearable Sensor Nodes" Sensors 15, no. 12: 31914-31929. https://doi.org/10.3390/s151229897
APA StyleCasson, A. J. (2015). An Analog Circuit Approximation of the Discrete Wavelet Transform for Ultra Low Power Signal Processing in Wearable Sensor Nodes. Sensors, 15(12), 31914-31929. https://doi.org/10.3390/s151229897






