Multiple-Parameter Estimation Method Based on Spatio-Temporal 2-D Processing for Bistatic MIMO Radar
Abstract
:1. Introduction
2. Data Model
3. Multiple-Parameter Estimation Spatio-Temporal 2-D Processing Method
3.1. Estimation of Transmitting-Receiving Azimuth
3.2. Estimation of the Doppler Frequency
4. Computer Simulation Analysis
4.1. Simulation 1: The Restrained Ability for Spatial Gaussian Colored Noise in the Proposed Method
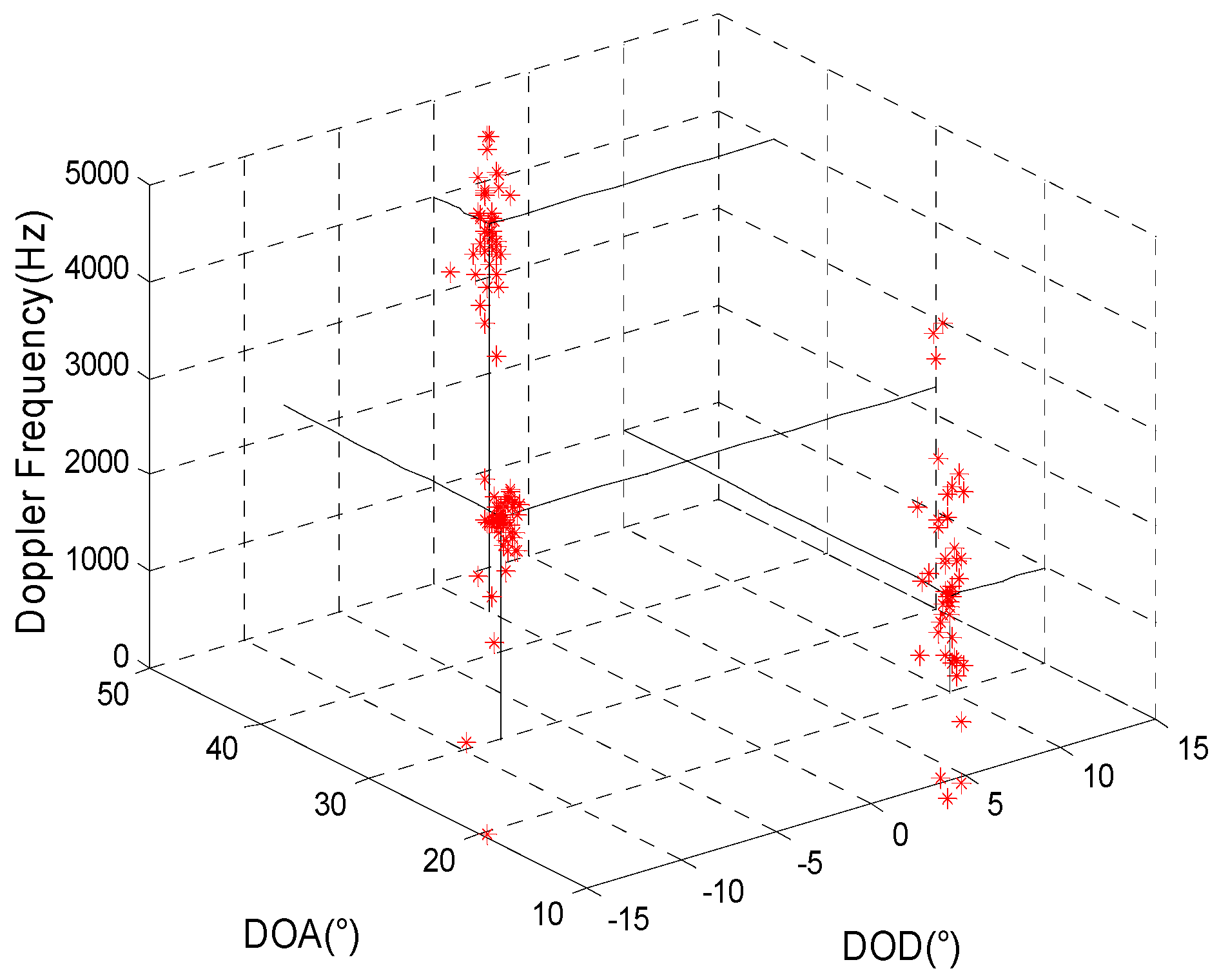
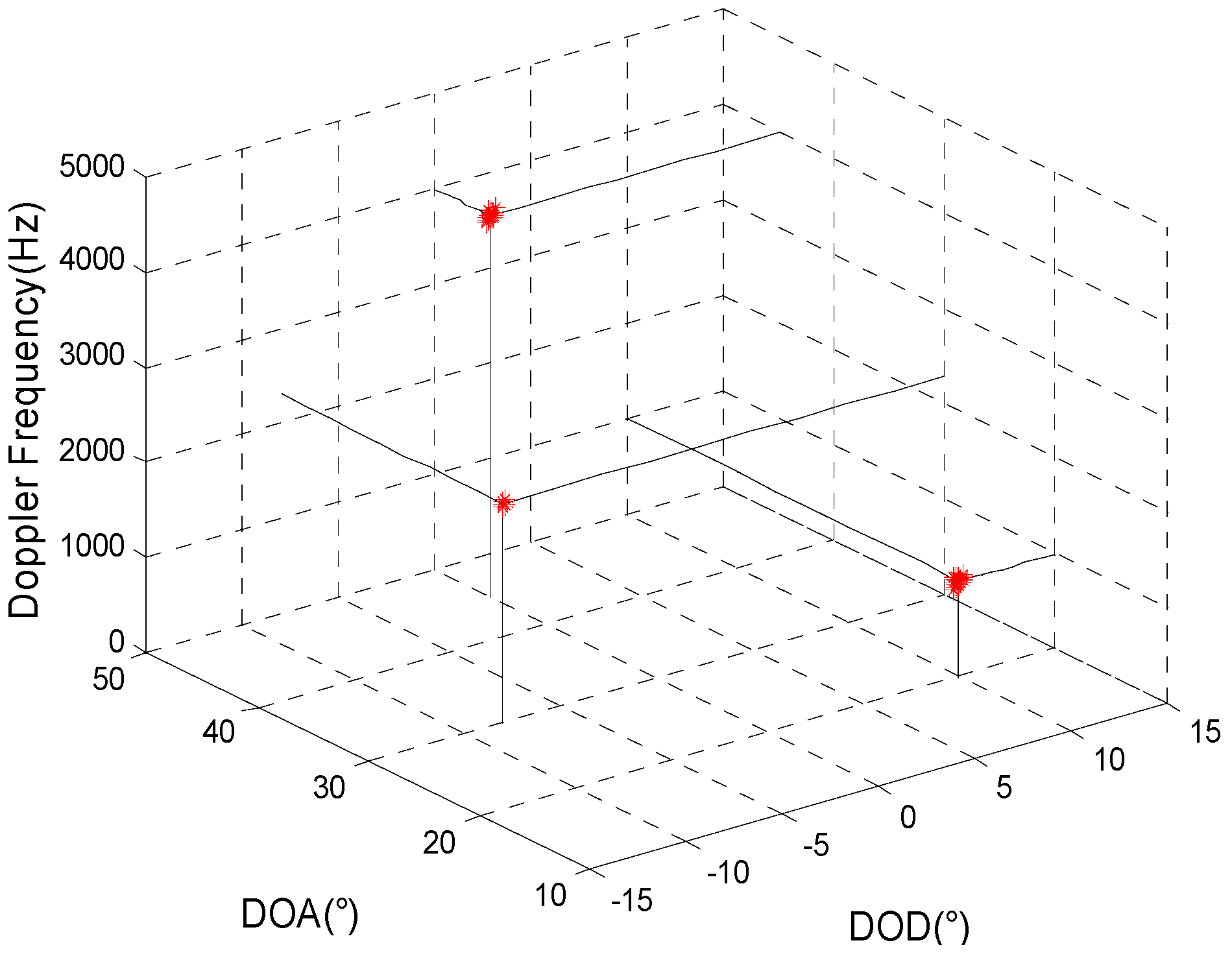
4.2. Simulation 2: When the Transmitting and Receiving Arrays are All Non-Uniform Linear Arrays, the Joint Estimation Results for the Target Parameters Using the Method Proposed here and the Algorithm Proposed in Reference [8]

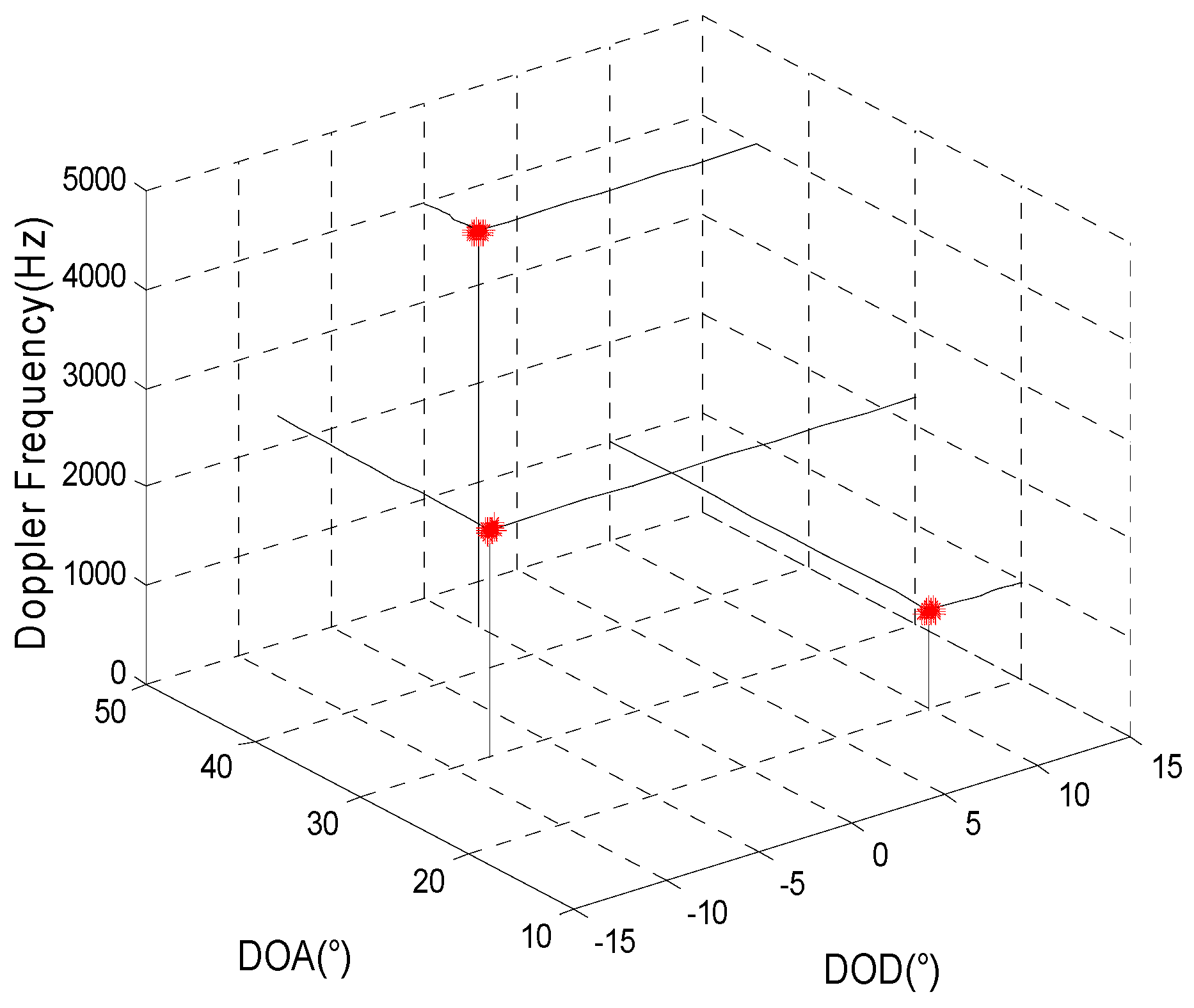
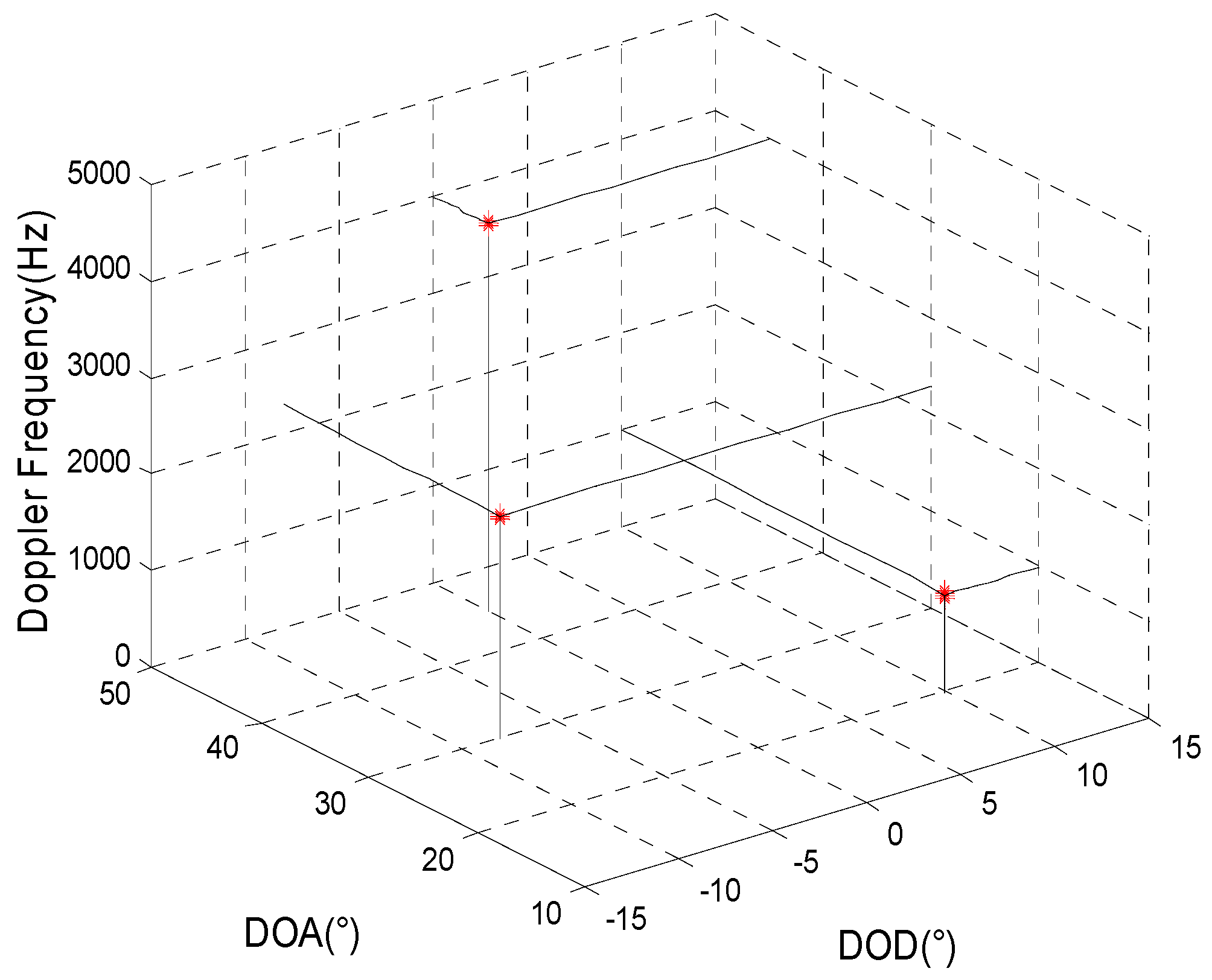

4.3. Simulation 3: The Comparison Curve of the Statistical Performance of the Algorithm


5. Conclusions
- (1)
- The prior estimate of the target number and the EVD of the data covariance matrix are not needed, thereby reducing the complexity and number of calculations.
- (2)
- The estimated parameters can be automatically paired, and array aperture losses can be avoided.
- (3)
- Compared with the algorithm in reference [13], the method proposed here does not include special demands on the structure of the transmitting and receiving arrays. The method is applied under a condition in which the transmitting and receiving arrays have an arbitrary geometrical configuration, and the method can greatly improve the parameter estimation performance. The algorithm in reference [13] can be used in transmitting and receiving arrays that do not satisfy conditions for translation invariant structure, but the distance between the two arbitrary elements of the transmitting and receiving arrays must not be more than 0.5 times the wavelength. Thus, the scope of the application of this method is limited to some degree.
- (4)
- In the method proposed here, the outputs of the matched filters for different moments are cross-correlated to eliminate the spatial colored noise. Thus, this method is suitable for a wider background of colored noise.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the IEEE National Radar Conference, Philadelphia, PA, USA, 26–29 April 2004; pp. 71–78.
- Farina, A.; Lesturgie, M. Special issue on bistatic and MIMO radar and their applications in surveillance and remote sensing. IET Radar Sonar Navig. 2014, 8, 73–74. [Google Scholar] [CrossRef]
- Li, H.; Wei, Q.; Jiang, J.; Tian, H.-L. Angle estimation and self-calibration for bistatic MIMO radar with mutual coupling of transmitting and receiving arrays. In Proceedings of the IEEE Workshop on Electronics, Computer and Applications, Ottawa, ON, Canada, 8–9 May 2014; pp. 354–357.
- Li, L. Joint parameter estimation and target localization for bistatic MIMO radar system on impulsive noise. Signal Image Video Process. 2015, 9, 1775–1783. [Google Scholar] [CrossRef]
- Guo, Y.D.; Zhang, Y.S.; Tong, N.N. Beamspace ESPRIT algorithm for bistatic MIMO radar. Electron. Lett. 2011, 47, 876–878. [Google Scholar] [CrossRef]
- Zhang, X.F.; Xu, D.Z. Angle Estimation in Bistatic MIMO Radar Using Improved Reduced Dimension Capon Algorithm. J. Syst. Eng. Electron. 2013, 24, 84–89. [Google Scholar] [CrossRef]
- Li, J.F.; Zhang, X.F.; Gao, X. A joint scheme for angle and array gain-phase error estimation in bistaitc MIMO radar. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1478–1482. [Google Scholar] [CrossRef]
- Yunhe, C. Joint estimation of angle and Doppler frequency for bistatic MIMO radar. Electron. Lett. 2010, 46, 170–172. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Z.; Li, X. An Algorithm for DOD-DOA and Doppler Frequency Jointly Estimating of Bistatic MIMO Radar. J. Electron. Inf. Technol. 2010, 32, 1843–1848. [Google Scholar] [CrossRef]
- Lu, H.; Feng, D.; He, J. A Novel Method for Target Location and Doppler Frequency Estimation in Bistatic MIMO Radar. J. Electron. Inf. Technol. 2010, 32, 2167–2171. [Google Scholar] [CrossRef]
- Zhang, Y.; Niu, X.; Zhao, G. Joint Estimation of Multi-Targets Angles-Doppler Frequency for the MIMO Bistatic Radar. J. Xidian Univ. 2011, 38, 16–21. [Google Scholar]
- Gong, J.; Lv, H.Q.; Guo, Y.D. Multidimensional Parameters Estimation for Bistatic MIMO Radar. In Proceedings of the 7th International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 23–25 September 2011; pp. 1–4.
- Fu, W.; Su, T.; Zhao, Y.; He, X. Joint Estimation of Angle and Doppler Frequency for Bistatic MIMO Radar in Spatial Colored Noise Based on Spatio-Temporal Structure. J. Electron. Inf. Technol. 2011, 33, 1649–1654. (In Chinese) [Google Scholar] [CrossRef]
- Moccia, A.; Renga, A. Bistatic synthetic aperture radar. In Distributed Space Missions for Earth System Monitoring; Springer: New York, NY, USA, 2013; pp. 3–59. [Google Scholar]
- Varotsos, C. Notes on the design and operation of aerospace vehicles. Astrophys. Space Sci. 1987, 134, 205–208. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Li, Y.; Zhang, K.; Tang, W. Multiple-Parameter Estimation Method Based on Spatio-Temporal 2-D Processing for Bistatic MIMO Radar. Sensors 2015, 15, 31442-31452. https://doi.org/10.3390/s151229865
Yang S, Li Y, Zhang K, Tang W. Multiple-Parameter Estimation Method Based on Spatio-Temporal 2-D Processing for Bistatic MIMO Radar. Sensors. 2015; 15(12):31442-31452. https://doi.org/10.3390/s151229865
Chicago/Turabian StyleYang, Shouguo, Yong Li, Kunhui Zhang, and Weiping Tang. 2015. "Multiple-Parameter Estimation Method Based on Spatio-Temporal 2-D Processing for Bistatic MIMO Radar" Sensors 15, no. 12: 31442-31452. https://doi.org/10.3390/s151229865
APA StyleYang, S., Li, Y., Zhang, K., & Tang, W. (2015). Multiple-Parameter Estimation Method Based on Spatio-Temporal 2-D Processing for Bistatic MIMO Radar. Sensors, 15(12), 31442-31452. https://doi.org/10.3390/s151229865





