A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver
Abstract
:1. Introduction
2. RTOD Algorithm and Software
2.1. Dynamical Model of LEO Satellite Orbit
2.2. GPS Measurements
2.3. Pseudo-Ambiguity Parameter
2.4. Properties of Pseudo-Ambiguity
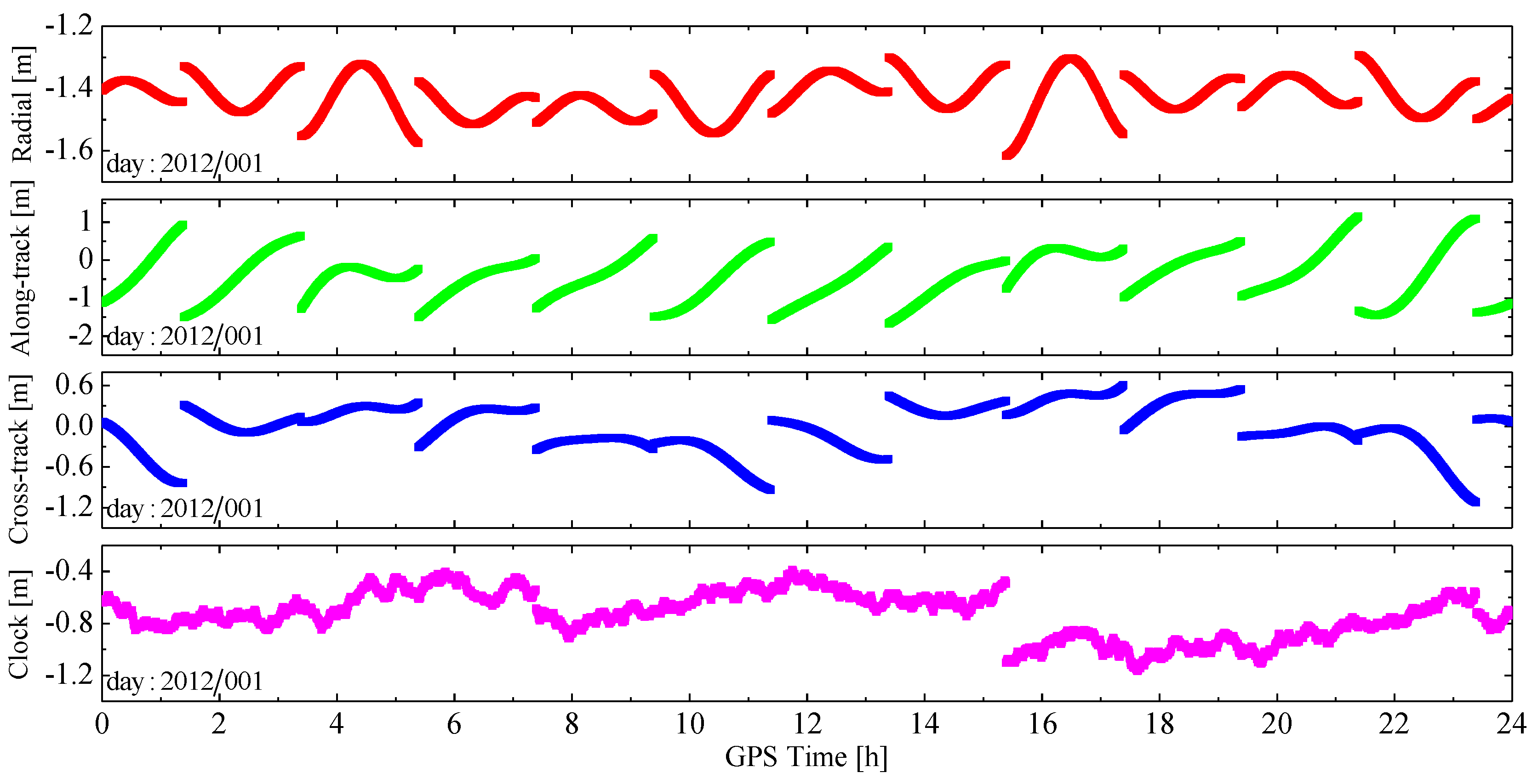
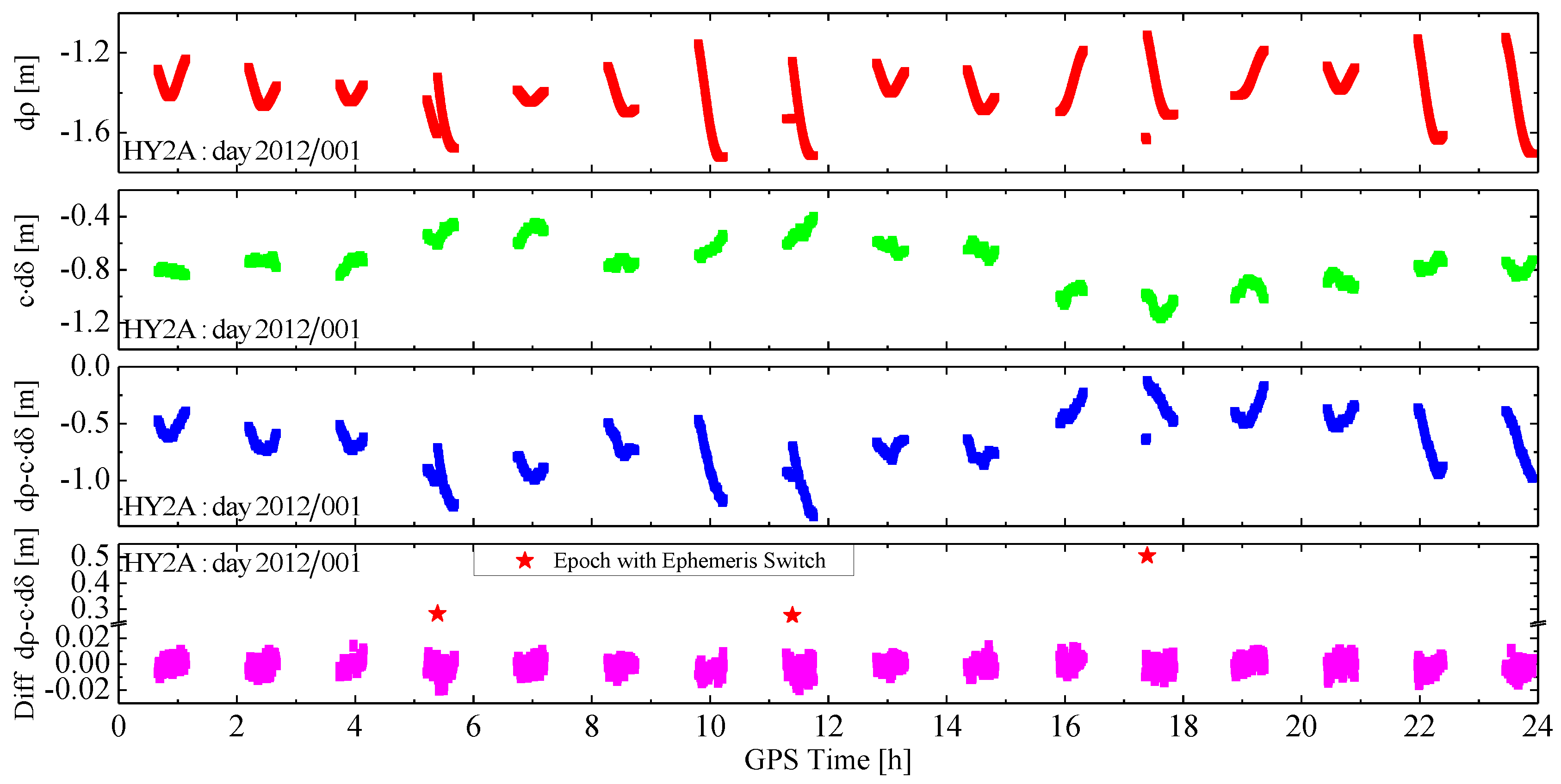

2.5. Parameter Estimation
2.6. Software
| Model/Parameter | Relevant Setting |
|---|---|
| Measurement model | |
| GPS data | Dual-frequency pseudo-range and carrier-phase data, sampling rate of 30 s |
| GPS orbit and clock | Broadcast ephemeris |
| Pseudo-ambiguity | Initial standard deviation , and the standard deviation of the process noise is , where is the epoch interval. |
| Dynamic model | |
| Earth Gravity Field | EGM 2008, adopt 45 × 45 for HY2A and 60 × 60 for ZY3 |
| Luni-solar gravitation | Low precision model, Moon and Sun’s position are computed via analytic method |
| Earth tides | Low precision model, k20 solid only |
| Atmosphere Drag | Modified Harris-Priester model (density), fixed effective area, estimates Cd parameter |
| Solar radiation pressure | Cannonball model, fixed effective area, estimates Cr parameter |
| Empirical acceleration | Dynamic Model Compensation (DMC) [4] with a first-order Gauss-Markov model, |
| Other perturbations | Neglected |
| Reference frame | |
| Coordinate system | WGS84 |
| Precession and nutation | IAU1976/IAU 1980 simplified model |
| Earth rotation parameter | Rapid predicted EOP in IERS Bulletin A |
3. Flight Data Analyses
3.1. Datasets
| Mission | Altitude (km) | Data Arc Year/Days | Noise (m) | |
|---|---|---|---|---|
| HY2A | 900 | 2012/001–005 | 2.172 | ≤0.006 |
| ZY3 | 500 | 2012/032–036 | 2.157 | ≤0.006 |
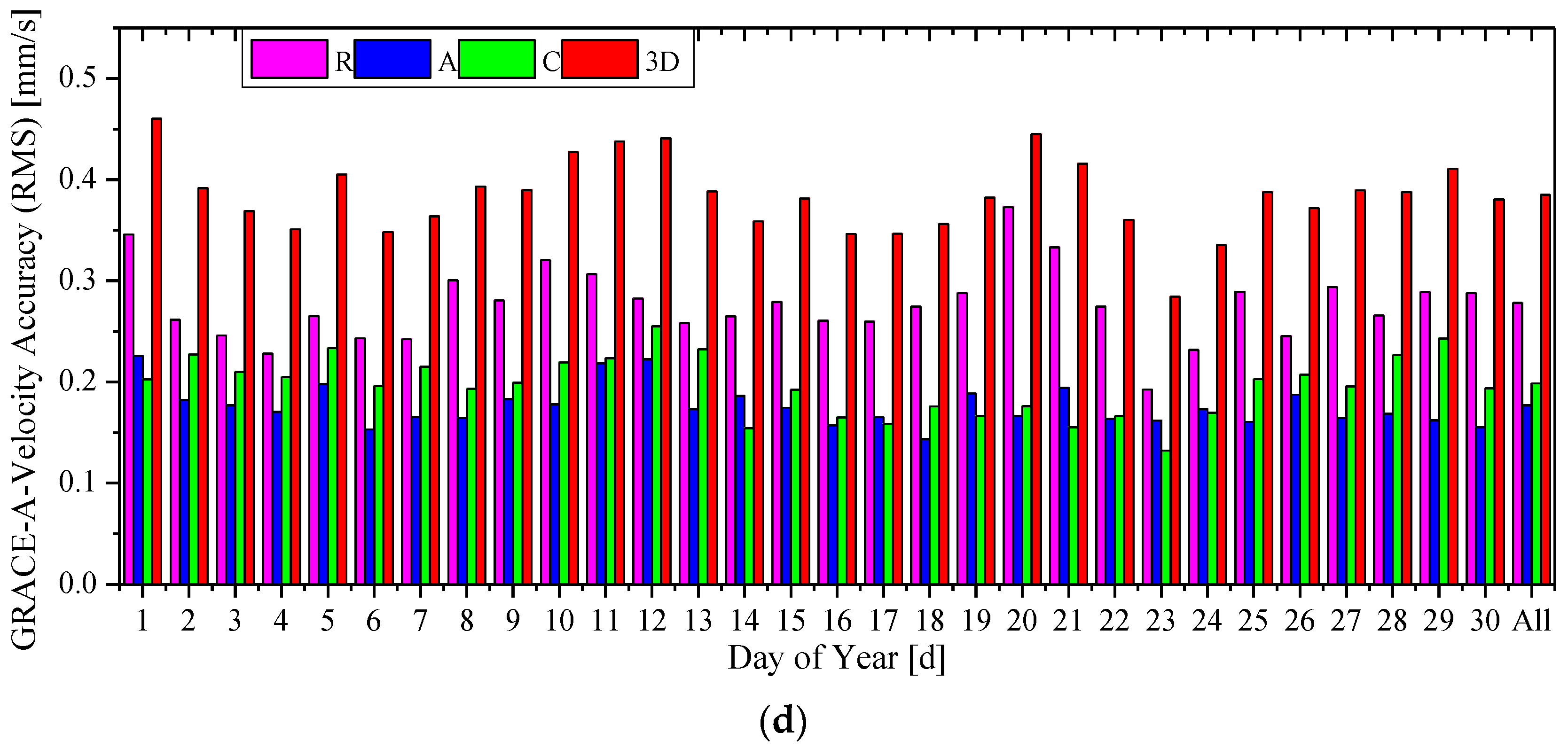
3.2. RTOD Accuracy Analysis
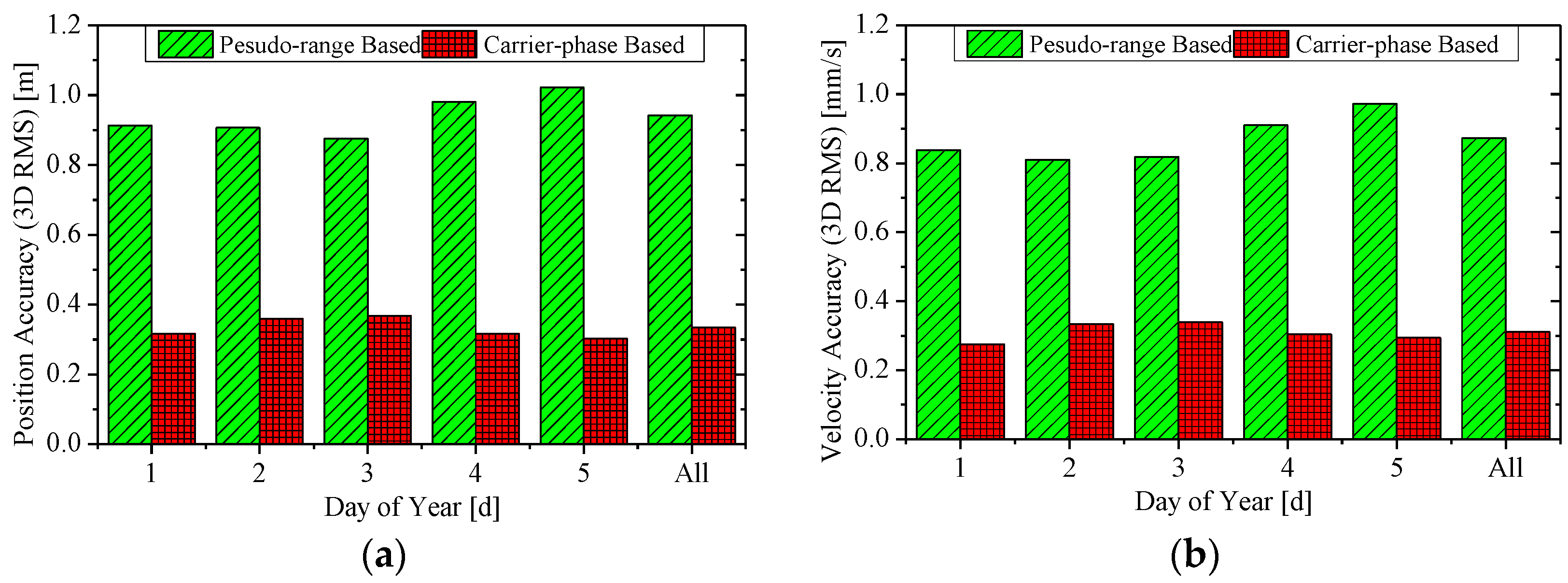
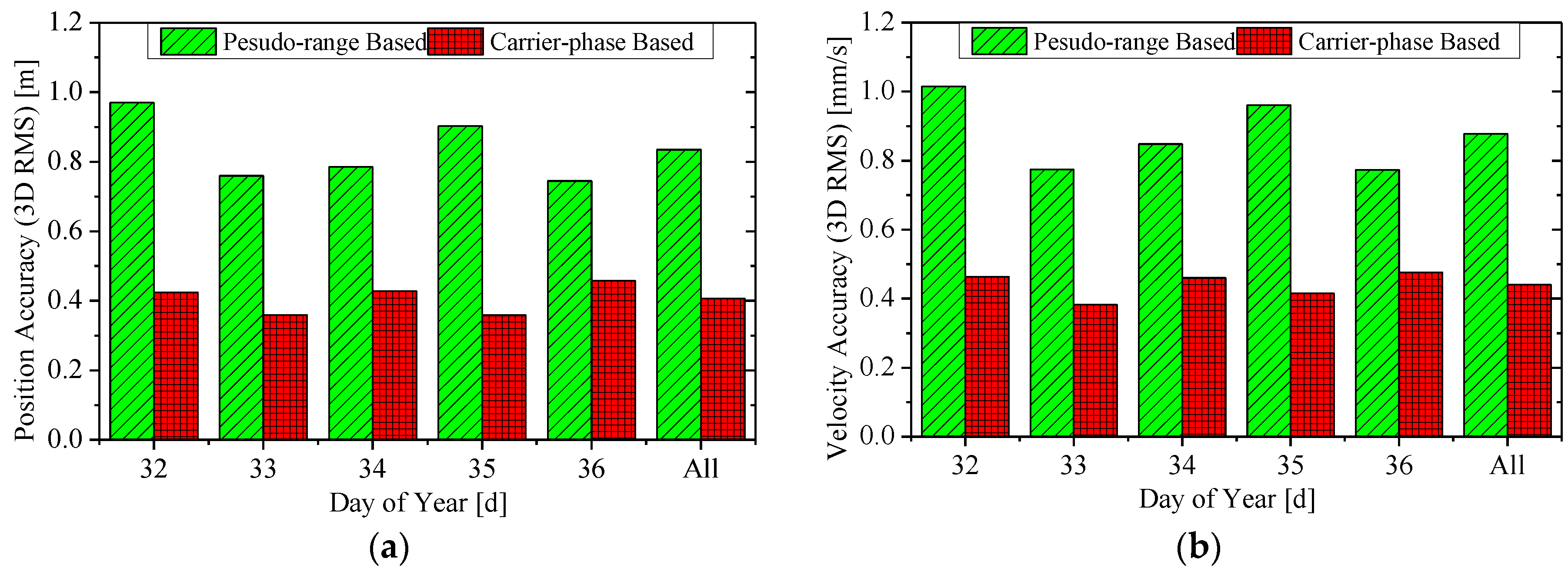
| Accuracy (RMS) | HY2A | ZY3 | |||
|---|---|---|---|---|---|
| Pseudo-Range Based | Carrier-Phase Based | Pseudo-Range Based | Carrier-Phase Based | ||
| Position (m) | R | 0.312 | 0.085 | 0.348 | 0.186 |
| A | 0.701 | 0.256 | 0.714 | 0.339 | |
| C | 0.547 | 0.197 | 0.255 | 0.128 | |
| 3D | 0.942 | 0.334 | 0.835 | 0.407 | |
| Velocity (mm/s) | R | 0.624 | 0.226 | 0.741 | 0.360 |
| A | 0.287 | 0.113 | 0.357 | 0.209 | |
| C | 0.538 | 0.181 | 0.304 | 0.142 | |
| 3D | 0.873 | 0.311 | 0.877 | 0.440 | |
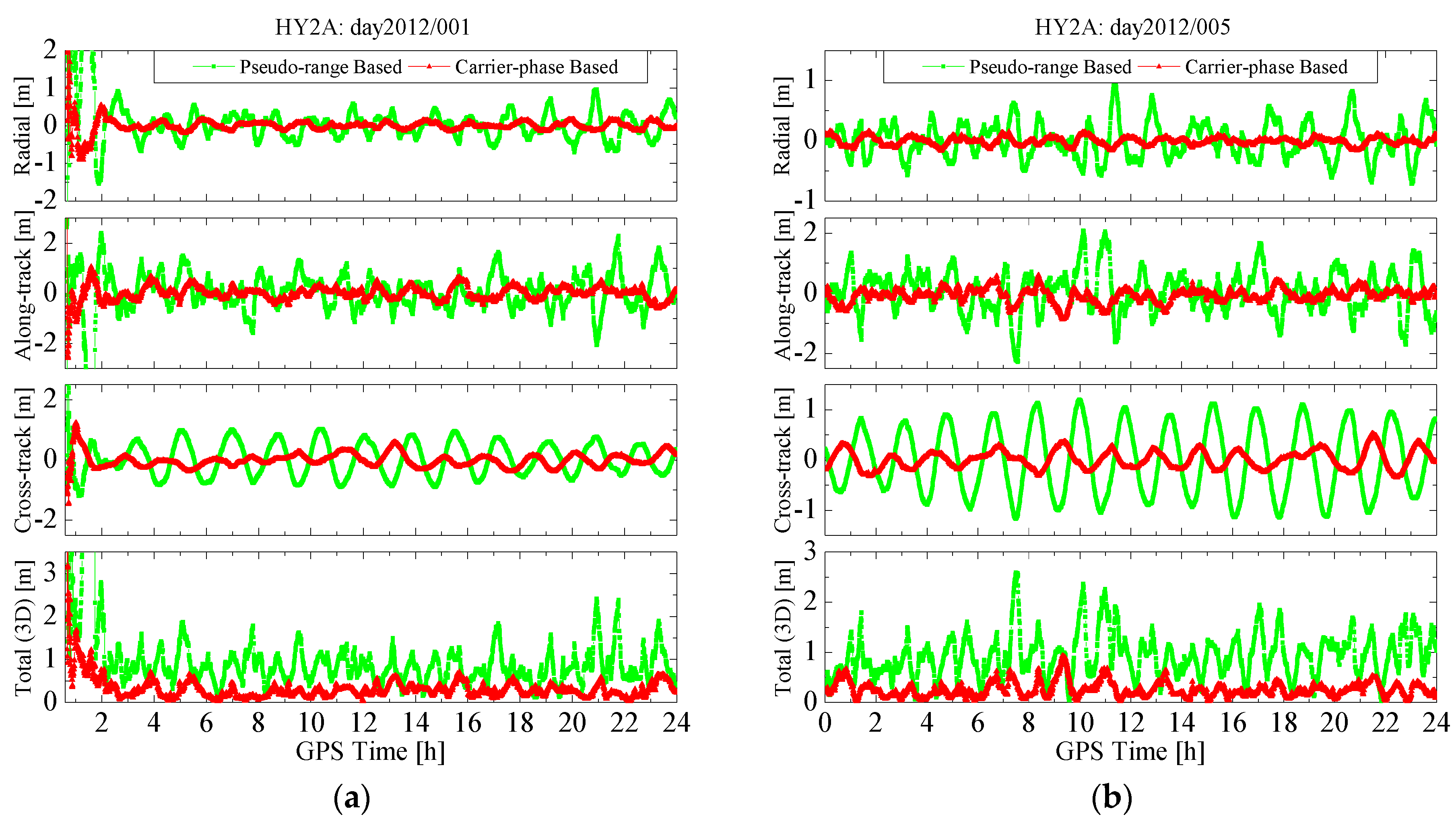
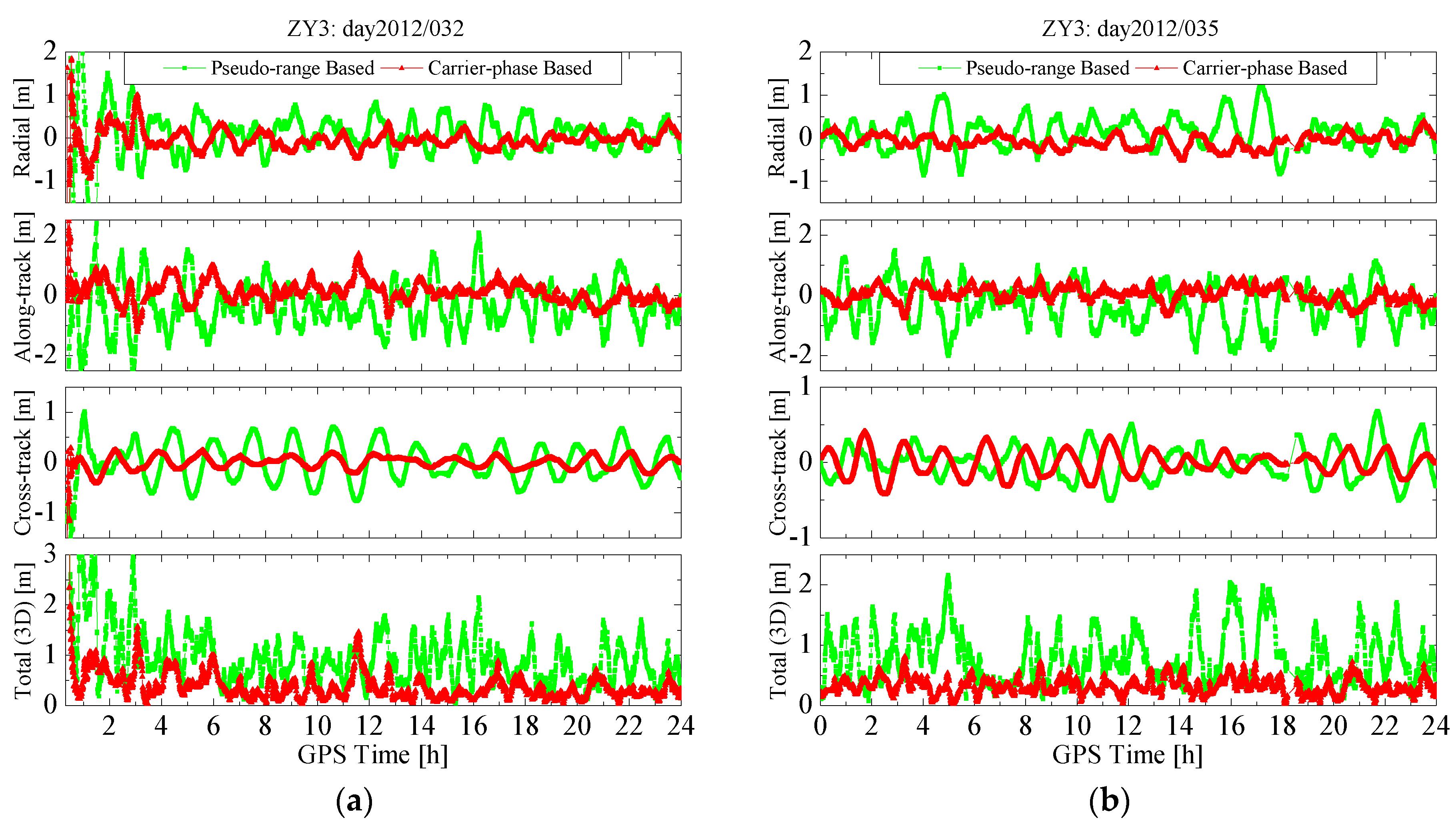

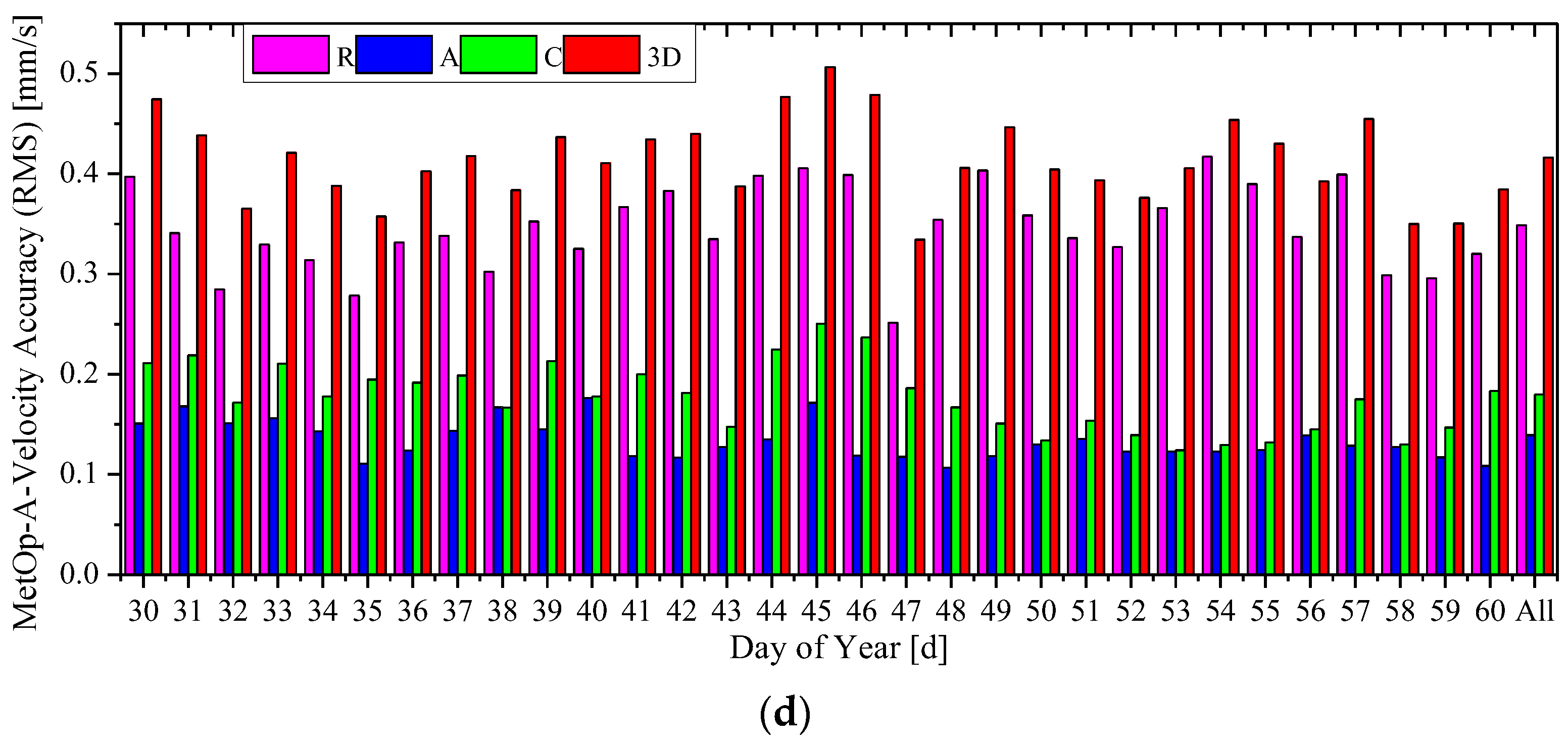
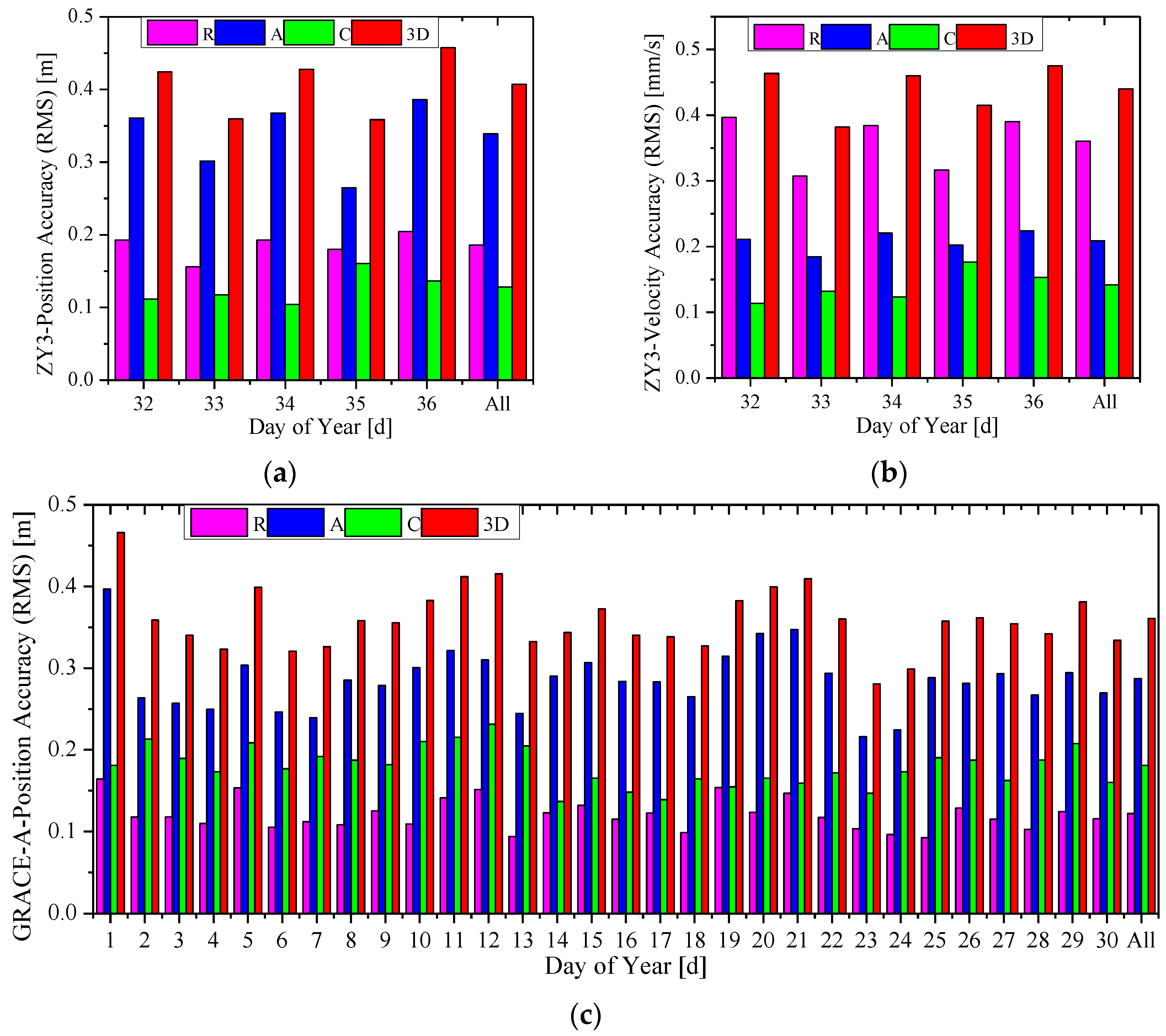
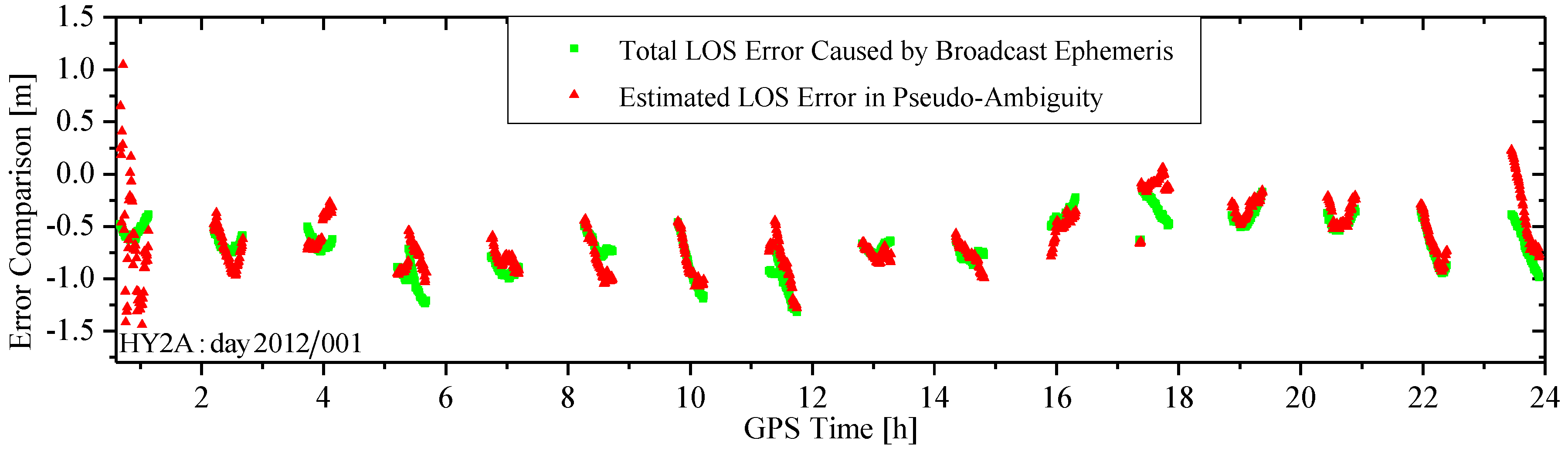
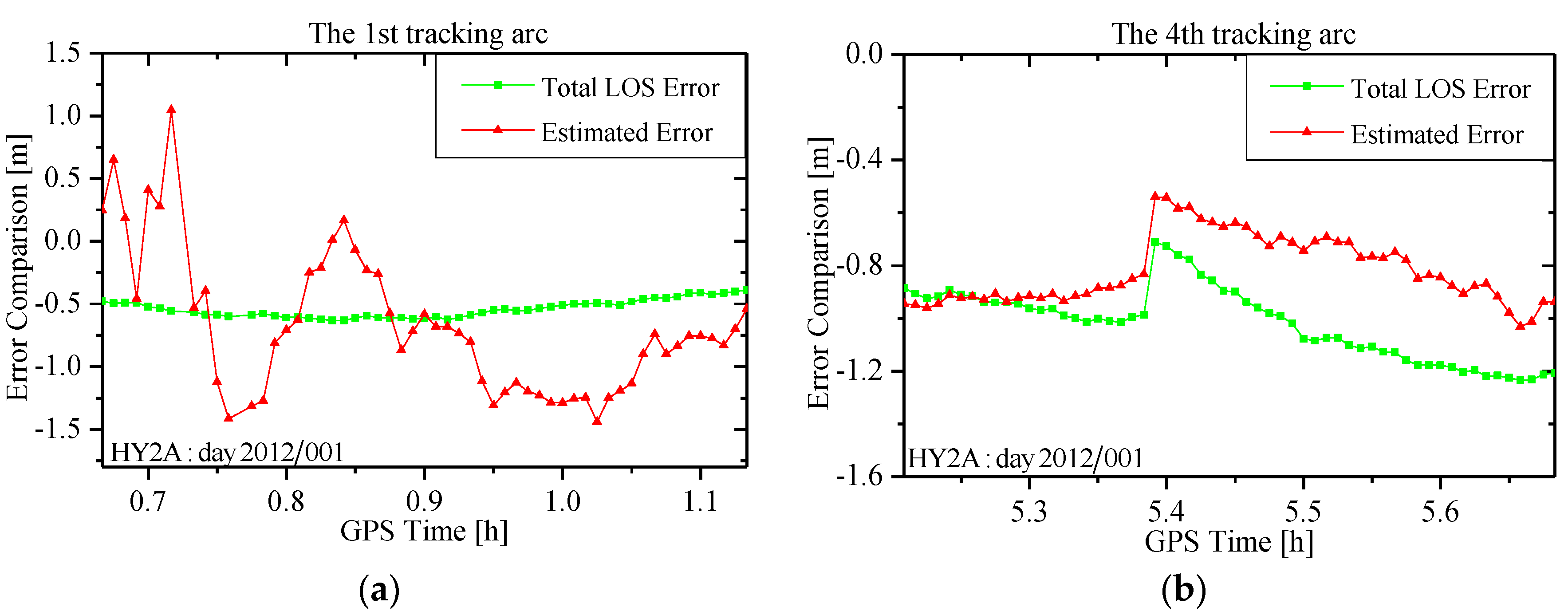
3.3. Effect of Pseudo-Ambiguity
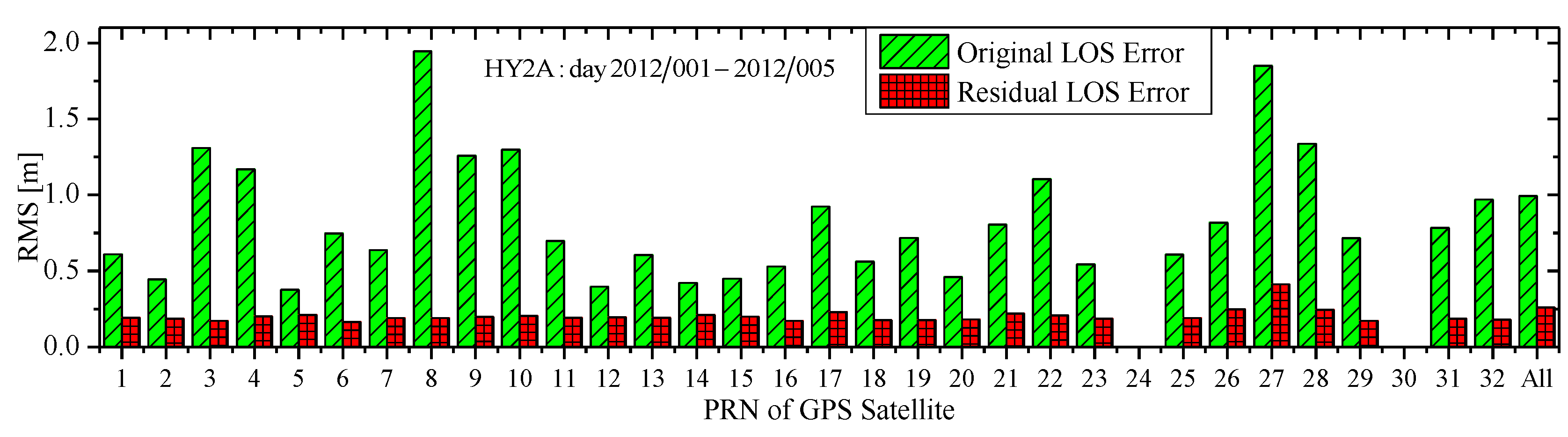
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Silvestrin, P.; Potti, J.; Carmona, J.C.; Bernedo, P. An autonomous GNSS-based orbit determination system for low-earth observation satellites. In Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION-GPS-1995), Palm Springs, CA, USA, 12–15 September 1995; pp. 173–182.
- Hart, R.C.; Hartman, K.R.; Long, A.C.; Lee, T.; Oza, D.H. Global Positioning System (GPS) Enhanced Orbit Determination Experiment (GEODE) on the small satellite technology initiative (SSTI) lewis spacecraft. In Proceedings of the ION-GPS-1996, Kansas City, MO, USA, 17–20 September 1996; pp. 1303–1312.
- Hart, R.C.; Long, A.C.; Lee, T. Autonomous navigation of the SSTI/Lewis spacecraft using the Global Positioning System (GPS). In Proceedings of the Flight Mechanics Symposium, GSFC, Greenbelt, MD, USA, 19–21 May 1997; pp. 19–32.
- Goldstein, D.B. Real-time, Autonomous Precise Satellite Orbit Determination Using the Global Positioning System. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2000. [Google Scholar]
- Bertiger, W.; Haines, B.; Kuang, D.; Lough, M.; Lichten, S.; Muellerschoen, R.J.; Vigue, Y.; Wu, S. Precise real-time low earth orbiter navigation with GPS. In Proceedings of the ION-GPS-1998, Nashville, TN, USA, 15–18 September 1998; pp. 1927–1936.
- Reichert, A.; Meehan, T.; Munson, T. Toward decimeter-level real-time orbit determination: A demonstration using the SAC-C and CHAMP spacecraft. In Proceedings of the ION-GPS-2002, Portland, OR, USA, 24–27 September 2002; pp. 24–27.
- Montenbruck, O.; Gill, E.; Markgraf, M. Phoenix-XNS—A miniature real-time navigation system for LEO satellites. In Proceedings of the NAVITEC’2006, Noordwijk, The Netherlands, 11–13 December 2006; pp. 11–13.
- Gill, E.; Montenbruck, O.; Arichandran, K.; Tan, S.H.; Bretschneider, T. High-precision onboard orbit determination for small satellites-the GPS-based XNS on X-SAT. In Proceedings of the 6th Symposium on Small Satellites Systems and Services, La Rochelle, France, 20–24 September 2004; pp. 47–52.
- Montenbruck, O.; Markgraf, M.; Naudet, J.; Santandrea, S.; Gantois, K.; Vuilleumier, P. Autonomous and precise navigation of the PROBA-2 spacecraft. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; pp. 7086–7103.
- Markgraf, M.; Montenbruck, O.; Stefano, S.; Joris, N. Phoenix-XNS navigation system onboard the PROBA-2 spacecraft-first flight results. In Proceedings of the Small Satellites Systems and Services the 4S Symposium, Madeira, Portugal, Slovenia, 4–8 June 2010; pp. 60–68.
- Chiaradia, A.P.M.; Kuga, H.K.; de Almeida, P.A.F.B. Onboard and real-time artificial satellite orbit determination using GPS. Math. Problems Eng. 2013, 2013, 1–8. [Google Scholar]
- De Florio, S. Precise Autonomous Orbit Control in Low Earth Orbit: From Design to Flight Validation. Ph.D. Thesis, The University of Glasgow, Glasgow, UK, 2013. [Google Scholar]
- Wang, F. Theory and Software Development on Autonomous Orbit Determination Using Space-Borne GPS Measurements. Ph.D. Thesis, Wuhan University, Wuhan, China, 2006. [Google Scholar]
- Montenbruck, O.; Ramos-Bosch, P. Precision real-time navigation of LEO satellites using global positioning system measurements. GPS Solut. 2008, 12, 187–198. [Google Scholar] [CrossRef]
- Wang, F. A kalman filtering algorithm for precision real-time orbit determination with space-borne GPS measurements. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 653–656. [Google Scholar]
- Montenbruck, O.; Helleputte, V.T.; Kroes, R.; Gill, E. Reduced dynamic orbit determination using GPS code and carrier measurements. Aerosp. Sci. Technol. 2005, 9, 261–271. [Google Scholar] [CrossRef]
- Montenbruck, O.; Yoon, Y.; Gill, E. Precise orbit determination for the TerraSAR-X mission. In Proceedings of the 19th International Symposium on Space Flight Dynamics, Kanazawa, Japan, 4–11 June 2006; pp. 613–618.
- Montenbruck, O.; Andres, Y.; Bock, H.; van Helleputte, T.; van den Ijssel, J.; Loiselet, M.; Marquardt, C.; Silvestrin, P.; Visser, P.; Yoon, Y. Tracking and orbit determination performance of the GRAS instrument on MetOp-A. GPS Solut. 2008, 12, 289–299. [Google Scholar] [CrossRef]
- Bock, H.; Jäggi, A.; Švehla, D.; Beutler, G.; Hugentobler, U.; Visser, P. Precise orbit determination for the GOCE satellite using GPS. Adv. Space Res. 2007, 39, 1638–1647. [Google Scholar] [CrossRef]
- Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geod. 2006, 80, 322–331. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Zou, X.; Xin, Y. The stochastic model refinement for precise orbit determination of GRACE. Chin. J. Geophys. 2010, 53, 1554–1561. [Google Scholar]
- Li, X.; Zhang, X.; Li, P. PPP for rapid precise positioning and orbit determination with zero-difference integer ambiguity fixing. Chin. J. Geophys. 2012, 55, 833–840. [Google Scholar]
- Zhang, Q.; Zhang, J.; Zhang, H.; Wang, R.; Jia, H. The study of HY2A satellite engineering development and in-orbit movement. Eng. Sci. 2013, 80, 12–18. [Google Scholar] [CrossRef]
- Li, D. China’s first civilian three-line-array stereo mapping satellite: ZY3. Acta Geod. Cartogr. Sin. 2012, 41, 317–322. [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Application; Springer: Berlin, Germeny, 2000. [Google Scholar]
- Cryer, J.D.; Chan, K.S. Time Series Analysis with Applications in R, 2nd ed.; China Machine Press: Beijing, China, 2011. [Google Scholar]
- Guo, J.; Zhao, Q.; Li, M.; Hu, Z. Centimeter level orbit determination for HY2A using GPS data. Geomat. Inf. Sci. Wuhan Univ. 2013, 28, 52–55. [Google Scholar]
- Zhao, C.; Tang, X. Precise orbit determination for the ZY-3 satellite mission using GPS receiver. J. Astronaut. 2013, 34, 1202–1206. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Gong, X.; Sang, J.; Zhang, X. A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver. Sensors 2015, 15, 30403-30418. https://doi.org/10.3390/s151229805
Wang F, Gong X, Sang J, Zhang X. A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver. Sensors. 2015; 15(12):30403-30418. https://doi.org/10.3390/s151229805
Chicago/Turabian StyleWang, Fuhong, Xuewen Gong, Jizhang Sang, and Xiaohong Zhang. 2015. "A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver" Sensors 15, no. 12: 30403-30418. https://doi.org/10.3390/s151229805
APA StyleWang, F., Gong, X., Sang, J., & Zhang, X. (2015). A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver. Sensors, 15(12), 30403-30418. https://doi.org/10.3390/s151229805





