4.1. Considered Scenarios
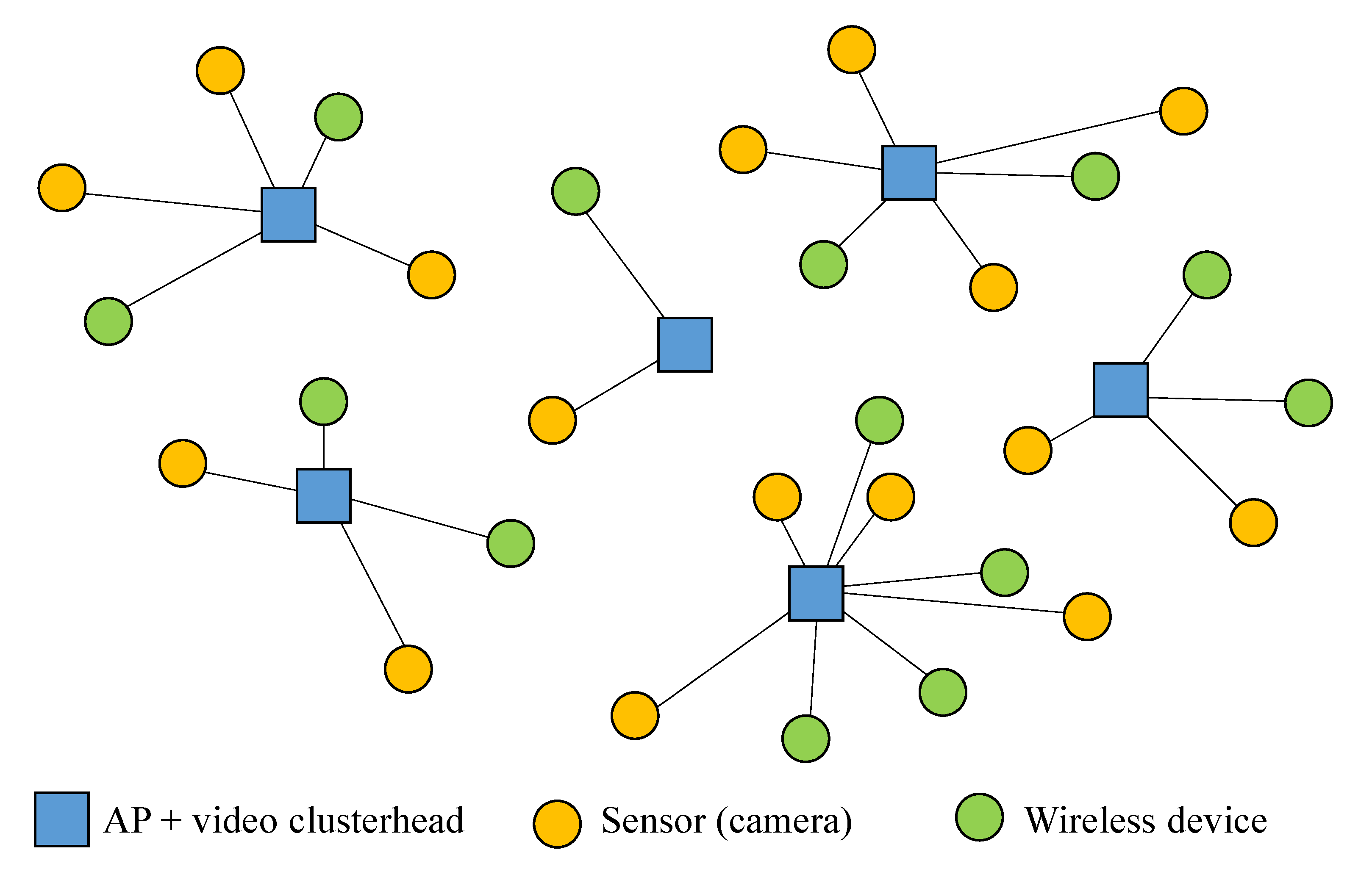
In this paper, we make the common assumption that sensor nodes (IP-based cameras) are static elements. As in our problem there is not any element that evolves with time, we deal with the problem of evaluating the performance of a particular frequency assignment strategy by means of the computation described in
Section 2. Please, note that the frequency strategy evolves with time, but it is computed in an offline manner.
We have taken into consideration three types of WSSN scenarios. In the first case, we have considered 50 APs and 350 (50 × 7) cameras; in the second one, 50 APs and 500 (50 × 10) cameras; and in the third one, 100 APs and 500 (100 × 5) cameras. The position where APs and wireless terminals are located in a plane is random, considering that a wireless terminal is associated with its closest AP. If a sensor (camera) is not in the coverage area of any AP (given by the sensitivity of its receptor, as explained in
Section 2.3), we have removed that sensor from the problem. Additionally, if an AP has no associated sensors, it is also removed from the problem. Obviously, as the density of nodes increases, the number of unconnected nodes decreases. For each type of scenario and due to their randomness, we have generated three specific scenarios, so we have studied nine scenarios. Moreover, given the non-deterministic nature of the different algorithms under study, we have run each algorithm ten times in each scenario.
Table 1 summarizes the scenarios under study, where we show the number of nodes (APs and sensors) initially deployed and the number of nodes that remain after removing the unconnected nodes (
ν). Moreover, for the sake of quantifying the density of each scenario, we also show the mean number of interference signals that each node in the network receives (
).
Table 1.
Summary of scenarios.
Table 1.
Summary of scenarios.
| Scenario | # APs | # Sensors | ν | |
|---|
| 1 | 50 | 350 | 237 | 22.53 |
| 2 | 50 | 350 | 241 | 21.53 |
| 3 | 50 | 350 | 240 | 21.81 |
| 4 | 50 | 500 | 439 | 34.72 |
| 5 | 50 | 500 | 414 | 39.26 |
| 6 | 50 | 500 | 427 | 34.30 |
| 7 | 100 | 500 | 490 | 47.62 |
| 8 | 100 | 500 | 487 | 51.57 |
| 9 | 100 | 500 | 527 | 48.63 |
4.3. Results
The choice of the configuration parameters for the studied scenarios has been driven by considering typical or reasonable parameters from a realistic point of view, as summarized in
Table 2. With these values, the coverage area is
m.
Firstly, we study the performance of the SA algorithm with different values for its configuration parameters: initial temperature (
T) and the number of iterations. In general, a higher initial temperature increases the chances for escaping from local maxima, although an excessive temperature can drive the optimizer to escape from the global maximum. For that reason, setting the initial temperature is usually a delicate matter and depends on the concrete application. For the case of the number of iterations, and as a general rule, a higher number of iterations provides more opportunities to improve the solution, but it also increases the time that the algorithm is operating with high temperatures and, so, the risk of escaping from the global maximum (in addition to the increased computation cost, of course). In
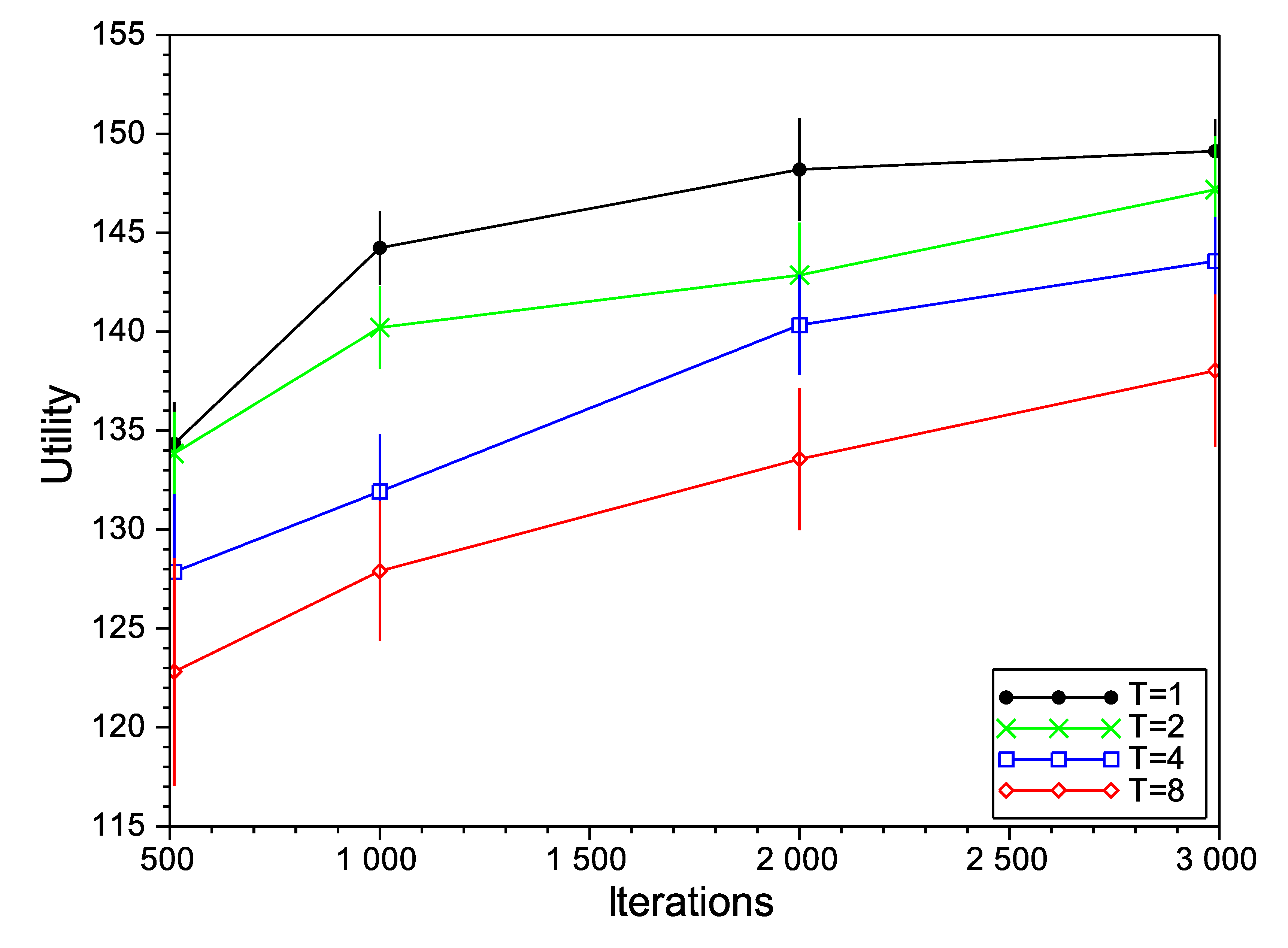
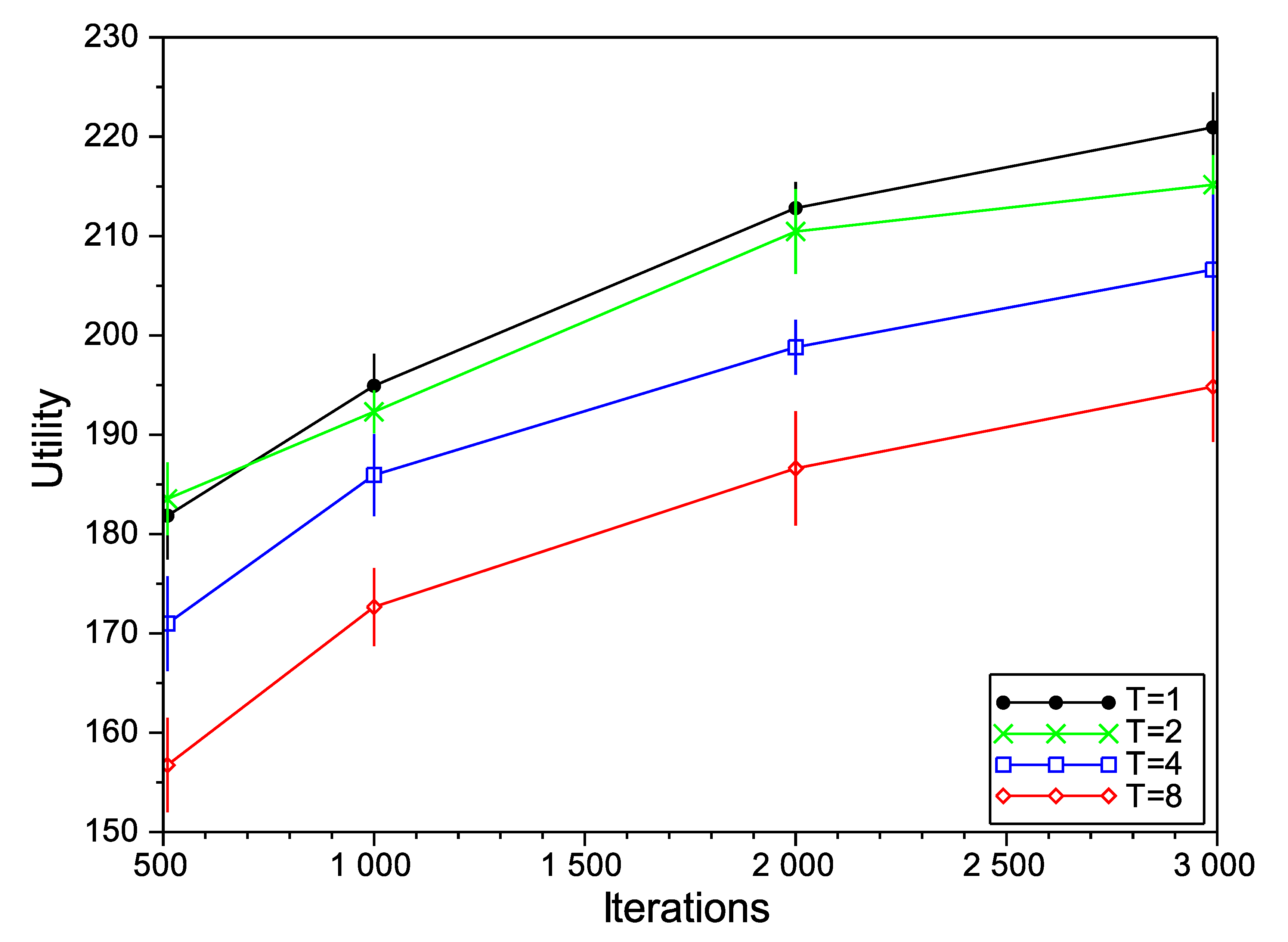
Figure 4,
Figure 5 and
Figure 6, we show the variation of the utility and the confidence intervals at 95% of the final negotiation outcome for different values of temperature and the number of iterations for Scenarios 3, 6 and 9 (we omit the rest of the scenarios, as the results obtained are very similar). In those figures, we notice that, for the number of iterations, the best choice is to choose the highest number as possible to obtain higher utilities. This effect occurs in all of the studied scenarios (not only the ones depicted in the figures), with the exception of one of them (Scenario 6 in
Figure 5 with
), where the utility function decreases from
to
for 2000 and 3000 iterations, respectively. Regarding the initial temperature
T, the best choice is
. From this point on, the SA algorithm will be executed with
and 3000 iterations.
Table 2.
Summary of the parameters (C, camera).
Table 2.
Summary of the parameters (C, camera).
| Parameter | Value |
|---|
| 30 mW |
| 0 dB |
| 0 dB |
| L | 40 dB |
| S | dBm |
| m |
| m |
| Ψ (APs) | 0.5 |
| Ψ (C) | 0.2 |
Figure 4.
Simulated annealing (SA) evaluation in Scenario 3.
Figure 4.
Simulated annealing (SA) evaluation in Scenario 3.
Figure 5.
SA evaluation in Scenario 6.
Figure 5.
SA evaluation in Scenario 6.
Figure 6.
SA evaluation in Scenario 9.
Figure 6.
SA evaluation in Scenario 9.
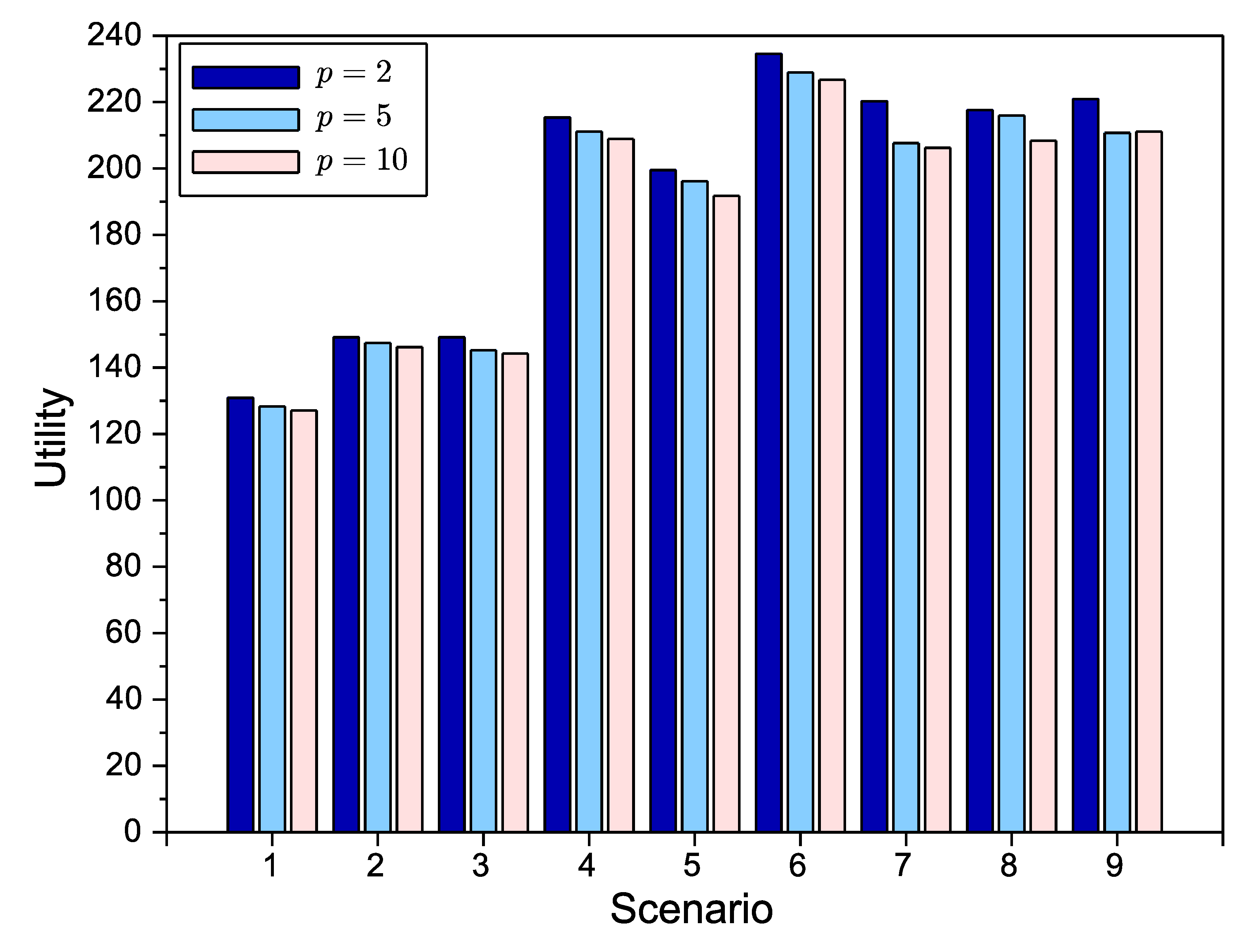
Once the SA algorithm has been tuned, the next experiments are focused on determining the impact of having a different number of agents or network providers (
p) in the negotiation. In
Figure 7, we have evaluated all of the scenarios under study with
. From the figure, we can conclude that, as expected, increasing the number of providers
p yields a progressive diminution of the global utility, since trade-off solutions involving access points in different providers will be more likely to be rejected. However, this reduction is moderate enough. From this point on, all of the results belong to the case
. The reason for this choice is two-fold. First, we think it is reasonable to consider a small number of providers offering surveillance services. Second, there are more works in complex bilateral negotiations than for the multilateral case (three or more agents).
Next, we compare the SA algorithm with the rest of the proposals: random channel assignment, SCS, HC and ALHSO. In
Table 3,
Table 4 and
Table 5, we show the average (avg), standard deviation (SD) and confidence intervals at 95% (CI) of the utility function for 10 executions of the algorithm in each of the proposed scenarios. Furthermore, we highlight in bold the best solution. As can be observed, regarding the mean utility, the SA algorithm is the best solution for all of the scenarios, except for Scenario 8, where ALHSO shows the best performance. The second best performance is obtained by ALHSO, followed, by far, by SCS. As could be expected, the worst performance is obtained by the random channel assignment, which obtains very low utility values. In the case of HC (which can be seen as an SA optimizer with
), we can note that it is able to obtain good results for the simplest scenarios (
Table 3), but its performance decreases in more complex scenarios (
Table 3,
Table 4 and
Table 5), due to its tendency of getting stuck in local maxima.
Figure 7.
SA evaluation with different numbers of network providers (p).
Figure 7.
SA evaluation with different numbers of network providers (p).
Table 3.
Utility in scenarios with 50 APs and 350 sensors. SCS, sequential channel search; ALHSO, augmented Lagrangian harmony search optimization; HC, hill-climber.
Table 3.
Utility in scenarios with 50 APs and 350 sensors. SCS, sequential channel search; ALHSO, augmented Lagrangian harmony search optimization; HC, hill-climber.
| | Scenario 1 | Scenario 2 | Scenario 3 |
|---|
| avg | SD | CI | avg | SD | CI | avg | SD | CI |
|---|
| Random | 59.36 | 9.61 | 6.87 | 73.74 | 10.68 | 7.64 | 65.81 | 13.76 | 9.84 |
| SCS | 106.74 | 4.30 | 3.08 | 121.20 | 7.18 | 5.14 | 122.78 | 4.46 | 3.19 |
| ALHSO | 121.64 | 4.17 | 2.98 | 141.09 | 3.56 | 2.55 | 132.92 | 3.95 | 2.83 |
| HC | 123.30 | 3.50 | 2.50 | 140.37 | 4.93 | 3.53 | 138.02 | 5.31 | 3.80 |
| SA | 130.89 | 2.65 | 1.90 | 149.16 | 1.65 | 1.18 | 149.13 | 2.27 | 1.62 |
Table 4.
Utility in scenarios with 50 APs and 500 sensors.
Table 4.
Utility in scenarios with 50 APs and 500 sensors.
| | Scenario 4 | Scenario 5 | Scenario 6 |
|---|
| avg | SD | CI | avg | SD | CI | avg | SD | CI |
|---|
| Random | 92.96 | 6.59 | 4.71 | 78.05 | 16.95 | 12.13 | 105.08 | 13.70 | 9.80 |
| SCS | 165.60 | 9.00 | 6.44 | 151.74 | 10.24 | 7.33 | 181.27 | 9.14 | 6.54 |
| ALHSO | 203.62 | 5.76 | 4.12 | 184.01 | 7.46 | 5.34 | 221.96 | 5.37 | 3.84 |
| HC | 196.82 | 9.94 | 7.11 | 179.11 | 11.06 | 7.91 | 211.76 | 11.05 | 7.90 |
| SA | 215.37 | 2.75 | 1.97 | 199.52 | 2.98 | 2.13 | 234.59 | 1.46 | 1.04 |
Table 5.
Utility in scenarios with 100 APs and 500 sensors.
Table 5.
Utility in scenarios with 100 APs and 500 sensors.
| | Scenario 7 | Scenario 8 | Scenario 9 |
|---|
| avg | SD | CI | avg | SD | CI | avg | SD | CI |
|---|
| Random | 90.13 | 9.14 | 6.54 | 95.73 | 15.87 | 11.35 | 88.79 | 11.64 | 8.33 |
| SCS | 164.94 | 9.34 | 6.68 | 168.28 | 13.09 | 9.36 | 172.70 | 11.53 | 8.25 |
| ALHSO | 216.36 | 6.40 | 4.58 | 223.02 | 5.03 | 3.60 | 217.53 | 4.86 | 3.48 |
| HC | 196.33 | 8.07 | 5.77 | 199.51 | 8.74 | 6.25 | 199.65 | 7.73 | 5.53 |
| SA | 220.29 | 5.17 | 3.70 | 217.60 | 5.24 | 3.75 | 220.94 | 4.92 | 3.52 |
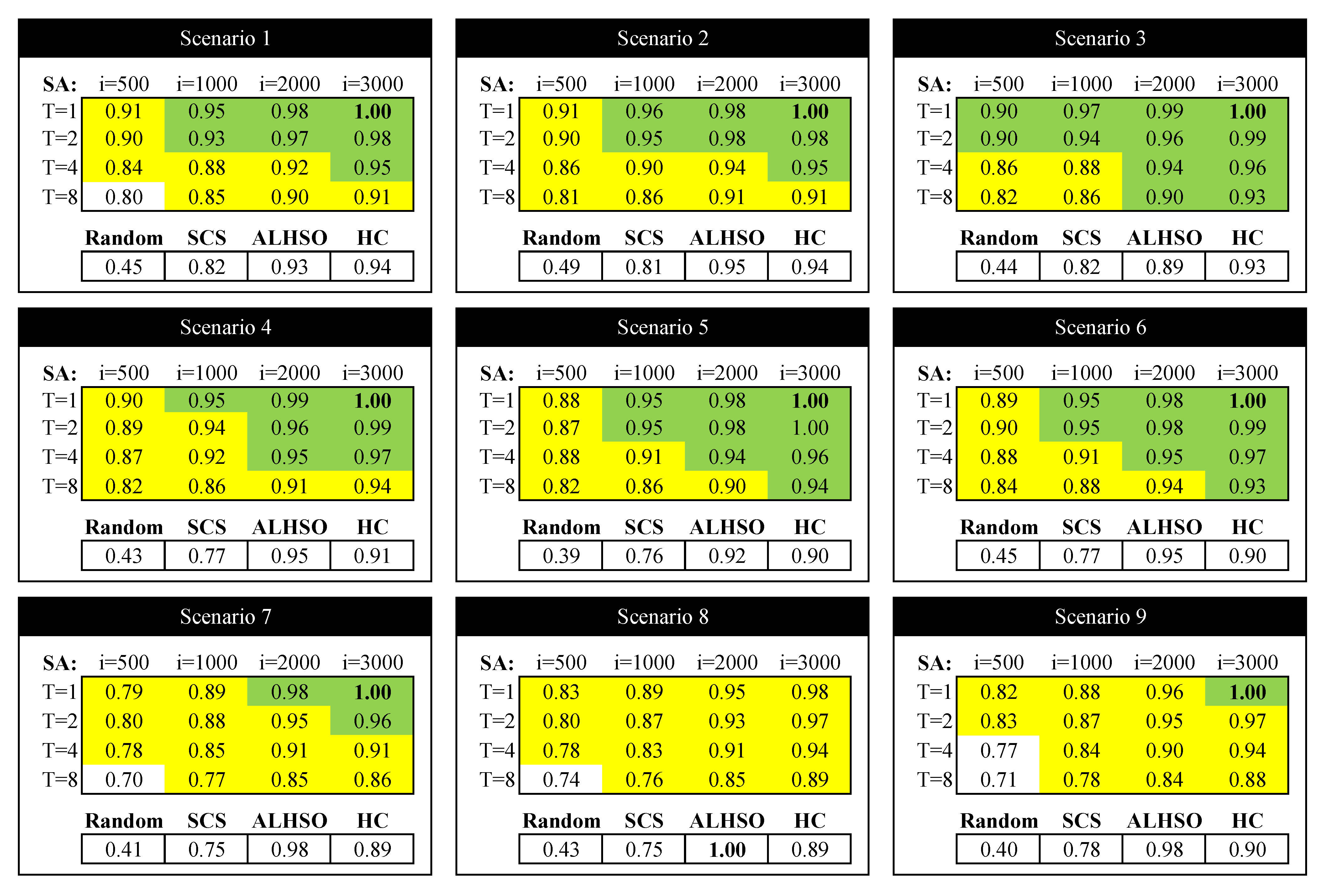
Regarding the standard deviation of the solutions, the algorithm that shows the lowest deviation is SA in almost every studied case (except in the most complex Scenarios 8 and 9, where SA is very similar to ALHSO), followed by ALHSO, SCS and random. As a conclusion, we can state that outperforming an optimization algorithm like ALHSO with negotiation techniques like SA shows that the use of negotiation techniques is advisable for the problem under study. Since the SA algorithm requires, as seen previously, the configuration of two parameters (initial temperature and the number of iterations), we finally include a comparison of all of the algorithms in a relative manner, with the purpose of analyzing the behavior of SA if it is not configured properly.
Figure 8.
Results relatives to the maximum.
Figure 8.
Results relatives to the maximum.
Figure 8 shows the mean value of the utility functions for the different scenarios and relative to their maximum value (in bold). To make the interpretation easier, in the table devoted to the results of the SA algorithm, we have highlighted in green those results that outperform or equal ALHSO (they also outperform SCS and random, as they are less restrictive). Moreover, we have highlighted in yellow the results where SA outperforms SCS. As a conclusion, for temperatures close to
and 1000 or more iterations, SA outperforms ALHSO. Moreover, we notice that, for almost all cases (except for very high temperatures and very few iterations), SA outperforms SCS. In the figure, we also show the results for HC (equivalent to SA with
) with 3000 iterations, and we observe that it has a worse performance than SA for the same number of iterations.
As a conclusion, we can recommend the use of negotiation techniques based on SA, as it is able to obtain better results than SCS in almost all cases, and it is not difficult to find configuration parameters that make SA even better than a nonlinear optimizer like ALHSO.