Maximum Measurement Range and Accuracy of SAW Reflective Delay Line Sensors
Abstract
:1. Introduction
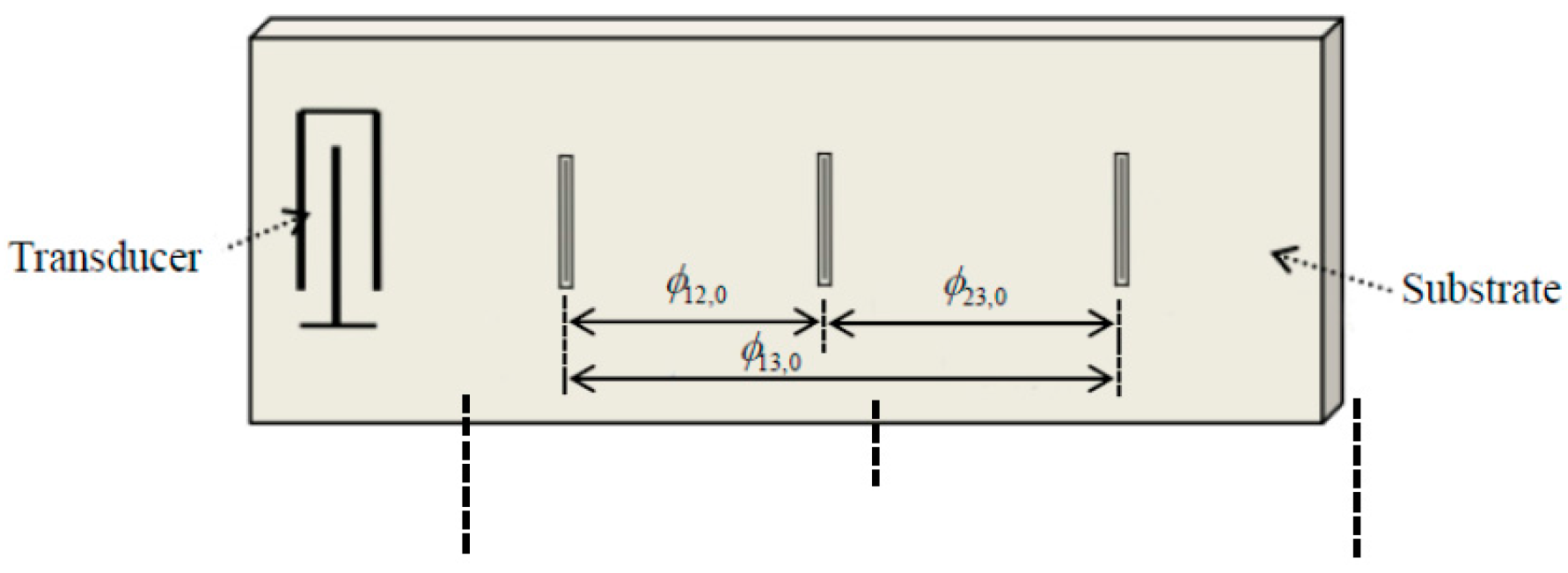
2. Principle of Sensing with Three Reflectors
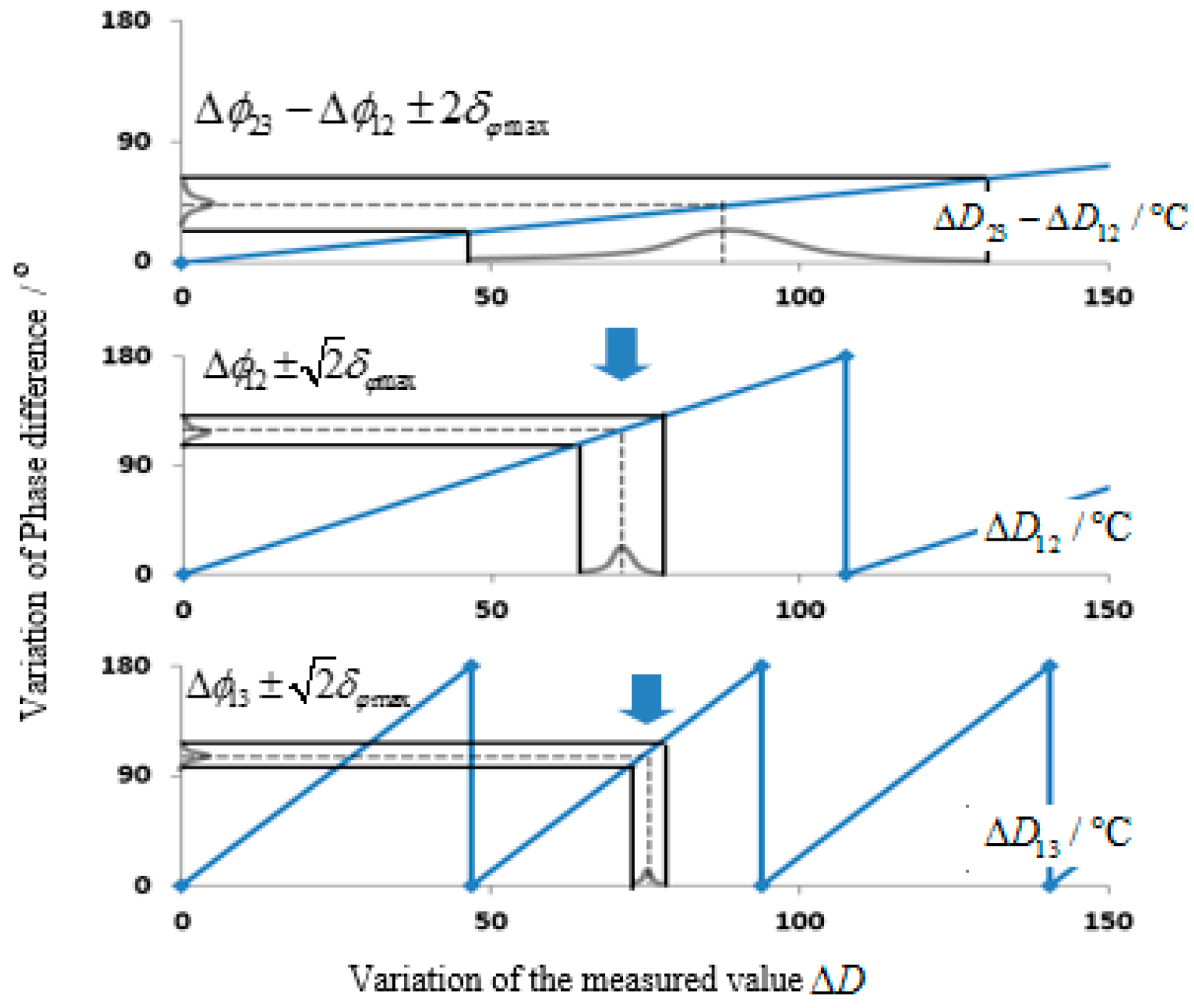
3. The Maximum Measurement Range and Accuracy
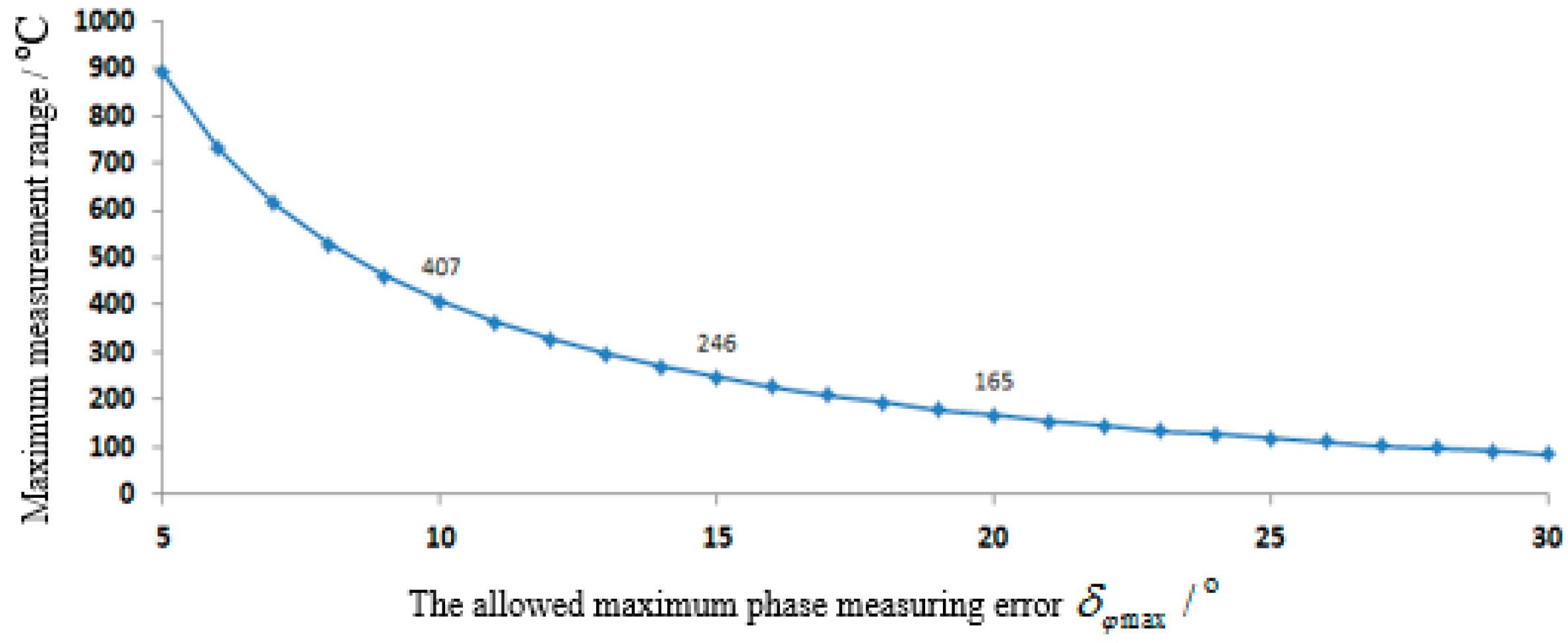
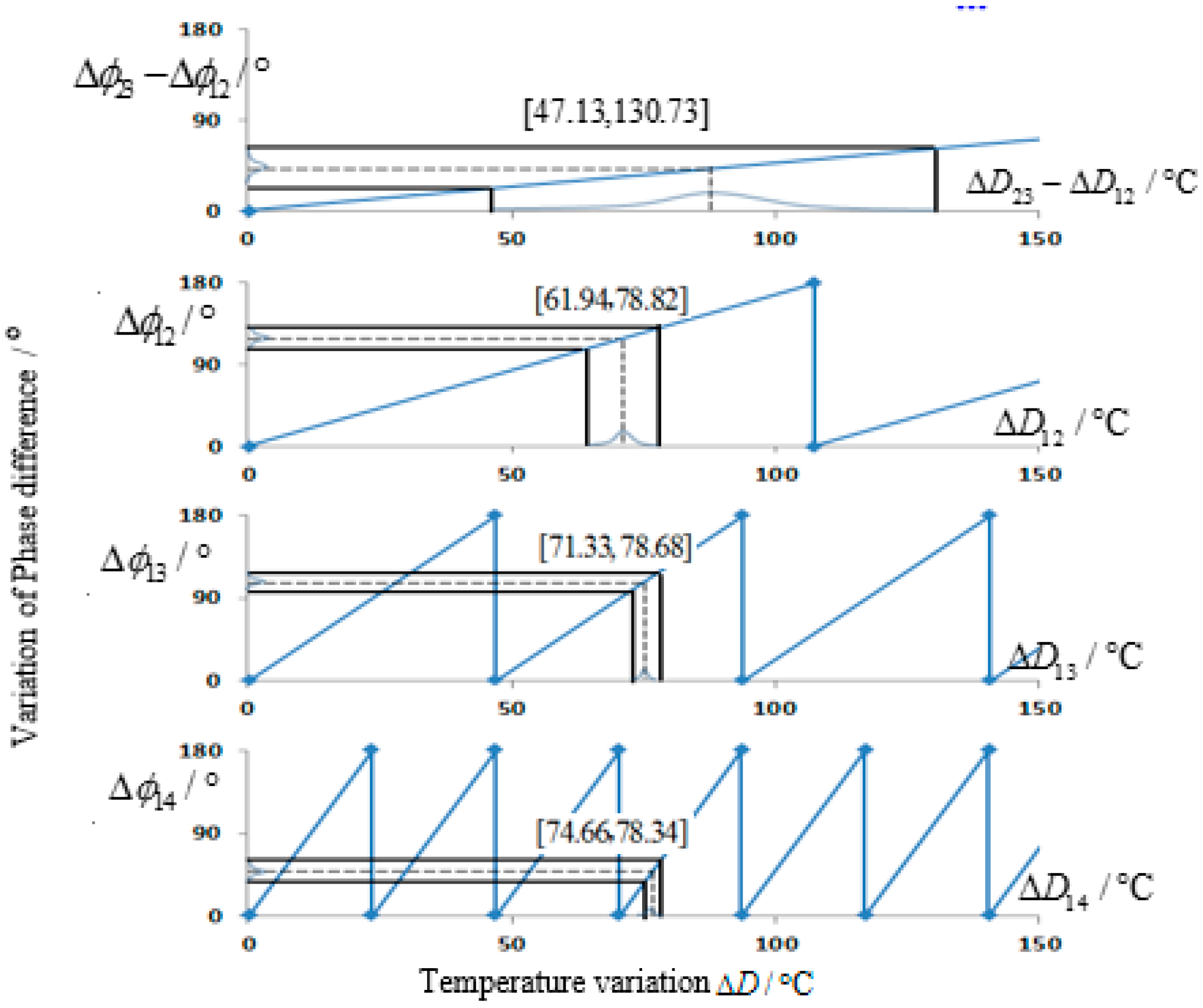
3.1. The Maximum Measurement Range
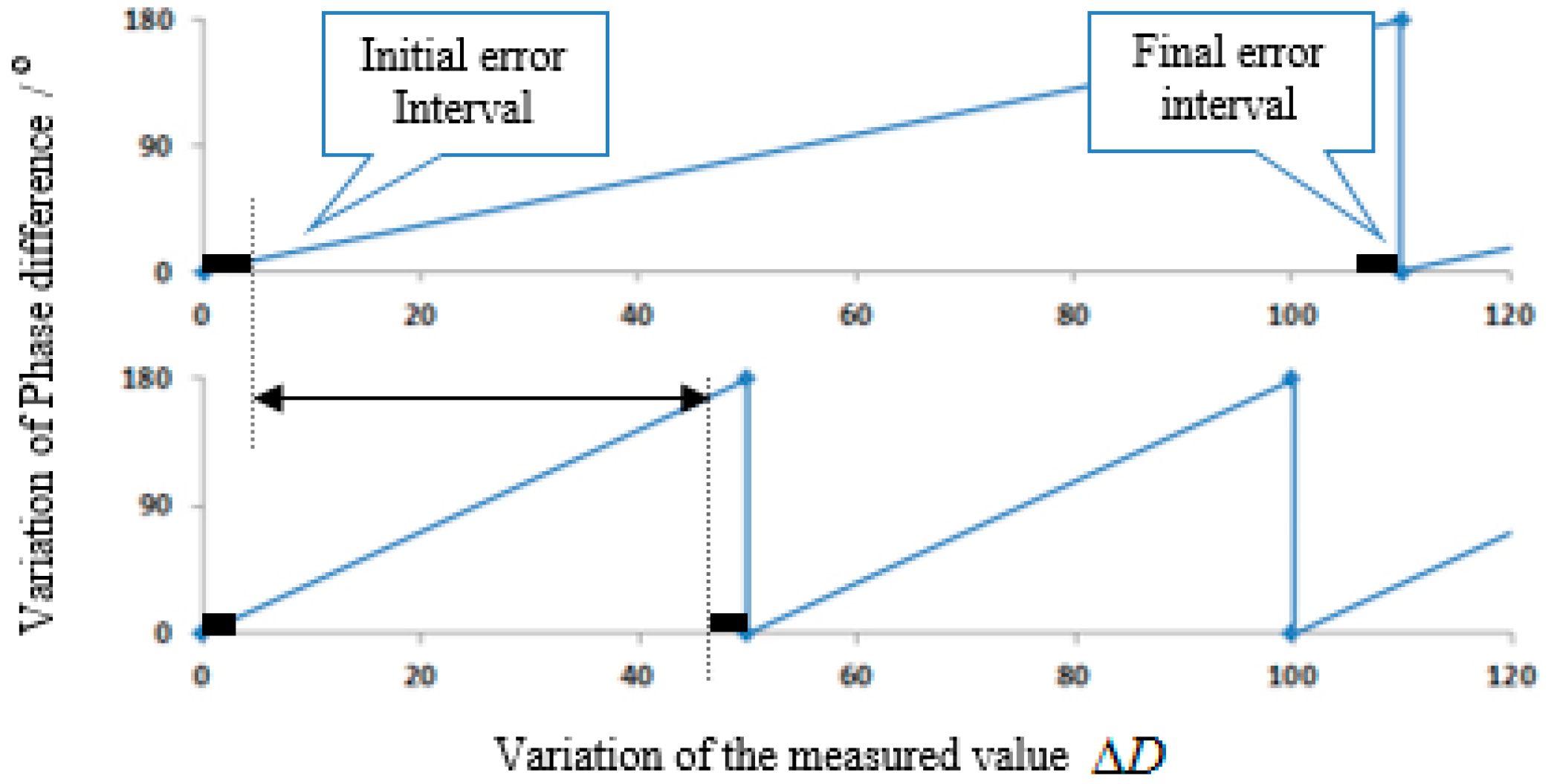
| Initial Error Interval | Final Error Interval | |
|---|---|---|
3.2. The Maximum Measurement Accuracy
4. Experimental Verification
4.1. VNA Test Results
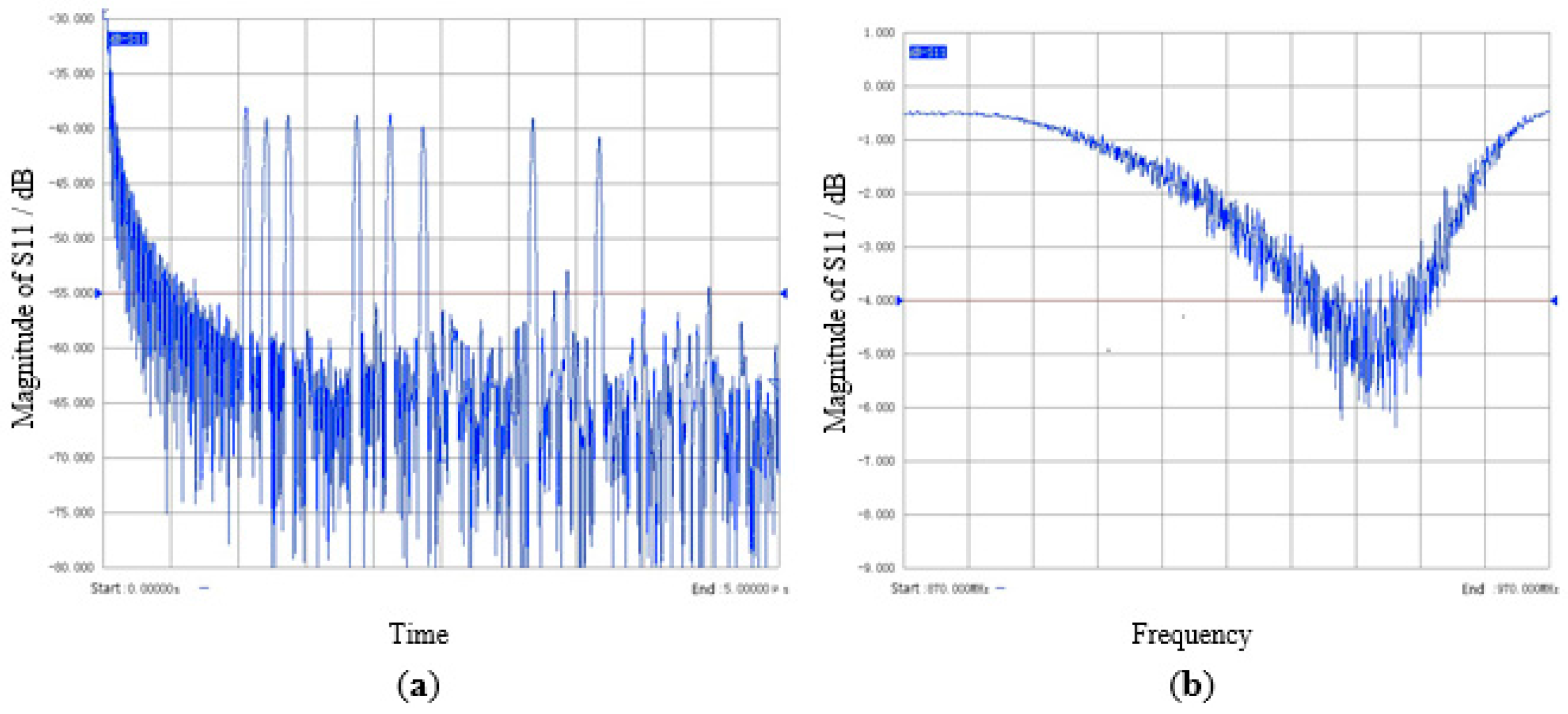

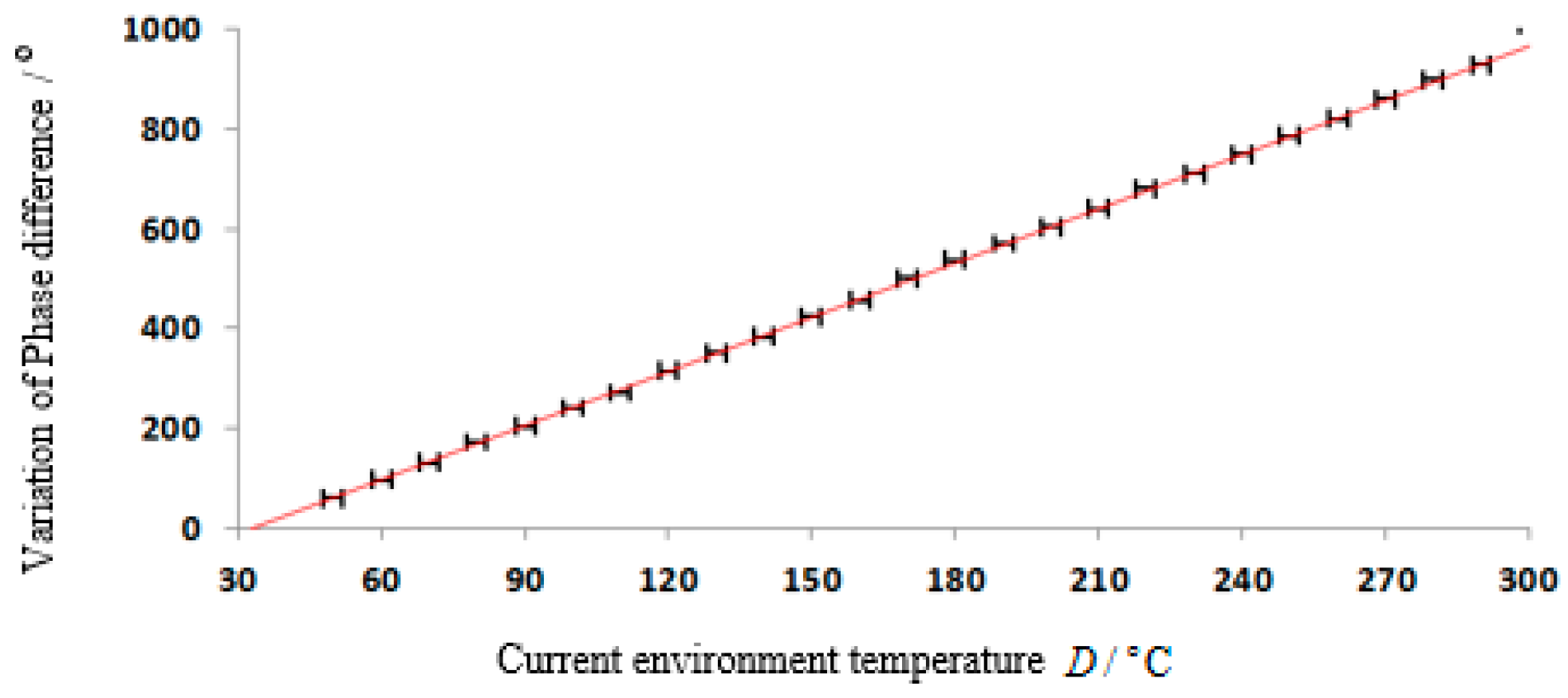
4.2. Reader Test Results
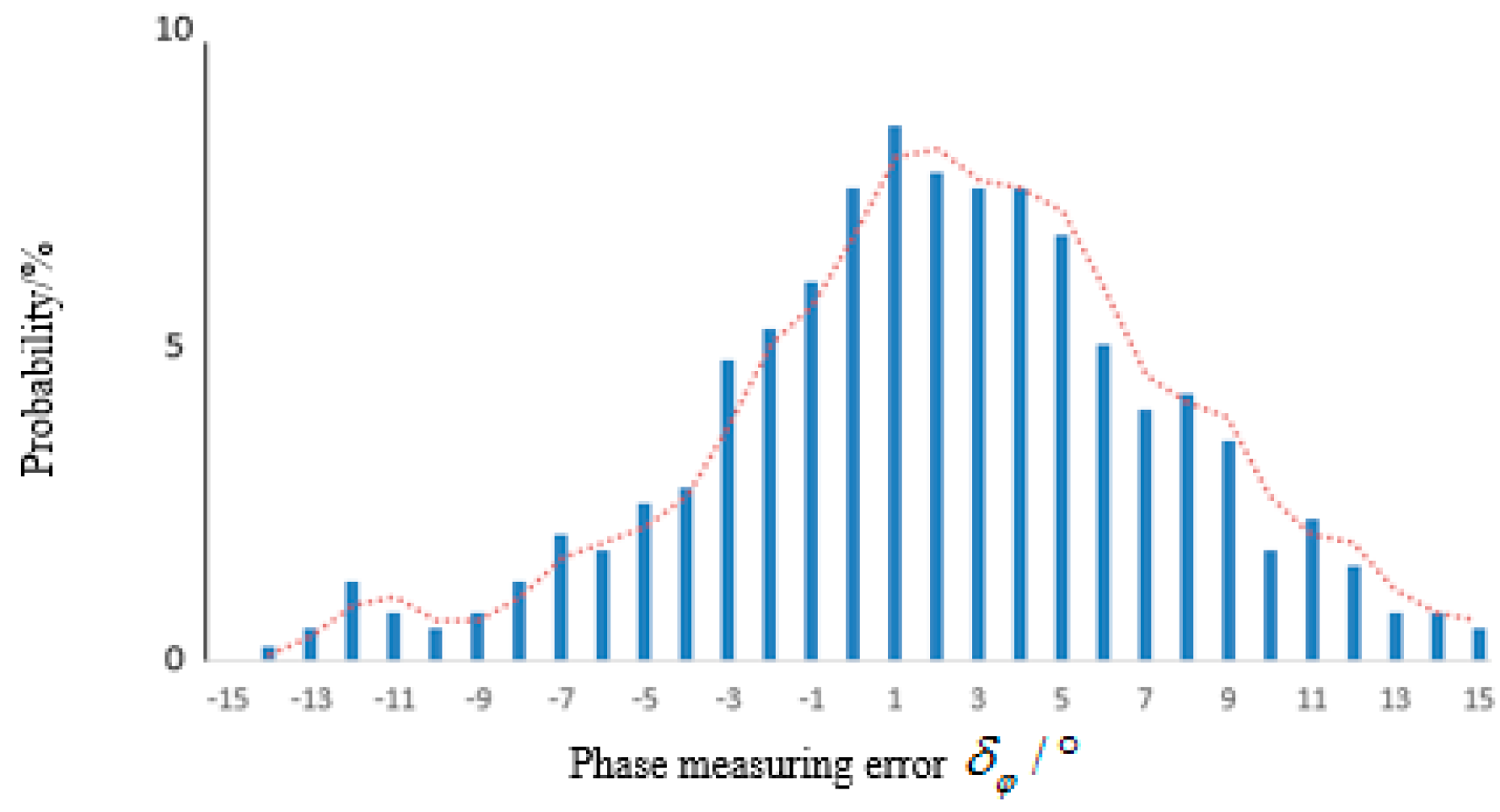
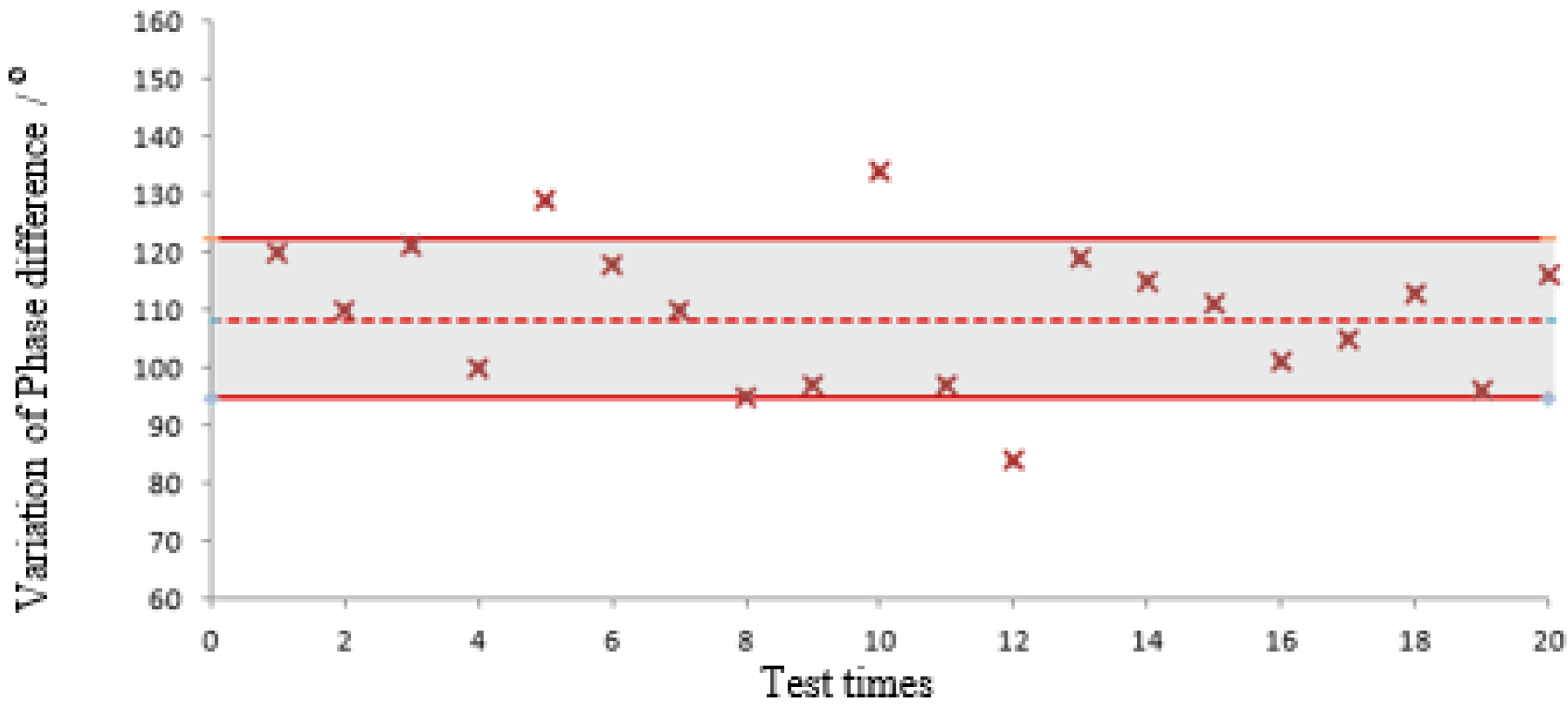
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pohl, A. A Review of wireless SAW sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 317–332. [Google Scholar] [CrossRef] [PubMed]
- Kang, A.L.; Zhang, C.R.; Ji, X.J.; Han, T.; Li, R.S.; Li, X.W. SAW-RFID enabled temperature sensor. Sens. Actuators A Phys. 2013, 201, 105–113. [Google Scholar] [CrossRef]
- Reindl, L.M.; Shrena, I.M. Wireless measurement of temperature using surface acoustic waves sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 1457–1463. [Google Scholar] [CrossRef] [PubMed]
- Li, B.D.; Yassine, O.; Kosel, J. A surface acoustic wave passive and wireless sensor for magnetic fields, temperature, and humidity. IEEE Sens. J. 2014, 15, 453–462. [Google Scholar] [CrossRef]
- Zheng, P.; Greve, D.W.; Oppenheim, I.J.; Chin, T.L. Langasite surface acoustic wave sensors: Fabrication and testing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 295–303. [Google Scholar] [CrossRef] [PubMed]
- da Cunha, M.P.; Lad, R.J.; Moonlight, T.; Moulzolf, S.; Canabal, A.; Behanan, R.; Davulis, P.M.; Frankel, D.; Bernhardt, G.; Pollard, T.; et al. Recent advances in harsh environment acoustic wave sensors for contemporary applications. In Proceedings of the 2011 IEEE Sensors Conferences, Limerick, Ireland, 28–31 October 2011; pp. 614–617.
- Shmaliy, Y.S.; Manzano, O.; Lucio, J.; Rojas-Laguna, R. Approximate estimates of limiting errors of passive wireless SAW sensing with DPM. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1797–1805. [Google Scholar] [CrossRef] [PubMed]
- Kuypers, J.; Reindl, L.; Tanaka, S.; Esashi, M. Maximum accuracy evaluation scheme for wireless SAW delay-line sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 1640–1652. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.; Scheiblhofer, S.; Reindl, L.; Stelzer, A. Performance evaluation of algorithms for SAW-based temperature measurement. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1177–1185. [Google Scholar] [CrossRef] [PubMed]
- Viikari, V.; Kokkonen, K.; Meltaus, J. Optimized signal processing for FMCW interrogated reflective delay line-type SAW sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2522–2526. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.D.; Dong, Y.G.; Feng, G. A multi-resolution wireless force sensing system based upon a passive SAW device. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 1438–1441. [Google Scholar] [CrossRef] [PubMed]
- Han, T.; Lin, W.; Lin, J.M.; Wang, W.B.; Wu, H.D.; Shui, Y.A. Errors of phases and group delays in SAW RFID tags with phase modulation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 2565–25705. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Han, T.; Qin, P. Maximum Measurement Range and Accuracy of SAW Reflective Delay Line Sensors. Sensors 2015, 15, 26643-26653. https://doi.org/10.3390/s151026643
Zheng Z, Han T, Qin P. Maximum Measurement Range and Accuracy of SAW Reflective Delay Line Sensors. Sensors. 2015; 15(10):26643-26653. https://doi.org/10.3390/s151026643
Chicago/Turabian StyleZheng, Zehua, Tao Han, and Peng Qin. 2015. "Maximum Measurement Range and Accuracy of SAW Reflective Delay Line Sensors" Sensors 15, no. 10: 26643-26653. https://doi.org/10.3390/s151026643
APA StyleZheng, Z., Han, T., & Qin, P. (2015). Maximum Measurement Range and Accuracy of SAW Reflective Delay Line Sensors. Sensors, 15(10), 26643-26653. https://doi.org/10.3390/s151026643





