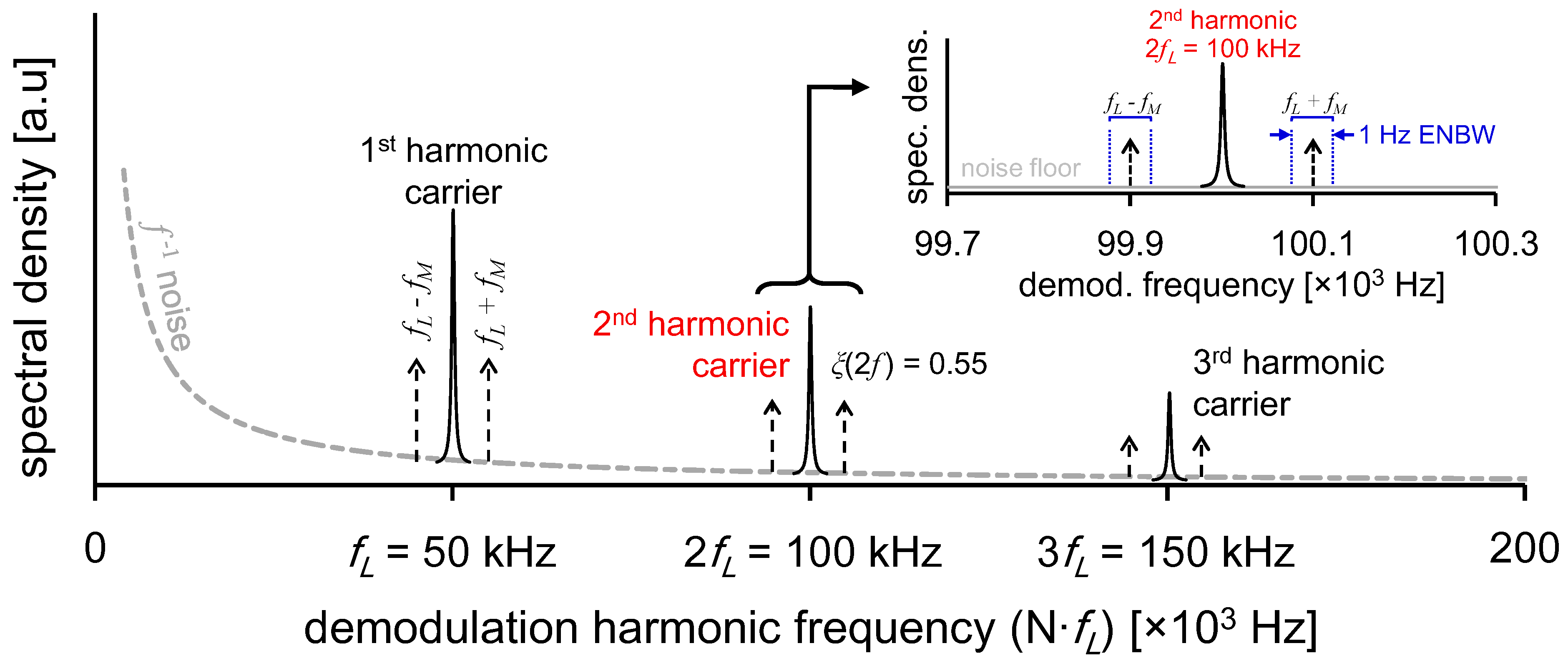
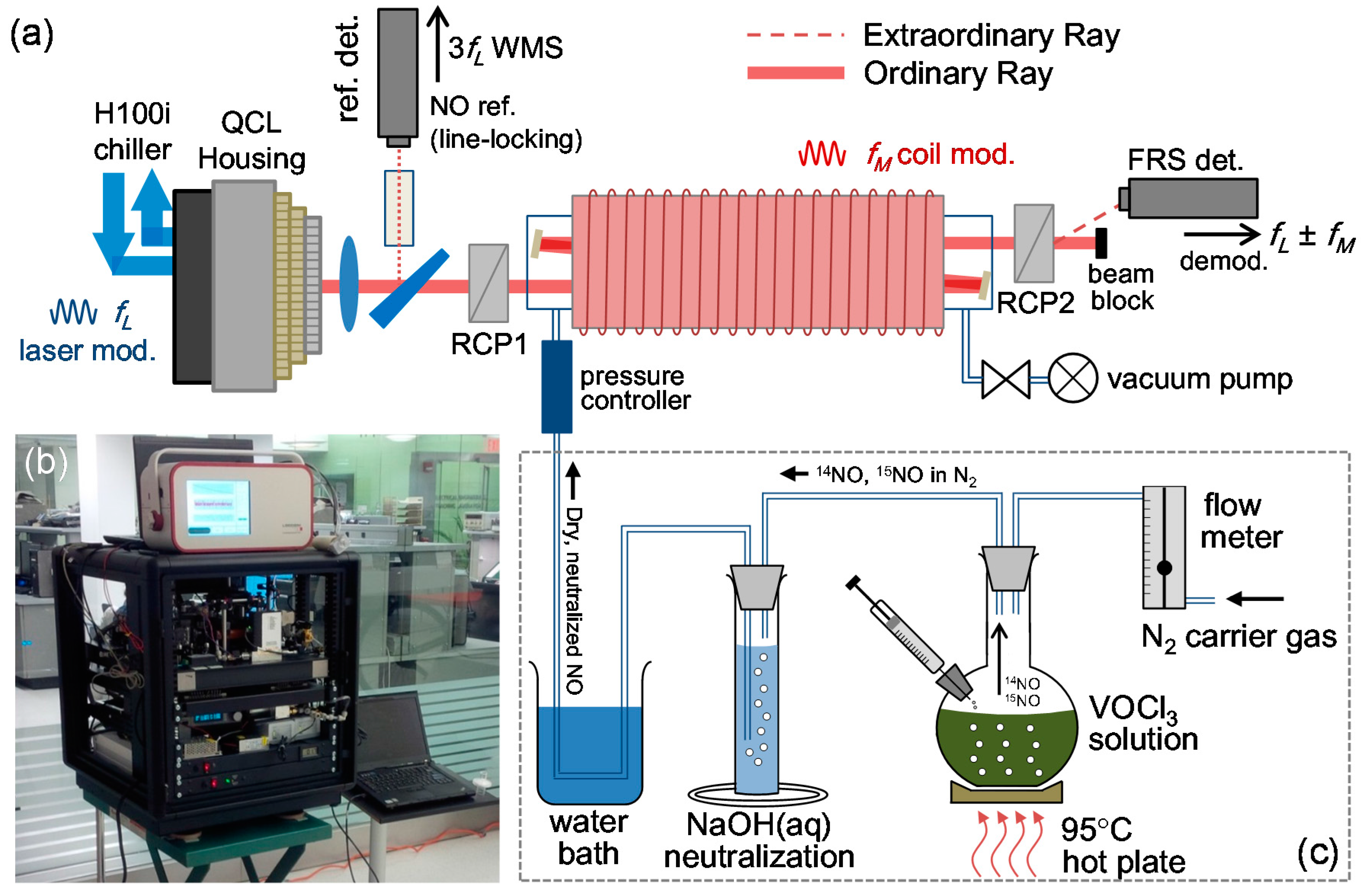
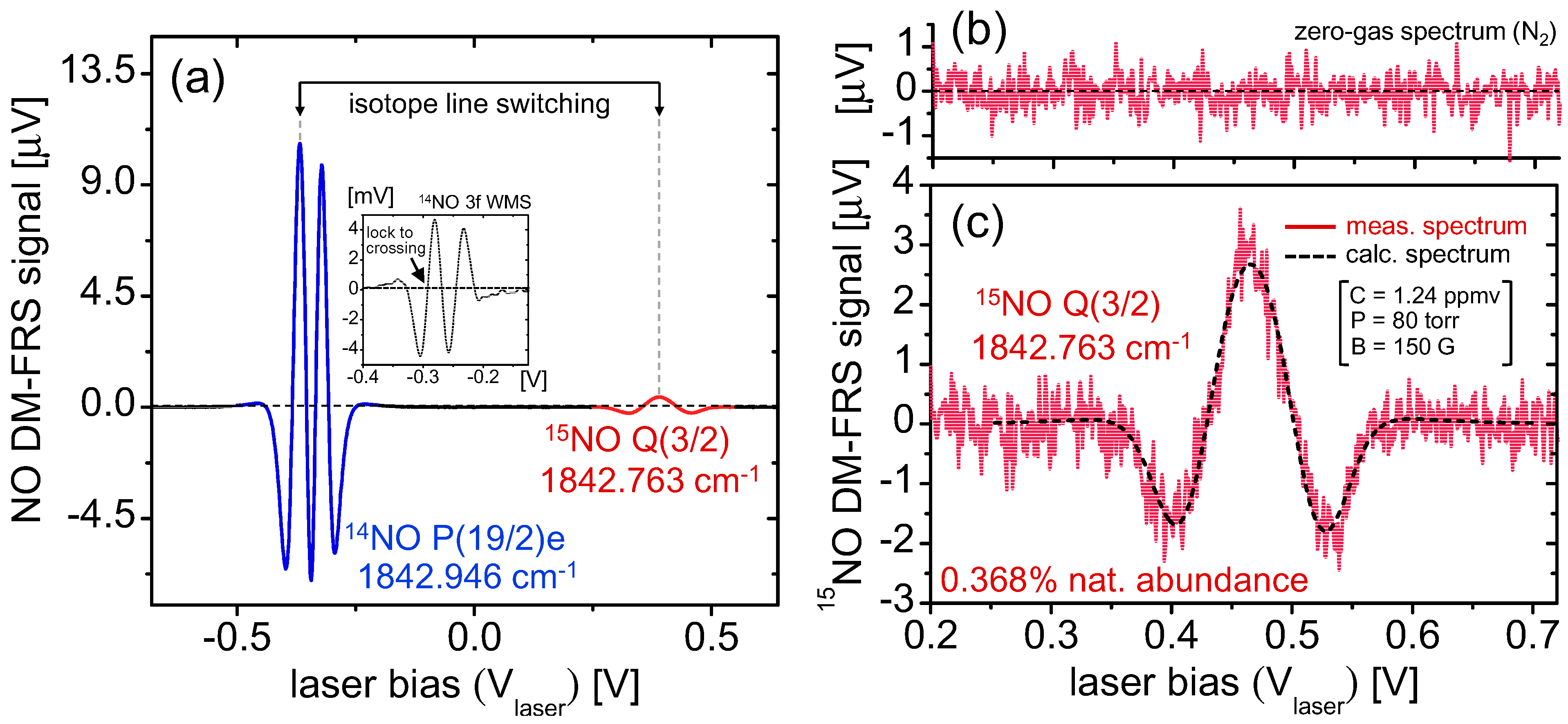
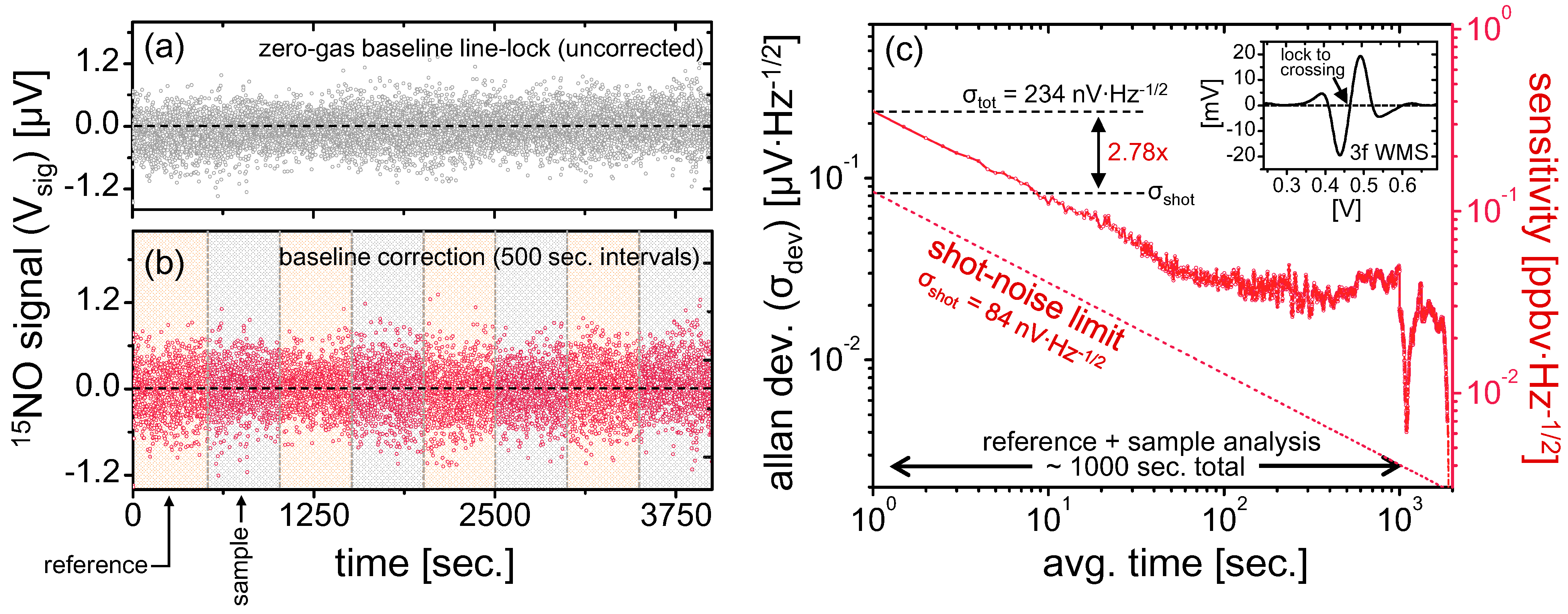
5.1. Real-Time Analysis of Gas Samples
In
Section 4, spectrometer noise characterization revealed a drift-free performance of approximately 1000 s, and it is expected that within this time frame the DM-FRS spectrometer provides high accuracy, and does not introduce measurement artefacts (
i.e., modification of the ratiometric value via instrument fractionation). The system measurements that are used to evaluate the isotopic ratios (δ
15N) are typically presented as permil (‰) values, defined according to [
25]:
where [N]
S and [N]
R represent the true sample and reference volume concentrations of NO. In the case of experimentally determined concentrations, we define an analogous ratiometric quantity:
We define the corresponding tilde notation to denote the raw measured signal on the spectrometer (typically measured in μV). The equality between volume concentration ratio (ppmv) defined in Equation (11) and raw signal ratio (μV) in Equation (12) generally holds true since [
15Ñ] = [
15N]·γ
15 and [
14Ñ] = [
14N]·γ
14 where γ is the ppmv to μV instrumental conversion factor for each isotope. Assuming sequential reference and sample measurements are made within the drift-free time-frame of the instrument (see
Section 4.3), we expect γ to remain the same (
i.e., γ
S14 = γ
R14 and γ
S15 = γ
R15), and therefore we expect δ
15N = δ
15Ñ (
i.e., the reference ratio to remain unchanged) within the stability time of the spectrometer. Within the preceding stability constraints and also for notational clarity, we use δ
15N to denote our measured isotopic ratio in the following discussion.
To evaluate the isotopic ratiometry performance of the system, we first consider the instantaneous ratiometric error Δ(δ
15N)(
t):
where we have defined our instantaneous signals [
15Ñ]
s(
t) and [
14Ñ]
s(
t) to be time dependent and our uncertainties Δ[
15Ñ]
s and Δ[
14Ñ]
s represent errors for data reported every 1 s (1 Hz measurements). The reference measurement error is assumed to be negligible, which can be assured through application of high concentration reference gases/liquid samples. By applying isotopic line switching with 50% measurement duty cycle between major and minor isotopes, it is appropriate to assume Δ[
15Ñ]
s/[
15Ñ]
s > Δ[
14Ñ]
s/[
14Ñ]
s. Propagation of the uncertainties in Equation (13) then gives:
For samples with near-natural abundance, Equation (14) reduces further to a straightforward relation between the ratiometric error and the relative precision of minor isotope detection:
From Equations (14) and (15), it is evident that error contributions of the spectrometer are inversely proportional to the minor isotope signal strength [
15Ñ]
s(
t). Thus, any noise and drifts in the system can be compensated by increasing the sample size for isotopic ratiometry measurements. As a rough approximation, with Δ[
15Ñ]
s = 234 nV·Hz
−1/2 indicated in
Figure 4c, a sub-permil precision can be achieved for 1 Hz measurements if ~100 ppmv NO samples are used, which would result in [
15Ñ]
s > 234 μV. With this relationship, one can predict minimum sample size required to achieve desirable instantaneous ratiometric precision.
Both the ratiometric precision and its concentration dependence as well as any potential fractionation effects of the gas analyzer can be conveniently evaluated using gas samples. To this end, we used the NO in N
2 mixture from the cylinder (with 1.24 ppmv
14NO concentration as calculated in
Section 4.2), which was manually diluted over a time span of 1200 s via mixing with dry nitrogen to produce a gradual concentration variation in the sample gas concentration with no modification to the relative isotopic composition of NO. For this test, only relative excursion from the mean isotopic composition is of importance, and the sample was assumed to have natural abundance of NO isotopes with nominal δ
15N = 0. The line-switch interval was set to 50 s (
Figure 5), with the gray shaded regions denoting
14NO measurement periods and the non-shaded regions denoting
15NO. Inherent to the line-switch process is the presence of gaps in the measurement of each isotope. To enable direct ratiometric calculation in the measurement regions of
15NO, we perform a polynomial interpolation of the
14NO signal (which has significantly higher SNR and negligible effect on the ratiometric error as shown in Equation (14)).
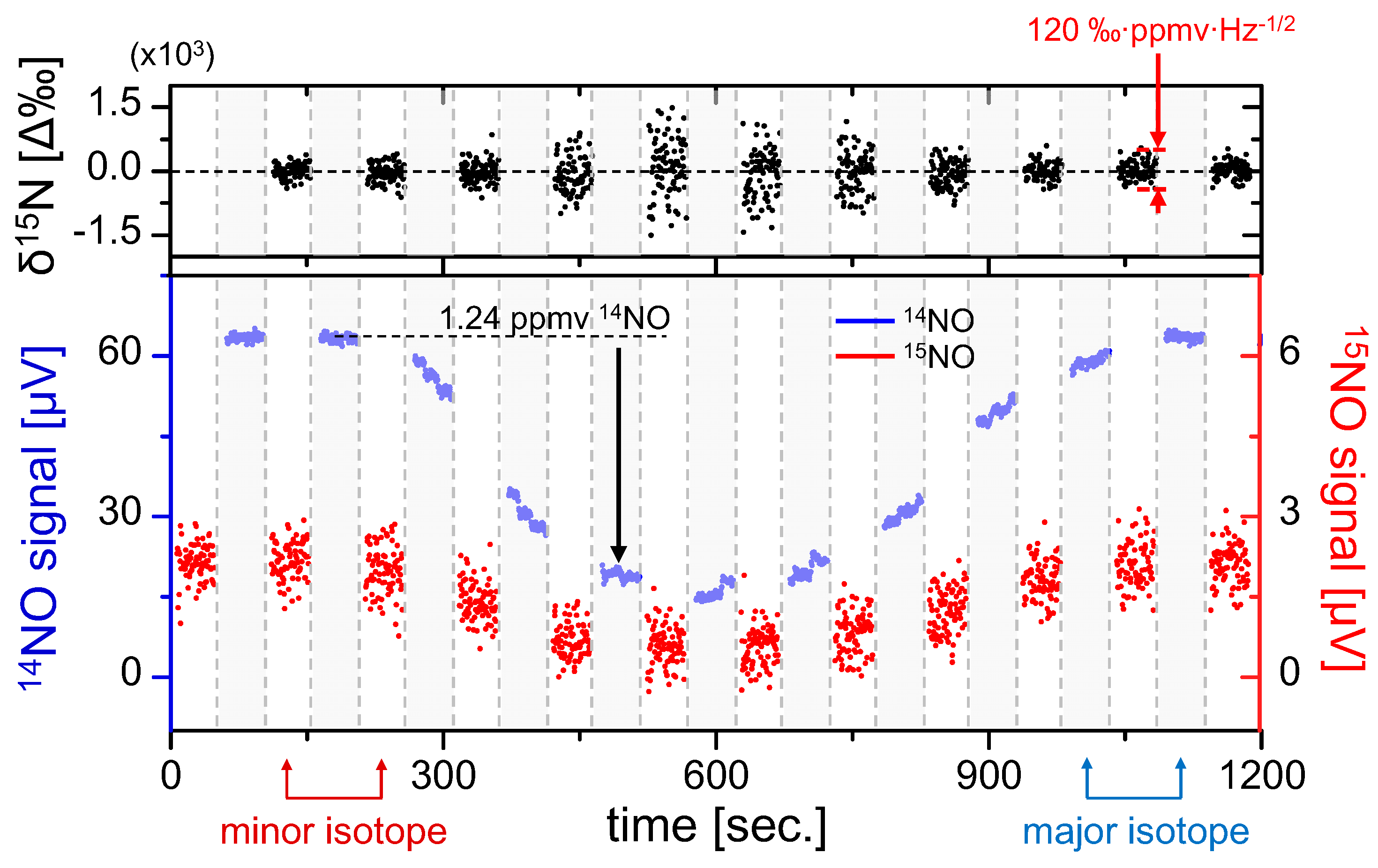
The results of isotopic analysis are shown in the top graph of
Figure 5, demonstrating negligible fractionation effects over the duration of NO variation. It is also clearly visible that the precision is degraded with smaller sample concentrations, which was predicted by Equations (14) and (15). Despite varying precision, during this test statistically the permil ratio does not deviate from the mean (0‰ assumed here), which confirms that the accuracy of the sensor is preserved over the ~1000 s measurement time, a result consistent with the Allan analysis in
Figure 4. Within a single 50 s measurement segment we have estimated a concentration-normalized ratiometric precision of 120‰·ppmv·Hz
−1/2. This confirms the previous estimate predicting that a sub-permil precision for a 1 Hz measurement near natural abundance requires NO concentrations of >100 ppmv.
Figure 5.
Quasi-simultaneous isotope measurement of 1.24 ppmv 14NO in N2 mixture diluted using pure nitrogen. Line-switching occurs every 50 s, and polynomial interpolation of 14NO is used to calculate the isotopic ratio (top graph). Gray regions denote 14NO measurements and white regions denote 15NO. Permil ratiometric values are calculated according to Equation (12), demonstrating fractionation-free system performance. A concentration-normalized precision of Δ(δ15N) = 120‰·ppmv·Hz−1/2 was determined from a typical measurement segment.
Figure 5.
Quasi-simultaneous isotope measurement of 1.24 ppmv 14NO in N2 mixture diluted using pure nitrogen. Line-switching occurs every 50 s, and polynomial interpolation of 14NO is used to calculate the isotopic ratio (top graph). Gray regions denote 14NO measurements and white regions denote 15NO. Permil ratiometric values are calculated according to Equation (12), demonstrating fractionation-free system performance. A concentration-normalized precision of Δ(δ15N) = 120‰·ppmv·Hz−1/2 was determined from a typical measurement segment.
5.2. Fluid Sample Analysis
To study real-time fractionation effects in the chemical conversion system for liquid sample analysis, it is necessary to preserve high ratiometric precision. Therefore in order to produce NO concentrations above 100 ppmv, we have used >1 μmol samples of liquid nitrate/nitrite solutions. As a demonstration of the quasi-simultaneous isotope measurement of fluid samples, we have injected 5 μmol (500 μL × 10 mM) KNO
3 (potassium nitrate) into the acidic vanadium(III) for measurement of NO isotopes as shown in
Figure 6. Broad peaks of ~100 s full-width half-maximum (FWHM) were obtained at a flow rate of 64 sccm, and line-switching at 15 s intervals was selected to ensure sufficient time resolution during the sample peak. In principle, the measurement duty cycle for each isotope (
14NO and
15NO) should be optimized such that the majority of time is spent on
15NO measurement (which has a lower SNR); however, this results in sparse and short
14NO segments, which in turn yields lower peak interpolation accuracy. From these experimental considerations we have chosen a simple 50% duty cycle between major/minor isotope switching. As mentioned in
Section 4.2, the PID line-lock requires 2.5 s settling time, and such an interval of data at the beginning of each measurement segment has been discarded prior to analyses. The final isotopic ratio (δ
15N
T) is referenced to a NO permeation device (G-Cal, Vici Metronics), whose isotopic ratio (B
R) has been characterized to remain independent of flow rate (tested from 10 sccm to 140 sccm) and concentration, and is therefore suitable as a stable reference for our measurements.
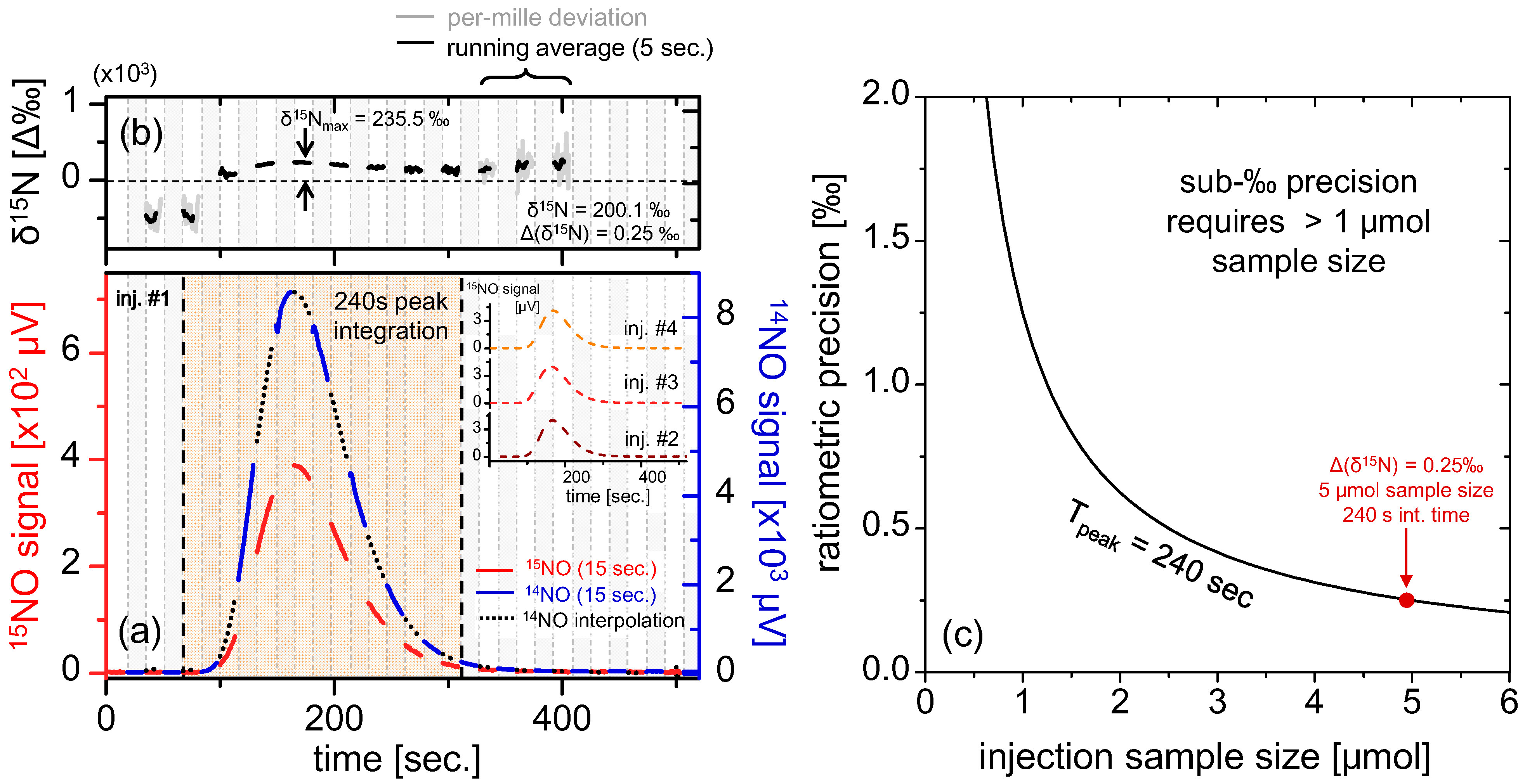
Figure 6.
(a) Real-time measurement of 5 μmol injection of KNO3 (500 μL of 10 mM solution) via line-switching every 15 s at 50% duty cycle for each isotope. The blue, red and black segments correspond to [14Ñ]S, [15Ñ]S and interpolated [14Ñ]S respectively. The resulting peak has FWHM of ~100 s, obtained in a flow rate of 64 sccm, and the inset shows three more repeat injections (only [15Ñ]S is shown for clarity); (b) Ratiometric curves derived from the quotient of [15Ñ]S(t) and interpolated [14Ñ]S. A clear time dependent curvature is apparent, with a maxima occurring at the measurement peak; (c) Calculation of ratiometric precision vs. sample size, using data obtained from (a). Generally, samples >1 μmol NO3− are required to ensure sub-permil precisions over the span of the peak.
Figure 6.
(a) Real-time measurement of 5 μmol injection of KNO3 (500 μL of 10 mM solution) via line-switching every 15 s at 50% duty cycle for each isotope. The blue, red and black segments correspond to [14Ñ]S, [15Ñ]S and interpolated [14Ñ]S respectively. The resulting peak has FWHM of ~100 s, obtained in a flow rate of 64 sccm, and the inset shows three more repeat injections (only [15Ñ]S is shown for clarity); (b) Ratiometric curves derived from the quotient of [15Ñ]S(t) and interpolated [14Ñ]S. A clear time dependent curvature is apparent, with a maxima occurring at the measurement peak; (c) Calculation of ratiometric precision vs. sample size, using data obtained from (a). Generally, samples >1 μmol NO3− are required to ensure sub-permil precisions over the span of the peak.
The data in
Figure 6b clearly demonstrate a varying instantaneous permil ratio over the sample peak. Provided that the spectrometer itself is fractionation-free as shown in the previous section, we conclude that the fractionation observed during the liquid sample analysis originates from the chemical conversion unit. Mass fractionation may result in shifted
15NO and
14NO peaks, and the δ
15N(
t) at any given point in time may not be an accurate representation of the sample composition. Therefore to reduce the effects of time-dependent fractionation it is critical to measure the entire peak (
i.e., integrating the entire peak ensures we have taken all chemically produced NO molecules into account). To calculate the total permil value δ
15N
T the ratio of the integrated peaks is used according to:
where we define B
R as the reference ratio (G-Cal permeation device), and T as the time-span used for
15NO measurement (peak integration time is ~50% total peak time due to isotope switching). Using [
15Ñ]
s(
t) = B
R·[δ
15N(
t)/10
3 + 1]·[
14Ñ]
s(
t) from Equation (12), we obtain
This demonstrates that the final isotopic ratio can be considered as a weighted average of the instantaneous permil ratio (
Figure 6b) over the major isotopic peak. Furthermore, Equation (17) indicates that as [
14Ñ]
s(
t) degrades near the wings of the peak, the relative contribution of δ
15N(
t) to δ
15N
T becomes proportionally smaller. Qualitatively, the accuracy of the final ratiometric calculation is hardly affected by the integration of the wings, and any residual accuracy deviation is corrected via calibration with known references.
Propagation of error in Equation (17) and noting that the 1 Hz precisions Δ[
15Ñ]
s are uncorrelated and sum in quadrature, will result in a simple extension of Equation (14) of the following form:
Intuitively, Equation (18) can be understood as the quotient of time-averaged noise and signal for the minor isotope, multiplied by a conversion factor (~10
3 for samples near B
R abundance) to convert to ratiometric (‰) units. Since in case of the liquid samples the entire sample peak is used for measurement, the time-averaging further improves ratiometric precision, which is also sample size dependent. The effect of sample size variation on ratiometric precision is plotted in
Figure 6c, which indicates sub-‰ precision for sample sizes >1 μmol. For the peak shown in
Figure 6a derived from a 5 μmol KNO
3 sample, we calculate δ
15N
T = 200.1‰ and Δ(δ
15N
T) = 0.25‰, demonstrating ratiometric precision well within sub-permil range. Multiple repeat injections yielded very similar ratiometric values (three [
15Ñ]
S(
t) measurements are shown in the inset, and [
14Ñ]
S(
t) is excluded for clarity) with the average isotopic ratio of (δ
15N
T)
avg = 199.0‰. The standard deviation of (δ
15N
T)
stdev = 5.08‰ was calculated for the best four out of five injections, which is significantly higher than: (i) instrument precision of 0.25‰ (calculated for 5 μmol KNO
3) and (ii) instrument drift (sub-‰ for ~10
3 s as calculated from
Figure 4c); therefore, we conclude the principal contribution to the measurement error originates from uncertainty introduced by the chemical reduction of nitrates within the sampling front-end.
5.3. Ratiometric Linearity
In
Section 5.1, fractionation-free system performance was demonstrated, supporting the conclusion that the real-time fractionation described in
Section 5.2 may be attributed to isotopic variations in the sample gas. At this point it is appropriate to consider how the ratiometric accuracy varies with isotopic composition. This sensor linearity test was conducted by performing 400 nmol injections of samples with known isotopic compositions with ratiometric values of 5‰, 1111‰, 2218‰, and 5536‰ prepared using a mixture of 99%
15N enriched potassium nitrate (Cambridge Isotopes) with natural abundance nitrate (Fisher Scientific). The samples injected were substantially smaller (by roughly 12.5×) than prior injections demonstrated in
Section 5.2, thus yielding lower ratiometric precision of Δ(δ
15N) = 2‰ (consistent with Equation (18) and
Figure 6b). Four repeat injections were conducted for each ratiometric sample, and the results are plotted in
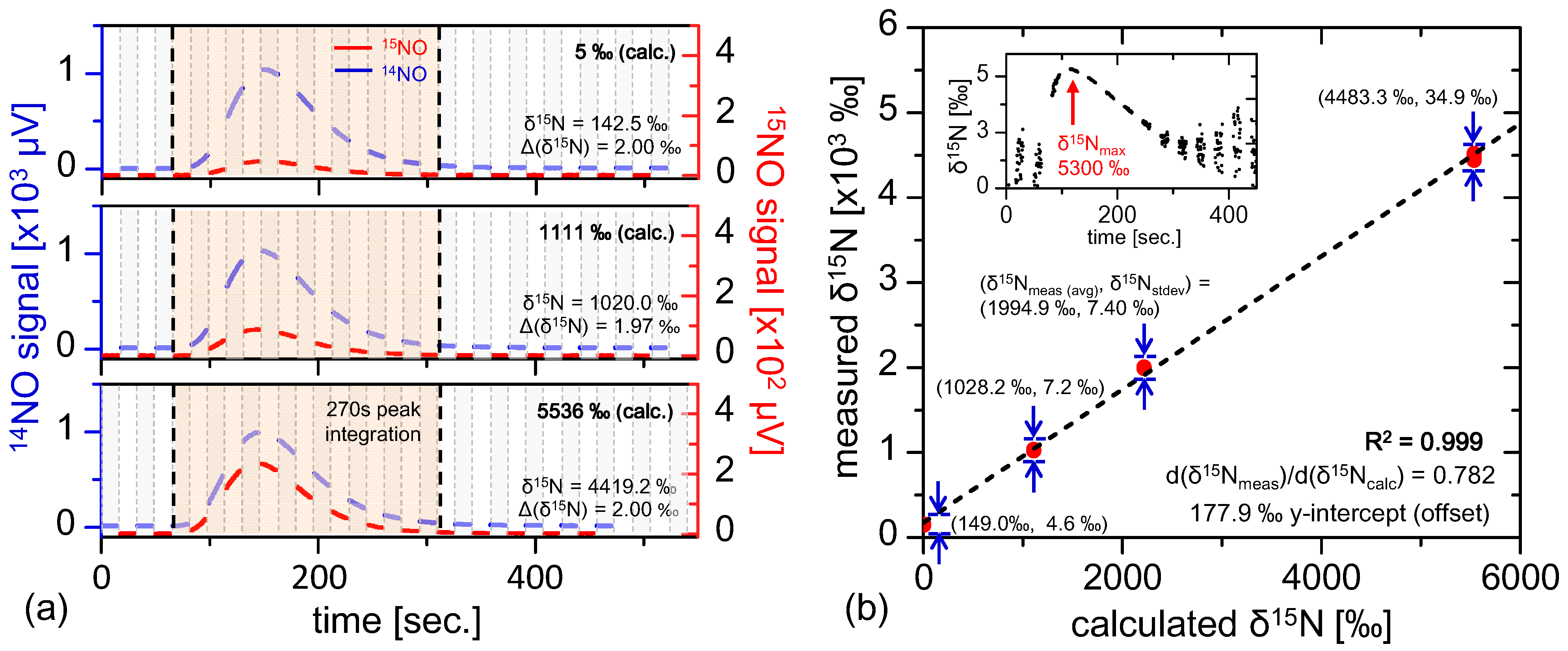
Figure 7b. The ratiometric analyses demonstrate excellent linearity (R
2 = 0.999), with a ratiometric offset of 177.9‰ that is consistent with those observed with near-natural abundance samples shown in
Figure 6a. Additionally, it is interesting to note that the ratio of measured to calculated isotopic ratio is not unity (dδ
15N
meas/dδ
15N
calc = 0.782), indicating possible preference of
14NO in the vanadium(III) conversion process. Different temperature dependence of the transition linestrength between
14NO and
15NO have been considered as a source of this effect, but calculations yield slope modification factors far below the observed deviation for temperature differences up to hundreds of Kelvin. Nevertheless, the excellent linearity demonstrates consistency in the sample conversion and measurement process, thus allowing any sample to be calibrated via known references.
Figure 7.
(
a) Multiple injections of known isotopically labeled references spanning from 5‰ to 5536‰, where the
15NO signal is clearly enhanced for enriched samples. The smaller 400 nmol injection size reduces ratiometric precision (Δ(δ
15N) ≈ 2‰), consistent with
Figure 6c and Equation (18); Plotted in (
b) are multiple labeled reference injections (4 points per calculated δ
15N value, and the plot demonstrates excellent linearity (R
2 = 0.999) with measured δ
15N offset consistent with fractionation observed in
Figure 6a. The inset shows the shape of real-time fractionation curve of the most enriched reference injection (δ
15N
calc = 5536‰), demonstrating results similar to those in
Section 5.2.
Figure 7.
(
a) Multiple injections of known isotopically labeled references spanning from 5‰ to 5536‰, where the
15NO signal is clearly enhanced for enriched samples. The smaller 400 nmol injection size reduces ratiometric precision (Δ(δ
15N) ≈ 2‰), consistent with
Figure 6c and Equation (18); Plotted in (
b) are multiple labeled reference injections (4 points per calculated δ
15N value, and the plot demonstrates excellent linearity (R
2 = 0.999) with measured δ
15N offset consistent with fractionation observed in
Figure 6a. The inset shows the shape of real-time fractionation curve of the most enriched reference injection (δ
15N
calc = 5536‰), demonstrating results similar to those in
Section 5.2.