Non-Rigid Structure Estimation in Trajectory Space from Monocular Vision
Abstract
:1. Introduction
2. The Problem of Non-Rigid Structure Estimation
3. The Calculation of Matrix S Using PTA
4. The Optimization of Matrix S Using the APG Algorithm
4.1. The Trace-Minimization Problem
4.2. The Application of the APG Algorithm
| Algorithm 1. The steps of the APG algorithm. |
| Step 1. Initialization: Given , , , K=1, 2, 3... |
| Step 2. While not converged do |
| Step 3. |
| Step 4. |
| Step 5. |
| Step 6. , |
| Step 7. End while. |
| Step 8. , namely the reconstructed structure matrix . |
5. Experiment Results
5.1. The Yoga Sequence Experiment
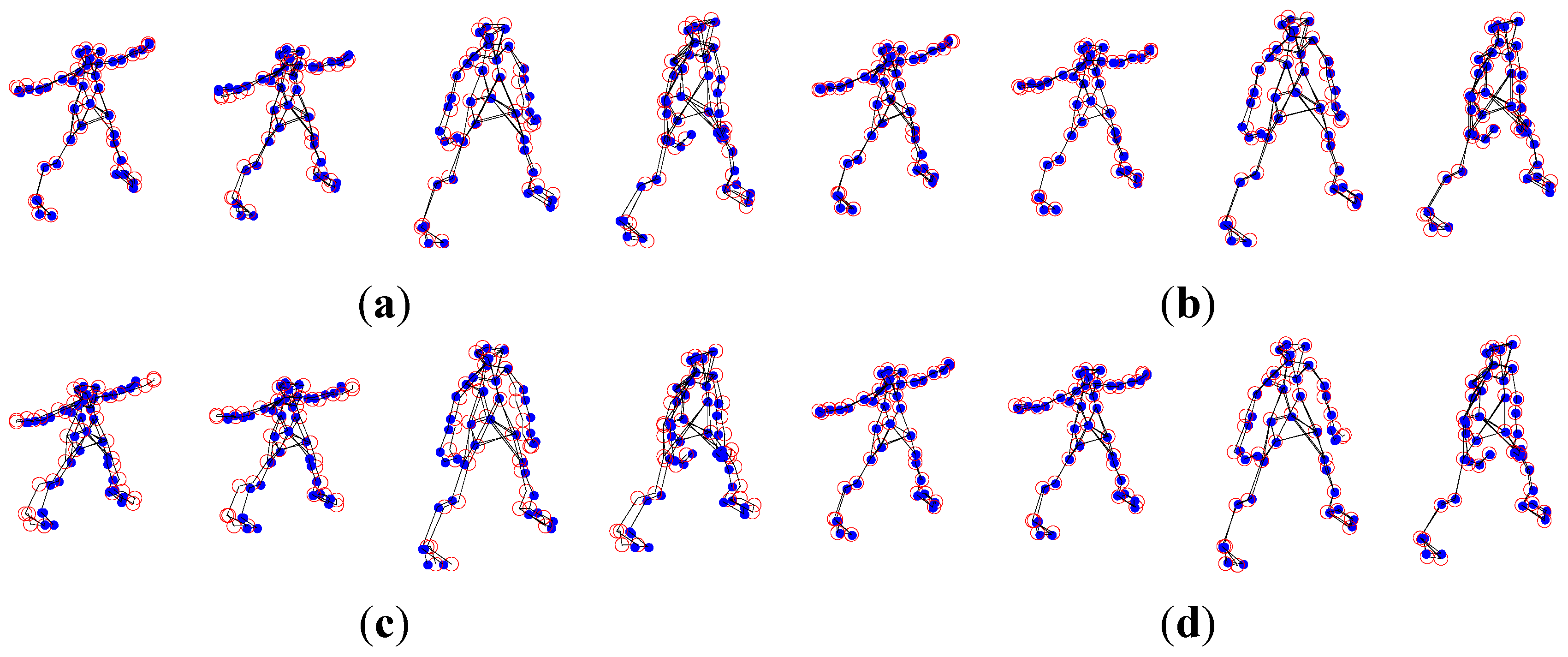
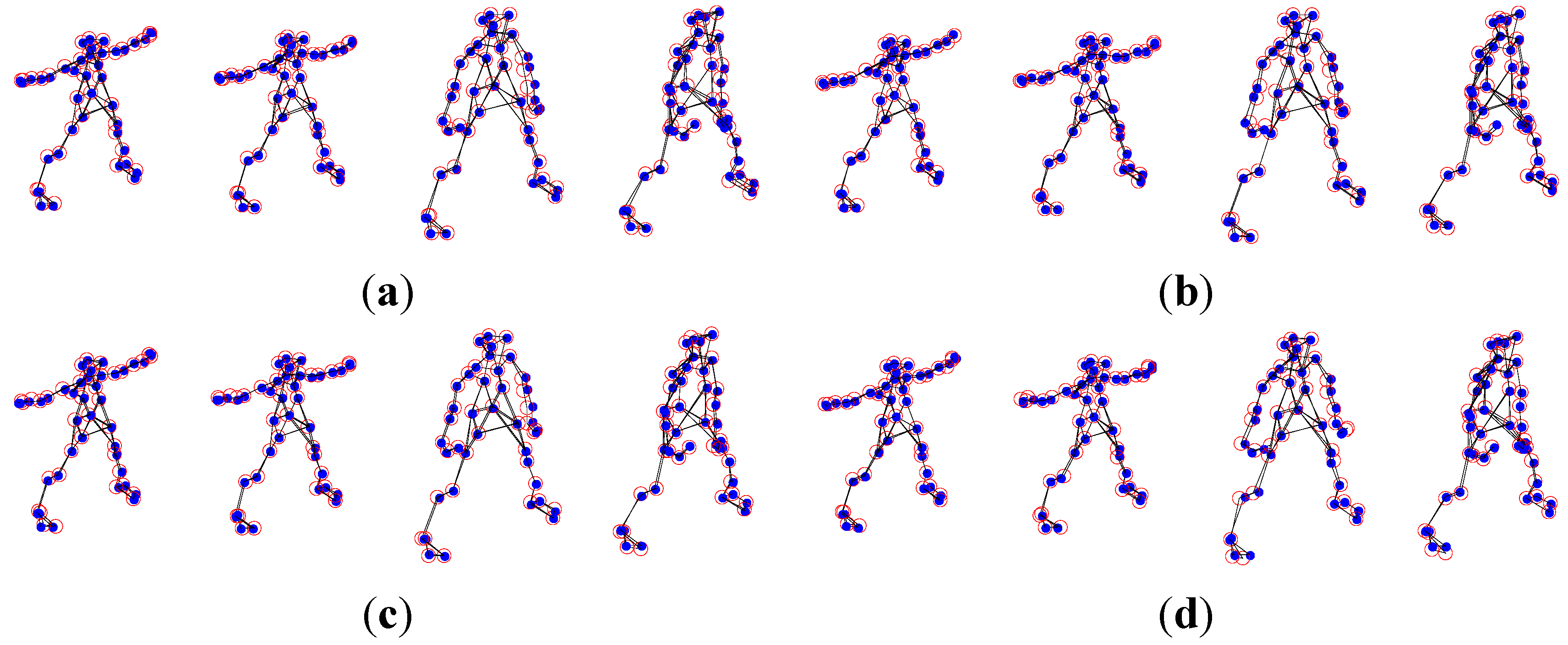
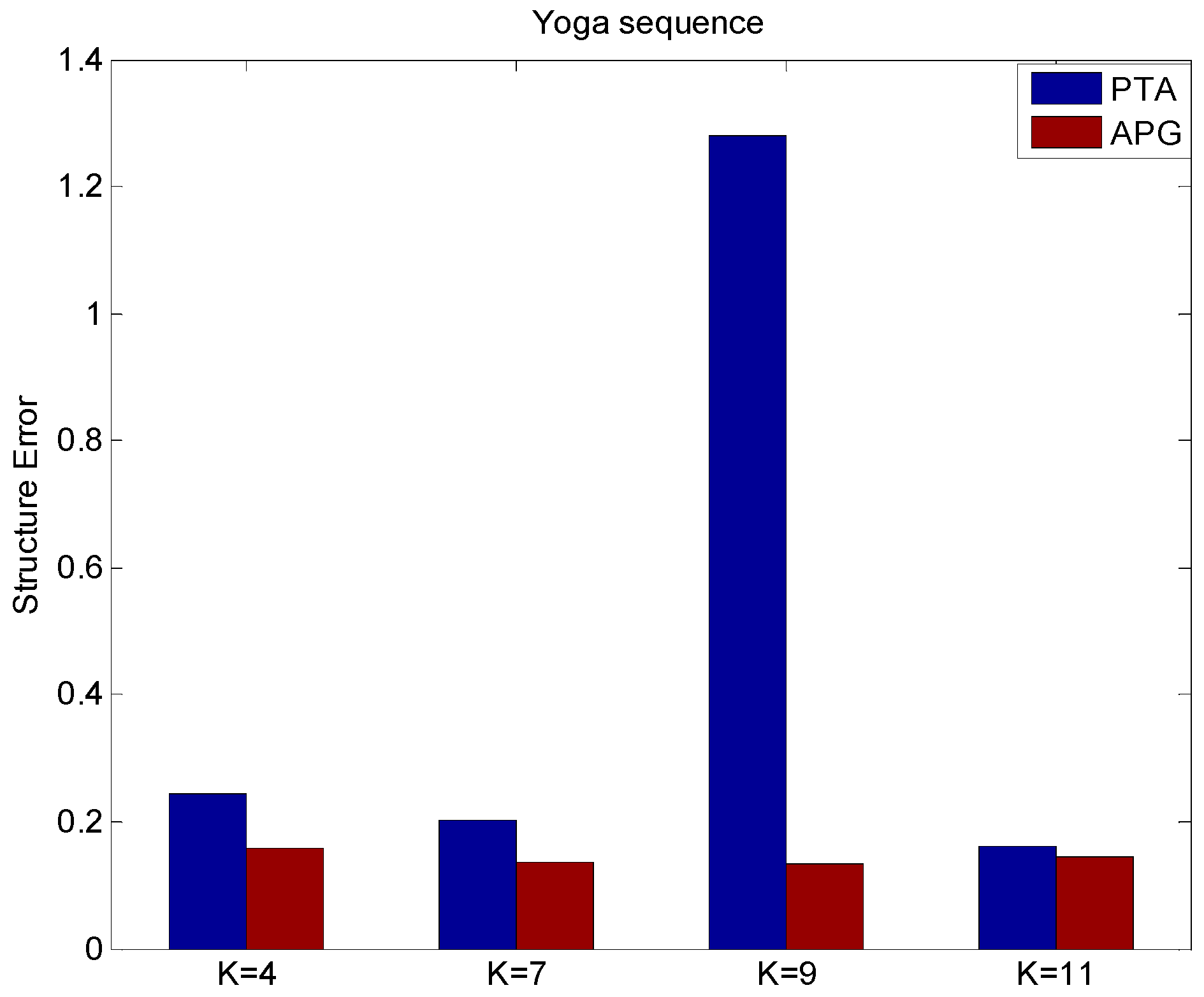
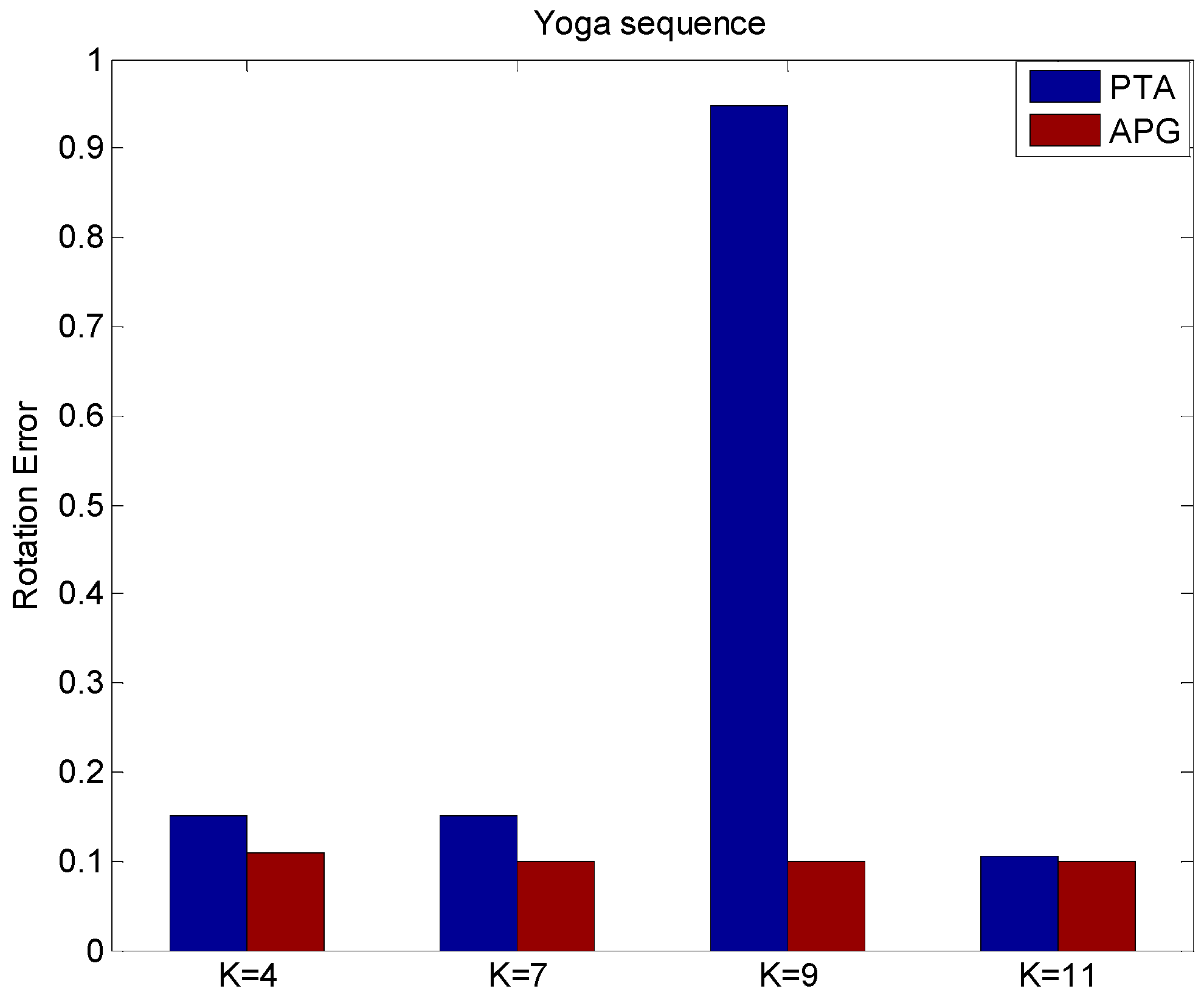
5.2. The Pickup Sequence Experiment
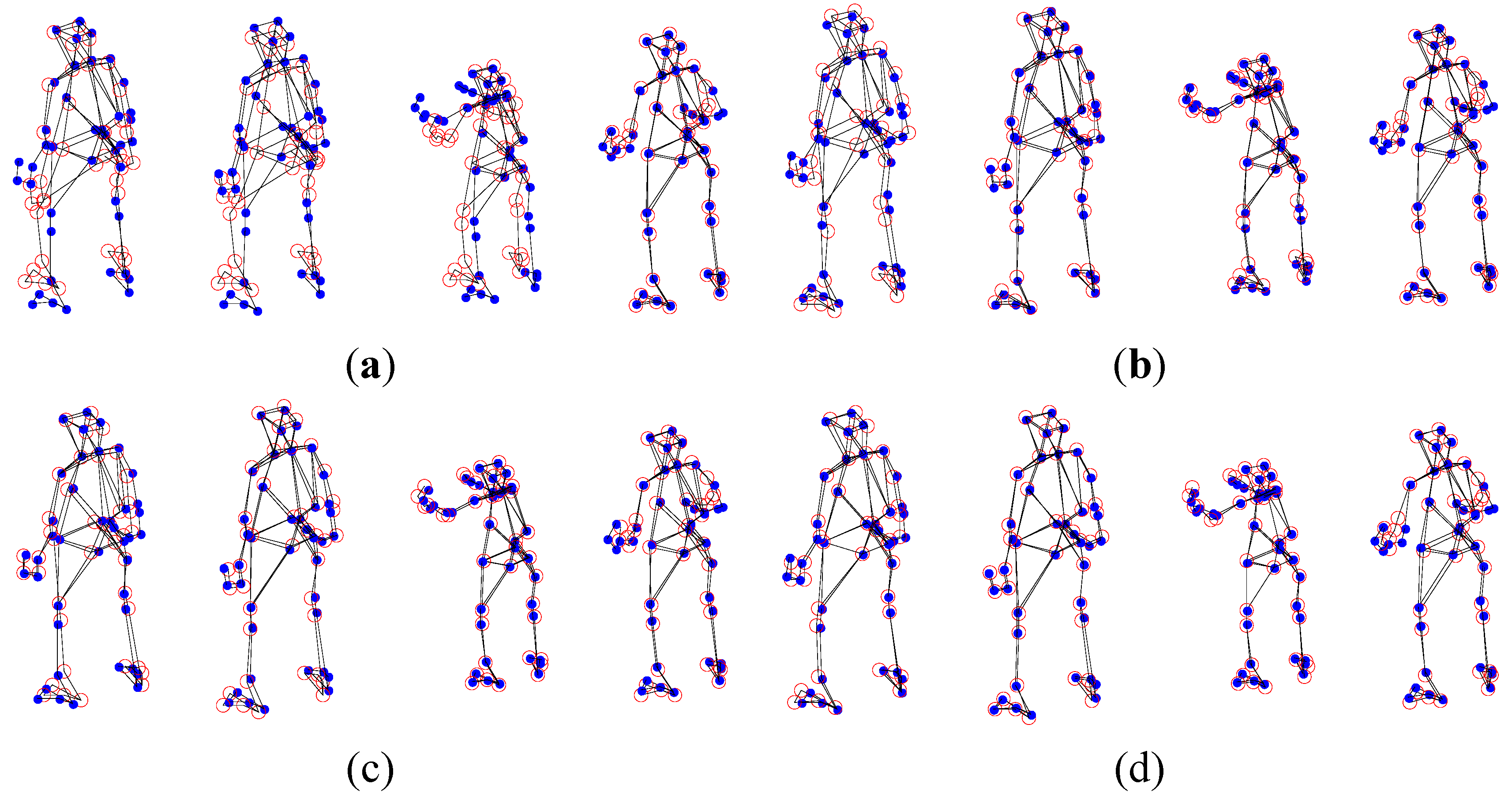
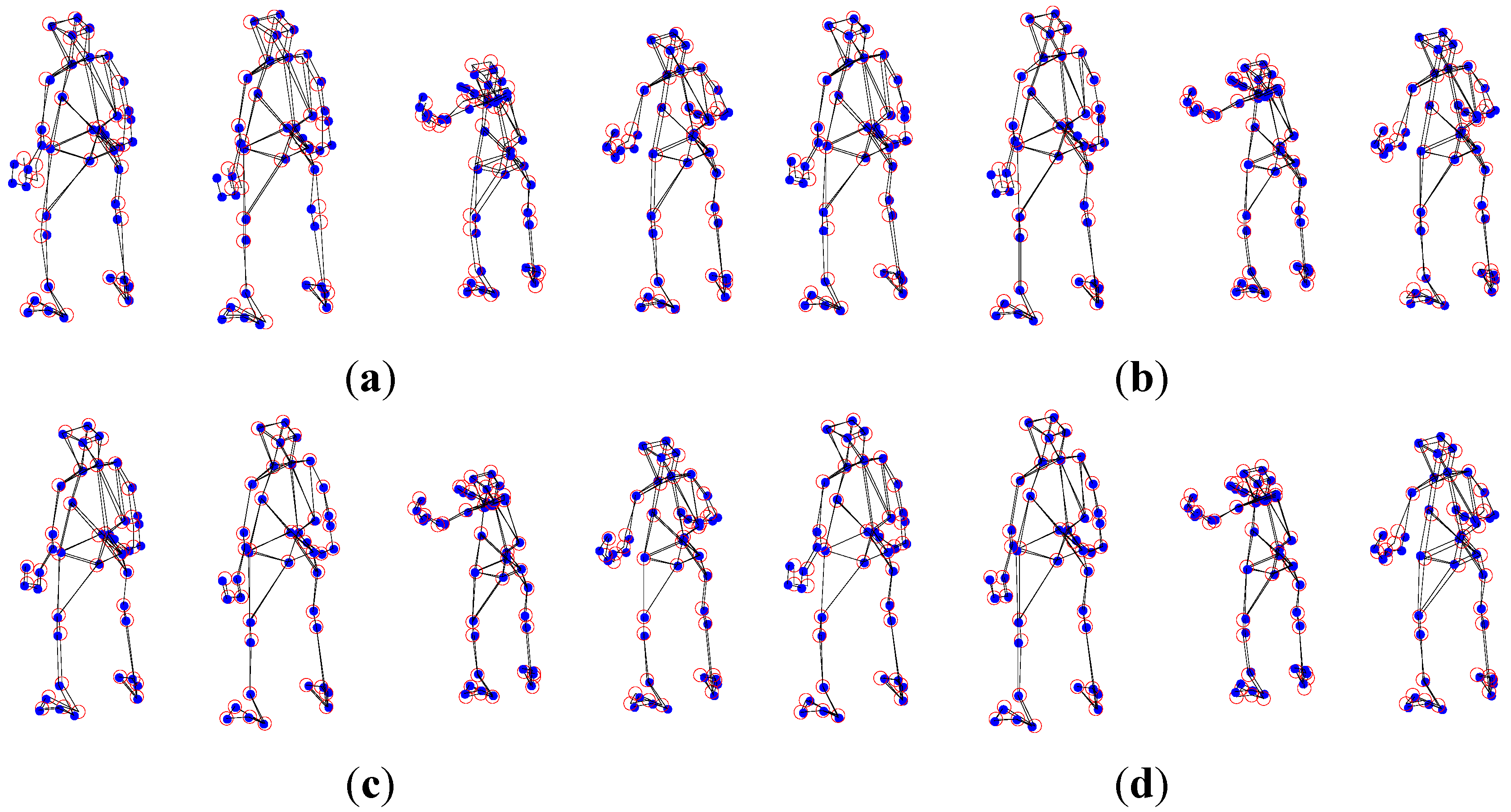
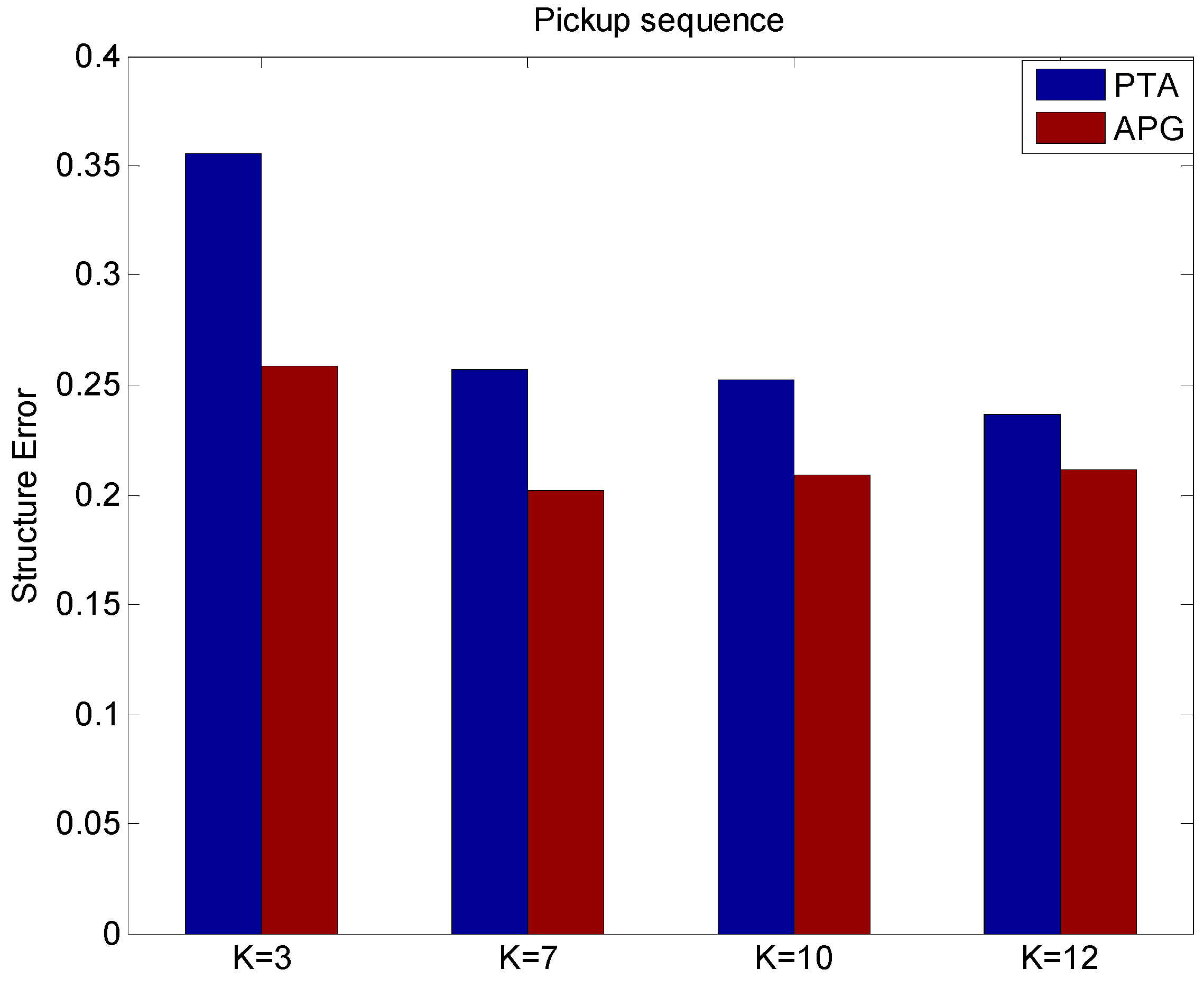
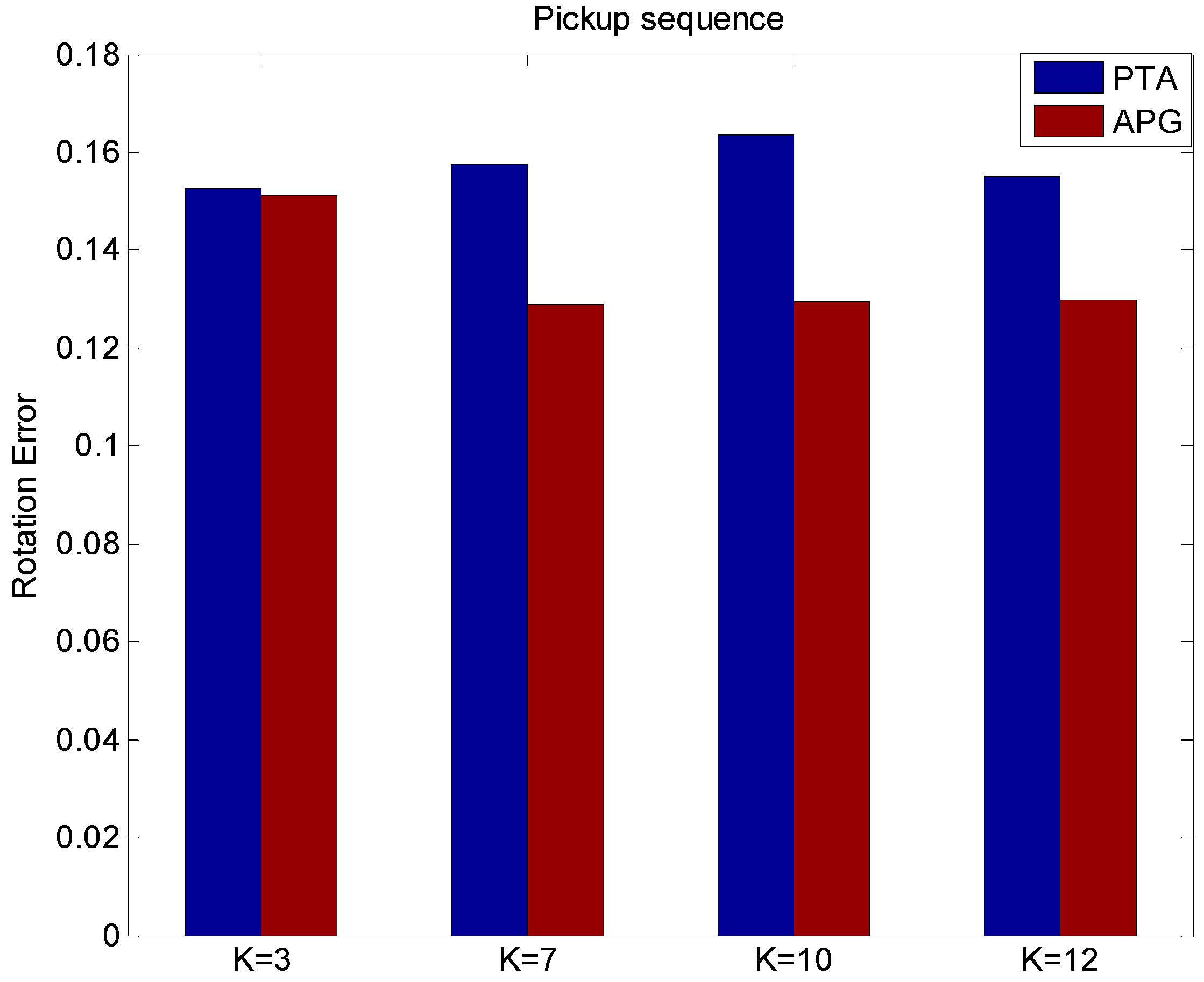
5.3. The Comparison of APG Method and Block Matrix Method
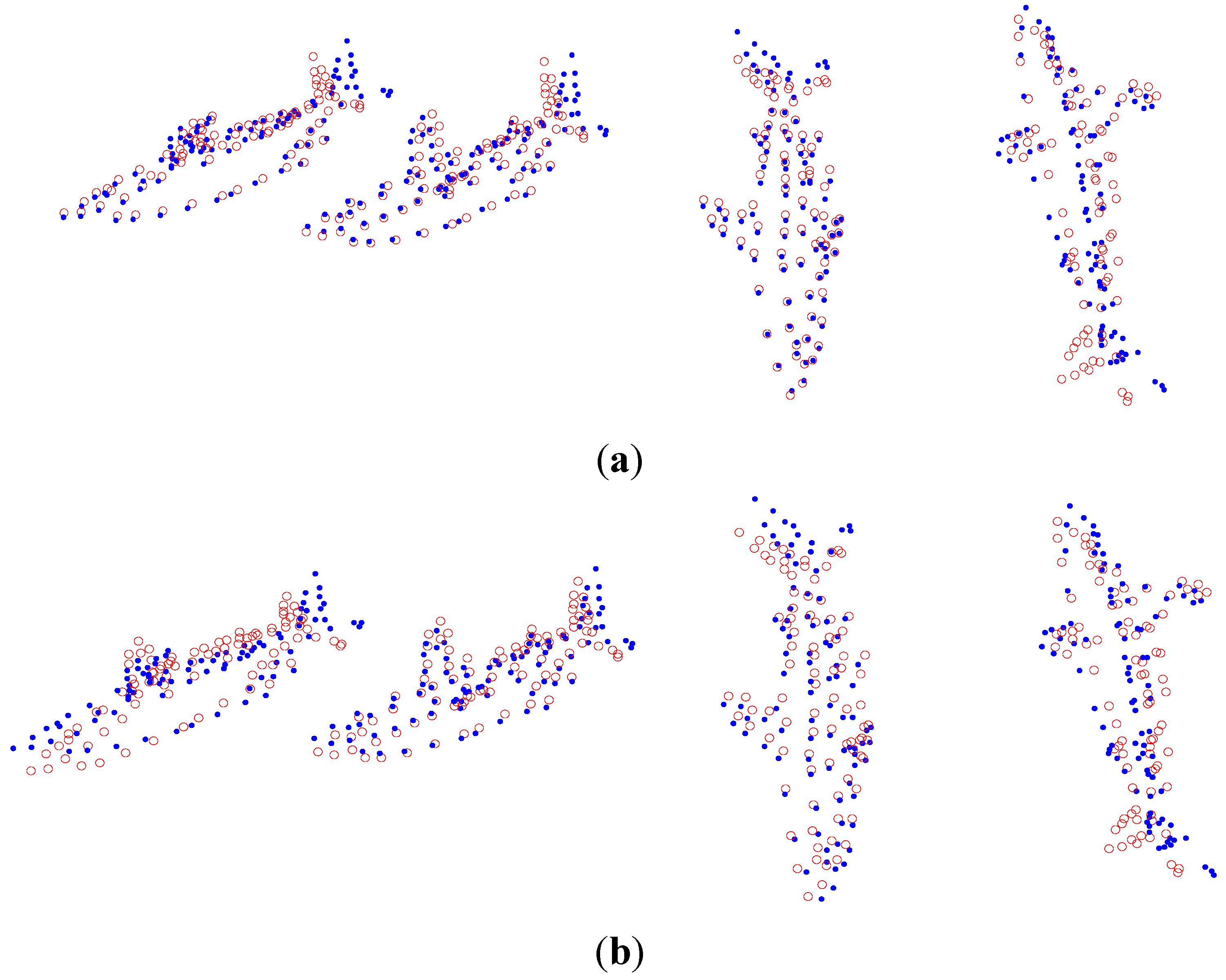
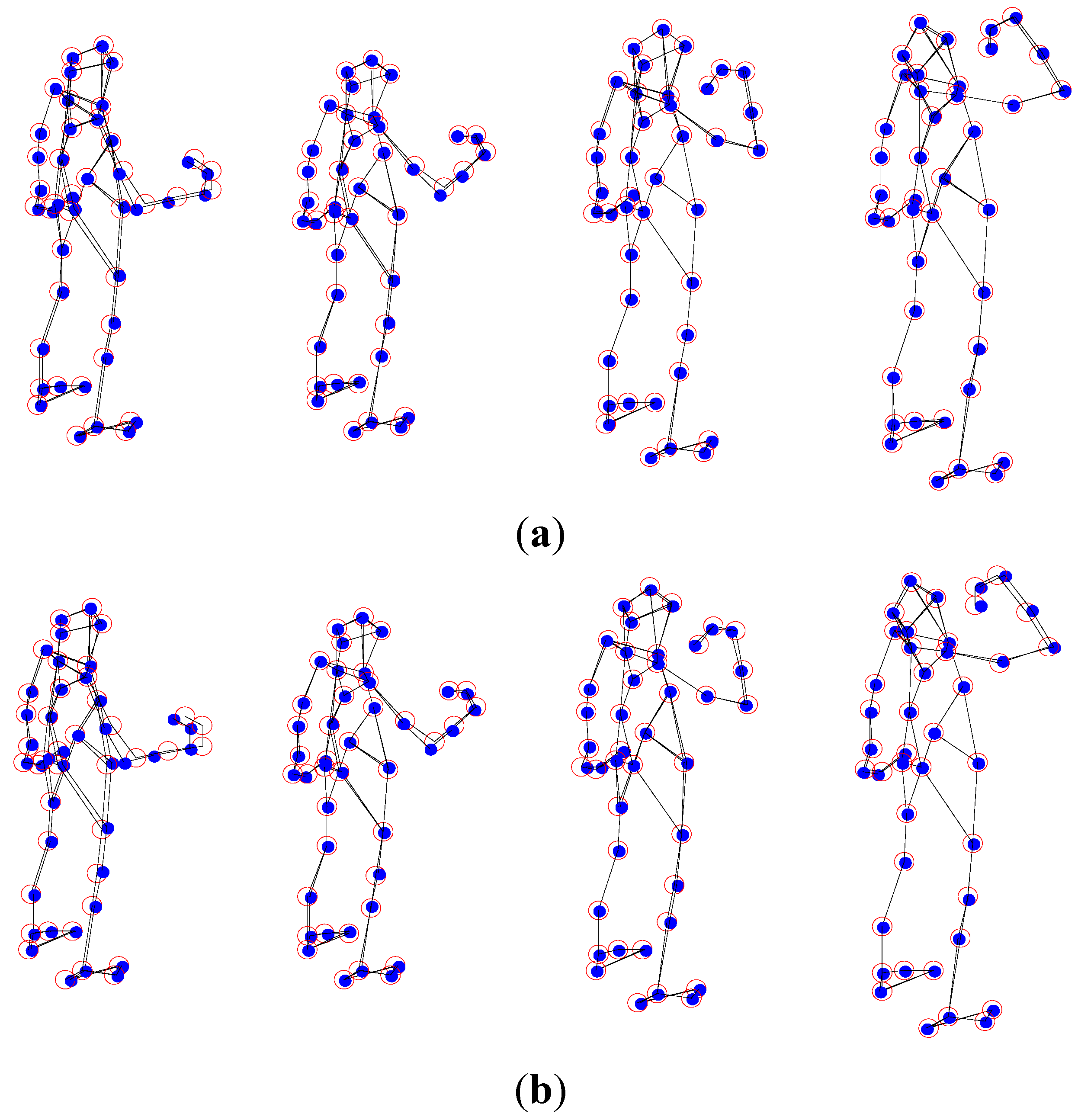
| Database | Shark | Drink | Yoga | Dance | Pickup |
|---|---|---|---|---|---|
| Block Matrix Method | 0.242(3) | 0.019(4) | 0.125(9) | 0.171(10) | 0.138(7) |
| APG method | 0.204(2) | 0.017(13) | 0.135(9) | 0.231(5) | 0.202(7) |
5.4. The Comparison of the APG Method and Existing Methods

| Database | Methods | ||||
|---|---|---|---|---|---|
| EM-PPCA | MP | PTA | CSF | APG | |
| Drink | 0.339 | 0.460 | 0.025 (3) | 0.022 (6) | 0.017 (13) |
| Dance | 0.984 | 0.264 | 0.296 (5) | 0.271 (2) | 0.231 (5) |
| Yoga | 0.810 | 0.804 | 0.162 (11) | 0.147 (7) | 0.135 (9) |
| Shark | 0.050 | 0.157 | 0.312 (2) | 0.254 (2) | 0.204 (2) |
| Pickup | 0.582 | 0.433 | 0.237 (12) | 0.230 (6) | 0.202 (7) |
| Time | Drink | Dance | Yoga | Shark | Pickup |
|---|---|---|---|---|---|
| T | 30.073 s | 1.9245 s | 2.4637 s | 0.8516 s | 3.7898 s |
| t/T | 4.99% | 19.1% | 3.12% | 23.9% | 2.62% |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tomasi, C.; Kanade, T. Shape and motion from image streams under orthography: A factorization method. Int. J. Comput. Vis. 1992, 9, 137–154. [Google Scholar] [CrossRef]
- Bregler, C.; Hertzmann, A.; Biermann, H. Recovering Non-Rigid 3D Shape from Image Streams. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 13–18 June 2000; pp. 690–696.
- Torresani, L.; Hertzmann, A.; Bregler, C. Learning Non-Rigid 3D Shape from 2D Motion. In Proceedings of the 17th Annual Conference on Neural Information Processing Systems, Vancouver, Canada, 8–13 December 2003.
- Brand, M. A Direct Method for 3D Factorization of Nonrigid Motion Observed in 2D. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Cabridge, MA, USA, 20–25 June 2005; pp. 122–128.
- Xiao, J.; Chai, J.; Kanade, T. A closed form solution to non-rigid shape and motion recovery. Int. J. Comput. Vis. 2006, 67, 233–246. [Google Scholar] [CrossRef]
- Akhter, I.; Sheikh, Y.; Khan, S.; Kanade, T. Trajectory space: A dual representation for nonrigid structure from motion. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1442–1456. [Google Scholar] [CrossRef] [PubMed]
- Akhter, I.; Sheikh, Y.; Khan, S.; Kanade, T. Nonrigid structure from motion in trajectory space. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 7, 1442–1456. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Cox, M.; Lucey, S. 3D Motion Reconstruction for Real-World Camera Motion. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1–8.
- Gotardo, P.F.U.; Martinez, A.M. Non-Rigid Structure from Motion with Complementary Rank-3 Spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3065–3072.
- Rehan, A.; Zaheer, A.; AKhter, I.; Saeed, A. NRSFM Using Local Rigidity. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Steamboat Springs, CO, USA, 24–26 March 2014; pp. 69–74.
- Minsik, L.; Jungchan, C.; Chong-Ho, C.; Songhwai, O. Procrustean Normal Distribution for Non-Rigid Structure from Motion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1280–1287.
- Minsik, L.; Chong-Ho, C.; Songhwai, O. A Procrustean Markov Process for Non-Rigid Structure Recovery. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1550–1557.
- Antonio, A.; Lourdes, A.; Begoña, C.; Montiel, J.M.M. Good Vibrations: A Modal Analysis Approach for Sequential Non-Rigid Structure from Motion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1558–1565.
- Akhter, I.; Sheikh, Y.; Khan, S. In Defense of Orthonormality Constraints for Nonrigid Structure from Motion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1534–1541.
- Wen, Z.W.; Goldfarb, D.; Yin, W. Alternating direction augmented Lagrangian methods for semi definite programming. Math. Program. Comput. 2010, 2, 203–230. [Google Scholar] [CrossRef]
- Wang, Y.M.; Cheng, J.M.; Zheng, J.B.; Xiong, Y.L. Analysis of wavelet basis selection in optimal trajectory space finding for 3D non-rigid structure from motion. Int. J. Wavelets Multiresolut. Inf. Process. 2014, 12, 1–14. [Google Scholar] [CrossRef]
- Torresani, L.; Hertzmann, A.; Bregler, C. Nonrigid structure-from motion: Estimating shape and motion with hierarchical priors. Pattern Anal. Mach. Intell. 2008, 30, 878–892. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Chai, J.; Kanade, T. A Closed-Form Solution to Non-rigid Shape and Motion Recovery; Springer Berlin Heidelberg: Berlin, Germany, 2004. [Google Scholar]
- Wright, J.; Ganesh, A.; Rao, S.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Adv. Neural Inf. Process. Syst. 2009, 1, 2080–2088. [Google Scholar]
- Gandy, S.; Yamada, I. Alternating Minimization Techniques for the Efficient Recovery of a Sparsely Corrupted Low-Rank Matrix. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 3638–3641.
- Dai, Y.C.; Li, H.D.; He, M.Y. A Simple Prior-Free Method for Non-Rigid Structure-from-Motionfactorization. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2018–2025. [CrossRef]
- Do, T.T.; Chen, Y.; Nguyen, N.; Lu, G. A Fast and Efficient Heuristic Nuclear-Norm Algorithm for Affine Rank Minimization. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Taipei, China, 19–24 April 2009; pp. 3393–3396.
- Recht, B.; Fazel, M.; Parrilo, P. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Tremoulheac, B.; Atkinson, D.; Arridge, S.R. Fast Dynamic MRI via Nuclear Norm Minimization and Accelerated Proximal Gradient. In Proceedings of the IEEE 10th International Symposium on Biomedical Imaging: From Nano to Macro, San Francisco, CA, USA, 7–11 April 2013; pp. 35–38.
- Lu, Y.; Zhang, L.W. The augmented Lagrangian method based on the APG strategy for an inverse damped gyroscopic eigenvalue problem. Comput. Optim. Appl. 2015, 1, 1–36. [Google Scholar] [CrossRef]
- Wang, Y.M.; Zheng, J.B.; Wang, Y.P.; Shi, X.Z. Estimation of Deformation Degree with Uncertainty and Missing data. In Proceedings of the International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009.
- Paladini, M.; Delbue, A.; Stosic, M. Factorization for Non-Rigid and Articulated Structure Using Metric Projections. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2898–2905.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tong, L.; Jiang, M.; Zheng, J. Non-Rigid Structure Estimation in Trajectory Space from Monocular Vision. Sensors 2015, 15, 25730-25745. https://doi.org/10.3390/s151025730
Wang Y, Tong L, Jiang M, Zheng J. Non-Rigid Structure Estimation in Trajectory Space from Monocular Vision. Sensors. 2015; 15(10):25730-25745. https://doi.org/10.3390/s151025730
Chicago/Turabian StyleWang, Yaming, Lingling Tong, Mingfeng Jiang, and Junbao Zheng. 2015. "Non-Rigid Structure Estimation in Trajectory Space from Monocular Vision" Sensors 15, no. 10: 25730-25745. https://doi.org/10.3390/s151025730
APA StyleWang, Y., Tong, L., Jiang, M., & Zheng, J. (2015). Non-Rigid Structure Estimation in Trajectory Space from Monocular Vision. Sensors, 15(10), 25730-25745. https://doi.org/10.3390/s151025730






