WSNs Data Acquisition by Combining Hierarchical Routing Method and Compressive Sensing
Abstract
: We address the problem of data acquisition in large distributed wireless sensor networks (WSNs). We propose a method for data acquisition using the hierarchical routing method and compressive sensing for WSNs. Only a few samples are needed to recover the original signal with high probability since sparse representation technology is exploited to capture the similarities and differences of the original signal. To collect samples effectively in WSNs, a framework for the use of the hierarchical routing method and compressive sensing is proposed, using a randomized rotation of cluster-heads to evenly distribute the energy load among the sensors in the network. Furthermore, L1-minimization and Bayesian compressed sensing are used to approximate the recovery of the original signal from the smaller number of samples with a lower signal reconstruction error. We also give an extensive validation regarding coherence, compression rate, and lifetime, based on an analysis of the theory and experiments in the environment with real world signals. The results show that our solution is effective in a large distributed network, especially for energy constrained WSNs.1. Introduction
Wireless sensor networks (WSNs) are used in a variety of applications, such as environmental data collection, dangerous event monitoring, and disaster prevention [1,2]. However, they have some performance limits (e.g., energy consumption). Conventional WSNs protocols, like location-based protocols [3] and hierarchical protocols [4], are helpful in reducing bandwidth requirements. The theory of compressive sensing (CS) [5,6], a novel sensing/sampling paradigm that goes against common wisdom in data acquisition, can further reduce the bandwidth requirements and save more energy.
Candès and Wakin [5] provided an introduction to compressive sampling, which is usually used in the field of efficient digital image compression. If a signal is known to be compressible, Donoho [6] found that the number of measurements M for this signal is dramatically smaller than the size of signal N (M ≪ N). Note that a signal being compressible means that it can be exploited to hold the correlation of the data both temporally and spatially based on some sparsification bases.
A number of papers focus on the combination of CS theory and WSNs [1,7,8]. Fazel et al. [1] proposed a distributed energy-efficient sensor network scheme based on random access compressed sensing. However, the authors in [1] do not address the scenario of multi-hop wireless networks. A recent survey of CS theory as applied in WSNs is given in [7], which recovers sparse data in WSNs by solving a convex optimization via L1 norm. The authors in [8] discussed EW-CS scheme that is better overall recovery quality for non-uniform compressible signals than ordinary CS schemes. However, it is not feasible to simply combine CS theory with WSNs since the recovery procedure would fail due to the coherence between measurement and sparsity matrices in a real WSN scenario as described later and reference [9].
The research group of Xiang, Luo, Vasilakos and Rosenberg has done great work in the field of data collection in wireless sensor networks [9–12]. Reference [9] illustrated two crucial insights: firstly, applying CS naively may not bring any improvement, which coincides with our viewpoint in this paper, such as the bad performance of L1 described in Table 1; and secondly, they put forward the idea that the hybrid-CS can achieve significant throughput improvements. Based on their previous hybrid-CS, reference [10] further proposed two solutions for data collection, i.e., the optimal solution and the near-optimal solution. Reference [11] proposed the Dual-lEvel Compressed Aggregation framework to recover the physical signal from incomplete data from WSNs, which is also able to be done from our HRM_CS. The amazing work of their group is the CS-based aggregation scheme, which achieves both recovery fidelity and energy efficiency in WSNs with arbitrary topology according to the reference [12]. They employed diffusion wavelets to design the sparse basis while we focus on the recovery method based on Bayesian Compressed Sensing and the problem of coherence in the model of HRM_CS, which is more practical under the environment with real world signals.
Quer et al. [13] proposed a sparsity model that allows the use of CS theory for the online recovery of large data sets. While some of our work was inspired by the study reported in [13], it not only extends the results given in [13] by using the hierarchical routing method, but also provides a mathematical analysis of sparsity and coherence. In our previous paper [2], we proposed a data fusion method based on CS, which was used to monitor the cyanobacteria bloom-forming in a lake using a single hop network.
In the past years, considering the energy consumption in the procedure of route, reference [14] put forward a recurrent neural network to realize the range-free localization of WSNs while we decrease the energy consumption by making use of compressive sampling. These are two different methods to solve a similar problem. Joining CS theory with a routing free algorithm would be a worthwhile topic for future work.
The main existing problems that limit widespread applications under the real WSN scenario are as follows: (1) lack of a suitable method for a large region covered by a multi-hop network; (2) lack on an effective analysis of sparsity and coherence; and (3) lack of a quantitative analysis of the lifetime of the whole WSN. In this paper we solve all of these issues by jointly employing the hierarchical routing method and compressive sensing in multi-hop networks. The main contributions of this paper are the following:
A model combining the hierarchical routing method and compressive sensing (called the HRM_CS) for WSN data acquisition, which includes some variant models, e.g., a model combining the hierarchical routing method and the Bayesian compressed sensing (BCS) based CS recovery algorithm (HRM_CS1), and a model combining the hierarchical routing method and the L1-minimization based CS recovery algorithm (HRM_CS2).
A quantitative mathematical analysis of the HRM_CS, which includes signal sparsity analysis, measurement matrix analysis, coherence analysis, and so on.
Design of a HRM_CS framework, being used for the online recovery of large data sets by collecting a small number of readings.
Proof of the effectiveness of our approach for the acquisition and recovery of signals measured in an actual WSN deployment.
The paper is structured as follows: in Sections 2 and 3, we present our HRM_CS model for WSN data acquisition and the corresponding analysis in terms of signal sparsity, signal recovery, and routing method. In Section 4, we provide a framework for implementing the HRM_CS. In Section 5, through comparison with standard approaches, we prove the effectiveness of our model. Finally, we present our conclusions in Section 6.
2. WSNs Data Acquisition Model
In this section we firstly review basic CS theory from a sparse signal model and recovery model. Then we present the hierarchical routing method. Finally, we introduce our HRM_CS model for WSN data acquisition, through the joint use of the hierarchical routing method and compressive sensing.
2.1. Compressive Sensing Theory
Consider a grid WSN, consisting of N (N = I × J) sensors located on a two-dimensional plane for monitoring an environment with I and J sensors in the x- and y-directions, respectively. Each sensor in the network grid independently acquires a measurement and transmits this data towards the sink along the routing path. We firstly transform the two-dimensional data matrix U of the original signal into one-dimensional data vector X by Equation (1):
Taking into account the sparsity of natural phenomena (e.g., the temporal correlation and spatial correlation) in the monitored environment [1,2], based on classic compressive sensing theory, we can create M random projections of X, that is, Y ∈ RM, and obtain the following mathematical model:
2.1.1. Signal Sparsity
Various common transforms can be used in the sparse signal model, such as Haar wavelets, the Fourier transform, principal component analysis (PCA) [15–17], and the discrete cosine transform (DCT). In the following, considering a real world signal [18], we focus on the latter two transforms, i.e., PCA and DCT, which are used in the later model. Based on matrix algebra, in order to identify patterns in data and express the data in such a way as to highlight their similarities and differences in X, we apply PCA to find patterns in the data and compress them, i.e., by reducing the number of dimensions, without much loss of information. First, we calculate the eigenvectors and eigenvalues of the covariance matrix. Then, we choose components to form a feature vector. DCT is another transform [19,20], defined as Ψ ∈ RN×N, ΨT Ψ = E. In our previous work, we used the observed chlorophyll-A data from the sensor nodes located in the Taihu Lake in China (longitude: 120.296, latitude: 31.387) as the original signal and applied DCT as a transform. From the results given in [2], almost 99% of the energy of size N = 92 is contained in only six important coefficients, i.e., K = 6.
2.1.2. Signal Recovery
Based on the previous work, if the original signal is sparse, it can be recovered with high probability using a method with some optimization techniques, such as L1-minimization [2,5,6] and BCS [21–23]. With a sufficient number of measurements, the sink is able to reconstruct the sensor readings by solving an L1-minimization problem [5,6]. By using L1-minimization technology [2], we reconstructed the chlorophyll-A signal from a smaller sample with higher accuracy; the mean of the reconstruction error for sampling point-1 was 0.17%, while that for sampling point-2 was 1.59%. As for the BCS method [23], its basic idea is to maximize the posterior from a Bayesian perspective, estimate sparse coefficients from the Bayesian framework, and then compute the estimated value of the original signal. In BCS, the estimated parameters are random variables with some prior distribution. By learning the ith sample xi and the Bayesian rule, P(xi | α) can be transformed into P(α | xi), a maximum a posteriori (MAP) estimate, where α is the estimated parameter. We employ BCS method in our later data acquisition model.
2.2. Traditional Hierarchical Routing Method
As pointed out in the previous section, a compressive sensing model can be used in most single-hop WSNs [1,2] or centralized environment [5,22]. In what follows, we present a method for gathering data for a multi-hop WSN in a distributed environment.
To avoid confusion, it is important to note that in this section interpretation of all the variables is involved. Suppose N sensors, denoted as x1, x2,…,xN, form a multi-hop route to the sink and the original signal vector is denoted as X ∈ RN. Let dj denote the readings obtained by node xj. There are two simple data collection schemes: the baseline and compressive methods in a multi-hop route, referred to as Equations (3) and (4), respectively [3]. To avoid excessive overloading in single-tier WSNs, a clustering method has been used in some routing approaches [23,24]. The hierarchical routing method utilizes randomized rotation of local cluster-head nodes to distribute the energy load evenly among the sensors in the network [25]:
2.3. Our HRM_CS Model
Inspired by the above theory and method, we put forward our HRM_CS model, which jointly applies the hierarchical routing method and compressive sensing to effectively compress and recover the original signal by exploiting the correlation of sensor readings. Next we describe the HRM_CS model in the formula form. In the HRM_CS model, based on the description of Equation (2), we design a hierarchical routing method to get the value of Y ∈ RM. According to LEACH in [4], we divide the N nodes into M clusters and randomly rotate cluster-heads, where the M cluster-head nodes, denoted by {Y1, Y2, Y3,…,YM}. However, in order to further reduce energy dissipation and enhance system lifetime, differing from LEACH, we only select a part of nodes to transmit data to the cluster head. Assume that {C1, C2, C3,…, CM} corresponds to the number of nodes in each of the M clusters and . Note that the original signal is X ∈ RN and the compressive signal from the M clusters is Y ∈ RM.
In order to balance the energy cost among all the nodes, when we create the measurement matrix Φ, in which each row corresponds to the whole N nodes in the WSN. We introduce random coefficients wk,c set to 0 or 1, where k denotes the kth cluster (Yk) and c denotes the cth node (xk,c) in this cluster. Each sensor contributes its readings to the sink with a non zero coefficient or zero otherwise. And now X can be expressed as X = {x1,1,x1,2,…,x1,C1,…,xM,1,xM,2,…,xM,CM}, where xk,c is the sensor value and 1 ≤ k ≤ M, C1 ≤ c ≤ CM. In this way, a randomly chosen subset of nodes participates in the sensing process so that the lifetime of the whole network is prolonged as long as the energy left in these nodes is higher than the threshold. At first, the sink node picks a random subset of M sensors for sampling and broadcasts the selected set of nodes at each round. Then, the selected nodes sample the physical value xk,c from the sensor. Furthermore, HRM_CS model of jointly applying the hierarchical routing method and compressive sensing process can be formally expressed as Equation (5):
3. Analysis and Optimization of HRM_CS Model
In Section 2 we presented a data acquisition model for WSNs, called the HRM_CS, which combines the hierarchical routing method and compressive sensing. To determine the effectiveness of the HRM_CS and investigate the impact of the routing method on the compression process, we present a formula analysis from multiple aspects. First, without loss of generality, we assume a simple radio model [4], where the radio dissipates Eelec = 50nJ/bit to run the transmitter or receiver circuitry and εamp = 100pJ/bit/m2 for the transmission amplifier. The formula to calculate the energy required to transmit a k-bit message along a distance of d, is given below:
In addition, the formula to calculate the energy required to receive a message, is:
Next we present an analysis of the HRM_CS model from four different aspects.
3.1. Sparsity Analysis
There are some common transforms that can be used in a sparse signal model. In this paper, we focus on DCT and PCA. For the DCT, the sparsity depends on the corresponding coefficients with low and middle frequency, whereas for the PCA, the sparsity is determined by the square root of the eigenvalues of the covariance matrix. Note that the default transform in the following section is the DCT.
3.2. Measurement Matrix Analysis
We consider two different schemes to build the measurement matrix, i.e., random sampling (RS) and the hierarchical routing method (HRM). The RS scheme is used to determine in a fully distributed way which sensors randomly transmit their data to the sink node at any given time k. In the HRM scheme every sensor node first sends its data to local cluster base stations and then these data are transferred to the sink node by the local clusters.
3.3. Coherence Analysis between Measurement Matrix and Sparsity Matrix
Coherence analysis between the measurement matrix and sparsity matrix is an important metric that affects the accuracy and stability of information recovery. The formula to compute the coherence μ [15] is given below:
The values of μ depend on a column in the CS matrix, where Hi = ΦΨi, Hj = ΦΨj, and . From the large number of experiments carried out, we find two methods are able to decrease μ and increase the stability of CS recovery: (1) Adopting the Gaussian random measurement matrix, i.e., the RS scheme. This is because occurrence probability of 0's and 1's in a row of the Gaussian random measurement matrix is relatively fixed so that the coherence being relatively stable; (2) Increasing the number of cluster-head nodes at some extent. This is because that the measurement matrix based on the HRM is built by setting the value of the local head node to “1” and that of the other nodes in this cluster to “0”. Therefore, with an increasing number of cluster-head nodes, both the number of non cluster-head nodes within each new cluster and the total number of occurrences of the value “1” in a row decrease. This leads to the coherence μ decreasing.
3.4. Optimization of HRM_CS Model
The HRM_CS objective is to provide a data acquisition method with longer lifetime and higher recovery accuracy under the real WSN environment. In this section, three performance metrics, namely, recovery accuracy (Error), communication cost and compression rate are analyzed. Based on this analysis, the optimized model from the two variant models of HRM_CS, i.e., HRM_CS1 with BCS and HRM_CS2 with L1-minimization can be obtained. Detailed experimental results are shown in Table 1, where the raw AD values denote the values from the card of Analog signals conversion Digital signals in a real WSN scenario GreenOrbs [18].
First, we investigate recovery accuracy (Error). The max Error is less than 1%, which meets the system demands. Although the HRM_CS1 is a little inferior to the HRM_CS2 with respect to recovery accuracy, HRM_CS1 is superior to the HRM_CS2 with respect to much more stability, i.e., the recovery method based on BCS has greater success than L1-minimization (hereafter called L1). Moreover, the number M of head nodes does not have a large effect on the error and variance of recovery in a BCS scenario. This is because BCS estimates the most probable value by maximizing a posteriori without depending on the particular WSN topology considered.
Second, we analyze communication cost. Here we compute the total number of packets in the HRM_CS. The main steps are as follows: (1) N − M nodes in the cluster send their own sensor readings to M cluster-head nodes with an associated cost O(N − M); (2) Next, superposition of the signal is carried out at the cluster-head node. In addition, the M cluster-head nodes transmit their own sensor readings to the sink along a routing path that minimizes the number of transmissions. On this path the packet is not processed but simply forwarded with the longest path O(N½); (3) The total cost of delivering packets to the sink from M cluster-head nodes is O(MN½).
Last, we consider compression rate. From a sink point of view, compression rate is defined as . It is related to the number M of head nodes and increases as M decreases, where N is the total number of sensor nodes.
From the above analysis, it can easily been seen that the WSN based on the HRM_CS has longer lifetime, compared with the classic approaches given by Equations (3) and (4), where the data are not well compressed. In particular, it can also been seen that the HRM_CS1 with M = 40 is our optimal choice since the higher compression rate and stability can be gotten at a little cost of recovery error, compared with the HRM_CS2.
4. HRM_CS Framework
In this section we present our framework for implementing the HRM_CS, which performs well for fully distributed compression in WSNs and centralized recovery of an N-dimensional signal from a compressed M-dimensional signal at the sink. We first present the HRM_CS framework from a holistic viewpoint, and then, we describe WSNs deployment and clustering scenarios. Finally, we introduce the preprocessing for monitoring data, which can optimize the HRM_CS performance.
4.1. HRM_CS Framework for WSNs
To implement the model in Equation (5) described in Section 2, we present our framework for WSNs data acquisition in detail. From Figure 1, we can see that the monitoring region is mapped with N = I × J nodes into two-dimensional matrix U in the first step. Note that U corresponding to the one-dimensional vector X in Equation (1). Then, in the next step, we logically re-organize U to build a clustering structure based on the hierarchical routing method, by randomly selecting cluster-heads and nodes within their clusters to evenly distribute the energy load among the sensors in the network. Each sensor node selected sends its data to local cluster base stations and then these data are transferred to the sink node. In the final step the superposition of the signal is completed and the original signal is recovered at the central sink node based on the optimization techniques.
4.2. WSN Deployment
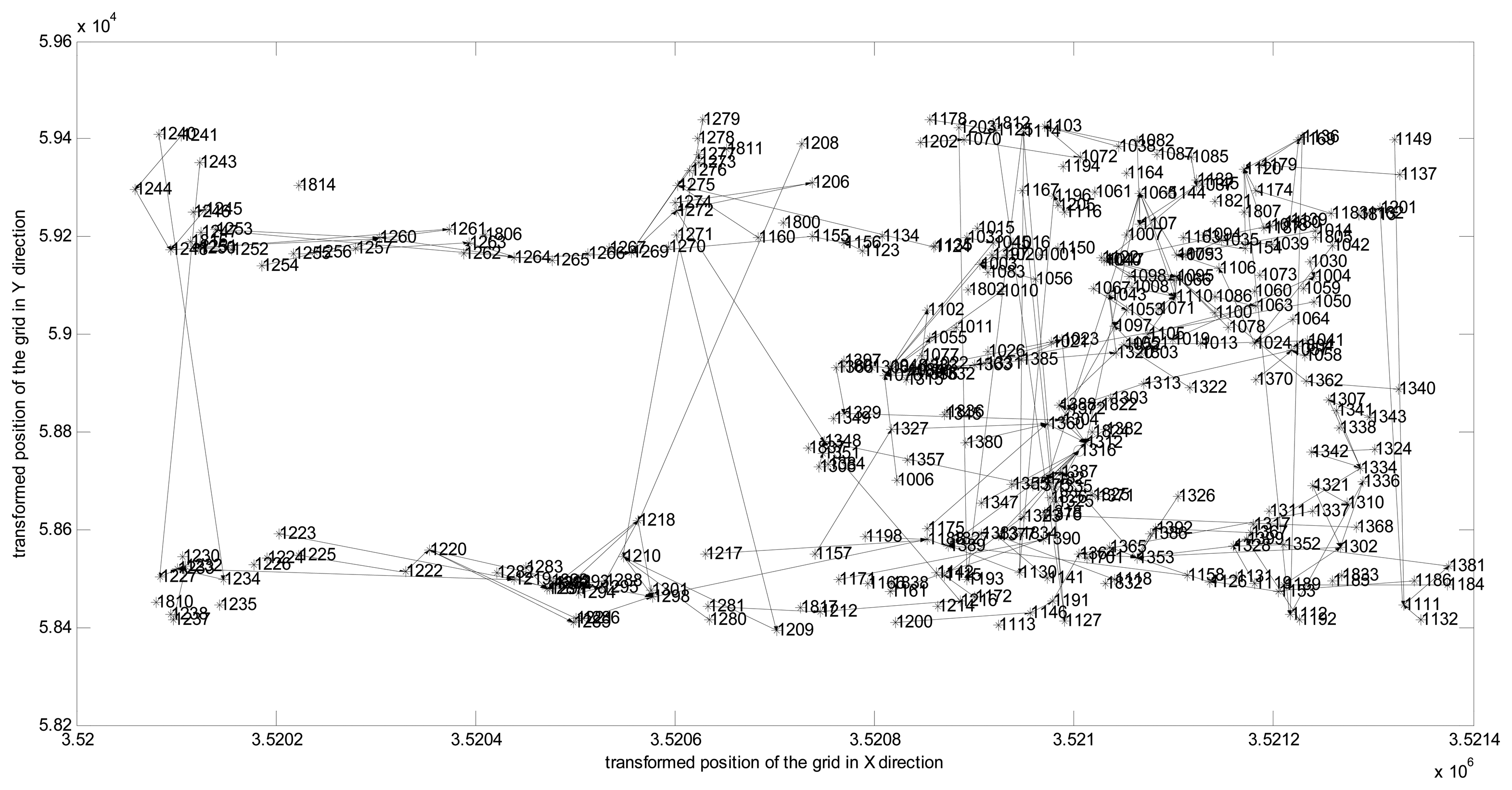
We consider the deployment in GreenOrbs [18], which is a real WSN scenario set up for long-term monitoring of temperature and humidity in a forest without human supervision. We depict these nodes with their ID and location as shown in Figure 2. The operation of HRM_CS is broken up into rounds, where some node becomes a cluster-head for the current round while each non-cluster-head node decides the cluster to which it will belong for this round. Furthermore, according to the path of the message transmission in one round, we obtain the corresponding screen-shot of hierarchical cluster topology as shown in Figure 3.
4.3. Monitored Data Preprocessing
In this section, we discuss the preprocessing of the monitored data. As the first step, based on the hierarchical cluster topology as shown in Figure 3, we select the top right region with the most densely distributed nodes as the experimental data. Let the relative position be depicted on the X- and Y-axis according to the grid structure preprocessing, while the raw AD values from the sensors corresponding to the monitored temperature are given on the Z-axis, as displayed in 3D in Figure 4. As is known, the AD raw values from the sensor must be converted into a natural signal temperature by the formula: temperature = −39.60 + 0.01 × (AD raw value) [18].
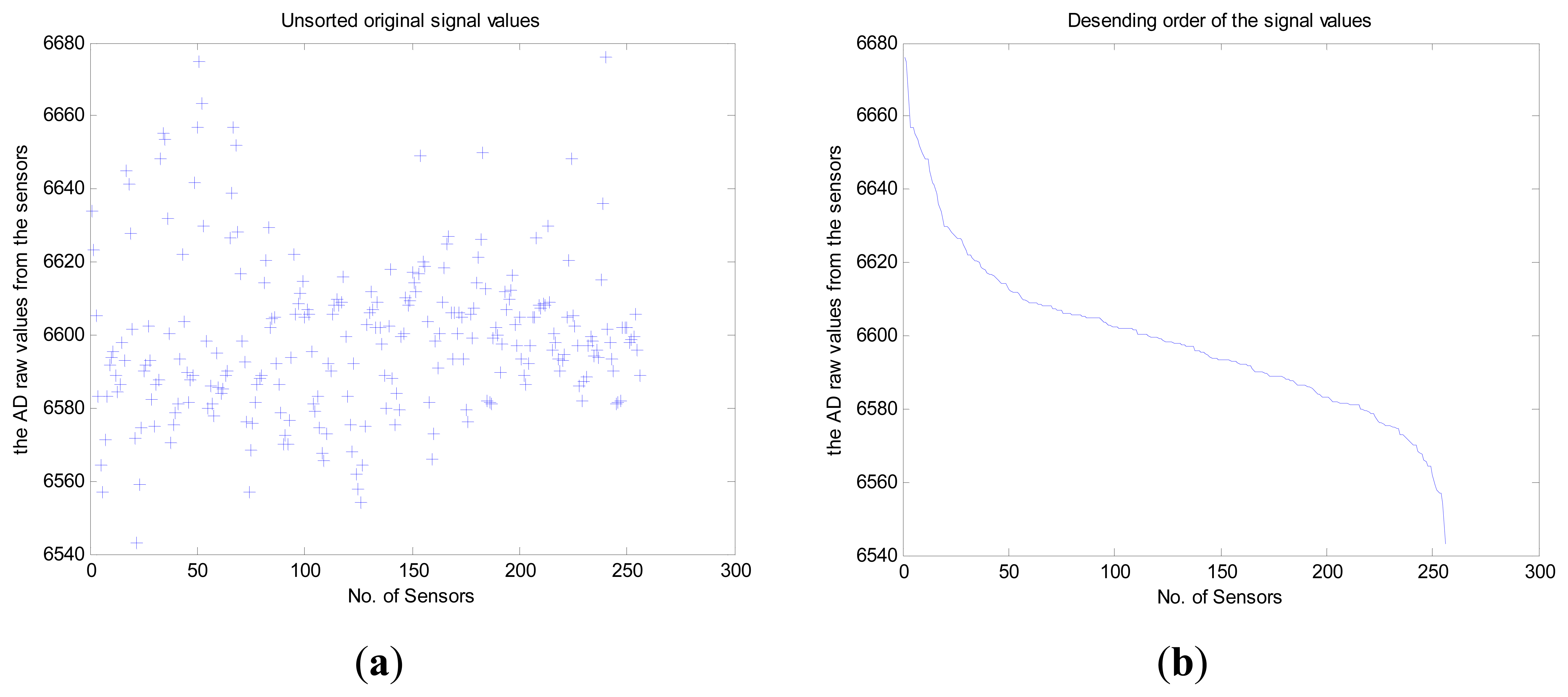
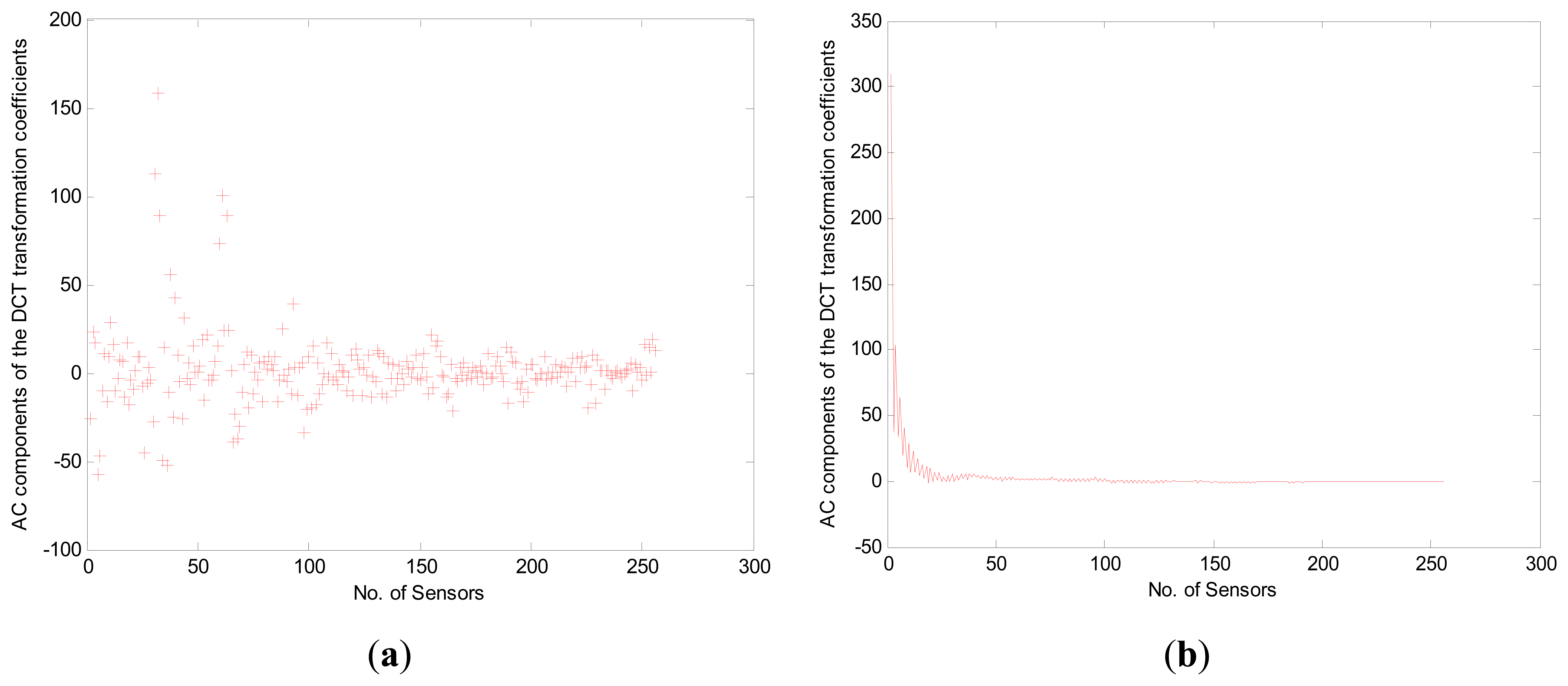
Then, in order to optimize the compression rate, we compared two cases: sorted and unsorted monitored data values during the preprocessing. The X-axis depicts the 256 nodes while the Y-axis gives the raw AD values from the sensors corresponding to the monitored temperature as shown in Figure 5. Note that the compression rate for the “Sorted” case (Figure 5b) is superior to that for the “Unsorted” case (Figure 5a) in the preprocessing since it is affected by a discrete signal characteristic in the frequency domain. To demonstrate the effectiveness of the preprocessing, we create a sparse representation of the “Unsorted” (Figure 6a) and “Sorted” (Figure 6b) monitored data values by DCT. As shown in Figure 6, the X-axis depicts the 256 nodes while the Y-axis gives the AC components of the DCT transformation coefficients. The “Sorted” case is superior to the “Unsorted” case with respect to compression rate during the preprocessing since “Sorted” case decreases the total communication cost, which coincides with the conclusion in reference [12].
5. Performance Comparison
To extensively validate our HRM_CS, we focus on recovery error, energy consumption, and lifetime, compared with other classic WSNs [3,13,25]. As for the limited computational power and communication bandwidth in WSNs, the lifetime of WSNs is the most important metric.
Energy Consumption
As the analysis in the previous section shows, compared with the traditional clustering method, the energy consumption of the HRM_CS is substantially reduced by introducing compressive sampling. To analyze the energy consumption, we focus on the sending and receiving phase although there are multiple other phases, such as the sensor computation during the data acquisition. We adopt the energy model given as Equations (6) and (7) in Section 3. For further details refer to [4,26].
Lifetime
Assume that each sensor is a tiny powered sensing unit with a finite amount of energy that determines its lifetime. According to the computation energy consumed, when the energy left is lower than zero, we refer to this sensor as dead; otherwise it is alive.
Recovery Error (err)
Assume an original signal X ∈ RN, and recovery signal X̃ ∈ RN, then:
First, let us consider the effects of preprocessing on L1-minimization recovery [27]. Figure 7a shows the referenced values after subtracting the minimum value from the original signal. Figure 7b shows the recovery effects with preprocessing and applying a DCT, while Figure 7c shows the recovery effects without preprocessing but applying a DCT. Figure 7d depicts the recovery effects without preprocessing and using PCA. From this experiment, we find that the following results: (1) the recovery error in Figure 7b is smaller than those in Figure 7c,d; (2) the recovery errors in Figure 7c,d are of the same magnitude, however, from the viewpoint of varying trends, the method using PCA in Figure 7d is inferior to that using DCT in Figure 7c since the DCT transform can characterize the original signal using more coefficients with low and middle frequency.
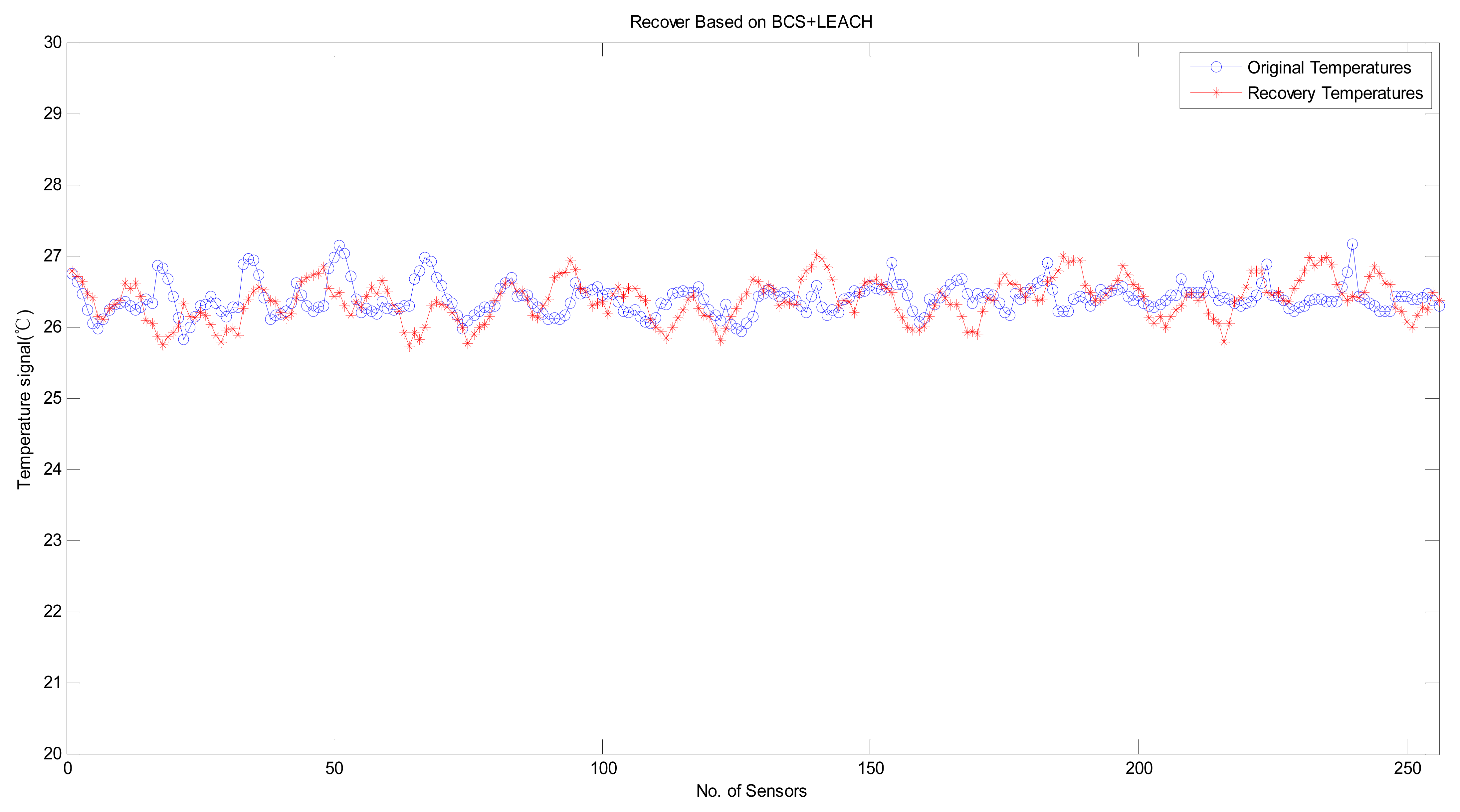
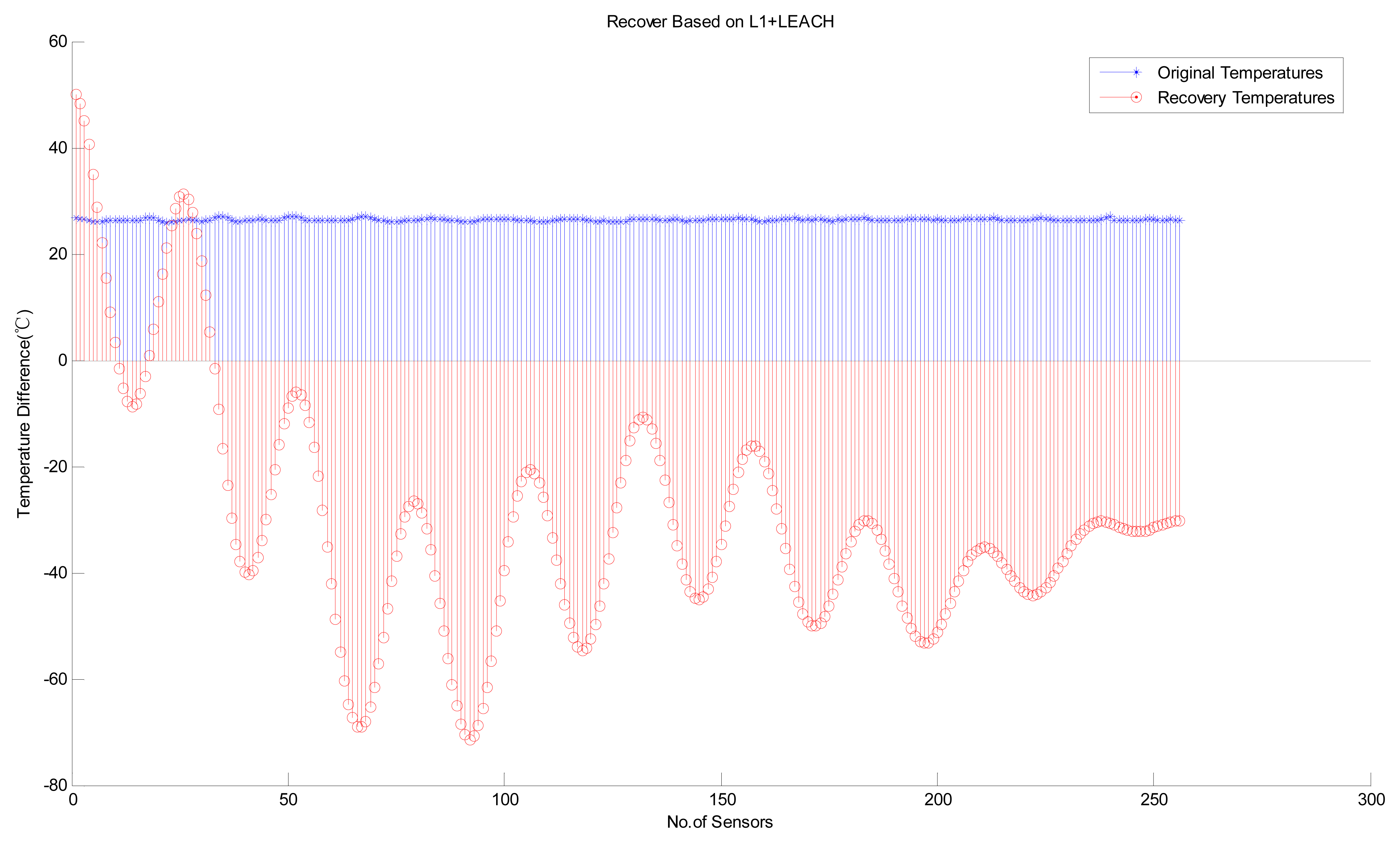
Next, we consider the performance of variants of the B HRM_CS model. Figure 8 shows the experimental results of the HRM_CS1, i.e., jointly using CS as the recovery algorithm and LEACH as the hierarchical routing method. Figure 9 depicts the experimental results with high recovery accuracy for the HRM_CS2, i.e., combining L1-minimization as the recovery algorithm and LEACH as the hierarchical routing method. Under the HRM_CS2 scenario, if there are too few 1's when creating the measurement matrix, i.e., there are too few nodes to participate in the measurement, it will lead to failure during the recovery operation since the coherence between the measurement and sparsity matrices increases, as shown in Figure 10. Based on the above experiments, as for the stability of information recovery, we find that the applying CS naively like L1-minimization may be not proper under the real scenario of WSNs and HRM_CS1 is superior to HRM_CS2.
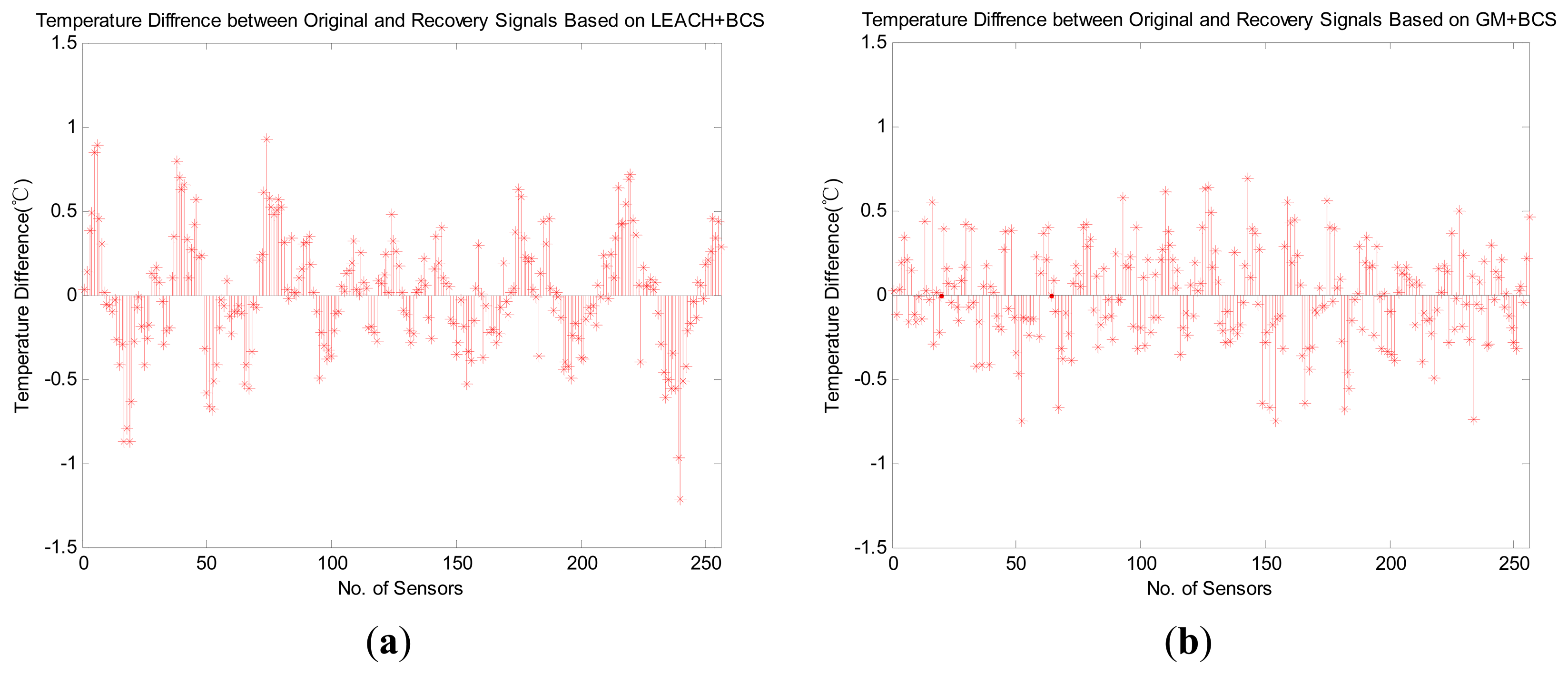
In Figure 11, we demonstrate the recovery accuracy by comparing the HRM_CS1 with the GM_CS [13] based on the same recovery method, BCS. Figure 11 depicts the experimental results for the original and recovered signals, for which the error is less than 1 °C. Furthermore, the mean error of our HRM_CS1 0.0101 is slightly greater than the mean error of the GM_CS 0.0084 while HRM_CS1 has much longer lifetime than that of the GM_CS, as shown in Figure 13.
As for the number of measurements M, i.e., the number of clusters in HRM_CS model, it is a vital parameter and has an influence on the lifetime of WSNs. Based on the basic compressive sensing theory [5], we know that M ≥ 4K, K is the number of significant components in original signal X while K varies with the different threshold value during the process of signal, which can be seen in Table 2. As a result, it can be seen from the Figure 12 that the lifetime of WSNs with different number of clusters also take the corresponding changes and the maximal lifetime is obtained at M = 40.
In the last graph, Figure 13, we show the impact of different data acquisition methods on the lifetime of WSNs. We compared four different methods, namely, HRM_CS, one_hop method [3], traditional LEACH [25] and GM_CS [13]. Here GM_CS means that we use the Gaussian random matrix as the routing matrix jointly with CS. As described in Table 1, L1-minimization is more unstable than BCS in this real WSN scenario. Therefore, here we use the BCS as CS recovery algorithm in our experiment. As shown in Figure 13, our solution HRM_CS, is superior to the other methods since the HRM_CS adopts compressive sampling, which decreases the number of communication packets and prolongs the lifetime as a consequence.
6. Conclusions
In this paper, we proposed the HRM_CS, a model for data acquisition in WSNs by jointly applying the hierarchical routing method and compressive sensing, which minimizes global energy usage by decreasing the number of samples. HRM_CS outperforms conventional LEACH by introducing the sparse representation technology of PCA and DCT to capture the similarities and differences of the original signal. We studied an approximate recovery of the original signal from this smaller number of WSNs samples with a lower signal reconstruction error, such as L1-minimization or Bayesian compressed sensing. Thereafter we compared the performance of these two signal reconstruction techniques combining a different measurement matrix. The extensive validation demonstrates that our solution is effective in reducing energy dissipation and enhancing system lifetime, although it is not necessarily the most accurate. Other supervised WSNs routing algorithms, such as the multicast tree, even for arbitrary topology [12] and routing-free [14], also have attractive features and should be compared when applied jointly with CS in our future work.
Supplementary Materials
Supplementary materials can be accessed at: https://www.mdpi.com/1424-8220/14/9/16766/s1.
sensors-14-16766-s001.rarGlossary
The table of the key letters and abbreviations in the paper.
| Symbol | Explanation | Symbol | Explanation | Symbol | Explanation |
|---|---|---|---|---|---|
| HRM_CS | Model of combining HRM and CS | μ | Coherence between the measurement and sparsity matrices | PCA | Principal Component Analysis |
| L1 | Recovery algorithm L1-minimization | Φ | Measurement matrix | BCS | Bayesian Compressed Sensing |
| HRM_CS1 | Model of combining the HRM and the BCS | Ψ | Transform Matrix | X | One-dimensional data vector |
| HRM_CS2 | Model of combining the HRM and the L1 | wk,c | Random Coefficients of cth node of kth cluster | Y | M random projec-tions vector X |
| χ̂ | Estimated value of χ | xk,c | Sensor value of cth node of kth cluster | χ | K-sparse value of the original signal X |
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Nos. 61170065, 61373137, 61171053, 61103195, 61203217), Six Industries Talent Peaks Plan of Jiangsu Province (No. 2013-DZXX-014), the Natural Science Foundation of Jiangsu Province (No. BK2012436, No. BK20141429), the Scientific and Technological Support Project (Society) of Jiangsu Province (No. BE2014718, No. BE2013666), Natural Science Key Fund for Colleges and Universities in Jiangsu Province (No. 11KJA520001, No. 12KJA520002), Scientific Research & Industry Promotion Project for Higher Education Institutions (No. JHB2012-7), the NJUPT Natural Science Foundation (No. NY213157 and No. NY213037), and the State University Student STITP of China (No. 0700412017). In addition, we are grateful to the anonymous reviewers for their insightful and constructive suggestions.
Author Contributions
Zhiqiang Zou is responsible for designing the model HRM_CS for data acquisition while Cunchen Hu and Fei Zhang is responsible for implementing this model. Hao Zhao and Shu Shen is responsible for verifying this model by doing extensive experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fazel, M.; Fazel, F.; Stojanovic, M. Random access compressed sensing for energy-efficient underwater sensor networks. IEEE J. Sel. Areas Commun. 2011, 29, 1160–1670. [Google Scholar]
- Zou, Z.Q.; Li, Z.T.; Zhao, H.; Hu, C.C.; Zhang, F. Compressed Sensing Data Fusion of Monitoring Cyanobacteria Bloom-Forming. In Advances in Wireless Sensor Networks; Wang, R., Xiao, F., Eds.; Springer: Berlin, Germany; pp. 744–752.
- Akkaya, K.; Younis, M. A survey on routing protocols for wireless sensor networks. Ad. Hoc. Netw. 2005, 3, 325–349. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.P.; Balakrishnan, H. Energy efficient communication protocol for wireless sensor networks. Proceedings of the 33rd Hawaii International Conference on System Sciences, Hawaii, HI, USA, 4–7 January 2000; pp. 1–10.
- Candès, E.J.; Wakin, M. An introduction to compressive sampling. IEEE Signal Proc. Mag. 2008, 25, 21–30. [Google Scholar]
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar]
- Balouchestani, M.; Raahemifar, K.; Krishnan, S. Robust wireless sensor networks with compressed sensing theory. Commun. Comput. Inf. Sci. 2012, 293, 608–619. [Google Scholar]
- Liu, Y.; Zhu, X.; Zhang, L.; Cho, S.H. Expanding window compressed sensing for non-uniform compressible signals. Sensors 2012, 12, 13034–13057. [Google Scholar]
- Luo, J.; Xiang, L.; Rosenberg, C. Does compressed sensing improve the throughput of wireless sensor networks. Proceedings of the IEEE ICC, Cape Town, South Africa, 23–27 May 2010; pp. 1–6.
- Xiang, L.; Luo, J.; Vasilakos, A.V. Compressed data aggregation for energy efficient wireless sensor networks. Proceedings of the 8th IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Salt Lake City, UT, USA, 27–30 June 2011; pp. 46–54.
- Xiang, L.; Luo, J.; Deng, C.; Vasilakos, A.; Lin, W. DECA: Recovering fields of physical quantities from incomplete sensory data. Proceedings of the 9th IEEE SECON, Seoul, Korea, 18–21 June 2012; pp. 107–115.
- Xiang, L.; Luo, J.; Rosenberg, C. Compressed data aggregation: Energy-Efficient and high-fidelity data collection. IEEE/ACM Trans. Netw. 2013, 12, 1722–1735. [Google Scholar]
- Quer, G.; Masiero, R.; Pillonetto, G.; Rossi, M.; Zorzi, M. Sensing compression and recovery for WSNS sparse signal modeling and monitoring framework. IEEE Trans. Wirel. Commnun. 2012, 11, 3447–3461. [Google Scholar]
- Li, S.; Qin, F. A dynamic neural network approach for solving nonlinear inequalities defined on a graph and its application to distributed, routing-free, range-free localization of WSNs. Neurocomputing 2013, 117, 72–80. [Google Scholar]
- Quer, G.; Masiero, R.; Munaretto, D.; Rossi, M.; Widmer, J.; Zorzi, M. On the interplay between routing and signal representation for Compressive Sensing in wireless sensor networks. Proceedings of the 2009 Information Theory and Applications Workshop, San Diego, CA, USA, 8–13 February 2009; pp. 206–215.
- Smith, L.I. A Tutorial on Principal Components Analysis. Available online: www.ce.yildiz.edu.tr/personal/songul/file/1097/principal_components.pdf (accessed on 2 September 2013).
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar]
- Liu, Y.; He, Y.; Li, M.; Wang, J.; Liu, K.; Li, X. Does wireless sensor network scale? A measurement study on GreenOrbs. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1983–1993. [Google Scholar]
- Masiero, R.; Quer, G.; Munaretto, D.; Rossi, M.; Widmer, J.; Zorzi, M. Data acquisition through joint compressive sensing and principal component analysis. Proceedings of the IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–4.
- Luo, C.; Wu, F.; Sun, J; Chen, C.W. Compressive data gathering for large-scale wireless sensor networks. Proceedings of the 15th Annual International Conference on Mobile Computing and Networking, Beijing, China, 20–25 September 2009; pp. 145–156.
- Masiero, R.; Quer, G.; Rossi, M.; Zorzi, M. A bayesian analysis of compressive sensing data recovery in wireless sensor networks. Proceedings of the 2009 International Conference on Ultra Modern Telecommunications & Workshops (ICUMT'09), St. Petersburg, FL, USA, 12–14 October 2009; pp. 1–6.
- Ji, S.H.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Proc. 2008, 56, 2346–2356. [Google Scholar]
- Yu, B.; Li, J.Z.; Li, Y.S. Distributed data aggregation scheduling in wireless sensor networks. Proceedings of the INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 2159–2167.
- Xu, X.; Li, M.; Mao, X.; Tang, S.; Wang, S. A Delay efficient algorithm for data aggregation in multi-hop wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 163–175. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.P.; Balakrishnan, H. An application specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar]
- Lindsey, S.; Raghavendra, C.S. PEGASIS: Power-Efficient gathering in sensor information systems. Proceedings of the 2002 IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; pp. 1125–1130.
- Candes, E.; Romberg, J. L1-Magic: Recovery Of Sparse Signals Via Convex Programming. Available online: www.acm.caltech.edu/l1magic/downloads/l1magic.pdf (accessed on 2 September 2013).







| Recovery Method | Threshold | Number of Cluster Heads M | Coherence μ | Success Recovery Rate (%) | Error (%) | Variance |
|---|---|---|---|---|---|---|
| L1 | 50 | 40 | 1.950 | 20 | 0.262 | 298.748 |
| BCS | 50 | 40 | 1.950 | 100 | 0.327 | 466.902 |
| L1 | 40 | 56 | 1.495 | 20 | 0.247 | 265.394 |
| BCS | 40 | 56 | 1.495 | 100 | 0.329 | 472.804 |
| L1 | 35 | 68 | 1.085 | 25 | 0.224 | 218.526 |
| BCS | 35 | 68 | 1.085 | 100 | 0.326 | 463.506 |
| L1 | 28 | 84 | 0.658 | 33 | 0.250 | 272.964 |
| BCS | 28 | 84 | 0.658 | 100 | 0.326 | 463.182 |
| L1 | 25 | 100 | 0.556 | 60 | 0.209 | 191.134 |
| BCS | 25 | 100 | 0.556 | 100 | 0.326 | 462.999 |
| L1 | 20 | 140 | 0.388 | 100 | 0.222 | 55.810 |
| BCS | 20 | 140 | 0.388 | 100 | 0.326 | 462.787 |
Error: recovery error; Variance: variance of raw AD values between original signal and recovery signal; L1: the recovery method based on L1-minimization; BCS: the recovery method based on BCS.
| Threshold Value | Number of Significant Components K | Number of Clusters M |
|---|---|---|
| 20 | 35 | 140 |
| 23 | 30 | 120 |
| 25 | 25 | 100 |
| 29 | 20 | 80 |
| 39 | 15 | 60 |
| 51 | 10 | 40 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zou, Z.; Hu, C.; Zhang, F.; Zhao, H.; Shen, S. WSNs Data Acquisition by Combining Hierarchical Routing Method and Compressive Sensing. Sensors 2014, 14, 16766-16784. https://doi.org/10.3390/s140916766
Zou Z, Hu C, Zhang F, Zhao H, Shen S. WSNs Data Acquisition by Combining Hierarchical Routing Method and Compressive Sensing. Sensors. 2014; 14(9):16766-16784. https://doi.org/10.3390/s140916766
Chicago/Turabian StyleZou, Zhiqiang, Cunchen Hu, Fei Zhang, Hao Zhao, and Shu Shen. 2014. "WSNs Data Acquisition by Combining Hierarchical Routing Method and Compressive Sensing" Sensors 14, no. 9: 16766-16784. https://doi.org/10.3390/s140916766
APA StyleZou, Z., Hu, C., Zhang, F., Zhao, H., & Shen, S. (2014). WSNs Data Acquisition by Combining Hierarchical Routing Method and Compressive Sensing. Sensors, 14(9), 16766-16784. https://doi.org/10.3390/s140916766




