Compressive Sensing Image Sensors-Hardware Implementation
Abstract
: The compressive sensing (CS) paradigm uses simultaneous sensing and compression to provide an efficient image acquisition technique. The main advantages of the CS method include high resolution imaging using low resolution sensor arrays and faster image acquisition. Since the imaging philosophy in CS imagers is different from conventional imaging systems, new physical structures have been developed for cameras that use the CS technique. In this paper, a review of different hardware implementations of CS encoding in optical and electrical domains is presented. Considering the recent advances in CMOS (complementary metal–oxide–semiconductor) technologies and the feasibility of performing on-chip signal processing, important practical issues in the implementation of CS in CMOS sensors are emphasized. In addition, the CS coding for video capture is discussed.1. Introduction
Image sensors are of increasing importance in applications such as biomedical imaging, sensor networks, hand-held digital cameras, as well as cameras in cell phones, computers, and for closed circuit television (CCTV) monitoring systems. The increasing demand for both high resolution and high frame rate cameras leads to a large amount of image data. With these large amounts of data, fast and accurate image compression algorithms to represent the data in a compact form are required. Typically, compression algorithms use the spatial and temporal correlations in image and video signals to remove redundant information while concurrently keeping the essential features intact. Different algorithms such as Huffman, arithmetic, dictionary, differential, sub-band and wavelet-based coding as well as quantization methods have been presented [1]. These algorithms perform the compression after the image acquisition.
In the compressive sensing (CS) method [2–7], instead of sensing the entire image and then subsequently removing redundant information during the compression step, only the required or non-redundant information is sensed. The CS paradigm has attracted increased interest in past decade because it intrinsically avoids sensing redundant information that exists in image or video data. In CS, a number of random projections of the image are being sensed as the compressed version of the image, thus leading to the faster image acquisition system.
The CS method has also found extensive applications because of its impact in decreasing the number of the sensors for a given image resolution and reducing the image acquisition time. Some of the main applications of the CS are in radar imaging [8,9], DNA microarrays [10,11], surface metrology [12], and biomedical imaging [13,14] including magnetic resonance imaging (MRI) [15–17], computed tomography (CT) imaging [18–20], ultrasound imaging [21–23], and fluorescent imaging [24,25].
As the CS paradigm invokes simultaneous sensing and compression, conventional architectures cannot be used for the implementation of CS encoding. This is because in standard cameras, the level of the light for each spot in the scene, i.e., the pixel value, is captured while the CS technique requires some transformed version of the light level of the entire scene. Therefore, new imaging structures have been proposed to implement CS-based imaging systems.
The first implementations of CS were in the optical domain. Here, the required transformation can be applied to the reflected light coming from the object. The resulting transform coefficients can be sensed by regular sensors and used in the decoder side to recover the pixel values for the image. However, the implementation can be performed in electrical domain as well. The recent advances in CMOS technology have provided for the development of smart imaging systems and the possibility of on-chip signal processing for CMOS-based sensors. Therefore, the CS method can be implemented in the focal-plane with a CMOS sensor in electrical domain. Although the electrical implementation does not lead to less image sensors, the shorter acquisition time can be achieved with a smaller camera size compared to the optical-domain CS cameras.
In this paper, different hardware implementations of the CS-based image acquisition encoding in optical and electrical domains for image and video coding are discussed. In Section 2, the compressive sensing framework including encoding and decoding schemes is discussed. A study of different hardware implementations of CS for image acquisition is presented in Section 3. Section 4 includes the CS system for video coding. Finally, in Section 5, the conclusions are presented.
2. Compressive Sensing Framework
2.1. Encoding
Natural images consist of highly structured information leading to a strong dependency between the adjacent pixels in the image. This dependency can be mathematically investigated by evaluating the expansion coefficients of the image in a special basis, ψ, e.g., discrete cosine transform (DCT), discrete wavelet transform (DWT), and contourlet transform. Considering an N-pixel image as the vector x which is made by column concatenation of the image, then the transformation of the image in basis ψ is:
Conventional transform coding schemes apply the transform ψ to the image and keep the k significant coefficients as the compressed version of the image. The image can be recovered in the decoding process using these coefficients and the inverse transform ψ−1. However, all N pixels should be acquired to extract the significant coefficients. Therefore, it is not efficient to capture N values while only k values are enough for the image reconstruction. Compressive sensing addresses the problem of inefficient sampling and then compression.
By sampling all of the pixels separately, their common information is sampled more than once. Although, this extra information can be removed later using image compression algorithms, in compressive sensing, only the necessary information is sampled from the beginning. Therefore, instead of sampling the level of the light from the different points in the scene, the projections of the level of the light for the entire scene are used as the CS measurements. These measurements can be used to recover the image that would be achieved by regular sampling schemes.
CS encoding is performed by acquiring several linear measurements from the image using different projection functions. Considering the image as the vector x, different projections of the image can be shown as follows:
As can be seen in Equation (3), the encoding process is a simple matrix multiplication. However, the important part is that the measurement matrix Φ should be properly chosen to extract the maximum information from the image. The measurement matrix can be chosen based on the particular properties of the image. However, the structure of the image is unknown, unless CS is used for the compression of an available image, but this is not its main purpose. Also, the structural information of the image might change from one image to another. Therefore, a universal measurement matrix which is applicable for all images is required.
It has been shown that when the number of the measurements (M) is greater than the order of sparsity of the image (k), then the necessary and sufficient condition for image reconstruction is the validity of the restricted isometry property (RIP) for the measurement matrix [5,26,27]. The RIP property is expressed as follows:
2.2. Decoding
Reconstruction algorithms use the measurement vector, y, the measurement matrix, Φ, and the basis, ψ, to recover the value of each pixel in the image. The reconstruction methods search for the sparsest vector such that its projection on the measurement matrix domain matches the available measurement values. The 0-norm is the best criterion function to measure the sparsity of a vector. Therefore, the problem can mathematically be expressed as follows:
The 0-norm minimization is an NP-complete problem. However, it can be shown that the 1-norm minimization, basis pursuit (BP) [2], and the linear programming algorithm can be used for reconstruction if the measurement matrix satisfies the restricted isometry property [26,27]. Therefore, considering the effect of the noise on the measurements values, the reconstruction problem can be shown to be:
Convex programming can be exploited to solve the above optimization problem. Although linear programming leads to promising results in terms of the reconstructed image quality, it is of high computational complexity, for instance in order of [29]. Some other fast convex programming methods, for example gradient methods [30], have been presented to improve the computational load of the algorithms. Also, for the optimization problem, some efficient iterative methods based on solving several optimization sub-problems with sparsity regularizer have proposed in [31,32] to improve the convergence time.
There is another family of algorithms based on iterative greedy methods that are computationally more efficient compared to BP methods. However, the cost is a lower image quality for the same number of measurements [33–38]. Greedy methods use iterative, non-optimization approach by successive approximation of the data and its residuals. Orthogonal matching pursuit (OMP) [33], stagewise OMP (StOMP) [34], and regularized OMP (ROMP) [35] are some of the greedy methods with computational complexity in order of O(KMN) [36]. Subspace pursuit (SP) [36], compressive sampling matching pursuit (CoSaMP) [37], and adaptive sparsity matching pursuit (ASMP) [38] are some of the other greedy methods with comparable reconstruction quality to the BP methods.
3. Hardware Implementation
3.1. Single Pixel Cameras
Conventional cameras represent the captured image in spatial domain by using multiple photodetectors as the pixels of the image [39]. Therefore, the resolution of the image increases with the number of photodetectors. However, the first implementations of a CS imaging system used a single photodetector to capture different CS measurements from the scene. Optical devices were used to represent the pixels of the image. Therefore, the resolution of the image was defined in the optical domain.
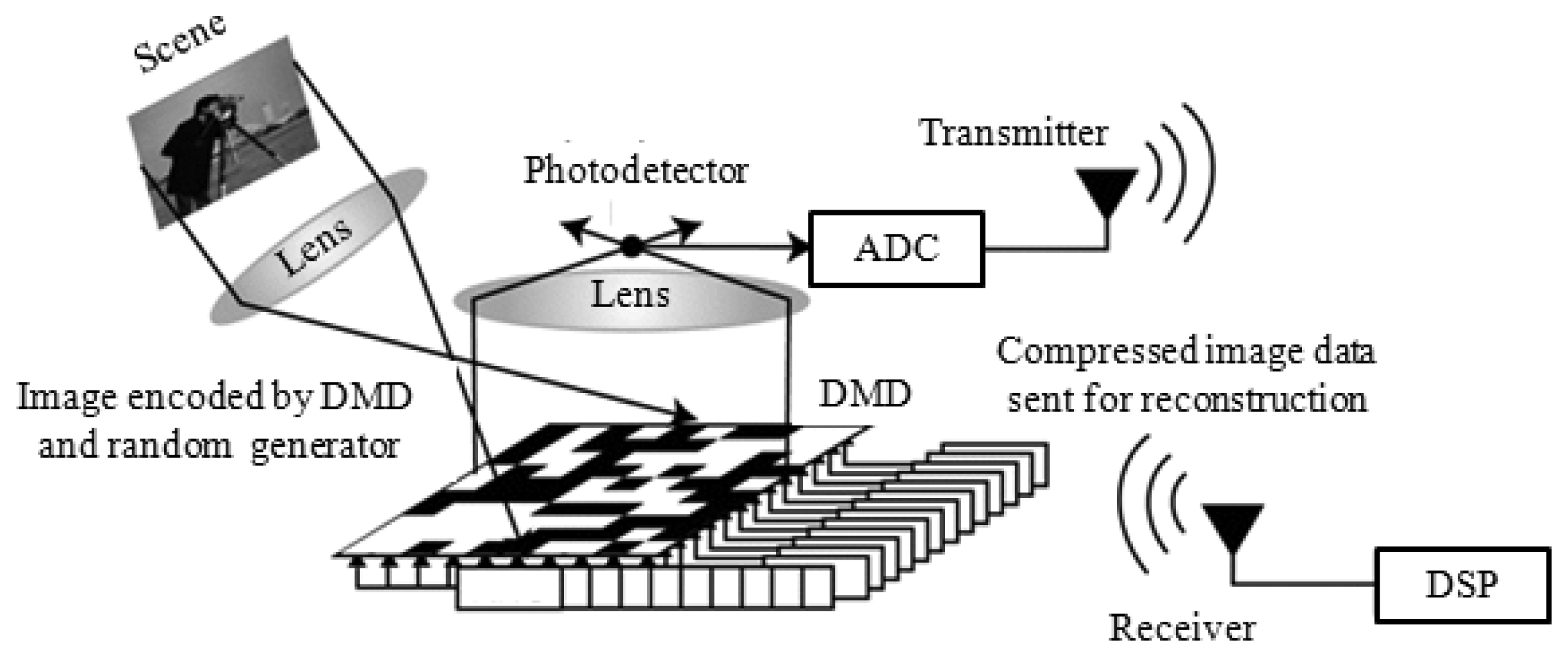
The digital micro-mirror device (DMD) and the CS paradigm were used to implement one of the first single-pixel cameras [40,41]. Figure 1 shows a general schematic of the implemented single-pixel imaging systems. Each mirror in the DMD array is tilting towards or away from the photodetector based on its applied random coefficient [42]. The aggregate level of the light, which is integrated by the photodetector, represents one CS measurement. Different measurements are then achieved by different random alignments of the micro-mirrors. A multi-pixel image is recovered using all measurement values and the CS reconstruction methods described in Section 2.2. The idea of single-pixel imaging is also used in compressive confocal microscopes [43,44].
In [45], a single detector terahertz imaging system is presented. A series of random masks have been exploited to make the CS measurements. Each mask represents a random pattern using a combination of transparent and opaque areas corresponding to random coefficients. In [46], structured light and a single detector have been used to measure specific features of the image. Instead of using uniform illumination for imaging, a set of spatially structured illumination patterns have been used to extract a sequence of measurements from the image.
All the single-pixel cameras described above are based on serial measurement extraction. Different measurements are made during consecutive time intervals. Therefore, the object should be stationary during the measurement process. This stationary requirement makes the designs unsuitable for video acquisition when there is movement in the scene from one measurement to the next.
3.2. Coded Aperture Cameras
Typical cameras use pinhole apertures and lenses to focus the incoming light from the object onto the sensor array. Therefore, each sensor in the array represents a pixel of the image. However, the optical field from the scene could be modulated using a coded aperture. Therefore, some specific image transformations can be implemented in optical domain [47]. Considering the CS measurements set as a random transformation of the image, then coded aperture can also be used in CS cameras. In [48], a high resolution coded aperture with a low resolution focal plane array aperture has been used for imaging. The aperture has been designed so that different CS measurement values are collected by the different pixels of the low resolution array. Therefore, the value measured by each sensor on the focal plane array is a CS measurement value formed in optical domain by the coded aperture. Contrary to the single-pixel imager, all CS measurement values are extracted in the same time interval.
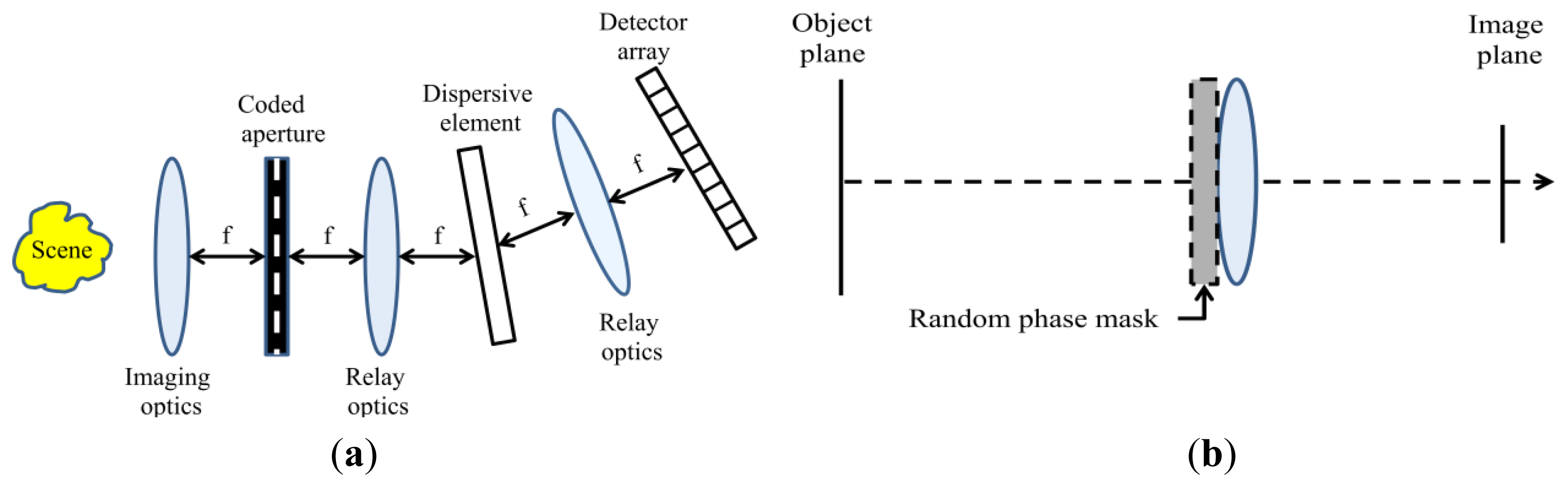
The coded aperture approach is also used for spectral imaging. In [49], a single shot spectral imager using the CS framework is presented. To improve the signal-to-noise ratio (SNR) of reconstruction, a multi-shot approach with multiple apertures and focal plane measurement sets is presented in [50]. The CS measurement can also be implemented by using a random mask placed on the lens. Here, the convolution of the image and mask signal is made at a single exposure to create the CS measurement values [51]. Figure 2 shows the spectral imaging structure [49], and the random mask set-up presented in [51].
3.3. Random Lens Imaging
An imaging system developed in [52] utilizes random lens made from multi-faceted mirrors for compressive image acquisition. The system is the same as in conventional cameras, but the input-output relationship of the light rays is randomized. The only extra hardware is some small mirror patches stitched around the sensors, thus leading to an ultra-thin design for multi-spectral and high dynamic range imaging [52].
3.4. CS-CMOS Cameras
In the hardware implementation of CS encoding discussed in Sections 3.1–3.3, the random transformation required for CS measurements is performed in the optical domain. This leads to an optimum usage of photodetectors to achieve high resolution imaging using low resolution sensor arrays at the cost of a larger camera size due to the optical components. However, the CS method can also be useful as an image compression method because of its straightforward encoding process. Due to the limitation in power and area, compression methods with simple encoding processes are of high interest for on-chip image compression in CMOS imaging systems. Therefore, on-chip implementation of CS algorithms in electrical domain would be useful for portable applications where there are limitations on camera size and power consumption.
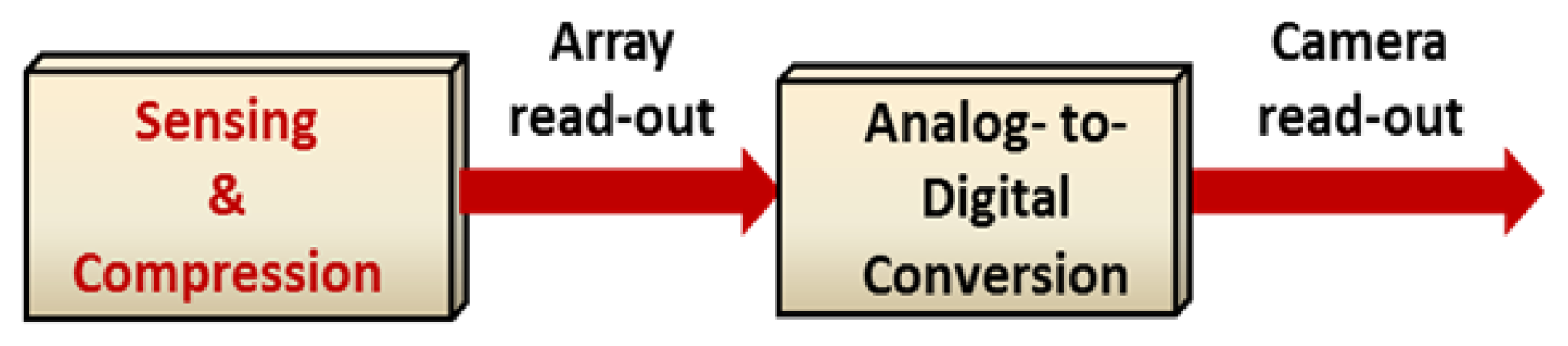
The electrical domain implementation of CS algorithm could be performed in digital domain. In this case, after the sensing and analog-to-digital (A/D) conversion, the digital values should be stored and then added together with random weights to make the CS measurements. A schematic representation of the digital implementation is shown in Figure 3.
Although the camera read-out time decreases in this implementation, the array read-out time and amount of the storage are the same as an imager with no compression. Also, the multiple memory accesses for the digital calculation increases the overall read-out time. However, all or some parts of the compression could be performed in analog domain before or as a part of the analog-to-digital conversion. This structure decreases the amount of the on-chip storage area. Also, the analog implementations of the arithmetic circuits are faster and require less area compared to the digital circuits. Figure 4 shows the block diagram representation for the analog implementation.
Several works have been presented on computational imaging and analog signal processing in image sensors [53,54]. These designs are intended to implement the image transformation in analog domain. However, they could be used as a CS encoder by choosing appropriate transform coefficients.
The main advantage of the CS encoding, which is the simultaneous sensing and compression, is disregarded for both structures in Figures 3 and 4. To be compatible with the CS concept, the compression should be performed in the array level and before the array read-out. Figure 5 shows the block diagram of a CS imaging system which is well-matched with the CS concept. In this implementation, only the compressed version of the image is read-out, so the entire imaging process is faster and more power efficient.
One of the major difficulties in realizing the CS-CMOS implementation shown in Figure 5 is the method of applying random coefficients to the pixels. The random selection and summation of the pixels can be performed after the light integration [55–57], but this is not based on the block diagram in Figure 5. In [55], a block-based CS encoding for digital pixel sensors (DPS) has been presented. The sensor array has been divided into different sub-blocks and one pixel is randomly selected in each block as the CS measurement for that block. The selected digital outputs are then saved in 8-bit memories to be used in the CS reconstruction process.
Another block-based implementation of CS at the A/D conversion level has been presented in [57]. The random measurement is performed with a CS multiplexer before a ΔΣ-based A/D converter. Row and column block selectors are used to connect different blocks to a CS multiplexer and a pseudo-random generator provides the random coefficients required for the CS multiplexer. Although the measurement process is not performed in parallel with sensing, the different measurements are extracted in parallel. This leads to a single-shot imaging scheme. However, to perform the simultaneous sensing and compression, the random sequence should be applied at the beginning of the integration time to make sure that the corresponding CS measurement is integrated during the light integration. Therefore, the technique of random selection of the pixels is important. Examples of the pixel selection techniques are discussed in the following three subsections 3.4.1 to 3.4.3.
3.4.1. In-Pixel Random Generators
Some designs use in-pixel memories or digital circuits to put all or part of the random generator inside the pixel. However, by putting non-photosensitive elements inside the pixel, the fill factor and sensitivity of the imager decreases [58,59]. Also, the size of the pixel increases, thus leading to lower image spatial resolution.
In [60], in-pixel memories with control logic, a finite state machine (FSM), three linear feedback shift registers (LFSRs) and a single analog processing unit were used to perform in-pixel convolution in real-time. Each pixel contains a three-transistor active pixel sensor (APS) [61,62] with one flip flop as the local memory plus control logic to implement the horizontal and vertical shifting. Using a two-dimensional scrambling technique, the random coefficients are applied in two dimensions over the entire array. Also, the measurement process is performed in two dimensions using the differential current output of each pixel which are connected to the corresponding outputs from other pixels. Finally, the accumulated differential currents are fed to a transimpedance amplifier (TIA) to calculate the final CS measurement. The measurement process is completely performed during the light integration in analog domain, although the scrambling technique needs extra time between the acquisitions of one measurement and the next.
3.4.2. Column-Row Random Selection
Random coefficients can be fed to the pixels from outside the array. However, because of layout restrictions, having individual access to each pixel is impractical for a large array sensor. It is because of the limited number of the metal layers in present-day standard CMOS technologies and the fact that the metal layers cannot pass through the photosensitive areas [63]. Therefore, different sub-regions of the pixels should share common paths to access the coefficients. Random coefficients can be partially fed to the array along the columns so that pixels in each row have the same coefficient. Then, the outputs of the columns are randomly combined outside the array to complete the random measurement.
In [64,65], passive pixel sensors (PPS) [66] were used to design a separable-transform image sensor which is also capable of implementing the CS encoding. Instead of sensing the pixel values for the image, the imager projects the image on a specific basis and produces the projection coefficients. The convolution and image transformation are performed for separate sub-regions of the image with 8 × 8 and 16 × 16 block sizes, respectively. The main capability of the design is to exploit the separability property to perform the image transformation in two steps:
- (1)
focal plane processing along the columns and during the sensing, and
- (2)
analog computational units outside the array and before the analog-to-digital converter.
Figure 6 shows the schematic representation of the imager in [64]. The image transformation is divided into two separate matrix multiplications. The first multiplication is performed by using differential transistors in the pixels and Kirchhoff's current law along the columns. The coefficients for each pixel are provided by the differential signal paths which are the same for the pixels in each row. The results for different columns are fed to an analog vector-matrix multiplier (VMM) to perform the second part of the matrix multiplication. The imager can be exploited for CS imaging by dividing the random multiplication of CS encoding into two separate matrix computations. However, the separability property and analog multiplication is too complicated for the CS implementation, although it is useful in performing other image transformations.
The APS and switched capacitor circuits are used in [67] to implement a separable transform imager. By adding one transistor and one capacitor to the three-transistor APS structure and using a switched capacitor circuit for each column, the random combination of the pixels for each column is achieved. The calculated values from all columns are fed to another switch capacitor circuit to make the final random measurement. The timing of the switching clocks can be adjusted to choose one coefficient from the set {0, +1, −1} for each pixel.
An implementation of CS encoding using random convolution was presented in [68]. The structure is a combination of in-pixel and column-row random selection. Binary random coefficients were provided by in-pixel memories and a LFS) to feed the initial values for the in-pixel memories. Each pixel contains a photodiode and a 1-bit memory which is connected to the memories in adjacent pixels to make an embedded shift register inside the array. The outputs of the pixels in each column are connected together, and Kirchhoff's current law applies along the columns to make a random light integration for each column. A time-domain multiplexer and an analog-to-digital converter are used to digitize the outputs for different columns. The rest of the measurement process is performed by doing several digital summations. To complete the randomness of the convolution process, a pseudo-random triggering LFSR was used after column integration, but before column read-out. Note that the CS measurement process has been performed in two steps, with the second step in digital domain and after the light integration. This is not the simultaneous sensing and compression expected in CS encoding.
3.4.3. Block Random Selection
Column-row random selection provides the possibility of feeding random sequences from outside the array by using the same signal paths for pixels in each column. However, the metal paths could be shared among different blocks of the images, instead of the columns. As the size of the block is small compared to the entire array, then the individual access to all pixels in the block from outside the array is feasible. Also, each pixel in the block could share the metal path with its corresponding pixels in other blocks. Therefore, each random coefficient is connected to all the corresponding pixels in different blocks. It is analogous to the column-row structure when all pixels in one column share the same random coefficient. Therefore, the array can be divided into separate blocks and the CS encoding can be implemented for different blocks separately. Individual access to all pixels in each block can be possible at the time of measurement time of the block.
In [63], a new block-based implementation of CS using a three-transistor APS structure, an off-array LFSR, and switched capacitor (SC) circuits, was designed. The SC branches and LFSR are designed outside the array and there is no extra in-pixel element for compression. The random coefficients produced by the LFSR are fed to the SC branches outside the array. However, to provide the individual connection of pixels and SC branches, the imager is designed in different blocks which share the same signal paths toward the SC branches. Figure 7(a) shows a block diagram of the connection between the pixels, SC branches and LFSR.
The connections between different 4 × 4 blocks in the array for block-by-block read-out are shown in Figure 7(b). In this structure, there is one set of SC branches for the entire array. Therefore, the CS measurement is performed for one block at a time. To improve the read-out time of the array, the measurement process can be performed in parallel for different columns of blocks, as shown in Figure 7(c). There is one integrator and one set of SC branches for each column of the blocks. Therefore, the measurement process is performed in parallel at the same time, for different columns of blocks.
Table 1 shows a summary of different CS-CMOS imager architectures discussed in this paper. The implementation can be in analog or digital domain. In the digital implementation, the random selection and measurement extraction are straightforward as they use the digital data outside the array. However, the analog implementation leads to a faster and more efficient encoding process. As can be seen in the table, different works use different methods of random selections. In-pixel random selection leads to the use of extra digital components inside the pixel which reduce the fill factor of the design. However, column-row and block random selection methods use the external random coefficients to avoid the use of internal digital circuits. Also, the block method is more efficient in terms of in-pixel and overall hardware usage.
4. CS Video Capture
The structures mentioned in the previous section can be used for video acquisition by encoding each frame of the image separately. In this case, the measurement values for each frame should be captured and sent off the camera before starting the measurement process for the next frame. The entire video acquisition scheme for n consecutive frames of the video is shown in Figure 8.
The spatial dependency of different pixels in the image is exploited as the sparsity objective function in the CS image decoding process. However, there are temporal correlations between the consecutive frames of a video which can be used to reduce the reconstruction time of a CS-encoded video.
In [69], the temporal information of the video was exploited to improve the overall reconstruction time. In one implementation, the decoded image for each reconstructed frame was used as the initial value for the reconstruction problem of the next frame. In another implementation, the CS decoding problem was solved for multiple frames at the same time with reasonable computation time by using the similarities between the subsequent frames.
While only the sparsity of the image derivative in temporal domain has been used in [69], the motion function of the video from one frame to another can be used to improve the reconstruction. In [70], considering the relationship between motion and CS coding, a method to estimate the motion information of the image was presented. Also, the motion parameters were included in the reconstruction problem to improve the quality of decoded frames.
Considering the timing diagram in Figure 8, the video frames cannot be captured during the read-out intervals. The fact that the read-out time increases with increasing imager size restricts the frame rate of the CS video camera. However, the measurement process can be performed in temporal domain as well as in spatial domain to improve the capture time of a constant number of frames. Therefore, the measurements can be captured for a three-dimensional cube of data instead of separate measurements for several two-dimensional data sets, i.e., image frames, as shown in Figure 9. Using the measurement process in Figure 9(a), the read-out time of the camera is reduced by the ratio of 1/n.
A new CS measurement method for video compression based on the read-out scenario shown in Figure 9 was presented in [71]. In this method, multiple cameras capture the CS measurements from the same scene. Each camera then produces a frame of the measurement values instead of n frames of pixel values. Different measurement frames captured from different cameras are exploited to reconstruct the video for n subsequent frames.
The measurement process is performed completely in time domain. One binary random vector with n entries is assigned to each pixel of the image in each camera. If the ith bit of the vector is “1”, the level of the light for that pixel in the ith frame is integrated and added to the measurement value for that pixel. The level of the light during each frame does not affect the measurement value when its corresponding bit in the random vector is “0”.
The simulation results for the image reconstruction are promising and lead to a high frame rate video recording system [71]. However, regular sensor structures cannot be used for the hardware implementation of this design. New pixel structure should be considered to perform the CS measurement process in time domain. Also, since each pixel needs a separate random sequence, new array architecture is required to apply the random bits to the pixels.
5. Conclusions
In this paper, we reviewed compressive sensing (CS) image acquisition with encoding and decoding techniques, and discussed several hardware implementations. Different implementations in optical domain by using digital micro-mirror device (DMD) arrays, coded aperture or random lens systems in early implementation of CS encoding were reviewed. However, the complexity of the optical components and the size of the camera make the optical implementation of the CS encoding unsuitable for portable applications. Also, because of the significant advances in complementary metal-oxide-semiconductor (CMOS) technology, the implementation of CS on focal plane of the CMOS sensors is very feasible. Therefore, we reviewed recent implementations of CS encoding in electrical domain for CMOS sensor structures. In addition, recent works on CS video coding were discussed.
Acknowledgments
The authors are grateful to the Natural Science and Engineering Research Council (NSERC) of Canada and the Canada Research Chair program for funding this work. Also, we would like to acknowledge CMC Microsystems for the provision of products and services that facilitated this research. One author (MJD) also expresses his thanks to the ITCE Division, POSTECH for hosting him as a Distinguished Visiting Professor through the S. Korean Ministry of Education, Science, and Technology Program (project R31-2008-000-10100-0), during the final preparations of the revised manuscript.
References
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann Publishers: New York, NY, USA; p. 1998.
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag 2008, 25, 21–30. [Google Scholar]
- Rombers, J. Imaging via compressive sampling [introduction to compressive sampling and recovery via convex programming]. IEEE Signal Process. Mag. 2008, 25, 14–20. [Google Scholar]
- Baraniuk, R.G. Compressive sensing [lecture notes]. IEEE Signal Process. Mag. 2007, 24, 118–124. [Google Scholar]
- Candes, E.J. Compressive Sampling. Proceeding of International Congress of Mathematicians, Madrid, Spain, 2–30 August 2006; Volume 3, pp. 1433–1452.
- Fornasier, M.; Rauhut, H. Compressive Sensing. In Handbook of Mathematical Methods in Imaging; Springer: Heidelberg, Germany, 2011; Volume 1, pp. 187–229. [Google Scholar]
- Herman, M.A.; Strohmer, T. High-resolution radar via compressed sensing. IEEE Trans. Signal Process 2009, 57, 2275–2284. [Google Scholar]
- Gurbuz, A.C.; McClellan, J.H.; Scott, W.R. A compressive sensing data acquisition and imaging method for stepped frequency GPRs. IEEE Trans. Signal Process. 2009, 57, 2640–2650. [Google Scholar]
- Sheikh, M.A.; Milenkovic, O.; Sarvotham, S.; Baraniuk, R.G. Compressed Sensing DNA Microarrays; Technical Report ECE-0706; ECE, Rice University: Houston, TX, USA, 2007. [Google Scholar]
- Parvaresh, F.; Vikalo, H.; Misra, S.; Hassibi, B. Recovering sparse signals using sparse measurement matrices in compressed DNA microarrays. IEEE J. Sel. Top. Signal Process. 2008, 2, 275–285. [Google Scholar]
- Ma, J. Compressed sensing for surface characterization and metrology. IEEE Trans. Instrum. Meas. 2010, 59, 1600–1615. [Google Scholar]
- Wang, G.; Bresler, Y.; Ntziachristos, V. Guest editorial compressive sensing for biomedical imaging. IEEE Trans. Med. Imag. 2011, 30, 1013–1016. [Google Scholar]
- Faramarzpour, N.; El-Desouki, M.M.; Deen, M.J.; Fang, Q.; Shirani, S.; Liu, L.W.C. CMOS imaging for biomedical applications. IEEE Potent. 2008, 27, 31–36. [Google Scholar]
- Lustig, M.; Donoho, D.; Pauly, J. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Resonance Med. 2007, 58, 1182–1195. [Google Scholar]
- Lusting, M.; Donoho, D.; Santos, J.; Pauly, J. Compressed sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar]
- Cukur, T.; Lusting, M.; Saritas, E.; Nishimura, D. Signal compensation and compressed sensing for magnetization-prepared MR angiography. IEEE Trans. Med. Imag. 2011, 30, 1017–1027. [Google Scholar]
- Chen, G.H.; Tang, J.; Leng, S. Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med. Phys. 2008, 35, 660–663. [Google Scholar]
- Sidky, E.Y.; Pan, X. Image reconstruction in circular conebeam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 2008, 53, 4777–4807. [Google Scholar]
- Yu, H.; Wang, G. Compressed sensing based interior tomography. Phys. Med. Biol. 2009, 54, 2791–2805. [Google Scholar]
- Quinsac, C.; Basarab, A.; Girault, J.; Kouame, D. Compressed sensing of ultrasound images: Sampling of apatial frequency domains. Proceedings of IEEE Workshop on Signal Processing Systems (SIPS), San Francisco, CA, USA, 6–8 October 2010; pp. 231–236.
- Achim, A.; Buxton, B.; Tzagkarakis, G.; Tsakalides, P. Compressive Sensing for Ultrasound and RF Echoes using Alpha-stable Distributions. Proceedings of 32nd Annual IEEE International Conference on Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 4304–4307.
- Tosic, I.; Jovanovic, I.; Frossard, P.; Vetterli, M.; Duric, N. Ultrasound tomography with learned dictionaries. Proceedings of IEEE International Conference on Acoustics, Speech Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 5502–5505.
- Coskun, A.F.; Sencan, I.; Su, T.; Ozcan, A. Lensless wide-field fluorescent imaging on a chip using compressive decoding of sparse objects. Opt. Express 2010, 18, 10510–10523. [Google Scholar]
- Kfouri, M.; Marinov, O.; Quevedo, P.; Faramarzpour, N.; Shirani, S.; Liu, L.W.; Fang, Q.; Deen, M.J. Towards a miniaturized wireless fluorescence-based diagnostic imaging system. IEEE J. Sel. Top. Quant. Electron. 2008, 14, 226–234. [Google Scholar]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. Compets Rendus Math. 2008, 349, 589–592. [Google Scholar]
- Dadkhah, M.R.; Shirani, S.; Deen, M.J. Compressive Sensing with Modified Total Variation Minimization Algorithm. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), allas, TX, USA, 14–19 March 2010; pp. 1310–1313.
- Nestrov, Y.; Nemrovski, A. Interior Point Polynomial Algorithms in Convex Programming; Studies in Applied Mathematics (SIAM): Philadelphia, PA, USA, 1994. [Google Scholar]
- Figueiredo, M.A.T.; Nowark, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A new TwIST: Two step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar]
- Wright, S.J.; Nowark, R.D.; Figueiredo, M.A.T. Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar]
- Needell, D.; Vershynin, R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit. IEEE J. Sel. Top. Signal Process. 2010, 4, 310–316. [Google Scholar]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar]
- Wu, H.; Wang, S. Adaptive sparsity matching pursuit algorithm for sparse reconstruction. IEEE Signal Process. Lett. 2009, 19, 471–474. [Google Scholar]
- Deen, M.J.; Basu, P.K. Silicon Photonics—Fundamentals and Devices; John Wiley & Sons Ltd.: Chichester, UK, 2012. [Google Scholar]
- Durate, M.F.; Devenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar]
- Rice Single-Pixel Camera Project. Available online: http://dsp.rice.edu/cscamera (accessed on 26 March 2013).
- Samspell, J. Digital micromirror device (DMD) and its application to projection displays. J. Vac. Sci. Technol. B 1994, 12, 3242–3246. [Google Scholar]
- Ye, P.; Paredes, J.L.; Wu, Y.; Chen, C.; Arce, G.R.; Parther, D.W. Compressive confocal microscopy: 3D reconstruction algorithms. Proc. SPIE 2009, 7210. [Google Scholar] [CrossRef]
- Wu, Y.; Ye, P.; Mirza, I.O.; Arce, G.R.; Parther, D.W. Experimental demonstration of an optical-sectioning compressive sensing microscope (CSM). Opt. Express 2010, 18, 24565–24578. [Google Scholar]
- Chan, W.L.; Charan, K.; Takhar, D.; Kelly, K.F.; Baraniuk, R.G.; Mittleman, D.M. A single-pixel terahertz imaging system based on compressed sensing. Appl. Phys. Lett. 2008, 93. [Google Scholar] [CrossRef]
- Baheti, P.K.; Neifeld, M.A. Feature-specific structured imaging. Appl. Opt. 2008, 45, 7382–7391. [Google Scholar]
- Gottesman, S.R.; Fenimore, E.E. New family of binary arrays for coded aperture imaging. Appl. Opt. 1989, 28, 4344–4352. [Google Scholar]
- Marcia, R.F.; Willet, R.M. Compressive Coded Aperture Superresolution Image Reconstruction. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 30 March–4 April 2008; pp. 833–836.
- Wagadarikar, A.; John, R.; Willet, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt. 2008, 47, B44–B51. [Google Scholar]
- Arguello, H.; Rueda, H.F.; Arce, G.R. Spatial super-resolution in code aperture spectral imaging. Proc. SPIE 2012, 8365. [Google Scholar] [CrossRef]
- Stern, A.; Javidi, B. Random projections imaging with extended space-bandwidth product. J. Disp. Technol. 2007, 3, 316–320. [Google Scholar]
- Fergus, R.; Torralba, A.; Freeman, W.T. Random Lens Imaging; Technical Report MIT-CSAIL-TR-2006-058; MIT-CASIL: Cambridge, MA, USA, 2006. [Google Scholar]
- Nilchi, A.; Aziz, J.; Genov, R. Focal-plane algorithmically-multiplying CMOS computational image sensor. IEEE J. Solid-State Circuits 2009, 44, 1829–1839. [Google Scholar]
- Njuguna, R.; Gruev, V. Low power programmable current mode computational imaging sensor. IEEE Sens. J 2012, 12, 727–736. [Google Scholar]
- Zhang, M.; Wang, Y.; Bermak, A. Block Based Compressive Sampling for Digital Pixel Sensor Array. Proceedings of 2nd Asia Symposium on Quality Electronic Design (ASQED), Penang, Malaysia, 3–4 August 2010; pp. 9–12.
- Zhang, M.; Bermak, A. Compressive acquisition CMOS image sensor—From algorithmic solution to hardware implementation. IEEE Trans. Very Large Scale Integr. Syst. 2010, 18, 490–500. [Google Scholar]
- Oike, Y.; Gamal, A.E. A 256 × 256 CMOS Image Sensor with ΔΣ-based Single-Shot Compressed Sensing. Proceedings of IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 19–23 February 2012; pp. 386–388.
- El-Desouki, M.M.; Marinov, O.; Deen, M.J.; Fang, Q. CMOS active-pixel sensor with in-situ memory for ultrahigh-speed imaging. IEEE Sens. J. 2011, 11, 1375–1379. [Google Scholar]
- El-Desouki, M.; Deen, M.J.; Fang, Q.; Liu, L.; Tse, F.; Armstrong, D. CMOS image sensors for high speed applications. Sensors 2009, 9, 430–444. [Google Scholar]
- Majidzadeh, V.; Jacques, L.; Schmid, A.; Vandergheynst, P.; Leblebici, Y. A (256 × 256) Pixel 76.7 mW CMOS Imager/Compressor Based on Real-Time In-Pixel Compressive Sensing. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS), Paris, France, 30 May–2 June 2010; pp. 2956–2959.
- Faramarzpour, N.; Deen, M.J.; Shirani, S.; Fang, Q.; Liu, L.W.C.; Desouza Campos, F.; Swart, J.W. CMOS based active pixel for low light-level detection. IEEE Trans. Electron. Devices 2007, 54, 3229–3237. [Google Scholar]
- Faramarzpour, N.; El-Desouki, M.M.; Deen, M.J.; Shirani, S.; Fang, Q. CMOS photodetector systems for low-level light applications. J. Mater. Sci.: Mater. Electron. 2009, 20 Suppl. 1, S87–S93. [Google Scholar]
- Dadkhah, M.R.; Deen, M.J.; Shirani, S. Block-based compressive sensing in a CMOS image sensor. IEEE Sens. J. 2012. in press. [Google Scholar]
- Robucci, R.; Gray, J.D.; Chiu, L.K.; Romberg, J.; Hasler, P. Compressive sensing on a CMOS separable-transform image sensor. Proc. IEEE 2010, 98, 1089–1101. [Google Scholar]
- Xiao, L.; Liu, K.; Han, D. CMOS low data rate imaging method based on compressed sensing. Opt. Laser Technol. 2012, 44, 1338–1345. [Google Scholar]
- Gamal, A.E.; Eltoukhy, H. CMOS image sensors. IEEE Circuits Devices Mag. 2005, 21, 6–20. [Google Scholar]
- Chi, Y.M.; Abbas, A.; Chakrabartty, S.; Cauwenberghs, G. An Active Pixel CMOS Separable Transform Image Sensor. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS), Taipei, Taiwan, 24–27 May 2009; pp. 1281–1284.
- Jacques, L.; Vandergheynst, P.; Bibet, A.; Majidzadeh, V.; Schmid, A.; Leblebici, Y. CMOS Compressed Imaging by Random Convolution. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Taipei, Taiwan, 19–24 April 2009; pp. 1113–1116.
- Marcia, R.F.; Willet, R.M. Compressive Coded Aperture Video Reconstruction. Proceedings of European Signal Processing Conference (EUSIPCO), Lausanne, Switzerland, 25–29 August 2008.
- Jacobs, N.; Schuh, S.; Pless, R. Compressive Sensing and Differential Image-Motion Estimation. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 718–721.
- Wu, X.; Pournaghi, R. High Frame Rate Video Capture by Multiple Cameras with Coded Exposure. Proceeding of IEEE International Conference on Image Processing (ICIP), Hong Kong, 26–29 September 2010; pp. 577–580.






| Ref. | Pixel Type | Tech. (cmos) | Array Size | In-pixel Components | Technique |
|---|---|---|---|---|---|
| [55] | DPS | -- | -- | 1 transistor, 2 inverters, 1 AND, 1 comparator | Digital domain, Random selection after integration |
| [57] | APS | 0.15 μm | 256 × 256 | 4 transistors | Analog-to-digital conversion level, Random selection after integration |
| [58] | APS | 0.18 μm | 256 × 256 | 3 transistors, 3 NAND, 1 D-flip flop | Analog domain, In-pixel random selection, Differential current & Trans-impedance amplifier |
| [63] | APS | 0.13 μm | 16 × 16 | 3 transistors | Analog domain, Block random selection, Switched capacitor (SC) circuits |
| [64] | PPS | 0.35 μm | 256 × 256 | 2 transistors | Analog domain, Column-row random selection Differential current & Vector matrix multiplier |
| [67] | APS | 0.5 μm | 128 × 128 | 4 transistors, 1 capacitor | Analog domain, Column-row random selection SC circuits |
| [68] | PPS | -- | -- | 1 transistor, 1 flip flop | Analog & digital domain, In-pixel & column-row random selection |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dadkhah, M.; Deen, M.J.; Shirani, S. Compressive Sensing Image Sensors-Hardware Implementation. Sensors 2013, 13, 4961-4978. https://doi.org/10.3390/s130404961
Dadkhah M, Deen MJ, Shirani S. Compressive Sensing Image Sensors-Hardware Implementation. Sensors. 2013; 13(4):4961-4978. https://doi.org/10.3390/s130404961
Chicago/Turabian StyleDadkhah, Mohammadreza, M. Jamal Deen, and Shahram Shirani. 2013. "Compressive Sensing Image Sensors-Hardware Implementation" Sensors 13, no. 4: 4961-4978. https://doi.org/10.3390/s130404961
APA StyleDadkhah, M., Deen, M. J., & Shirani, S. (2013). Compressive Sensing Image Sensors-Hardware Implementation. Sensors, 13(4), 4961-4978. https://doi.org/10.3390/s130404961






