Arrhythmia Identification with Two-Lead Electrocardiograms Using Artificial Neural Networks and Support Vector Machines for a Portable ECG Monitor System
Abstract
:1. Introduction
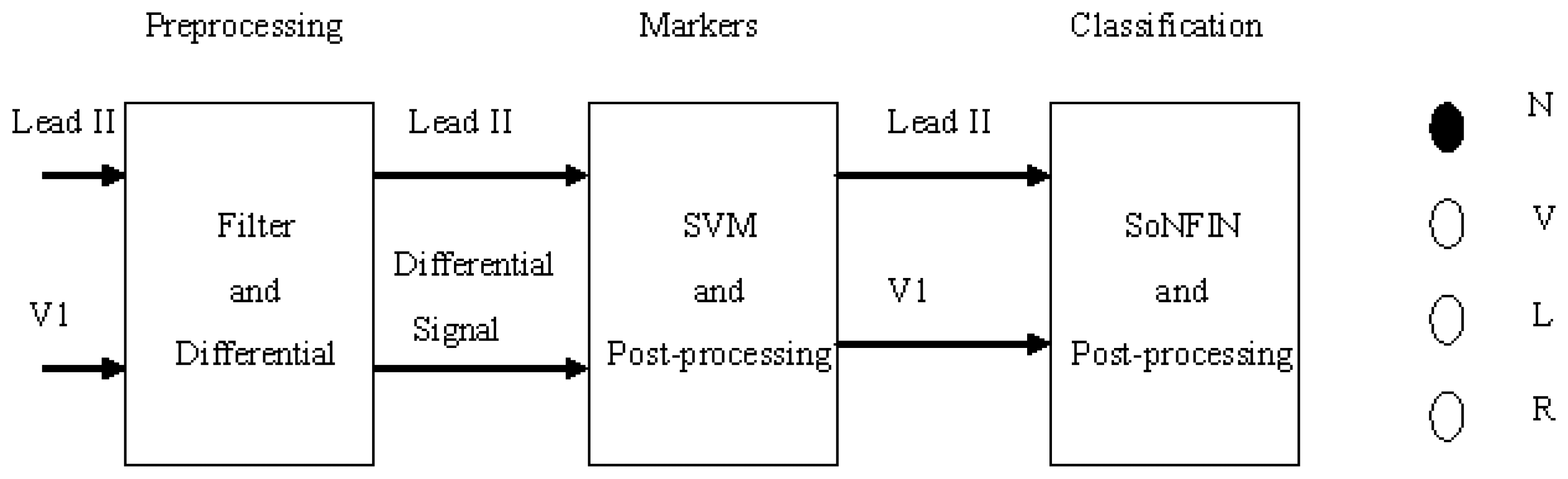
- The Lead II signals were normalized and filtered to reduce the coupled noise (Section 2.2).
- The positions of QRS-complexes in Lead II were detected and marked via a well-trained SVM. Two waveforms of each heartbeat in Lead II and V1 were individually extracted according the markers in Lead II (Section 2.3).
- The extracted waveform was used as a feature to recognize the arrhythmic type of a heartbeat. In this configuration, a self-constructing neural fuzzy inference network (SoNFIN) was used to recognize the arrhythmic type of the heartbeat using the raw Lead II and V1 signals (Section 2.4).
2. Experimental Section
2.1. Database
2.2. Filtering and Normalization
2.3. QR-Complexes Detection and Waveform Extraction
2.3.1. Support Vector Machine (SVM)
2.3.2. Training Phase of SVM
2.3.3. Test and Post-Processing Phases of SVM
2.4. Arrhythmia Classification
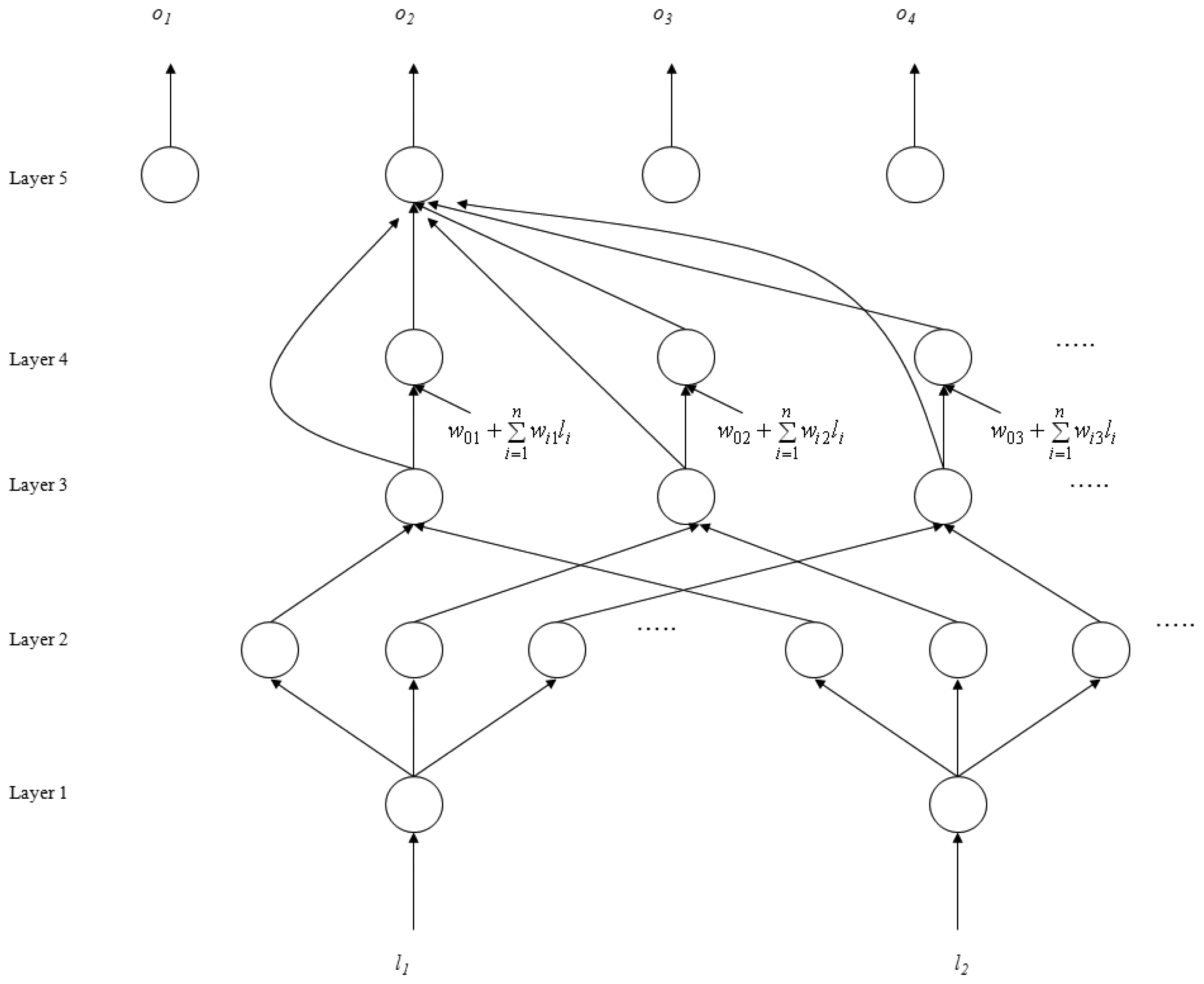
2.4.1. Self-Constructing Neural Fuzzy Inference Network (SoNFIN)
- Layer 1: No computation is performed in this layer. Each node in this layer corresponds to one input variable. Only transmitted input values are forwarded to the next layer directly:
- Layer 2: For fuzzy set Aij, a Gaussian membership function is used to describe the degree that the input variable lj belongs to the i-th fuzzy set. Its mathematical function is defined as follows:where mij and σij are the center and width of the membership function, respectively. This function is implemented by each node.
- Layer 3: A node in this layer represents one fuzzy logic rule and performs precondition matching of a rule. Here we use the following product operation for each Layer-3 node:
- Layer 4: Nodes in this layer are called consequent nodes. Each node is linked to Layer-3 output, and the linear association of the weight in this layer is as follows:
- Layer 5: Each node in this layer corresponds to one output variable. The node integrates all the actions recommended by Layer 5 and acts as a defuzzifier with:
2.4.2. Training and Test Phases of SoNFIN
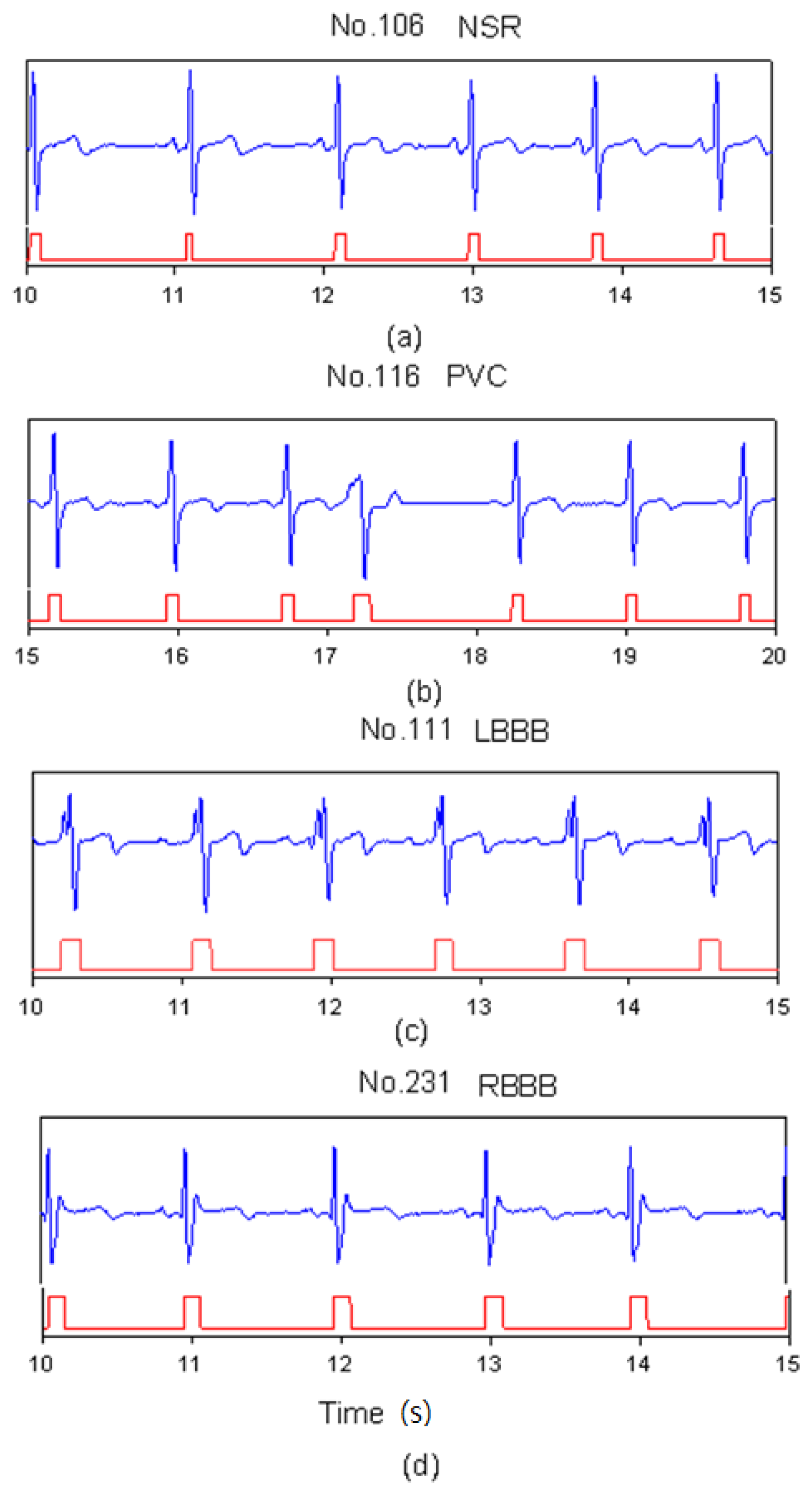
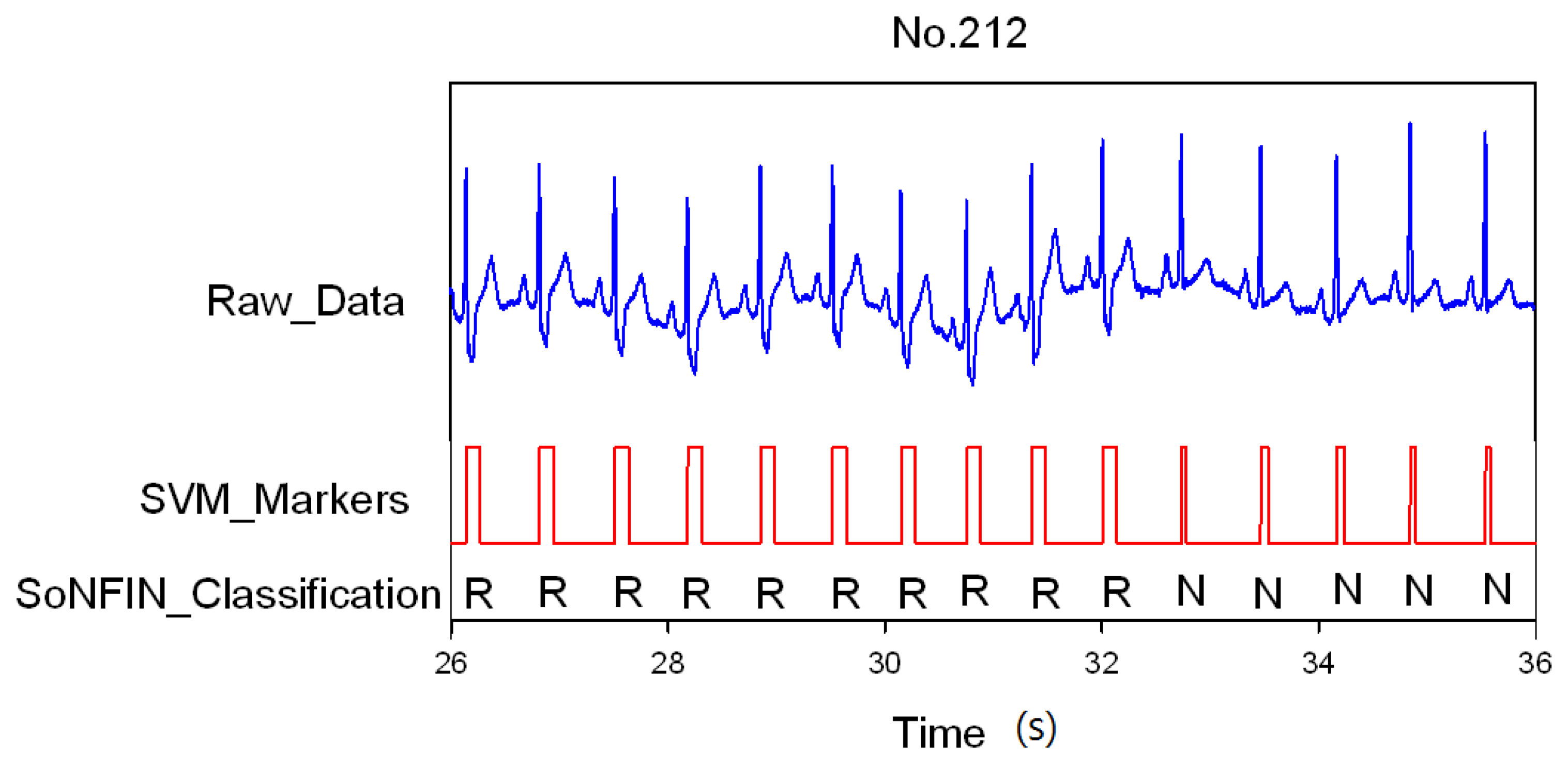
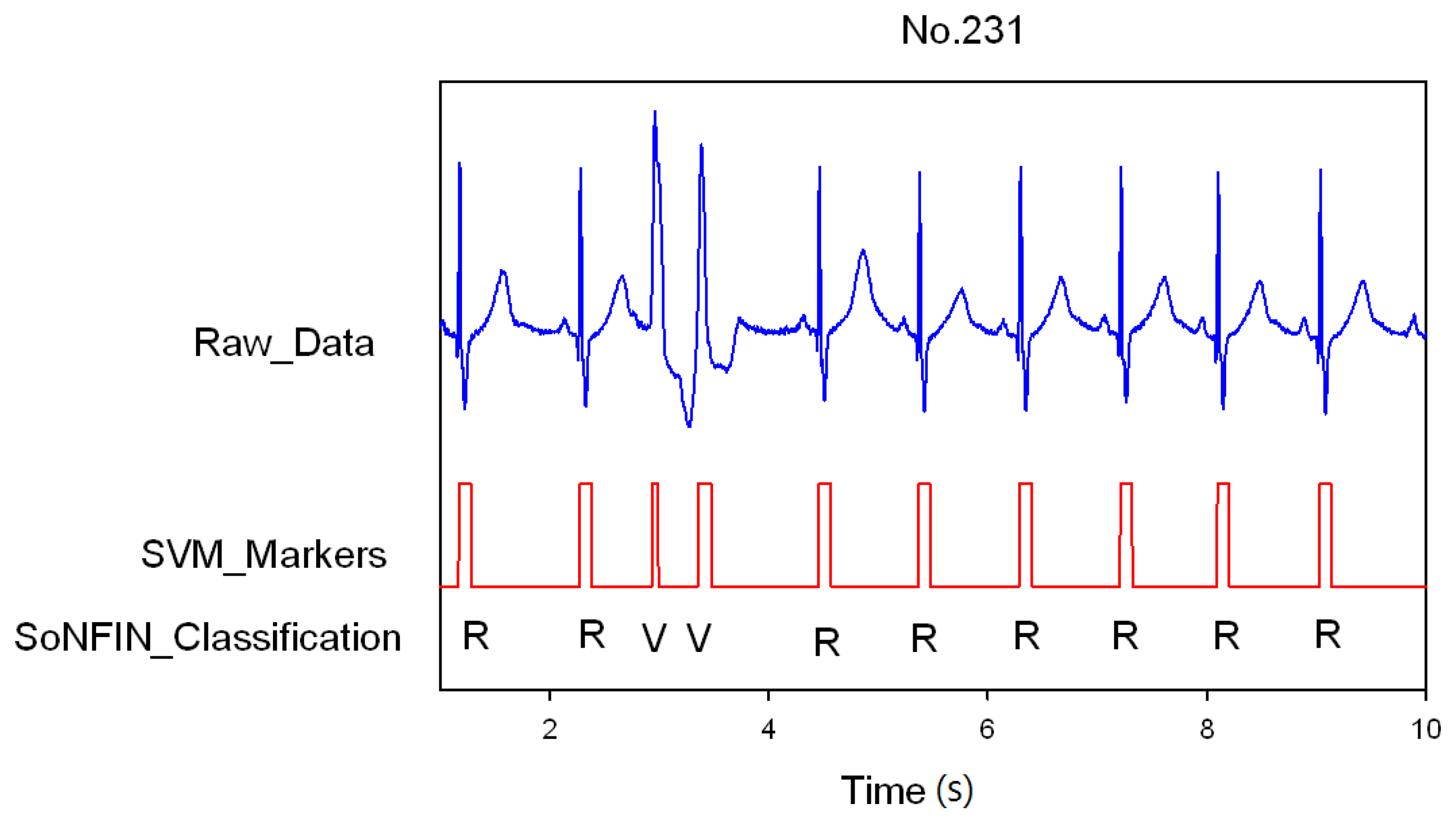
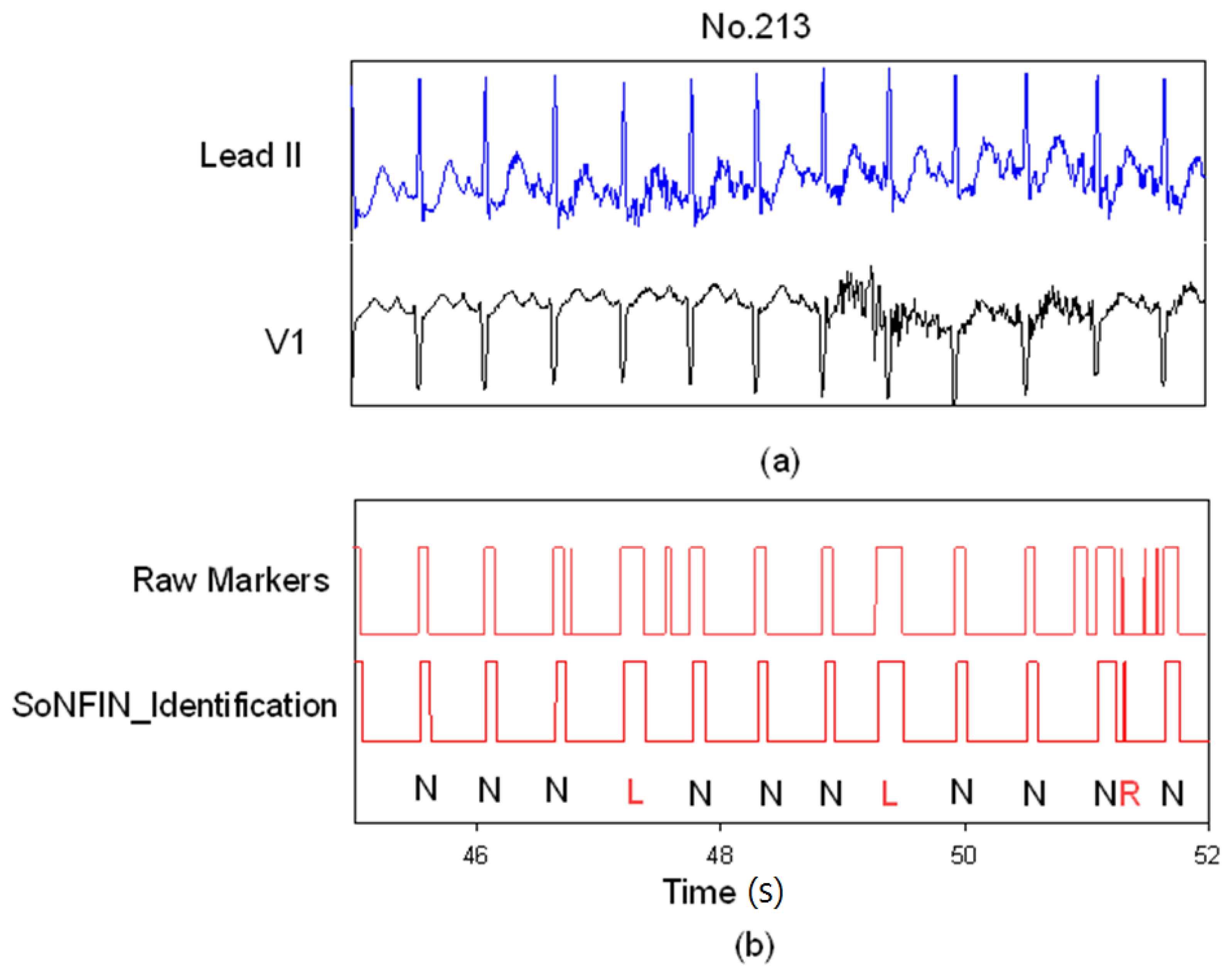
3. Results and Discussion
4. Conclusions
Acknowledgments
References
- Hii, P.-C.; Chung, W.-Y. A comprehensive ubiquitous healthcare solution on an android mobile device. Sensors 2011, 11, 6799–6815. [Google Scholar]
- Friesen, G.M.; Jannett, T.C.; Jadallah, M.A.; Yates, S.L.; Quint, S.R.; Troynagle, H. A comparison of the noise sensitivity of nine qrs detection algorithms. IEEE Trans. Biomed. Eng. 1990, 37, 85–98. [Google Scholar]
- Okada, M. A digital filter for the ors complex detection. IEEE Trans. Biomed. Eng. 1979, 26, 700–703. [Google Scholar]
- Pan, J.; Tompkins, W.J. A real-time qrs detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar]
- Trahanias, P.E. An approach to qrs complex detection using mathematical morphology. IEEE Trans. Biomed. Eng. 1993, 40, 201–205. [Google Scholar]
- Li, C.-W.; Zheng, C.-X.; Tai, C.-F. Detection of ecg characteristic points using wavelet transforms. IEEE Trans. Biomed. Eng. 1995, 42, 21–28. [Google Scholar]
- Gritzali, F. Towards a generalized scheme for qrs detection in ecg waveforms. Signal Process 1988, 15, 183–192. [Google Scholar]
- Yeh, Y.-C.; Wan, W.-J. Qrs complexes detection for ecg signal: The difference operation method. Comput. Methods Programs Biomed. 2008, 91, 245–254. [Google Scholar]
- Mehta, S.S.; Lingayat, N.S. Identification of qrs complexes in 12-lead electrocardiogram. Expert Syst. Appl. 2009, 36, 820–828. [Google Scholar]
- Throne, R.D.; Jenkins, J.M.; DiCarlo, L.A.A. Comparison of four new time-domain techniques for discriminating monomorphic ventricular tachycardia from sinus rhythm using ventricular waveform morphology. IEEE Trans. Biomed. Eng. 1991, 38, 561–570. [Google Scholar]
- Clayton, R.H.; Murray, A.; Campbell, R.W.F. Recognition of ventricular fibrillation using neural networks. Med. Biol. Eng. Comput. 1994, 32, 217–220. [Google Scholar]
- Tsipouras, M.G.; Fotiadis, D.I.; Sideris, D. An arrhythmia classification system based on the rr-interval signal. Artif. Intell. Med. 2005, 33, 237–250. [Google Scholar]
- Moavenian, M.; Khorrami, H. A qualitative comparison of artificial neural networks and support vector machines in ecg arrhythmias classification. Expert Syst. Appl. 2010, 37, 3088–3093. [Google Scholar]
- Thakor, N.V.; Zhu, Y.-S. Applications of adaptive filtering to ecg analysis: Noise cancellation and arrhythmia detection. IEEE Trans. Biomed. Eng. 1991, 18, 785–794. [Google Scholar]
- Chang, K.-M. Arrhythmia ecg noise reduction by ensemble impirical mode decomposition. Sensors 2010, 10, 6063–6080. [Google Scholar]
- Fan, S.-Z.; Yeh, J.-R.; Chen, B.-C.; Shieh, J.-S. Comparison of eeg approximate entropy and complexity measures of depth of anaesthesia during inhalational general anaesthesia. J. Med. Biol. Eng. 2011, 31, 359–366. [Google Scholar]
- Mehta, S.S.; Shete, D.A.; Lingayat, N.S.; Chouhanc, V.S. K-means algorithm for the detection and delineation of qrs-complexes in electrocardiogram. IRBM 2010, 31, 48–54. [Google Scholar]
- Osowski, S.; Linh, T.H. Ecg beat recognition using fuzzy hybrid neural network. IEEE Trans. Biomed. Eng. 2001, 48, 1265–1271. [Google Scholar]
- Lagerholm, M.; Peterson, C.; Braccini, G.; Ebendrandt, L.; Sornmo, L. Clustering ecg complexes using hermite functions and self-organizing maps. IEEE Trans. Biomed. Eng. 2000, 47, 838–848. [Google Scholar]
- Al-Fahoum, A.S.; Howitt, I. Combined wavelet transformation and radial basis neural networks for classifying life threatening cardiac arrhythmias. Med. Biol. Eng. Comput. 1999, 37, 566–573. [Google Scholar]
- MIT-BIH. Database Distribution; Massachusetts Institute of Technology: Cambridge, MA, USA, 1998. [Google Scholar]
- Widrow, B.; Glover, J.R.; Mccool, J.M.; Kaunitz, J.; Williams, C.; Hean, R.H.; Zeidler, J.R.; Dong, E.; Goodlin, R.C. Adaptive noise cancelling: Principles and applications. Proc. IEEE. 1975, 63, 1692–1716. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 955–971. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. Libsvm: A Library for Support Vector Machines; National Taiwan University: Taipei, Taiwan, 2004. [Google Scholar]
- Jung, C.-F.; Lin, C.-T. An on-line self-constructing neural fuzzy inference network and its application. IEEE Trans. Fuzzy Syst. 1998, 6, 12–32. [Google Scholar]
- Arzeno, N.M.; Poon, C.S.; Deng, Z.D. Quantitative analysis of qrs detection algorithms based on first derivative of the ecg. Proceedings of 28th IEEE EMBS Annual International Conference, New York, NY, USA; 2006; pp. 1788–1791. [Google Scholar]
- Adnane, M.; Jiang, Z.; Choi, S. Development of qrs detection algorithm designed for wearable cardiorespiratory system. Comput. Methods Programs Biomed. 2009, 93, 20–31. [Google Scholar]
- Benitez, D.; Gaydecki, P.A.; Zaidi, A.; Fitzpatrick, A.P. The use of hilbert transform in ecg signal analysis. Comput. Biol. Med. 2001, 31, 399–406. [Google Scholar]
- Chen, S.W.; Chen, H.C.; Chan, H.L. A real time qrs detection method based on moving-averaging incorporating with wavelet denoising. Comput. Methods Programs Biomed. 2006, 82, 187–195. [Google Scholar]
- Israel, S.A.; Irvine, J.M.; Cheng, A.; Wiederbold, M.D.; Wiederhold, B.K. Ecg to identify individuals. Pattern Recognit 2005, 38, 133–142. [Google Scholar]
- Paoletti, M.; Marchesi, C. Discovering dangerous patterns in long-term ambulatory ecg recordings using a fast qrs detection algorithm and explorative data analysis. Comput. Methods Programs Biomed. 2006, 82, 20–30. [Google Scholar]
- Conflict of Interest: The authors declare that they have no conflict of interest.

| N | V | R | L | A | total | |
|---|---|---|---|---|---|---|
| 105 | 401 | 15 | 0 | 0 | 0 | 416 |
| 106 | 312 | 2 | 0 | 0 | 0 | 314 |
| 108 | 275 | 5 | 0 | 0 | 2 | 282 |
| 109 | 0 | 7 | 0 | 411 | 2 | 420 |
| 111 | 0 | 0 | 0 | 343 | 0 | 343 |
| 112 | 428 | 0 | 0 | 0 | 0 | 428 |
| 113 | 288 | 0 | 0 | 0 | 1 | 289 |
| 115 | 316 | 0 | 0 | 0 | 0 | 316 |
| 116 | 384 | 11 | 0 | 0 | 0 | 395 |
| 118 | 0 | 3 | 347 | 0 | 11 | 361 |
| 119 | 245 | 80 | 0 | 0 | 0 | 325 |
| 121 | 301 | 0 | 0 | 0 | 0 | 301 |
| 122 | 421 | 0 | 0 | 0 | 0 | 421 |
| 201 | 441 | 0 | 0 | 0 | 0 | 441 |
| 202 | 261 | 4 | 0 | 0 | 0 | 265 |
| 205 | 449 | 3 | 0 | 0 | 0 | 452 |
| 207 | 0 | 0 | 0 | 349 | 0 | 349 |
| 208 | 242 | 245 | 0 | 0 | 0 | 487 |
| 209 | 365 | 0 | 0 | 0 | 178 | 543 |
| 212 | 140 | 0 | 319 | 0 | 0 | 459 |
| 213 | 501 | 48 | 0 | 0 | 0 | 549 |
| 214 | 0 | 33 | 0 | 346 | 1 | 380 |
| 219 | 364 | 15 | 0 | 0 | 0 | 379 |
| 220 | 352 | 0 | 0 | 0 | 1 | 353 |
| 221 | 327 | 80 | 0 | 0 | 0 | 407 |
| 222 | 366 | 0 | 0 | 0 | 0 | 366 |
| 223 | 390 | 16 | 0 | 0 | 0 | 406 |
| 228 | 312 | 18 | 0 | 0 | 0 | 330 |
| 230 | 392 | 0 | 0 | 0 | 0 | 392 |
| 231 | 13 | 1 | 287 | 0 | 0 | 301 |
| 232 | 0 | 0 | 330 | 0 | 0 | 330 |
| 233 | 372 | 138 | 0 | 0 | 4 | 514 |
| 234 | 462 | 0 | 0 | 0 | 0 | 462 |
| Total | 9,120 | 724 | 1,283 | 1,449 | 200 | 12,776 |
| No. | TP | FN | FP |
|---|---|---|---|
| 105 | 416 | 0 | 24 |
| 106 | 312 | 2 | 26 |
| 108 | 282 | 0 | 37 |
| 109 | 419 | 1 | 10 |
| 111 | 343 | 0 | 186 |
| 112 | 428 | 0 | 81 |
| 113 | 289 | 0 | 0 |
| 115 | 316 | 0 | 0 |
| 116 | 395 | 0 | 4 |
| 118 | 361 | 0 | 11 |
| 119 | 325 | 0 | 12 |
| 121 | 301 | 0 | 20 |
| 122 | 421 | 0 | 0 |
| 201 | 441 | 0 | 0 |
| 202 | 265 | 0 | 1 |
| 205 | 452 | 0 | 0 |
| 207 | 349 | 0 | 13 |
| 208 | 480 | 7 | 11 |
| 209 | 541 | 2 | 52 |
| 212 | 455 | 4 | 9 |
| 213 | 548 | 1 | 4 |
| 214 | 376 | 4 | 8 |
| 219 | 378 | 1 | 9 |
| 220 | 353 | 0 | 0 |
| 221 | 407 | 0 | 0 |
| 222 | 366 | 0 | 5 |
| 223 | 406 | 0 | 0 |
| 228 | 330 | 0 | 1 |
| 230 | 392 | 0 | 0 |
| 231 | 301 | 0 | 41 |
| 232 | 330 | 0 | 3 |
| 233 | 514 | 0 | 4 |
| 234 | 462 | 0 | 0 |
| Total | 12,754 | 22 | 572 |
| N | Estimate | Sensitivity | Specificity | Accuracy | ||
|---|---|---|---|---|---|---|
| N | Non_N | |||||
| Real | N | 9,189 | 107 | 98.8% | 99.2% | 98.9% |
| Non_N | 25 | 3,433 | ||||
| V | Estimate | 95.1% | 99.4% | 99.1% | ||
| V | Non_V | |||||
| Real | V | 684 | 35 | |||
| Non_V | 72 | 11,998 | ||||
| R | Estimate | 99.7% | 99.8% | 99.8% | ||
| R | Non_R | |||||
| Real | R | 1,287 | 3 | |||
| Non_R | 20 | 11,444 | ||||
| L | Estimate | 97.9% | 99.4% | 99.3% | ||
| L | non_L | |||||
| Real | L | 1,419 | 30 | |||
| Non_L | 58 | 11,247 | ||||
| Averaged accuracy | 98.8% | |||||
| N | Estimate | Sensitivity | Specificity | Accuracy | ||
|---|---|---|---|---|---|---|
| N | Non_N | |||||
| Real | N | 9,189 | 107 | 98.8% | 96.9% | 98.2% |
| Non_N | 121 | 3,909 | ||||
| V | Estimate | 95.1% | 98.1% | 97.9% | ||
| V | Non_V | |||||
| Real | V | 684 | 35 | |||
| Non_V | 239 | 12,368 | ||||
| R | Estimate | 99.7% | 99.7% | 99.7% | ||
| R | Non_R | |||||
| Real | R | 1,287 | 3 | |||
| Non_R | 31 | 12,005 | ||||
| L | Estimate | 97.9% | 99.2% | 99.1% | ||
| L | non_L | |||||
| Real | L | 1,419 | 30 | |||
| Non_L | 85 | 11,792 | ||||
| noise | Estimate | 47.7% | 100% | 97.7% | ||
| noise | Non_noise | |||||
| Real | n | 271 | 301 | |||
| Non_noise | 0 | 12,754 | ||||
| Averaged accuracy | 96.4% | |||||
| Reference | Method | Accuracy (%) |
|---|---|---|
| Proposed algorithm | SVM | 97.5% |
| J. Pan, and W. J. Tompkins [4] | Dynamic threshold | 99.3% |
| P. E. Trahanias [5] | Mathematical morphology | 99.48% |
| F. Gritzali [7] | Length and energy transformation | 99.6% |
| Y. -C. Yeh, and W. -J. Wanga [8] | Difference operation method | 99.81 |
| M. Adnane et al. [28] | Morphological features | 99.64% |
| M. Paoletti and C. Marchesi [32] | Karhunen-Loève transform | 99.15% |
| S. S. Mehta and N. S. Lingayat [9] | SVM | 98.12% |
| S. S. Mehta et al. [17] | K-mean | 98.66% |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, S.-H.; Cheng, D.-C.; Lin, C.-M. Arrhythmia Identification with Two-Lead Electrocardiograms Using Artificial Neural Networks and Support Vector Machines for a Portable ECG Monitor System. Sensors 2013, 13, 813-828. https://doi.org/10.3390/s130100813
Liu S-H, Cheng D-C, Lin C-M. Arrhythmia Identification with Two-Lead Electrocardiograms Using Artificial Neural Networks and Support Vector Machines for a Portable ECG Monitor System. Sensors. 2013; 13(1):813-828. https://doi.org/10.3390/s130100813
Chicago/Turabian StyleLiu, Shing-Hong, Da-Chuan Cheng, and Chih-Ming Lin. 2013. "Arrhythmia Identification with Two-Lead Electrocardiograms Using Artificial Neural Networks and Support Vector Machines for a Portable ECG Monitor System" Sensors 13, no. 1: 813-828. https://doi.org/10.3390/s130100813
APA StyleLiu, S.-H., Cheng, D.-C., & Lin, C.-M. (2013). Arrhythmia Identification with Two-Lead Electrocardiograms Using Artificial Neural Networks and Support Vector Machines for a Portable ECG Monitor System. Sensors, 13(1), 813-828. https://doi.org/10.3390/s130100813






