Non-Linearity Analysis of Depth and Angular Indexes for Optimal Stereo SLAM
Abstract
:1. Introduction
2. System Structure
2.1. 3D Features
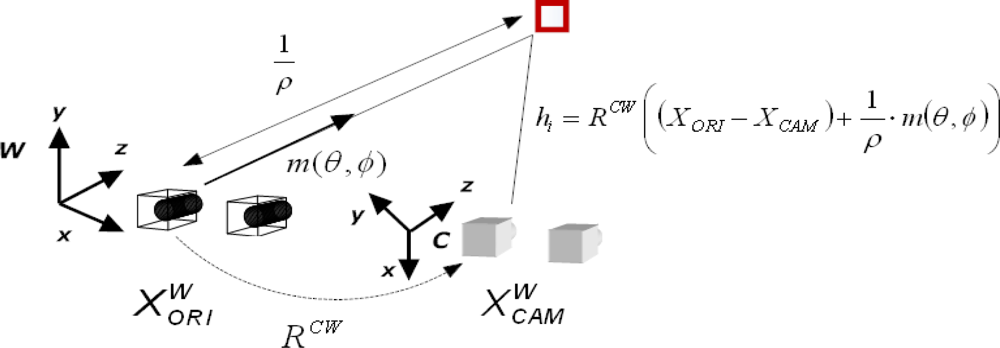
2.2. Inverse depth Features
3. Non-Linearity Analysis of Depth and Angular Information
- If the non-linearity index Lf is equal to zero for a point Zi, this implies that the function f is linear in interval ΔZ.
- If the non-linearity index Lf takes values higher than zero, this implies that the function f is not linear in the interval ΔZ.
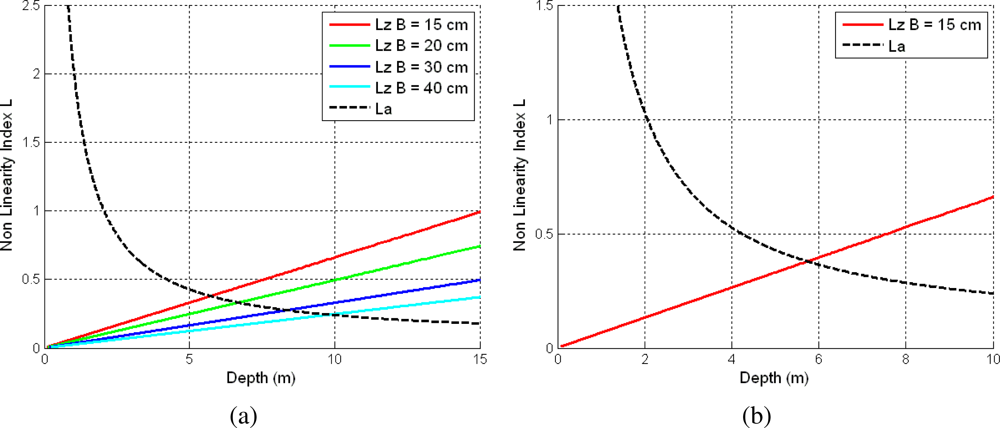
3.1. Depth Non-Linearity
3.2. Angular Non-Linearity
3.3. Optimal Depth Threshold
4. EKF SLAM Overview
- Prediction Step
- Update Step
4.1. Motion Model
4.2. Measurement Model
4.2.1. Measurement Prediction
4.2.2. Measurement Search
4.2.3. Filter Update
4.3. Feature Management
4.4. Switching between Inverse Depth and 3D Features
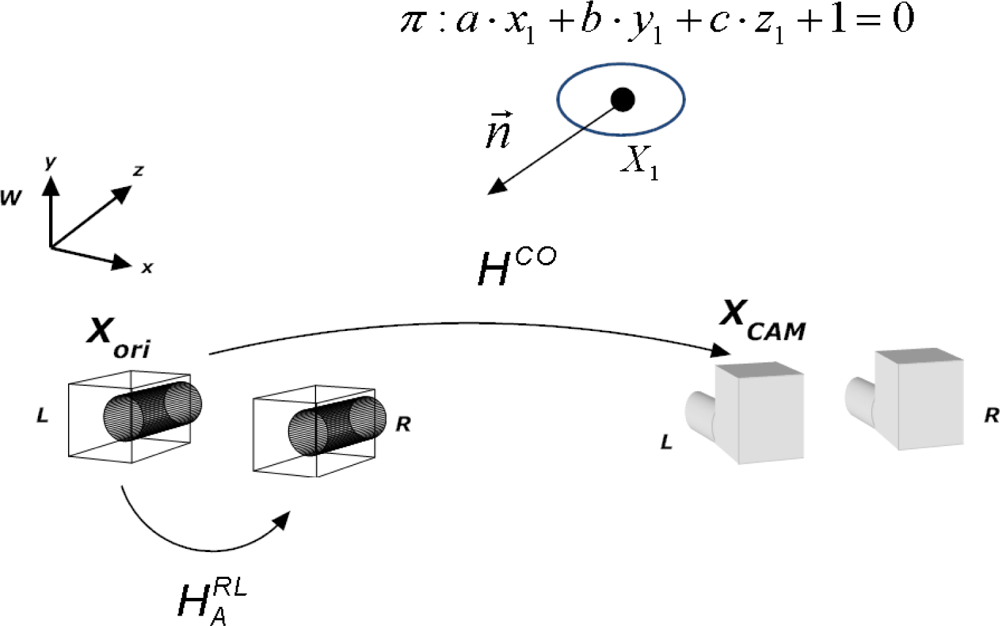
5. 2D Homography Warping
6. Experiments in Indoor Environments
- % Inverse Features: Is the percentage of the total number of features in the map that were initialized with an inverse depth parametrization.
- ɛi: Is the absolute mean error in m, for the cartesian coordinates (X, Z).
- Mean PYY Trace: Is the mean trace of the covariance matrix PYY for each of the features that compose the final map. This parameter is indicative of the uncertainty of the features, i.e., the quality of the map.
- Case: No patch transformation or 2D patch warping.
- Sequence: The test sequences for which we performed the comparison. We selected the corridor and L sequence. In the corridor sequence the changes in appearance are mainly due to changes in scale, whereas in the L sequence changes in appearance are mainly due to changes in scale and viewpoint.
- # Features Map: Is the total number of features in the map at the end of the sequence.
- # Total Attempts: Is the total number of feature measurement attempts during all the sequence.
- # Successful Attempts: Is the total number of successful feature measurement attempts during all the sequence.
- Ratio: Is the ratio between the number of successful measurement attempts and the total number of attempts.
7. Conclusions and Future Works
Acknowledgments
References
- Broida, T.; Chandrashekhar, S.; Chellappa, R. Recursive 3-D Motion Estimation from a Monocular Image Sequence. IEEE Trans. Aerosp. Electron. Syst 1990, 26, 639–656. [Google Scholar]
- Broida, T.; Chellappa, R. Estimating the Kinematics and Structure of a Rigid Object from a Sequence of Monocular Images. IEEE Trans. Pattern Anal. Machine Intell 1991, 13, 497–513. [Google Scholar]
- Mountney, P.; Stoyanov, D.; Davison, A.J.; Yang, G.Z. Simultaneous Stereoscope Localization and Soft-Tissue Mapping for Minimally Invasive Surgery. Proceedings of Medical Image Computing and Computer Assisted Intervention (MICCAI), Copenhagen, Denmark, October 1–6, 2006.
- Klein, G.; Murray, D. Parallel Tracking and Mapping for Small AR Workspaces. Proceedings of the 6th IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Phoenix, AZ, USA, October 28–November 2, 2007.
- Schleicher, D.; Bergasa, L.M.; Barea, R.; Lóez, E.; Ocaña, M.; Nuevo, J. Real-Time Wide-Angle Stereo Visual SLAM on Large Environments Using SIFT Features Correction. Proceedings of IEEE /RSJ International Conference on Intelligent Robots and Systems (IROS), San Diego, CA, USA, October 29–November 2, 2007.
- Schleicher, D.; Bergasa, L.M.; Barea, R.; Lóez, E.; Ocaña, M. Real-Time Simultaneous Localization and Mapping with a Wide-Angle Stereo Camera and Adaptive Patches. Proceedings of IEEE /RSJ International Conference on Intelligent Robots and Systems (IROS), Beijing, China, October 9–15, 2006.
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Machine Intell 2007, 29, 1052–1067. [Google Scholar]
- Civera, J.; Davison, A.J.; Montiel, J.M. Inverse Depth Parametrization for Monocular SLAM. IEEE Trans. Robotics 2008, 24, 932–945. [Google Scholar]
- Walker, B.N.; Lindsay, J. Navigation Performance with a Virtual Auditory Display: Effects of Beacon Sound, Capture Radius, and Practice. Human Factors 2006, 48, 265–278. [Google Scholar]
- Li, L.J.; Socher, R.; Li, F.F. Towards Total Scene Understanding:Classification, Annotation and Segmentation in an Automatic Framework. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (2009), Miami, FL, USA, June 20–26, 2009.
- Oh, S.; Tariq, S.; Walker, B.; Dellaert, F. Map-Based Priors for Localization. Proceedings of IEEE /RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, September 28–October 2, 2004.
- Saéz, J.M.; Escolano, F.; Penalver, A. First Steps towards Stereo-Based 6DOF SLAM for the Visually Impared. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, June 20–26, 2005.
- Paz, L.M.; Piniés, P.; Tardós, J.D.; Neira, J. Large Scale 6DOF SLAM with Stereo-in-hand. IEEE Trans. Robotics 2008, 24, 946–957. [Google Scholar]
- Paz, L.M.; Guivant, J.; Tardós, J.D.; Neira, J. Data Association in O(n) for Divide and Conquer SLAM. Proceedings of Robotics: Science and Systems, Atlanta, GA, USA, June 27–30, 2007.
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. Proceedings of the 4th Alvey Vision Conference, Manchester, UK, August 30–September 2, 1988; pp. 147–151.
- Eade, E.; Drummond, T. Monocular SLAM as a Graph of Coalesced Observations. Proceedings of International Conference on Computer Vision (ICCV), Rio de Janeiro, Brazil, October 14–20, 2007.
- Liang, B.; Pears, N. Visual Navigation Using Planar Homographies. Proceedings of IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, May 11–15, 2002.
- Molton, N.; Davison, A.J.; Reid, I. Locally Planar Patch Features for Real-Time Structure from Motion. Proceedings of British Machine Vision Conference (BMVC), London, UK, September 7–9, 2004.
- Chum, O.; Pajdla, T.; Sturm, P. The Geometric Error for Homographies. Comput. Vision Image Underst 2005, 97, 86–102. [Google Scholar]
- Documentation: Camera Calibration Toolbox for Matlab. 2007. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 20 April 2010).
- Piniés, P.; Tardós, J.D. Large Scale SLAM Building Conditionally Independent Local Maps: Application to Monocular Vision. IEEE Trans. Robotics 2008, 24, 1094–1106. [Google Scholar]
- Kaess, M.; Ranganathan, A.; Dellaert, F. iSAM: Incremental Smoothing and Mapping. IEEE Trans. Robotics 2008, 24, 1365–1378. [Google Scholar]
- Agrawal, M.; Konolige, K.; Blas, M.R. CenSurE: Center Surround Extremas for Realtime Feature Detection and Matching. Proceedings of the 10th European Conference on Computer Vision (ECCV), Marseille, France, October 12–18, 2008.
- Schleicher, D.; Bergasa, L.M.; Ocaña, M.; Barea, R.; Lóez, E. Real-Time Hierarchical Outdoor SLAM Based on Stereovision and GPS Fusion. IEEE Trans. Intell. Transp. Systems 2009, 10, 440–452. [Google Scholar]
- Lowe, D. Distinctive Image Features from Scale-Invariant Keypoints. Intl. J. Comput. Vision 2004, 60, 91–110. [Google Scholar]
- Angeli, A.; Filliat, D.; Doncieux, S.; Meyer, J.A. Fast and Incremental Method for Loop-Closure Detection Using Bags of Visual Words. IEEE Trans. Robotics 2008, 24, 1027–1037. [Google Scholar]
- Cummins, M.; Newman, P. Highly Scalable Appearance-Only SLAM–FAB-MAP 2.0. Proceedings fo Robotics: Science and Systems (RSS09), Seattle, WA, USA, June 29–July 01, 2009.
- Triggs, B.; McLauchlan, P.; Hartley, R.; Fitzgibbon, A. Bundle Adjustment—A Modern Synthesis. In Vision Algorithms: Theory and Practice; Triggs, W., Zisserman, A., Szeliski, R., Eds.; Springer Verlag: New York, NY, USA, 1999; pp. 298–375. [Google Scholar]
- Llorca, F.D.; Sotelo, A.M.; Parra, I.; Ocaña, M.; Bergasa, M.L. Error Analysis in a Stereo Vision-Based Pedestrian Detection Sensor for Collision Avo idance Applications. Sensors 2010, 10, 3741–3758. [Google Scholar]



| Stereo Baseline (cm) | Depth Threshold (m) |
|---|---|
| 15 | 5.71 |
| 20 | 6.69 |
| 30 | 8.35 |
| 40 | 9.81 |
| Sequence | Case | % Inverse Features | ɛX | ɛZ | Mean PYY Trace |
|---|---|---|---|---|---|
| Corridor | Without Inverse Par. | 0.00 | 0.9394 | 0.4217 | 0.1351 |
| Corridor | With Inverse Par., Zt = 10 m | 5.23 | 0.9259 | 0.4647 | 0.0275 |
| Corridor | With Inverse Par., Zt = 5.7 m | 24.32 | 0.7574 | 0.3777 | 0.0072 |
| L | Without Inverse Par. | 0.00 | 0.5047 | 0.3985 | 0.1852 |
| L | With Inverse Par., Zt = 10 m | 7.85 | 0.5523 | 0.1017 | 0.0245 |
| L | With Inverse Par., Zt = 5.7 m | 19.21 | 0.5534 | 0.2135 | 0.0078 |
| Loop | Without Inverse Par. | 0.00 | 0.4066 | 0.9801 | 0.2593 |
| Loop | With Inverse Par., Zt = 10 m | 5.27 | 0.3829 | 0.63030 | 0.0472 |
| Loop | With Inverse Par., Zt = 5.7 m | 12.36 | 0.2191 | 0.3778 | 0.0310 |
| Case | Sequence | # Features Map | # Total Attempts | # Successful Attempts | Ratio % |
|---|---|---|---|---|---|
| No Patch Transformation | Corridor | 85 | 6,283 | 5,612 | 89.32 |
| 2D Warping | Corridor | 68 | 6,398 | 5,781 | 90.35 |
| No Patch Transformation | L | 116 | 11,627 | 8,922 | 76.73 |
| 2D Warping | L | 105 | 10,297 | 9,119 | 88.71 |
| Filter Step | Time ms |
|---|---|
| Feature Initialization (15) | 18.00 |
| Prediction | 0.47 |
| Measurement | 10 |
| Update | 4.96 |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Bergasa, L.M.; Alcantarilla, P.F.; Schleicher, D. Non-Linearity Analysis of Depth and Angular Indexes for Optimal Stereo SLAM. Sensors 2010, 10, 4159-4179. https://doi.org/10.3390/s100404159
Bergasa LM, Alcantarilla PF, Schleicher D. Non-Linearity Analysis of Depth and Angular Indexes for Optimal Stereo SLAM. Sensors. 2010; 10(4):4159-4179. https://doi.org/10.3390/s100404159
Chicago/Turabian StyleBergasa, Luis M., Pablo F. Alcantarilla, and David Schleicher. 2010. "Non-Linearity Analysis of Depth and Angular Indexes for Optimal Stereo SLAM" Sensors 10, no. 4: 4159-4179. https://doi.org/10.3390/s100404159
APA StyleBergasa, L. M., Alcantarilla, P. F., & Schleicher, D. (2010). Non-Linearity Analysis of Depth and Angular Indexes for Optimal Stereo SLAM. Sensors, 10(4), 4159-4179. https://doi.org/10.3390/s100404159




