Response Ant Colony Optimization of End Milling Surface Roughness
Abstract
:1. Introduction
2. Theoretical Background
2.1. Response Surface Method
2.2. Ant Colony Optimisation
- a search space S defined over a finite set of discrete decision variables and a set Ω of constraints among the variables;
- an objective function f: to be minimized
3. Experimental Setup
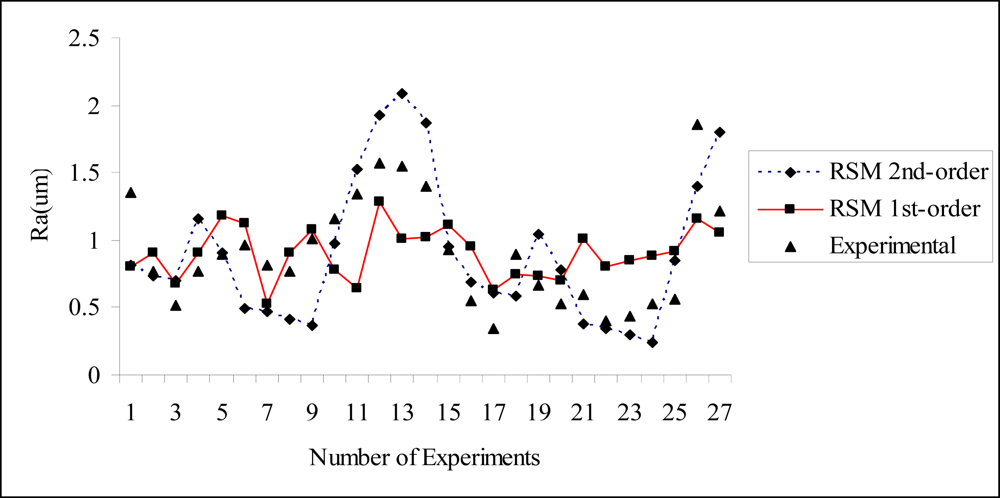
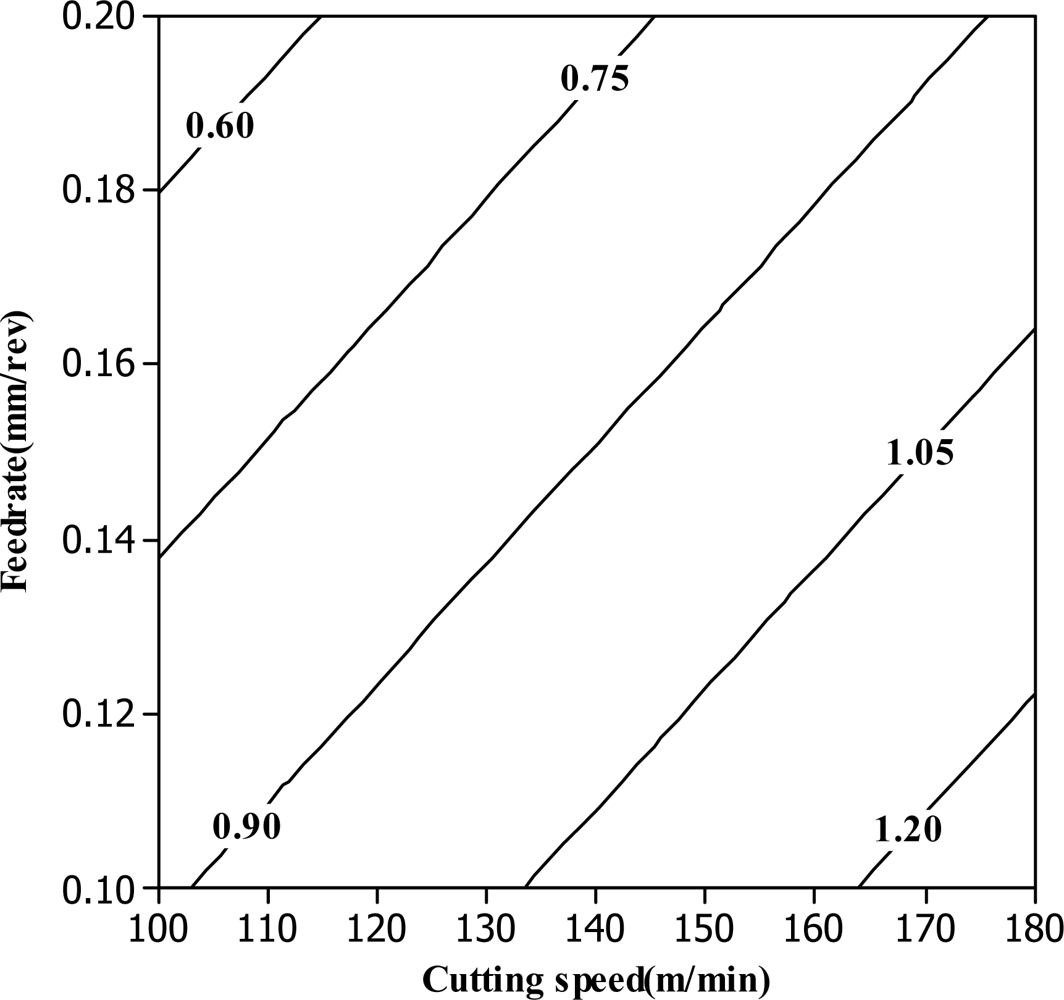
4. Results and Discussion
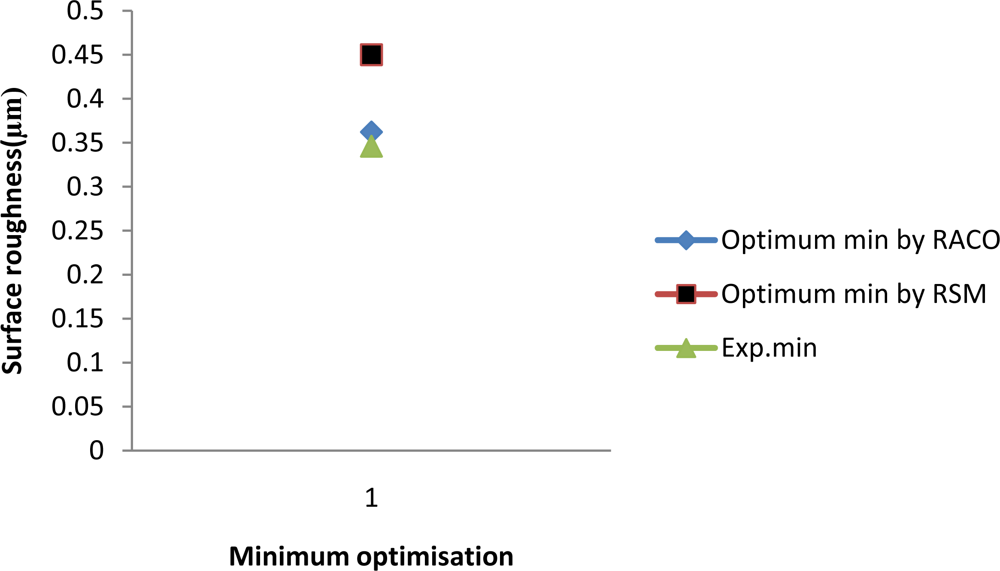
5. Test Validation
6. Conclusions
Acknowledgments
References and Notes
- Chen, D.C.; Chen, C.F. Use of Taguchi method to study a robust design for the sectioned beams curvature during rolling. J. Mater. Proc. Tech 2007, 190, 130–137. [Google Scholar]
- Fung, C.P.; Kang, P.C. Multi-response optimization in friction properties of PBT composites using Taguchi method and principle component analysis. J. Mater. Proc. Tech 2005, 170, 602–610. [Google Scholar]
- Tang, S.H.; Tan, V.J.; Sapuan, S.M.; Sulaiman, S.; Ismail, N.; Samin, R. The use of Taguchi method in the design of plastic injection mould for reducing warpage. J. Mater. Proc. Tech 2007, 182, 418–426. [Google Scholar]
- Vijian, P.; Arunachalam, V.P. Optimization of squeeze cast parameters of LM6 aluminium alloy for surface roughness using Taguchimethod. J. Mater. Proc. Tech 2006, 180, 161–166. [Google Scholar]
- Yang, L.J. The effect of specimen thickness on the hardness of plasma surface hardened ASSAB 760 steel specimens. J. Mater. Proc. Tech 2007, 185, 113–119. [Google Scholar]
- Zhang, J.Z.; Chen, J.C.; Kirby, E.D. Surface roughness optimization in a end-milling operation using the Taguchi design method. J. Mater. Proc. Tech 2007, 184, 233–239. [Google Scholar]
- Aslan, E.; Camuscu, N.; Birgoren, B. Design optimization of cutting parameters when turning hardened AISI 4140 steel (63 HRC) with Al2O3 + TiCN mixed ceramic tool. Mater. Des 2007, 28, 1618–1622. [Google Scholar]
- Nalbant, M.; Gokkaya, H.; Sur, G. Application of Taguchi method in the optimization of cutting parameters for surface roughness in turning. Mater. Des 2007, 28, 1379–1385. [Google Scholar]
- Kalpakjian, S.; Schmid, S.R. Manufacturing Engineering and Technology, International, 4th ed; Prentice Hall: Upper Saddle River, NJ, USA, 2001; pp. 536–681. [Google Scholar]
- EI Baradie, M.A. Cutting fluids: part I characterization. J. Mat. Proc. Tech 1996, 56, 786–797. [Google Scholar]
- Alauddin, M.; EL Baradie, M.A.; Hashmi, M.S.J. Prediction of tool life in end milling by response surface methodology. J. Mater. Proc. Tech 1997, 71, 456–465. [Google Scholar]
- Hasegawa, M.; Seireg, A.; Lindberg, R.A. Surface roughness model for turning. Tribol. Int 1976, 6, 285–289. [Google Scholar]
- Alauddin, M.; El Baradie, M.A.; Hashmi, M.S.J. Computer-aided analysis of a surface-roughness model for end milling. J. Mat. Proc. Tech 1995, 55, 123–127. [Google Scholar]
- Alauddin, M.; El Baradie, M.A.; Hashmi, M.S.J. Optimization of surface finish in end milling Inconel 718. J. Mat. Proc. Tech 1996, 56, 54–65. [Google Scholar]
- EI-Baradie, M.A. Surface roughness model for turning grey cast iron 1154 BHN. Proc. IMechE 1993, 207, 43–54. [Google Scholar]
- Bandyopadhyay, B.P.; Teo, E.H. Application of factorial design of experiment in high speed turning. Proc. Manuf. Int. Part 4, Advances in Materials & Automation, Atlanta, GA, USA, ASME, NY; 1990; pp. 3–8. [Google Scholar]
- Gorlenko, O.A. Assessment of starface roughness parameters and their interdependence. Precis. Eng 1981, 3, 105–108. [Google Scholar]
- Thomas, T.R. Characterisation of surface roughness. Precis. Eng 1981, 3, 2–8. [Google Scholar]
- Mital, M. Mehta, Surface roughness prediction models for fine turning. Int. J. Pro. Re 1988, 26, 1861–1876. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Box, G.E.P.; Draper, N.R. Empirical Model-Building and Response Surfaces; John Wiley & Sons Inc: New York, NY, USA, 1986; p. 669. [Google Scholar]
- Box, G.E.P.; Behnken, D.W. Some new three level designs for the study of quantitative variables. Technometrics 1960, 2, 455–475. [Google Scholar]
- Camazine, S.; Deneubourg, J.L.; Franks, N.; Sneyd, J.; Theraulaz, G.; Bonabeau, E. Self-Organization in Biological Systems; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Grassé, P.P. La reconstruction du nid et les coordinations inter individuelles chez bellicositermes natalensis et cubitermes sp. La théorie de la stigmergie: essai d’interprétation du comportement des termites constructeurs. Insect. Soc 1959, 6, 41–48. [Google Scholar]
- Dorigo, M.; Di Caro, G. The Ant Colony Optimization Meta-Heuristic. In New Ideas in Optimization; Corne, D., Dorigo, M., Glover, F., Eds.; McGraw-Hill: New York, NY, USA, 1999; p. 11. [Google Scholar]
- Dorigo, M.; Di Caro, G.; Gambardella, L.M. Ant algorithms for discrete optimization. Artif. Life 1999, 5, 137–172. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Positive Feedback as a Search Strategy, Technical report 91-016; Dipartimento di Elettronica, Politecnico di Milano: Milan, Italy, 1991. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms, Ph.D. thesis,; Dipartimento di Elettronica, Politecnico di Milano: Milan, Italy, 1992.
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant System: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man. Cybern 1996, 26, 29–41. [Google Scholar]
- Kadirgama, K.; Noor, M.M.; Zuki, N.M.; Rahman, M.M.; Rejab, M.R.M.; Daud, R.; Abou-El-Hossein, K.A. Optimization of surface roughness in end milling on mould aluminium alloys (aa6061-t6) using response surface method and radian basis function network. Jordan J. Mech. Ind. Eng 2008, 2, 209–214. [Google Scholar]

| Component | Al | Cr | Cu | Fe | Mg | Mn | Si | Ti | Zn |
|---|---|---|---|---|---|---|---|---|---|
| Wt % | 95.8–98.6 | 0.04–0.35 | 0.15–0.4 | Max 0.7 | 0.8–1.2 | Max 0.15 | 0.4–0.8 | Max 0.15 | Max 0.25 |
| Cutting speed (m/min) | Feedrate (mm/rev) | Axial depth (mm) | Radial depth (mm) |
|---|---|---|---|
| 140 | 0.15 | 0.10 | 5.0 |
| 140 | 0.15 | 0.15 | 3.5 |
| 100 | 0.15 | 0.15 | 5.0 |
| 140 | 0.15 | 0.15 | 3.5 |
| 180 | 0.15 | 0.20 | 3.5 |
| 180 | 0.15 | 0.15 | 2.0 |
| 100 | 0.20 | 0.15 | 3.5 |
| 140 | 0.15 | 0.15 | 3.5 |
| 180 | 0.15 | 0.15 | 5.0 |
| 100 | 0.15 | 0.20 | 3.5 |
| 140 | 0.20 | 0.10 | 3.5 |
| 180 | 0.10 | 0.15 | 3.5 |
| 140 | 0.15 | 0.20 | 2.0 |
| 180 | 0.15 | 0.10 | 3.5 |
| 140 | 0.10 | 0.15 | 2.0 |
| 140 | 0.15 | 0.20 | 5.0 |
| 100 | 0.15 | 0.10 | 3.5 |
| 140 | 0.20 | 0.15 | 2.0 |
| 100 | 0.15 | 0.15 | 2.0 |
| 140 | 0.20 | 0.15 | 5.0 |
| 140 | 0.10 | 0.10 | 3.5 |
| 140 | 0.20 | 0.20 | 3.5 |
| 140 | 0.15 | 0.10 | 2.0 |
| 100 | 0.10 | 0.15 | 3.5 |
| 180 | 0.20 | 0.15 | 3.5 |
| 140 | 0.10 | 0.20 | 3.5 |
| 140 | 0.10 | 0.15 | 5.0 |
| Hardness, Brinell | 95 |
| Hardness, Knoop | 120 |
| Hardness, Rockwell A | 40 |
| Hardness, Rockwell B | 60 |
| Hardness, Vickers | 107 |
| Ultimate Tensile Strength | 310 MPa |
| Tensile Yield Strength | 276 MPa |
| Elongation at Break | 12 % |
| Elongation at Break | 17 % |
| Modulus of Elasticity | 68.9 GPa |
| Density | 2.7 g/cc |
| Source | DOF | Seq. SS | Adj. SS | Adj. MS | F | P |
|---|---|---|---|---|---|---|
| Regression | 4 | 0.9309 | 0.9309 | 0.2327 | 0.78 | 0.552 |
| Linear | 4 | 0.9309 | 0.9309 | 0.2327 | 0.78 | 0.552 |
| Residual Error | 22 | 6.5937 | 6.5937 | 0.2997 | ||
| Lack-of-Fit | 20 | 6.3151 | 6.3151 | 0.3158 | 2.27 | 0.351 |
| Pure Error | 2 | 0.2786 | 0.2786 | 0.1393 | ||
| Total | 26 | 7.5246 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kadirgama, K.; Noor, M.M.; Alla, A.N.A. Response Ant Colony Optimization of End Milling Surface Roughness. Sensors 2010, 10, 2054-2063. https://doi.org/10.3390/s100302054
Kadirgama K, Noor MM, Alla ANA. Response Ant Colony Optimization of End Milling Surface Roughness. Sensors. 2010; 10(3):2054-2063. https://doi.org/10.3390/s100302054
Chicago/Turabian StyleKadirgama, K., M. M. Noor, and Ahmed N. Abd Alla. 2010. "Response Ant Colony Optimization of End Milling Surface Roughness" Sensors 10, no. 3: 2054-2063. https://doi.org/10.3390/s100302054
APA StyleKadirgama, K., Noor, M. M., & Alla, A. N. A. (2010). Response Ant Colony Optimization of End Milling Surface Roughness. Sensors, 10(3), 2054-2063. https://doi.org/10.3390/s100302054







