Next Article in Journal
16S rRNA Gene-Based Metagenomic Analysis of Ozark Cave Bacteria
Previous Article in Journal
A Unique Coral Community in the Mangroves of Hurricane Hole, St. John, US Virgin Islands
Previous Article in Special Issue
Turnover Dynamics of Breeding Land Birds on Islands: is Island Biogeographic Theory ‘True but Trivial’ over Decadal Time-Scales?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Diversity
Volume 9
Issue 3
10.3390/d9030030
diversity-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Biodiversity Dynamics on Islands: Explicitly Accounting for Causality in Mechanistic Models

by
Ludwig Leidinger
* and
Juliano Sarmento Cabral
Ecosystem Modeling, Center for Computational and Theoretical Biology, Faculty of Biology, University of Würzburg, 97074 Würzburg, Germany
*
Author to whom correspondence should be addressed.
Diversity 2017, 9(3), 30; https://doi.org/10.3390/d9030030
Submission received: 28 June 2017 / Revised: 26 July 2017 / Accepted: 28 July 2017 / Published: 7 August 2017
(This article belongs to the Special Issue Selected Papers from The ISLAND BIOLOGY–2016 - An International Conference on Island Evolution, Ecology, and Conservation (18-22 July 2016))
Browse Figures
Versions Notes

Abstract

:
Island biogeography remains a popular topic in ecology and has gained renewed interest due to recent theoretical development. As experimental investigation of the theory is difficult to carry out, mechanistic simulation models provide useful alternatives. Several eco-evolutionary mechanisms have been identified to affect island biodiversity, but integrating more than a few of these processes into models remains a challenge. To get an overview of what processes mechanistic island models have integrated so far and what conclusions they came to, we conducted an exhaustive literature review of studies featuring island-specific mechanistic models. This was done using an extensive systematic literature search with subsequent manual filtering. We obtained a list of 28 studies containing mechanistic island models, out of 647 total hits. Mechanistic island models differ greatly in their integrated processes and computational structure. Their individual findings range from theoretical (such as humped-shaped extinction rates for oceanic islands) to system-specific dynamics (e.g., equilibrium and non-equilibrium dynamics for Galápagos’ birds). However, most models so far only integrate theories and processes pair-wise, while focusing on hypothetical systems. Trophic interactions and explicit micro-evolution are largely underrepresented in models. We expect future models to continue integrating processes, thus promoting the full appraisal of biodiversity dynamics.

1. Introduction

Islands remain popular model systems for studying mechanisms determining species diversity [1,2]. Reasons for this include the possibility to define isolation and area [3], while still retaining a degree of connectivity via rare long-distance dispersal events. At the same time, islands showcase all major types of mechanisms thus far indicated to influence biodiversity dynamics, such as physiological, demographic, dispersal, interaction, genetic and environmental processes [4,5,6].
One of the most prominent and earliest theories describing island diversity as a function of ecological mechanisms and external drivers is the seminal equilibrium theory of island biogeography (ETIB; [7]). In their theory, MacArthur and Wilson suggest that species numbers on an island are determined by a dynamic equilibrium between opposing rates of colonization and extinction. These rates are, in turn, dependent on the isolation and size of an island, respectively. A decade ago, island biogeography theory received new momentum with the formulation of the general dynamic model (GDM; [8]). This conceptual model considers changes of carrying capacity and niche opportunities over the ontogeny of oceanic islands and its effect on species numbers and their rates of change, including predictions on speciation rates. The typical ontogenic trajectory of hotspot islands starts with a small island size at the time of island emergence via volcanic activity, corresponding to low carrying capacity. As the island grows older, elevation and overall area increases and, thus, also carrying capacity. Later, after the island drifts out of the volcanic hotspot, erosion leads to higher topographic complexity, facilitating species radiations. The last stage sees further erosion of the island and ultimately atoll formation, resulting in increased numbers of locally extinct species.
While biodiversity theories, in particular the ETIB, were developed and tested experimentally, nowadays, conservation considerations render it unfeasible to conduct experiments of a scale comparable to that of the classical experiment by Simberloff and Wilson [9]. Moreover, Borregaard et al. [10] and Whittaker and Fernández-Palacios [11] among others point out that issues such as anthropogenic disturbances and above all the long timescales relevant when considering evolution make studying phenomena affecting the dynamics and maintenance of island biodiversity difficult and complex.
As a general consequence of these limitations, many studies investigating species diversity patterns on islands can only draw conclusions of a correlative nature, often by fitting regression models [12]. This has helped in identifying many possible drivers of biodiversity distribution [13,14]. However, the underlying causal relationships remain generally debatable, considering that the representation of causality in correlative models is limited. Therefore, definitive statements on evolution and on the impact of geological processes based solely on field data are generally inconclusive. This holds true particularly for islands, due to the destructive nature of geological phenomena, such as volcanism or erosion. One way to overcome this data limitation is to employ a space-for-time substitution using islands of different ontogenic stages as snapshots in time [15]. However, archipelagic dynamics, such as geomorphological changes in island size, connectivity and heterogeneity, as well as island hopping, might have confounding effects on empirical data [16]. Another possible alternative, still involving empirical testing, is using smaller scaled model systems such as microbiota [17,18]. Yet, for studying biogeography dynamics of longer living organisms, process-explicit models remain the most viable option to date.
With the advances in technology and scientific knowledge, process-explicit simulation models have become even more feasible, both in implementation, as well as conducting. In principle, process-explicit (or mechanistic) models reflect hypotheses about how mechanisms interact to produce observed patterns. In this context, we define mechanisms (or processes) as actions that causally link elements in a model. The produced patterns are thus direct results of the interplay between integrated processes. The advantage of these models lies in their flexibility. Such flexibility can be characterized in two ways: (1) through variation of model parameter values and thus their impact [19]; and (2) switching off particular processes or varying the model structure, e.g., the order of processes [20]. The combination of both allows for a multitude of possible alternative simulation arenas or scenarios and enables us to test the robustness, but also the importance of the respective mechanistic assumptions, while maintaining complete mechanistic control of the experiments.
To get an overview of which processes and drivers have been considered thus far in mechanistic island models, what patterns they produce and what they found out about their systems, we conducted an extensive literature review. We systematically searched for aspects, like for example, the theories models are based on, whether they are stochastic or deterministic, spatially implicit or explicit and what focal level they consider. The scope of our review also entails any model explicitly assessing island biogeography theories or assumptions. In contrast to the recent review by Borregaard et al. [10], we only consider models that specifically feature causal mechanisms, detached from the scope of the GDM. Our review is similar to Cabral et al. [21], but we focus specifically on island models and perform an exhaustive, systematic literature search.

2. Results

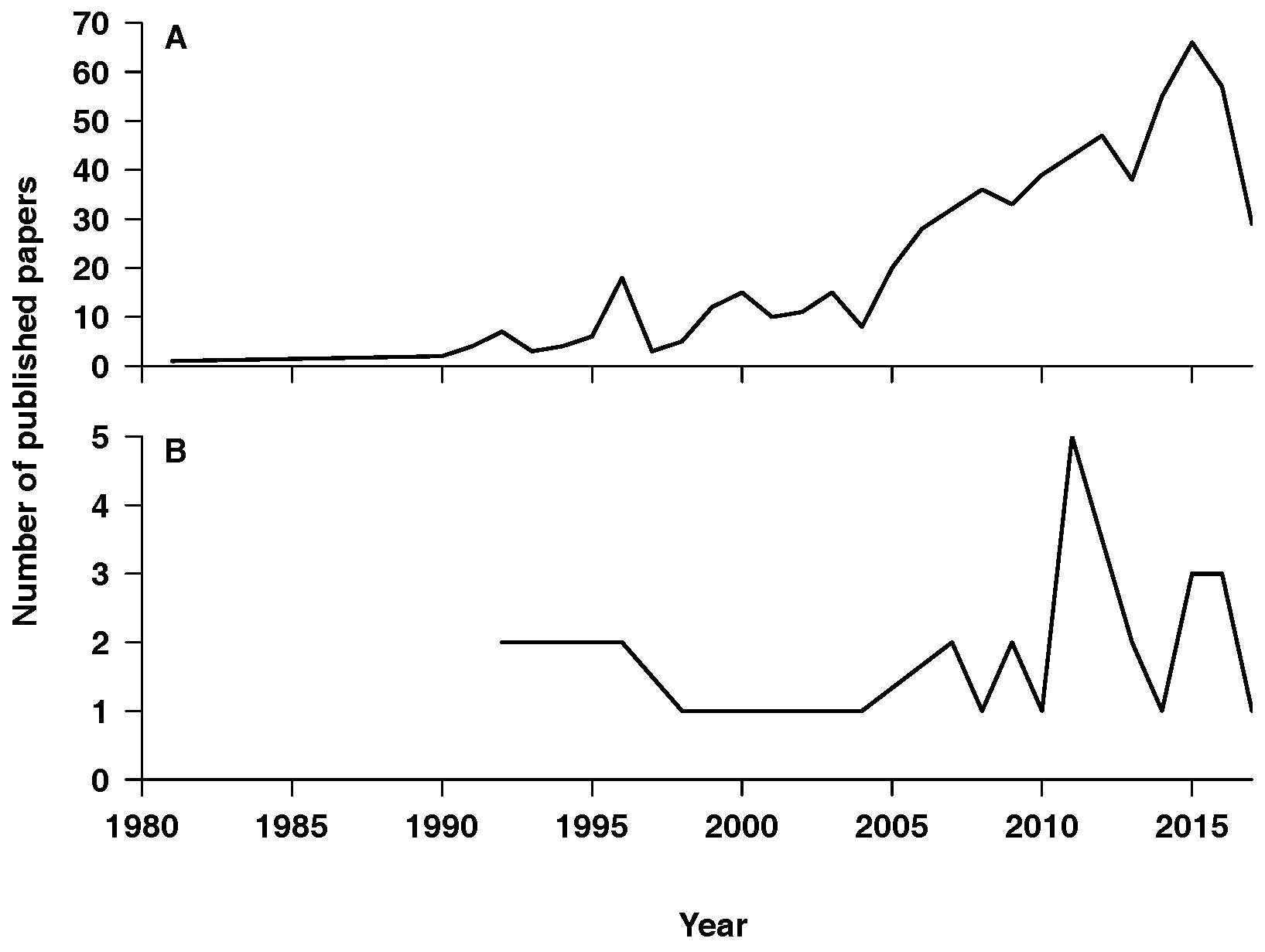
2.1. Description

The search for “archipelago OR island OR model OR equilibrium” in the title field and “(island OR archipelago) AND (species) AND (evolution OR speciation OR theory) AND (simulation OR model)” as the topics yielded 647 hits on the Web of Science (https://apps.webofknowledge.com), spanning years from 1981 to 2017 (Figure 1), which we filtered manually on the basis of whether the papers actually contained mechanistic models and whether they were island related, i.e., whether they assessed island biogeography theories or dealt explicitly with islands and/or archipelagos. This procedure meant not including all models that could potentially be relevant to islands (e.g., metacommunity models), but which unfortunately did not explicitly state so in their text, thus making it difficult to find all of them in a systematic way. After this filtering, we attained 28 hits in total (Table 1).

2.2. Properties

Island biogeography models developed so far are very diverse in their properties (see the spread in Figure 2). Common to most models is the implementation of basic demographic processes (birth/death) and dispersal, but also, evolution is an often integrated process (Table 1, “processes”). A fundamental property found in the models lies in their implementation of stochasticity. Most of the studies use stochastic models (Figure 2). These are characterized by employing stochasticity in at least one of their mechanisms. This might be, e.g., the selection of the number of offspring in a reproduction event (e.g., [22]) or dispersal decisions (e.g., [23]). In contrast, deterministic models are often described purely analytically by a set of differential equations [24,25], although in some deterministic models, stochasticity can be easily switched on [26].
Some of the models explicitly consider the spatial configuration and position of state variables of their environment, i.e., they are spatially explicit. While spatially explicit and stochastic models were common in the earliest studies [22,27], more recently published models tend to be less often spatially explicit [28,29], which mirrors the popularity of the unified neutral theory of biodiversity (UNTB; [30]). Because the UNTB inspired a large portion of the later models, we considered it an additional category. Consequently, models are “neutral” if they follow neutral dynamics, i.e., ecological equivalence between individuals of different species. Additional underlying theories are also summed up in Table 1.
Models also varied in their metacommunity scenarios. The most common arena is of a mainland-island configuration (or source-sink), with a source species pool on the (continental) mainland. In some cases, more than one island is modeled, creating an archipelago-type system (Table 1). Most models furthermore explore hypothetical systems (Table 1), which represent islands in a simplified way and have no direct connection to real-world systems, although they are often inspired by real-world examples.
The integration of evolutionary processes emerges as another discriminating factor (Figure 2). This has been achieved at different levels of detail. With a genome-explicit model, Gavrilets and Vose [31] consider the accumulation of micro-evolution in genes encoding for ecological niche preferences, which leads to the isolation of populations and eventually in speciation, and recent papers opt to implement speciation in a more simplified way using submodels like “protracted speciation” [32] or point speciation as in the original UNTB [30].
An important factor contributing to the distribution of the studies’ models is the implemented agent level, which determines whether processes directly act on individuals, populations or species. This also shows a positive trend with stochasticity, with deterministic analytical models usually focusing on higher organizational levels (see the diametrical axes “focal.level” and “stochastic” in Figure 2), such as population or species numbers [26,33]. In contrast, stochastic models often are individual based [22,31]. The agent level often also determines the focal level (Table 1), which is on the same or a higher organizational level as the agent level. Noteworthy here are two studies, which integrate genetic properties into their models to investigate the genetic structures of populations [34,35].
While in most of the models, there is no differences between species, some models allow species to carry their own particular parameter values. This can, for instance, be the reproductive output [22,24] or the competition strength [36] and is reflected as the number of non-neutral niche axes (Table 1). The total number of parameters ranges from one to 14 (Table 1). However, as parameters were not equally apparent in all papers, these numbers might be underestimated.
Furthermore, we discriminated models with static environments and models where the environment was subject to change. This change affects the geographic configuration of the environments, altering island size, suitability or carrying capacity. Examples for this are the models inspired by the GDM, which simulate island ontogenies [25,26,37].
Lastly, we took into consideration whether studies investigated purely hypothetical scenarios (models marked “h” in the system column of Table 1) or if they applied their models to real-world systems, e.g., by fitting or calibrating them to empirical data (models marked “r”). Of the 28 included studies, only five studies include a systematic comparison with real-world systems. For instance, Birand and Howard [38] and Rosindell and Phillimore [39] use parameter screening to obtain realistic rates of extinction, reproduction, speciation and migration compared with archipelago species numbers (including information on endemics) from plants and arthropods, or birds, respectively. Two other studies used representations of real geography as their model arena [23,34] for the investigation of radiation or speciation histories. Only a single study actually fitted their model to data, using a maximum likelihood approach and dated phylogenies of Galápagos land birds to obtain rates of diversification and radiation [29].
Some of the aforementioned characteristics often go together, representing commonly-used model structures (Figure 3). For example, island models following the framework of the UNTB usually employ evolution, as well. This highlights especially those studies that extend classical neutral dynamics with speciation [28,39,40]. Another example of a frequent characteristics combination are spatially-explicit models with static environments, which can be found among the earliest published models included in this study [22,24,27,41]. This co-occurrence of spatially-explicit and static environment properties is further strengthened by a number of studies displaying the exact opposite of this combination, namely spatially-implicit models with dynamic environments, as implemented by models having a GDM background [25,26,37]. One interesting property that is rather isolated in the property space is the consideration of inter-specific differences (niche-based, Figure 3). While the contrast of niche-based models to neutral models could be expected, the accompanying opposition to models including evolution is surprising. In fact, when marking the relevant studies according to whether models consider niche differences between species (green cluster, Figure 2) and whether they employ evolution in any form (orange cluster, Figure 2), only one study [31] joins both of these clusters and can thus be understood as the only one to investigate evolution in an explicitly adaptive context.

2.3. Findings

The reviewed studies investigate a variety of patterns in the spectrum of biodiversity. Commonly investigated patterns include the proportion of endemism and species-area relationships (SAR). For SAR, studies found that in additional to the extinction and immigration rates as proposed by MacArthur and Wilson [7]) [27,41,42], species numbers also depend on explicit competition [41], trophic interactions [50,52], environmental heterogeneity [33,47] and evolutionary processes, like mutations and speciation [25,38]. Figure 4 shows a representation of all of the processes and drivers implemented in the models, explicitly highlighting causal relationships and under-explored links.
A group of models simulating hypothetical systems concentrated on testing particular predictions from theoretical frameworks like ETIB and was thus able to confirm power law species-area-relationships [27,41,42] or the hump-shaped trajectories following island ontogenies of the GDM [26,37]. This investigation of theoretical prediction includes a trend of models integrating different existing theories or improving theory considering additional mechanisms, mostly on the basis of classical island biogeography, such as disturbance [22], trophic interactions [50], evolution and speciation [39,43], competition [24,36] and inter-specific differentiation (e.g., niche-based) [47]. In many cases, these extended models are able to explain field observations that could not be explained by any one isolated theoretical component, e.g., the ETIB (model generality [20]).
The models that simulate real-world systems [23,29,34] shed light on the mechanisms behind distribution patterns of real-world species; for instance, diversification of Philippine shrews shaped by competitive exclusion over dispersal ability [23], bluebirds on Bermuda as cryptic introductions [34] or presently increasing species richness in some bird lineages on the Galápagos, while other lineages already attained equilibrium dynamics [29]. The models of Birand and Howard [38] and Rosindell and Phillimore [39] were able to produce realistic species distribution and endemism patterns, when compared to empirical data of species numbers, while Valente et al. [29] used Bayesian information criterion weights for selection of the best model that explains current diversification patterns on the basis of phylogenetic data.
Some models reveal the impacts of spatial and temporal factors and mechanisms on island biodiversity. For instance, along island chains, species richness does not necessarily decrease, but can even increase with distance from the mainland, if speciation rates are adequately high [40]. When considering temporal scales relevant for geological dynamics, island biodiversity follows island ontogeny as predicted by the GDM [26,37]. Moreover, island biodiversity does not necessarily follow either equilibrium or non-equilibrium dynamics exclusively [29]. Furthermore, species abundances provide a better measure of immigration/extinction rates on islands than only species richness: low abundances follow immigration and may precede extinction [28]. Interestingly, the extension of island biogeography with niche theory leads to complex emergent patterns. For example, Kadmon and Allouche [33] revealed a uni-modal relationship between species richness and habitat heterogeneity, owing to the reduced suitable area on a given island at high degrees of heterogeneity. Relaxing the habitat specificity of species to allow for a niche breadth, however, restores the positive relationship between species richness and habitat heterogeneity as predicted by classical niche theory [47]. Thus, integrating multiple processes results in both complex emergent patterns and provides detailed information about the study system.

3. Discussion

3.1. General Modeling Trends

Although actual mechanistic models in island biogeography are still scarce in comparison to other fields in ecology [21], the rate of publication of models has increased (Figure 1). This reflects a renewed popularity in island biogeography theory over the past two decades (Figure 1), highlighting the importance of islands as model systems for biodiversity dynamics. Therefore, we expect a persistence of the increasing trend in the number of island models in the near future, particularly because several processes and process combinations remain un- or under-explored.
The sequence of underlying theories that studies try to test or extend shows that modelers are often inspired by the important current theories. Early papers [22,42] are mainly based on MacArthur and Wilson’s ETIB. In the 2000s, the popularity of the neutral theory of island biogeography [30] inspired a series of studies following the publication of the theory [28,39,55]. More recently, the general dynamic model of oceanic island biogeography [8] is also employed in models [26,37]. This regular switching in underlying theories suggests that a universal theory of ecology is highly sought after (see Lawton [56]). The effort to develop such a universal theory is often made explicit in the usage of adjectives like “generalized” or “unified” in paper titles [25,29,36,39]. Yet, unifying studies have only integrated parts, mostly pair-wise, of the many ecological theories. More importantly, the majority of mechanistic models do indeed integrate theories by simulating processes particular to each theory. Exemplary processes include colonization and extinction, representing the ETIB [22,42], or island ontogeny, representing the GDM [26,37].
The advantage of island models simulating hypothetical systems [42,43,50] is that they facilitate understanding the effects of fundamental processes. Furthermore, hypothetical systems are more easily employed, because they do not need data to setup simulation arenas and have parameters set by assumptions and study design, which follow the model’s theoretical background and study question, respectively. However, more specific questions can only be answered by simulating real-world systems [23,34]. The gained knowledge can also be used to extrapolate the development of the system into the future, taking into account different climate or disturbance scenarios. A mechanistic model is thus a powerful tool for conservation biology. These kinds of models do not have to be specific for a particular system. The model of Valente et al. [29], for instance, was later used to assess the impact of anthropogenic extinctions on equilibrium dynamics in another system, namely Caribbean bats [57].

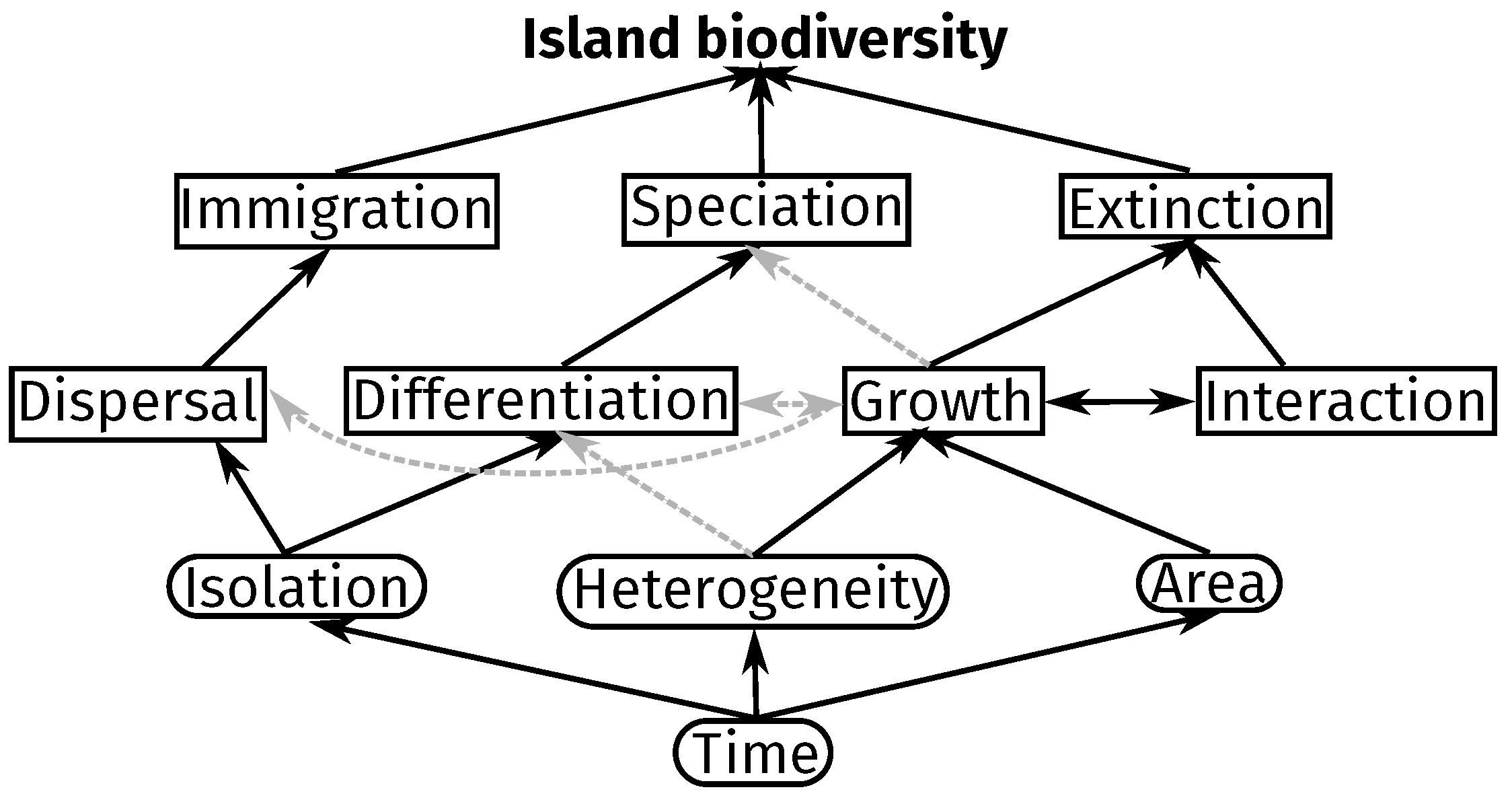
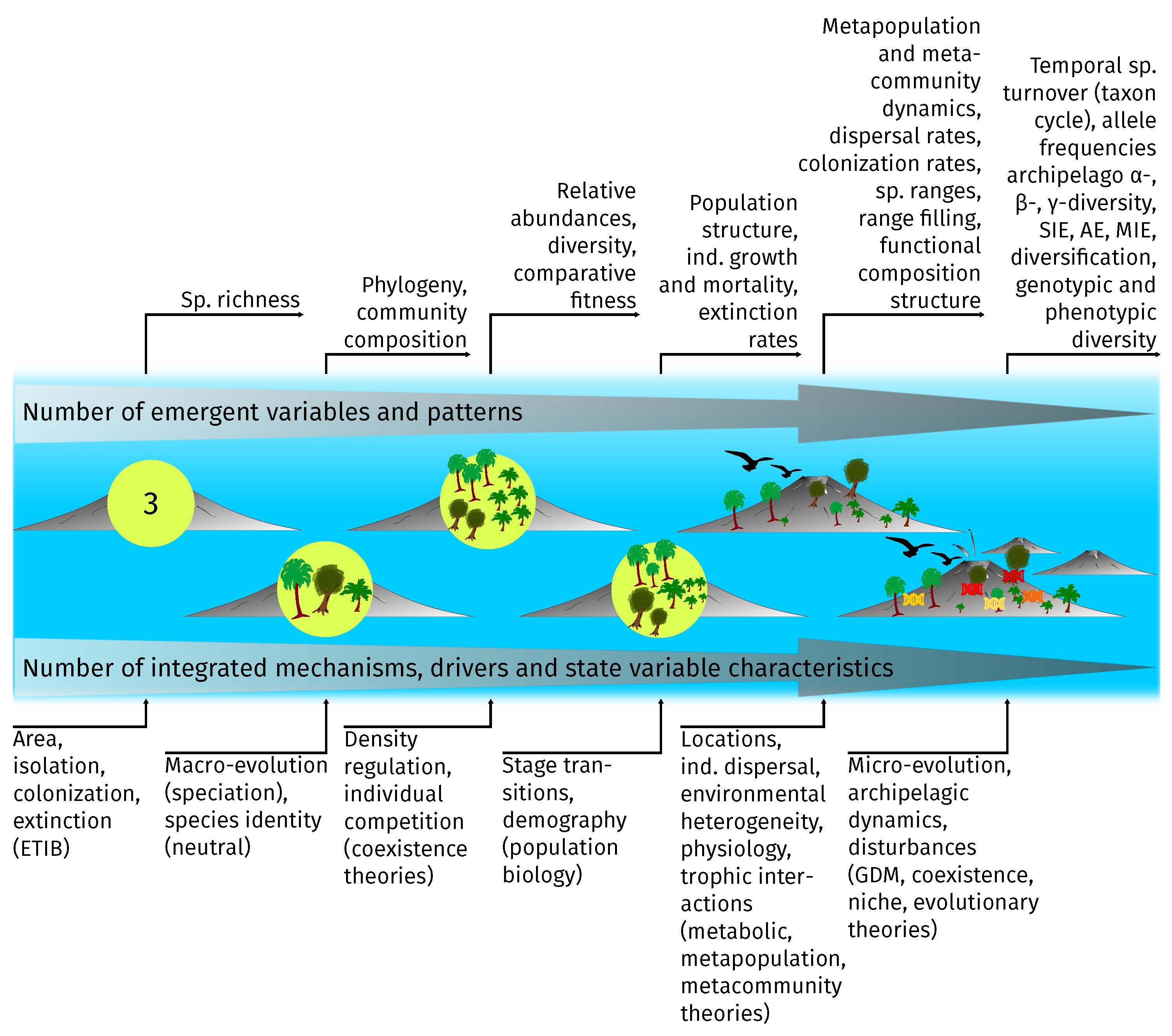
3.2. Integrated Processes and Emergent Patterns

The observed studies often focus on specific ecological aspects, which affect the implemented processes (or characteristics of the state variables), for example spatial arrangement [40,48] or inter-specific variability [33,47]. However, some of the mechanisms, like disturbances or explicit competition, were rarely explicitly integrated (e.g., [22,24,27]). Most notably, only one model considers trophic interactions [50]. Given the importance of higher trophic levels acting as top-down regulators on biodiversity [58], it is surprising that not more direct species interactions are being considered yet.
A possible reason for this limited process integration is the required mechanistic complexity and resulting computational demand. The latter is an issue that still seems to scare ecologists and showcases that despite today’s computational feasibility, ecological modeling is not as developed as other fields in biology (e.g., -omics studies) or other natural science fields. This underdevelopment of computational abilities highlights the need for teaching computer programming to undergraduate students of ecology. To also educate today’s researchers, current modelers should explain their models better and make them more accessible, by, e.g., user-friendly interfaces and proper documentation. As a first step, however, it should be considered good practice to always publish computer code alongside the publication [59,60].
Another particularly understudied field in island models is evolution based on the accumulation of explicit gene mutations that result in fitness differences. Only one study of the investigated papers employed such a detailed micro-evolutionary mechanism, with a palm population adapting to different soil types and diverging in its phenology [31]. Given that selection on oceanic islands has been one of the foundations of evolution theory [61], the explicit evolution of traits and species will hopefully be more often implemented in island models. A first step towards this is the concept of protracted speciation, where a mutation event triggers a speciation process, but the new species emerges only after a certain period of implicit accumulation of mutations and genomic isolation from the sister clade [32]. Among non-island models there are further examples for such micro-evolutionary processes and consideration of genetic diversity (e.g., [62,63,64]). Some of their integrated evolutionary processes could ultimately result in reproductive isolation of populations and thus speciation, and there are already examples for actual adaptive speciation and radiation in landscape ecology and metacommunity models [65,66,67]. Applying their findings to island systems could provide the perfect framework to increase and unify efforts in studying the (micro-)evolution of species.
Biological models for nowadays complex questions should aim at producing patterns over different spatial, temporal or organizational scales (pattern-oriented modeling; [68,69]). The mechanistic complexities of many models, with up to ten model parameters or more (Table 1), would easily be able to produce more patterns, but the respective studies concentrated on only a few patterns at a time, for instance species numbers [27] or biogeographic rates [28]. One model that investigated the interaction between micro-evolutionary and ecological mechanism [6], thus producing eco-evolutionary dynamics, was unfortunately not considered by our web of knowledge search. Another example of a very complex stochastic archipelago model including evolutionary dynamics, niche theory and geomorphological processes was not captured in our search, as it represents a book chapter [70]. This reduction of investigated processes and patterns, and thus complexity, can be a consequence of the peer-review process, which often requires a focus on one or few specific and simple questions, or it can result from models developed specifically to only address a certain problem.
While simple models do have their place for, e.g., preliminary investigations of particular processes in a hypothetical system, they do not need to be developed from scratch. For example, if one is interested in assessing the role of positive density dependence (i.e., Allee effects) on islands, one would not need to implement a model de novo, but could simply apply a pre-existing model with Allee effects to islands. In the quest for more cooperation, reproducibility and re-use of code, we thus encourage modelers to rather develop existing models further. For this to work, modeling scientists should embrace open source principles. A complex model integrating multiple processes and generating multiple patterns could thus be used to investigate multiple questions, problems and systems (e.g., higher model generality [20]). For example, a model integrating trait evolution (changes in individual or species function) could be used to investigate both neutral and niche-based assumptions and is thus more general than purely neutral models.

3.3. Limitations and Modeling Agenda

Two great difficulties in constructing process-based models lie in the number of parameters and the calibration of these parameters with adequate values, as some of the investigated models did for example with phylogenetic data. The number of parameters increases with each additional process, which requires additional empirical data for parameterization. Additionally, after calibration, calibrated parameter values should be cross-checked with field observations, which further increases the need for specific data. Furthermore, additional processes and parameters increase the risk of equifinality, i.e., a model that will produce similar results, despite different parameter combinations [12]. To deal with this issue, more detailed data are needed to correctly identify processes and parameters. Due to the destructive nature of geomorphological processes acting on islands, the wish for comprehensive data for island systems over evolutionary timescales will likely never be fulfilled, but many hypotheses generated through simulations models could be selectively tested with fieldwork. For this to work, modelers and empiricists will need to collaborate more closely. This can be achieved if modelers communicate what kind of data they need and if the empiricists consider model predictions to be testable hypotheses.
Until now, island models mainly focused on single islands, preventing confounding effects emerging from archipelagic dynamics, such as archipelago biodiversity positively correlating with archipelago island number [14]. Borregaard et al. [26] considers archipelago dynamics implicitly by employing an emigration function, which represents individuals migrating between islands. Notable exceptions are the models of Warren [48] and Gascuel et al. [40], which both provide a simplified framework of archipelagos using island chain systems and dispersal between neighboring islands. This way, they are able to reveal that archipelago species richness is higher than species richness on a single island with a matched size. However, the linear, evenly-spaced arrangement of islands is one simple representation of an archipelago and cannot capture more diverse connection patterns of archipelagos that occur in nature. Additionally, theory predicts that real-world archipelagos are also subject to change over time, due to geomorphological and climatic processes, which in turn affects biodiversity [8].
Other processes known to have major impacts on biodiversity, but hitherto absent explicitly in models, include glaciation-induced sea level oscillations [71,72] or anthropogenic influences [73]. However, one initialization scenario of Rosindell and Harmon [28] reflects a sea level change that separates a landmass from the mainland, which thus harbors a subset of the mainland species pool. Furthermore, processes like range shifts under climate change and resulting evolutionary effects, which currently are a hot topic in ecological modeling in general [62,74], are not explored by island models yet. A more collaborative approach between researchers of these different ecological fields is thus a promising perspective for ecological modeling in general. With models integrating many different processes, which are able to produce several plausible patterns, researchers will have a valuable tool to make new hypotheses and thus guide field ecologists efficiently to conduct necessary experiments.

3.4. Conclusions

In this paper, we reviewed mechanistic island models, revealing a high diversity of investigated questions and integrated processes. Integrated processes were often inspired by current influential theories and highlight the search for a universal theory of ecology/island biogeography. An important step towards this will be the development of models integrating evolutionary, ecological and environmental processes, thus far recognized as relevant by biodiversity theories.
While in island models, patterns and processes at intermediate ecological levels (e.g., population, species) predominate, more realistic, and thus more widely applicable, models will need to integrate more processes at the individual level, such as interactions, genetics and behavior. These individual-level processes should not only affect individuals, but should also influence patterns at the population, community and metacommunity level (Figure 5). Additionally, processes acting on higher spatial and temporal scales, like archipelago structure and geomorphological changes, as well as human-induced environmental change will also need to be considered explicitly (far right in Figure 5). While most of these processes are already implemented in the reviewed models, hardly any model integrates more than two aspects at a time. Yet, the models were able to shed light on a variety of ecological questions in island biogeography regarding the past, present and future. Therefore, we anticipate that integrating multiple processes should untap an even larger number of potential (more complex) questions by increasing model generality.
Lastly, island biogeography theory was never applied solely to islands, as several ETIB-inspired metapopulation and metacommunity studies indicate. We regret that we had to exclude many potentially relevant metacommunity studies from our review, because they did not specifically relate their models to islands, but hope that in the future, researchers will more often apply their models to other related systems, as well. Because of their many advantageous qualities, like clearly-defined isolation and structure, islands will likely remain an ideal model system for studying biodiversity dynamics in general. The next generation of island models will therefore, much like the ETIB did and still does, continue to inspire fields like landscape ecology, metapopulation and metacommunity ecology, marine biology and be applied to systems such as sky islands, coral reefs and forest fragments. This will help with promoting the usefulness of mechanistic models to an even wider range of researchers, which ultimately will result in increasingly better models and better predictions.

4. Materials and Methods

The raw compilation of studies was obtained by running an ISI Web of Science search with the string “archipelago OR island OR model OR equilibrium” in the title field and “(island OR archipelago) AND (species) AND (evolution OR speciation OR theory) AND (simulation OR model)” as the topics. We did also try a more restrictive title search string (“(archipelago OR island) AND (model OR equilibrium)”), but this string resulted in far fewer hits and missed some modeling papers we knew explicitly included islands. This conservative search captured a broad range of studies even if it resulted in many false positives. The initial search result was refined by manual review of all 647 found studies evaluating two criteria: (1) whether the study has a direct island relation; and (2) whether the study employs a mechanistic model. Only if both of these questions could be answered with yes was a study incorporated into our review. We are aware that this focus on island-specific studies is somewhat arbitrary, as many metacommunity- and metapopulation-like systems, such as lakes, caves or coral reefs, could also be applied to islands (e.g., [75,76]). However, finding all of them would be systematically challenging via a structured literature search, because although plentiful and highly relevant to islands, these models failed to explicitly relate their findings to island biogeography theory, which was one of our manual screening targets. Additionally, metapopulation and metacommunity studies are usually restricted to ecological timescales and, thus, often lack evolutionary and/or (geomorphological) environmental processes, which are relevant to island biodiversity. Nevertheless, we believe that summarizing the findings of such models and relating them to island biogeography theory, as well as to other biodiversity theories would be a very useful exercise and should be aimed for in future reviews.
We analyzed the obtained paper list with special attention on the nature of the employed models and the theoretical backgrounds. For this, we characterized the models by several categories: (a) whether they employ stochasticity, e.g., in the demographics; (b) whether or not they are spatially explicit, that is the spatial position and arrangement actually impacts the system; (c) if they consider their environments to be static (yes) or if islands for example follow an ontogenic trajectory (no); (d) if they consider evolutionary processes like mutation, speciation or selection; and (e) whether they regard their systems as following neutral theory [30]. Some categories rather represent spectra like the agent level, i.e., the organizational level of the state variables on which processes act (individuals, populations, species) or the number of niche axes (number of biological parameters, whose values may be different between species in the case of niche-based models). Furthermore, we considered the focal level: the organizational level at which most emergent patterns are investigated. Additionally, we included the year of publication, the type of system that is modeled (single island, archipelago, mainland-island, mainland-archipelago) and whether this is real-world or hypothetical, as well as the theoretical background of the model, if specified. We also looked for the integrated processes, the number of model parameters as we were able to identify them and the investigated patterns.
We then used some of this information (agent level, static environment, number of niche axes, spatially explicitness, stochasticity, neutrality and evolutionary processes) to conduct multidimensional scaling (MDS) employing the R packages MASS, vegan and smacof [77,78,79] and thus get an overview of how different studies are assembled and whether there are specific under-explored areas to be found. For the ordination of papers, we used mds from the smacof package [79]and metaMDS from the MASS package for the ordination of model properties. Contrary to ordination methods like principal component analyses, in MDS, the goodness of fit is not indicated by the sum of explained variance of the first dimensions, but the Stress-1 value, with values close to zero indicating a good fit [79]. The code for running these analyses and producing the plots can be found in the Supplementary Materials.

Supplementary Materials

The following are available online at https://github.com/lleiding/mechislandmodels, code.R: R-code for running MDS and producing plots.

Acknowledgments

We thank two anonymous reviewers for helpful comments on an earlier version of this manuscript. J.S.C. and L.L. received funding from the Julius-Maximilians University of Wuerzburg. This publication was funded by the German Research Foundation (DFG) and the University of Wuerzburg in the funding program Open Access Publishing.

Author Contributions

J.S.C. conceived of and designed the review. L.L. performed the literature search. L.L. analyzed the data. L.L. led the writing with contributions by J.S.C.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Vitousek, P.M. Oceanic islands as model systems for ecological studies. J. Biogeogr. 2002, 29, 573–582. [Google Scholar] [CrossRef]
  2. Warren, B.H.; Simberloff, D.; Ricklefs, R.E.; Aguilée, R.; Condamine, F.L.; Gravel, D.; Morlon, H.; Mouquet, N.; Rosindell, J.; Casquet, J.; et al. Islands as model systems in ecology and evolution: Prospects fifty years after MacArthur-Wilson. Ecol. Lett. 2015, 18, 200–217. [Google Scholar] [CrossRef] [PubMed]
  3. Weigelt, P.; Kreft, H. Quantifying island isolation—Insights from global patterns of insular plant species richness. Ecography 2013, 36, 417–429. [Google Scholar] [CrossRef]
  4. Singer, A.; Johst, K.; Banitz, T.; Fowler, M.S.; Groeneveld, J.; Gutiérrez, A.G.; Hartig, F.; Krug, R.M.; Liess, M.; Matlack, G.; et al. Community dynamics under environmental change: How can next generation mechanistic models improve projections of species distributions? Ecol. Model. 2016, 326, 63–74. [Google Scholar] [CrossRef]
  5. Urban, M.; Bocedi, G.; Hendry, A.; Mihoub, J.B.; Pe’er, G.; Singer, A.; Bridle, J.; Crozier, L.; de Meester, L.; Godsoe, W.; et al. Improving the forecast for biodiversity under climate change. Science 2016, 353, aad8466. [Google Scholar] [CrossRef] [PubMed]
  6. Cabral, J.S.; Wiegand, K.; Kreft, H. Interactions between ecological, evolutionary, and environmental processes unveil complex dynamics of island biodiversity. bioRxiv 2017. [Google Scholar] [CrossRef]
  7. MacArthur, R.H.; Wilson, E.O. An equilibrium theory of insular zoogeography. Evolution 1963, 17, 373–387. [Google Scholar] [CrossRef]
  8. Whittaker, R.J.; Triantis, K.A.; Ladle, R.J. A general dynamic theory of oceanic island biogeography. J. Biogeogr. 2008, 35, 977–994. [Google Scholar] [CrossRef]
  9. Simberloff, D.S.; Wilson, E.O. Experimental zoogeography of islands: The colonization of empty islands. Ecology 1969, 50, 278–296. [Google Scholar] [CrossRef]
  10. Borregaard, M.K.; Amorim, I.R.; Borges, P.A.; Cabral, J.S.; Fernández-Palacios, J.M.; Field, R.; Heaney, L.R.; Kreft, H.; Matthews, T.J.; Olesen, J.M.; et al. Oceanic island biogeography through the lens of the general dynamic model: Assessment and prospect. Biol. Rev. 2017, 92, 830–853. [Google Scholar] [CrossRef] [PubMed]
  11. Whittaker, R.J.; Fernández-Palacios, J.M. Island Biogeography: Ecology, Evolution, and Conservation; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
  12. Dormann, C.F.; Schymanski, S.J.; Cabral, J.; Chuine, I.; Graham, C.; Hartig, F.; Kearney, M.; Morin, X.; Römermann, C.; Schröder, B.; et al. Correlation and process in species distribution models: Bridging a dichotomy. J. Biogeogr. 2012, 39, 2119–2131. [Google Scholar] [CrossRef]
  13. Weigelt, P.; Jetz, W.; Kreft, H. Bioclimatic and physical characterization of the world’s islands. Proc. Natl. Acad. Sci. USA 2013, 110, 15307–15312. [Google Scholar] [CrossRef] [PubMed]
  14. Cabral, J.S.; Weigelt, P.; Kissling, W.D.; Kreft, H. Biogeographic, climatic and spatial drivers differentially affect α-, β- and γ-diversities on oceanic archipelagos. Proc. R. Soc. Lond. B Biol. Sci. 2014, 281, 20133246. [Google Scholar] [CrossRef] [PubMed]
  15. Borges, P.A.; Brown, V.K. Effect of island geological age on the arthropod species richness of Azorean pastures. Biol. J. Linn. Soc. 1999, 66, 373–410. [Google Scholar] [CrossRef]
  16. Buskirk, R.E. Zoogeographic patterns and tectonic history of Jamaica and the northern Caribbean. J. Biogeogr. 1985, 12, 445–461. [Google Scholar] [CrossRef]
  17. Meyer, K.M.; Leveau, J.H. Microbiology of the phyllosphere: A playground for testing ecological concepts. Oecologia 2012, 168, 621–629. [Google Scholar] [CrossRef] [PubMed]
  18. Maignien, L.; DeForce, E.A.; Chafee, M.E.; Eren, A.M.; Simmons, S.L. Ecological succession and stochastic variation in the assembly of Arabidopsis thaliana phyllosphere communities. MBio 2014, 5, e00682-13. [Google Scholar] [CrossRef] [PubMed]
  19. Jeltsch, F.; Moloney, K.A.; Schurr, F.M.; Köchy, M.; Schwager, M. The state of plant population modelling in light of environmental change. Perspect. Plant Ecol. Evol. Syst. 2008, 9, 171–189. [Google Scholar] [CrossRef]
  20. Evans, M.R.; Grimm, V.; Johst, K.; Knuuttila, T.; De Langhe, R.; Lessells, C.M.; Merz, M.; O’Malley, M.A.; Orzack, S.H.; Weisberg, M.; et al. Do simple models lead to generality in ecology? Trends Ecol. Evol. 2013, 28, 578–583. [Google Scholar] [CrossRef] [PubMed]
  21. Cabral, J.S.; Valente, L.; Hartig, F. Mechanistic simulation models in macroecology and biogeography: State-of-art and prospects. Ecography 2017, 40, 267–280. [Google Scholar] [CrossRef]
  22. Villa, F.; Rossi, O.; Sartore, F. Understanding the role of chronic environmental disturbance in the context of island biogeographic theory. Environ. Manag. 1992, 16, 653–666. [Google Scholar] [CrossRef]
  23. Esselstyn, J.A.; Maher, S.P.; Brown, R.M. Species interactions during diversification and community assembly in an island radiation of shrews. PLoS ONE 2011, 6, e21885. [Google Scholar] [CrossRef] [PubMed]
  24. Cantrell, R.; Cosner, C.; Hutson, V. Spatially explicit models for the population dynamics of a species colonizing an island. Math. Biosci. 1996, 136, 65–107. [Google Scholar] [CrossRef]
  25. Chen, X.; Jiao, J.; Tong, X. A generalized model of island biogeography. Sci. China Life Sci. 2011, 54, 1055–1061. [Google Scholar] [CrossRef] [PubMed]
  26. Borregaard, M.K.; Matthews, T.J.; Whittaker, R.J. The general dynamic model: Towards a unified theory of island biogeography? Glob. Ecol. Biogeogr. 2015, 25, 805–816. [Google Scholar] [CrossRef]
  27. Durrett, R.; Levin, S. Spatial models for species-area curves. J. Theor. Biol. 1996, 179, 119–127. [Google Scholar] [CrossRef]
  28. Rosindell, J.; Harmon, L.J. A unified model of species immigration, extinction and abundance on islands. J. Biogeogr. 2013, 40, 1107–1118. [Google Scholar] [CrossRef]
  29. Valente, L.M.; Phillimore, A.B.; Etienne, R.S. Equilibrium and non-equilibrium dynamics simultaneously operate in the Galápagos islands. Ecol. Lett. 2015, 18, 844–852. [Google Scholar] [CrossRef] [PubMed]
  30. Hubbell, S. The Unified Neutral Theory of Species Abundance and Diversity; Hubbell, SP (2004) Quarterly Review of Biology; Princeton University Press: Princeton, NJ, USA, 2001; Volume 79, pp. 96–97. [Google Scholar]
  31. Gavrilets, S.; Vose, A. Case studies and mathematical models of ecological speciation. 2. Palms on an oceanic island. Mol. Ecol. 2007, 16, 2910–2921. [Google Scholar] [CrossRef] [PubMed]
  32. Rosindell, J.; Cornell, S.J.; Hubbell, S.P.; Etienne, R.S. Protracted speciation revitalizes the neutral theory of biodiversity. Ecol. Lett. 2010, 13, 716–727. [Google Scholar] [CrossRef] [PubMed]
  33. Kadmon, R.; Allouche, O. Integrating the effects of area, isolation, and habitat heterogeneity on species diversity: A unification of island biogeography and niche theory. Am. Nat. 2007, 170, 443–454. [Google Scholar] [CrossRef] [PubMed]
  34. Avery, J.D.; Fonseca, D.M.; Campagne, P.; Lockwood, J.L. Cryptic introductions and the interpretation of island biodiversity. Mol. Ecol. 2013, 22, 2313–2324. [Google Scholar] [CrossRef] [PubMed]
  35. Yamaguchi, R.; Iwasa, Y. Parapatric speciation in three islands: dynamics of geographical configuration of allele sharing. Open Sci. 2017, 4, 160819. [Google Scholar] [CrossRef] [PubMed]
  36. Kessler, D.A.; Shnerb, N.M. Generalized model of island biodiversity. Phys. Rev. E 2015, 91, 042705. [Google Scholar] [CrossRef] [PubMed]
  37. Valente, L.M.; Etienne, R.S.; Phillimore, A.B. The effects of island ontogeny on species diversity and phylogeny. Proc. R. Soc. Lond. B Biol. Sci. 2014, 281, 20133227. [Google Scholar] [CrossRef] [PubMed]
  38. Birand, A.; Howard, D.J. The relationship between proportion of endemics and species diversity on islands: Expectations from a null model. Ecography 2008, 31, 286–288. [Google Scholar] [CrossRef]
  39. Rosindell, J.; Phillimore, A.B. A unified model of island biogeography sheds light on the zone of radiation. Ecol. Lett. 2011, 14, 552–560. [Google Scholar] [CrossRef] [PubMed]
  40. Gascuel, F.; Laroche, F.; Bonnet-Lebrun, A.S.; Rodrigues, A.S. The effects of archipelago spatial structure on island diversity and endemism: predictions from a spatially-structured neutral model. Evolution 2016, 70, 2657–2666. [Google Scholar] [CrossRef] [PubMed]
  41. De Blasio, F. Diversity variation in isolated environments: Species-area effects from a stochastic model. Ecol. Model. 1998, 111, 93–98. [Google Scholar]
  42. Wissel, C.; Maier, B. A stochastic model for the species-area relationship. J. Biogeogr. 1992, 19, 355–361. [Google Scholar] [CrossRef]
  43. Johnson, K.P.; Adler, F.R.; Cherry, J.L. Genetic and phylogenetic consequences of island biogeography. Evolution 2000, 54, 387–396. [Google Scholar] [CrossRef] [PubMed]
  44. Ricklefs, R.E.; Bermingham, E. Application of Johnson et al.’s speciation threshold model to apparent colonization times of island biotas. Evolution 2004, 58, 1664–1673. [Google Scholar] [CrossRef] [PubMed]
  45. Emerson, B.C.; Kolm, N. Species diversity can drive speciation. Nature 2005, 434, 1015–1017. [Google Scholar] [CrossRef] [PubMed]
  46. Chen, X.Y.; He, F. Speciation and endemism under the model of island biogeography. Ecology 2009, 90, 39–45. [Google Scholar] [CrossRef] [PubMed]
  47. Hortal, J.; Triantis, K.A.; Meiri, S.; Thébault, E.; Sfenthourakis, S. Island species richness increases with habitat diversity. Am. Nat. 2009, 174, E205–E217. [Google Scholar] [CrossRef] [PubMed]
  48. Warren, P.B. Biodiversity on island chains: Neutral model simulations. Phys. Rev. E 2010, 82, 051922. [Google Scholar] [CrossRef] [PubMed]
  49. Lambert, A. Species abundance distributions in neutral models with immigration or mutation and general lifetimes. J. Math. Biol. 2011, 63, 57–72. [Google Scholar] [CrossRef] [PubMed]
  50. Gravel, D.; Massol, F.; Canard, E.; Mouillot, D.; Mouquet, N. Trophic theory of island biogeography. Ecol. Lett. 2011, 14, 1010–1016. [Google Scholar] [CrossRef] [PubMed]
  51. Chen, Y. An island biogeography model for beta diversity and endemism: The roles of speciation, extinction and dispersal. Int. J. Biomath. 2015, 8, 1550011. [Google Scholar] [CrossRef]
  52. Jacquet, C.; Mouillot, D.; Kulbicki, M.; Gravel, D. Extensions of Island Biogeography Theory predict the scaling of functional trait composition with habitat area and isolation. Ecol. Lett. 2017, 20, 135–146. [Google Scholar] [CrossRef] [PubMed]
  53. Brown, J.H.; Kodric-Brown, A. Turnover rates in insular biogeography: Effect of immigration on extinction. Ecology 1977, 58, 445–449. [Google Scholar] [CrossRef]
  54. Lomolino, M.V. The Target Area Hypothesis: The Influence of Island Area on Immigration Rates of Non-Volant Mammals. Oikos 1990, 57, 297–300. [Google Scholar] [CrossRef]
  55. Keil, P.; Herben, T.; Rosindell, J.; Storch, D. Predictions of Taylor’s power law, density dependence and pink noise from a neutrally modeled time series. J. Theor. Biol. 2010, 265, 78–86. [Google Scholar] [CrossRef] [PubMed]
  56. Lawton, J.H. Are There General Laws in Ecology? Oikos 1999, 84, 177–192. [Google Scholar] [CrossRef]
  57. Valente, L.; Etienne, R.S.; Dávalos, L.M. Recent extinctions disturb path to equilibrium diversity in Caribbean bats. Nat. Ecol. Evol. 2017, 1, 0026. [Google Scholar] [CrossRef]
  58. Terborgh, J.W. Toward a trophic theory of species diversity. Proc. Nat. Acad. Sci. USA 2015, 112, 11415–11422. [Google Scholar] [CrossRef] [PubMed]
  59. Barnes, N. Publish your computer code: It is good enough. Nature 2010, 467, 753. [Google Scholar] [CrossRef] [PubMed]
  60. Mislan, K.; Heer, J.M.; White, E.P. Elevating the status of code in ecology. Trends Ecol. Evol. 2016, 31, 4–7. [Google Scholar] [CrossRef] [PubMed]
  61. Darwin, C. On the Origin of the Species by Natural Selection; J. Murray: London, UK, 1859. [Google Scholar]
  62. Schiffers, K.; Bourne, E.C.; Lavergne, S.; Thuiller, W.; Travis, J.M. Limited evolutionary rescue of locally adapted populations facing climate change. Philos. Trans. R. Soc. B 2013, 368, 20120083. [Google Scholar] [CrossRef] [PubMed]
  63. Vellend, M. Species diversity and genetic diversity: Parallel processes and correlated patterns. Am. Nat. 2005, 166, 199–215. [Google Scholar] [CrossRef] [PubMed]
  64. Laroche, F.; Jarne, P.; Lamy, T.; David, P.; Massol, F. A neutral theory for interpreting correlations between species and genetic diversity in communities. Am. Nat. 2014, 185, 59–69. [Google Scholar] [CrossRef] [PubMed]
  65. Aguilée, R.; Claessen, D.; Lambert, A. Adaptive radiation driven by the interplay of eco-evolutionary and landscape dynamics. Evolution 2013, 67, 1291–1306. [Google Scholar] [CrossRef] [PubMed]
  66. Thibert-Plante, X.; Gavrilets, S. Evolution of mate choice and the so-called magic traits in ecological speciation. Ecol. Lett. 2013, 16, 1004–1013. [Google Scholar] [CrossRef] [PubMed]
  67. Gascuel, F.; Ferrière, R.; Aguilée, R.; Lambert, A. How ecology and landscape dynamics shape phylogenetic trees. Syst. Biol. 2015, 64, 590–607. [Google Scholar] [CrossRef] [PubMed]
  68. Grimm, V.; Frank, K.; Jeltsch, F.; Brandl, R.; Uchmański, J.; Wissel, C. Pattern-oriented modelling in population ecology. Sci. Total Environ. 1996, 183, 151–166. [Google Scholar] [CrossRef]
  69. Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.H.; Weiner, J.; Wiegand, T.; DeAngelis, D.L. Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science 2005, 310, 987–991. [Google Scholar] [CrossRef] [PubMed]
  70. Haydon, D.; Radtkey, R.R.; Pianka, E.R. Experimental Biogeography: Interactions between Stochastic, Historical, and Ecological Processes in a Model Archipelago. In Species Diversity in Ecological Communities: Historical and Geographical Perspectives; The University of Chicago Press: Chicago, IL, USA, 1993; pp. 117–130. [Google Scholar]
  71. Weigelt, P.; Steinbauer, M.J.; Cabral, J.S.; Kreft, H. Late Quaternary climate change shapes island biodiversity. Nature 2016, 532, 99–114. [Google Scholar] [CrossRef] [PubMed]
  72. Fernández-Palacios, J.M.; Rijsdijk, K.F.; Norder, S.J.; Otto, R.; Nascimento, L.; Fernández-Lugo, S.; Tjørve, E.; Whittaker, R.J. Towards a glacial-sensitive model of island biogeography. Glob. Ecol. Biogeogr. 2016, 25, 817–830. [Google Scholar] [CrossRef]
  73. Helmus, M.R.; Mahler, D.L.; Losos, J.B. Island biogeography of the Anthropocene. Nature 2014, 513, 543–546. [Google Scholar] [CrossRef] [PubMed]
  74. Kubisch, A.; Winter, A.M.; Fronhofer, E.A. The downward spiral: Eco-evolutionary feedback loops lead to the emergence of ‘elastic’ranges. Ecography 2015, 39, 261–269. [Google Scholar] [CrossRef]
  75. Prevedello, J.A.; Gotelli, N.J.; Metzger, J.P. A stochastic model for landscape patterns of biodiversity. Ecol. Monogr. 2016, 86, 462–479. [Google Scholar] [CrossRef]
  76. Stier, A.C.; Hanson, K.M.; Holbrook, S.J.; Schmitt, R.J.; Brooks, A.J. Predation and landscape characteristics independently affect reef fish community organization. Ecology 2014, 95, 1294–1307. [Google Scholar] [CrossRef] [PubMed]
  77. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
  78. Oksanen, J.; Blanchet, F.G.; Friendly, M.; Kindt, R.; Legendre, P.; McGlinn, D.; Minchin, P.R.; O’Hara, R.B.; Simpson, G.L.; Solymos, P.; et al. Vegan: Community Ecology Package, R package version 2.4-1. 2016.
  79. De Leeuw, J.; Mair, P. Multidimensional Scaling Using Majorization: SMACOF in R. J. Stat. Softw. 2009, 31, 1–30. [Google Scholar] [CrossRef]
Diversity 09 00030 g001 550
Figure 1. Number of paper hits from the literature search over publication years. (A) Total (raw) numbers of all paper types; (B) numbers of studies containing mechanistic simulation models. Note the different y-axis scales of both graphs.
Figure 1. Number of paper hits from the literature search over publication years. (A) Total (raw) numbers of all paper types; (B) numbers of studies containing mechanistic simulation models. Note the different y-axis scales of both graphs.
Diversity 09 00030 g001
Diversity 09 00030 g002 550
Figure 2. Multidimensional scaling of the refined list of papers according to the model characteristics ( S t r e s s − 1 = 0.144 , better than permutation-based null solutions with p < 0.05 ). Blue arrows represent category axes with significant importance ( p < 0.05 ). Arrow directions are from the absence to the presence of a property or in increasing order (number of niche axes and focal level). Clusters show groupings of papers based on whether models consider niche differences between species (green cluster) and whether they employ evolution in any form (orange cluster). Meaning of arrow labels: neutral: whether the model follows neutral theory [30]; evolution: whether the model employs evolution; stochastic: whether the model architecture is deterministic (zero) or stochastic (one); spatially.explicit: whether the model explicitly considers space; no.niche.axes: the number of parameters that relate to biological differences between species; static.environment: whether the model arena is subject to change (zero) or static (one); agent.level: the organizational level at which the model processes act (from individual, one, to population, two, to species, three). The underlying data are shown in Table 1. Note that for the creation of the plot, a jitter was applied to the data to make points better distinguishable.
Figure 2. Multidimensional scaling of the refined list of papers according to the model characteristics ( S t r e s s − 1 = 0.144 , better than permutation-based null solutions with p < 0.05 ). Blue arrows represent category axes with significant importance ( p < 0.05 ). Arrow directions are from the absence to the presence of a property or in increasing order (number of niche axes and focal level). Clusters show groupings of papers based on whether models consider niche differences between species (green cluster) and whether they employ evolution in any form (orange cluster). Meaning of arrow labels: neutral: whether the model follows neutral theory [30]; evolution: whether the model employs evolution; stochastic: whether the model architecture is deterministic (zero) or stochastic (one); spatially.explicit: whether the model explicitly considers space; no.niche.axes: the number of parameters that relate to biological differences between species; static.environment: whether the model arena is subject to change (zero) or static (one); agent.level: the organizational level at which the model processes act (from individual, one, to population, two, to species, three). The underlying data are shown in Table 1. Note that for the creation of the plot, a jitter was applied to the data to make points better distinguishable.
Diversity 09 00030 g002
Diversity 09 00030 g003 550
Figure 3. Multidimensional scaling of the model properties in the refined list of papers ( S t r e s s − 1 = 0.126 ). The closer two properties are, the more often these properties are implemented simultaneously in models. The underlying data are shown in Table 1. ind.based: individual-based; pop.based: population-based; sp.based: species-based; other properties as in Figure 2. For this analysis, we used the same data as for producing Figure 2 .
Figure 3. Multidimensional scaling of the model properties in the refined list of papers ( S t r e s s − 1 = 0.126 ). The closer two properties are, the more often these properties are implemented simultaneously in models. The underlying data are shown in Table 1. ind.based: individual-based; pop.based: population-based; sp.based: species-based; other properties as in Figure 2. For this analysis, we used the same data as for producing Figure 2 .
Diversity 09 00030 g003
Diversity 09 00030 g004 550
Figure 4. Summary of typical processes and drivers affecting island biodiversity implemented in the models with their assumed causal relationships (Table 1, columns “processes”, “focal level”, “agent level”, “investigated patterns”). Round and square boxes denote drivers and processes, respectively. The bottom row of processes represents processes usually acting on individual-/population-levels, the top row of processes metacommunity-level processes. Black boxes and text mark factors and relationships regularly integrated in models, while grey arrows stand for thus far under- or un-explored relationships. Note that authors may opt to implement models that skip certain organizational levels, for example for investigating the direct effect of isolation on extinction as predicted by the ETIB. Additional relationships not explicitly stated in the chart include rescue-effects [53] between isolation and extinction and target effects [54] from area to immigration. For clarity, these kinds of relationships have been excluded from the graphic. Furthermore, “growth” combines both birth and death processes, while “interactions” include positive, neutral and negative interactions, for example competition or trophic interactions, and “differentiation” encompasses micro-evolutionary processes, such as mutation and gene flow. For a more complete overview of processes, patterns and organizational levels, the reader may refer to Figure 5.
Figure 4. Summary of typical processes and drivers affecting island biodiversity implemented in the models with their assumed causal relationships (Table 1, columns “processes”, “focal level”, “agent level”, “investigated patterns”). Round and square boxes denote drivers and processes, respectively. The bottom row of processes represents processes usually acting on individual-/population-levels, the top row of processes metacommunity-level processes. Black boxes and text mark factors and relationships regularly integrated in models, while grey arrows stand for thus far under- or un-explored relationships. Note that authors may opt to implement models that skip certain organizational levels, for example for investigating the direct effect of isolation on extinction as predicted by the ETIB. Additional relationships not explicitly stated in the chart include rescue-effects [53] between isolation and extinction and target effects [54] from area to immigration. For clarity, these kinds of relationships have been excluded from the graphic. Furthermore, “growth” combines both birth and death processes, while “interactions” include positive, neutral and negative interactions, for example competition or trophic interactions, and “differentiation” encompasses micro-evolutionary processes, such as mutation and gene flow. For a more complete overview of processes, patterns and organizational levels, the reader may refer to Figure 5.
Diversity 09 00030 g004
Diversity 09 00030 g005 550
Figure 5. Representation of exemplary integrated processes and drivers in island models (bottom) and emerging variables and patterns (top). Model complexity, and thus generality [20], increases from left to right. We assume that processes and drivers add up from left to right. Thus, a given model representation includes also all processes and drivers of the less complex models to its left and is therefore also able to produce the respective patterns. Mechanisms and drivers are closely related to different theories (exemplary theories are shown in brackets at the bottom), e.g., colonization and extinction as the fundamental rates of the equilibrium theory of island biogeography (ETIB). As can be seen, some emergent patterns of more complex models are the same as the drivers for simpler models. For instance, the second model on the right produces colonization rates as an emergent pattern, which at the same time are necessary input parameters for the far left model. AE: archipelago endemics; ind.: individual. MIE: multiple island endemics; SIE: single island endemics; sp.: species; GDM: general dynamic model.
Figure 5. Representation of exemplary integrated processes and drivers in island models (bottom) and emerging variables and patterns (top). Model complexity, and thus generality [20], increases from left to right. We assume that processes and drivers add up from left to right. Thus, a given model representation includes also all processes and drivers of the less complex models to its left and is therefore also able to produce the respective patterns. Mechanisms and drivers are closely related to different theories (exemplary theories are shown in brackets at the bottom), e.g., colonization and extinction as the fundamental rates of the equilibrium theory of island biogeography (ETIB). As can be seen, some emergent patterns of more complex models are the same as the drivers for simpler models. For instance, the second model on the right produces colonization rates as an emergent pattern, which at the same time are necessary input parameters for the far left model. AE: archipelago endemics; ind.: individual. MIE: multiple island endemics; SIE: single island endemics; sp.: species; GDM: general dynamic model.
Diversity 09 00030 g005
Table
Table 1. Studies with process-based models for island biogeography. Papers are sorted chronologically. The system column also contains information on whether the model simulates a purely hypothetical (h) or real-world system (calibrated with data, r). Columns that were used for Figure 2 and Figure 3 are marked with an asterisk (*). A: archipelago; AID: area-isolation-dependency; com.: community; comp.: competition; dep.: dependent; disp.: dispersal (includes immigration for species-based models and establishment for population-based models; dist.: disturbance; div.: diversity; E: endemics; eq.: equilibrium; ETIB: equilibrium theory of island biogeography; Ev.: evolutionary processes; ext.: extinction; GDM: general dynamic model of oceanic island biogeography; I: island; ind.: individual; MA: mainland-archipelago; MI: mainland-island; mut.: mutation; No. nn.: number of non-neutral niche axes, specific to species or individuals; No. par.: minimum number of easily identifiable parameters (e.g., constants, rates); Nt.: neutral; phyl.: phylogenetic; pop.: population; repr.: reproduction; SAD: species-abundance-distribution; SAR: species-area-relationship; SHR: species-heterogeneity-relationship; SIR: species-isolation-relationship; spec.: speciation; sp.: species; Spt. exp.: spatially explicit; st/dn: static or dynamic environment; Stoc.: stochastic; th.: theory.
Table 1. Studies with process-based models for island biogeography. Papers are sorted chronologically. The system column also contains information on whether the model simulates a purely hypothetical (h) or real-world system (calibrated with data, r). Columns that were used for Figure 2 and Figure 3 are marked with an asterisk (*). A: archipelago; AID: area-isolation-dependency; com.: community; comp.: competition; dep.: dependent; disp.: dispersal (includes immigration for species-based models and establishment for population-based models; dist.: disturbance; div.: diversity; E: endemics; eq.: equilibrium; ETIB: equilibrium theory of island biogeography; Ev.: evolutionary processes; ext.: extinction; GDM: general dynamic model of oceanic island biogeography; I: island; ind.: individual; MA: mainland-archipelago; MI: mainland-island; mut.: mutation; No. nn.: number of non-neutral niche axes, specific to species or individuals; No. par.: minimum number of easily identifiable parameters (e.g., constants, rates); Nt.: neutral; phyl.: phylogenetic; pop.: population; repr.: reproduction; SAD: species-abundance-distribution; SAR: species-area-relationship; SHR: species-heterogeneity-relationship; SIR: species-isolation-relationship; spec.: speciation; sp.: species; Spt. exp.: spatially explicit; st/dn: static or dynamic environment; Stoc.: stochastic; th.: theory.
StudyYearSystem (h/r)Theoretical BackgroundProcesses (st/dn) *No. par.Stoc. *Spt. Exp. *Ev. *Nt. *No. nn. *Agent Level * Focal LevelInvestigated Patterns
Wissel and Maier [42]1992MI (h)ETIB, target effectdisp., repr., (st)7yesnonoyes0pop.com.SAR
Villa et al. [22]1992MA (h)ETIBdisp., repr., dist., (st)9yesyesnono4ind.com.SAR, eq.
Durrett and Levin [27]1996A (h)ETIBdisp., comp., spec., (st)4yesyesyesyes0sp.com.SAR
Cantrell et al. [24]1996MI (h)ETIB, Allee effectsdisp., repr., comp., (st)6noyesnono2pop.sp.trait-dep. colonization
De Blasio [41]1998MI (h)ETIBdisp., comp., (st)5yesyesnoyes0pop.com.SAR
Johnson et al. [43]2000MI (h)ETIB, genetic divergencedisp., spec., ext., divergence, (st)7nonoyesyes0pop.pop.AID of diverging lineages over time
Ricklefs and Bermingham [44]2004MI (h)[43]mut., spec., (st)6yesnoyesyes0sp.sp.SIR, divergence-dep. no. of lineages
Gavrilets and Vose [31]2007MI (h)sympatric spec.disp., sex. repr., mut., (st)6yesyesyesno5ind.com.time- & niche-dep. trait distribution
Kadmon and Allouche [33]2007MI (h)ETIB, UNTB, nichedisp., repr., ext., (st)5nononono1ind.com.SAR, SHR
Birand and Howard [38]2008A (h)[45]disp., spec., ext., (st)4yesnoyesyes0sp.com.sp.-div.-dep.E
Chen and He [46]2009MI (h)ETIBdisp., spec., ext., (st)4nonoyesyes0sp.com.rate-dep. E
Hortal et al. [47]2009MI (r)[33]disp, repr., (st)5yesnonono2ind.com.SAR, SHR
Warren [48]2010MA (h)UNTBdisp, spec., (st)6yesnoyesyes0ind.com.SIR, rate-dep. β -div.
Rosindell and Phillimore [39]2011MI (r)UNTBdisp., repr., spec., (st)5yesnoyesyes0ind.com.SAD, SAR, SIR
Lambert [49]2011MI (h)ETIB, UNTBdisp., repr., mut., (st)6yesnoyesyes0pop.com.rate-dep. SAD
Esselstyn et al. [23]2011A (r)not explicitdisp., (st)1yesyesyesyes0sp.sp.radiation history
Gravel et al. [50]2011MI (r)ETIB, trophic th.disp, ext., (st)2yesnonono1sp.com.SAR
Chen et al. [25]2011MI (h)GDM, ETIBdisp, spec., ext., (dn)12nonoyesyes0sp.com.time-dep. E & sp. richness
Avery et al. [34]2013MI (r)not explicitdisp., repr., mut., (dn)6yesnoyesyes0ind.pop.colonization history
Rosindell and Harmon [28]2013MI (h)UNTB, ETIBdisp., death, (st)6yesnonoyes0ind.com.rate-dep. SAD
Valente et al. [37]2014MI (h)GDM, ETIBdisp., spec., ext., (dn)4yesnoyesyes0sp.com.rate- & time-dep. sp. richness
Chen [51]2015MA (h)[45,46]disp., ext., spec., (st)3nonoyesyes0sp.sp.rate-dep. E & β -div.
Kessler and Shnerb [36]2015MI (h)ETIB, UNTB, Lotka-Volterradisp., repr., comp., (st)4yesnonono1pop.com.comp.-dep.com. assembly
Valente et al. [29]2015MI (r)UNTB, ETIBdisp., spec., ext., (st)6yesnoyesyes0sp.com.time-dep. phyl. rates
Borregaard et al. [26]2016I (h)GDMdisp., spec., ext., (dn)13nonoyesyes0sp.com.time-dep. SAR, SHR
Gascuel et al. [40]2016MA (h)UNTB, [39]repr., disp., spec., (st)6yesyesyesyes0ind.com.SIR, E in A
Jacquet et al. [52]2017MI (h)ETIB, trophic th.disp., ext., (st)14yesnonono1sp.com.AID of traits
Yamaguchi and Iwasa [35]2017A (h)pop. geneticsdisp., mut., (st)4yesnoyesyes0pop.pop.time-dep. SIR

Share and Cite

MDPI and ACS Style

Leidinger, L.; Cabral, J.S. Biodiversity Dynamics on Islands: Explicitly Accounting for Causality in Mechanistic Models. Diversity 2017, 9, 30. https://doi.org/10.3390/d9030030

AMA Style

Leidinger L, Cabral JS. Biodiversity Dynamics on Islands: Explicitly Accounting for Causality in Mechanistic Models. Diversity. 2017; 9(3):30. https://doi.org/10.3390/d9030030

Chicago/Turabian Style

Leidinger, Ludwig, and Juliano Sarmento Cabral. 2017. "Biodiversity Dynamics on Islands: Explicitly Accounting for Causality in Mechanistic Models" Diversity 9, no. 3: 30. https://doi.org/10.3390/d9030030

APA Style

Leidinger, L., & Cabral, J. S. (2017). Biodiversity Dynamics on Islands: Explicitly Accounting for Causality in Mechanistic Models. Diversity, 9(3), 30. https://doi.org/10.3390/d9030030

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop