Abstract
The accuracy of ten methods of scaling (Smalian, Huber, Newton, Neloïd, paraboloid, cone, paracone, cylinder, truncated cone and truncated Neloïd) was evaluated on logs of 0.5, 1, 2 and 3 m cut to different heights of 27 teak trees. For this purpose, the volumes estimated by the ten formulas were compared with real volumes obtained by the technique of xylometer. The results obtained showed that the method of Huber was more efficient to calculate the volume of logs throughout the stem when the length was 0.5 m. For the other length logs, it was also the best formula when the logs came from the base of the stem. The formulas of Newton and Smalian gave in the center and top of the stem, in the case of 1 m and 2 m logs, relatively similar results and were better than other methods of scaling. As might be expected, the dendrometric method (cylinder, paraboloid, Neloïd, cone) gave worse results regardless of the length of logs considered. With logs of 0.5, 1, 2 and 3 m long, truncated forms of cone and Neloïd could also be used without significant errors in estimating the volume of teak logs. The model scaling obtained for the entire tree expresses the logarithm of the volume against the logarithm of the diameter and the logarithm of height.
1. Introduction
The estimated volume of forest trees is fairly sensitive, despite the research and development of cubage made in the timber trade. Taking into account the commercial considerations always omnipresent, it returns to the forest manager, not a research institute, to choose the appropriate method of scaling during sales or inventory management. However, comparisons between “management” and “research” cubage are inevitable when field data, such as price per cubic meter, are used in applied research.
Indeed, wood cubage is used to determine the volume of the logs. This is very important for sale, because it is one of the essential elements of wood value. This volume is the basis of the commercial transaction between buyers and sellers of wood. It is also useful in forest management and monitoring. Finally, it is necessary for resource assessment and forest production, which contribute to evaluating strategic guidance at every level. Thus, the sustainable management of forest resources requires appropriate data collection [1]. One of the most widely used indicators is cubage. Prediction of individual volume and merchantable volume of the trunk is necessary in the management of forestry. In order to do this, sample-based inventory procedures are used, in which tree volume is determined through volumetric equations and other procedures, such as volume ratio or taper models [2]. The most widely used procedure is that of volumetric equations, usually adjusted by using data from scaling of the sample trees. In scaling, stem volume may be obtained through water displacement (xylometer), which considers the real volume, or through mathematical equations, such as Huber’s, Newton’s, Smalian’s, Hohenald’s, Pressler’s, the centroid method and Hossfeld’s equation, among others, all of which are estimative of the real volume [3,4,5]. In volumes of log calculation, there are two major sources that contribute to the total error in volume estimation [6]. First, there is the choice of the equation used in determining volume. The accuracy of a volume equation's prediction depends upon the underlying shape of the log (geometric solid). A second source of error is introduced when diameters and lengths of logs are not accurately measured.
Opinions regarding the most precise formulas for carrying out scaling differ among authors. The most widely used are Newton’s, Huber’s and Smalian’s formulas [7]. Goulding [8] and Husch et al. [9] affirm that Newton’s is the most precise formula, as it takes into account the different forms the tree stem can assume: cone, paraboloid, Neloïd and cylinder. Finger [7] highlights that the Huber and Smalian formulas are precise only when the stem resembles a paraboloid.
There is also a difference in use of formulas according to continents and countries. Huber’s formula is more used in Europe due to its accuracy, while the Smalian is preferred in the USA due to its practicality, especially if the aim is also to quantify the logs piled together [3]. In Brazil, the Smalian formula is widely used to determine tree volume and to adjust volumetric equations of different native and exotic species [10,11,12,13,14,15,16,17]. According to Machado and Figueiredo Filho [5], this is due more to practicality than to accuracy.
In Benin, the difficulty of having an appropriate cubage pushes managers to use only formulas established for tropical trees by Dawkings [18] to estimate the total volume or marketable volume. For Dawkings [18], the value of the form factor of tropical species is 0.55 to estimate the total volume and 0.70 for stem volume. These values are not consistent with the morphology of the trees in the Sudanian zone. Fonton et al. [19] noted an underestimation of about 10% of the volume four species (Isoberlinia doka, Isoberlinia tomentosa, Anogeissus leiocarpa and Daniellia oliveri) with the form factor proposed by Dawkins [18]. Consequently, sometimes significant discrepancies can be observed between the mensuration characteristics estimated and the real characteristics of the stands, hence errors in estimation and forest planning.
The study aims to evaluate the influence of the log length in determining the volume of teak trees. The choice of this species is justified by the fact that, during the past few decades, many private operators interest is more to install teak plantation, given its technological quality. According to the increase of production, Benin is currently an exporter of teak wood. Teak is, therefore, the best opportunity for producing tropical timber quality [20,21].
2. Material and Method
2.1. Study Area
The study was carried out in Savè District in central Benin (Figure 1). The district is located between 7.42 °–8.45 ° north latitude and 2.15 °–2.45 ° east longitude. It covers an area of 2,228 km2.
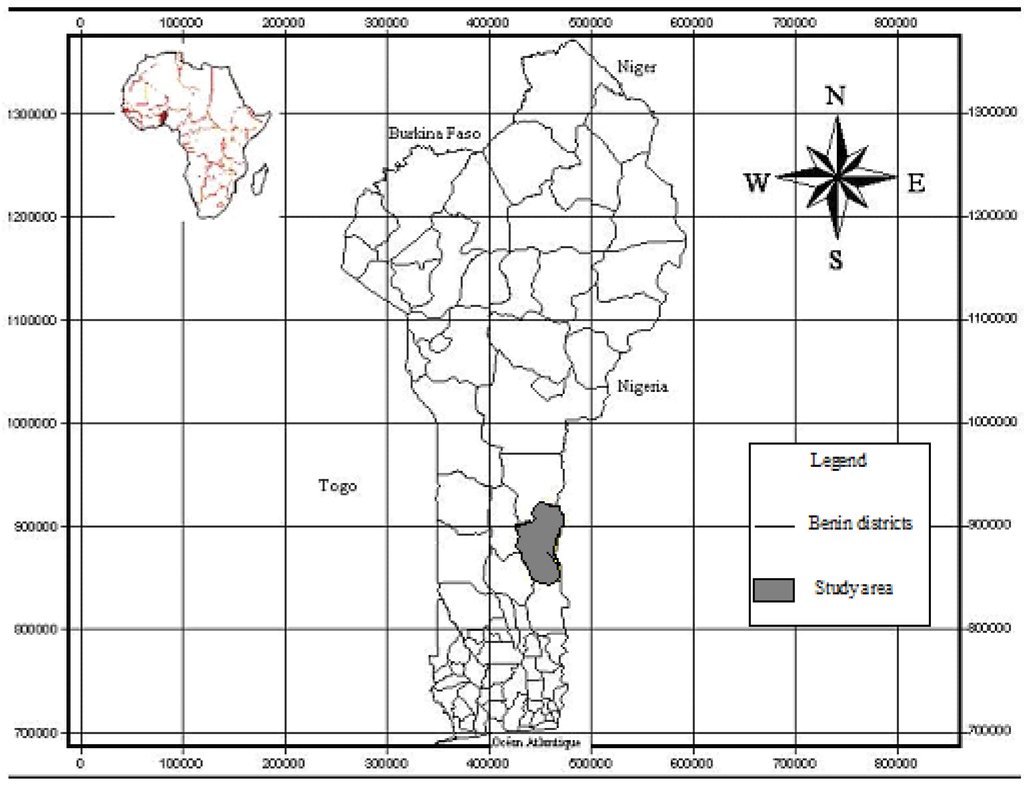
Figure 1.
Localization of the study area.
Savè District is a transition zone between the Guinean climate, with four seasons, and the Sudanian climate with two seasons. It enjoys a climate with contrasting seasons, very marked temperature fluctuations and an average annual rainfall of 1,200 mm. However, in recent years, there has been a trend towards the Sudanese type characterized by a rainy season and a dry season, with an average height of 1,100 mm of rainfall per year. The average annual temperature is 27 °C and an average relative humidity of 31% for the minimum and 98% for the maximum. Soil types are tropical ferruginous concretions of crystalline basement, or hydromorphic along the river.
2.2. Methods
2.2.1. Method of Data Collection
Determining the volume of felled trees has been studied extensively, and many formulas have been proposed by various authors. According to [4], in addition to the graphical method and the method by integration, we can distinguish in the practical point of view three techniques of scaling. The first technique assimilates trees as a solid of revolution called dendrometric type (cylinder, paraboloid, Neloïd, cone or truncated form of the last three solids). The second method involves the use of formulas expressing the tree volume according to circumferences measured on this tree at fixed heights. These formulas, however, become impractical when a high accuracy is required. In addition, the measurement of a large number of circumferences at heights determined is difficult. The third technique, which is often used, consists of dividing the log into several lengths. The volume of the different sections is then obtained by a simple formula, such as the Huber, Smalian or Newton formula [3,4,5,22]. The total volume is obviously equal to the sum of the volumes of the different sections. In this study, the approach is based on the latest technique of scaling. The real value of the volume of each log was determined by the water displacement technique (xylometer).
The data used come from three (3) plantations located in Savè District. In each of these plantations, nine (9) trees with upright trunks were randomly selected. The characteristics of the sample trees are given in Table 1.

Table 1.
Mean values and standard deviation in parentheses of trees characteristics.
| Plantations | Age | Diameter (cm) | Total height (m) | Merchantable height (m) | Bark thickness (mm) |
|---|---|---|---|---|---|
| 1 | 28 (4) | 20.32 (2.24) | 14.68 (1.20) | 9.78 (1.06) | 12.33 (1.87) |
| 2 | 29 (5) | 20.83 (1.68) | 13.78 (0.97) | 9.11 (1.27) | 12.00 (2.24) |
| 3 | 28 (5) | 22.00 (2.52) | 14.84 (0.71) | 10.20 (0.77) | 11.90 (1.55) |
2.2.2. Scaling Methods
Techniques for scaling trees are numerous, and the studies in order to compare the various methods are insufficient to clearly define a protocol for data collection [23]. If the scaling of an individual tree on the ground may seem relatively simple, it needs to respect a number of conditions for implementation. It is therefore imperative to work with rigor and a method to ensure sufficient reliability of the results.
To do this, the xylometer technique, or water displacement, which provides the real volume of each log, was used initially. Then, an estimate of each of these volumes was made by ten formulas listed in Table 2 to assess the approximation of the real volume by these formulas.
Thus, each sample tree was felled with a chainsaw and cut successively in sections of 0.5 m.
The sampling position of each log on the axis of the stem was noted. The real volume of logs of lengths of 1, 2 and 3 m were obtained by the successive addition of a volume of logs of length 0.5 m, in accordance with their position on the axis of the stem. The sampling position of logs of 1, 2 and 3 m were also noted.

Table 2.
Scaling Formulas of dendrometric types and their truncated forms.
| Scaling formulas | Volume of the solid |
|---|---|
| Cylinder | 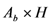 |
| Paraboloid | 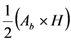 |
| Cone | 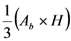 |
| Paracone | 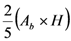 |
| Neloïd | 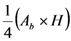 |
| Huber | 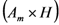 |
| Smalian | 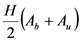 |
| Newton | 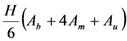 |
| Truncated cone | 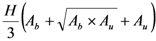 |
| Truncated Neloïd | 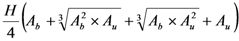 |
Note: Ab: section at the base. Au: section at the top. Am: section in the middle. H: length.
2.2.3. Xylometer Method
The objective of this work was to evaluate the accuracy of different volume equations for predicting the real volume of logs. The xylometer method has been used for this purpose to have the real volume. The method consists in immersing the logs of lengths of 0.5 m in a barrel of water to 3/4 and measuring the volume of water displaced. The increase in water level (water level increased, denoted ha) is obtained by the difference between the water level after the immersion of the logs (final water height hf) and the level of initial water (initial water depth hi). The volume of water displaced (Ve), therefore, corresponds to the real volume of the logs and is obtained by the expression:
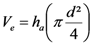 where d is the diameter of the barrel and Ve the real volume of the logs.
where d is the diameter of the barrel and Ve the real volume of the logs.
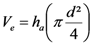
In order to minimize water loss by absorption and by friction, logs were surrounded by very thin plastic film, and after each operation, the initial level of the water was measured again prior to the introduction of another log. We assume that the teak logs immersed were not subjected to deformation relative to their initial state.
2.2.4. Scaling of the Whole Tree
Selecting a model to predict the total volume and merchantable volume of the tree was carried out by selecting the best model among the six models in Table 3. The first four are forms of linear regression and the last two non-linear regression.

Table 3.
Scaling formulas of total volume andmerchantable volume of the teak tree.
| Model | Equation |
|---|---|
| M1 | 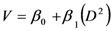 |
| M2 | 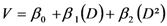 |
| M3 | 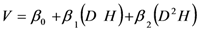 |
| M4 | 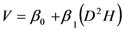 |
| M5 | 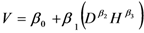 |
| M6 | 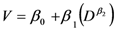 |
Note: V = volume; D = diameter at 1.30 m; H = height; β0, β1, β2 and β 3 are constants to be estimated.
2.2.5. Criteria for Evaluating Models
The influence of the length of the logs on a scaling formula is highlighted by the analysis of two fundamental criteria: systematic error committed by the use of the formula and the mean square error.
The systematic error (SE) calculated for each category of logs indicates the average difference between a real value of volume (reference volume) and is estimated by scaling formulas (volume tested). It is expressed as a percentage of the real volume:
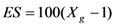 where
where 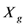 is the angular coefficient of the straight line passing through the origin and expressing the test volume according to the reference volume (the real volume):
is the angular coefficient of the straight line passing through the origin and expressing the test volume according to the reference volume (the real volume):
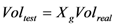
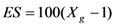
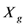 is the angular coefficient of the straight line passing through the origin and expressing the test volume according to the reference volume (the real volume):
is the angular coefficient of the straight line passing through the origin and expressing the test volume according to the reference volume (the real volume):
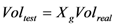
If ES is positive, the scaling formula tested gives an average volume greater than the real volume. In contrary, if ES is negative, the real volume will be greater than the average volume obtained by the scaling formula.
The Root-Mean-Squared error is the square root of the mean square error. It was calculated for each category of logs. It is obtained by the following formula:
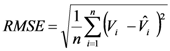 where n is the sample size (n varies according to the location of the logs on the axis of the stem. Its greatest value obtained at the base is 27 corresponding to the logs of the 27 sample trees of the study. This number decreases as one moves along the axis, because the sample trees do not have the same height.
where n is the sample size (n varies according to the location of the logs on the axis of the stem. Its greatest value obtained at the base is 27 corresponding to the logs of the 27 sample trees of the study. This number decreases as one moves along the axis, because the sample trees do not have the same height. 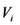 , the real volume of logs i at position i of the stem i and,
, the real volume of logs i at position i of the stem i and, 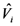 , its estimate by one of the formulas.
, its estimate by one of the formulas.
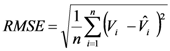
 , the real volume of logs i at position i of the stem i and,
, the real volume of logs i at position i of the stem i and,  , its estimate by one of the formulas.
, its estimate by one of the formulas. Volume equations for whole tree are compared on the basis of the residual variance and the adjusted coefficient of determination.
3. Results
3.1. Comparison of Scaling Formulas
The analysis of Table 4 shows that cone, Neloïd, paraboloid and paracone formulas have negative biases, while cylinder, Huber, truncated Neloïd, Newton, Smalian and truncated cone formulas give, in most cases, a positive bias. A negative bias leads to an underestimation of the real value of volume, while a positive bias leads instead to an overestimation of the real volume. It follows that cone, Neloïd, paraboloid and paracone formulas underestimate the real volume, while cylinder, Huber, truncated Neloïd, Newton, Smalian and truncated cone formulas overestimate this value. Error is more important in the formulas that underestimate the volume value than those that overestimate. For example, for logs of 0.5 m, the negative bias reaches 64.9% in the case of the cone formula, 73.7% in the case of Neloïd, 47.4% in the case of paraboloid and 57.9% in the case of paracone. The maximum value of positive bias is 10% for the cylinder method, 3% for the Huber’s method and Newton's methods and 4% for truncated Neloïd, Smalian and truncated cone methods. Thus, the assumption of conical logs, Neloïd logs or paraboloid logs does not prove accurate for estimating the volume of logs of 0.5 m, because it underestimates about 50% the volume of these logs.
It is a result from Table 5 that regardless of the level of the log collection, the squared error increases as the length of the logs increases. For the cone formula, for example, it is 8.6 for logs of 0.5 m, 17.57 for logs of 1 m and 43.52 of logs of 3 m.
For a given length of logs, the error decreases as the level increases on the axis of the stem. For example, the cone formula error is 8.6 when the position is 3 m, and it decreases to 3.64 when the log is removed from 6 m and 0.73 when the log is removed from 9 m to the axis of the stem.
The comparison of the formulas shows that Huber’s formula gives, in most cases, the best results, with low quadratic error ranging between 0.21 and 7.45. It is followed by Newton's formula, with a range of 0.21 to 10.4. Cone, cylinder and Neloïd formulas exhibit, instead, the greatest bias. Maximum values are 43.52, 73.48 and 57.67 respectively for the cone, cylinder and Neloïd formulas.

Table 4.
Mean values of the systematic error (SE) by sampling height and length of the logs for different methods of scaling.
| Log length (m) | Stem height (m) | Scaling formula | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cone | Cylinder | Huber | Neloïd | Truncated Neloïd | Newton | Paraboloid | Smalian | Truncated cone | Paracone | ||
| 0.5 | 3 | -64.9 | 5.0 | 1.0 | -73.7 | 2.0 | 1.0 | -47.4 | 2.0 | 2.0 | -57.9 |
| 6 | -63.2 | 10.0 | 3.0 | -72.4 | 4.0 | 3.0 | -44.8 | 4.0 | 4.0 | -55.9 | |
| 9 | -64.6 | 6.0 | -0.6 | -73.4 | -0.3 | -0.4 | -46.9 | -0.1 | -0.3 | -57.5 | |
| 1 | 3 | -63.0 | 11.0 | 0.0 | -72.3 | 2.0 | 1.0 | -44.5 | 2.0 | 2.0 | -55.6 |
| 6 | -62.1 | 14.0 | 7.0 | -71.5 | 4.0 | 6.0 | -43.1 | 4.0 | 4.0 | -54.5 | |
| 9 | -60.7 | 18.0 | 8.0 | -70.5 | 8.0 | 8.0 | -41.1 | 9.0 | 8.0 | -52.9 | |
| 3 | 3 | -42.9 | 71.0 | 1.0 | -57.2 | 20.0 | 9.0 | -14.4 | 24.0 | 21.0 | -31.5 |
| 6 | -56.2 | 31.0 | 2.0 | -67.1 | 3.0 | 3.0 | -34.3 | 5.0 | 3.0 | -47.4 | |
| 9 | -53.9 | 38.0 | 10.0 | -65.4 | 0.0 | 8.0 | -30.9 | 3.0 | 1.0 | -44.7 | |

Table 5.
Mean values of the root mean square error (RMSE) by sampling height and length of the ridge of different methods of scaling.
| Log length (m) | Stem height (m) | Scaling formula | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cone | Cylinder | Huber | Neloïd | Truncated Neloïd | Newton | Paraboloid | Smalian | Truncated cone | Paracone | ||
| 0.5 | 3 | 8.6 0 | 1.59 | 0.24 | 9.75 | 0.92 | 0.37 | 6.31 | 0.93 | 0.92 | 7.68 |
| 6 | 4.96 | 1.82 | 0.38 | 5.66 | 1.08 | 0.49 | 3.59 | 1.12 | 1.09 | 4.4 0 | |
| 9 | 2.91 | 0.62 | 0.21 | 3.31 | 0.49 | 0.21 | 2.13 | 0.49 | 0.49 | 2.6 0 | |
| 1 | 3 | 17.57 | 4. 00 | 1.47 | 20.14 | 1.58 | 1.18 | 12.47 | 1.61 | 1.59 | 15.52 |
| 6 | 10.14 | 5.01 | 2.58 | 11.62 | 2.91 | 2.01 | 7.32 | 3.05 | 2.94 | 8.98 | |
| 9 | 4.82 | 1.89 | 0.93 | 5.59 | 1.36 | 1.04 | 3.31 | 1.36 | 1.36 | 4.21 | |
| 3 | 3 | 43.52 | 73.48 | 7.45 | 57.67 | 22.45 | 10.4 0 | 16.61 | 26.48 | 23.45 | 32.36 |
| 6 | 33.41 | 21.27 | 5.82 | 39.79 | 6.5 0 | 4.41 | 20.92 | 7.03 | 6.62 | 28.35 | |
| 9 | 19.94 | 15.18 | 6.47 | 24.13 | 3. 00 | 4.63 | 11.71 | 3.18 | 2.98 | 16.61 | |
As an illustration, the Figure 2, Figure 3 show the trend of the mean square error and systematic error along the axis of the stem of the different formulas. These figures confirm the various findings, as noted above.
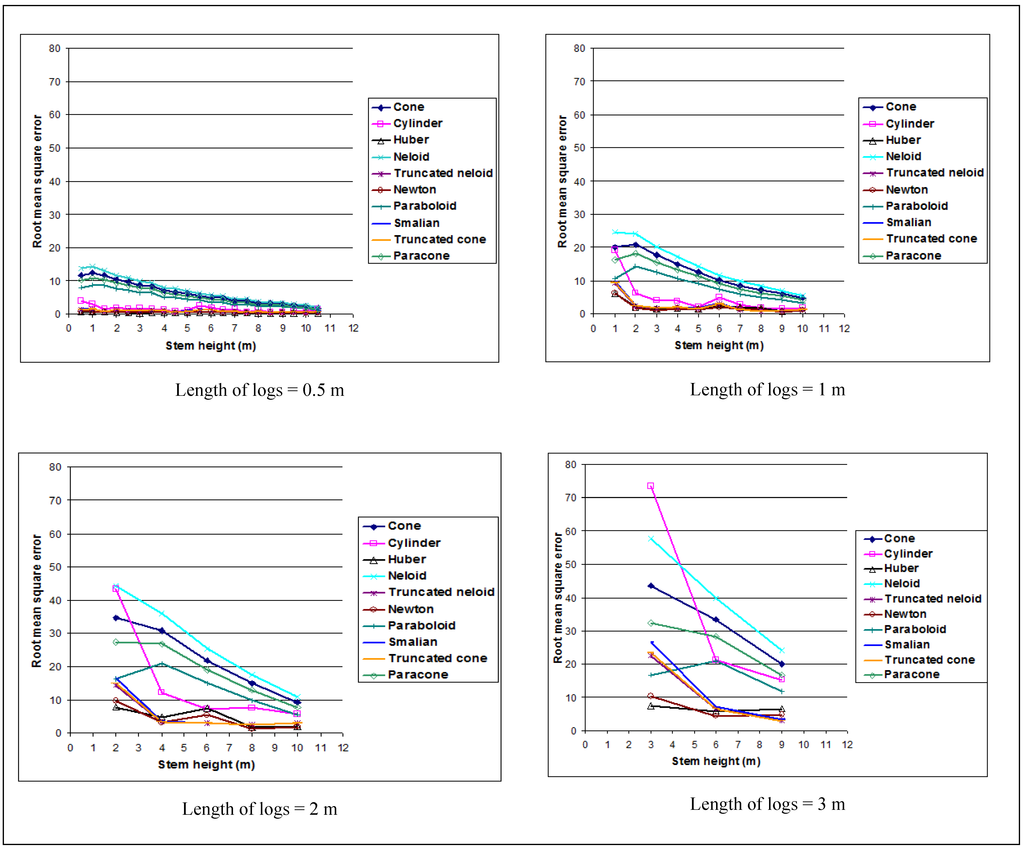
Figure 2.
Trend of the mean squared error along the stem.
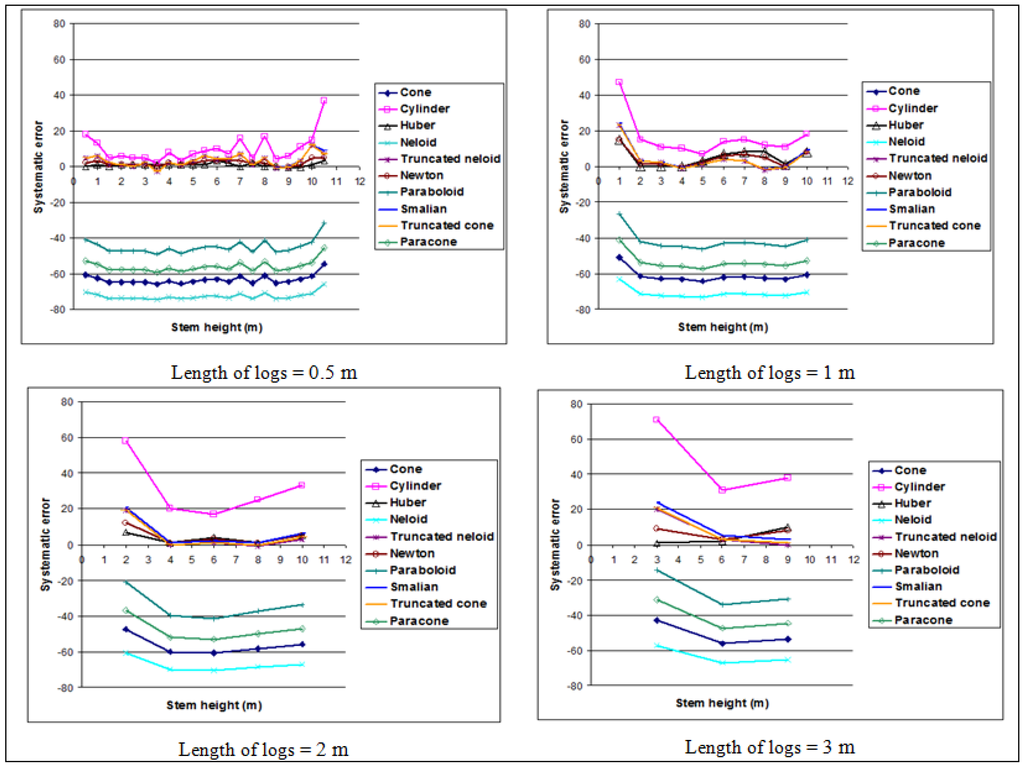
Figure 3.
Trend of the systematic error along the stem.
The analysis of the overall results allows a synthesis of the best volume equations based on the length of the logs and position on the stem shown in Table 6. This synthesis shows that the Huber formula has the lowest values of the squared error and systematic error along the stem of the tree for logs of 0.5 m. It is also suitable for scaling the base of the stem to a cutting height of 4 m in the case of logs of 1 m, at the first cut (first two meters of the stem) for logs of 2 m and three meters for logs of 3 m; while Newton’s formula is suitable for scaling logs of 1 m from the center to the top (stem portion between 4 m and 10 m). It is also suitable for scaling logs of 2 m taken at 2 m and 10 m. Finally, it is also suitable for logs of 3 m taken from the center (3 m and 6 m) on the axis of the stem. For the logs of 3 m taken at the top (6 to 9 m) of the stem, the formula of the truncated cone is more appropriate.

Table 6.
Improved formula scaling according to the length of the logs and cutting level.
| Length of the logs (m) | Stem height (m) | ||
|---|---|---|---|
| low | center | top | |
| 0.5 | Huber | Huber | Huber |
| 1 | Huber | Newton | Newton |
| 2 | Huber | Newton | Newton |
| 3 | Huber | Newton | truncated cone |
3.2. Estimate of Tree Volume
The best model for predicting the total and merchantable volume of the tree was chosen from the models presented above. In view of the results (Table 7), it appears that the best model for prediction of the total volume and the merchantable volume is the M5 model, as it has in each case the lowest value of the residual error and the highest value of the adjusted coefficient of determination.
The graphical analysis of the residuals against the predicted values showed that the assumption of homogeneity of variance is observed. Under these conditions, the prediction equations are:
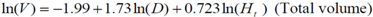 and
and
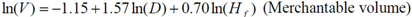
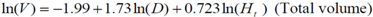
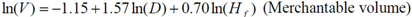

Table 7.
Models for estimating the total volume and the merchantable volume.
| Volume | Model | s | Adjusted R2 | |
|---|---|---|---|---|
| Total and merchantable | M1 | 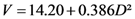 | 21.522 | 74.00 |
| M2 | 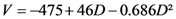 | 21.043 | 75.10 | |
| M6 | 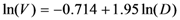 | 0.111 | 76.80 | |
| Total | M3 | 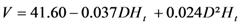 | 20.735 | 75.80 |
| M4 | 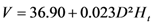 | 20.319 | 76.80 | |
| M5 | 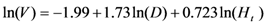 | 0.101 | 80.70 | |
| Merchantable | M3 | 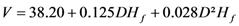 | 17.322 | 83.10 |
| M4 | 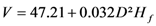 | 17.000 | 83.75 | |
| M5 | 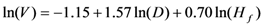 | 0.084 | 86.70 | |
In these relations, V is the volume, D is the diameter at breast height, Ht total height and Hf bole height.
4. Discussions
In the literature, many approaches are used to determine the real volume value of logs. In this study, the approach is based on the scaling technique of dividing the stem into several logs section of 0.5 m and determining the real volume of logs by the xylometer technique. The advantage of this approach is to have a high accuracy of the real volume value in contrast to the approach of estimating the volume by the simple scaling formulas, e.g., Huber, Smalian or Newton formulas proposed by [3,4,5,22]. Bigin [6] mentioned that if volume is being determined via water displacement, there can be other sources of measurement error if water adheres to the log. The use of plastic film can minimize this source of error.
Huber’s formula has the lowest values of the squared error and systematic error along the stem of the tree for logs of 0.5 m. It adapts to the length of logs of 1, 2 and 3 m from the base of the stem (stem height less than or equal to 4 m). Beyond this height (stem height greater than 4 m), the formulas of Newton, truncated cone and Smalian are more precise for logs of 1 m, and Newton’s formula is suitable for logs of 2 m. For logs of 3 m, Newton's formula is suitable for logs in the center of the stem (3 to 6 m) and the truncated cone formula bolts at the top of the stem (6 to 9 m). Similar results were obtained by other authors, including [24], comparing the accuracy of different volume equations on Pinus elliottii trees, believes that Huber’s formula is more efficient than other approaches for estimating the volume of any length of ridge considered. These authors also noted that Huber's formula is the formula most accurate on several species, whatever the age of the trees and geographic region.
Fonton et al. [19] mentioned the hypothesis of the succession of truncated cones along the stem of four species (Isoberlinia doka, Isoberlinia tomentosa, Anogeissus leiocarpa and Daniellia oliveri) and think that it is more reasonable, because it is less dependent on the length of the logs and more suited to the general taper of a tree [25,26,27].
Whatever the length of the log, mean square error decreases from the bottom to the top of the stem. Altherr [28] also showed in a study of 15,000 trees the influence of the length of the logs. He finds that the use of logs of 2 m along the stem leads to a systematic error of 1%, compared to the volume obtained for logs of 1 m. He also demonstrates that the error focuses on the first five meters of the trunk, while it is almost zero for the central part of the stem and very low for the last five meters. This fact can be explained by the irregularities of the stem, which are larger at the base than the upper end of the shaft. These irregularities can be explained by the plantation regime and type of thinning performed. Indeed, the plantations from which come the trees of the present study Huber are coppice and the type of thinning is selective. The results of research on pre-commercial and commercial thinning demonstrated the relationship between crown length and stem taper. Barbour et al. [29] found in red spruce (Picea rubens Sarg.), following a pre-commercial thinning conducted in Nova Scotia fifteen years ago, that the crown was longer and that higher stems taper in thinned stands. According to Thomson and Barclay [30], a strong commercial thinning reduces pruning at the base of the crown. After treatment, more light can enter in the stand, and lower branches remain active for photosynthesis. This results in a slower crown recession in individual trees of thinned stands. The radial growth in the lower part of the stem is therefore increased, since the auxin fall faster across the stem, resulting in a greater scroll [31]. Newnham [32] also observed that when the cover is released, the stem have a form, which is closer to a cone or Neloïd form, due to a more pronounced extension of the crown.
According to Viens [33], four hypotheses can be used to explain the differences in the shape and distribution of growth on the stem. One hypothesis, which is connected to a mechanical compensation order, has been described by [34]. It states that the external mechanical stress tends to alter and change the shape of the stem.
Two mechanical forces influence the straightness of a stem [34]. The first is the vertical force, which is the weight of the stem itself plus the weight of snow and ice. The second is the horizontal force imposed by the wind. Therefore, the greatest growth observed at the base of the stem of trees from thinned stands may be due to increased wind penetration in the canopy and lower mutual support of the stems, which leads to the formation of the reaction wood [33].
A second hypothesis relates to the conductivity of the water [34,35]. Assuming that the shape of the stem is a response to the needs of the hydraulic tree, thinning causes a rise of the surface conduction of the water in the non-leaves of the rod, due to an increase in photosynthetic activity and transpiration.
The third hypothesis, posed by Pressler, offers another explanation of the changes of form caused by thinning [34]. This assumption is based only on the fact that radial growth is connected to the leaf biomass. He mentioned that the radial growth at a location on the stem is a function of leaf biomass present above this point. Also, the point where the maximum radial growth is to be located lower on the stem of trees treated as thinning induces a decrease in the height of the crown base.
Finally, the changes of form after thinning would not necessarily be due to a change in tree growth, but may be caused by the morphology of residual trees. For example, at a low thinning, the dominant trees are preserved, which artificially increases the average scroll of the stem [34]. A strong low thinning will therefore select trees with a scroll larger than lower thinning [34].
Models expressing the volume as a function of the square of the diameter are most relevant for estimating the volume of individual trees [27,36,37,38]. However, the models obtained for scaling the entire tree in this study express the logarithm of the volume (total and merchantable volume) according to the logarithm of the diameter and height. These models have the best fit parameters (residual error and adjusted coefficient of determination).
5. Conclusion
The present study has evaluated the influence of the length of logs on different volume equations by the water displacement method. It follows from the results that the length of the logs has a different effect on the volume equations. The longer the log, the larger the volume estimation error. Moreover, regardless of the length of the logs, the mean squared error decreases from the bottom to the top of the stem. Among the formulas compared, Huber’s formula is best suited to logs of 0.5 m along the stem and for logs of 1, 2 and 3 m derived at the base of the stem. For these three last categories of logs, Newton, truncated cone and Smalian formulas are more accurate for the rest of the axis of the stem. The results obtained allow loggers to have more appropriate equations for estimating the volume of teak trees.
References
- Akinsanmi, F.A.; Akindele, S.O. Teak productivity in relation to soil conditions: A re-assessment of teak plantations in the dry high forest area of south-western Nigeria. Nigerian J. For. 1995, 24 & 25, 7–10. [Google Scholar]
- Campos, J.C.C.; Leite, H.G. Mensuração Florestal: Perguntas e Respostas, 2nd ed; Viçosa: Editora UFV, 2009; p. 542. [Google Scholar]
- Loëtsch, F.; Zoöhrer, F.; Haller, K.E. Forest inventory, 2nd ed; BLV: Verlagsgesellschaft, Munich, 1973; pp. 1–469. [Google Scholar]
- Palm, R. Comparaison de méthodes de cubage d’arbres abattus. R.F.F. 1976, 28, 48–54. [Google Scholar] [CrossRef]
- Machado, S.A.; Figueiredo Filho, A. Dendrometria, 1st ed; Edição dos autores: Curitiba, Brasil, 2003; pp. 1–309. [Google Scholar]
- Bigin, G.S. Estimating the accuracy of volume equations using taper equations of stem profile. Can. J. For. Res. 1988, 18, 1002–1007. [Google Scholar] [CrossRef]
- Finger, C.A.G. Fundamentos de biometria florestal; UFSM/CEPEF/FATEC: Santa Maria, Brazil, 1992; pp. 1–269. [Google Scholar]
- Goulding, C.J. Cubic spline curves and calculation of volume of sectionally measured trees. New Zeal. J. For. Sci. 1979, 9, 89–99. [Google Scholar]
- Husch, B.; Miller, C.I.; Beers, T.W. Forest Mensuration, 2nd ed; J. Willey: New York, NY, USA, 1982; pp. 1–398. [Google Scholar]
- Machado, S.A.; Mello, J.M.; Barros, D.A. Comparação entre métodos para a avaliação de volume total de madeira por unidade de área. para o Pinheiro do Paraná. na Região Sul do Brasil. (in Portuguese). Cerne 2000, 6, 55–66. [Google Scholar]
- Machado, S.A.; Conceição, M.B.; Figueiredo, D.J. Modelagem do volume individual para diferentes idades e regimes de desbaste em plantações de Pinus oocarpa. (in Portuguese). Ciências Exatas e Naturais 2002, 4, 185–196. [Google Scholar]
- Machado, S.A.; Téo, S.J.; Urbano, E.; Figura, M.A.; Silva, L.C.R. Comparação de métodos de cubagem absolutos com o volume obtido pelo xilômetro para Bracatinga (Mimosa scabrella Bentham). (in Portuguese). Cerne 2006, 12, 239–253. [Google Scholar]
- Ribeiro, C.A.S.; Silva, J.A.A.; Ferreira, R.L.C.; Meunier, I.M.J.; Ferraz, I. Seleção de modelos volumétricos para Leucena no agreste do estado de Pernambuco. (in Portuguese). Brasil Florestal 2001, 20, 37–45. [Google Scholar]
- Schneider, P.R.; Tonini, H. Utilização de variáveis dummy em equações de volume para Acácia mearnsii. (in Portuguese). Ciência Florestal 2003, 13, 121–129. [Google Scholar]
- Silva, J.A.A.; Paula Neto, F.; Brandi, R.M. Análise de modelos volumétricos para a construção de tabelas de volume comercial para Eucalyptus spp.. segundo a espécie. região e método de regeneração. (in Portuguese). Revista Árvore 1978, 2, 86–89. [Google Scholar]
- Soares, C.P.B.; Paula Neto, F. Determinação do tamanho da amostra em um inventário volumétrico e de biomassa de troncos. (in Portuguese). Revista Ceres. 1997, 44, 142–151. [Google Scholar]
- Tonini, H.; Arco-Verde, M.F.; Sá, S.P.P. Dendrometria de espécies nativas em plantios homogêneos no estado de Roraima – Andiroba (Carapa guianensis Aubl). Castanha-do-Brasil (Bertholletia excelsa Bonpl.). Ipê-roxo (Tabebuia avellanedae Lorentz ex Griseb) e Jatobá (Hymenaea courbaril L.). (in Portuguese). Acta Amazônica 2005, 35, 353–362. [Google Scholar]
- Dawkings, H.C. Estimating total volume of some Caribbean trees. Caribb For. 1961, 22, 62–63. [Google Scholar]
- Fonton, N.H.; Yabi, C.C.; Dah-Dovonon, J.Z.; Adoko, F.K.; Dotchamou, T. Modélisation du volume du fût d'arbre pour une gestion durable des écosystèmes forestiers soudaniens. (in French). Bois et Forêt des Tropiques 2009, 300, 95–100. [Google Scholar]
- Keogh, R.M. Teak 2000: a consortium support for greatly increasing the contribution of quality tropical hardwood plantations to sustainable development. International Institute for Environment and Development (IIED): London, UK, 1996. [Google Scholar]
- FAO. Le teck. Unasylva 2000, 201, 1–65.
- Soares, C.P.B.; Paula Neto, F.; SOUZA, A.L. Dendrometria e Inventário Florestal; (in Portuguese). MG: Universidade Federal de Viçosa, Viçosa, 2006; pp. 1–276. [Google Scholar]
- Palm, R. Contribution méthodologique au cubage des arbres et à la construction de tables de cubage et d’assortiments. (in French). Thèse de doctorat, Faculté des Sciences Agronomiques de l'Etat Gembloux: Belgique, 1981; pp. 1–295. [Google Scholar]
- Afonso, F.F.; Sebastião, A.M.; Maurício, R.A.C. Testing accuracy of log volume calculation procedures against water displacement technique (xylometer). Can. J. For. Res. 2000, 30, 990–997. [Google Scholar] [CrossRef]
- Palm, R. Influence de la formule de cubage et de la longueur des billons sur la détermination du volume des arbres abattus. (in French). Anales des Sciences Forestières 1982, 39, 231–238. [Google Scholar] [CrossRef]
- Pauwels, D.; Rondeux, J. Tarifs de cubage pour les petits bois de Mélèze (Larix sp.) en Ardenne. (in French). Available online: http://orbi.ulg.ac.be/handle/2268/96128/ (accessed on 26 February 2013).
- Thibaut, A.; Rondeux, J.; Claessens, H. Tarifs de cubage pour l'Aulne Glutineux (Alnus glutineux (L.) Gaertn.) en Belgique Méridionale. (in French). Rev. For. Fr. 1998, 50, 244–250. [Google Scholar] [CrossRef]
- Altherr, E. Die Genauigkeit verschiedener Verfahren der Sektionierung in absoluten und relativen Schaftlàngen. Allg. Forst- und Jagdztg 1960, 131, 226–236. [Google Scholar]
- Barbour, R.J.; Fayle, D.C.F.; Chauret, G.; Cook, J.; Karsh, M.B.; Ran, S. Breastheight relative density and radial growth in mature jack pine (Pinus banksiarza) for 38 years after thinning. Can. J. For. Res. 1994, 24, 2439–2447. [Google Scholar] [CrossRef]
- Thomson, A.J.; Barclay, H.J. Effects of thinning and urea fertilization on the distribution of the area increment dong the boles of Douglas-fir at Shawnigan Lake, British Colombia. Can. For. Res. 1984, 14, 879–884. [Google Scholar] [CrossRef]
- Jozsa, L.A.; Middleton, G.R. Les Caractéristiques Déterminant La Qualité Du Bois: Nature et Conséquences Pratiques; (in French). Forintek Canada Corp, 1997; pp. 1–42. [Google Scholar]
- Newnham, R.M. Stem form and the variation of taper with age and thinning regime. Forestry 1965, 38, 218–224. [Google Scholar] [CrossRef]
- Viens, E. Effets de l'éclaircie commerciale sur la croissance et la forme de la tige du pin gris (Prm banksuna LM) en Abiti, Québec. (in French). Mémoire de Maîtrise en Ressources Renouvelables, Université du Québec à Chicoutimi, Bibliothèque National de Canada: Québec, Canada, 2001; pp. 1–63. [Google Scholar]
- Larson, P.R. Stem form development of forest trees. In Forest Science; Society of American Foresters: Washington, DC, USA, 1963; pp. 1–42, Monograph 5. [Google Scholar]
- Shinozaki, K.; Yoda, K.; Hozowi, K.; Kira, T. A quantitative analysis of form-The pipe mode1 theory 1-Basic analysis. Jpn. J. Ecol. 1964, 14, 97–105. [Google Scholar]
- Rondeux, J. La Mesure Des Arbres Et Des Peuplements Forestiers; (in French). Presses agronomiques de Gembloux: Gembloux, Belgique, 1999; pp. 1–521. [Google Scholar]
- Laumans, P. Tables de cubage à deux entrées pour le volume bois sciable du Teck (Tectona grandis L. f.) au Sud Bénin. Wittelsbacherstr 11, D-8016 Feldkirchen, 1991; pp. 11–18. [Google Scholar]
- Fonton, N.H.; Glele Kakaï, R.; Rondeux, J. Étude dendrométrique de Acacia auriculiformis A. Cunn ex Benth en mélange sur vertisol au Bénin. Biotechnologie. (in French). Agronomie. Société et Environnement 2002, 6, 29–37. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).