1. Introduction
Plant community phylogenetic diversity, including Faith’s phylogenetic diversity, mean pairwise distance, and mean nearest taxon distance, represents the cumulative branch length of species within a community on a phylogenetic tree [
1], serving as a crucial complement to traditional species diversity metrics. In the context of rangeland conservation, phylogenetic diversity provides unique insights into the evolutionary resilience of ecosystems under anthropogenic pressures like grazing and fencing—key management strategies for sustainable pastoralism. Compared with traditional indicators that focus merely on the number of species, phylogenetic diversity provides insights into the evolutionary heterogeneity and functional potential of species within a community. It offers distinct advantages in elucidating the mechanisms of community assembly, ecological processes, and ecosystem functioning [
2]. Phylogenetic diversity also plays a crucial role in key conservation [
3] and restoration efforts [
4], including the identification of priority areas for biodiversity protection and the evaluation of ecological restoration outcomes. Specifically for alpine rangelands, which cover 40% of the Qinghai-Tibet Plateau and face escalating climate and land-use pressures, phylogenetic metrics are critical for assessing conservation priorities under contrasting management regimes. Therefore, investigating the phylogenetic diversity of plant communities not only enhances our understanding of the underlying mechanisms governing community assembly and functional stability, but also offers theoretical foundations and decision support frameworks for ecological conservation, restoration management, and global change research.
Recently, advancements in ecological modeling and data science have led to the widespread application of model simulation techniques in the study of phylogenetic diversity [
5,
6]. Our focus on alpine grasslands—a system where grazing exclusion (fencing) and traditional pastoralism create stark ecological contrasts—necessitates modeling approaches capable of capturing these management-driven phylogenetic patterns. For example, early studies predominantly employed conventional statistical methods—such as multiple linear regression, generalized linear models, and redundancy analysis—to investigate the relationships between phylogenetic diversity and environmental variables (e.g., climate, hydrology, soil properties, and land use patterns) [
7]. Although these models offer strong explanatory power and interpretability, they have limited capacity to capture nonlinear relationships and variable interactions, which restricts their effectiveness in handling high-dimensional and heterogeneous data from complex ecosystems. Furthermore, with advances in spatial ecological modeling, species distribution models, such as MaxEnt, BIOMOD, and ecological niche models, have increasingly been applied to spatial prediction studies of phylogenetic diversity [
8]. These approaches infer the geographic patterns of phylogenetic diversity based on species’ spatial distribution data [
9]. However, these models are usually established at the species level, neglecting the direct modeling ability of phylogenetic relationships among species within communities.
The choice to model phylogenetic (rather than functional or taxonomic) diversity stems from its unique capacity to (1) reflect deep evolutionary legacies that constrain community responses to management; (2) provide proxy measures of unmeasured functional traits via phylogenetic signal; and (3) identify conservation priorities for evolutionarily distinct lineages. Recently, machine learning models like random forests, XGBoost, SVMs, and ANNs have become widely used in phylogenetic diversity studies due to their ability to handle complex ecological data, model nonlinear relationships, and assess variable importance. For example, Cadotte et al. (2017) proposed that ensemble learning methods can effectively assess the impacts of ecological processes, such as environmental filtering and competitive interactions, on phylogenetic diversity [
10]. In recent decades, numerous studies have increasingly sought to integrate multiple algorithms to enhance the robustness of predictive models [
11]. Despite continuous advancements in model simulation technology, research on plant community phylogenetic diversity still faces several challenges as follows: firstly, the lack of high-resolution and comprehensive phylogenetic tree data; secondly, inconsistent applicability of various algorithms to community-scale phylogenetic structure indices, such as PD, MPD, and MNTD; thirdly, alpine grasslands exhibit high climate sensitivity [
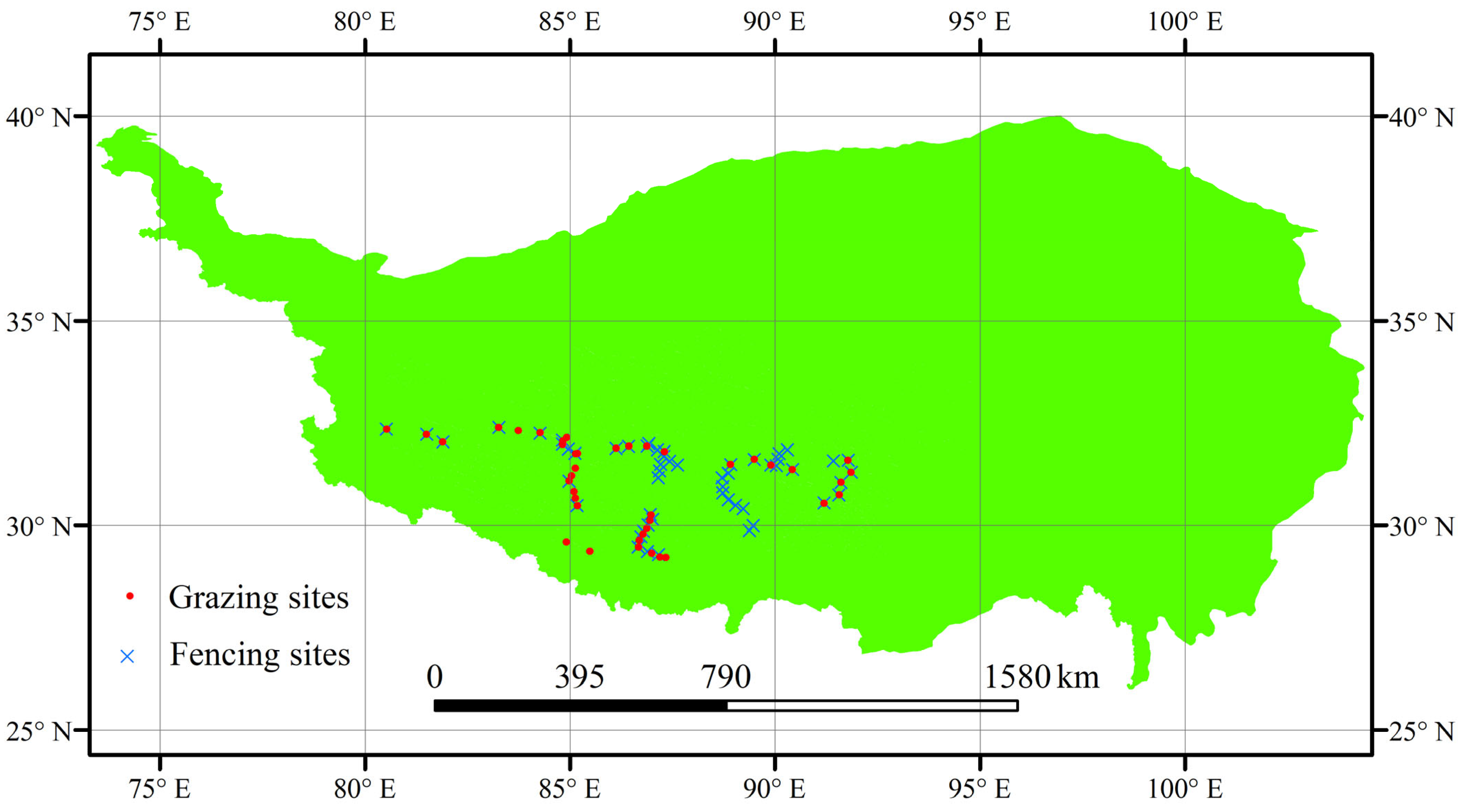
12], and the mechanisms underlying changes in their phylogenetic diversity are complex. Our study specifically targets the Qinghai-Tibet Plateau’s Stipa-Carex-Kobresia dominated ecosystems (28–38° N, 80–100° E; 3000–5000 m elevation), where grazing/fencing contrasts create natural laboratories for testing model performance under real-world conservation scenarios. Therefore, a comprehensive analysis of the response characteristics of plant community phylogenetic diversity under various management scenarios—such as fencing and grazing—in alpine grasslands is essential for elucidating the mechanisms underlying grassland community assembly, maintaining ecological functions, and developing sustainable management strategies.
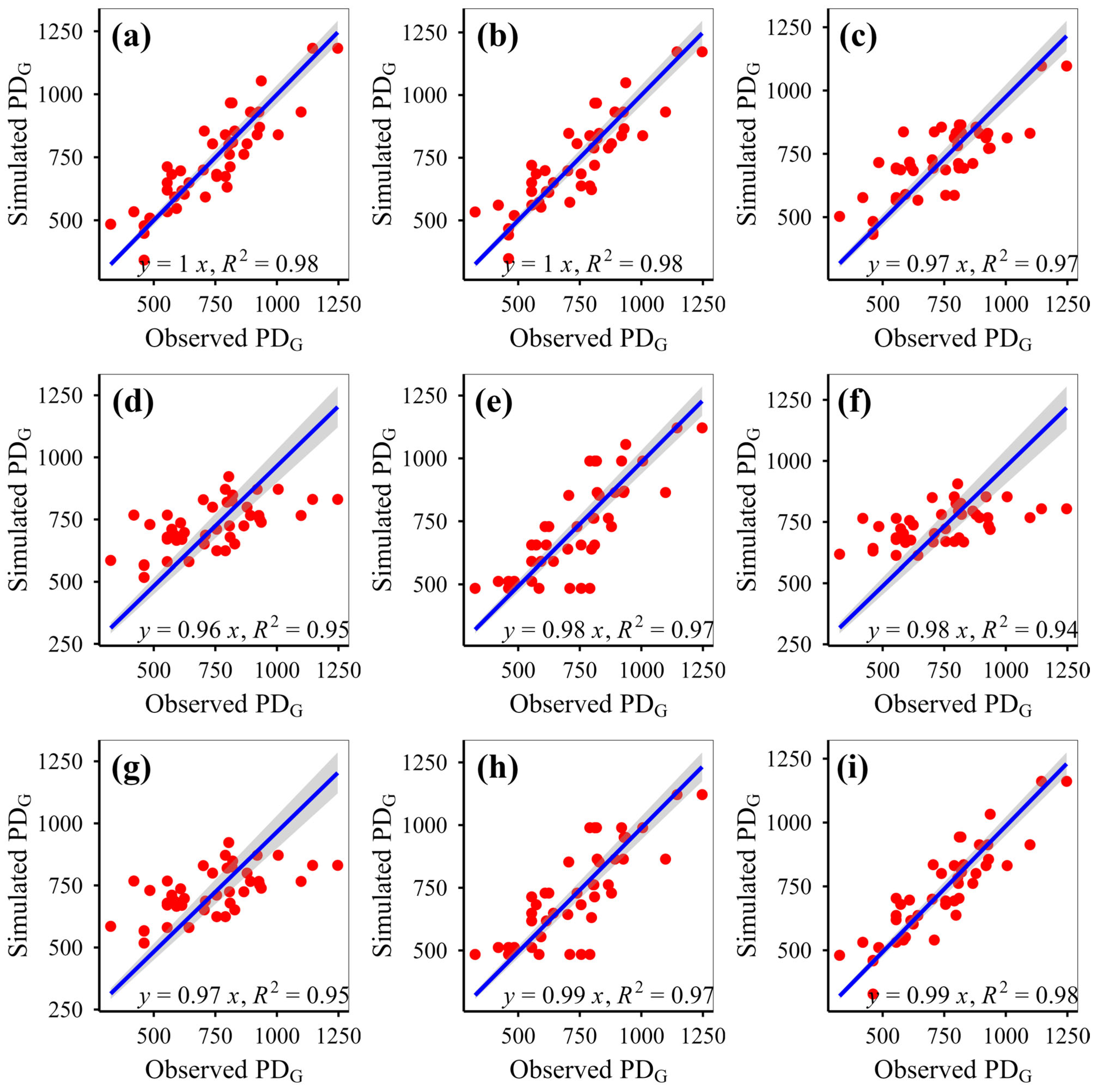
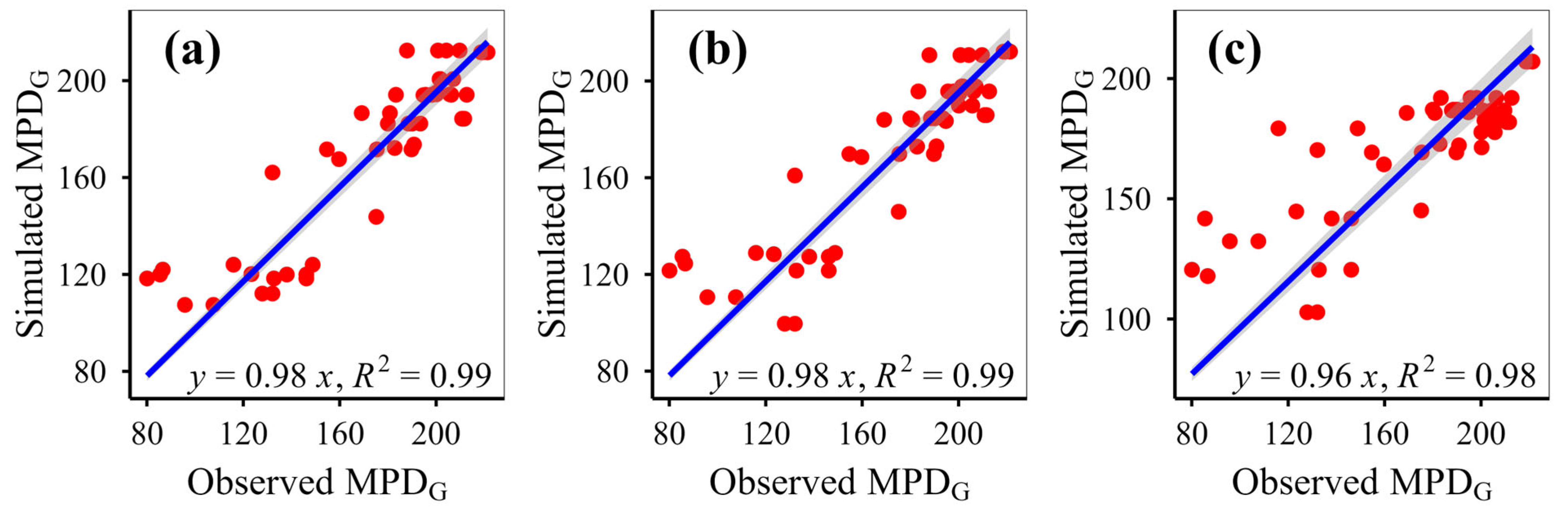
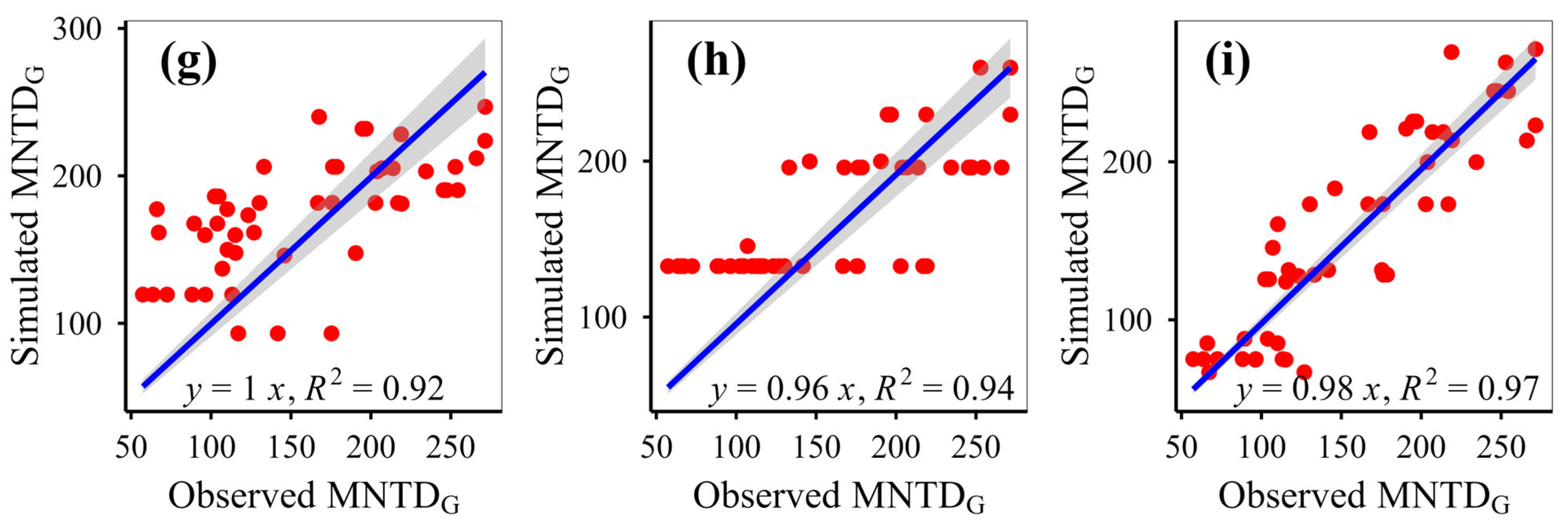
In this study, the metrics of plant community phylogenetic diversity—including phylogenetic diversity (PD), mean pairwise distance (MPD), and mean nearest taxon distance (MNTD)—were computed using remote sensing and climatic variables such as the normalized difference vegetation index, temperature, precipitation, and solar radiation. These computations were carried out employing nine data mining techniques: random forest, generalized boosted regression, support vector machine, multiple linear regression, recursive regression tree, artificial neural network, generalized linear regression, conditional inference tree, and extreme gradient boosting. The central aim of this research was to assess and compare the predictive accuracy of these modeling approaches in estimating plant community phylogenetic diversity under contrasting rangeland management strategies, thereby bridging the gap between computational ecology and practical conservation decision making.
5. Conclusions
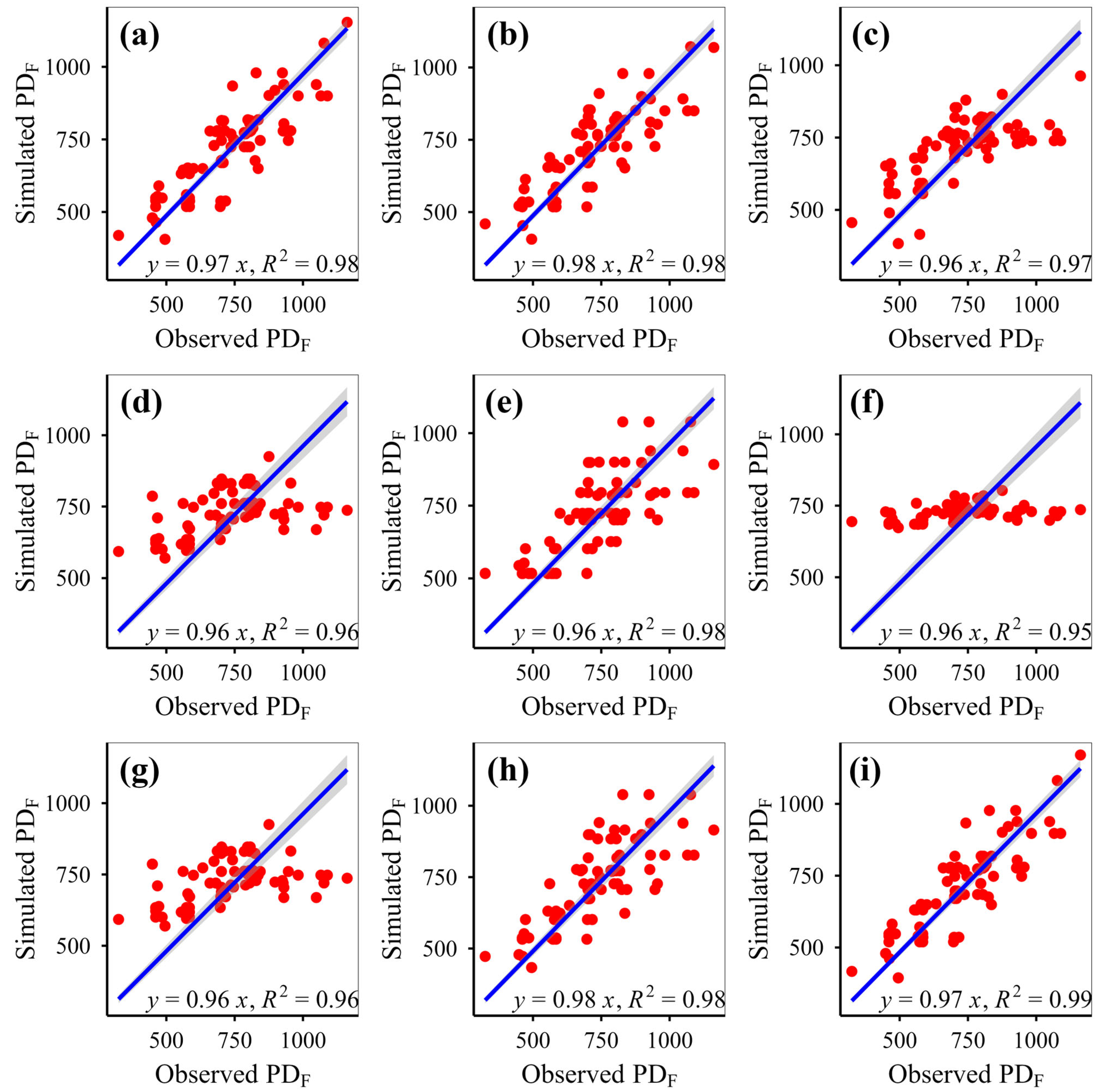
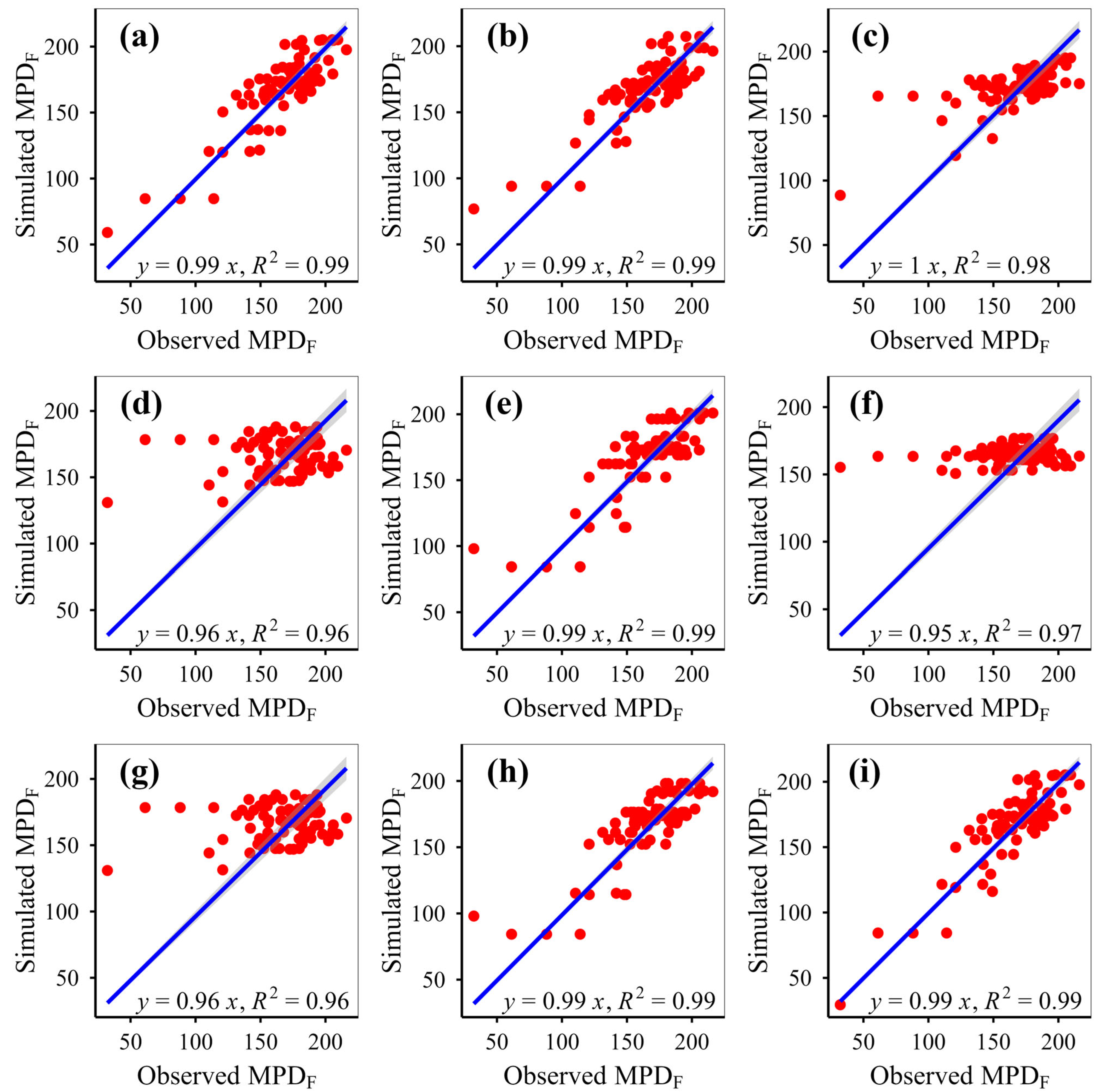
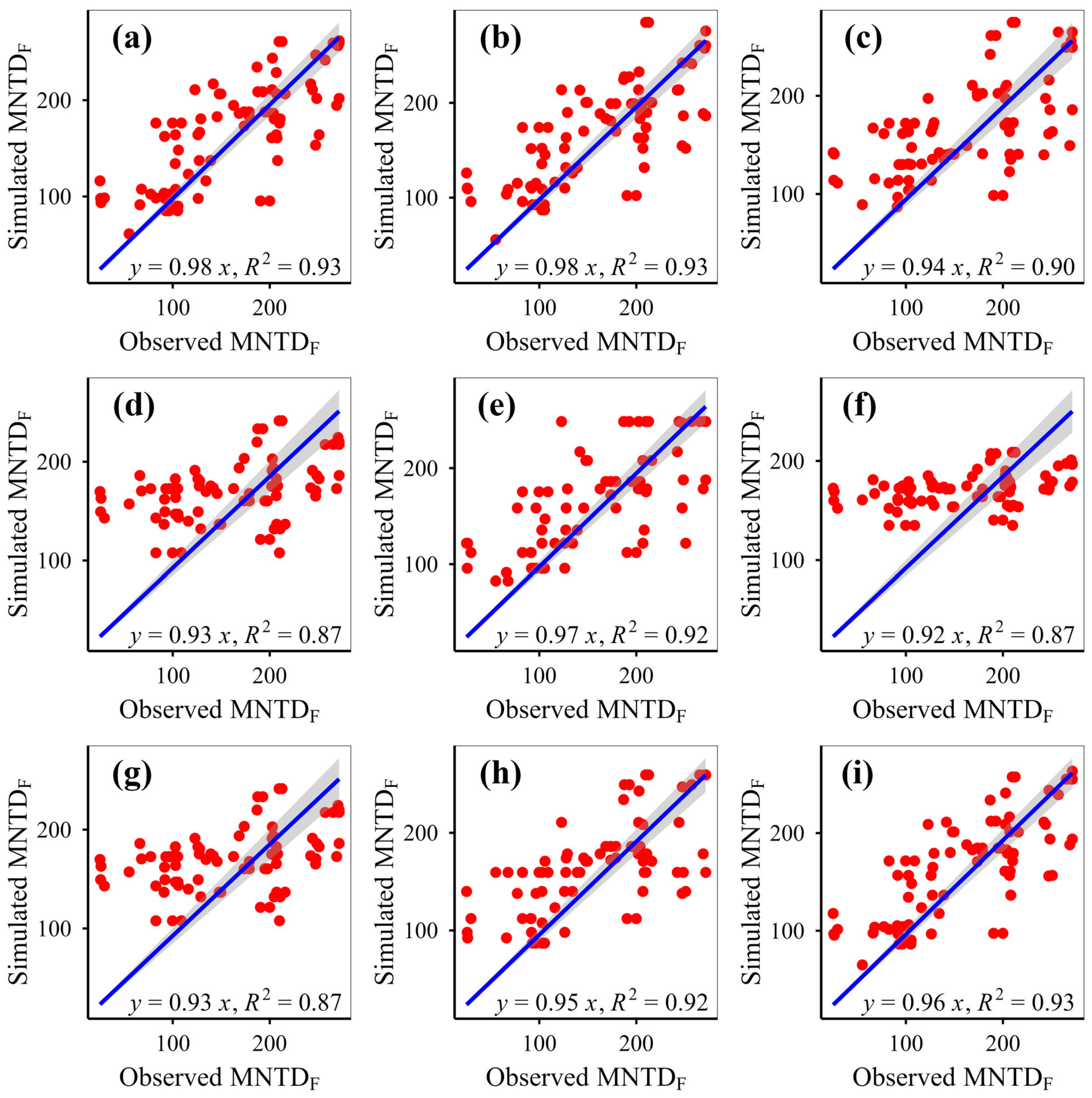
This study simulated plant phylogenetic diversity under different scenarios (fenced vs. grazed) on the Qinghai-Xizang Plateau using nine models based on various algorithms. This study demonstrates that eXGB, RF, and GBR are the most reliable algorithms for predicting plant community phylogenetic diversity, outperforming the other six models (MLR, RRT, GLR, ANN, CIT, SVM). The eXGB model excels in predicting MPD and MNTD under fencing conditions and PD under grazing conditions, but its accuracy declines for grazing-related distance metrics (MPD/MNTD). In contrast, RF delivers consistent performance, achieving high precision for MPD/MNTD under grazing and PD under fencing, thus offering balanced predictive capability across diverse scenarios. Critically, evaluation of scatterplot integrity (e.g., symmetry along 1:1 lines) and multi-metric validation (bias, RMSE, R2, slope) proves essential for robust model assessment. While no single algorithm dominates all scenarios, eXGB and RF emerge as contextually optimal choices, highlighting the necessity for condition-specific model selection in ecological diversity studies.