Elucidating the Disrupted Seasonal Cycle of Eodiaptomus japonicus (Calanoida, Copepoda) in Lake Biwa: Insights from an Individual-Based Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Purpose and Patterns
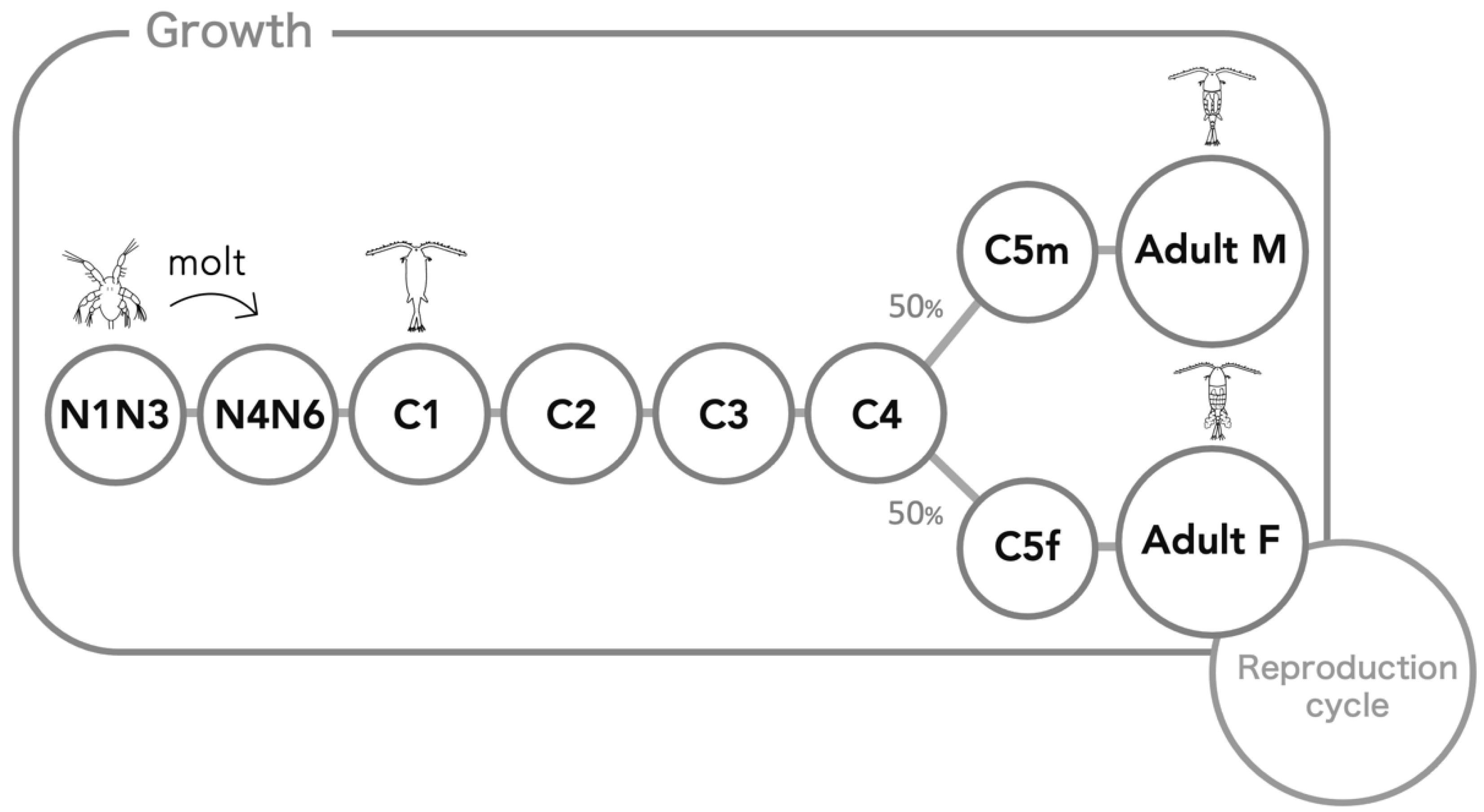
2.2. Entities, State Variables, and Scales
2.3. Process Overview and Scheduling
2.4. Design Concepts
2.4.1. Basic Principles
2.4.2. Emergence
2.4.3. Adaptation
2.4.4. Sensing
2.4.5. Interactions
2.4.6. Stochasticity
2.4.7. Observation
2.5. Initialization
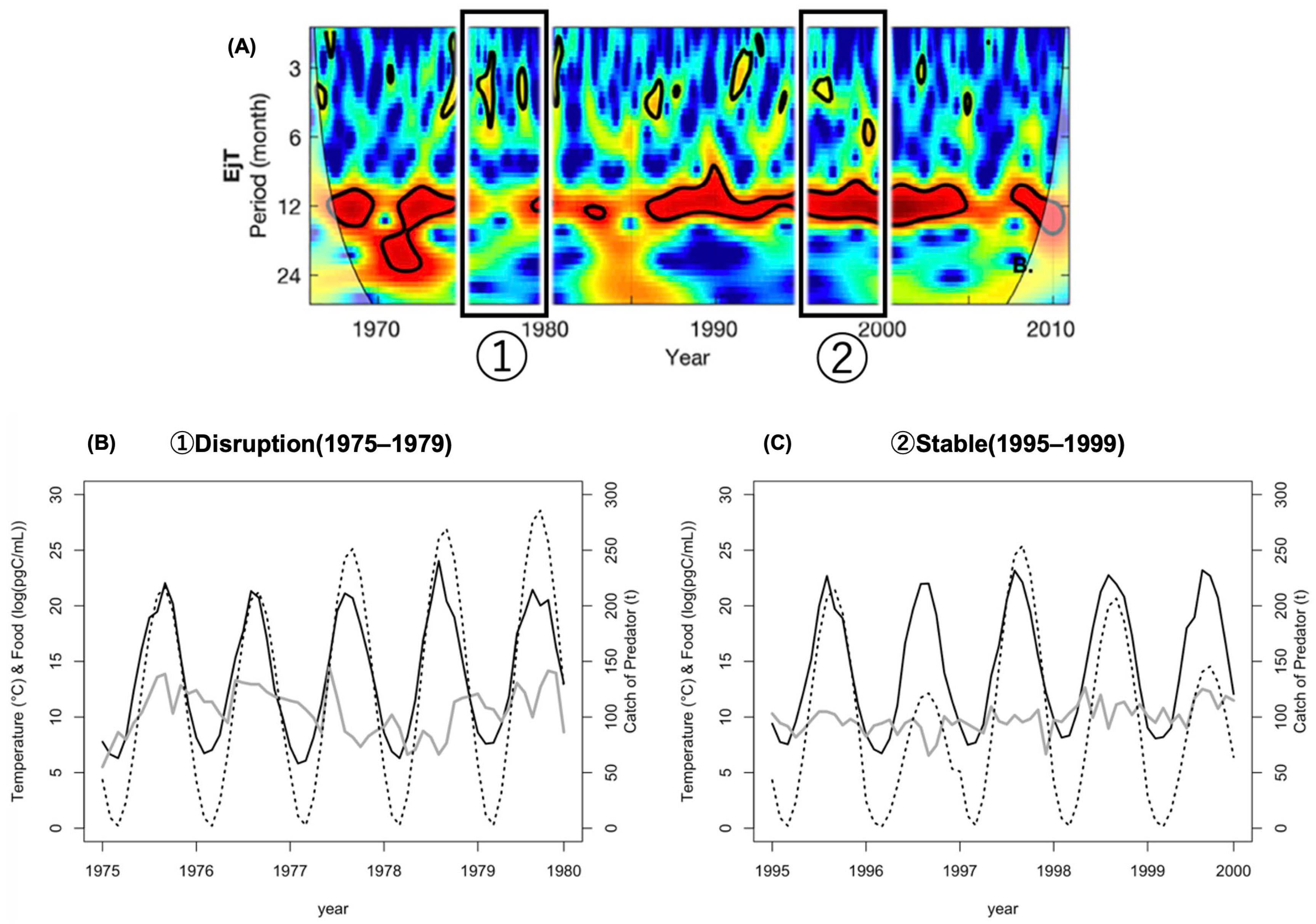
- Disruption period (1975–1979)—when the disruption of the seasonal cycle of this species was observed;
- Stable period (1995–1999)—when its seasonal cycle was stable.
2.6. Input Data
- (a)
- Set water temperature, food concentration, and predators;
- (b)
- Set water temperature and food concentration;
- (c)
- Set water temperature and predators.
2.7. Submodels
2.7.1. Environmental Conditions
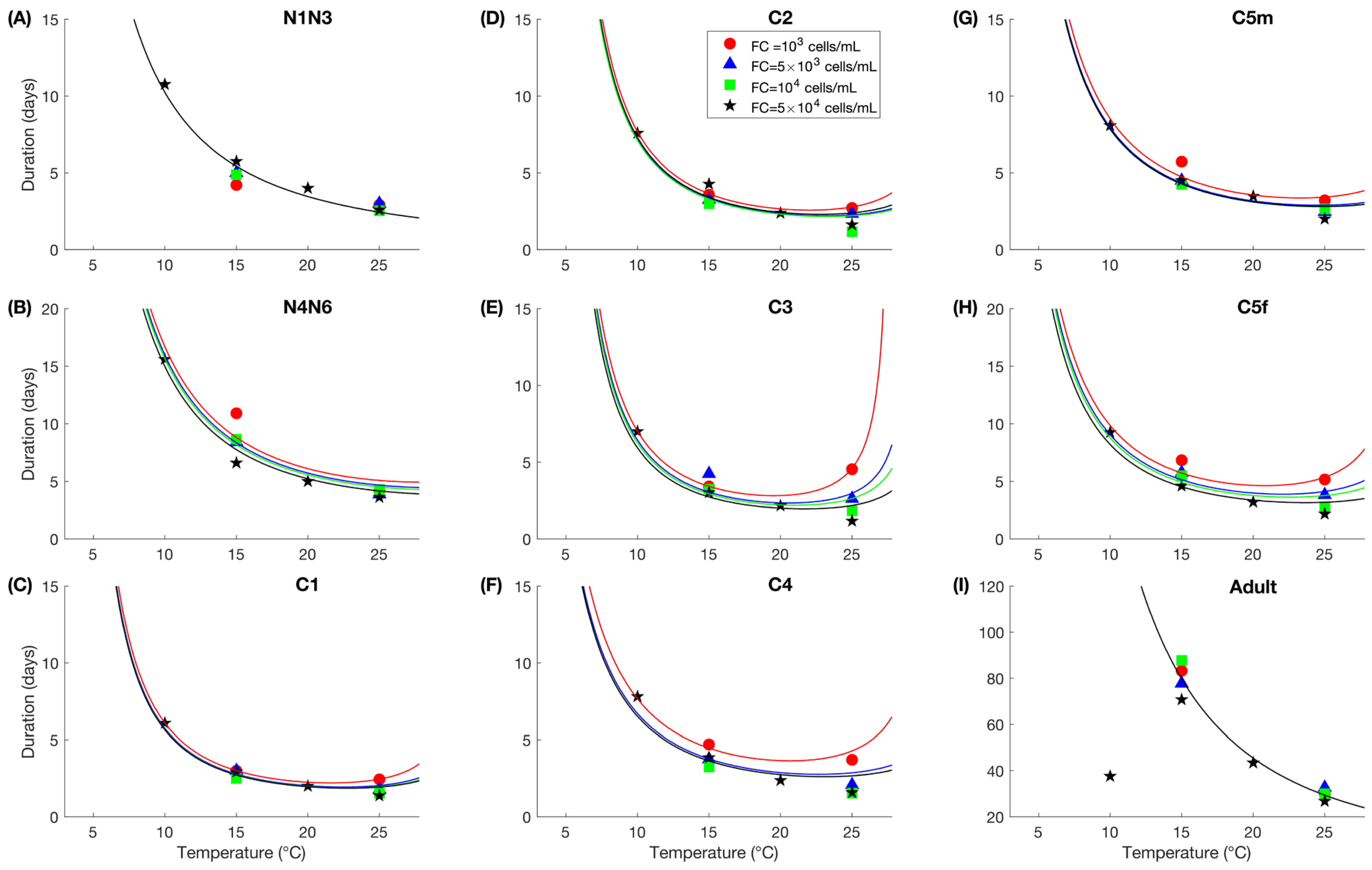
2.7.2. Growth
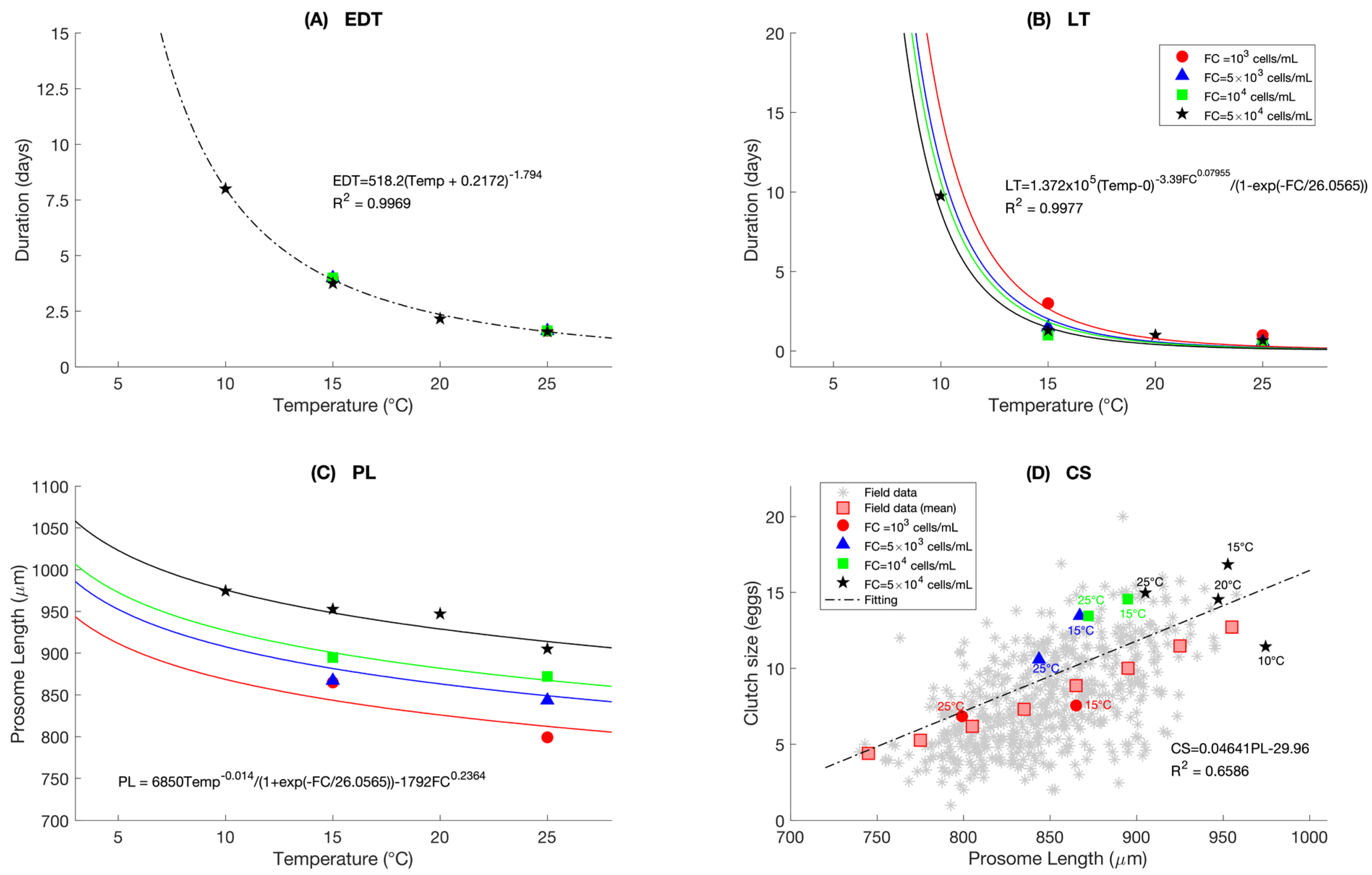
2.7.3. Reproduction
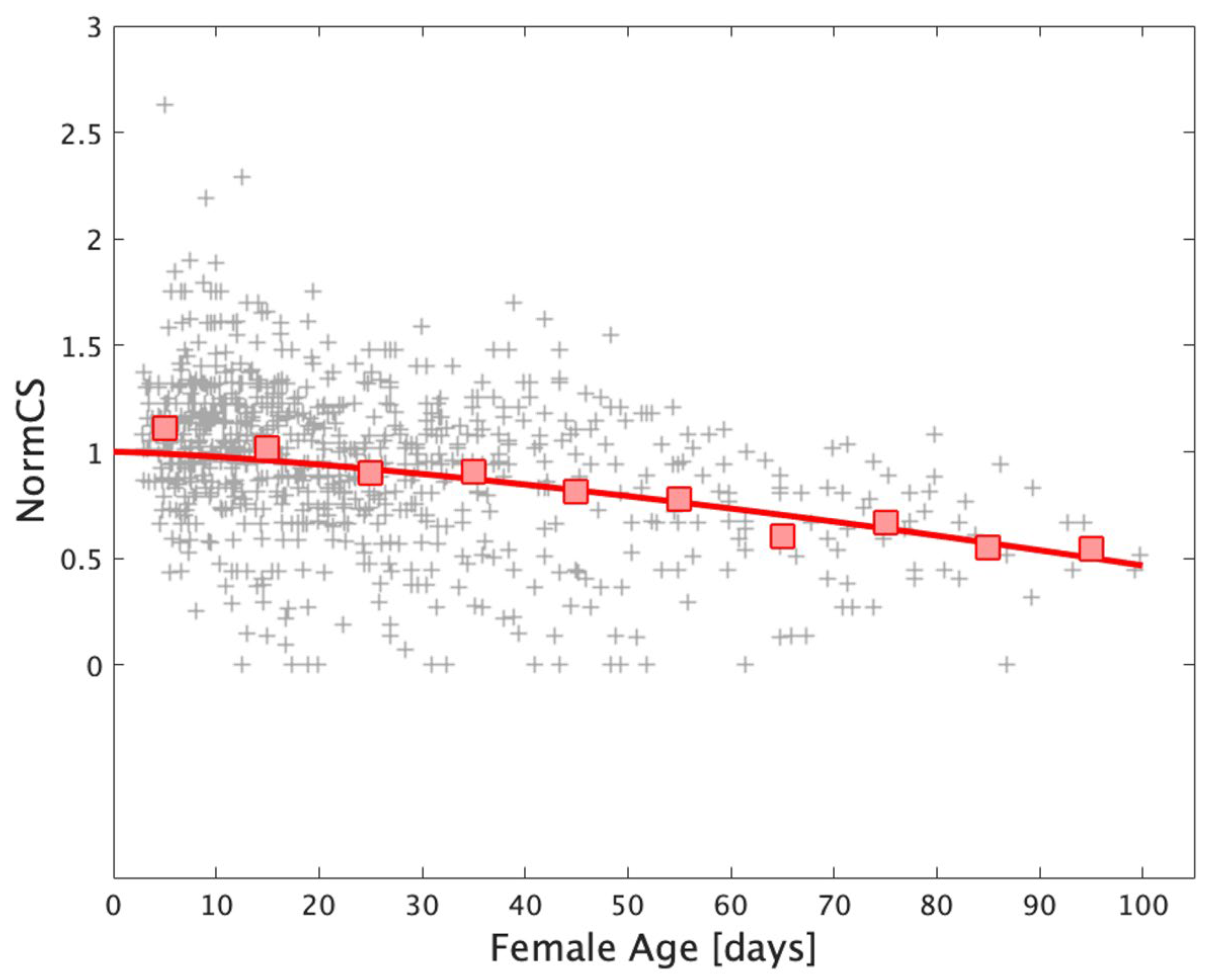
2.7.4. Survival Rate
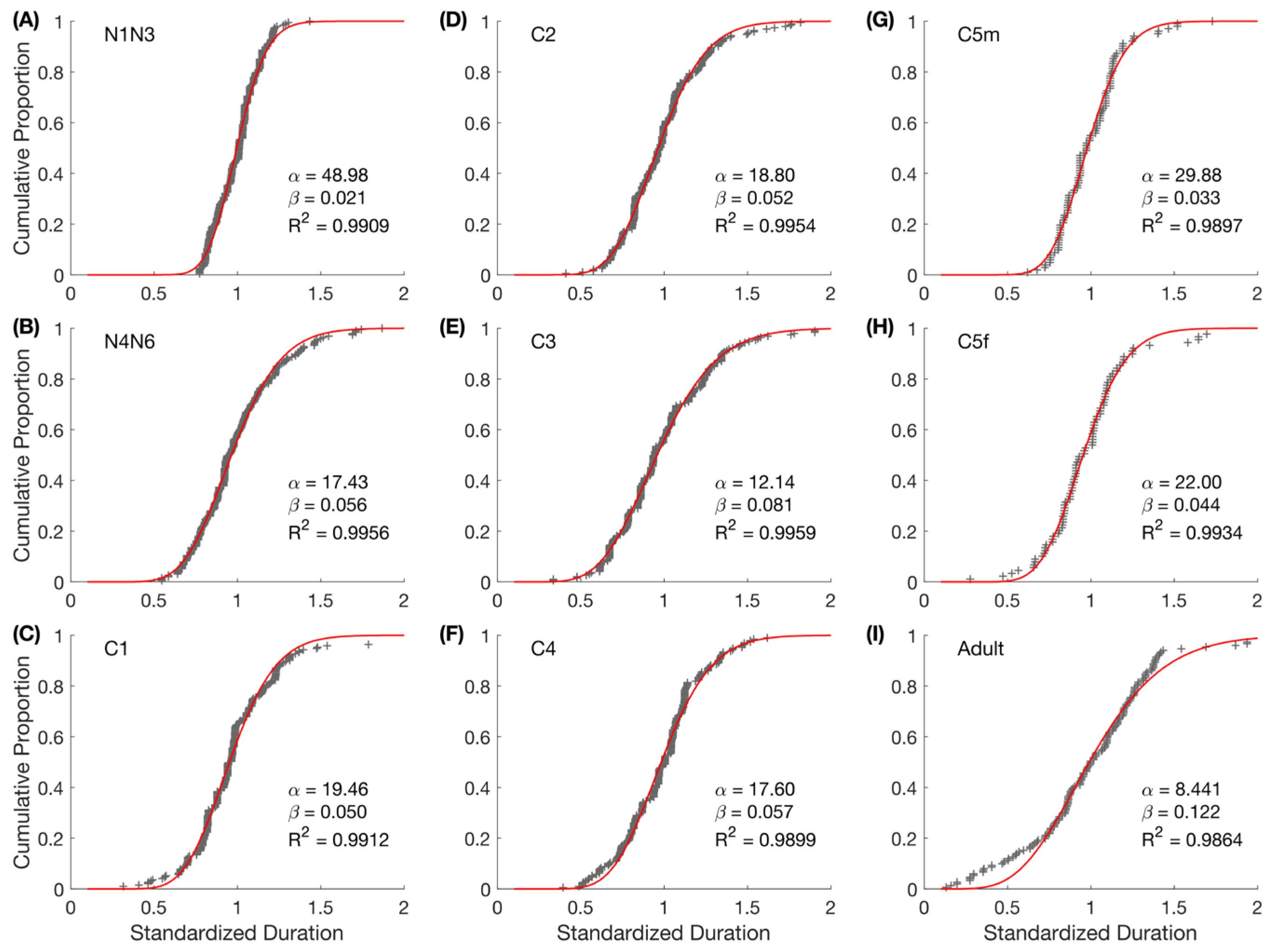
2.7.5. Individual Variability
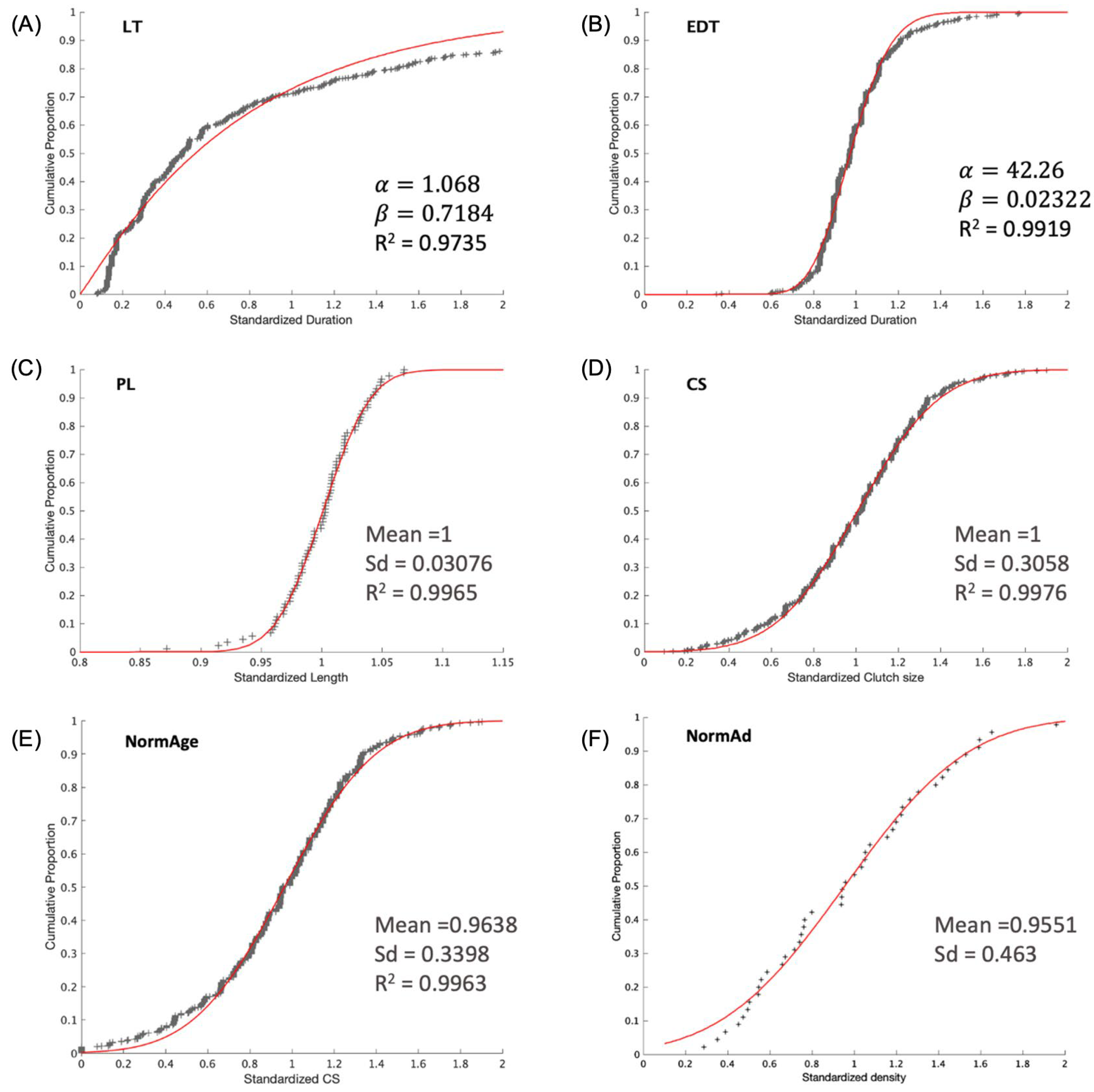
2.8. Model Verification
3. Results
3.1. Simulation (a)—Effects of Water Temperature, Food Concentration, and Predators
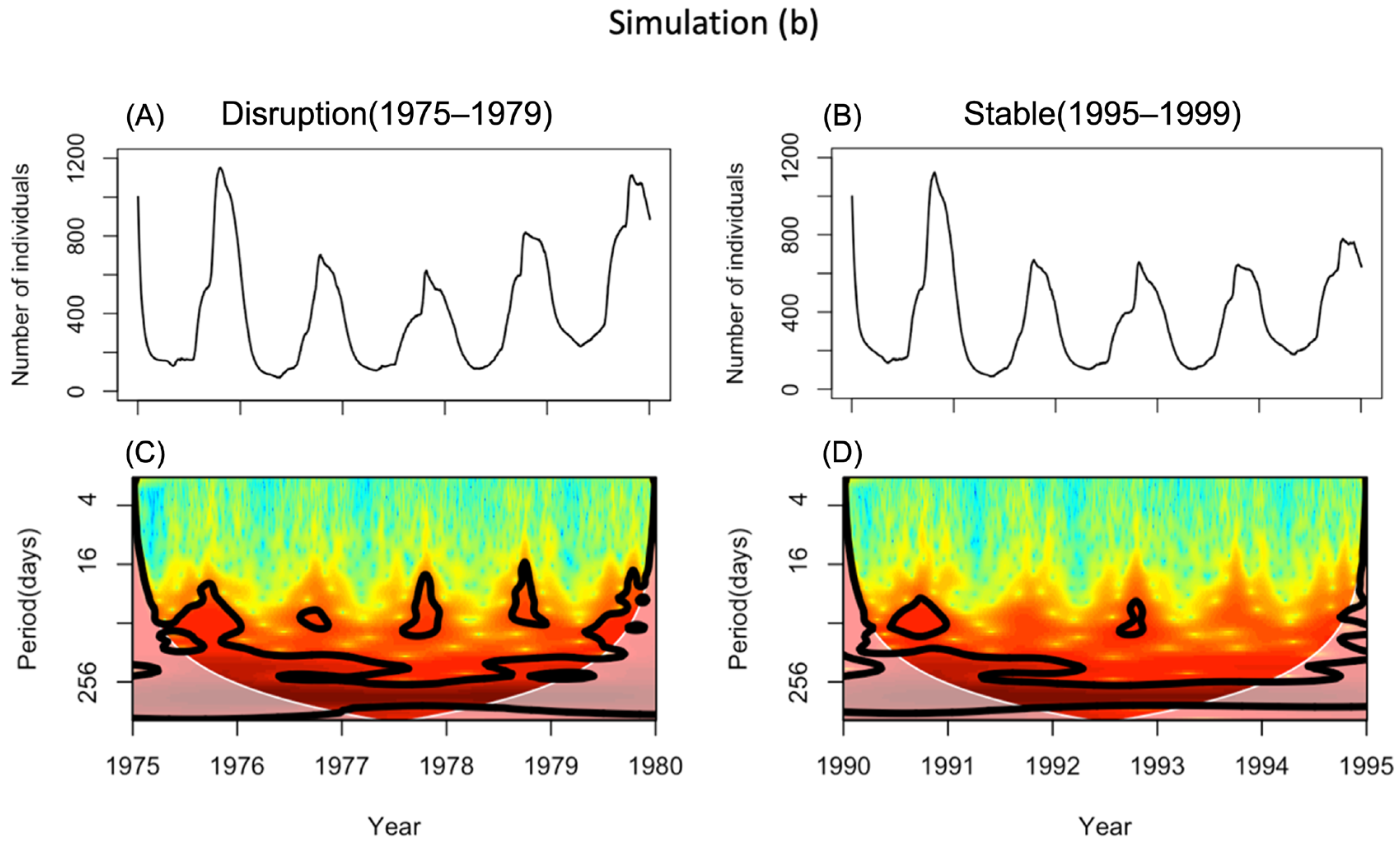
3.2. Simulation (b)—Effects of Water Temperature and Food Concentration
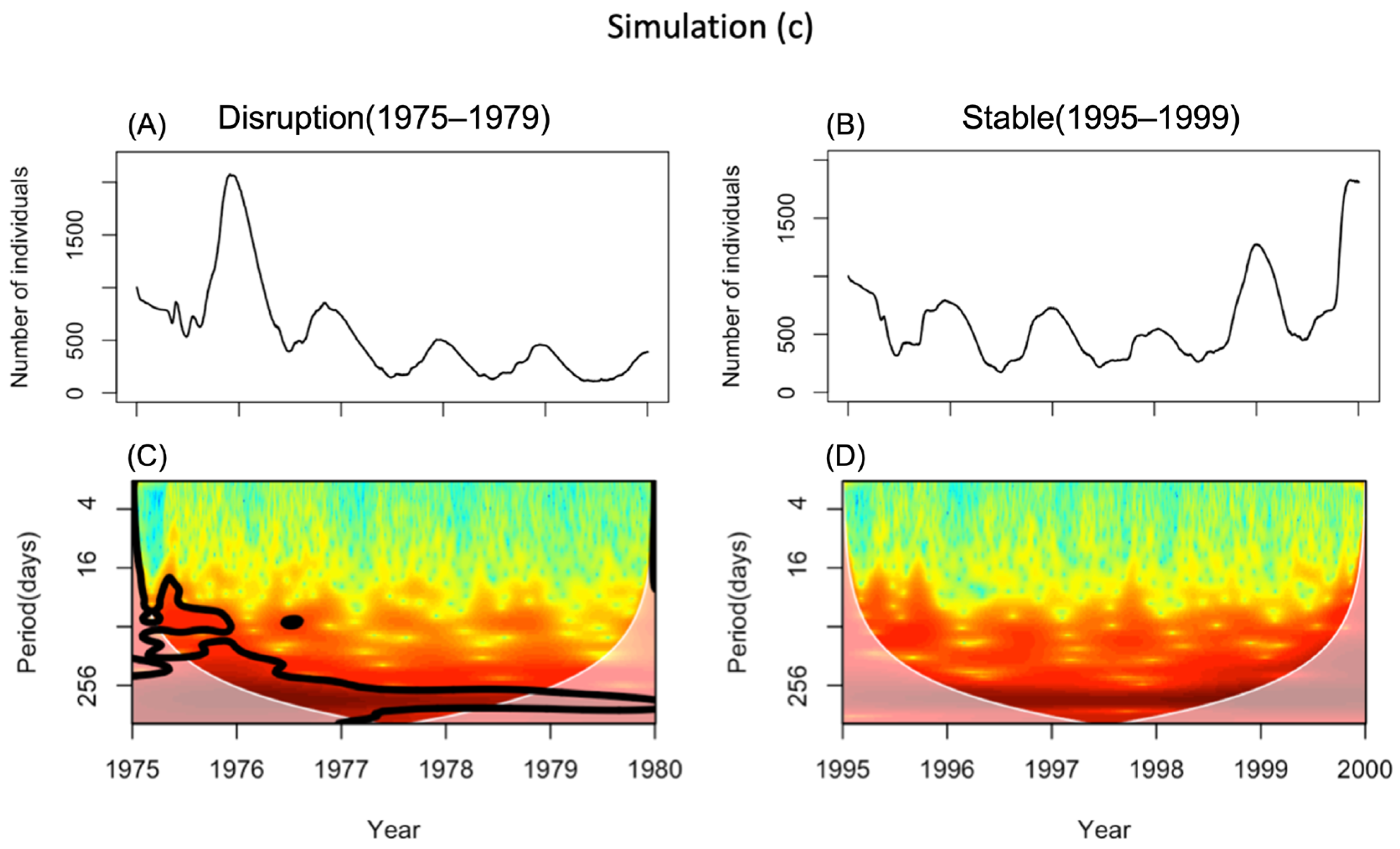
3.3. Simulation (c)—Effects of Water Temperature and Predation
4. Discussion
4.1. The Simulation Results
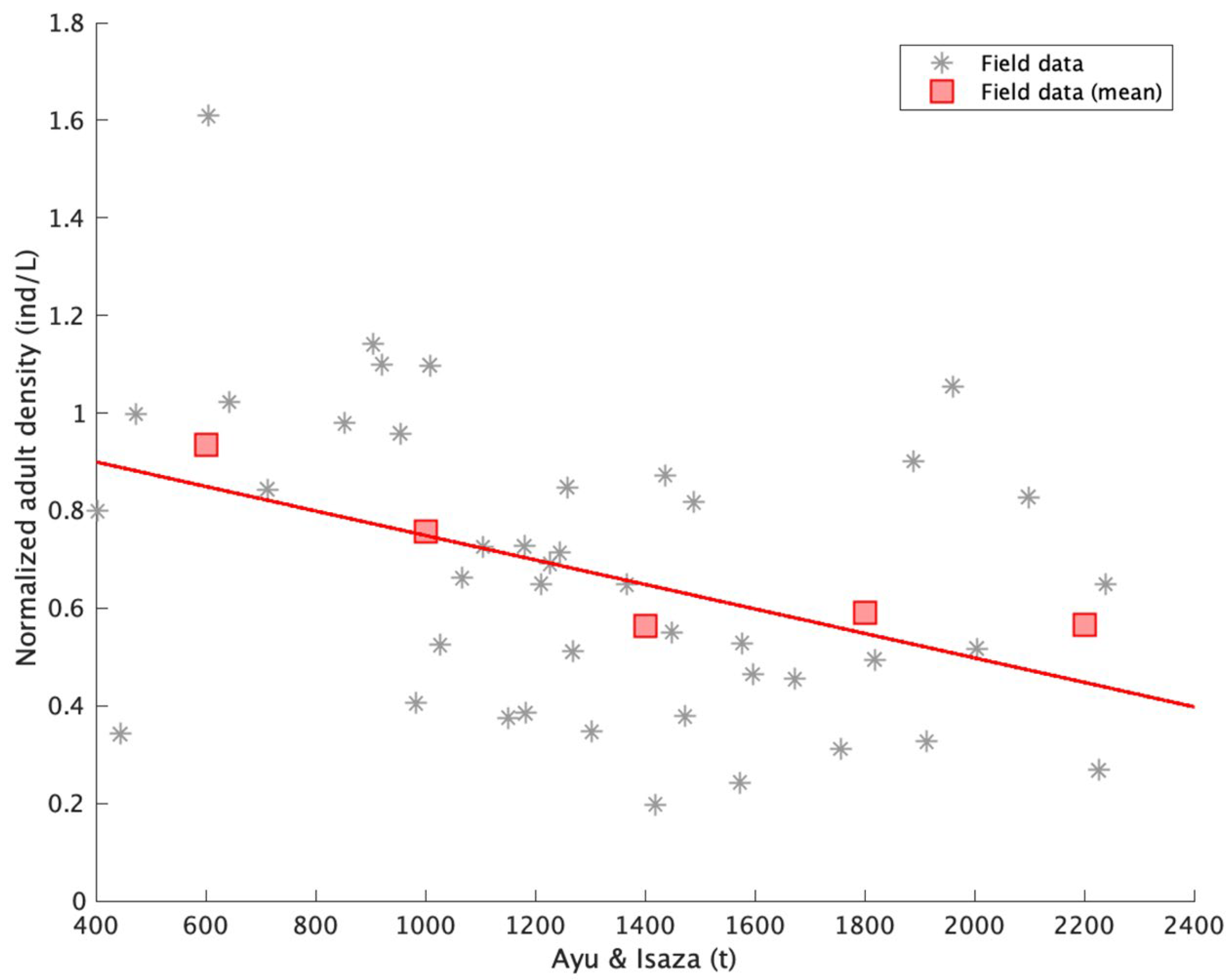
4.2. Comparison of Simulation Output and Field Population Density
4.3. The Predators’ Effect in the Model
4.4. Future Development and Model Potential
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adrian, R.; Wilhelm, S.; Gerten, D. Life-history traits of lake plankton species may govern their phenological response to climate warming. Glob. Change Biol. 2006, 12, 652–661. [Google Scholar] [CrossRef]
- Nakazawa, T.; Doi, H. A perspective on match/mismatch of phenology in community contexts. Oikos 2012, 121, 489–495. [Google Scholar] [CrossRef]
- Kawanabe, H.; Nishino, M.; Maehata, M. Lake Biwa: Interactions between Nature and People, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Tsugeki, N.; Oda, H.; Urabe, J. Fluctuation of the zooplankton community in Lake Biwa during the 20th century: A paleolimnological analysis. Limnology 2003, 4, 101–107. [Google Scholar] [CrossRef]
- Hyodo, F.; Tsugeki, N.; Azuma, J.; Urabe, J.; Nakanishi, M.; Wada, E. Changes in stable isotopes, lignin-derived phenols, and fossil pigments in sediments of Lake Biwa, Japan: Implications for anthropogenic effects over the last 100 years. Sci. Total Environ. 2008, 403, 139–147. [Google Scholar] [CrossRef]
- Hsieh, C.H.; Sakai, Y.; Ban, S.; Ishikawa, K.; Ishikawa, T.; Ichise, S.; Yamamura, N.; Kumagai, M. Eutrophication and warming effects on long-term variation of zoo- plankton in Lake Biwa. Biogeosciences 2011, 8, 1383–1399. [Google Scholar] [CrossRef]
- Okubo, T.; Azuma, Y. Last 35 years variation for water quality and watershed environments in Lake Biwa. Trans. Res. Inst. Oceanochem. 2016, 29, 2–16. (In Japanese) [Google Scholar]
- Hsieh, C.H.; Ishikawa, K.; Sakai, Y.; Ishikawa, T.; Ichise, S.; Yamamoto, Y.; Kuo, T.C.; Park, H.D.; Yamamura, N.; Kumagai, M. Phytoplankton community reorganization driven by eutrophication and warming in Lake Biwa. Aquat. Sci. 2010, 72, 467–483. [Google Scholar] [CrossRef]
- Maehata, M. Environmental conservation of Lake Biwa. In Lake Biwa: Interactions between Nature and People; Kawanabe, H., Nishino, M., Maehata, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 419–513. [Google Scholar] [CrossRef]
- Liu, X.; Dur, G.; Ban, S.; Sakai, Y.; Ohmae, S.; Morita, T. Planktivorous fish predation masks anthropogenic disturbances on decadal trends in zooplankton biomass and body size structure in Lake Biwa, Japan. Limnol. Oceanogr. 2020, 65, 667–682. [Google Scholar] [CrossRef]
- Kawabata, K.; Narita, T.; Nagoshi, M.; Nishino, M.; Kawabata, K.; Nagoshi, M.; Nishino, M. Stomach contents of the landlocked dwarf ayu in Lake Biwa, Japan. Limnology 2002, 3, 135–142. [Google Scholar] [CrossRef]
- Kawabata, K. Abundance and distribution of Eodiaptomus japonicus (Copepoda: Calanoida) in Lake Biwa. Bull. Plankton Soc. Jpn. 1987, 34, 173–183. [Google Scholar]
- Kawabata, K. Seasonal changes in abundance and vertical distribution of Mesocyclops thermocyclopoides, Cyclops vicinus and Daphnia longispina in Lake Biwa. Jpn. J. Limnol. 1989, 50, 9–13. [Google Scholar] [CrossRef]
- Kawabata, K. Mortality Rate of Eodiaptomus japonicus (Copepoda: Calanoida) in Lake Biwa. Jpn. J. Limnology 1993, 54, 131–136. [Google Scholar] [CrossRef]
- Kawabata, K. Ontogenetic niches of a planktonic copepod in Lake Biwa studied on a fine temporal scale. Ecol. Res. 1995, 10, 207–215. [Google Scholar] [CrossRef]
- Kawabata, K. Clearance rate of the cyclopoid copepod Mesocyclops dissimilis on the calanoid copepod Eodiaptomus japonicus. Plankton Benthos Res. 2006, 1, 68–70. [Google Scholar] [CrossRef]
- Kawabata, K.; Urabe, J. Population dynamics of planktonic crustacea studied during BITEX’93. Jpn. J. Limnol. 1996, 57, 545–552. [Google Scholar] [CrossRef]
- Kawabata, K.; Narita, T. Feeding rate of naupliar Eodiaptomus japonicus. Plankton Biol. Ecol. 2003, 50, 27–29. [Google Scholar]
- Kawabata, K.; Narita, T.; Nishino, M. Predator–prey relationship between the landlocked dwarf ayu and planktonic crustacea in Lake Biwa, Japan. Limnology 2006, 7, 199–203. [Google Scholar] [CrossRef]
- Nagata, T.; Okamoto, K. Filtering rates on natural bacteria by Daphnia longispina and Eodiaptomus japonicus in Lake Biwa. J. Plankton Res. 1988, 10, 835–850. [Google Scholar] [CrossRef]
- Liu, X.; Ban, S. Effects of acclimatization on metabolic plasticity of Eodiaptomus japonicus (Copepoda: Calanoida) determined using an optical oxygen meter. J. Plankton Res. 2017, 39, 111–121. [Google Scholar] [CrossRef]
- Liu, X.; Ban, S. Effects of temperature and nutritional conditions on physiological responses of the freshwater copepod Eodiaptomus japonicus in Lake Biwa, (Japan). Limnol. Study 2018, 5, 13–24. [Google Scholar]
- Liu, X.; Beyrend-Dur, D.; Dur, G.; Ban, S. Effects of temperature on life history traits of Eodiaptomus japonicus (Copepoda: Calanoida) from Lake Biwa (Japan). Limnology 2014, 15, 85–97. [Google Scholar] [CrossRef]
- Liu, X.; Beyrend, D.; Dur, G.; Ban, S. Combined effects of temperature and food concentration on growth and reproduction of Eodiaptomus japonicus (Copepoda: Calanoida) from Lake Biwa (Japan). Freshw. Biol. 2015, 60, 2003–2018. [Google Scholar] [CrossRef]
- Liu, X.; Dur, G.; Ban, S.; Sakai, Y.; Ohmae, S.; Morita, T. Quasi-decadal periodicities in growth and production of the copepod Eodiaptomus japonicus in Lake Biwa, Japan, related to the Arctic Oscillation. Limnol. Oceanogr. 2021, 66, 3783–3795. [Google Scholar] [CrossRef]
- Gao, H.; Liu, X.; Ban, S. Effect of acute acidic stress on survival and metabolic activity of zooplankton from Lake Biwa, Japan. Inland Waters 2022, 12, 488–498. [Google Scholar] [CrossRef]
- Dur, G.; Liu, X.; Sakai, Y.; Hsieh, C.H.; Ban, S.; Souissi, S. Disrupted seasonal cycle of the warm-adapted and main zooplankter of Lake Biwa, Japan. J. Great Lakes Res. 2022, 48, 1206–1218. [Google Scholar] [CrossRef]
- Halsband-Lenk, C.; Carlotti, F.; Greve, W. Life-history strategies of calanoid congeners under two different climate regimes: A comparison. ICES J. Mar. Sci. 2004, 61, 709–720. [Google Scholar] [CrossRef]
- Herzig, A. The ecological significance of the relationship between temperature and duration of embryonic development in planktonic freshwater copepods. Hydrobiologia 1983, 100, 65–91. [Google Scholar] [CrossRef]
- Ban, S. Effect of temperature and food concentration on post-embryonic development, egg production and adult body size of calanoid copepod Eurytemora affinis. J. Plankton Res. 1994, 16, 721–735. [Google Scholar] [CrossRef]
- Jiménez-Melero, R.; Santer, B.; Guerrero, F. Embryonic and naupliar development of Eudiaptomus gracilis and Eudiaptomus graciloides at different temperatures: Comments on individual variability. J. Plankton Res. 2005, 27, 1175–1187. [Google Scholar] [CrossRef]
- Kiørboe, T.; Møhlenberg, F.; Hamburger, K. Bioenergetics of the planktonic copepod Acartia tonsa: Relation between feeding, egg production and respiration, and composition of specific dynamic action. Mar. Ecol. Prog. Ser. 1985, 26, 85–97. [Google Scholar] [CrossRef]
- Klein Breteler, W.C.M.; Gonzalez, S.R.; Schogt, N. Development of Pseudocalanus elongatus (Copepoda, Calanoida) cultured at different temperature and food conditions. Mar. Ecol. Prog. Ser. 1995, 119, 99–110. [Google Scholar] [CrossRef]
- Jiménez-Melero, R.; Parra, G.; Guerrero, F. Effect of temperature, food and individual variability on the embryonic development time and fecundity of Arctodiaptomus salinus (Copepoda: Calanoida) from a shallow saline pond. Hydrobiologia 2012, 686, 241–256. [Google Scholar] [CrossRef]
- Lee, H.; Ban, S.; Ikeda, T.; Matsuishi, T. Effect of temperature on development growth and reproduction in the marine copepod Pseudocalanus newmani at satiating food condition. J. Plankton Res. 2003, 25, 261–271. [Google Scholar] [CrossRef]
- Svensson, J.E. Fish predation on Eudiaptomus gracilis in relation to clutch size, body size, and sex: A field experiment. Hydrobiologia 1997, 344, 155–161. [Google Scholar] [CrossRef]
- Jeppesen, E.; Jensen, J.P.; Søndergaard, M.; Lauridsen, T.; Pedersen, L.J.; Jensen, L. Top-down control in fresh-water lakes: The role of nutrient state, submerged macrophytes and water depth. Hydrobiologia 1997, 342, 151–164. [Google Scholar] [CrossRef] [PubMed]
- Verheye, H.M.; Richardson, A.J.; Hutchings, L.; Marska, G.; Gianakouras, D. Long-term trends in the abundance and community structure of coastal zooplankton in the southern Benguela system, 1951–1996. Afr. J. Mar. Sci. 1998, 19, 317–332. [Google Scholar] [CrossRef]
- Daskalov, G.M. Overfishing drives a trophic cascade in the Black Sea. Mar. Ecol. Prog. Ser. 2002, 225, 53–63. [Google Scholar] [CrossRef]
- Brooks, J.L.; Dodson, S.I. Predation, body size, and composition of plankton. Science 1965, 150, 28–35. [Google Scholar] [CrossRef]
- Rettig, J.E. Zooplankton responses to predation by larval bluegill: An enclosure experiment. Freshw. Biol. 2003, 48, 636–648. [Google Scholar] [CrossRef]
- Hambright, K.D. Long-term zooplankton body size and species changes in a subtropical lake: Implications for lake management. Fundam. Appl. Limnol. Arch. Hydrobiol. 2008, 173, 1–13. [Google Scholar] [CrossRef]
- Dorman, J.G.; Sydeman, W.J.; Bograd, S.J.; Powell, T.M. An individual-based model of the krill Euphausia pacifica in the California current. Prog. Oceanogr. 2015, 138, 504–520. [Google Scholar] [CrossRef]
- Xu, Y.; Rose, K.A.; Chai, F.; Chavez, F.P.; Ayon, P. Does spatial variation in environmental conditions affect recruitment? A study using a 3-D model of Peruvian anchovy. Prog. Oceanogr. 2015, 138, 417–430. [Google Scholar] [CrossRef]
- Stillman, R.A.; Railsback, S.F.; Giske, J.; Berger, U.; Grimm, V. Making predictions in a changing world: The benefits of individual-based ecology. BioScience 2015, 65, 140–150. [Google Scholar] [CrossRef]
- DeAngelis, D.L.; Mooij, W.M. Individual-based modeling of ecological and evolutionary processes. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 147–168. [Google Scholar] [CrossRef]
- Grimm, V.; Railsback, S. Individual-Based Modeling and Ecology; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; Bastiansen, F.; Eliassen, S.; Ginot, V.; Giske, J.; Goss-Custard, J.; Grand, T.; Heinz, S.K.; Huse, G.; et al. A standard protocol for describing individual-based and agent-based models. Ecol. Model. 2006, 198, 115–126. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; DeAngelis, D.L.; Polhill, J.G.; Giske, J.; Railsback, S.F. The ODD protocol: A review and first update. Ecol. Model. 2010, 221, 2760–2768. [Google Scholar] [CrossRef]
- Grimm, V.; Railsback, S.F.; Vincenot, C.E.; Berger, U.; Gallagher, C.; Deangelis, D.L.; Edmonds, B.; Ge, J.; Giske, J.; Groeneveld, J.; et al. The ODD protocol for describing agent-based and other simulation models: A second update to improve clarity, replication, and structural realism. JASSS 2020, 23, 7. [Google Scholar] [CrossRef]
- El Messoussi, S.; Hafid, H.; Lahrouni, A.; Afif, M. Simulation of Temperature Effect on the Population Dynamic of the Mediterranean Fruit Fly Ceratitis capitata (Diptera; Tephritidae). J. Agron. 2007, 6, 374–377. [Google Scholar] [CrossRef]
- Souissi, S.; Ban, S. The consequence of individual variability in moulting probability and the aggregation of stages for modelling copepod population dynamics models. J. Plankton Res. 2001, 23, 1279–1296. [Google Scholar] [CrossRef]
- Dur, G.; Souissi, S.; Devreker, D.; Ginot, V.; Schmitt, F.G.; Hwang, J.S. An individual-based model to study the reproduction of egg bearing copepods: Application to Eurytemora affinis (Copepoda Calanoida) from the Seine estuary, France. Ecol. Model. 2009, 220, 1073–1089. [Google Scholar] [CrossRef]
- Briones, J.C.; Tsai, C.-H.; Nakazawa, T.; Sakai, Y.; Papa, R.D.S.; Hsieh, C.; Okuda, N. Long-term changes in the diet of Gymnogobius isaza from Lake Biwa, Japan: Effects of body size and environmental prey availability. PLoS ONE 2012, 7, e53167. [Google Scholar] [CrossRef] [PubMed]
- Devreker, D.; Pierson, J.J.; Souissi, S.; Kimmel, D.G.; Roman, M.R. An experimental approach to estimate egg production and development rate of the calanoid copepod Eurytemora affinis in Chesapeake Bay, USA. J. Exp. Mar. Biol. Ecol. 2012, 416–417, 72–83. [Google Scholar] [CrossRef]
- Gerten, D.; Adrian, R. Species-specific changes in the phenology and peak abundance of freshwater copepods in response to warm summers. Freshw. Biol. 2002, 47, 2163–2173. [Google Scholar] [CrossRef]
- Winder, M.; Schindler, D.E.; Essington, T.E.; Litt, A.H. Disrupted seasonal clockwork in the population dynamics of a freshwater copepod by climate warming. Limnol. Oceanogr. 2009, 54 6Pt 2, 2493–2505. [Google Scholar] [CrossRef]
- Burnsd, C.W.; Hegarty, B. Diet selection by copepods in the presence of cyanobacteria. J. Plankton Res. 1994, 16, 1671–1690. [Google Scholar] [CrossRef]
- Poulet, S.A. Factors controlling utilization of non-a1ga1 diets by particle-grazing copepods. Oceanol. Acta 1983, 6, 221–234. [Google Scholar]
- Kiørboe, T. Fluid dynamic constraints on resource acquisition in small pelagic organisms. Eur. Phys. J. Spec. Top. 2016, 225, 669–683. [Google Scholar] [CrossRef]
- Daewel, U.; Hjøllo, S.S.; Huret, M.; Ji, R.; Maar, M.; Niiranen, S.; Travers-Trolet, M.; Peck, M.A.; van de Wolfshaar, K.E. Predation control of zooplankton dynamics: A review of observations and models. ICES J. Mar. Sci. 2014, 71, 254–271. [Google Scholar] [CrossRef]
- Bryant, A.D.; Heath, M.R.; Broekhuizen, N.; Ollason, J.G.; Gurney, W.S.C.; Greenstreet, S.P.R. Modeling the predation, growth and population dynamics of fish within a spatially-resolved shelf-sea ecosystem model. Neth. J. Sea Res. 1995, 33, 407–421. [Google Scholar] [CrossRef]
- Maury, O.; Faugeras, B.; Shin, Y.-J.; Poggiale, J.-C.; Ari, T.B.; Marsac, F. Modeling environmental effects on the size-structured energy flow through marine ecosystems. Part 1: The model. Prog. Oceanogr. 2007, 74, 479–499. [Google Scholar] [CrossRef]
- Baird, M.E.; Suthers, I.M. A size-resolved pelagic ecosystem model. Ecol. Model. 2007, 203, 185–203. [Google Scholar] [CrossRef]
- Zhou, M.; Carlotti, F.; Zhu, Y. A size-spectrum zooplankton closure model for ecosystem modelling. J. Plankton Res. 2010, 32, 1147–1165. [Google Scholar] [CrossRef]
- Jeppesen, E.; Meerhoff, M.; Holmgren, K.; González-Bergonzoni, I.; Teixeira de Mello, F.; Declerck, S.; De Meester, L.; Søndergaard, M.; Lauridsen, T.L.; Bjerring, R.; et al. Impacts of climate warming on lake fish community structure and potential effects on ecosystem function. Hydrobiologia 2010, 646, 73–90. [Google Scholar] [CrossRef]
- Jaime, S.; Cervantes-Martínez, A.; Gutiérrez-Aguirre, M.A.; Jùares-Morales, J.R.; Reyes-Solares, E.M.; Delgado-Blas, V.H. Historical zooplankton composition indicates eutrophication stages in a Neotropical aquatic system: The case of Lake Amatitlàn, Central America. Diversity 2021, 13, 432. [Google Scholar] [CrossRef]

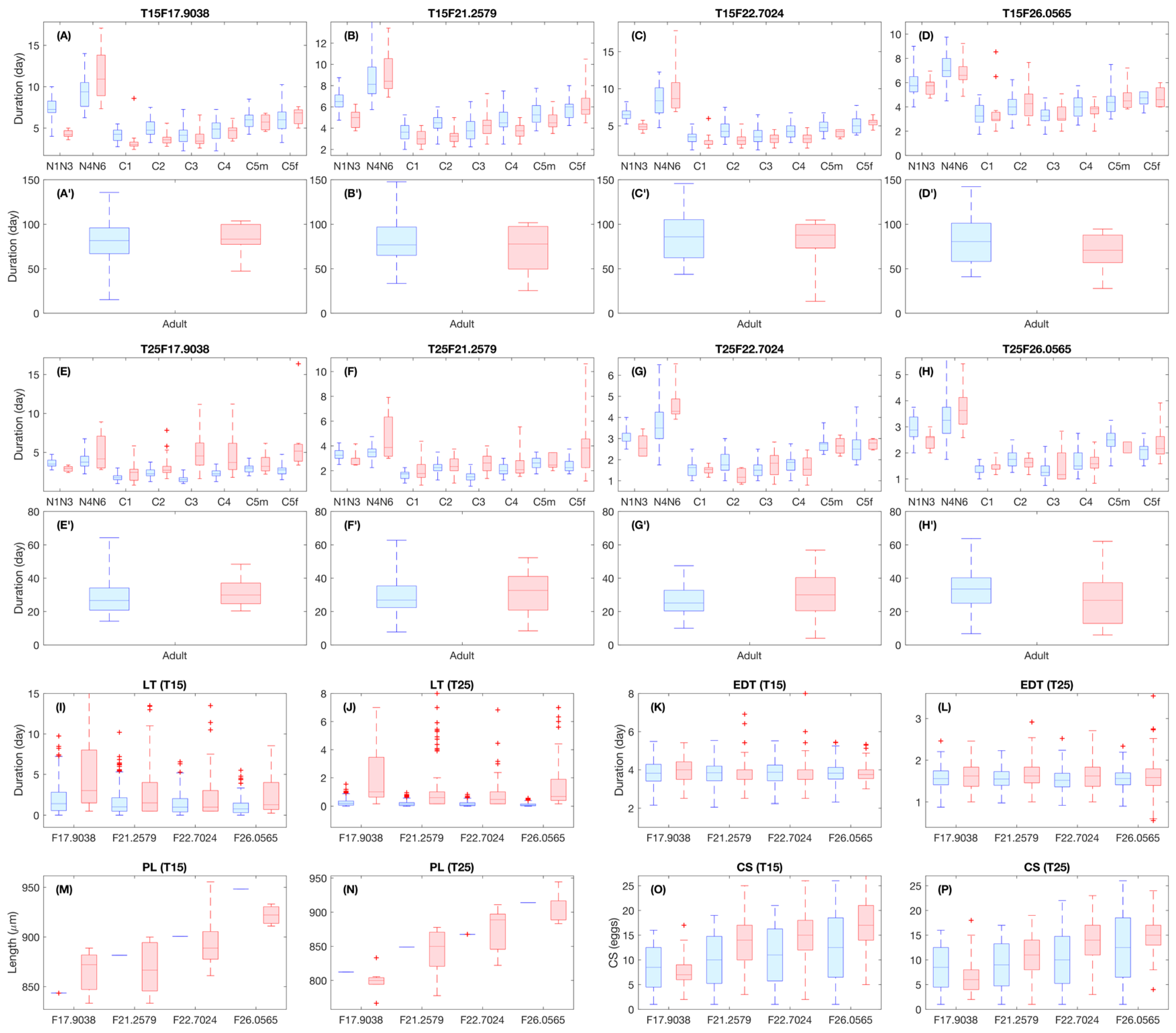

| Attribute | Unit | Meaning | Holder | Initial Value |
|---|---|---|---|---|
| age | °Cday | Cumulative time step counted immediately after molting | All | 0 |
| duration | °Cday | Stage duration defined under temperature and food conditions | All | Equations (1) and (2) |
| survival | %/day | Survival probability of individuals | All | 100% or Equations (10) and (11) |
| sexratio | - | The ratio of male to female | C4 | 0.5 |
| EDT | °Cday | Time from spawning to hatching | AdultF | 0 |
| LT | °Cday | Time from hatching to spawning | AdultF | Equation (4) |
| CS | eggs | Clutch size (number of eggs/female) | AdultF | 0 |
| HS | % | Hatching success of a clutch | AdultF | 98.17 |
| PL | µm | Length of the body on the front side of the female | AdultF | Equation (6) |
| ovigerous | - | Ovigerous state of females | AdultF | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, A.; Ban, S.; Liu, X.; Souissi, S.; Oda, T.; Dur, G. Elucidating the Disrupted Seasonal Cycle of Eodiaptomus japonicus (Calanoida, Copepoda) in Lake Biwa: Insights from an Individual-Based Model. Diversity 2024, 16, 309. https://doi.org/10.3390/d16060309
Takahashi A, Ban S, Liu X, Souissi S, Oda T, Dur G. Elucidating the Disrupted Seasonal Cycle of Eodiaptomus japonicus (Calanoida, Copepoda) in Lake Biwa: Insights from an Individual-Based Model. Diversity. 2024; 16(6):309. https://doi.org/10.3390/d16060309
Chicago/Turabian StyleTakahashi, Amane, Syuhei Ban, Xin Liu, Sami Souissi, Tomohiro Oda, and Gaël Dur. 2024. "Elucidating the Disrupted Seasonal Cycle of Eodiaptomus japonicus (Calanoida, Copepoda) in Lake Biwa: Insights from an Individual-Based Model" Diversity 16, no. 6: 309. https://doi.org/10.3390/d16060309
APA StyleTakahashi, A., Ban, S., Liu, X., Souissi, S., Oda, T., & Dur, G. (2024). Elucidating the Disrupted Seasonal Cycle of Eodiaptomus japonicus (Calanoida, Copepoda) in Lake Biwa: Insights from an Individual-Based Model. Diversity, 16(6), 309. https://doi.org/10.3390/d16060309







