Invasion Consequences in Communities Maintained by Niche and Intransitive Coexistence Mechanisms
Abstract
1. Introduction
2. Methods
2.1. Native Dynamic Model
2.1.1. Model Construction
2.1.2. Competition Matrix
2.1.3. Coexistence Mechanisms Analysis
2.2. Invasion of Alien Species
2.3. Metrics for Species Short-Term Response to Invasion
3. Results
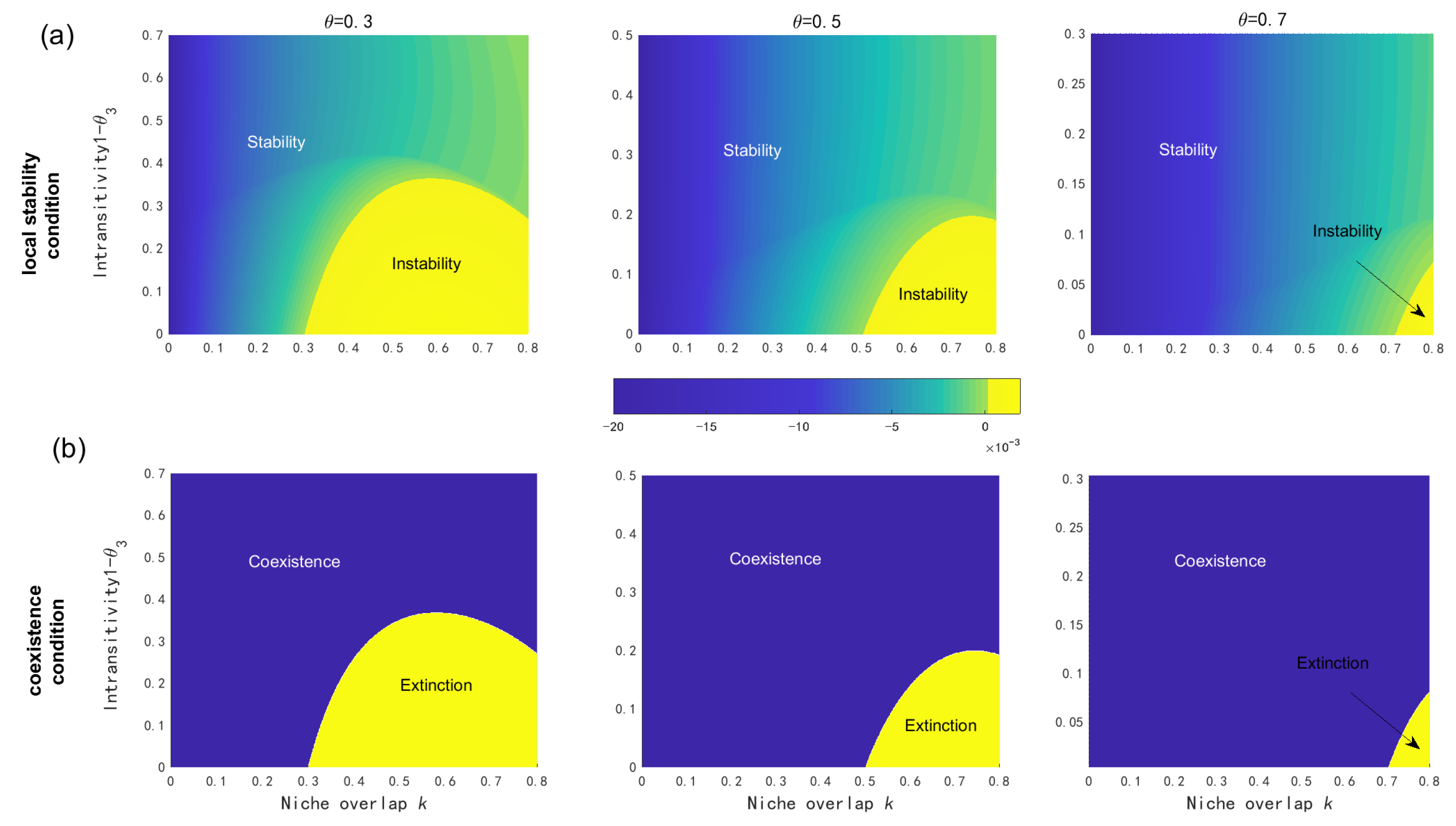
3.1. Native Coexistence Mechanisms
3.2. Invasion Consequences
3.2.1. Three Coexistence Mechanisms
3.2.2. Invasion When Only Competing with One Native Species
3.2.3. Long-Term Population Evolution and Short-Term Response
3.2.4. Invasion Consequence for the Other Scenarios
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation of Native Coexistence Conditions
Appendix A.1. The Existence of Positive Equilibrium Point

The Locally Asymptotic Stable Analysis
Appendix B. Calculation of Matrix for Species Short-Term Response
References
- Van Kleunen, M.; Dawson, W.; Essl, F.; Pergl, J.; Winter, M.; Weber, E.; Kreft, H.; Weigelt, P.; Kartesz, J.; Nishino, M.; et al. Global exchange and accumulation of non-native plants. Nature 2015, 525, 100–103. [Google Scholar] [CrossRef] [PubMed]
- McGeoch, M.A.; Latombe, G. Characterizing common and range expanding species. J. Biogeogr. 2016, 43, 217–228. [Google Scholar] [CrossRef]
- Coates, D. Strategic Plan for Biodiversity (2011–2020) and the Aichi Biodiversity Targets; Finlayson, C.M., Everard, M., Irvine, K., Mclnnes, R.J., Middleton, B.A., van Dam, A.A., Davidson, N.C., Eds.; The Wetland Book; Springer: Dordrecht, The Netherlands, 2016; pp. 1–7. [Google Scholar]
- Kolar, C.S.; Lodge, D.M. Progress in invasion biology: Predicting invaders. Trends Ecol. Evol. 2001, 16, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Keane, R.M.; Crawley, M.J. Exotic plant invasions and the enemy release hypothesis. Trends Ecol. Evol. 2002, 17, 164–170. [Google Scholar] [CrossRef]
- Hierro, J.L.; Maron, J.L.; Callaway, R.M. A biogeographical approach to plant invasions: The importance of studying exotics in their introduced and native range. J. Ecol. 2005, 93, 5–15. [Google Scholar] [CrossRef]
- Diez, J.M.; Dickie, I.; Edwards, G.; Hulme, P.E.; Sullivan, J.J.; Duncan, R.P. Negative soil feedbacks accumulate over time for non-native plant species. Ecol. Lett. 2010, 13, 803–809. [Google Scholar] [CrossRef]
- Pyšek, P.; Richardson, D.M. Traits associated with invasiveness in alien plants: Where do we stand? Biol. Invasions 2007, 193, 97–125. [Google Scholar]
- Ortega, Y.K.; Greenwood, L.F.; Callaway, R.M.; Pearson, D.E. Different responses of congeneric consumers to an exotic food resource: Who gets the novel resource prize? Biol. Invasions 2014, 16, 1757–1767. [Google Scholar] [CrossRef]
- Hobbs, R.J. The nature and effects of disturbance relative to invasions. In Biological Invasions: A Global Perspective; John Wiley & Sons: Chichester, UK, 1989; pp. 389–406. [Google Scholar]
- Colautti, R.I.; Ricciardi, A.; Grigorovich, I.A.; MacIsaac, H.J. Is invasion success explained by the enemy release hypothesis? Ecol. Lett. 2004, 7, 721–733. [Google Scholar] [CrossRef]
- Mitchell, C.E.; Agrawal, A.A.; Bever, J.D.; Gilbert, G.S.; Hufbauer, R.A.; Klironomos, J.N.; Maron, J.L.; Morris, W.F.; Parker, I.M.; Power, A.G.; et al. Biotic interactions and plant invasions. Ecol. Lett. 2006, 9, 726–740. [Google Scholar] [CrossRef]
- Traveset, A.; Richardson, D.M. Mutualistic interactions and biological invasions. Annu. Rev. Ecol. Evol. Syst. 2014, 45, 89–113. [Google Scholar] [CrossRef]
- Minoarivelo, H.O.; Hui, C. Invading a mutualistic network: To be or not to be similar. Ecol. Evol. 2016, 6, 4981–4996. [Google Scholar] [CrossRef] [PubMed]
- Godoy, O. Coexistence theory as a tool to understand biological invasions in species interaction networks: Implications for the study of novel ecosystems. Funct. Ecol. 2019, 33, 1190–1201. [Google Scholar] [CrossRef]
- Romanuk, T.N.; Zhou, Y.; Brose, U.; Berlow, E.L.; Williams, R.J.; Martinez, N.D. Predicting invasion success in complex ecological networks. Philos. Trans. R. Soc. B Biol. 2009, 364, 1743–1754. [Google Scholar] [CrossRef] [PubMed]
- Hui, C.; Richardson, D.M.; Landi, P.; Minoarivelo, H.O.; Garnas, J.; Roy, H.E. Defining invasiveness and invasibility in ecological networks. Biol. Invasions 2016, 18, 971–983. [Google Scholar] [CrossRef]
- Hutchinson, G.E. Homage to Santa Rosalia or why are there so many kinds of animals? Am. Nat. 1959, 93, 145–159. [Google Scholar] [CrossRef]
- Diamond, J.M. Assembly of species communities. In Ecology and Evolution of Communities; Wiley: Hoboken, NJ, USA, 1975; pp. 342–444. [Google Scholar]
- MacArthur, R.H.; Wilson, E.O. The Theory of Island Biogeography. In The Theory of Island Biogeography; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Fargione, J.; Brown, C.S.; Tilman, D. Community assembly and invasion: An experimental test of neutral versus niche processes. Proc. Natl. Acad. Sci. USA 2003, 100, 8916–8920. [Google Scholar] [CrossRef]
- Fridley, J.D.; Stachowicz, J.J.; Naeem, S.; Sax, D.; Seabloom, E.; Smith, M.; Stohlgren, T.; Tilman, D.; Holle, B.V. The invasion paradox: Reconciling pattern and process in species invasions. Ecology 2007, 88, 3–17. [Google Scholar] [CrossRef]
- Mack, R.N. Phylogenetic constraint, absent life forms, and preadapted alien plants: A prescription for biological invasions. Int. J. Plant Sci. 2003, 164, S185–S196. [Google Scholar] [CrossRef]
- Stachowicz, J.J.; Tilman, D. Species invasions and the relationships between species diversity, community saturation, and ecosystem functioning. In Species Invasions: Insights into Ecology, Evolution, and Biogeography; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2005; pp. 41–64. [Google Scholar]
- MacDougall, A.S.; Gilbert, B.; Levine, J.M. Plant invasions and the niche. J. Ecol. 2009, 97, 609–615. [Google Scholar] [CrossRef]
- Leffler, A.J.; James, J.J.; Monaco, T.A.; Sheley, R.L. A new perspective on trait differences between native and invasive exotic plants. Ecology 2014, 95, 298–305. [Google Scholar] [CrossRef] [PubMed]
- Bruno, J.; Fridley, J.; Bromberg, K.; Bertness, M. Insights into biotic interactions from studies of species invasions. Species Invasions Insights Ecol. Evol. Biogeogr. 2005, 97, 13–40. [Google Scholar]
- Laird, R.A.; Schamp, B.S. Competitive intransitivity promotes species coexistence. Am. Nat. 2006, 168, 182–193. [Google Scholar] [CrossRef]
- Allesina, S.; Levine, J.M. A competitive network theory of species diversity. Proc. Natl. Acad. Sci. USA 2011, 108, 5638–5642. [Google Scholar] [CrossRef]
- Lankau, R.A.; Strauss, S.Y. Mutual feedbacks maintain both genetic and species diversity in a plant community. Science 2007, 317, 1561–1563. [Google Scholar] [CrossRef] [PubMed]
- Soliveres, S.; Allan, E. Everything you Always Wanted to Know about Intransitive Competition But Were Afraid to Ask. J. Ecol. 2018, 106, 807–814. [Google Scholar] [CrossRef]
- Gallien, L.; Zimmermann, N.E.; Levine, J.M.; Adler, P.B. The effects of intransitive competition on coexistence. Ecol. Lett. 2017, 20, 791–800. [Google Scholar] [CrossRef]
- Godoy, O.; Stouffer, D.B.; Kraft, N.J.; Levine, J.M. Intransitivity is Infrequent and Fails to Promote Annual Plant Coexistence without Pairwise Niche Differences. Ecology 2017, 98, 1193–1200. [Google Scholar] [CrossRef]
- Yang, Y.; Hui, C. How competitive intransitivity and niche overlap affect spatial coexistence. Oikos 2021, 130, 260–273. [Google Scholar] [CrossRef]
- Chesson, P. Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 2000, 31, 343–366. [Google Scholar] [CrossRef]
- Uricchio, L.H.; Daws, S.C.; Spear, E.R.; Mordecai, E.A. Priority effects and nonhierarchical competition shape species composition in a complex grassland community. Am. Nat. 2019, 193, 213–226. [Google Scholar] [CrossRef] [PubMed]
- Levine, S.H. Competitive interactions in ecosystems. Am. Nat. 1976, 110, 903–910. [Google Scholar] [CrossRef]
- Mitchell, C.E.; Power, A.G. Release of invasive plants from fungal and viral pathogens. Nature 2003, 421, 625–627. [Google Scholar] [CrossRef]
- Bulleri, F.; Bruno, J.F.; Benedetti-Cecchi, L. Beyond competition: Incorporating positive interactions between species to predict ecosystem invasibility. PLoS Biol. 2008, 6, e162. [Google Scholar] [CrossRef] [PubMed]
- Adler, P.B.; HilleRisLambers, J.; Levine, J.M. A niche for neutrality. Ecol. Lett. 2007, 10, 95–104. [Google Scholar] [CrossRef]
- Hui, C.; Richardson, D.M. How to invade an ecological network. Trends Ecol. Evol. 2019, 34, 121–131. [Google Scholar] [CrossRef]
- Latombe, G.; Richardson, D.M.; McGeoch, M.A.; Altwegg, R.; Catford, J.A.; Chase, J.M.; Courchamp, F.; Esler, K.J.; Jeschke, J.M.; Landi, P.; et al. Mechanistic reconciliation of community and invasion ecology. Ecosphere 2021, 12, e03359. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Schreiber, S.J.; Killingback, T.P. Spatial heterogeneity promotes coexistence of rock–paper–scissors metacommunities. Theor. Popul. Biol. 2013, 86, 1–11. [Google Scholar] [CrossRef]
- Leung, A.W. Systems of Nonlinear Partial Differential Equations: Applications to Biology and Engineering; Springer Science & Business Media: Berlin, Germany, 2013; Volume 49. [Google Scholar]
- Pao, C.V. Nonlinear Parabolic and Elliptic Equations; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Takeuchi, Y. Global Dynamical Properties of Lotka-Volterra Systems; World Scientific: Singapore, 1996. [Google Scholar]
- Waltman, P. Competition Models in Population Biology; SIAM: Philadelphia, PA, USA, 1983. [Google Scholar]
- Lotka, A.J. Elements of Physical Biology; Williams & Wilkins: Philadelphia, PA, USA, 1925. [Google Scholar]
- Volterra, V. Variations and fluctuations of the number of individuals in animal species living together. ICES J. Mar. Sci. 1928, 3, 3–51. [Google Scholar] [CrossRef]
- Lyapunov, A.M. The general problem of the stability of motion. Int. J. Control 1992, 55, 531–534. [Google Scholar] [CrossRef]
- Gantmacher, F. Matrix Theory; Chelsea Publishing Company: New York, NY, USA, 1959. [Google Scholar]
- Miller, T.E. Direct and indirect species interactions in an early old-field plant community. Am. Nat. 1994, 143, 1007–1025. [Google Scholar] [CrossRef]
- Levine, J.M.; Bascompte, J.; Adler, P.B.; Allesina, S. Beyond pairwise mechanisms of species coexistence in complex communities. Nature 2017, 546, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Soliveres, S.; Lehmann, A.; Boch, S.; Altermatt, F.; Carrara, F.; Crowther, T.W.; Delgado-Baquerizo, M.; Kempel, A.; Maynard, D.S.; Rillig, M.C.; et al. Intransitive competition is common across five major taxonomic groups and is driven by productivity, competitive rank and functional traits. J. Ecol. 2018, 106, 852–864. [Google Scholar] [CrossRef]
- Gallardo, B.; Clavero, M.; Sánchez, M.I.; Vilà, M. Global ecological impacts of invasive species in aquatic ecosystems. Glob. Chang. Biol. 2016, 22, 151–163. [Google Scholar] [CrossRef]
- Barabás, G.; Michalska-Smith, M.J.; Allesina, S. The effect of intra-and interspecific competition on coexistence in multispecies communities. Am. Nat. 2016, 188, E1–E12. [Google Scholar] [CrossRef]
- Northfield, T.D.; Laurance, S.G.; Mayfield, M.M.; Paini, D.R.; Snyder, W.E.; Stouffer, D.B.; Wright, J.T.; Lach, L. Native turncoats and indirect facilitation of species invasions. Proc. R. Soc. B Biol. Sci. 2018, 285, 20171936. [Google Scholar] [CrossRef]
- Warren, R.J.; Reed, K.; Mathew, A.; Krupp, K.; Goodman, M.; Archibald, K.; Spiering, D.J. Release from intraspecific competition promotes dominance of a non-native invader. Biol. Invasions 2019, 21, 895–909. [Google Scholar] [CrossRef]
- Allesina, S.; Tang, S. Stability criteria for complex ecosystems. Nature 2012, 483, 205–208. [Google Scholar] [CrossRef]
- Suweis, S.; Grilli, J.; Banavar, J.R.; Allesina, S.; Maritan, A. Effect of localization on the stability of mutualistic ecological networks. Nat. Commun. 2015, 6, 10179. [Google Scholar] [CrossRef]
- Villa Martín, P.; Bonachela, J.A.; Levin, S.A.; Muñoz, M.A. Eluding catastrophic shifts. Proc. Natl. Acad. Sci. USA 2015, 112, E1828–E1836. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Billick, I.; Case, T.J. Higher order interactions in ecological communities: What are they and how can they be detected? Ecology 1994, 75, 1529–1543. [Google Scholar] [CrossRef]
- Grilli, J.; Barabás, G.; Michalska-Smith, M.J.; Allesina, S. Higher-order interactions stabilize dynamics in competitive network models. Nature 2017, 548, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Valentin, R.E.; Nielsen, A.L.; Wiman, N.G.; Lee, D.H.; Fonseca, D.M. Global invasion network of the brown marmorated stink bug, Halyomorpha halys. Sci. Rep. 2017, 7, 9866. [Google Scholar] [CrossRef] [PubMed]
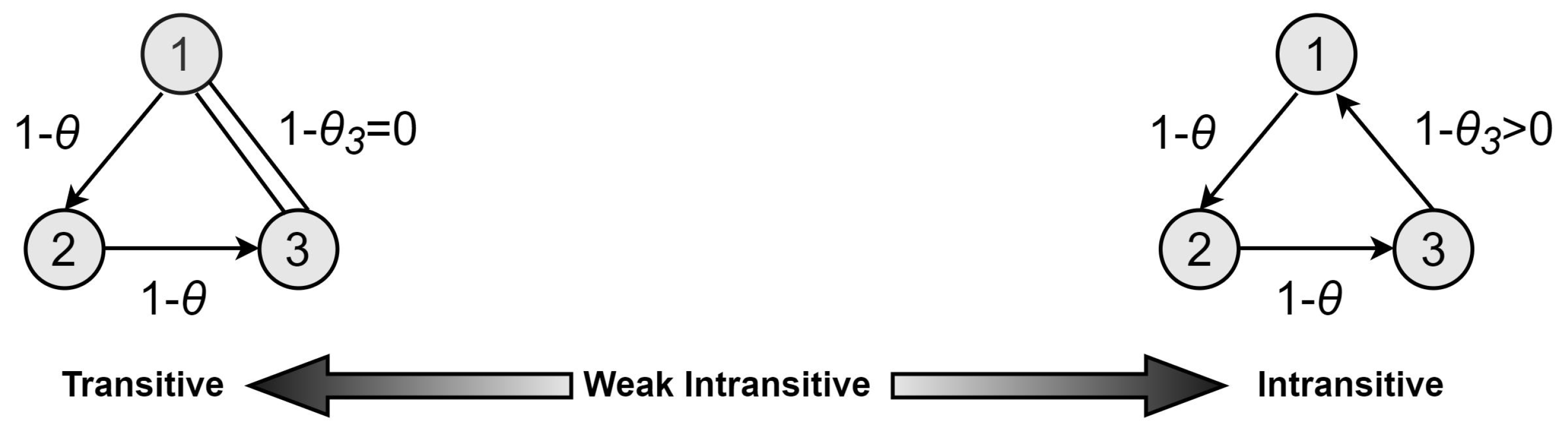





| Scenario | The Meaning of Different Scenarios | Parameter Range |
|---|---|---|
| Case 1 | Strong niche differentiation | |
| Case 2 | Combination of niche differentiation and intransitive competition | |
| Case 3 | Intransitive competition |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Guo, X.; Bao, L.; Yang, Y. Invasion Consequences in Communities Maintained by Niche and Intransitive Coexistence Mechanisms. Diversity 2023, 15, 554. https://doi.org/10.3390/d15040554
Zhang B, Guo X, Bao L, Yang Y. Invasion Consequences in Communities Maintained by Niche and Intransitive Coexistence Mechanisms. Diversity. 2023; 15(4):554. https://doi.org/10.3390/d15040554
Chicago/Turabian StyleZhang, Bozhong, Xiaolong Guo, Liping Bao, and Yinghui Yang. 2023. "Invasion Consequences in Communities Maintained by Niche and Intransitive Coexistence Mechanisms" Diversity 15, no. 4: 554. https://doi.org/10.3390/d15040554
APA StyleZhang, B., Guo, X., Bao, L., & Yang, Y. (2023). Invasion Consequences in Communities Maintained by Niche and Intransitive Coexistence Mechanisms. Diversity, 15(4), 554. https://doi.org/10.3390/d15040554





