Combining Geographic Distribution and Trait Information to Infer Predator–Prey Species-Level Interaction Properties
Abstract
1. Introduction
2. Materials and Methods
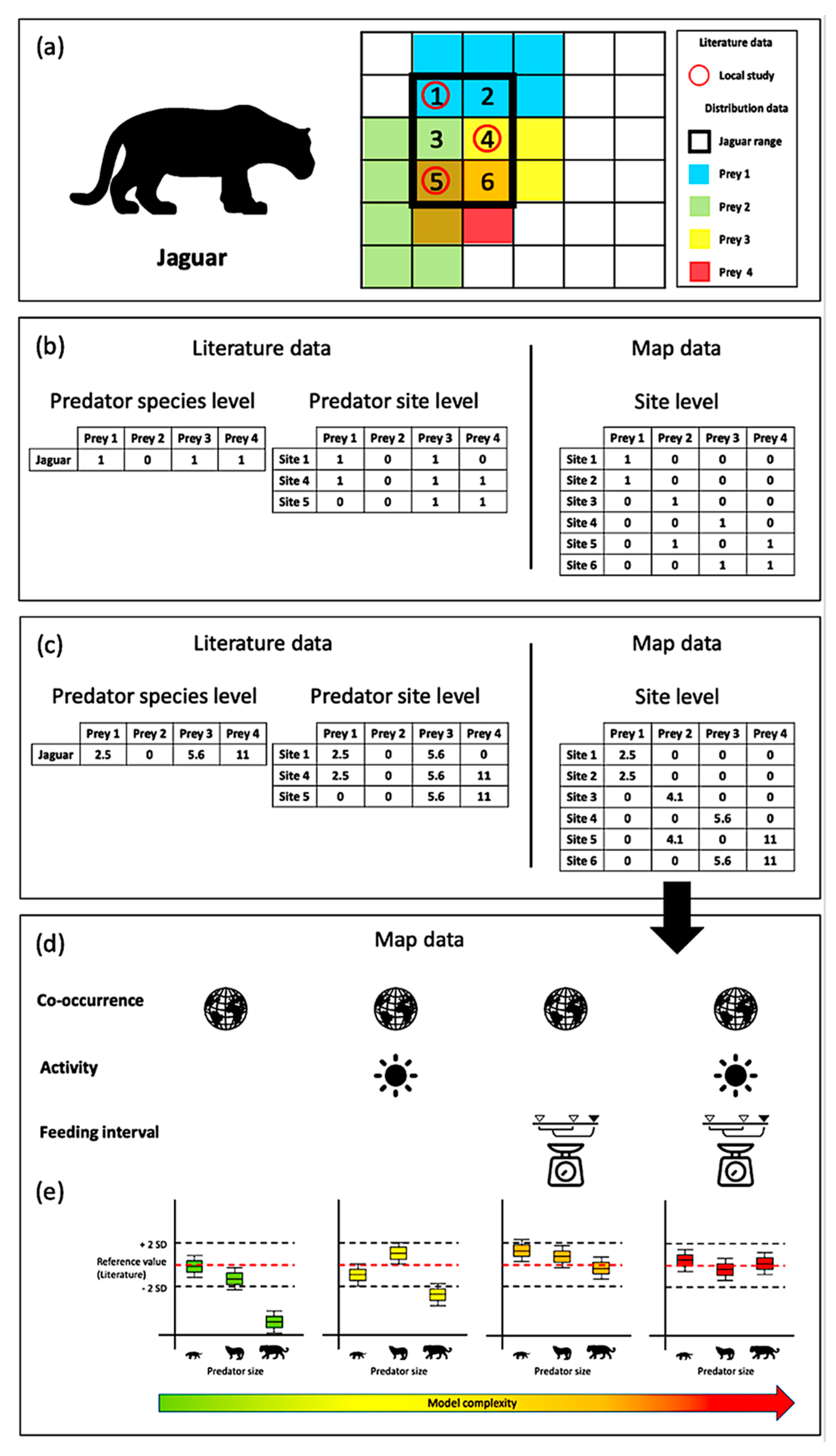
2.1. Data Collection
2.2. Interaction Properties: Summary of the Approach
2.3. Trait Combinations and Interaction Models
2.4. Model Performance
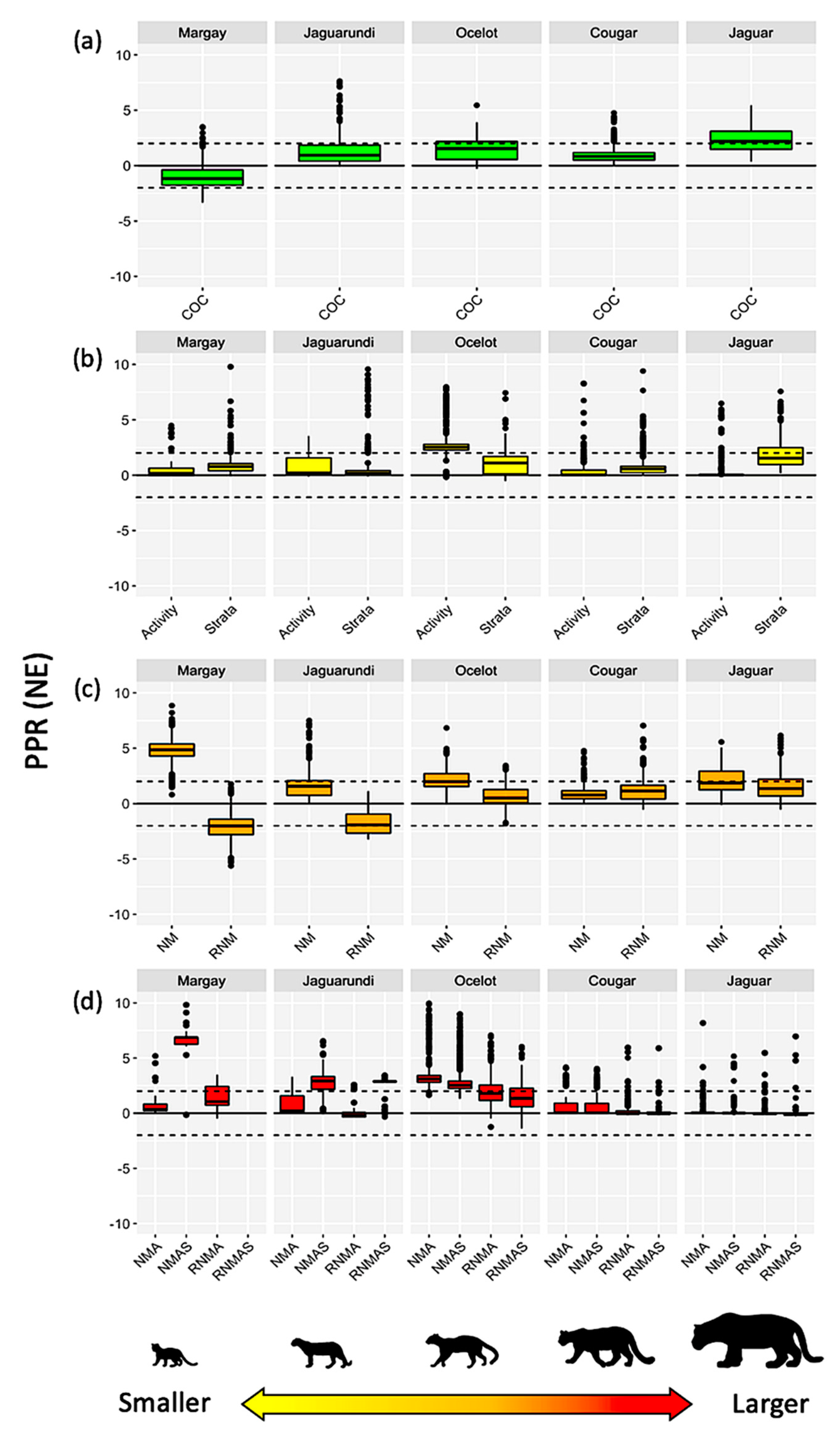
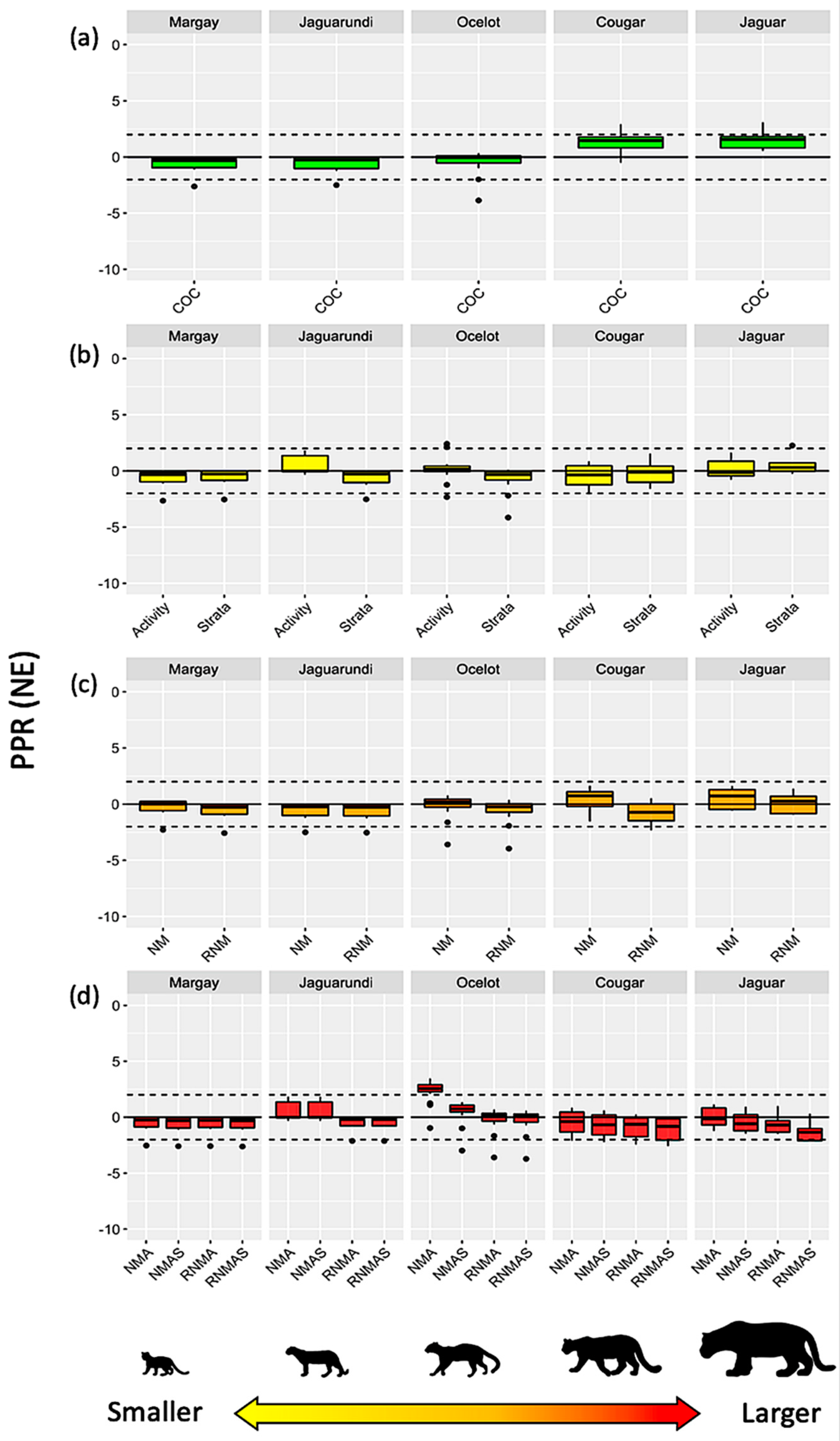
3. Results
Interaction Models vs. Reference Values
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hortal, J.; de Bello, F.; Diniz-Filho, J.A.F.; Lewinsohn, T.M.; Lobo, J.M.; Ladle, R.J. Seven shortfalls that beset large-scale knowledge of biodiversity. Annu. Rev. Ecol. Evol. Syst. 2015, 46, 523–549. [Google Scholar] [CrossRef]
- Poisot, T.; Stouffer, D.B.; Gravel, D. Beyond species: Why ecological interaction networks vary through space and time. Oikos 2015, 124, 243–251. [Google Scholar] [CrossRef]
- Gravel, D.; Baiser, B.; Dunne, J.A.; Kopelke, J.P.; Martinez, N.D.; Nyman, T.; Poisot, T.; Stouffer, D.B.; Tylianakis, J.M.; Wood, S.A.; et al. Bringing Elton and Grinnell together: A quantitative framework to represent the biogeography of ecological interaction networks. Ecography 2019, 42, 401–415. [Google Scholar] [CrossRef]
- Poelen, J.H.; Simons, J.D.; Mungall, C.J. Global biotic interactions: An open infrastructure to share and analyze species-interaction datasets. Ecol. Inform. 2014, 24, 148–159. [Google Scholar] [CrossRef]
- Kopelke, J.P.; Nyman, T.; Cazelles, K.; Gravel, D.; Vissault, S.; Roslin, T. Food-web structure of willow-galling sawflies and their natural enemies across Europe. Ecology 2017, 98, 1730. [Google Scholar] [CrossRef]
- Blanchet, F.G.; Cazelles, K.; Gravel, D. Co-occurrence is not evidence of ecological interactions. Ecol. Lett. 2020, 23, 1050–1063. [Google Scholar] [CrossRef]
- Valiente-Banuet, A.; Aizen, M.A.; Alcántara, J.M.; Arroyo, J.; Cocucci, A.; Galetti, M.; García, M.B.; García, D.; Gómez, J.M.; Jordano, P.; et al. Beyond species loss: The extinction of ecological interactions in a changing world. Funct. Ecol. 2015, 29, 299–307. [Google Scholar] [CrossRef]
- Wood, C.L.; Zgliczynski, B.J.; Haupt, A.J.; Guerra, A.S.; Micheli, F.; Sandin, S.A. Human impacts decouple a fundamental ecological relationship—The positive association between host diversity and parasite diversity. Glob. Chang. Biol. 2018, 24, 3666–3679. [Google Scholar] [CrossRef]
- Forbes, S. On the Local Distribution of Certain Illinois Fishes: An Essay in Statistical Ecology. Bull. Ill State Lab. Nat. History 1907, 12, 273–303. [Google Scholar]
- Morales-Castilla, I.; Matias, M.G.; Gravel, D.; Araújo, M.B. Inferring biotic interactions from proxies. Trends Ecol. Evol. 2015, 30, 347–356. [Google Scholar] [CrossRef]
- Pappalardo, P.; Morales-Castilla, I.; Park, A.W.; Huang, S.; Schmidt, J.P.; Stephens, P.R. Comparing methods for mapping global parasite diversity. Glob. Ecol. Biogeogr. 2020, 29, 182–193. [Google Scholar] [CrossRef]
- Elton, C.S. Animal Ecology, 1st ed.; Macmillan: New York, NY, USA, 1927; p. 50. [Google Scholar]
- O’Connor, L.M.; Pollock, L.J.; Braga, J.; Ficetola, G.F.; Maiorano, L.; Martinez-Almoyna, C.; Montemaggiori, A.; Ohlmann, M.; Thuiller, W. Unveiling the food webs of tetrapods across Europe through the prism of the Eltonian niche. J. Biogeogr. 2020, 47, 181–192. [Google Scholar] [CrossRef]
- Williams, R.J.; Anandanadesan, A.; Purves, D. The probabilistic niche model reveals the niche structure and role of body size in a complex food web. PLoS ONE 2010, 5, e12092. [Google Scholar] [CrossRef] [PubMed]
- Gravel, D.; Poisot, T.; Albouy, C.; Velez, L.; Mouillot, D. Inferring food web structure from predator–prey body size relationships. Methods Ecol. Evol. 2013, 4, 1083–1090. [Google Scholar] [CrossRef]
- Rosado, B.H.; Figueiredo, M.S.; de Mattos, E.A.; Grelle, C.E. Eltonian shortfall due to the Grinnellian view: Functional ecology between the mismatch of niche concepts. Ecography 2016, 39, 1034–1041. [Google Scholar] [CrossRef]
- Soberón, J. Grinnellian and Eltonian niches and geographic distributions of species. Ecol. Lett. 2007, 10, 1115–1123. [Google Scholar] [CrossRef] [PubMed]
- Kissling, W.D.; Dormann, C.F.; Groeneveld, J.; Hickler, T.; Kühn, I.; McInerny, G.J.; Montoya, J.M.; Römermann, C.; Schiffers, K.; Schurr, F.M.; et al. Towards novel approaches to modelling biotic interactions in multispecies assemblages at large spatial extents. J. Biogeogr. 2012, 39, 2163–2178. [Google Scholar] [CrossRef]
- Pichler, M.; Boreux, V.; Klein, A.M.; Schleuning, M.; Hartig, F. Machine learning algorithms to infer trait-matching and predict species interactions in ecological networks. Methods Ecol. Evol. 2019, 11, 281–293. [Google Scholar] [CrossRef]
- Carbone, C.; Mace, G.M.; Roberts, S.C.; Macdonald, D.W. Energetic constraints on the diet of terrestrial carnivores. Nature 1999, 402, 286–288. [Google Scholar] [CrossRef]
- Riede, J.O.; Brose, U.; Ebenman, B.; Jacob, U.; Thompson, R.; Townsend, C.R.; Jonsson, T. Stepping in Elton’s footprints: A general scaling model for body masses and trophic levels across ecosystems. Ecol. Lett. 2011, 14, 169–178. [Google Scholar] [CrossRef]
- Tucker, M.A.; Rogers, T.L. Examining predator–prey body size, trophic level and body mass across marine and terrestrial mammals. Proc. R Soc. B Biol. Sci. 2014, 281, 20142103. [Google Scholar] [CrossRef]
- Smith, F.A.; Lyons, S.K. How big should a mammal be? A macroecological look at mammalian body size over space and time. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 2364–2378. [Google Scholar] [CrossRef]
- Palomares, F.; Caro, T.M. Interspecific killing among mammalian carnivores. Am. Nat. 1999, 153, 492–508. [Google Scholar] [CrossRef]
- Wilman, H.; Belmaker, J.; Simpson, J.; de la Rosa, C.; Rivadeneira, M.M.; Jetz, W. EltonTraits 1.0: Species-level foraging attributes of the world's birds and mammals: Ecological Archives E095-178. Ecology 2014, 95, 2027. [Google Scholar] [CrossRef]
- Kissling, W.D.; Schleuning, M. Multispecies interactions across trophic levels at macroscales: Retrospective and future directions. Ecography 2015, 38, 346–357. [Google Scholar] [CrossRef]
- Pacifici, M.; Santini, L.; Di Marco, M.; Baisero, D.; Francucci, L.; Marasini, G.G.; Visconti, P.; Rondinini, C. Generation length for mammals. Nat. Conserv. 2013, 5, 89. [Google Scholar]
- Sánchez-Barradas, A.; Villalobos, F. Species geographical co-occurrence and the effect of Grinnellian and Eltonian niche partitioning: The case of a Neotropical felid assemblage. Ecol. Res. 2020, 35, 382–393. [Google Scholar] [CrossRef]
- Villalobos, F.; Rangel, T.F.; Diniz-Filho, J.A.F. Phylogenetic fields of species: Cross-species patterns of phylogenetic structure and geographical coexistence. Proc. R Soc. B Biol. Sci. 2013, 280, 20122570. [Google Scholar] [CrossRef] [PubMed]
- Villalobos, F.; Olalla-Tárraga, M.Á.; Cianciaruso, M.V.; Rangel, T.F.; Diniz-Filho, J.A.F. Global patterns of mammalian co-occurrence: Phylogenetic and body size structure within species ranges. J. Biogeogr. 2017, 44, 136–146. [Google Scholar] [CrossRef]
- Williams, R.J.; Martinez, N.D. Simple rules yield complex food webs. Nature 2000, 404, 180–183. [Google Scholar] [CrossRef]
- Emmons, L.H. Comparative feeding ecology of felids in a neotropical rainforest. Behav. Ecol. Sociobiol. 1987, 20, 271–283. [Google Scholar] [CrossRef]
- Knopff, K.H.; Boyce, M.S. Prey specialization by individual cougars in multiprey systems. In Transactions of the North American Wildlife and Natural Resources Conference; FAO: Rome, Italy, 2007. [Google Scholar]
- Van Valkenburgh, B. Iterative evolution of hypercarnivory in canids (Mammalia: Carnivora): Evolutionary interactions among sympatric predators. Paleobiology 1991, 17, 340–362. [Google Scholar] [CrossRef]
- Giordano, A.J. Ecology and status of the jaguarundi Puma yagouaroundi: A synthesis of existing knowledge. Mammal Rev. 2016, 46, 30–43. [Google Scholar] [CrossRef]
- López-González, C.A.; Miller, B.J. Do jaguars (Panthera onca) depend on large prey? West. N. Am. Nat. 2002, 62, 218–222. [Google Scholar]
- Brodie, J.F. Is research effort allocated efficiently for conservation? Felidae as a global case study. Biodivers. Conserv. 2009, 18, 2927–2939. [Google Scholar] [CrossRef]
- Hernández-Lara, C.; Carbó-Ramírez, P.; Santiago-Alarcon, D. Effects of land use change (rural-urban) on the diversity and epizootiological parameters of avian Haemosporida in a widespread neotropical bird. Acta Tropica 2020, 209, 105542. [Google Scholar] [CrossRef]
- Sunquist, M.E.; Sunquist, F.C. Wild Cats of the World, 1st ed.; University of Chicago Press: Chicago, IL, USA, 2002; p. 451. [Google Scholar]
- Massara, R.L.; de Oliveira Paschoal, A.M.; Bailey, L.L.; Doherty, P.F., Jr.; de Frias Barreto, M.; Chiarello, A.G. Effect of humans and pumas on the temporal activity of ocelots in protected areas of Atlantic Forest. Mamm. Biol. 2018, 92, 86–93. [Google Scholar] [CrossRef]
| Models | Distribution | Traits | Model Complexity | |||
|---|---|---|---|---|---|---|
| Activity Period | Foraging Strata | Prey Body Mass | ||||
| Interval | Preference | |||||
| Co-occurrence | 1 | 0 | 0 | 0 | 0 |  |
| Activity | 1 | 1 | 0 | 0 | 0 | |
| Strata | 1 | 0 | 1 | 0 | 0 | |
| NM | 1 | 0 | 0 | 1 | 0 | |
| RNM | 1 | 0 | 0 | 1 | 1 | |
| NMA | 1 | 1 | 0 | 1 | 0 | |
| NMAS | 1 | 1 | 1 | 1 | 0 | |
| RNMA | 1 | 1 | 0 | 1 | 1 | |
| RNMAS | 1 | 1 | 1 | 1 | 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Barradas, A.; Dáttilo, W.; Santiago-Alarcon, D.; Kissling, W.D.; Villalobos, F. Combining Geographic Distribution and Trait Information to Infer Predator–Prey Species-Level Interaction Properties. Diversity 2023, 15, 61. https://doi.org/10.3390/d15010061
Sánchez-Barradas A, Dáttilo W, Santiago-Alarcon D, Kissling WD, Villalobos F. Combining Geographic Distribution and Trait Information to Infer Predator–Prey Species-Level Interaction Properties. Diversity. 2023; 15(1):61. https://doi.org/10.3390/d15010061
Chicago/Turabian StyleSánchez-Barradas, Alejandro, Wesley Dáttilo, Diego Santiago-Alarcon, W. Daniel Kissling, and Fabricio Villalobos. 2023. "Combining Geographic Distribution and Trait Information to Infer Predator–Prey Species-Level Interaction Properties" Diversity 15, no. 1: 61. https://doi.org/10.3390/d15010061
APA StyleSánchez-Barradas, A., Dáttilo, W., Santiago-Alarcon, D., Kissling, W. D., & Villalobos, F. (2023). Combining Geographic Distribution and Trait Information to Infer Predator–Prey Species-Level Interaction Properties. Diversity, 15(1), 61. https://doi.org/10.3390/d15010061







