The Effect of Grapevine Variety and Wine Region on the Primer Parameters of Wine Based on 1H NMR-Spectroscopy and Machine Learning Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Apparatus and Measurement
2.3. Classification Methods
2.3.1. Linear Discriminant Analysis (LDA)
2.3.2. Neural Networks (NN)
2.3.3. Random Forest
2.3.4. Support Vector Machines (SVM)
2.4. Model Evaluations
2.5. Visualization
3. Results
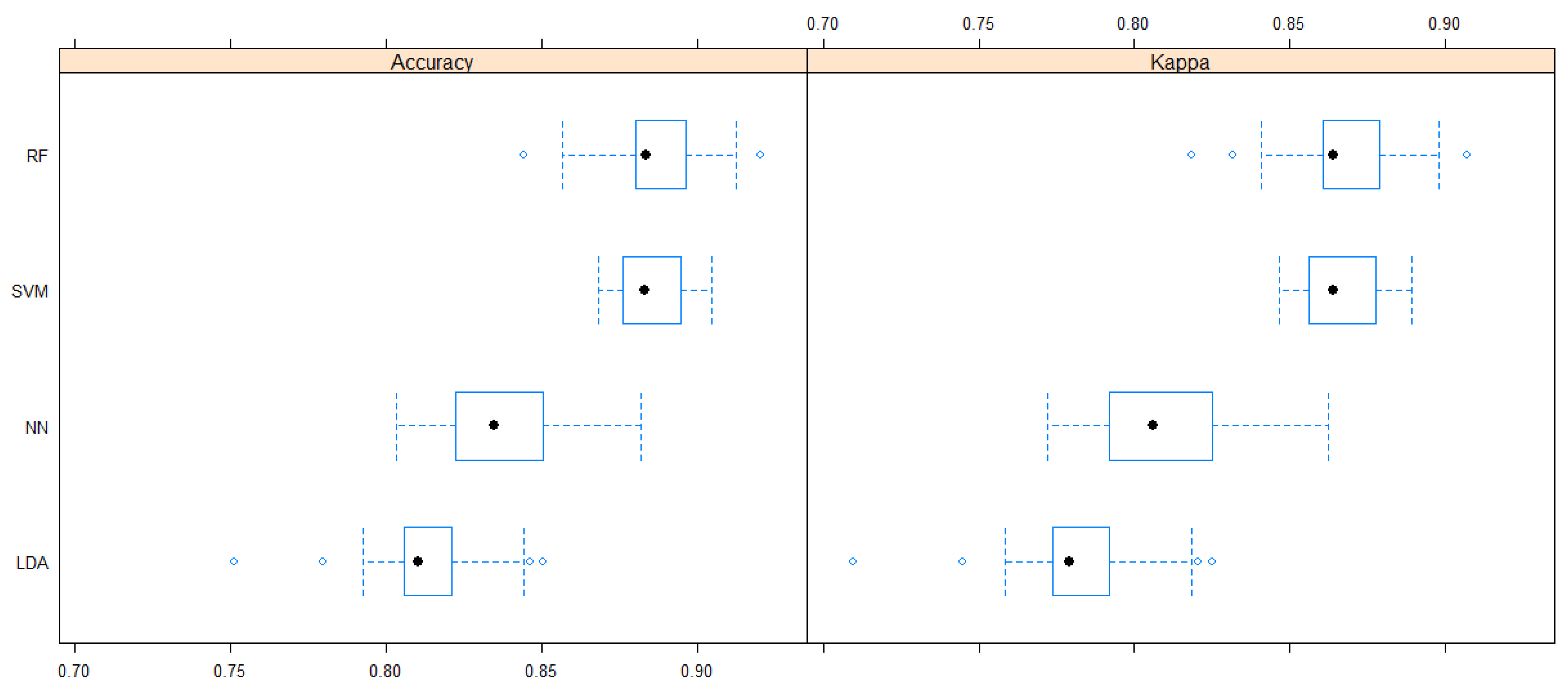
3.1. Linear Discriminant Analysis and Neural Networks
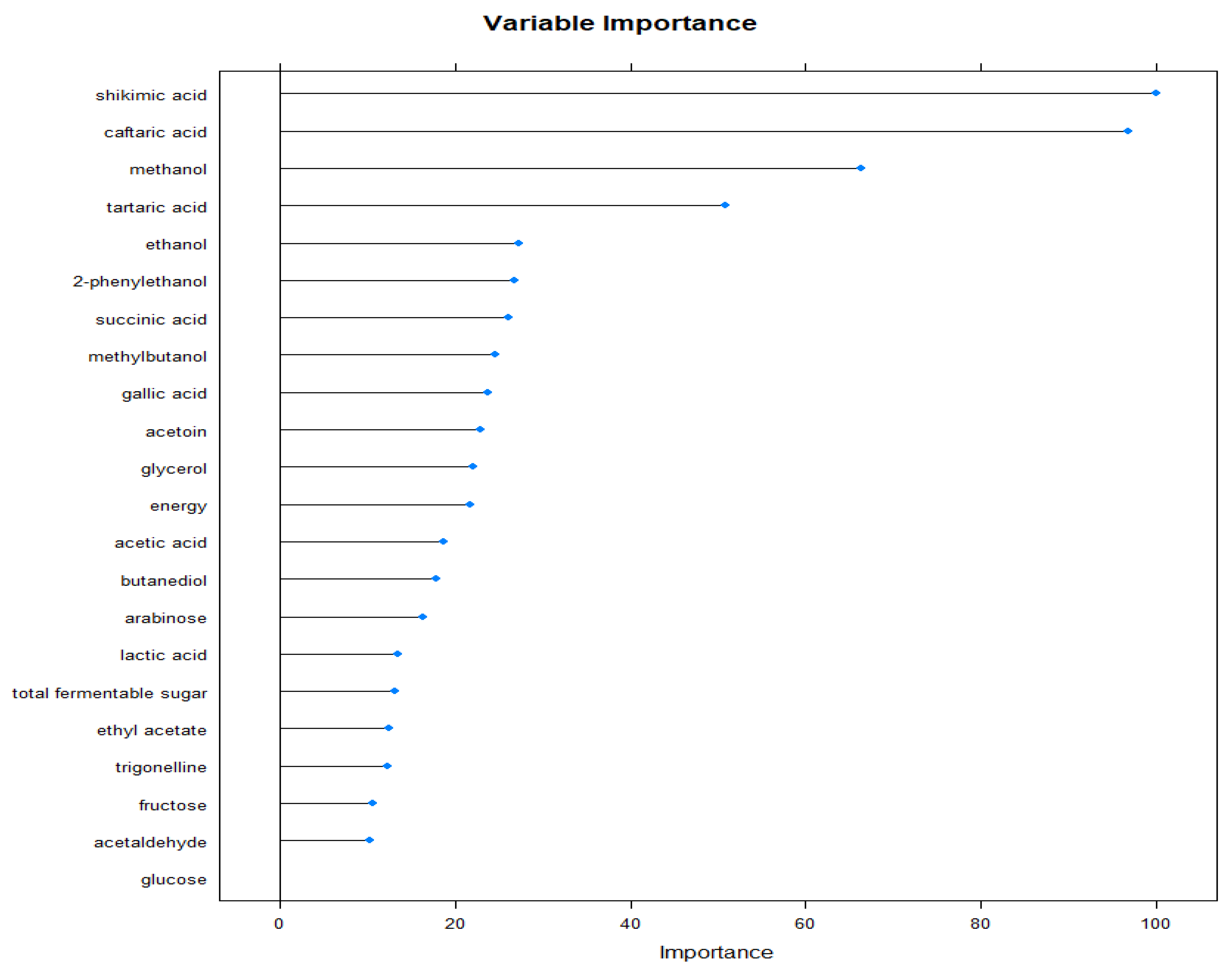
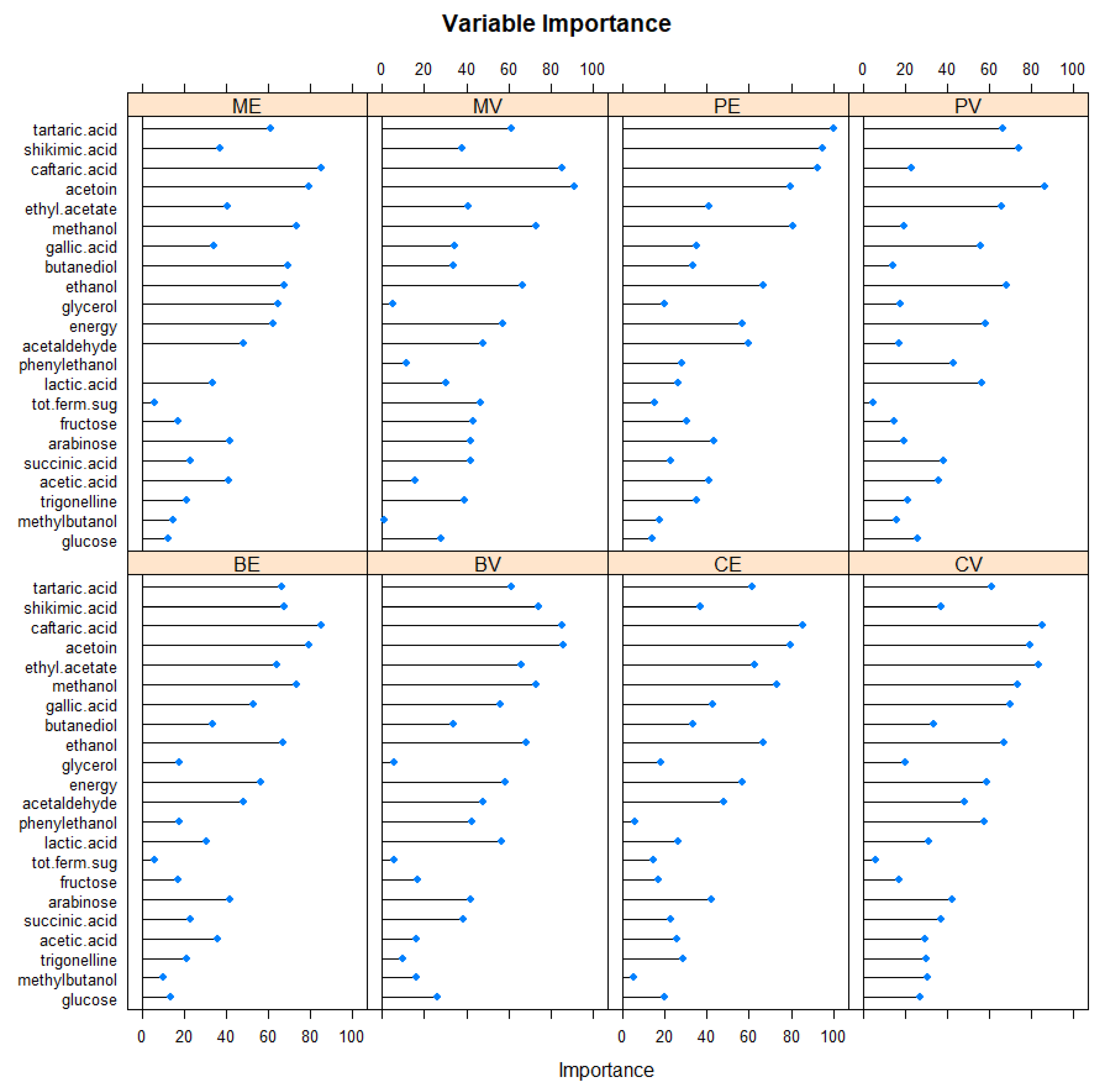
3.2. Random Forest (RF) and Support Vector Machines (SVM)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Simmler, C.; Napolitano, J.G.; McAlpine, J.B.; Chen, S.N.; Pauli, G.F. Universal quantitative NMR analysis of complex natural samples. Curr. Opin. Biotechnol. 2014, 25, 51–59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Consonni, R.; Cagliani, L.R. The potentiality of NMR-based metabolomics in food science and food authentication assessment. Magn. Reson. Chem. MRC 2019, 57, 558–578. [Google Scholar] [CrossRef]
- Du, Y.Y.; Bai, G.Y.; Zhang, X.; Liu, M.L. Classification of wines based on combination of 1H NMR spectroscopy and principal component analysis. Chin. J. Chem. 2007, 25, 930–936. [Google Scholar] [CrossRef]
- Consonni, R.; Cagliani, L.R.; Guantieri, V.; Simonato, B. Identification of metabolic content of selected Amarone wine. Food Chem. 2017, 129, 693–699. [Google Scholar] [CrossRef]
- Anastasiadi, M.; Zir, A.; Magiatis, P.; Haroutounian, S.A.; Skaltsounis, A.L.; Mikros, E. 1H NMR-based metabolomics for the classification of Greek wines according to variety, region, and vintage. Comparison with HPLC data. J. Agric. Food Chem. 2009, 57, 11067–11074. [Google Scholar] [CrossRef] [PubMed]
- Minoja, A.P.; Napoli, C. NMR screening in the quality control of food and nutraceuticals. Food. Res. Int. 2014, 63, 126–131. [Google Scholar] [CrossRef]
- Consonni, R.; Cagliani, L.R. Chapter 4—Nuclear magnetic resonance and chemometrics to assess geographical origin and quality of traditional food products. In Advances in Food and Nutrition Research; Steve, L.T., Ed.; Cambridge Academic Press: Cambridge, UK, 2010; Volume 59, pp. 87–165. [Google Scholar] [CrossRef]
- Spyros, A.; Dais, P. NMR Spectroscopy in Food Analysis; Cambridge RSC: Cambridge, UK, 2012; pp. 1–343. ISBN 978-1-84973-175-1. [Google Scholar] [CrossRef] [Green Version]
- Spyros, A. Application of NMR in food analysis. In Specialist Periodical Reports: Nuclear Magnetic Resonance; Ramesh, V., Ed.; London RSC: London, UK, 2016; Volume 45, pp. 269–307. [Google Scholar]
- Consonni, R.; Astraka, K.; Cagliani, L.R.; Nenadis, N.; Petrakis, E.; Polissiou, M. Authenticity of food. In Encyclopedia of Food and Health; Caballero, B., Finglas, P., Toldrá, F., Eds.; Oxford Academic Press: Oxford, UK, 2016; pp. 285–293. [Google Scholar]
- Bloch, F. Nuclear induction. Am. Phys. Soc. 1946, 70, 460–474. [Google Scholar] [CrossRef]
- Abdul-Hamid, N.A.; Abas, F.; Ismail, I.S.; Tham, C.L.; Maulidiani, M.; Mediani, A.; Swarup, S.; Umashankar, S.; Zolkeflee, N.K. Metabolites and biological activities of Phoenix dactylifera L. pulp and seeds: A comparative MS and NMR based metabolomics approach. Phytochem. Lett. 2019, 31, 20–32. [Google Scholar] [CrossRef]
- Godelmann, R.; Fang, F.; Humpfer, E.; Schütz, B.; Bansbach, M.; Schäfer, H.; Spraul, M. Targeted and Nontargeted Wine Analysis by 1H NMR Spectroscopy Combined with Multivariate Statistical Analysis. Differentiation of Important Parameters: Grape Variety, Geographical Origin, Year of Vintage. Agric. Food Chem. 2013, 61, 5610–5619. [Google Scholar] [CrossRef]
- Holmes, E.; Nicholls, A.W.; Lindon, J.C.; Connor, S.C.; Connelly, J.C.; Haselden, J.N.; Damment, S.J.; Spraul, M.; Neidig, P.; Nicholson, J.K. Chemometric models for toxicity classification based on NMR spectra of biofluids. Chem. Res. Toxicol. 2000, 13, 471–478. [Google Scholar] [CrossRef]
- Lindon, J.C.; Nicholson, J.K.; Holmes, E.; Everett, J.R. Metabonomics: Metabolic processes studied by NMR spectroscopy of biofluids. Concepts Magn. Reson. 2000, 12, 289–320. [Google Scholar] [CrossRef]
- Mazzei, P.; Francesca, N.; Moschetti, G.; Piccolo, A. NMR spectroscopy evaluation of direct relationship between soils and molecular composition of red wines from Aglianico grapes. Anal. Chim. Acta 2010, 673, 167–172. [Google Scholar] [CrossRef] [PubMed]
- Monkahova, Y.B.; Schäfer, H.; Humpfer, E.; Spraul, M.; Kuballa, T.; Lachenmeier, D.W. Application of automated eightfold suppression of water and ethanol signals in 1H NMR to provide sensitivity for analyzing alcoholic beverages. Magn. Reson. Chem. 2011, 49, 734–739. [Google Scholar] [CrossRef] [PubMed]
- McClure, C.K. Structural Chemistry Using NMR Spectroscopy, Organic Molecules. In Encyclopedia of Spectroscopy and Spectrometry, 3rd ed.; Lindon, J.C., Tranter, G.E., Koppenaal, D.W., Eds.; Academic Press: Oxford, UK, 2017; pp. 281–292. [Google Scholar]
- Liu, M.; Nicholson, J.K.; Lindon, J.C. High resolution diffusion and relaxation edited one- and two-dimensional 1H NMR spectroscopy of biological fluids. Anal. Chem. 1996, 68, 3370–3376. [Google Scholar] [CrossRef]
- Alsante, K.M.; Baertschi, S.W.; Brian, M.C.; Marquez, L.; Sharp, T.R.; Zelesky, T.C. Degradation and Impurity Analysis for Pharmaceutical Drug Candidates. Sep. Sci. Technol. 2011, 10, 59–169. [Google Scholar]
- Magda, D.A.; Pirnau, A.; Feher, I.; Guyon, F.; Cozar, B.I. Alternative approach of applying 1H NMR in conjunction with chemometrics for wine classification. Lebensm. Wiss. Technol. 2019, 109, 422–428. [Google Scholar] [CrossRef]
- Amargianitaki, M.; Spyros, A. NMR-based metabolomics in wine quality control and authentication. Chem. Biol. Technol. Agric. 2017, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Masetti, O.; Sorbo, A.; Nisini, L. NMR Tracing of Food Geographical Origin: The Impact of Seasonality, Cultivar and Production Year on Data Analysis. Separations 2021, 8, 230. [Google Scholar] [CrossRef]
- Kalogiouri, N.P.; Samanidou, V.F. Liquid chromatographic methods coupled to chemometrics: A short review to present the key workflow for the investigation of wine phenolic composition as it is affected by environmental factors. Environ. Sci. Pollut. Res. 2021, 28, 59150–59164. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.C. The utilization of multiple measurements in problems of biological classification. J. R. Stat. Soc. Ser. B 1948, 10, 159–203. [Google Scholar] [CrossRef]
- Nisbet, R.; Miner, G.; Yale, K. Handbook of Statistical Analysis and Data Mining Applications, 2nd ed.; Academic Press: Cambridge, MA, USA, 2018; ISBN 9780124166325. [Google Scholar] [CrossRef]
- Fausett, L. Fundamentals of Neural Networks; Prentice Hall: New York, NY, USA, 1994. [Google Scholar]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000; ISBN 0-521-78019-5. [Google Scholar]
- Breiman, L.; Cutler, A.; Liaw, A.; Wiener, M. Breiman and Cutler’s Random Forests for Classification and Regression, R package Version 4.6–14; 2018. Available online: https://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 18 January 2022).
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168–192. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; Wiley: New York, NY, USA, 2000; pp. 160–164. ISBN 978-0-470-58247-3. [Google Scholar]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Cor-relation. J. Mach. Learn. Technol. 2011, 2, 37–63. Available online: https://bioinfopublication.org/files/articles/2_1_1_JMLT.pdf (accessed on 18 January 2022).
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Augustin, T. Unbiased split selection for classification trees based on the Gini Index. Comput. Stat. Data Anal. 2006, 52, 483–501. [Google Scholar] [CrossRef] [Green Version]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [Green Version]
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. In Advances in Neural Information Processing Systems; Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Lake Tahoe, CA, USA, 2013; pp. 431–439. [Google Scholar]
- Gregorutti, B.; Michel, B.; Saint Pierre, P. Grouped variable importance with random forests and application to multiple functional data analysis. Comput. Stat. Data Anal. 2015, 90, 15–35. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. 2020. Available online: https://www.R-project.org/ (accessed on 18 January 2022).
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth & Brooks/Cole Advanced Books & Software: Monterey, CA, USA, 1984. [Google Scholar]
- Tuszynski, J. caTools: Tools: Moving window statistics, GIF, Base64, ROC AUC, etc. R Package Version 1.18.0. 2020. Available online: https://CRAN.R-project.org/package=caTools (accessed on 18 January 2022).
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R Package Version 1.7-3. 2019. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 18 January 2022).
- Kuhn, M. caret: Classification and Regression Training. R Package Version 6.0-86. 2020. Available online: https://CRAN.R-project.org/package=caret (accessed on 18 January 2022).
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T. ROCR: Visualizing classifier performance in R. Bioinformatics 2005, 21, 7881. Available online: https://academic.oup.com/bioinformatics/article/21/20/3940/202693 (accessed on 18 January 2022). [CrossRef]
- Filho, E.J.A.; Silva, L.M.A.; Ribeiro, P.R.V.; de Brito, E.S.; Zocolo, G.J.; Souza-Leao, P.C.; Marquez, A.T.B.; Quintela, A.L.; Larsen, F.H.; Canuto, K.M. 1H NMR and LC-MS-based metabolomic approach for evaluation for the seasonality and viticultural practices in wines from Sao Francisco River Valley, a Brazilian semi-arid region. Food Chem. 2019, 289, 558–567. [Google Scholar] [CrossRef]
- Mascellani, A.; Hoca, G.; Babisz, M.; Krska, P.; Kloucek, P.; Havlik, J. 1H NMR chemometric models for classification of Czech wine type and variety. Food Chem. 2021, 339, 127852. [Google Scholar] [CrossRef]
- Gougeon, L.; da Costa, G.; Le Mao, I.; Ma, W.; Teissedre, P.L.; Guyon, F.; Richard, T. Wine analysis and authenticity using 1H NMR metabolomics data: Application to Chinese wines. Food Anal. Methods 2018, 11, 3425–3434. [Google Scholar] [CrossRef]
- Geana, E.I.; Popescu, R.; Costinel, D.; Dinca, O.R.; Ionete, R.E.; Stefanescu, I.; Artem, V.; Balaet, C. Classification of red wines using suitable markers coupled with multivariate statistic analysis. Food Chem. 2016, 192, 1015–1024. [Google Scholar] [CrossRef]
- Caruso, M.; Galgano, F.; Castiglione Morelli, M.A.; Viggiani, L.; Lencioni, L.; Giussani, B.; Favati, F. Chemical profile of white wines produced from ‘Greco bianco’ grape variety indifferent Italian areas by Nuclear Magnetic Resonance (NMR) and conventional physico chemical analyses. J. Agric. Food Chem. 2012, 60, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Pereira, G.E.; Gaudillere, J.P.; Van Leeuwen, C.; Hilbert, G.; Lavialle, O.; Maucourt, M.; Deborde, C.; Moing, A.; Rolin, D. 1H NMR and chemometrics to characterize mature grape berries in four wine-growing areas in Bordeaux, France. J. Agric. Food Chem. 2005, 53, 6382–6389. [Google Scholar] [CrossRef]
- Papotti, G.; Bertelli, D.; Graziosi, R.; Silvestri, M.; Bertacchini, L.; Durante, C.; Plessi, M. Application of One and two-dimensional NMR spectroscopy for the characterization of Protected Designation of Origin Lambrusco wines of Modena. J. Agric. Food Chem. 2013, 61, 1741–1746. [Google Scholar] [CrossRef]
- Monakhova, Y.B.; Godelmann, R.; Kuballa, T.; Mushtakova, S.P.; Rutledge, D.H. Independent components analysis to increase efficiency of discriminant analysis methods (FDA and LDA): Application to NMR fingerprinting of wine. Talanta 2015, 141, 60–65. [Google Scholar] [CrossRef]
- Viggiani, L.; Castiglione Morelli, M.A. Characterization of wines by Nuclear Magnetic Resonance: A work study on wines from the Basilicata region in Italy. J. Agric. Food Chem. 2008, 56, 8273–8279. [Google Scholar] [CrossRef] [PubMed]
- Son, H.S.; Ki, M.K.; Van Den Berg, F.; Hwang, G.S.; Park, W.M.; Lee, C.H.; Hong, Y.S. 1H nuclear magnetic resonance-based metabolomic characterization of wines by grape varieties and production areas. J. Agric. Food Chem. 2008, 56, 8007–8016. [Google Scholar] [CrossRef] [PubMed]
- Ali, K.; Maltese, F.; Toepfer, R.; Choi, Y.H.; Verpoorte, R. Metabolic characterization of Palatinate German white wines according to sensory attributes, varieties, and vintages using NMR spectroscopy and multivariate data analyses. J. Biomol. NMR 2011, 49, 255–266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martelo-Vidal, M.J.; Vázquez, M. Polyphenolic Profile of Red Wines for the Discrimination of Controlled Designation of Origin. Food Anal. Methods 2016, 9, 332–341. [Google Scholar] [CrossRef]
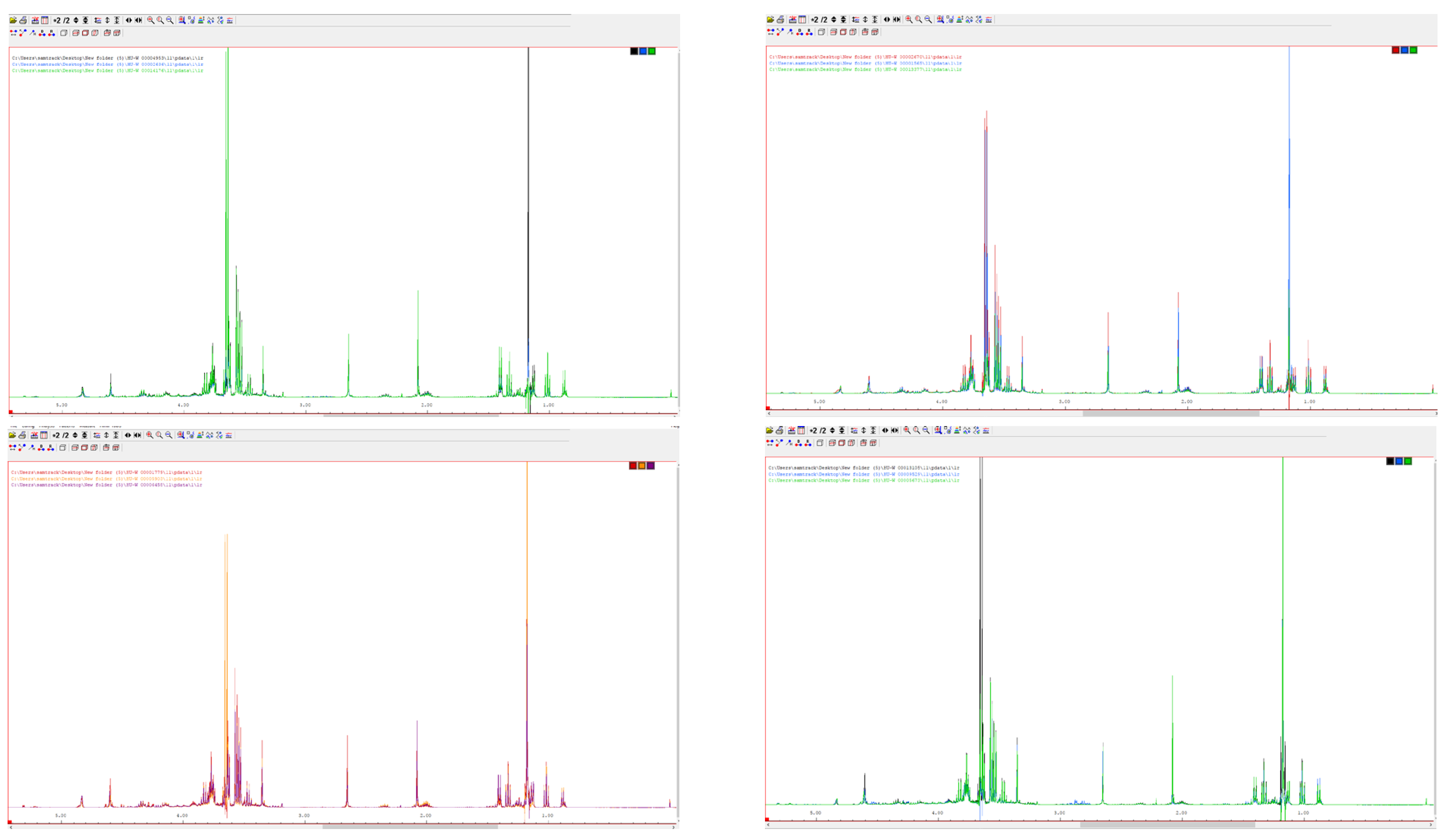


| Wine Region | Vintage | Cabernet Sauvignon | Blaufränkisch | Merlot | Pinot Noir | Total |
|---|---|---|---|---|---|---|
| Villány | 2015 | 65 | 65 | 127 | 56 | 313 |
| 2016 | 61 | 66 | 9 | 60 | 196 | |
| Total | 126 | 131 | 136 | 116 | 509 | |
| Eger | 2015 | 104 | 9 | 34 | 35 | 182 |
| 2016 | 44 | 17 | 57 | 52 | 170 | |
| Total | 148 | 26 | 91 | 87 | 352 |
| Overall Statistics | Overall Accuracy | Weighted Kappa | OOB Error Rate | Accuracy Ratio Test/Train | ||||
|---|---|---|---|---|---|---|---|---|
| 0.95 CI (0.91, 0.97) | 0.95 *** | 12.14% | 0.99 | |||||
| Group Statistics | ||||||||
| Categories | CE | CV | BE | BV | ME | MV | PE | PV |
| OOB class eror rate | 0.07 | 0.12 | 0.20 | 0.05 | 0.18 | 0.09 | 0.15 | 0.03 |
| Class Accuracy | 0.98 | 0.99 | 0.98 | 1.00 | 0.98 | 0.98 | 0.99 | 1.00 |
| Sensitivity or Recall (TPi/(TPi + FNi)) | 0.95 | 0.97 | 0.50 | 1.00 | 0.91 | 0.91 | 1.00 | 1.00 |
| Specificity (TNi/(TNi + FPi)) | 0.99 | 0.97 | 0.97 | 0.96 | 0.97 | 0.99 | 0.99 | 0.99 |
| Positive Prediction Value or Precision PPVi = (TPi/(TPi + FPi)) | 0.95 | 0.94 | 0.60 | 1.00 | 0.91 | 0.97 | 0.92 | 1.00 |
| Negative Prediction Value NPVi = (TNi/(TNi + FNi)) | 0.99 | 0.99 | 0.99 | 1.00 | 0.99 | 0.98 | 1.00 | 1.00 |
| Prevalence ((TPi + FNi)/N) | 0.17 | 0.16 | 0.03 | 0.15 | 0.11 | 0.16 | 0.10 | 0.13 |
| Detection Rate (TPi/N) | 0.16 | 0.15 | 0.01 | 0.15 | 0.10 | 0.14 | 0.10 | 0.13 |
| Detection Prevalence ((TPi + FPi)/N) | 0.17 | 0.16 | 0.02 | 0.15 | 0.11 | 0.15 | 0.11 | 0.13 |
| Balanced Accuracy ((Sensitivityi + Specificityi)/2) | 0.97 | 0.97 | 0.73 | 0.98 | 0.94 | 0.95 | 0.99 | 0.99 |
| AUC | 0.99 | 0.99 | 0.93 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| F1 score (2*PPV*Sensitivity/(PPV + Sensitivity)) | 0.95 | 0.96 | 0.55 | 1.00 | 0.91 | 0.94 | 0.96 | 1.00 |
| Overall Statistics | Overall Accuracy | Weighted Kappa | Accuracy Ratio Test/Train | |||||
|---|---|---|---|---|---|---|---|---|
| 0.94 CI (0.89, 0.96) | 0.95 *** | 0.94 | ||||||
| Group Statistics | ||||||||
| Categories | CE | CV | BE | BV | ME | MV | PE | PV |
| Class Accuracy | 0.98 | 0.98 | 0.98 | 0.99 | 0.98 | 0.99 | 0.98 | 1.00 |
| Sensitivity or Recall (TPi/(TPi + FNi)) | 0.97 | 0.91 | 0.67 | 0.94 | 0.91 | 0.94 | 0.91 | 1.00 |
| Specificity (TNi/(TNi + FPi)) | 0.98 | 0.97 | 0.96 | 0.96 | 0.96 | 0.97 | 0.98 | 0.98 |
| Positive Prediction Value or Precision PPVi = (TPi/(TPi + FPi)) | 0.92 | 0.97 | 0.57 | 1.00 | 0.91 | 0.97 | 0.87 | 0.97 |
| Negative Prediction Value NPVi = (TNi/(TNi + FNi)) | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 |
| Prevalence ((TPi + FNi)/N) | 0.17 | 0.16 | 0.03 | 0.15 | 0.11 | 0.16 | 0.10 | 0.13 |
| Detection Rate (TPi/N) | 0.17 | 0.14 | 0.02 | 0.14 | 0.10 | 0.15 | 0.09 | 0.13 |
| Detection Prevalence ((TPi + FPi)/N) | 0.18 | 0.15 | 0.03 | 0.14 | 0.11 | 0.15 | 0.11 | 0.14 |
| Balanced Accuracy ((Sensitivityi + Specificityi)/2) | 0.98 | 0.94 | 0.81 | 0.95 | 0.94 | 0.95 | 0.94 | 0.99 |
| AUC | 0.97 | 0.97 | 0.73 | 0.98 | 0.94 | 0.95 | 0.99 | 0.99 |
| F1 score (2*PPV*Sensitivity/(PPV + Sensitivity)) | 0.95 | 0.94 | 0.62 | 0.97 | 0.91 | 0.96 | 0.89 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyitrainé Sárdy, Á.D.; Ladányi, M.; Varga, Z.; Szövényi, Á.P.; Matolcsi, R. The Effect of Grapevine Variety and Wine Region on the Primer Parameters of Wine Based on 1H NMR-Spectroscopy and Machine Learning Methods. Diversity 2022, 14, 74. https://doi.org/10.3390/d14020074
Nyitrainé Sárdy ÁD, Ladányi M, Varga Z, Szövényi ÁP, Matolcsi R. The Effect of Grapevine Variety and Wine Region on the Primer Parameters of Wine Based on 1H NMR-Spectroscopy and Machine Learning Methods. Diversity. 2022; 14(2):74. https://doi.org/10.3390/d14020074
Chicago/Turabian StyleNyitrainé Sárdy, Ágnes Diána, Márta Ladányi, Zsuzsanna Varga, Áron Pál Szövényi, and Réka Matolcsi. 2022. "The Effect of Grapevine Variety and Wine Region on the Primer Parameters of Wine Based on 1H NMR-Spectroscopy and Machine Learning Methods" Diversity 14, no. 2: 74. https://doi.org/10.3390/d14020074
APA StyleNyitrainé Sárdy, Á. D., Ladányi, M., Varga, Z., Szövényi, Á. P., & Matolcsi, R. (2022). The Effect of Grapevine Variety and Wine Region on the Primer Parameters of Wine Based on 1H NMR-Spectroscopy and Machine Learning Methods. Diversity, 14(2), 74. https://doi.org/10.3390/d14020074







