Genetic Contributions of Genes on Sex Chromosomes and Mitochondrial DNA in a Pedigreed Population
Abstract
1. Introduction
2. Materials and Methods
2.1. Genetic Contribution of an Individual with Respect to Autosomal Genes
2.2. Genetic Contribution with Respect to Genes on Sex Chromosomes and Mitochondrial DNA
2.3. Average Genetic Contribution of an Individual to a Target Population
2.4. Coefficient of Variation of Genetic Contribution
2.5. Example Pedigree Data
2.6. Data Analysis
3. Results and Discussion
3.1. Calculated Genetic Contribution
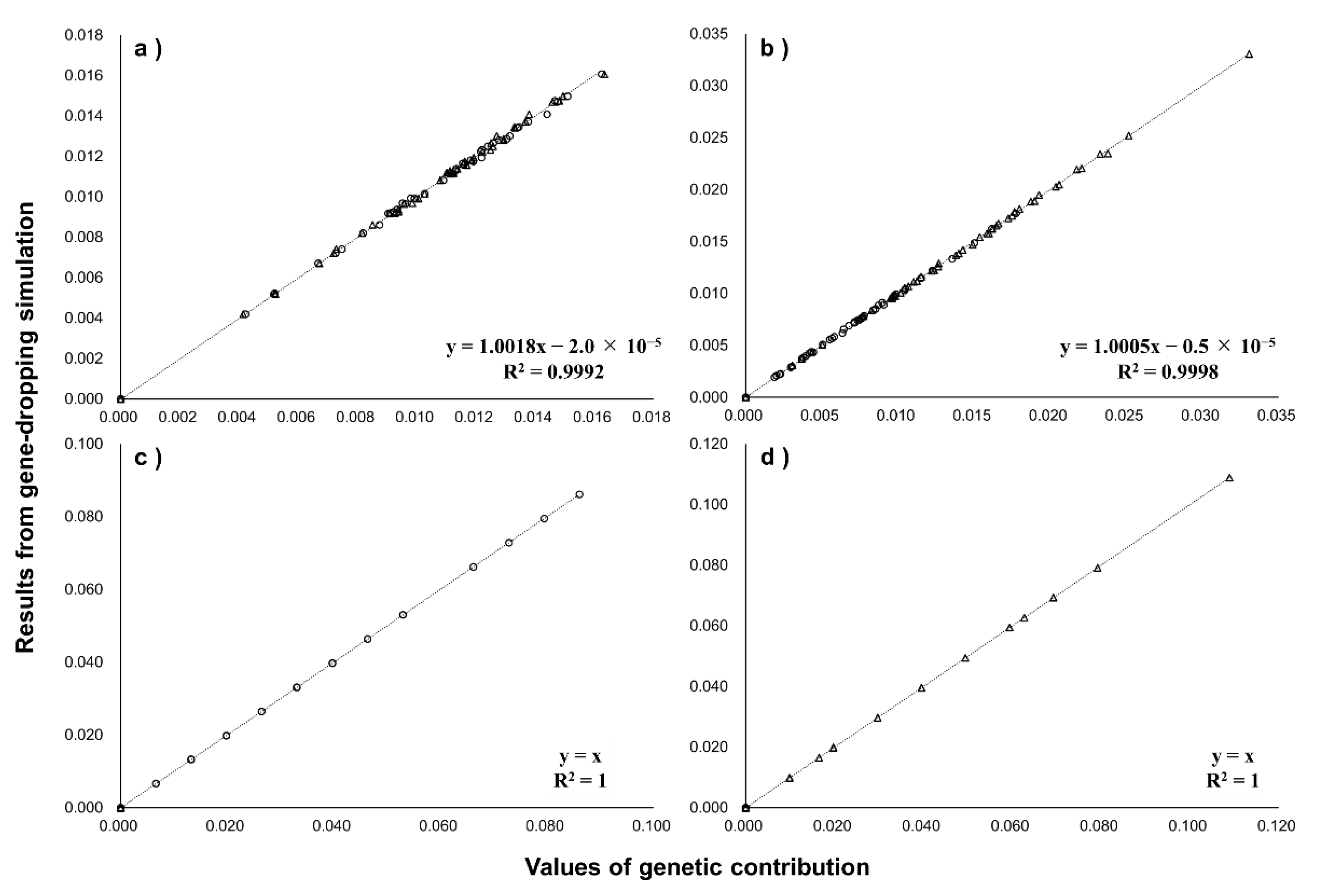
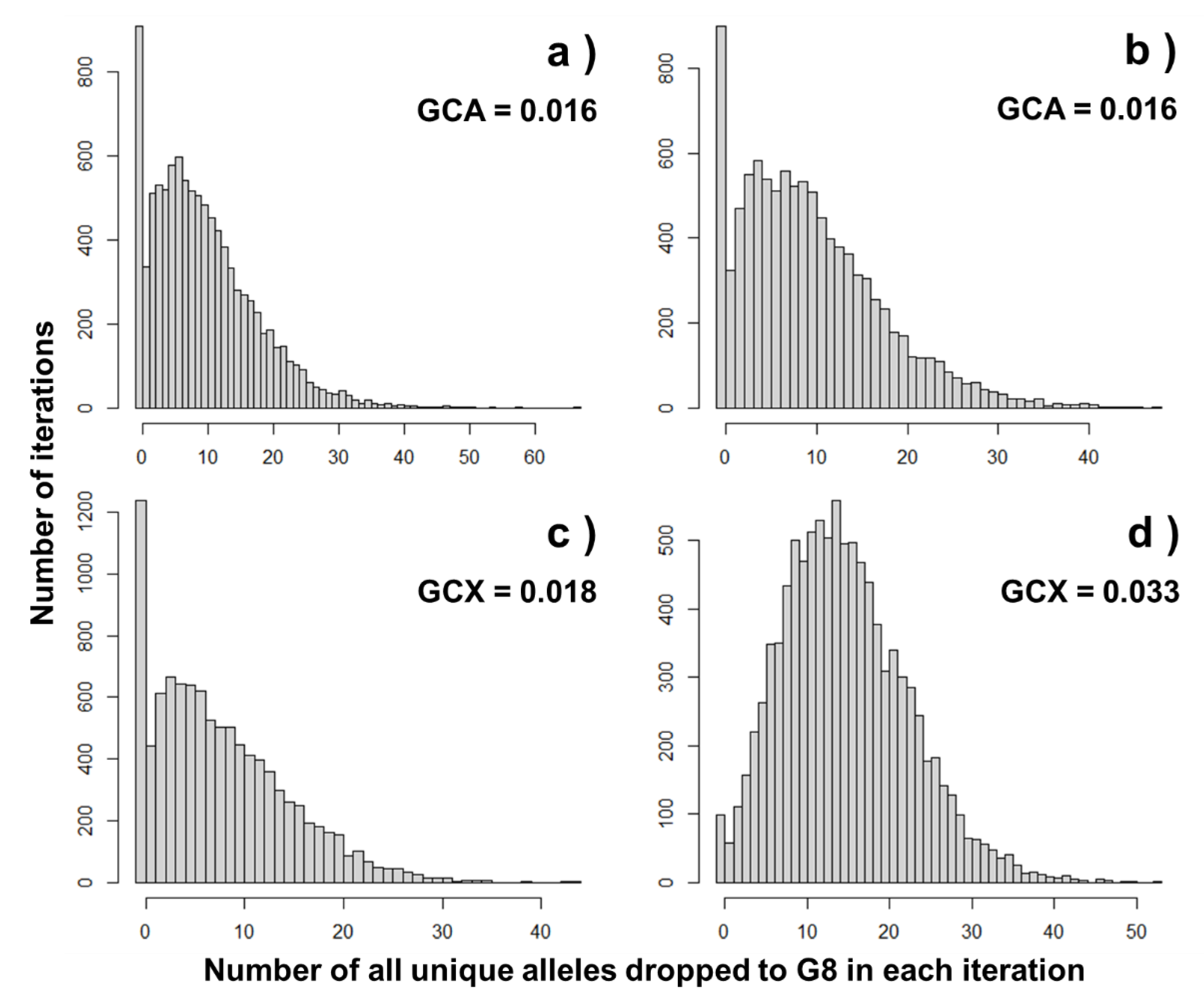
3.2. Comparing with Gene-Dropping Simulation Results
3.3. Effect of Pedigree Errors on Genetic Contribution Calculation
3.4. Calculating Coefficient of Variation of Genetic Contribution
3.5. General Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thornton, P.K. Livestock production: Recent trends, future prospects. Phil. Trans. R. Soc. B Biol. Sci. 2010, 365, 2853–2867. [Google Scholar] [CrossRef]
- Henderson, C.R. Estimation of variances in animal model and reduced animal model for single traits and single records. J. Dairy Sci. 1986, 69, 1394–1402. [Google Scholar] [CrossRef]
- Hofer, A. Variance component estimation in animal breeding: A review. J. Anim. Breed. Genet. 1998, 115, 247–265. [Google Scholar] [CrossRef]
- Thompson, R. Estimation of quantitative genetic parameters. Proc. R. Soc. B Biol. Sci. 2008, 27, 679–686. [Google Scholar] [CrossRef]
- Oyama, K. Genetic variability of Wagyu cattle estimated by statistical approaches. Anim. Sci. J. 2011, 82, 367–373. [Google Scholar] [CrossRef] [PubMed]
- Akanno, E.C.; Schenkel, F.S.; Quinton, V.M.; Friendship, R.M.; Robinson, J.A.B. Meta-analysis of genetic parameter estimates for reproduction, growth and carcass traits of pigs in the tropics. Livest Sci. 2013, 152, 101–113. [Google Scholar] [CrossRef]
- Jembere, T.; Dessie, T.; Rischkowsky, B.; Kebede, K.; Okeyo, A.M.; Haile, A. Meta-analysis of average estimates of genetic parameters for growth, reproduction and milk production traits in goats. Small Rumin. Res. 2017, 153, 71–80. [Google Scholar] [CrossRef]
- Suzuki, K.; Kadowaki, H.; Shibata, T.; Uchida, H.; Nishida, A. Selection for daily gain, loin-eye area, backfat thickness and intramuscular fat based on desired gains over seven generations of Duroc pigs. Livest. Prod. Sci. 2005, 97, 193–202. [Google Scholar] [CrossRef]
- Sasaki, Y.; Miyake, T.; Gaillard, C.; Oguni, T.; Matsumoto, M.; Ito, M.; Kurahara, T.; Sasae, Y.; Fujinaka, K.; Ohtagaki, S.; et al. Comparison of genetic gains per year for carcass traits among breeding programs in the Japanese Brown and the Japanese Black cattle. J. Anim. Sci. 2006, 84, 317–323. [Google Scholar] [CrossRef]
- García-Ruiz, A.; Cole, J.B.; VanRaden, P.M.; Wiggans, G.R.; Ruiz-López, F.J.; Van Tassell, C.P. Changes in genetic selection differentials and generation intervals in US Holstein dairy cattle as a result of genomic selection. Proc. Natl. Acad. Sci. USA 2016, 113, E3995–E4004. [Google Scholar] [CrossRef]
- Doekes, H.P.; Veerkamp, R.F.; Bijma, P.; Hiemstra, S.J.; Windig, J.J. Trends in genome-wide and region-specific genetic diversity in the Dutch-Flemish Holstein–Friesian breeding program from 1986 to 2015. Genet. Sel. Evol. 2018, 50, 15. [Google Scholar] [CrossRef] [PubMed]
- Forutan, M.; Mahuari, S.A.; Baes, C.; Melzer, N.; Schenkel, F.S.; Sargolzaei, M. Inbreeding and runs of homozygosity before and after genomic selection in North American Holstein cattle. BMC Genom. 2018, 19, 98. [Google Scholar] [CrossRef] [PubMed]
- Doublet, A.-C.; Croiseau, P.; Fritz, S.; Michenet, A.; Hozé, C.; Danchin-Burge, C.; Laloë, D.; Restoux, G. The impact of genomic selection on genetic diversity and genetic gain in three French dairy cattle breeds. Genet. Sel. Evol. 2019, 51, 52. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E.; Sonesson, A.K.; Gebregiwergis, G.; Woolliams, J.A. Management of genetic diversity in the era of genomics. Front. Genet. 2020, 11, 880. [Google Scholar] [CrossRef]
- Polak, G.; Gurgul, A.; Jasielczuk, I.; Szmatoła, T.; Krupiński, J.; Bugno-Poniewierska, M. Suitability of pedigree information and genomic methods for analyzing inbreeding of polish cold-blooded horses covered by conservation programs. Genes 2021, 12, 429. [Google Scholar] [CrossRef] [PubMed]
- Villanueva, B.; Fernández, A.; Saura, M.; Caballero, A.; Fernández, J.; Morales-González, E.; Toro, M.A.; Pong-Wong, R. The value of genomic relationship matrices to estimate levels of inbreeding. Genet. Sel. Evol. 2021, 53, 42. [Google Scholar] [CrossRef]
- Leroy, G.; Danchin-Burge, C.; Palhiere, I.; Baumung, R.; Fritz, S.; Mériaux, J.C.; Gautier, M. An ABC estimate of pedigree error rate: Application in dog, sheep and cattle breeds. Anim. Genet. 2012, 43, 309–314. [Google Scholar] [CrossRef]
- Zhang, J.; Song, H.; Zhang, Q.; Ding, X. Assessment of relationships between pigs based on pedigree and genomic information. Animal 2020, 14, 697–705. [Google Scholar] [CrossRef]
- Komiya, R.; Ogawa, S.; Aonuma, T.; Satoh, M. Performance of using opposing homozygotes for paternity testing in Japanese Black cattle. J. Anim. Breed. Genet. 2022, 139, 113–124. [Google Scholar] [CrossRef]
- Sørensen, M.K.; Sørensen, A.C.; Baumung, R.; Borchersen, S.; Berg, P. Optimal genetic contribution selection in Danish Holstein depends on pedigree quality. Livest. Sci. 2008, 118, 212–222. [Google Scholar] [CrossRef]
- Oliehoek, P.A.; Bijma, P. Effects of pedigree errors on the efficiency of conservation decisions. Genet. Sel. Evol. 2009, 41, 9. [Google Scholar] [CrossRef]
- Reid, J.M.; Keller, L.F.; Marr, A.B.; Nietlisbach, P.; Sardell, R.J.; Arcese, P. Pedigree error due to extra-pair reproduction substantially biases estimates of inbreeding depression. Evolution 2014, 68, 802–815. [Google Scholar] [CrossRef]
- Kadowaki, H.; Suzuki, E.; Kojima-Shibata, C.; Suzuki, K.; Okamura, T.; Onodera, W.; Shibata, T.; Kano, H. Selection for resistance to swine mycoplasmal pneumonia over 5 generations in Landrace pigs. Livest Sci. 2012, 147, 20–26. [Google Scholar] [CrossRef]
- Ogawa, S.; Satoh, M. Random regression analysis of calving interval of Japanese Black cows. Animals 2021, 11, 202. [Google Scholar] [CrossRef] [PubMed]
- Zoda, A.; Urakawa, M.; Oono, Y.; Ogawa, S.; Satoh, M. Estimation of genetic parameters for superovulatory response traits in Japanese Black cows. J. Anim. Sci. 2021, 99, skab265. [Google Scholar] [CrossRef] [PubMed]
- Okamura, T.; Maeda, K.; Onodera, W.; Kadowaki, H.; Kojima-Shibata, C.; Suzuki, E.; Uenishi, H.; Satoh, M.; Suzuki, K. Correlated responses of respiratory disease and immune capacity traits of Landrace pigs selected for Mycoplasmal pneumonia of swine (MPS) lesion. Anim. Sci. J. 2016, 87, 1099–1105. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, S.; Ohnishi, C.; Ishii, K.; Uemoto, Y.; Satoh, M. Genetic relationship between litter size traits at birth and body measurement and production traits in purebred Duroc pigs. Anim. Sci. J. 2020, 91, e13497. [Google Scholar] [CrossRef]
- Bottje, W.; Iqbal, M.; Tang, Z.X.; Cawthon, D.; Okimoto, R.; Wing, T.; Cooper, M. Association of mitochondrial function with feed efficiency within a single genetic line of male broilers. Poult. Sci. 2002, 81, 546–555. [Google Scholar] [CrossRef]
- Tsai, T.; John, J.C. The role of mitochondrial DNA copy number, variants, and haplotypes in farm animal developmental outcome. Domest. Anim. Endocrinol. 2016, 56, S133–S146. [Google Scholar] [CrossRef]
- Srirattana, K.; McCosker, K.; Schatz, T.; John, J.C. Cattle phenotypes can disguise their maternal ancestry. BMC Genet. 2017, 18, 59. [Google Scholar] [CrossRef]
- Darhan, H.; Zoda, A.; Kukusato, M.; Toyomizu, M.; Katoh, K.; Roh, S.; Ogawa, S.; Uemoto, Y.; Satoh, M.; Suzuki, K. Correlations between mitochondrial respiration activity and residual feed intake after divergent genetic selection for high- and low-oxygen consumption in mice. Anim. Sci. J. 2019, 90, 818–826. [Google Scholar] [CrossRef] [PubMed]
- Fortes, M.R.S.; Porto-Neto, L.R.; Satake, N.; Nguyen, L.T.; Freitas, A.C.; Melo, T.P.; Scalez, D.C.B.; Hayes, B.; Raidan, F.S.S.; Reverter, A.; et al. X chromosome variants are associated with male fertility traits in two bovine populations. Genet. Sel. Evol. 2020, 52, 46. [Google Scholar] [CrossRef] [PubMed]
- Meester, I.; Manilla-Muñoz, E.; León-Cachón, R.B.R.; Paniagua-Frausto, G.A.; Carrión-Alvarez, D.; Ruiz-Rodríguez, C.O.; Rodríguez-Rangel, Y.; García-Martínez, J.M. SeXY chromosomes and the immune system: Reflections after a comparative study. Biol. Sex Differ. 2020, 11, 3. [Google Scholar] [CrossRef] [PubMed]
- Gibson, J.P.; Freeman, A.E.; Boettcher, P.J. Cytoplasmic and mitochondrial inheritance of economic traits in cattle. Livest. Prod. Sci. 1997, 47, 115–124. [Google Scholar] [CrossRef]
- Yue, X.P.; Dechow, C.; Liu, W.S. A limited number of Y chromosome lineages is present in North American Holsteins. J. Dairy Sci. 2015, 98, 2738–2745. [Google Scholar] [CrossRef]
- Diaz, I.D.P.S.; de Camargo, G.M.F.; da Cruz, V.A.R.; Hermisdorff, I.C.; Carvalho, C.V.D.; de Albuquerque, L.G.; Costa, R.B. Effect of the X chromosome in genomic evaluations of reproductive traits in beef cattle. Anim. Reprod. Sci. 2021, 225, 106682. [Google Scholar] [CrossRef]
- Leroy, G.; Danchin-Burge, C.; Verrier, E. Impact of the use of cryobank samples in a selected cattle breed: A simulation study. Genet. Sel. Evol. 2011, 43, 36. [Google Scholar] [CrossRef]
- Doekes, H.P.; Veerkamp, R.F.; Bijma, P.; Hiemstra, S.J.; Windig, J. Value of the Dutch Holstein Friesian germplasm collection to increase genetic variability and improve genetic merit. J. Dairy Sci. 2018, 101, 10022–10033. [Google Scholar] [CrossRef]
- Eynard, S.E.; Windig, J.J.; Hulsegge, I.; Hiemstra, S.-J.; Calus, M.P.L. The impact of using old germplasm on genetic merit and diversity—A cattle breed case study. J. Anim. Breed. Genet. 2018, 135, 311–322. [Google Scholar] [CrossRef]
- Gibson, J.P.; Candiff, L.V. Developing straight breeding and crossbreeding structures for extensive grazing systems which utilize exotic animal genetic resources. In Developing Breeding Strategies for Lower Input Animal Production Environments; ICAR Technical Series; Galal, S., Boyazoglu, J., Hammond, K., Eds.; ICAR: Rome, Italy, 2000; Volume 3, pp. 207–242. [Google Scholar]
- Bolet, G.; Bidanel, J.P.; Olliver, L. Selection for litter size in pigs. II. Efficiency of closed and open selection lines. Genet. Sel. Evol. 2001, 33, 515. [Google Scholar] [CrossRef]
- Anderson, D.; Toma, R.; Negishi, Y.; Okuda, K.; Ishiniwa, H.; Hinton, T.G.; Nanba, K.; Tamate, H.B.; Kaneko, S. Mating of escaped domestic pigs with wild boar and possibility of their offspring migration after the Fukushima Daiichi Nuclear Power Plant accident. Sci. Rep. 2019, 9, 11537. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, R. Detection of Inobuta from wild boar population in Japan by genetic analysis. Rev. Agric. Sci. 2018, 6, 61–71. [Google Scholar] [CrossRef]
- Anderson, D.; Negishi, Y.; Ishiniwa, H.; Okuda, K.; Hinton, T.G.; Toma, R.; Nagata, J.; Tamate, H.B.; Kaneko, S. Introgression dynamics from invasive pigs into wild boar following the March 2011 natural and anthropogenic disasters at Fukushima. Proc. R. Soc. B. 2020, 288, 20210874. [Google Scholar] [CrossRef] [PubMed]
- Wiener, G. Breed structure in the pedigree Ayrshire cattle population in Great Britain. J. Agric. Sci. 1953, 43, 123–130. [Google Scholar] [CrossRef]
- Vozzi, P.A.; Marcondes, C.R.; Magnabosco, C.U.; Bezerra, L.A.F.; Lôbo, R.B. Structure and genetic variability in Nellore (Bos indicus) cattle by pedigree analysis. Genet. Mol. Biol. 2006, 29, 482–485. [Google Scholar] [CrossRef]
- Carolino, N.; Vitorino, A.; Carolino, I.; Pais, J.; Henriques, N.; Silveira, M.; Vicente, A. Genetic diversity in the Portuguese Mertolenga cattle breed assessed by pedigree analysis. Animals 2020, 10, 1990. [Google Scholar] [CrossRef]
- Honda, T.; Nomura, T.; Yamaguchi, Y.; Mukai, F. Monitoring of genetic diversity in the Japanese Black cattle population by the use of pedigree information. J. Anim. Breed. Genet. 2004, 121, 242–252. [Google Scholar] [CrossRef]
- Honda, T.; Fujii, T.; Nomura, T.; Mukai, F. Evaluation of genetic diversity in Japanese Brown cattle population by pedigree analysis. J. Anim. Breed. Genet. 2006, 123, 172–179. [Google Scholar] [CrossRef]
- Uemoto, Y.; Suzuki, K.; Yasuda, J.; Roh, S.; Satoh, M. Evaluation of inbreeding and genetic diversity in Japanese Shorthorn cattle by pedigree analysis. Anim. Sci. J. 2021, 92, e13643. [Google Scholar] [CrossRef]
- Okamura, T. An R program for inbreeding coefficient, relationship coefficient, genetic rate of contribution. Jpn. J. Swine Sci. 2020, 57, 108–115. [Google Scholar] [CrossRef]
- Ohnishi, C.; Satoh, S. Estimation of genetic parameters for performance and body measurement traits in Duroc pigs selected for average daily gain, loin muscle area, and backfat thickness. Livest. Sci. 2018, 214, 161–166. [Google Scholar] [CrossRef]
- Yazaki, N.; Ogawa, S.; Ohnishi, C.; Ishii, K.; Uemoto, Y.; Satoh, M. Effectiveness of body measurement traits for improving production traits in Duroc pigs. Nihon Chikusan Gakkaiho 2020, 91, 9–16. [Google Scholar] [CrossRef]
- Nishida, A.; Shinohara, H.; Ohtomo, Y.; Suzuki, K. A method for evaluating the change in genetic constitution of pig line. Jpn. J. Swine Science 2005, 42, 34–36. [Google Scholar] [CrossRef]
- Nagai, K.; Takahashi, Y.; Nomura, K.; Furukawa, T. Calculation of inbreeding coefficient, relationship coefficient and genetic rate of contribution using spreadsheet software. Jpn. J. Swine Sci. 2015, 52, 29–36. [Google Scholar] [CrossRef]
- Fernando, R.L.; Grossman, M. Genetic evaluation with autosomal and X-chromosomal inheritance. Theor. Appl. Genet. 1990, 80, 75–80. [Google Scholar] [CrossRef]
- Ogawa, S.; Satoh, M. Relationship between litter size at birth and within-litter birth weight characteristics in laboratory mice as pilot animal for pig. Anim. Sci. J. 2020, 91, e13488. [Google Scholar] [CrossRef] [PubMed]
- MacCluer, J.W.; VandeBerg, J.L.; Read, B.; Ryder, O.A. Pedigree analysis by computer simulation. Zoo Biol. 1986, 5, 147–160. [Google Scholar] [CrossRef]
- Arishima, T.; Sasaki, S.; Isobe, T.; Ikebata, Y.; Shimbara, S.; Ikeda, S.; Kawashima, K.; Suzuki, Y.; Watanabe, M.; Sugano, S.; et al. Maternal variant in the upstream of FOXP3 gene on the X chromosome is associated with recurrent infertility in Japanese Black cattle. BMC Genet. 2017, 18, 103. [Google Scholar] [CrossRef]
- Acquaviva, L.; Boekuhout, M.; Karasu, M.E.; Brick, K.; Pratto, F.; Li, T.; van Overbeek, M.; Kauppi, L.; Camerini-Otero, R.D.; Jasin, M.; et al. Ensuring meiotic DNA break formation in the mouse pseudoautosomal region. Nature 2020, 582, 426–431. [Google Scholar] [CrossRef]
- Zhang, J.; Kadri, N.K.; Mullaart, E.; Spelman, R.; Fritz, S.; Boichard, D.; Charlier, C.; Georges, M.; Druet, T. Genetic architecture of individual variation in recombination rate on the X chromosome in cattle. Heredity 2020, 125, 304–316. [Google Scholar] [CrossRef]
- Quaas, R.L. Additive genetic model with groups and relationships. J. Dairy Sci. 1988, 71, 1338–1345. [Google Scholar] [CrossRef]
- Legarra, A.; Christensen, O.F.; Vitezica, Z.G.; Aguilar, I.; Misztal, I. Ancestral relationships using metafounders: Finite ancestral populations and across population relationships. Genetics 2015, 200, 455–468. [Google Scholar] [CrossRef] [PubMed]
- Nwogwugwu, C.P.; Kim, Y.; Chung, Y.J.; Jang, S.B.; Roh, S.H.; Kim, S.; Lee, J.H.; Choi, T.J.; Lee, S.H. Effect of errors in pedigree on the accuracy of estimated breeding value for carcass traits in Korean Hanwoo cattle. Asian-Australas. J. Anim. Sci. 2020, 33, 1057–1067. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, Y.; Matsuda, H.; Yamada, T.; Sugiyama, T.; Homma, K.; Kaneko, Y.; Yamagishi, S.; Iwaisaki, H. Genome-wide SNP and STR discovery in the Japanese Crested Ibis and genetic diversity among founders of the Japanese population. PLoS ONE 2013, 8, e72781. [Google Scholar] [CrossRef]
- Moore, K.; Vilela, C.; Kaseja, K.; Mrode, R.; Coffey, M. Forensic use of the genomic relationship matrix to validate and discover livestock pedigrees. J. Anim. Sci. 2019, 97, 35–42. [Google Scholar] [CrossRef]
- Eusebi, P.G.; Martinez, A.; Cortes, O. Genomic tools for effective conservation of livestock breed diversity. Diversity 2019, 12, 8. [Google Scholar] [CrossRef]
- Suezawa, R.; Nikadori, H.; Sasaki, S. Genetic diversity and genomic inbreeding in Japanese Black cows in the islands of Okinawa Prefecture evaluated using single-nucleotide polymorphism array. Anim. Sci. J. 2021, 92, e13525. [Google Scholar] [CrossRef]
- Zoda, A.; Ogawa, S.; Matsuda, H.; Taniguchi, Y.; Watanabe, T.; Sugimoto, Y.; Iwaisaki, H. Inferring genetic characteristics of Japanese Black cattle populations using genome-wide single nucleotide polymorphism markers. J. Anim. Genet. 2021, in press. [Google Scholar]
- Frank, S.A. Evolution: Mitochondrial burden on male health. Curr. Biol. 2012, 22, R797–R799. [Google Scholar] [CrossRef]
- Vaught, R.C.; Dowling, D.K. Maternal inheritance of mitochondria: Implications for male fertility? Reproduction 2018, 155, R159–R168. [Google Scholar] [CrossRef]
- Subrini, J.; Turner, J. Y chromosome functions in mammalian spermatogenesis. eLife 2021, 10, e67345. [Google Scholar] [CrossRef] [PubMed]
- Druet, T.; Legarra, A. Theoretical and empirical comparisons of expected and realized relationships for the X-chromosome. Genet. Sel. Evol. 2020, 52, 50. [Google Scholar] [CrossRef] [PubMed]
- Ghafouri-Kesbi, F.; Abbasi, M.A. Autosomal and X-linked additive genetic effects on body weight, body measurements and efficiency-related traits in sheep. Small Rumin. Res. 2019, 180, 21–26. [Google Scholar] [CrossRef]
- Noorian, M.; Joezy-Shekalgorabi, S.; Kashan, N.E.J. Analysis of X chromosome and autosomal genetic effects on growth and efficiency-related traits in sheep. Anim. Prod. Sci. 2020, 61, 363–370. [Google Scholar] [CrossRef]
- Latifi, M.; Naderi, Y.; Mortazavi, A.; Bohlouli, M.; Sadeghi, S. Variation in autosomal and sex-linked genetic effects for growth traits in Markhoz goat using multivariate animal models. Trop. Anim. Health Prod. 2020, 52, 2917–2923. [Google Scholar] [CrossRef]
- Meyer, K. Scope for estimation of variances due to sex-linked, maternal and dominance effects in mixed model analyses. Proc. Assoc. Advmt. Anim. Breed. Genet. 2007, 17, 407–410. [Google Scholar]
- Wittenburg, D.; Teuscher, F.; Reinsch, N. Statistical tools to detect genetic variation for a sex dimorphism in piglet birth weight. J. Anim. Sci. 2011, 89, 622–629. [Google Scholar] [CrossRef][Green Version]
- Götherström, A.; Anderung, C.; Hellborg, L.; Elburg, R.; Smith, C.; Bradley, D.G.; Ellegren, H. Cattle domestication in the Near East was followed by hybridization with aurochs bulls in Europe. Proc. Royal Soc. B. 2005, 272, 2345–2351. [Google Scholar] [CrossRef]
- Wutke, S.; Sandoval-Castellanos, E.; Benecke, N.; Döhle, H.J.; Friederich, S.; Gonzalez, J.; Hofreiter, M.; Lõugas, L.; Magnell, O.; Malaspinas, A.S.; et al. Decline of genetic diversity in ancient domestic stallions in Europe. Sci. Adv. 2018, 4, eaap9691. [Google Scholar] [CrossRef]
- Jaton, C.; Koeck, A.; Sargolzaei, M.; Malchiodi, F.; Price, C.A.; Schenkel, F.S.; Miglior, F. Genetic analysis of superovulatory response of Holstein cows in Canada. J. Dairy Sci. 2016, 99, 3612–3623. [Google Scholar] [CrossRef]
- Parker Gaddis, K.L.; Dikmen, S.; Null, D.J.; Cole, J.B.; Hansen, P.J. Evaluation of genetic components in traits related to superovulation, in vitro fertilization, and embryo transfer in Holstein cattle. J. Dairy Sci. 2017, 100, 2877–2891. [Google Scholar] [CrossRef] [PubMed]
- Bouquet, A.; Sørensen, A.C.; Juga, J. Genomic selection strategies to optimize the use of multiple ovulation and embryo transfer schemes in dairy cattle breeding programs. Livest. Sci. 2015, 174, 18–25. [Google Scholar] [CrossRef]
- Thomasen, J.R.; Willam, A.; Egger-Danner, C.; Sørensen, A.C. Reproductive technologies combine well with genomic selection in dairy breeding programs. J. Dairy Sci. 2016, 99, 1331–1340. [Google Scholar] [CrossRef] [PubMed]
- Fujii, T.; Naito, A.; Hirayama, H.; Kashima, M.; Yoshino, H.; Hanamure, T.; Domon, Y.; Hayakawa, H.; Watanabe, T.; Moriyasu, S.; et al. Potential of preimplantation genomic selection for carcass traits in Japanese Black cattle. J. Reprod. Dev. 2019, 65, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Gandini, G.; Pizzi, F.; Stella, A.; Boettcher, P.J. The costs of breed reconstruction from cryopreserved material in mammalian livestock species. Genet. Sel. Evol. 2007, 39, 465. [Google Scholar] [CrossRef][Green Version]
- Fernández, J.; Meuwissen, T.H.E.; Toro, M.A.; Mäki-Tanila, A. Management of genetic diversity in small farm animal populations. Animal 2011, 5, 1684–1698. [Google Scholar] [CrossRef]
- Woelders, H.; Windig, J.; Hiemstra, S.J. How developments in cryobiology, reproductive technologies and conservation genomics could shape gene banking strategies for (farm) animals. Reprod. Domest. Anim. 2012, 47, 264–273. [Google Scholar] [CrossRef]
- Kameyama, K.; Nishi, T.; Yamada, M.; Masujin, K.; Morioka, K.; Kokuho, T.; Fukai, K. Experimental infection of pigs with a classical swine fever virus isolated in Japan for the first time in 26 years. J. Vet. Med. Sci. 2019, 81, 1277–1284. [Google Scholar] [CrossRef]
- Shimizu, Y.; Hayama, Y.; Murato, Y.; Sawai, K.; Yamaguchi, E.; Yamamoto, T. Epidemiology of classical swine fever in Japan—a descriptive analysis of the outbreaks in 2018–2019. Front. Vet. Sci. 2020, 7, 573480. [Google Scholar] [CrossRef]
- Shimizu, Y.; Hayama, Y.; Murato, Y.; Sawai, K.; Yamaguchi, E.; Yamamoto, T. Epidemiological analysis of classical swine fever in wild boars in Japan. BMC Vet. Res. 2021, 17, 188. [Google Scholar] [CrossRef]
- Sonesson, A.; Goddard, M.E.; Meuwissen, T.H.E. The use of frozen semen to minimize inbreeding in small populations. Genet. Res. Camb. 2002, 80, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Boettcher, P.J.; Stella, A.; Pizzi, F.; Gandini, G. The combined use of embryos and semen for cryogenic conservation of mammalian livestock genetic resources. Genet. Sel. Evol. 2005, 37, 657. [Google Scholar] [CrossRef] [PubMed]
- Howard, J.G.; Lynch, C.; Santymire, R.M.; Marinari, P.E.; Wildt, D.E. Recovery of gene diversity using long-term cryopreserved spermatozoa and artificial insemination in the endangered black-footed ferret. Anim. Conserv. 2016, 19, 102–111. [Google Scholar] [CrossRef]
- Oyama, K.; Nojima, M.; Shojo, M.; Fukushima, M.; Anada, K.; Mukai, F. Effect of sire mating patterns on future genetic merit and inbreeding in a closed beef cattle population. J. Anim. Breed. Genet. 2007, 124, 73–80. [Google Scholar] [CrossRef][Green Version]
- Heidaritabar, M.; Vereijken, A.; Muir, W.M.; Meuwissen, T.; Cheng, H.; Megens, H.-J.; Groenen, M.A.M.; Bastiaansen, J.W.M. Systematic differences in the response of genetic variation to pedigree and genome-based selection methods. Heredity 2014, 113, 503–513. [Google Scholar] [CrossRef]
- Gómez-Romano, F.; Villanueva, B.; Fernández, J.; Wooliams, J.A.; Pong-Wong, R. The use of genomic coancestry matrices in the optimisation of contributions to maintain genetic diversity at specific regions of the genome. Genet. Sel. Evol. 2016, 48, 2. [Google Scholar] [CrossRef]
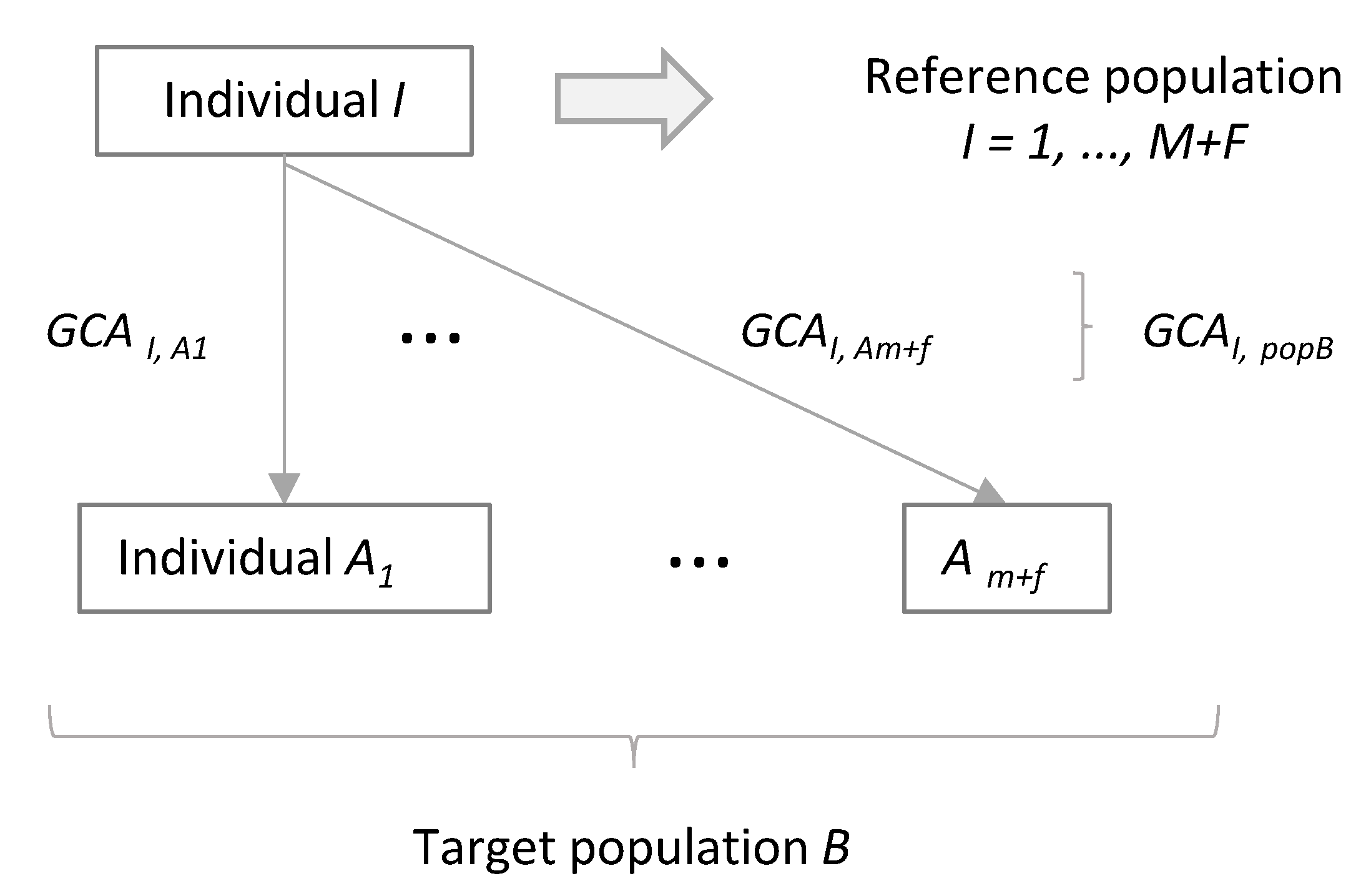



| Individual | Sex | Sire | Dam |
|---|---|---|---|
| 1 | Male | Unknown | Unknown |
| 2 | Female | Unknown | Unknown |
| 3 | Male | 1 | Unknown |
| 4 | Female | 1 | 2 |
| 5 | Male | 3 | 4 |
| 6 | Female | 1 | 4 |
| 7 | Male | 5 | 6 |
| 8 | Female | 5 | 6 |
| Generation | No. of Males | No. of Females | No. of Known Sires | No. of Known Dams |
|---|---|---|---|---|
| G1 | 50 | 50 | 0 | 0 |
| G2 | 186 | 173 | 46 | 46 |
| G3 | 248 | 249 | 124 | 124 |
| G4 | 149 | 146 | 95 | 95 |
| G5 | 174 | 171 | 112 | 112 |
| G6 | 158 | 154 | 103 | 103 |
| G7 | 151 | 156 | 100 | 100 |
| G8 | 151 | 152 | 101 | 101 |
| Total | 1267 | 1251 | 681 | 681 |
| I | A | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Autosomes (GCAI,A) | X chromosome (GCXI,A) | |||||||||||||||
| 1 | 1 | 0 | 0.5 | 0.5 | 0.5 | 0.75 | 0.625 | 0.625 | 1 | 0 | 0 | 0.5 | 0.5 | 0.75 | 0.75 | 0.625 |
| 2 | 0 | 1 | 0 | 0.5 | 0.25 | 0.25 | 0.25 | 0.25 | 0 | 1 | 0 | 0.5 | 0.5 | 0.25 | 0.25 | 0.375 |
| 3 | 0 | 0 | 1 | 0 | 0.5 | 0 | 0.25 | 0.25 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0 | 0 | 0 | 1 | 1 | 0.5 | 0.5 | 0.75 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0.5 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0.5 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Y chromosome (GCYI,A) | Mitochondrial DNA (GCMI,A) | |||||||||||||||
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Error Rate | GCAI,popB | GCXI,popB | GCYI,popB | GCMI,popB | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Min | Max | Mean | SD | Min | Max | Mean | SD | Min | Max | Mean | SD | Min | Max | |
| 1% | 1.07 | 0.23 | 0.37 | 2.20 | 1.57 | 0.40 | 0.47 | 3.18 | 6.74 | 2.95 | 0 | 19.06 | 6.58 | 3.34 | 0 | 24.27 |
| 2% | 1.53 | 0.24 | 0.74 | 2.56 | 2.25 | 0.42 | 0.89 | 4.07 | 9.88 | 3.09 | 1.87 | 23.80 | 9.79 | 3.62 | 1.14 | 27.40 |
| 4% | 2.14 | 0.27 | 1.16 | 3.27 | 3.17 | 0.46 | 1.61 | 5.04 | 14.00 | 3.18 | 3.50 | 26.85 | 14.07 | 3.81 | 3.85 | 30.88 |
| 8% | 2.97 | 0.31 | 1.87 | 4.31 | 4.41 | 0.50 | 2.81 | 6.60 | 19.53 | 3.36 | 7.25 | 34.08 | 19.73 | 3.90 | 8.08 | 36.12 |
| 16% | 4.02 | 0.36 | 2.69 | 5.39 | 5.97 | 0.59 | 3.98 | 8.31 | 26.23 | 3.66 | 13.64 | 42.57 | 26.69 | 3.95 | 13.32 | 42.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogawa, S.; Satoh, M. Genetic Contributions of Genes on Sex Chromosomes and Mitochondrial DNA in a Pedigreed Population. Diversity 2022, 14, 142. https://doi.org/10.3390/d14020142
Ogawa S, Satoh M. Genetic Contributions of Genes on Sex Chromosomes and Mitochondrial DNA in a Pedigreed Population. Diversity. 2022; 14(2):142. https://doi.org/10.3390/d14020142
Chicago/Turabian StyleOgawa, Shinichiro, and Masahiro Satoh. 2022. "Genetic Contributions of Genes on Sex Chromosomes and Mitochondrial DNA in a Pedigreed Population" Diversity 14, no. 2: 142. https://doi.org/10.3390/d14020142
APA StyleOgawa, S., & Satoh, M. (2022). Genetic Contributions of Genes on Sex Chromosomes and Mitochondrial DNA in a Pedigreed Population. Diversity, 14(2), 142. https://doi.org/10.3390/d14020142






