Prioritizing Management of Non-Native Eurasian Watermilfoil Using Species Occurrence and Abundance Predictions
Abstract
1. Introduction
2. Materials and Methods
2.1. Invasion History of Eurasian Watermilfoil
2.2. Occurrence and Abundance of Eurasian Watermilfoil
2.3. Explanatory Variables
2.4. Predicting Eurasian Watermilfoil Occurrence
2.5. Predicting Eurasian Watermilfoil Abundance
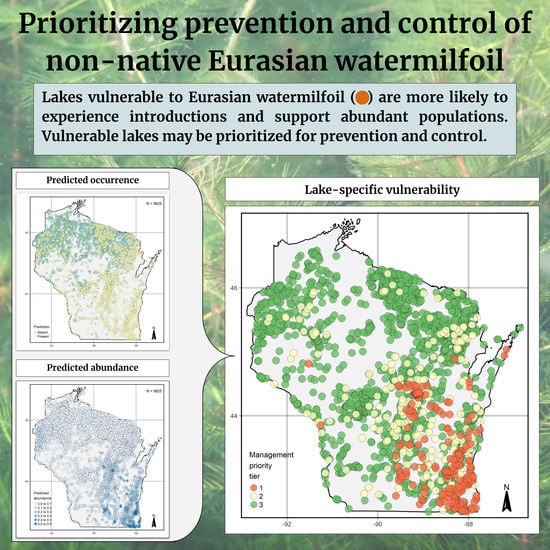
2.6. Defining and Prioritizing Management Targets
3. Results
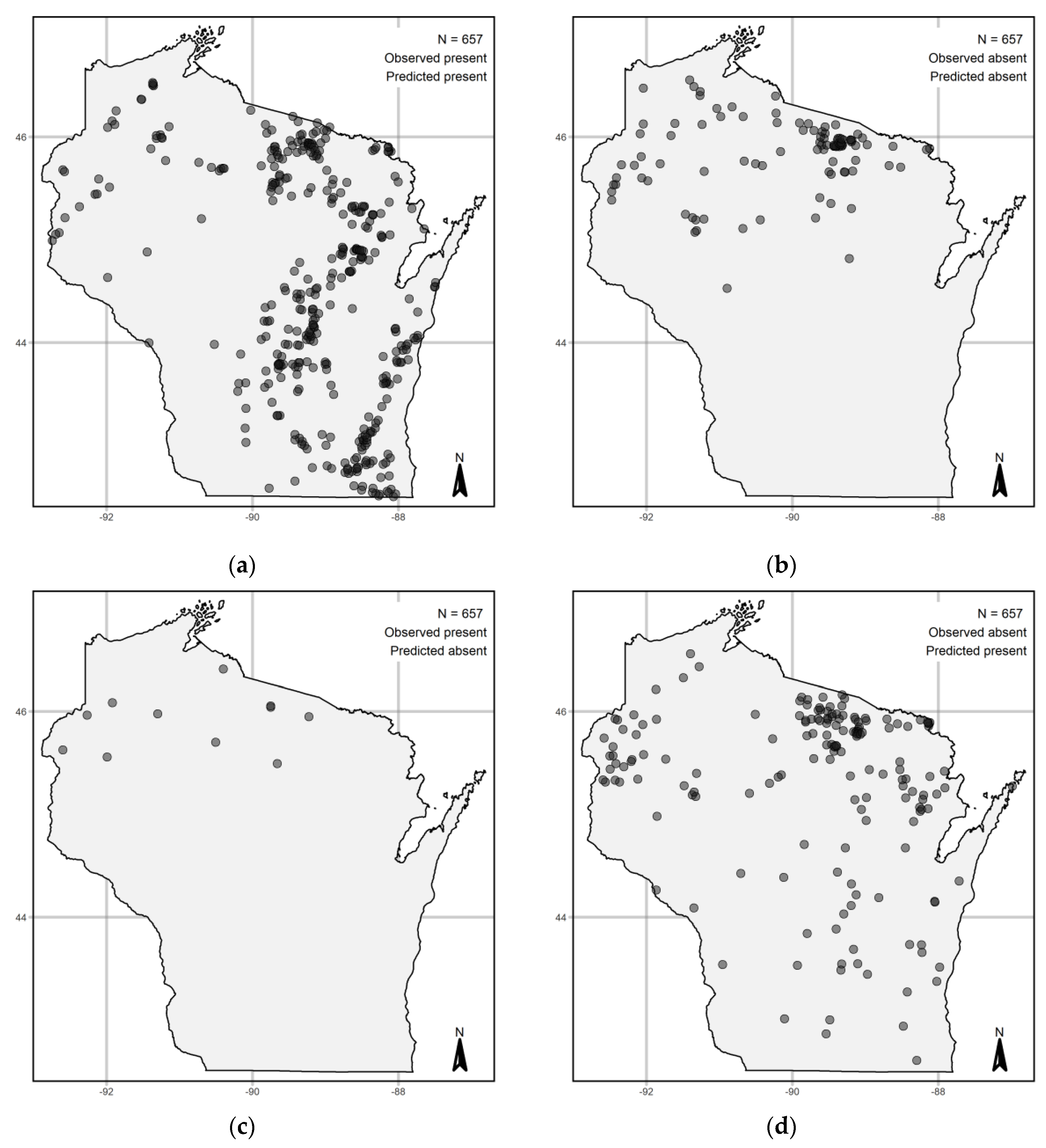
3.1. Occurrence Models
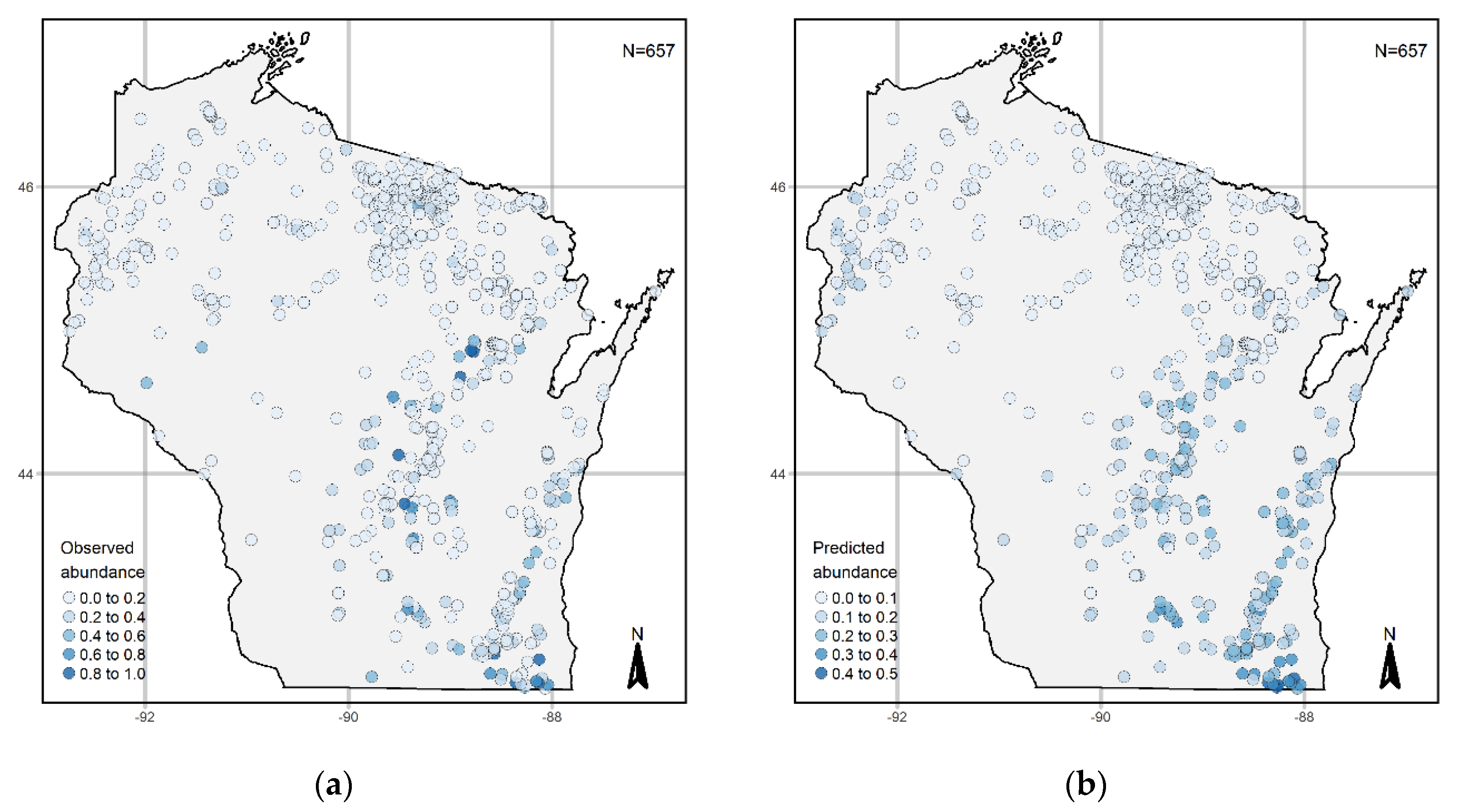
3.2. Abundance Models
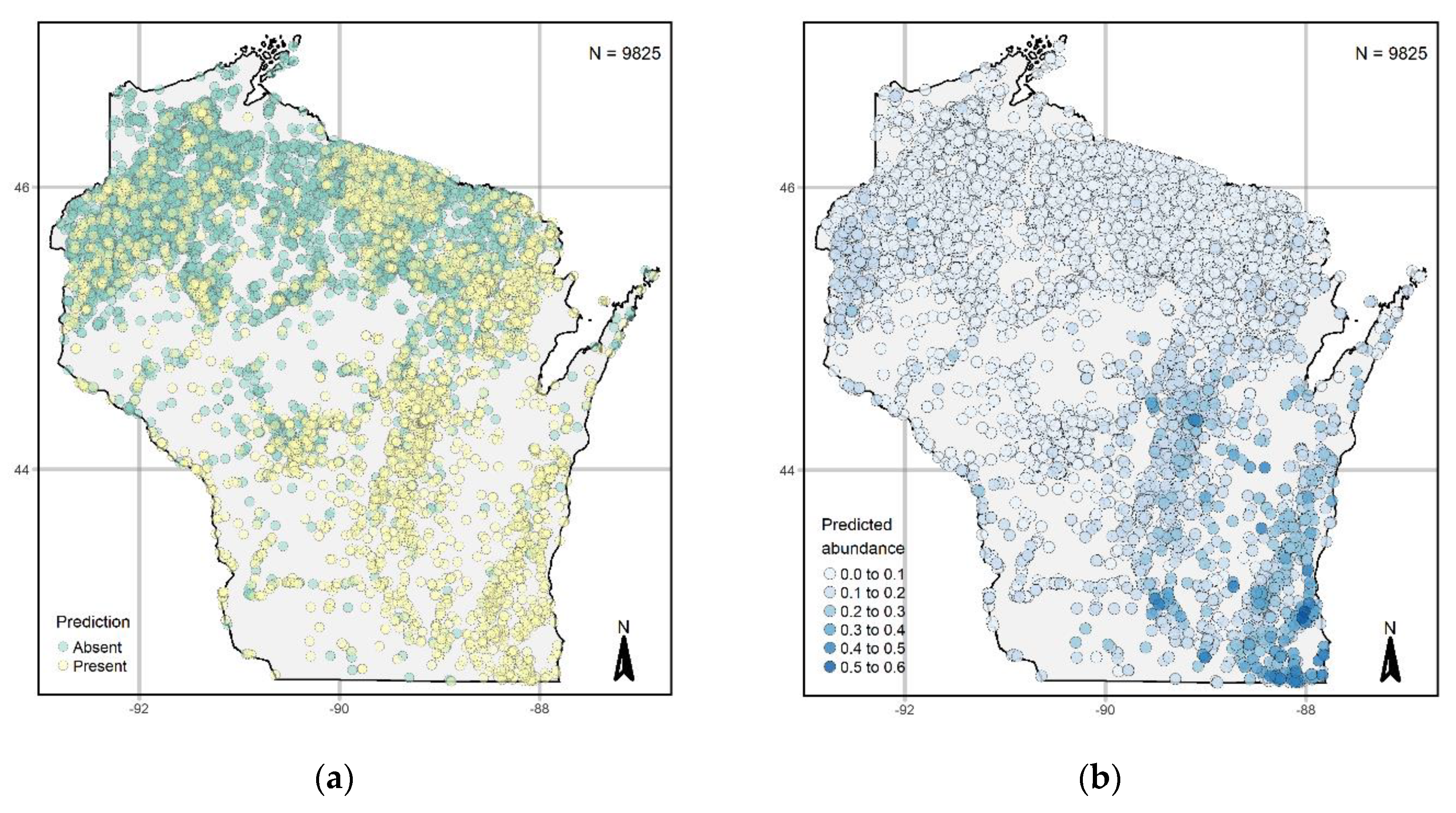
3.3. Statewide Predictions
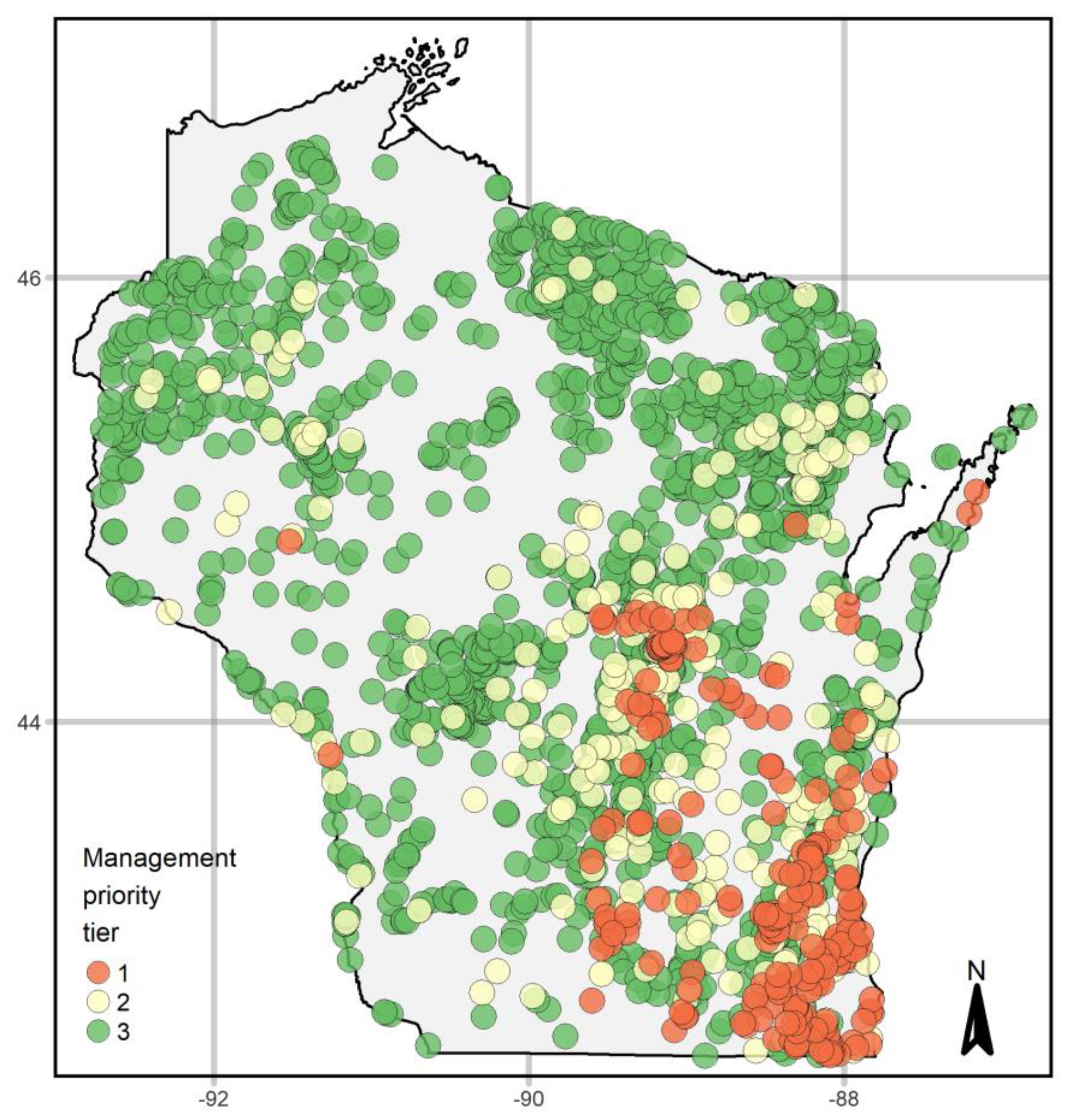
3.4. Prioritizing Management
4. Discussion
4.1. Occurrence Models
4.2. Abundance Models
4.3. Management Prioritization: Uniting Occurrence and Abundance
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mack, R.N.; Simberloff, D.; Lonsdale, W.M.; Evans, H.; Clout, M.; Bazzaz, F.A. Biotic invasions: Causes, epidemiology, global consequences, and control. Ecol. Appl. 2000, 10, 689–710. [Google Scholar] [CrossRef]
- Simberloff, D. How common are invasion-induced ecosystem impacts? Biol. Invasions 2011, 13, 1255–1268. [Google Scholar] [CrossRef]
- Vitousek, P.; DAntonio, C.; Loope, L.; Rejmanek, M.; Westbrooks, R. Introduced species: A significant component of human-caused global change. N. Zea. J. Ecol. 1997, 21, 1–16. [Google Scholar]
- Wilcove, D.S.; Rothstein, D.; Dubow, J.; Phillips, A.; Losos, E. Quantifying threats to imperiled species in the United States. Bioscience 1998, 48, 607–615. [Google Scholar] [CrossRef]
- Neill, P.; Arim, M. Human Health Link to Invasive Species. In Encyclopedia of Environmental Health; Elsevier BV: Amsterdam, The Netherlands, 2011; pp. 116–123. [Google Scholar]
- Pimentel, D.; Zuniga, R.; Morrison, D. Update on the environmental and economic costs associated with alien-invasive species in the United States. Ecol. Econ. 2005, 52, 273–288. [Google Scholar] [CrossRef]
- AquaNIS Editorial Board. Information System on Aquatic Non-Indigenous and Cryptogenic Species. World Wide Web Electronic Publication. 2015. Available online: http://www.corpi.ku.lt/databases/aquanis (accessed on 23 April 2020).
- Integrated Taxonomic Information System (ITIS). 2020. Available online: http://www.itis.gov (accessed on 23 April 2020).
- Invasive Species Specialist Group (ISSG). The Global Invasive Species Database. 2015. Available online: http://www.iucngisd.org/gisd/ (accessed on 23 April 2020).
- Simpson, A.; Eyler, M.C.; Sikes, D.; Bowser, M.; Sellers, E.; Guala, G.F.; Cannister, M.; Libby, R.; Kozlowski, N. A Comprehensive List of Non-Native Species Established in Three Major Regions of the United States: Version 2.0; U.S. Geological Survey: Reston, VA, USA, 2019. [CrossRef]
- Vander Zanden, M.J.; Olden, J.D.; Thorne, J.H.; Mandrak, N.E. Predicting occurrences and impacts of smallmouth bass introductions in north temperate lakes. Ecol. Appl. 2004, 14, 132–148. [Google Scholar] [CrossRef]
- Guisan, A.; Thuiller, W. Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 2005, 8, 993–1009. [Google Scholar] [CrossRef]
- Rushton, S.; Ormerod, S.J.; Kerby, G. New paradigms for modelling species distributions? J. Appl. Ecol. 2004, 41, 193–200. [Google Scholar] [CrossRef]
- Elith, J.; Graham, C.; Anderson, R.P.; Dudík, M.; Ferrier, S.; Guisan, A.; Hijmans, R.; Huettmann, F.; Leathwick, J.R.; Lehmann, A.; et al. Novel methods improve prediction of species’ distributions from occurrence data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef]
- Guisan, A.; Lehmann, A.; Ferrier, S.; Austin, M.; Overton, J.M.C.; Aspinall, R.; Hastie, T. Making better biogeographical predictions of species’ distributions. J. Appl. Ecol. 2006, 43, 386–392. [Google Scholar] [CrossRef]
- Václavík, T.; Meentemeyer, R.K. Invasive species distribution modeling (iSDM): Are absence data and dispersal constraints needed to predict actual distributions? Ecol. Model. 2009, 220, 3248–3258. [Google Scholar] [CrossRef]
- Dick, J.T.A.; Alexander, M.E.; Jeschke, J.M.; Ricciardi, A.; MacIsaac, H.J.; Robinson, T.B.; Kumschick, S.; Weyl, O.; Dunn, A.M.; Hatcher, M.J.; et al. Advancing impact prediction and hypothesis testing in invasion ecology using a comparative functional response approach. Biol. Invasions 2013, 16, 735–753. [Google Scholar] [CrossRef]
- Hall, J.L.W.; Anderson, R.D.; Killen, W.D.; Hosmer, A.J.; A Brain, R. Assessment of periphyton, aquatic macrophytes, benthic communities, and physical habitat in midwestern United States streams coinciding with varying historical concentrations of atrazine. J. Environ. Sci. Health Part A 2014, 49, 1091–1099. [Google Scholar] [CrossRef] [PubMed]
- Latzka, A.W.; Hansen, G.J.A.; Kornis, M.; Zanden, M.J.V. Spatial heterogeneity in invasive species impacts at the landscape scale. Ecosphere 2016, 7, e01311. [Google Scholar] [CrossRef]
- Parker, I.; Simberloff, D.; Lonsdale, W.; Goodell, K.; Wonham, M.; Kareiva, P.; Williamson, M.; Von Holle, B.; Moyle, P.; Byers, J.; et al. Impact: Toward a framework for understanding the ecological effects of invaders. Biol. Invasions 1999, 1, 3–19. [Google Scholar] [CrossRef]
- Strayer, D.L. Non-native species have multiple abundance-impact curves. Ecol. Evol. 2020, 10, 6833–6843. [Google Scholar] [CrossRef] [PubMed]
- Yokomizo, H.; Possingham, H.P.; Thomas, M.B.; Buckley, Y.M. Managing the impact of invasive species: The value of knowing the density-impact curve. Ecol. Appl. 2009, 19, 376–386. [Google Scholar] [CrossRef]
- Buchan, L.A.J.; Padilla, D.K. Predicting the likelihood of Eurasian watermilfoil presence in lakes, a macrophyte monitoring tool. Ecol. Appl. 2000, 10, 1442–1455. [Google Scholar] [CrossRef]
- Roley, S.S.; Newman, R. Predicting Eurasian watermilfoil invasions in Minnesota. Lake Reserv. Manag. 2008, 24, 361–369. [Google Scholar] [CrossRef]
- Tamayo, M.; Olden, J.D. Forecasting the vulnerability of lakes to aquatic plant invasions. Invasive Plant Sci. Manag. 2014, 7, 32–45. [Google Scholar] [CrossRef]
- Decker, K.L.; Allen, C.R.; Acosta, L.; Hellman, M.L.; Jorgensen, C.F.; Stutzman, R.J.; Unstad, K.M.; Williams, A.; Yans, M. Land Use, Landscapes, and Biological Invasions. Invasive Plant Sci. Manag. 2017, 5, 108–116. [Google Scholar] [CrossRef]
- Mikulyuk, A.; Sharma, S.; Van Egeren, S.; Erdmann, E.; Nault, M.E.; Hauxwell, J. The relative role of environmental, spatial, and land-use patterns in explaining aquatic macrophyte community composition. Can. J. Fish. Aquat. Sci. 2011, 68, 1778–1789. [Google Scholar] [CrossRef]
- Smith, C.S.; Barko, J.W. Ecology of Eurasian watermilfoil. J. Aquat. Plant Manag. 1990, 28, 55–64. [Google Scholar]
- Eiswerth, M.E.; Donaldson, S.G.; Johnson, W.S. Potential environmental impacts and economic damages of Eurasian watermilfoil (Myriophyllum spicatum) in Western Nevada and Northeastern California. Weed Technol. 2000, 14, 511–518. [Google Scholar] [CrossRef]
- EDDMapS. Early Detection & Distribution Mapping System; The University of Georgia-Center for Invasive Species and Ecosystem Health: Athens, GA, USA, 2017. [Google Scholar]
- Trebitz, A.S.; Nichols, S.A.; Carpenter, S.R.; Lathrop, R.C. Patterns of vegetation change in Lake Wingra following a Myriophyllum spicatum decline. Aquat. Bot. 1993, 46, 325–340. [Google Scholar] [CrossRef]
- Boylen, C.W.; Eichler, L.W.; Madsen, J.D. Loss of native aquatic plant species in a community dominated by Eurasian watermilfoil. Hydrobiologia 1999, 415, 207–211. [Google Scholar] [CrossRef]
- Provencher, B.; Lewis, D.J.; Anderson, K. Disentangling preferences and expectations in stated preference analysis with respondent uncertainty: The case of invasive species prevention. J. Environ. Econ. Manag. 2012, 64, 169–182. [Google Scholar] [CrossRef]
- Zipp, K.Y.; Lewis, D.J.; Provencher, B.; Zanden, M.J.V. The spatial dynamics of the economic impacts of an aquatic invasive species: An empirical analysis. Land. Econ. 2019, 95, 1–18. [Google Scholar] [CrossRef]
- Mikulyuk, A.; Kujawa, E.; Nault, M.E.; Van Egeren, S.; Wagner, K.I.; Barton, M.; Hauxwell, J.; Zanden, M.J.V. Is the cure worse than the disease? Comparing the ecological effects of an invasive aquatic plant and the herbicide treatments used to control it. FACET 2020, 5, 353–366. [Google Scholar] [CrossRef]
- Di Nino, F.; Thiébaut, G.; Muller, S. Response of Elodea nuttallii (Planch.) H. St. John to Manual Harvesting in the North-East of France. Hydrobiologia 2005, 551, 147–157. [Google Scholar] [CrossRef]
- Torn, K.; Martin, G.; Kotta, J.; Kupp, M. Effects of different types of mechanical disturbances on a charophyte dominated macrophyte community. Estuar. Coast. Shelf Sci. 2010, 87, 27–32. [Google Scholar] [CrossRef]
- Omernik, J.M.; Chapman, S.S.; Lillie, R.A.; Dumke, R.T. Transactions of the Wisconsin Academy of Sciences, Arts and Letters. Ecoregions Wis. 2000, 88, 77–103. [Google Scholar]
- Mikulyuk, A.; Hauxwell, J.; Rasmussen, P.; Knight, S.; Wagner, K.I.; Nault, M.E.; Ridgely, D. Testing a methodology for assessing plant communities in temperate inland lakes. Lake Reserv. Manag. 2010, 26, 54–62. [Google Scholar] [CrossRef]
- Hauxwell, J.; Knight, S.; Mikulyuk, A.; Nault, M.E.; Porzky, M.; Chase, S. Recommended Baseline Monitoring of Aquatic Plant in Wisconsin: Sampling Design, Field and Laboratory Procedures, Data Entry and Analysis, and Applications; Wisconsin Department of Natural Resources: Madison, WI, USA, 2010.
- Crow, G.E.; Hellquist, C.B. Aquatic and Wetland Plants of Northeastern North America. Vol 1. Pteridophytes, Gymnosperms and Angiosperms: Dicotyledons; University of Wisconsin Press: Madison, WI, USA, 2000. [Google Scholar]
- Crow, G.E.; Hellquist, C.B. Aquatic and Wetland Plants of Northeastern North America. Vol. 2. Angiosperms: Monocotyledons; University of Wisconsin Press: Madison, WI, USA, 2000. [Google Scholar]
- Menuz, D.R.; Ruesch, A.S.; Diebel, M.W. 1:24K Hydrography Attribution Metadata; Wisconsin Department of Natural Resources: Madison, WI, USA, 2013.
- Olson, J.R.; Hawkins, C.P. Predicting natural base-flow stream water chemistry in the western United States. Water Resour. Res. 2012, 48, 1–19. [Google Scholar] [CrossRef]
- Moebius-Clune, B. Soil Health Initiatives of the USDA Natural Resources Conservation Service (NRCS); RePEc; USDA: Washington, WA, USA, 2017.
- Wang, G.; Wu, B.; Zhang, L.; Jiang, H.; Xu, Z. Role of soil erodibility in affecting available nitrogen and phosphorus losses under simulated rainfall. J. Hydrol. 2014, 514, 180–191. [Google Scholar] [CrossRef]
- Jin, S.; Yang, L.; Danielson, P.; Homer, C.; Fry, J.; Xian, G. A comprehensive change detection method for updating the National Land Cover Database to circa 2011. Remote Sens. Environ. 2013, 132, 159–175. [Google Scholar] [CrossRef]
- Allouche, O.; Steinitz, O.; Rotem, D.; Rosenfeld, A.; Kadmon, R. Incorporating distance constraints into species distribution models. J. Appl. Ecol. 2008, 45, 599–609. [Google Scholar] [CrossRef]
- Reed-Andersen, T.; Bennett, E.M.; Jorgensen, B.S.; Lauster, G.; Lewis, D.B.; Nowacek, D.; Riera, J.L.; Sanderson, B.L.; Stedman, R. Distribution of recreational boating across lakes: Do landscape variables affect recreational use? Freshw. Biol. 2000, 43, 439–448. [Google Scholar] [CrossRef]
- Open Street Map. Roads Data for Wisconsin. Downloaded from GeoFabrik Website in June, 2014. 2014. Available online: http://www.geofabrik.de/data/download.html (accessed on 2 October 2020).
- Ruesch, A.S.; Menuz, D.R.; Diebel, M.W. 1:24K Wisconsin Hydrography Dataset Creation Toolset; Wisconsin Department of Natural Resources: Madison, WI, USA, 2013.
- The Register of Waterbodies; Wisconsin Department of Natural Resources: Madison, WI, USA, 2008.
- Bivand, R.; Keitt, T.; Rowlingson, B. rgdal: Bindings for the ’Geospatial’ Data Abstraction Library. R Package Version 0.8–13. 2019. Available online: https://cran.r-project.org/web/packages/rgdal/index.html (accessed on 13 October 2020).
- Bivand, R.; Rundel, C. rgeos: Interface to Geometry Engine—Open Source (’GEOS’). R Package Version 0.2–2. 2018. Available online: https://cran.r-project.org/web/packages/rgdal/index.html (accessed on 13 October 2020).
- Ryden, K. Environmental Systems Research Institute Mapping. Am. Cartogr. 1987, 14, 261–263. [Google Scholar] [CrossRef]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. 2017. Available online: https://rspatial.org/raster/ (accessed on 2 October 2020).
- Papes, M.; Vander Zanden, J. Wisconsin Lake Historical Limnological Parameters 2010, 1925–2009. Available online: https://doi.org/10.6073/pasta/66320ff8063706f6b3ee83a0ef3ef439 (accessed on 7 October 2020).
- Van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate Imputation by Chained Equations inR. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 2nd ed.; SAGE Publications: Thousand Oaks, CA, USA, 2011. [Google Scholar]
- Firth, D. Bias reduction of maximum likelihood estimates. Biometrika 1993, 80, 27–38. [Google Scholar] [CrossRef]
- Fielding, A.H.; Bell, J.F. A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ. Conserv. 1997, 24, 38–49. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sánchez, J.C.; Mueller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef] [PubMed]
- Tjur, T. Coefficients of Determination in Logistic Regression Models—A New Proposal: The Coefficient of Discrimination. Am. Stat. 2009, 63, 366–372. [Google Scholar] [CrossRef]
- Chen, J.; Shiyomi, M.; Hori, Y.; Yamamura, Y. Frequency distribution models for spatial patterns of vegetation abundance. Ecol. Model. 2008, 211, 403–410. [Google Scholar] [CrossRef]
- Ferrari, S.L.P.; Cribari-Neto, F. Beta Regression for Modelling Rates and Proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Simas, A.B.; Barreto-Souza, W.; Rocha, A.V. Improved estimators for a general class of beta regression models. Comput. Stat. Data Anal. 2010, 54, 348–366. [Google Scholar] [CrossRef]
- Hunger, M.; Baumert, J.; Holle, R. Analysis of SF-6D Index Data: Is Beta Regression Appropriate? Value Health 2011, 14, 759–767. [Google Scholar] [CrossRef]
- Cribari-Neto, F.; Zeileis, A. Beta Regression inR. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef]
- Smithson, M.; Verkuilen, J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol. Methods 2006, 11, 54–71. [Google Scholar] [CrossRef]
- Grün, B.; Kosmidis, I.; Zeileis, A. Extended Beta Regression inR: Shaken, Stirred, Mixed, and Partitioned. J. Stat. Softw. 2012, 48, 1–25. [Google Scholar] [CrossRef]
- Potts, J.; Elith, J. Comparing species abundance models. Ecol. Model. 2006, 199, 153–163. [Google Scholar] [CrossRef]
- Couch, R.; Nelson, E. Myriophyllum spicatum in North America. In Proceedings of the First International Symposium on Watermilfoil (Myriophyllum spicatum) and Related Haloragaciae Species, Vicksburg, MS, USA, 23–24 July 1985; Aquatic Plant Management Society: Vicksburg, MS, USA, 1985. [Google Scholar]
- Vestergaard, O.; Sand-Jensen, K. Alkalinity and trophic state regulate aquatic plant distribution in Danish lakes. Aquat. Bot. 2000, 67, 85–107. [Google Scholar] [CrossRef]
- Santamaría, L. Why are most aquatic plants widely distributed? Dispersal, clonal growth and small-scale heterogeneity in a stressful environment. Acta Oecol. 2002, 23, 137–154. [Google Scholar] [CrossRef]
- Johnstone, I.; Coffey, B.; Howard-Williams, C. The role of recreational boat traffic in interlake dispersal of macrophytes: A New Zealand case study. J. Environ. Manag. 1985, 20, 263–279. [Google Scholar]
- Havel, J.E.; Shurin, J.B.; Jones, J.R. Estimating dispersal from patterns of spread: Spatial and local control of lake invasions. Ecology 2002, 83, 3306–3318. [Google Scholar] [CrossRef]
- Rech, P.H.; Wetzel, R.G.; Thuy, N. Distribution, production and role of aquatic macrophytes in a southern Michigan marl lake. Freshw. Biol. 1971, 1, 3–21. [Google Scholar] [CrossRef]
- GBIF.org. 7 Aug 2020. GBIF Occurrence Download. Available online: https://www.gbif.org/occurrence/search?taxon_key=5361760 (accessed on 7 October 2020).
- Carpenter, S.R. Enrichment of Lake Wingra, Wisconsin, by submersed macrophyte decay. Ecology 1980, 61, 1145–1155. [Google Scholar] [CrossRef]
- Kovalenko, K.E.; Dibble, E.D.; Slade, J.G. Community effects of invasive macrophyte control: Role of invasive plant abundance and habitat complexity. J. Appl. Ecol. 2010, 47, 318–328. [Google Scholar] [CrossRef]
- Madsen, J.D.; Sutherland, J.W.; Bloomfield, J.A.; Eichler, L.W.; Boylen, C.W. The decline of native vegetation under dense Eurasian watermilfoil canopies. J. Aquat. Plant Manag. 1991, 29, 94–99. [Google Scholar]
- Wilson, S.J.; Ricciardi, A. Epiphytic macroinvertebrate communities on Eurasian watermilfoil (Myriophyllum spicatum) and native milfoils Myriophyllum sibiricum and Myriophyllum alterniflorum in eastern North America. Can. J. Fish. Aquat. Sci. 2009, 66, 18–30. [Google Scholar] [CrossRef]
- Horsch, E.J.; Lewis, D.J. The Effects of Aquatic Invasive Species on Property Values: Evidence from a Quasi-Experiment. Land Econ. 2009, 85, 391–409. [Google Scholar] [CrossRef]
- Olden, J.D.; Tamayo, M. Incentivizing the Public to Support Invasive Species Management: Eurasian Milfoil Reduces Lakefront Property Values. PLoS ONE 2014, 9, e110458. [Google Scholar] [CrossRef]
- Hutchinson, G.E. The chemical ecology of three species of Myriophyllum (Angionspermae, Haloragaceae). Limnol. Oceanogr. 1970, 15, 1–5. [Google Scholar] [CrossRef]
- Verheyen, D.; Van Gaelen, N.; Ronchi, B.; Batelaan, O.; Struyf, E.; Govers, G.; Merckx, R.; Diels, J. Dissolved phosphorus transport from soil to surface water in catchments with different land use. Ambio 2015, 44, 228–240. [Google Scholar] [CrossRef] [PubMed]
- Parry, R. Agricultural Phosphorus and Water Quality: A U.S. Environmental Protection Agency Perspective. J. Environ. Qual. 1998, 27, 258–261. [Google Scholar] [CrossRef]
- Egertson, C.J.; Kopaska, J.A.; Downing, J.A. A Century of change in macrophyte abundance and composition in response to agricultural eutrophication. Hydrobiology 2004, 524, 145–156. [Google Scholar] [CrossRef]
- Smith, V.H. Eutrophication of freshwater and coastal marine ecosystems a global problem. Environ. Sci. Pollut. Res. 2003, 10, 126–139. [Google Scholar] [CrossRef]
- Grace, J.B.; Wetzel, R.G. The production biology of Eurasian watermilfoil (Myriophyllum spicatum L.): A Review. J. Aquat. Plant Manag. 1978, 16, 1–11. [Google Scholar]
- Carpenter, S.R. The decline of Myriophyllum spicatum in a eutrophic Wisconsin lake. Can. J. Bot. 1980, 58, 527–535. [Google Scholar] [CrossRef]
- Newman, R.M.; Biesboer, D.D. A decline of Eurasian watermilfoil in Minnesota associated with the milfoil weevil, Euhrychiopsis lecontei. J. Aquat. Plant Manag. 2000, 38, 105–111. [Google Scholar]
- Hansen, G.J.A.; Zanden, M.J.V.; Blum, M.J.; Clayton, M.K.; Hain, E.F.; Hauxwell, J.; Izzo, M.; Kornis, M.S.; McIntyre, P.B.; Mikulyuk, A.; et al. Commonly rare and rarely common: Comparing population abundance of invasive and native aquatic species. PLoS ONE 2013, 8, e77415. [Google Scholar] [CrossRef] [PubMed]
- Vander Zanden, M.J.; Olden, J.D. A management framework for preventing the secondary spread of aquatic invasive species. Can. J. Fish. Aquat. Sci. 2008, 65, 1512–1522. [Google Scholar] [CrossRef]
| Predictor | Coefficient |
|---|---|
| Intercept | 0.13 *** (0.07−0.21) |
| Road density (log (m/ha +1)) | 1.93 *** (1.42−2.74) |
| Surface area (log ha) | 1.72 *** (1.33−2.31) |
| Maximum air temp. (°C × 10) | 1.69 ** (1.23−2.40) |
| Maximum depth (log m +1) | 1.55 ** (1.20−2.06) |
| Conductivity (log μS/cm) | 1.47 (0.72−3.20) |
| Alkalinity (log mg CaCO3 +1) | 1.44 (0.67−3.03) |
| Soil erodibility (kwfact) | 1.17 (0.93−1.49) |
| Watershed urban () | 1.07 (0.77−1.53) |
| pH | 1.06 (0.80−1.41) |
| Secchi depth (log m +1) | 0.85 (0.62−1.16) |
| Watershed agriculture () | 0.81 (0.58−1.10) |
| CaO () | 0.74 ** (0.57−0.92) |
| Annual temp. range (°C × 10) | 0.64 * (0.42−0.92) |
| Mean distance source (log m) | 0.61 *** (0.45−0.82) |
| Observed | |||
|---|---|---|---|
| Absent | Present | ||
| Predicted | Absent | 100 | 11 |
| Present | 169 | 377 | |
| Mean Submodel | Precision Submodel | |||||||
|---|---|---|---|---|---|---|---|---|
| Linear | Quadratic | Linear | Quadratic | |||||
| Predictors | Estimate | SE | Estimate | SE | Estimate | SE | Estimate | SE |
| Intercept | −3.71 *** | 0.28 | 2.11 *** | 0.31 | ||||
| Conductivity (log μS/cm) | 1.27 *** | 0.24 | −0.52 *** | 0.11 | −1.74 *** | 0.31 | 0.61 *** | 0.14 |
| Road density (log (m/ha +1)) | 0.34 * | 0.14 | −0.06 | 0.06 | −0.24 | 0.17 | 0.12 | 0.07 |
| Alkalinity (log mg CaCO3 +1) | 0.31 | 0.23 | −0.01 | 0.11 | −0.73 * | 0.30 | 0.41 ** | 0.14 |
| Maximum air temp. (°C x 10) | 0.28 * | 0.11 | −0.11 | 0.10 | 0.00 | 0.12 | 0.15 | 0.11 |
| Mean distance source (log m) | 0.22 | 0.16 | 0.19 * | 0.09 | −0.30 | 0.18 | −0.23 * | 0.10 |
| Watershed agriculture () | 0.10 | 0.13 | 0.03 | 0.08 | −0.31 * | 0.15 | 0.02 | 0.09 |
| Watershed urban () | 0.10 | 0.14 | 0.02 | 0.04 | −0.23 | 0.16 | 0.00 | 0.04 |
| Maximum depth (log m +1) | 0.07 | 0.11 | −0.10 | 0.06 | 0.09 | 0.13 | 0.11 | 0.07 |
| Soil erodibility (kwfact) | 0.04 | 0.08 | −0.23 ** | 0.09 | −0.03 | 0.09 | 0.37 *** | 0.10 |
| Surface area (log ha) | 0.02 | 0.19 | 0.02 | 0.05 | 0.09 | 0.22 | −0.02 | 0.06 |
| Secchi depth (log m +1) | −0.08 | 0.10 | −0.09 | 0.06 | 0.00 | 0.11 | 0.03 | 0.06 |
| pH | −0.11 | 0.11 | 0.01 | 0.05 | 0.27 | 0.15 | −0.06 | 0.06 |
| CaO () | −0.23 * | 0.10 | 0.06 | 0.05 | 0.22 | 0.12 | −0.06 | 0.05 |
| Annual temp. range (°C x 10) | −0.54 * | 0.21 | −0.05 | 0.07 | 0.42 | 0.23 | 0.05 | 0.07 |
| Log-likelihood | 1856 | |||||||
| Df | 58 | |||||||
| Pseudo R2 | 0.24 | |||||||
| Abundance | ||||
|---|---|---|---|---|
| High (0.36–1) | Med. (0.18–0.36) | Low (0–0.18) | ||
| Presence | High (0.75–1) | 28 | 188 | 227 |
| Med. (0.50–0.75) | 1 | 70 | 644 | |
| Low (0.25–0.50) | 0 | 28 | 1171 | |
| Prevention and Control Priority | Tier 1 | Tier 2 | Tier 3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikulyuk, A.; Hein, C.L.; Van Egeren, S.; Kujawa, E.R.; Vander Zanden, M.J. Prioritizing Management of Non-Native Eurasian Watermilfoil Using Species Occurrence and Abundance Predictions. Diversity 2020, 12, 394. https://doi.org/10.3390/d12100394
Mikulyuk A, Hein CL, Van Egeren S, Kujawa ER, Vander Zanden MJ. Prioritizing Management of Non-Native Eurasian Watermilfoil Using Species Occurrence and Abundance Predictions. Diversity. 2020; 12(10):394. https://doi.org/10.3390/d12100394
Chicago/Turabian StyleMikulyuk, Alison, Catherine L. Hein, Scott Van Egeren, Ellen Ruth Kujawa, and M. Jake Vander Zanden. 2020. "Prioritizing Management of Non-Native Eurasian Watermilfoil Using Species Occurrence and Abundance Predictions" Diversity 12, no. 10: 394. https://doi.org/10.3390/d12100394
APA StyleMikulyuk, A., Hein, C. L., Van Egeren, S., Kujawa, E. R., & Vander Zanden, M. J. (2020). Prioritizing Management of Non-Native Eurasian Watermilfoil Using Species Occurrence and Abundance Predictions. Diversity, 12(10), 394. https://doi.org/10.3390/d12100394