Investigation of the Peninsula Effect Using the Latitudinal Abundance Pattern for Tree Species in Florida
Abstract
1. Introduction
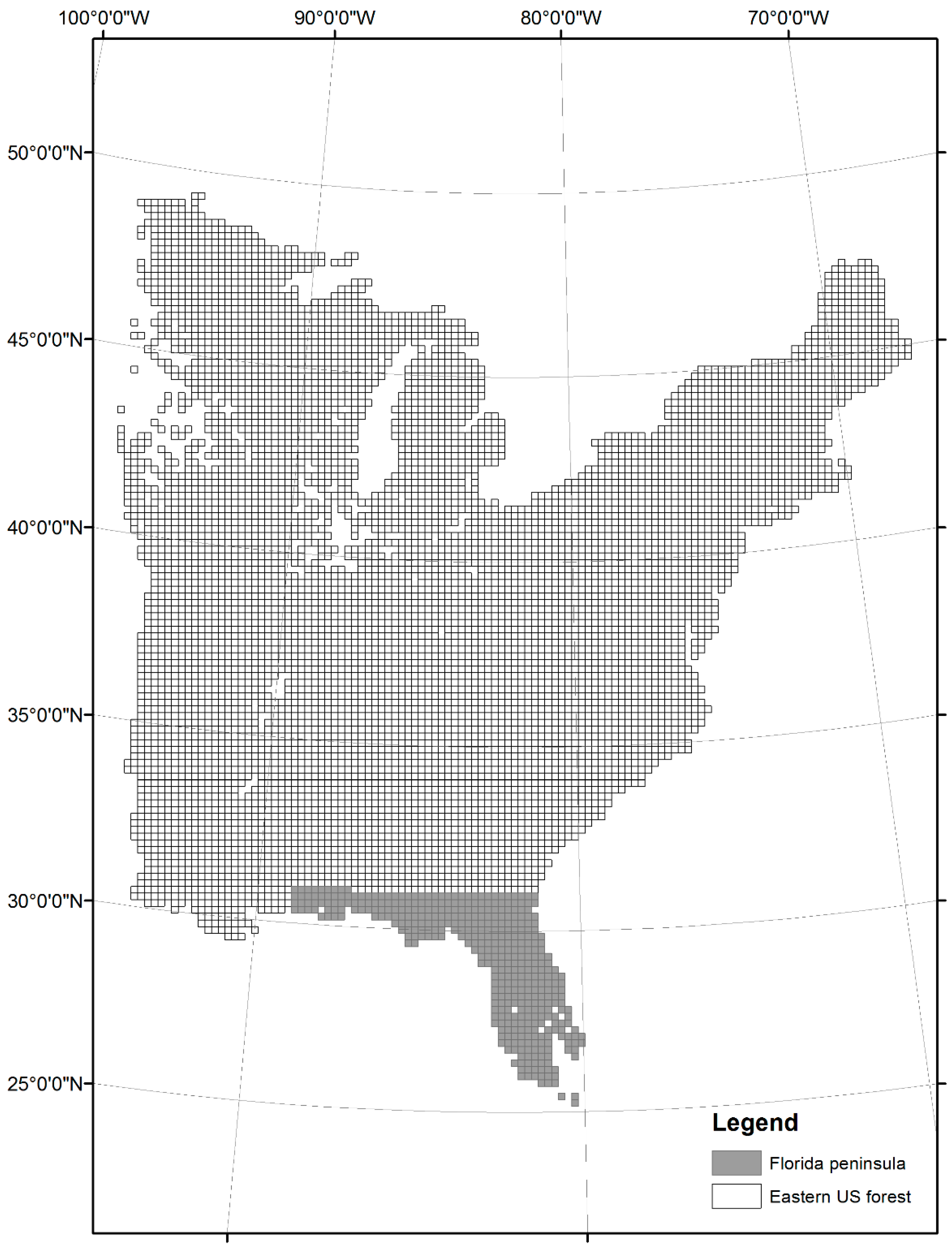
2. Materials and Methods
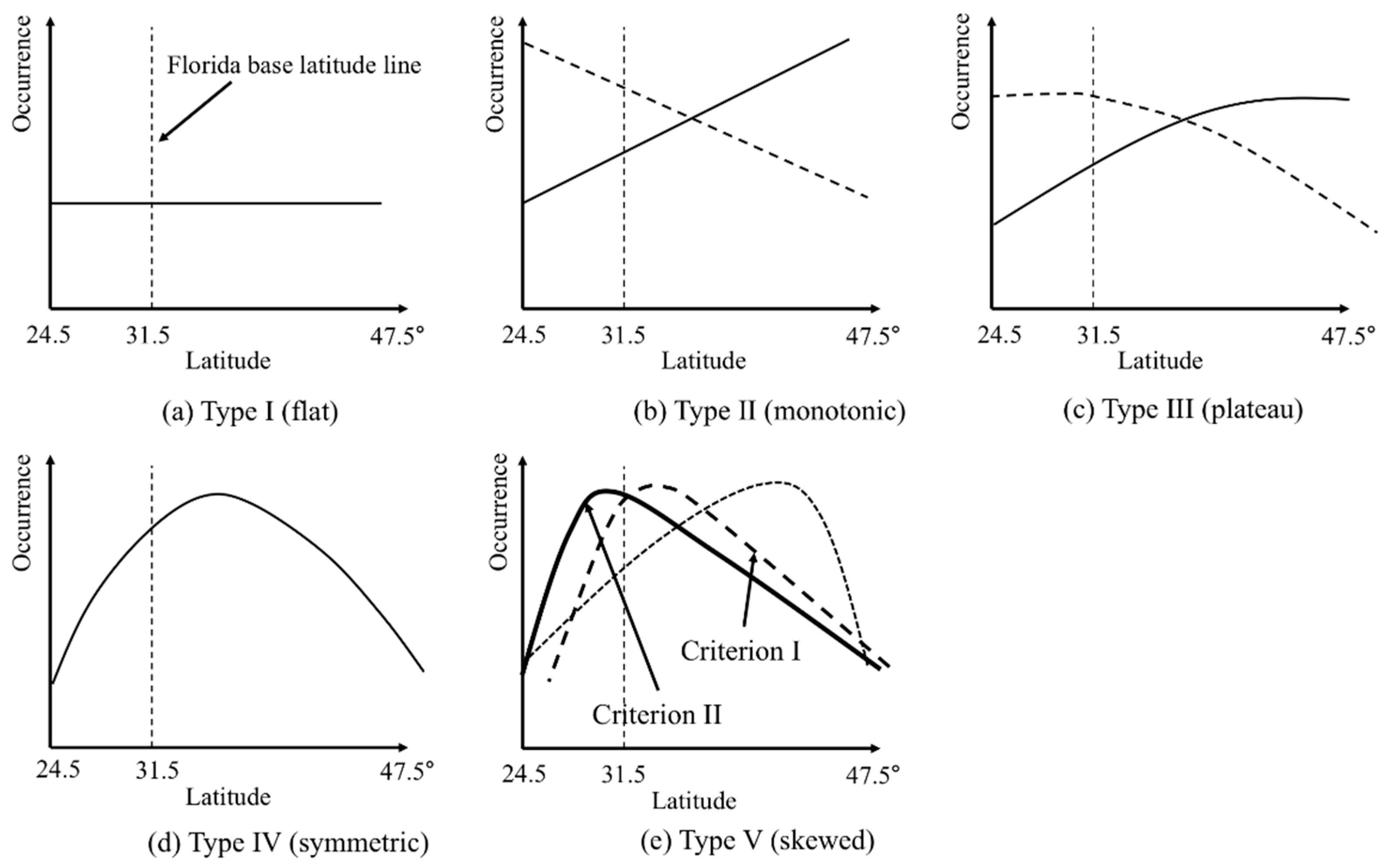
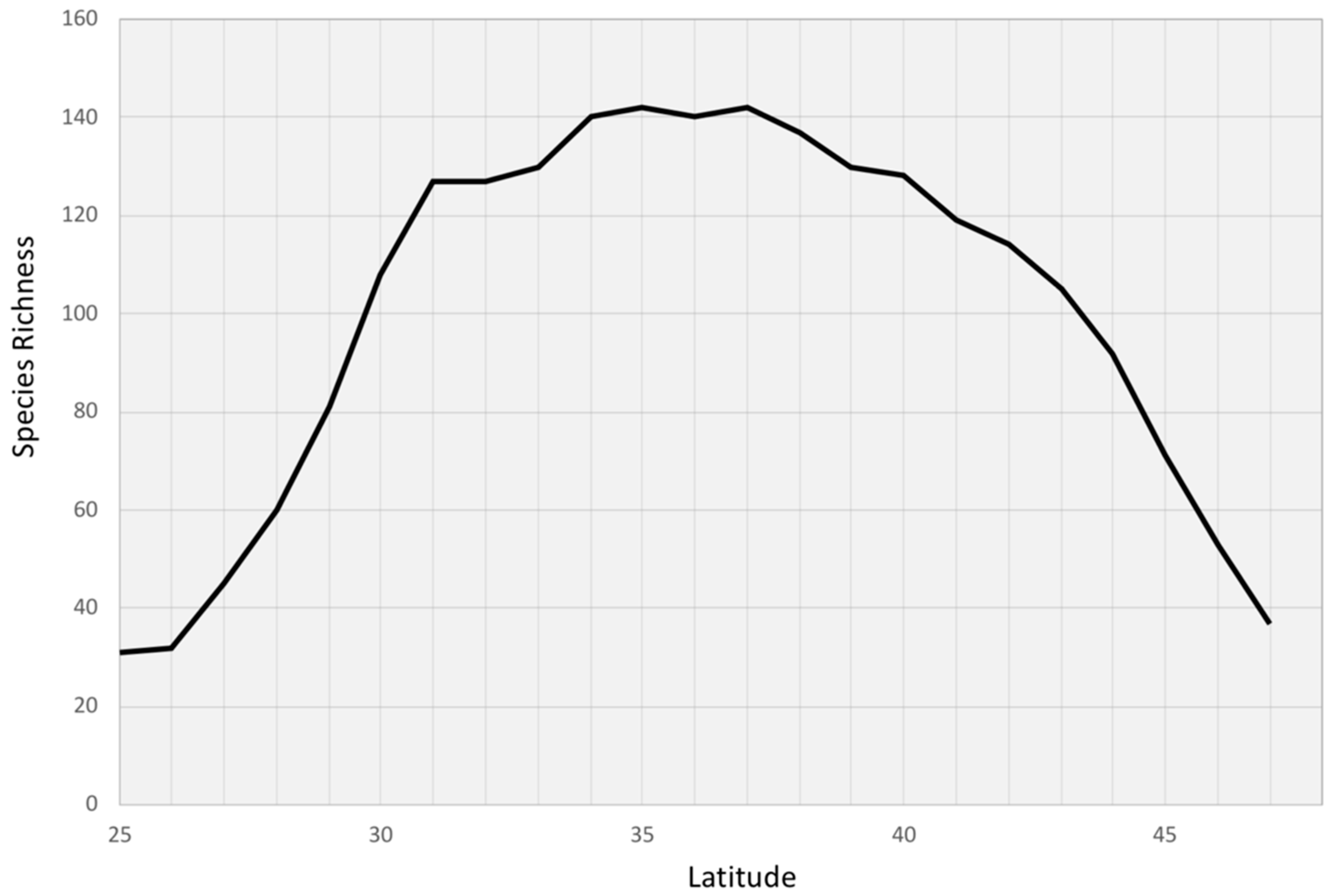
3. Results
4. Discussion
4.1. Comparison with Other Peninsula Effect Studies
4.2. Thoughts Regarding Other Hypotheses for the Peninsula Effect in Florida
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gleason, H.A. On the relation between species and area. Ecology 1922, 3, 158–162. [Google Scholar] [CrossRef]
- Fisher, R.A. Allowance for double reduction in the calculation of genotype frequencies with polysomic inheritance. Ann. Eugen. 1943, 12, 169–171. [Google Scholar] [CrossRef]
- Rohde, K. Latitudinal gradients in species diversity: The search for the primary cause. Oikos 1992, 65, 514–527. [Google Scholar] [CrossRef]
- Rosenzweig, M.L. Species Diversity in Space and Time; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Blackburn, T.M.; Gaston, K.J. Spatial patterns in the species richness of birds in the New World. Ecography 1996, 19, 369–376. [Google Scholar] [CrossRef]
- Willig, M.R.; Kaufman, D.M.; Stevens, R.D. Latitudinal gradients of biodiversity: Pattern, process, scale, and synthesis. Annu. Rev. Ecol. Evol. Syst. 2003, 34, 273–309. [Google Scholar] [CrossRef]
- Kiester, A.R. Species density of North American amphibians and reptiles. Syst. Zool. 1971, 20, 127–137. [Google Scholar] [CrossRef]
- Brown, J.H.; Lomolino, M.V. Biogeography, 2nd ed.; Sinauer: Sunderland, MA, USA, 1998. [Google Scholar]
- Wang, Z.; Fang, J.; Tang, Z.; Lin, X. Patterns, determinants and models of woody plant diversity in China. Proc. R. Soc. Lond. B Biol. Sci. 2010, 278. [Google Scholar] [CrossRef]
- Condamine, F.L.; Sperling, F.A.H.; Wahlberg, N.; Rasplus, J.; Kergoat, G.J. What causes latitudinal gradients in species diversity? Evolutionary processes and ecological constraints on swallowtail biodiversity. Ecol. Lett. 2012, 15, 267–277. [Google Scholar] [CrossRef]
- Mittelbach, G.G.; Schemske, D.W.; Cornell, H.V.; Allen, A.P.; Brown, J.M.; Bush, M.B.; Harrison, S.P.; Hurlbert, A.H.; Knowlton, N.; Lessios, H.A.; et al. Evolution and the latitudinal diversity gradient: Speciation, extinction and biogeography. Ecol. Lett. 2007, 10, 315–331. [Google Scholar] [CrossRef]
- Battisti, C. Peninsular patterns in biological diversity: Historical arrangement, methodological approaches and causal processes. J. Nat. Hist. 2014, 48, 2701–2732. [Google Scholar] [CrossRef]
- Robertson, W.B. An analysis of the breeding-bird populations of tropical Florida in relation to the vegetation. Ph.D. Thesis, University of Illinois Urbana-Champaign, Urbana, IL, USA, 1955. [Google Scholar]
- Simpson, G.G. Species density of North American recent mammals. Syst. Zool. 1964, 13, 57–73. [Google Scholar] [CrossRef]
- Olivier, P.I.; Rolo, V.; Van Aarde, R.J. Pattern or process? Evaluating the peninsula effect as a determinant of species richness in coastal dune forests. PLoS ONE 2017, 12, e0173694. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Wilson, E.O. The Theory of Island Biogeography; Princeton University Press: Princeton, NJ, USA, 1967. [Google Scholar]
- Taylor, R.J.; Regal, P.J. The peninsular effect on species diversity and the biogeography of Baja California. Am. Nat. 1978, 112, 583–593. [Google Scholar] [CrossRef]
- Milne, B.T.; Forman, R.T.T. Peninsulas in Maine: Woody plant diversity, distance, and environmental patterns. Ecology 1986, 67, 967–974. [Google Scholar] [CrossRef]
- González-Taboada, F.; Nores, C.; Ángel Álvarez, M. Breeding bird species richness in Spain: Assessing diversity hypothesis at various scales. Ecography 2007, 30, 241–250. [Google Scholar] [CrossRef]
- Peck, S.B.; Larivee, M.; Browne, J. Biogeography of ground beetles of Florida (Coleoptera: Carabidae): The peninsula effect and beyond. Ann. Entomol. Soc. Am. 2005, 98, 951–959. [Google Scholar] [CrossRef]
- Due, A.D.; Polis, G.A. Trends in scorpion diversity along the Baja California peninsula. Am. Nat. 1986, 128, 460–468. [Google Scholar] [CrossRef]
- Tackaberry, R.; Kellman, M. Patterns of tree species richness along peninsular extensions of tropical forests. Glob. Ecol. Biogeogr. Lett. 1996, 5, 85–90. [Google Scholar] [CrossRef]
- Jenkins, D.G.; Rinne, D. Red herring or low illumination? The peninsula effect revisited. J. Biogeogr. 2008, 35, 2128–2137. [Google Scholar] [CrossRef]
- Colautti, R.I.; Grigorovich, I.A.; MacIsaac, H.J. Propagule pressure: A null model for biological invasions. Biol. Invasions 2006, 8, 1023–1037. [Google Scholar] [CrossRef]
- Lavergne, S.; Molina, J.; Debussche, M.A.X. Fingerprints of environmental change on the rare mediterranean flora: A 115-year study. Glob. Chang. Biol. 2006, 12, 1466–1478. [Google Scholar] [CrossRef]
- Sutton, F.M.; Morgan, J.W. Functional traits and prior abundance explain native plant extirpation in a fragmented woodland landscape. J. Ecol. 2009, 97, 718–727. [Google Scholar] [CrossRef]
- Huisman, J.; Olff, H.; Fresco, L.F.M. A hierarchical set of models for species response analysis. J. Veg. Sci. 1993, 4, 37–46. [Google Scholar] [CrossRef]
- Smith, W.B. Forest inventory and analysis: A national inventory and monitoring program. Environ. Pollut. 2002, 116, S233–S242. [Google Scholar] [CrossRef]
- Bechtold, W.A.; Patterson, P.L. The Enhanced Forest Inventory and Analysis Program: National Sampling Design and Estimation Procedures; US Department of Agriculture Forest Service, Southern Research Station: Asheville, NC, USA, 2005. [Google Scholar]
- Gibson, J.; Moisen, G.; Frescino, T.; Edwards, T.C. Using publicly available forest inventory data in climate-based models of tree species distribution: Examining effects of true versus altered location coordinates. Ecosystems 2014, 17, 43–53. [Google Scholar] [CrossRef]
- Prisley, S.P.; Wang, H.-J.; Radtke, P.J.; Coulston, J. Combining FIA plot data with topographic variables: Are precise locations needed? In Forest Inventory and Analysis (FIA) Symposium 2008; October 21–23, 2008; Park City, UT Proc RMRS-P-56CD; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2009; Available online: https://www.fs.fed.us/rm/pubs/rmrs_p056.pdf (accessed on 29 January 2019).
- McRoberts, R.E.; Bechtold, W.A.; Patterson, P.L.; Scott, C.T.; Reams, G.A. The enhanced Forest Inventory and Analysis program of the USDA Forest Service: Historical perspective and announcement of statistical documentation. J. For. 2005, 103, 304–308. [Google Scholar]
- Kwon, Y.; Larsen, C.P.S.; Lee, M. Tree species richness predicted using a spatial environmental model including forest area and frost frequency, eastern USA. PLoS ONE 2018, 13, e0203881. [Google Scholar] [CrossRef]
- Whittaker, R.H. Evolution of species diversity in land communities. Evol. Biol. 1977, 10, 1–67. [Google Scholar]
- Magurran, A.E. An Index of Diversity; Meas Biol Divers; Blackwell Science Ltd.: Oxford, UK, 2004; pp. 100–133. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Oksanen, J.; Minchin, P.R. Continuum theory revisited: What shape are species responses along ecological gradients? Ecol. Model. 2002, 157, 119–129. [Google Scholar] [CrossRef]
- Documentation, P. PostgreSQL Global Development Group. 2006. Available online: https://www.postgresql.org/docs/9.6/index.html (accessed on 29 January 2019).
- R Development Core Team. R: A Language and Environment for Statistical Computing, Vienna, Austria. 2008. Available online: http://www.R-project.org (accessed on 29 January 2019).
- Murphy, H.T.; VanDerWal, J.; Lovett-Doust, J. Signatures of range expansion and erosion in eastern North American trees. Ecol. Lett. 2010, 13, 1233–1244. [Google Scholar] [CrossRef]
- Carrascal, L.M.; Díaz, L. Asociación entre distribución continental y regional. Análisis con la avifauna forestal y de medios arbolados de la Península Ibérica. Graellsia 2003, 59, 179–207. [Google Scholar] [CrossRef]
- Schwartz, M.W. Species diversity patterns in woody flora on three North American peninsulas. J. Biogeogr. 1988, 15, 759–774. [Google Scholar] [CrossRef]
- Little, E.L.; Viereck, L.A. Atlas of United States Trees: Conifers and Important Hardwoods; US Department of Agriculture, Forest Service: Washington, DC, USA, 1971. [Google Scholar]
- Grismer, L.L. Evolutionary biogeography on Mexico’s Baja California peninsula: A synthesis of molecules and historical geology. Proc. Natl. Acad. Sci. USA 2000, 97, 14017–14018. [Google Scholar] [CrossRef] [PubMed]
- Means, D.B.; Simberloff, D. The peninsula effect: Habitat-correlated species decline in Florida’s herpetofauna. J. Biogeogr. 1987, 14, 551–568. [Google Scholar] [CrossRef]
- Ewel, J.J.; Myers, R.L. Ecosystems of Florida; University of Central Florida Press: Orlando, FL, USA, 1990. [Google Scholar]
- Stevens, G.C. The latitudinal gradient in geographical range: How so many species coexist in the tropics. Am. Nat. 1989, 133, 240–256. [Google Scholar] [CrossRef]
- Busack, S.D.; Hedges, S.B. Is the peninsular effect a red herring? Am. Nat. 1984, 123, 266–275. [Google Scholar] [CrossRef]
| Type | Direction | Number of Species (%) | % | The Five Most Abundant Species in Each Category |
|---|---|---|---|---|
| Endemic | 21 | 18.5 (out of 113 species) | Guapira discolor; Avicennia germins; Laguncularia racemosa; Rhizophora mangle; Swietenia mahagoni | |
| I—Flat | 7 | 7.6 (out of 92 general species) | Ulmus crassifolia; Quercus marilandica; Carya illinoinensis; Cinmomum camphora; Gleditsia aquatica | |
| II—Monotonic | South | 13 | 14.1 | Gordonia lasianthus; Fraxinus pennsylvanica; Persea borbonia; Ostrya virginia; Morus alba |
| North | 13 | 14.1 | Sabal palmetto; Taxodium ascendens; Nyssa aquatica; Salix carolinia; Quercus virginia | |
| III—Plateau | South | 1 | 1 | Platanus occidentalis |
| North | 2 | 2.1 | Quercus veluti; Planera aquatica | |
| IV—Gaussian | 13 | 14.1 | Chamaecyparis thyoides; Oxydendrum arboreum; Nyssa sylvatica; Carya glabra; Celtis laevigata | |
| V—Skewed | South | 22 | 23.9 | Pinus taeda; Pinus elliottii; Pinus clausa; Liquidambar styraciflua; Nyssa biflora |
| North | 21 | 43.7 | Acer rubrum; Liriodendron tulipifera; Pinus palustris; Fagus grandifolia; Pinus echita |
| SPCD 1 | Common Name | Genus | Species | Peak Abundance Latitude |
|---|---|---|---|---|
| 653 | Sweetbay | Magnolia | virginiana | 29.8 |
| 694 | Swamp tupelo | Nyssa | biflora | 30.9 |
| 107 | Sand pine | Pinus | clausa | 29.5 |
| 111 | Slash pine | Pinus | elliottii | 29.8 |
| 813 | Cherrybark oak | Quercus | pagoda | 31.4 |
| 841 | Dwarf live oak | Quercus | minima | 28.4 |
| 820 | Laurel oak | Quercus | laurifolia | 30 |
| 822 | Overcup oak | Quercus | lyrata | 31.3 |
| 828 | Texas red oak | Quercus | texa | 31.1 |
| 827 | Water oak | Quercus | nigra | 31.5 |
| 831 | Willow oak | Quercus | phellos | 31.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, Y.; Feng, L. Investigation of the Peninsula Effect Using the Latitudinal Abundance Pattern for Tree Species in Florida. Diversity 2019, 11, 20. https://doi.org/10.3390/d11020020
Kwon Y, Feng L. Investigation of the Peninsula Effect Using the Latitudinal Abundance Pattern for Tree Species in Florida. Diversity. 2019; 11(2):20. https://doi.org/10.3390/d11020020
Chicago/Turabian StyleKwon, Youngsang, and Lian Feng. 2019. "Investigation of the Peninsula Effect Using the Latitudinal Abundance Pattern for Tree Species in Florida" Diversity 11, no. 2: 20. https://doi.org/10.3390/d11020020
APA StyleKwon, Y., & Feng, L. (2019). Investigation of the Peninsula Effect Using the Latitudinal Abundance Pattern for Tree Species in Florida. Diversity, 11(2), 20. https://doi.org/10.3390/d11020020





