Abstract
Betaines of squaric acid have gained research interest because of their structural and spectral properties. We elucidated the crystal and molecular structure of the triethylammonium betaine of squaric acid (1) by X-ray crystallography, IR, and NMR spectroscopy augmented by Hirshfeld surface analysis and DFT calculations. The crystal structure determination using Hirshfeld atom refinement reveals that the resonance hybrid structure with partial enolate character of the two lateral squaric acid C=O groups describes 1 best. The solid-state supramolecular structure features weak intermolecular C−H···O hydrogen bonds. The number of C=O bands in the IR spectrum in the solid-state is consistent with local C2v symmetry of the squaric acid residue in 1. The 13C NMR signals of this group in solution were assigned based on 2D NMR experiments and computational prediction using the Gauge-Independent Atom Orbital (GIAO) method. The present study provides the first structural characterization of a betaine of squaric acid containing a four-coordinate nitrogen atom directly attached to the four-membered ring.
1. Introduction
The name betaine originates from the naturally occurring compound N,N,N-trimethylammonioacetate and has been expanded to similar zwitterionic molecules having separate positively and negatively charged functional groups that cannot be described without formal charges [1]. The positively charged group that bears no hydrogen atom is usually an onium moiety, and the negatively charged group may be a carboxylate, sulfonate, or phenolate group, for example. In the 1980s, Schmidt et al. were the first to describe a variety of betaines of squaric acid [2,3,4]. In particular, pyridinium betaines of squaric attracted research interest because of their spectral properties and potential applications as non-linear optical materials [5,6,7].
In the course of our studies of squaramides as antimycobacterial drug candidates [8], we unintentionally isolated the triethylammonium betain of squaric acid, the title compound (1). Scheme 1 shows three resonance structures (I–III) and the hybrid structure IV for the compound. In I and III, the squarate moiety exhibits formal enolate character, whereas resonance structure II with adjacent formal charges represents an N-ylide rather than a betaine.
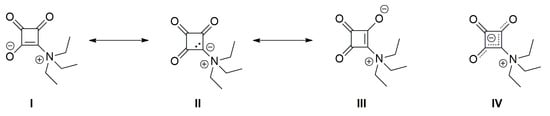
Scheme 1.
Resonance structures (I, II, and III) and hybrid structure (IV) of 1.
Herein, we report a combined crystallographic, IR and NMR spectroscopic and computational study on the triethylammonium betaine of squaric acid. To the best of our knowledge and based on a search of the Cambridge Structural Database (CSD) via WebCSD in August 2023 [9], 1, originally reported in the literature nearly 30 years ago [2], is the first structurally characterized betaine of squaric acid containing a four-coordinate nitrogen atom attached directly to the four-membered ring.
2. Results and Discussion
2.1. Structural Description of 1 in the Solid-State
Compound 1 was obtained when squaric acid was treated with trifluoromethanesulfonic anhydride and triethylamine. It forms pale yellow-greenish crystals (Figure S1). The structure was unambiguously confirmed by X-ray crystallography. The compound crystallized in the monoclinic centrosymmetric space group P21/n. Figure 1 shows the molecular structure of 1 in the crystal and a structure overlay diagram with the DFT-optimized molecular structure (B3LYP/G def2-TZVPP). Table 1 compares selected bond lengths and angles. The structure overlay reveals that the molecular structure in the crystal is close to the DFT-calculated minimum energy structure of the isolated molecule. The root mean square deviation (RMSD) is 0.1444 Å for all atoms. As can be seen in Figure 1b, the difference between the two structures is essentially a ca. 10° rotation of the triethylammonium group about the C1−N1 bond, which most likely results from packing effects in the crystal. The eight-membered C4NO3 fragment is almost planar (RMSD: 0.035 Å). A deformation density plot illustrates the bent bond feature of the four-membered carbon ring (Figure S2), indicating strain, as previously described for the squarate ion [10]. In the crystal, the C2−O1 and C4−O3 bond lengths are equal within 3σ, whereas the C3−O2 bond is significantly shorter than the C2−O1 and C4−O3 bonds by ca. 0.02 Å. Within the four-membered ring, the C1−C2 and C1−C4 and the C2−C3 and C3−C4 bond lengths each are likewise equal within 3σ, but the average length of the C1−C2 and C1−C4 bonds is significantly longer by ca. 0.10 Å than the average of the C2−C3 and C3−C4 bond lengths. These geometric parameters indicate that the resonance hybrid structure IV in Scheme 1 is the predominant form rather than the N-ylide structure II. This is consistent with previous structure reports of betaines of squaric acid containing a three-coordinate nitrogen atom [11,12,13,14,15,16,17] and the triphenylphosphonium betaine (CSD refcode: PIDDEL) [18], the only previously reported structurally characterized betaine of squaric acid featuring a four-coordinate group 15 atom. The CSD entry FEFLEI as an exception exhibits slightly different lateral C−O bond lengths, obviously resulting from intramolecular hydrogen bonding [19]. The C1−N1 bond in 1 is longer by ca. 0.05 Å than the average C−N(sp2) bond length in betaines of squaric acid with a three-coordinate nitrogen atom [11,12,13,14,15,16,17,19], but as expected markedly shorter by ca. 0.30 Å than the corresponding C−P bond in PIDDEL. The corresponding C−N distances in betaines of squaric acid in which the formal positive charge resides elsewhere in the molecule instead of the nitrogen atom bonded to the four-membered ring are significantly shorter than the C1−N1 bond length in 1 by ca. 0.12 Å, reflecting the squaramide nature of these structures [20,21,22,23]. The C4−C1−C2 bond angle in 1 is comparable to the average of the corresponding bond angle of 96.2° of the aforementioned previously reported betaines [11,12,13,14,15,16,17,19]. In PIDDEL, the corresponding angle is markedly smaller at 94.6 (1)° [18].
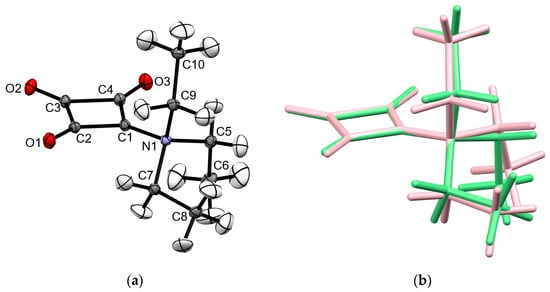
Figure 1.
(a) Molecular structure of 1 in the crystal. Displacement ellipsoids are drawn at the 50% probability level. (b) Structure overlay plot of the C4O3 entities of the molecular structure in the crystal (green) and the DFT-optimized structure of the free molecule (pink).

Table 1.
Selected bond lengths and angles for 1 (Å, °).
According to Kitajgorodskij, the space group P21/n is available for the densest packing of molecules of arbitrary shape. In the crystal, the molecules of 1 are found densely packed, as indicated by a high packing index of 78.0% [24]. Dipole–dipole interactions between the zwitterionic molecules can be considered the dominant intermolecular interaction in the solid state. Figure 2 depicts a section of the crystal structure and the molecular electrostatic potential mapped on the Hirshfeld surface. It can be seen that the positive charge is distributed over the triethylammonium group, whereas the negative charge is mainly located on the C3O3 entity. The distance between the mean planes through the four-membered rings stacked about a center of symmetry is 3.20 Å and the corresponding centroid-centroid distance is long at 4.15 Å. The solid-state supramolecular structure of 1 features short C−H···O contacts between an ethyl group and a carbonyl group with partial enolate character (Figure 3), which are indicative of weak hydrogen bonds (Table 2) [25]. It is reasonable to assume that the opposite partial charges on the triethylammonium group and the C3O3 entity facilitate weak intermolecular hydrogen bonding in this case. The strands of molecules so formed extend along a 21 screw axis parallel to the crystallographic b-axis direction. A Hirshfeld surface analysis and the corresponding 2D fingerprint plot reveal the dominance of the short O···H contacts, resulting from the accepting bifurcated intermolecular C−H···O hydrogen bonding (Figure 4).
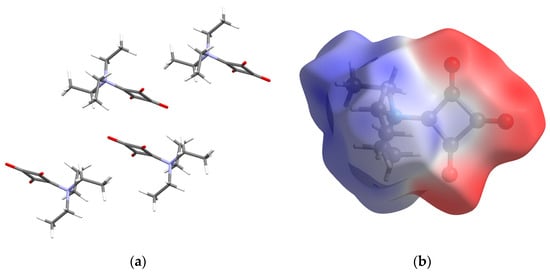
Figure 2.
(a) Section of the crystal structure of 1, viewed along the [011] direction. (b) Molecular electrostatic potential of 1 mapped on the Hirshfeld surface over the range −0.1 au (red), through zero (white) to 0.1 au (blue). Color scheme for the atoms: C, gray; H, white; N, blue; O, red.
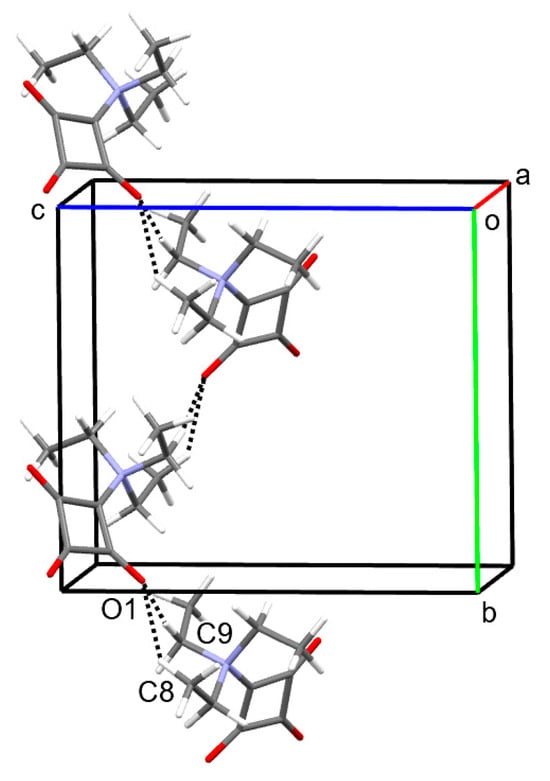
Figure 3.
Part of the crystal structure of 1, viewed approximately along the a-axis direction, showing C−H···O hydrogen-bonded chains extending along a 21 screw axis parallel to the b-axis direction. Color scheme: C, gray; H, white; N, blue; O, red.

Table 2.
Intermolecular hydrogen bond geometry for 1 (Å, °).
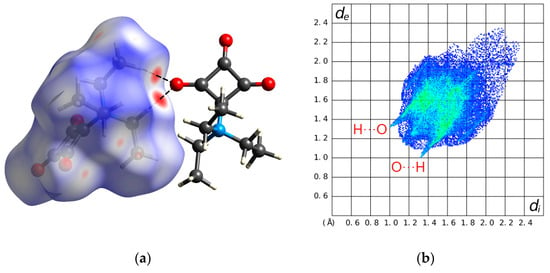
Figure 4.
(a) Hirshfeld surface mapped with dnorm (red areas indicate short contacts) and (b) the corresponding 2D fingerprint plot for 1. Color scheme for the atoms: C, gray; H, white; N, blue; O, red.
2.2. FT-IR Spectroscopy
An FT-IR spectrum of 1 was measured in the range of 4000–400 cm−1 (Figure S3). The IR bands arising from vibrations of the carbonyl groups are of particular interest. Assuming local C2v point group symmetry for the C4O3 fragment, three C=O bands (2A1 + B2) are expected. Indeed, the experimental IR spectrum exhibits three intense bands in the respective region (Table 3). These agree with those reported by Schmidt et al., albeit without detailed assignments [2]. Thus, we made tentative assignments based on DFT calculations (B3LYP/G def2-TZVPP) and the literature [6,13,26,27]. The band at 1789 cm−1 is assigned to the vibrational mode that can be predominantly described as C=O stretching vibration parallel to the local C2 axis. The band observed at 1735 cm−1 is ascribed to the mode that can be described essentially as stretching vibration of the two lateral C⸚O groups symmetric to the C2 axis, whereas the strongest band in the spectrum (1614 cm−1) belongs to the corresponding stretching mode antisymmetric with respect to the C2 axis.

Table 3.
Selected experimental (ATR) and theoretical (DFT) IR bands (cm−1) of 1.
2.3. NMR Spectroscopy
Compound 1 was also studied by NMR spectroscopy. The 1H NMR spectrum in methanol-d4 at room temperature (Figure S4) exhibits one set of signals for the ethyl groups, consistent with C3 symmetry of the triethylammonium group in solution. The ali-phatic region of the 13C NMR spectrum (Figure S5) shows two signals corresponding to the methyl (8.4 ppm) and methylene groups (55.4 ppm). Consistent with local C2v symmetry, three 13C NMR signals arise from the C4O3 unit (Figure 5 and Table 4). For the related 2-imidazol [1,2-a]pyridine of squaric acid, similar 13C NMR shifts have been reported for these carbon atoms but assignments have not been made [14]. We assign the signal with the largest downfield shift (211.0 ppm) to C3. The signal at 169.1 ppm can be attributed to C1 based on a cross peak from the methylene protons in the 2D 1H,13C HMBC NMR spectrum (Figure S7). The remaining signal at 193.4 ppm is assigned to the chemically equivalent nuclei of C2 and C4 based on their relative integral compared to C1 and C3. The shift of the signal assigned to C3 is also close to that reported for cyclobutanone (208.6 ppm), whereas that attributed to C2, C4 is similar to that reported for cyclobutane-1,3-dione (197.9 ppm) [29]. The NMR shifts for 1 predicted computationally using the Gauge-Independent Atom Orbital (GIAO) method corroborate the assignments made.
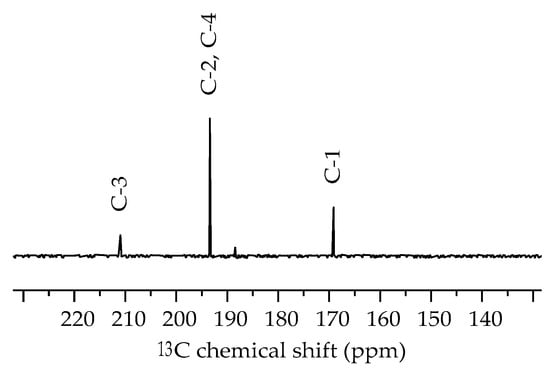
Figure 5.
Part of the 13C NMR spectrum of 1 in methanol-d4 at room temperature. The full spectrum can be found in the Supplementary Materials (Figure S5).

Table 4.
Experimental and predicted 13C NMR shifts (ppm) for the C4O3 fragment in 1.
3. Materials and Methods
3.1. General
All chemicals were of reagent-grade quality and used as received. Dichloromethane was stored over molecular sieves (4 Å). The IR spectrum was recorded on a Bruker Alpha FT-IR spectrometer with a resolution of 4 cm−1, using the ATR technique; 32 scans were accumulated (abbreviations: m = medium, s = strong). NMR spectra were recorded on a Bruker Avance Neo 600 MHz NMR spectrometer equipped with a BBO cryoprobe (abbreviations: t = triplet, q = quartet). Chemical shifts are reported relative to the residual solvent signals of methanol-d4 (δH = 3.31 ppm, δc = 49.00 ppm). The ESI mass spectrum was measured on a Q ExactiveTM Plus Orbitrap mass spectrometer (Thermo Scientific, Bremen, Germany).
3.2. Synthesis and Crystallization of 1
Squaric acid (1.14 g, 10 mmol) was suspended in 30 mL of dichloromethane, and triethylamine (2.8 mL, 20 mmol) was added. After ultra-sonication for 2 min., the mixture was degassed with argon-bubbling for 5 min, and subsequently, the mixture was cooled to 0 °C in an ice bath. Trifluoromethanesulfonic anhydride (1.68 mL, 10 mmol) was added dropwise with stirring. After stirring for 12 h and allowing the reaction mixture to warm up to room temperature, a precipitate formed and an additional 2.8 mL of triethylamine (20 mmol) was added. After the mixture had become clear, the solvent was removed under reduced pressure. HPLC analysis suggested that the crude product (3.61 g) consisted of ca. 45% 1 and large amounts of triethylammonium salts of squaric acid. Approximately 100 mg of the crude product were subjected to reversed-phase preparative HPLC (C18 column, acetonitrile/water gradient), which proved elusive. NMR analysis of the product thus obtained indicated a mixture of 1 and triethylammonium triflate. Crystallization from a solution in dichloromethane upon diffusion of heptane into the solvent afforded few pale yellow-green crystals of 1 after several days at room temperature, which were subjected to single-crystal X-ray diffraction and spectroscopic analyses. IR (ATR) ν 1789 [m, ν(C=O)], 1735 [m, νs(C⸚O)], 1614 [s, νas(C⸚O)] cm−1. 1H NMR (600 MHz, methanol-d4) δ 3.84 (q, J = 7.2 Hz, 6H, CH2), 1.35 (t, J = 7.2 Hz, 9H, CH3) ppm. 13C NMR (151 MHz, methanol-d4) δ 211.0, 193.4, 169.1, 55.4 (CH2), 8.4 (CH3) ppm. HRMS (ESI+): m/z 220.09433, calcd. for [C10H15NNaO3]+ 220.09441.
3.3. X-ray Crystallography
The crystals were coated with perfluoropolyether PFO-XR75 and mounted using a MiTeGen cryo-loop. The X-ray diffraction data were measured on a Bruker AXS D8 Venture diffractometer, equipped with an Incoatec IµS Diamond microfocus X-ray source, Incoatec multilayer optics, and a CMOS Photon III detector. The APEX 4.1.0 software was used to control the diffractometer [30]. The raw data were processed with the SAINT V8.40B software [31] and corrected for absorption effects with SADABS-2016/2 [32], using the Gaussian method based on indexed crystal faces.
The crystal structure was solved with SHELXT [33] and an initial independent atom model (IAM) refinement was carried out with SHELXL-2019/3 [34]. The structure was subsequently refined using Hirshfeld atom refinement (HAR) with NoSpherA2 [35,36] in Olex2 [37,38] with anisotropic atomic displacement parameters (ADPs) for all atoms. Regarding IAM refinement versus HAR, we should note that the conclusions drawn would be essentially the same in the present case, but HAR has some advantages. In particular, a better bond precision (average s.u. 0.0091 Å for IAM versus 0.0004 Å for HAR) can be mentioned. Furthermore, HAR allows for refinement of anisotropic ADPs for hydrogen atoms and results in C−H bond lengths that are 0.1 Å longer than those obtained by the IAM refinement and closer to those that one would expect using neutron diffraction. Crystal data and refinement details are listed in Table 3. Structure pictures were drawn with Mercury [39]. Hirshfeld surface analysis was carried out with CrystalExplorer [40], and the molecular electrostatic potential was calculated with Tonto [41]. The packing index was calculated with PLATON [42].
Crystal data for 1: C10H15NO3, Mr = 197.236, T = 100(2) K, λ = 0.71073 Å, monoclinic, space group P21/n, a = 7.4155(1), b = 10.9495(2), c = 11.9060(2) Å, β = 90.101(1)°, V = 966.72(3) Å3, Z = 4, ρcalc = 1.355 g cm−3, μcalc = 0.100 mm−1, F(000) = 424.278, crystal size = 0.164 × 0.096 × 0.072 mm, θ range = 2.53 − 33.14°, 189,165 reflections collected, 3695 reflections unique, Rint = 0.0908, observed reflections [I > 2σ(I)] 3236, 0 restraints, 262 parameters, S = 1.1708, R1 [I > 2σ(I)] = 0.0179, wR2 = 0.0344, Δρmax = 0.1319 eÅ−3, Δρmin = −0.1342 eÅ−3.
3.4. Computational Methods
DFT calculations were performed using ORCA (version 5.0) [43] with a B3LYP/G (VWN1) hybrid functional (20% HF exchange) [44,45,46], using a def2-TZVPP basis set [46] with an auxiliary def2/J basis [47]. Optimization of the structure used the BFGS method from an initial Hessian according to Almoef’s model with a very tight self-consistent field convergence threshold [48]. Calculations were made on the free molecule of 1. The optimized local minimum-energy structures exhibited only positive modes. Cartesian coordinates of the DFT-optimized structure of 1 can be found in the Supplementary Material. Structure pictures were generated with Mercury [39]. The DFT-calculated IR spectrum was evaluated with Avogadro [49]. 13C NMR shifts were predicted for the optimized structure of 1 with ORCA (version 5.0), using the default algorithm based on GIAOs [50,51]. The predicted shifts are reported relative to tetramethylsilane, calculated at the same level of theory.
4. Conclusions
We characterized the structure of 1 in the solid state by X-ray crystallography, using Hirshfeld atom refinement, and IR spectroscopy, augmented by DFT calculations. Geometric parameters of the molecular structure indicate that the resonance hybrid structure is the best representation of the betaine. Within the four-membered ring, the bond angle at C1 attached to the nitrogen atom is ca. 8° larger than the average of the other three bond angles. The observed number of carbonyl bands in the IR solid-state agrees with the local C2v symmetry assumed for the squarate moiety. Apart from close packing, dipole–dipole interactions and weak intermolecular C−H···O hydrogen bonds govern the supramolecular solid-state structure. Based on the HMBC spectrum and prediction by the GIAO method, we assigned 13C NMR signals arising from the squarate moiety.
Supplementary Materials
Cartesian coordinates of the DFT-optimized structures of 1; Figure S1: Microscope image of 1; Figure S2: Fcalc(HAR)-Fcalc(IAM) deformation density plot of 1; Figure S3: FT-IR spectrum of 1; Figure S4: 1H NMR spectrum of 1 in methanol-d4; Figure S5: 13C NMR spectrum of 1 in methanol-d4; Figure S6: 2D 1H,13C-edited-HSQC NMR spectrum of 1 in methanol-d4; Figure S7: 2D 1H,13C-HMBC NMR spectrum of 1 in methanol-d4; Figure S8: ESI+ mass spectrum of 1 in methanol.
Author Contributions
Conceptualization, R.G. and R.W.S.; methodology, P.R.P., R.G., M.L. and R.W.S.; validation, R.G., M.L. and R.W.S.; formal analysis, R.G., M.L. and R.W.S.; investigation, P.R.P., R.G. and M.L.; resources, R.G., M.L. and P.I.; data curation, R.G., M.L. and R.W.S.; writing—original draft preparation, R.W.S.; writing—review and editing, R.G., M.L., A.R. and P.I.; visualization, R.G., M.L. and R.W.S.; supervision, A.R. and P.I.; project administration, R.W.S. All authors have read and agreed to the published version of the manuscript.
Funding
No specific funding was received for this research.
Data Availability Statement
CCDC 2290391 contains the supplementary crystallographic data for this paper. The data can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/structures (accessed on 4 October 2023). Cartesian coordinates for the DFT-calculated structure of 1 can be found in the Supplementary Materials.
Acknowledgments
We would like to thank Christian W. Lehmann and Christophe Farès for providing access to the X-ray diffraction facility and the NMR facility, respectively, at the Max-Planck-Institut für Kohlenforschung. Heike Schucht and Dirk Kampen are gratefully acknowledged for technical assistance with the X-ray intensity data collection and for performing the ESI-MS analysis, respectively.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- IUPAC. Compendium of Chemical Terminology, 2nd ed.; The “Gold Book”. Compiled by A. D. McNaught and A. Wilkinson; Blackwell Scientific Publications: Oxford, UK, 1997. [Google Scholar] [CrossRef]
- Schmidt, A.H.; Aimène, A.; Schneider, M. Eine neue Klasse von Stickstoff-Betainen der Quadratsäure. Synthesis 1984, 1984, 436–439. [Google Scholar] [CrossRef]
- Schmidt, A.H.; Aimène, A. Cyclobutendione mit Triorganyl-phosphonio-Substituenten: Neue Quadratsäureabkömmlinge sowie Vertreter “push-pull” substitutierter Pseudooxokohlenstoffe. Chem. Ztg. 1983, 107, 299–304. [Google Scholar]
- Schmidt, A.H.; Botzet, D.; Straus, M. Oxokohlenstoffe und verwandte Verbindungen, XI. Eine Variante der Dreikomponenten-Reaktion zur Darstellung von Betainen der Quadratsäure. Chem. Ztg. 1986, 110, 273–275. [Google Scholar]
- Kolev, T.M.; Yancheva, D.Y.; Stoyanov, S.I. Synthesis and Spectral and Structural Elucidation of Some Pyridinium Betaines of Squaric Acid: Potential Materials for Nonlinear Optical Applications. Adv. Funct. Mater. 2004, 14, 799–805. [Google Scholar] [CrossRef]
- Kolev, T.; Stamboliyska, B.; Yancheva, D. Spectral and structural study of two acceptor-substituted pyridinium-betaines of squaric acid: Promising chromophores for nonlinear optical applications. Chem. Phys. 2006, 324, 489–496. [Google Scholar] [CrossRef]
- Kolev, T.M.; Yancheva, D.Y.; Stamboliyska, B.A.; Dimitrov, M.D.; Wortmann, R. Nonlinear optical properties of pyridinium-betaines of squaric acid: Experimental and theoretical study. Chem. Phys. 2008, 348, 45–52. [Google Scholar] [CrossRef]
- Courbon, G.M.; Palme, P.R.; Mann, L.; Richter, A.; Imming, P.; Rubinstein, J.L. Mechanism of mycobacterial ATP synthase inhibition by squaramides and second generation diarylquinolines. EMBO J. 2023, 42, e113687. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Ranganathan, A.; Kulkarni, G.U. An Experimental Electron Density Investigation of Squarate and Croconate Dianions. J. Phys. Chem. A 2002, 106, 7813–7819. [Google Scholar] [CrossRef]
- Kolev, T.; Yancheva, D.; Schürmann, M.; Kleb, D.-C.; Preut, H.; Spiteller, M. 4-Dimethylaminopyridinium-1-squarate. Acta Crystallogr. E 2002, 58, o1267–o1268. [Google Scholar] [CrossRef]
- Kolev, T.; Yancheva, D.; Shivachev, B.; Petrova, R.; Spiteller, M. 2-(3-Benzoyl-1-pyridinio)-3,4-dioxocyclobutenolate. Acta Crystallogr. C 2005, 61, o213–o215. [Google Scholar] [CrossRef] [PubMed]
- Kolev, T.; Wortmann, R.; Spiteller, M.; Sheldrick, W.S.; Mayer-Figge, H. 4-Methoxypyridinium betaine of squaric acid. Acta Crystallogr. E 2004, 60, o1449–o1450. [Google Scholar] [CrossRef]
- Grünefeld, J.; Kunick, C.; Jones, P.G. 1-(Imidazo[1,2-a]pyridin-1-ium-1-yl)-2,3,4-trioxocyclobutan-1-ide. Molbank 2019, 2019, M1072. [Google Scholar] [CrossRef]
- Kolev, T.; Yancheva, D.; Kleb, D.C.; Preut, H.; Bleckmann, P. Crystal structure of 4-benzoylpyridinium-1-squarate, C16H9NO4. Z. Kristallogr. NCS 2001, 216, 65–66. [Google Scholar] [CrossRef]
- Kolev, T.; Yancheva, D.; Shivachev, B.; Petrova, R. The pyridinium-betaine of squaric acid. Acta Crystallogr. E 2007, 63, o3259. [Google Scholar] [CrossRef]
- Kolev, T.; Wortmann, R.; Spiteller, M.; Sheldrick, W.S.; Mayer-Figge, H. 4-Phenylpyridinium betaine of squaric acid. Acta Crystallogr. E 2005, 61, o1090–o1092. [Google Scholar] [CrossRef]
- Bestmann, H.J.; Fürst, T.G.; Schier, A. Structures and Reactions of the Oxidation Products of Dimeric Ketenylidene(triphenyl)phosphorane. Angew. Chem. Int. Ed. 1993, 32, 1746–1747. [Google Scholar] [CrossRef]
- Ucar, I.; Bulut, A.; Yesilel, O.Z.; Odabasoglu, M.; Buyukgungor, O. 3-Acetoxy-2-(acetylamino)pyridinium-1-squarate. Acta Crystallogr. C 2005, 61, o148–o150. [Google Scholar] [CrossRef]
- Sanna, E.; Martínez, L.; Rotger, C.; Blasco, S.; González, J.; García-España, E.; Costa, A. Squaramide-Based Reagent for Selective Chromogenic Sensing of Cu(II) through a Zwitterion Radical. Org. Lett. 2010, 12, 3840–3843. [Google Scholar] [CrossRef]
- Portell, A.; Font-Bardia, M.; Prohens, R. Self-Assembling of Zwitterionic Squaramides through Electrostatically Compressed Face-to-Face π-Stacking: A New Supramolecular Synthon. Cryst. Growth Des. 2013, 13, 4200–4203. [Google Scholar] [CrossRef]
- Reis, F.D.D.; Gatti, I.C.; Garcia, H.C.; de Oliveira, V.E.; de Oliveira, L.F.C. Squaraines: Crystal Structures and Spectroscopic Analysis of Hydrated and Anhydrous Forms of Squaric Acid-Isoniazid Species. J. Phys. Chem. A 2014, 118, 11521–11528. [Google Scholar] [CrossRef]
- Prohens, R.; Portell, A.; Font-Bardia, M.; Bauzá, A.; Frontera, A. A combined crystallographic and theoretical study of weak intermolecular interactions in crystalline squaric acid esters and amides. CrystEngComm 2017, 19, 3071–3077. [Google Scholar] [CrossRef]
- Kitajgorodskij, A.I. Molecular Crystals and Molecules; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Thakuria, R.; Sarma, B.; Nangia, A. 7.03—Hydrogen Bonding in Molecular Crystals. In Comprehensive Supramolecular Chemistry II; Atwood, J.L., Ed.; Elsevier: Oxford, UK, 2017; pp. 25–48. [Google Scholar]
- Kolev, T.M.; Stamboliyska, B.A.; Yancheva, D.Y.; Enchev, V. Experimental and computational studies of the structure and vibrational spectra of 4-dimethylamino pyridinium-betaine of squaric acid. J. Mol. Struct. 2004, 691, 241–248. [Google Scholar] [CrossRef]
- Kolev, T.M.; Yancheva, D.Y.; Stamboliyska, B.A. Experimental and computational studies of the structure and vibrational spectra of pyridinium-betaine of squaric acid. Spectrochim. Acta A 2003, 59, 1805–1813. [Google Scholar] [CrossRef] [PubMed]
- Scott, A.P.; Radom, L. Harmonic Vibrational Frequencies: An Evaluation of Hartree−Fock, Møller−Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. J. Phys. Chem. 1996, 100, 16502–16513. [Google Scholar] [CrossRef]
- Gurst, J.E.; Schubert, E.M.; Boiadjiev, S.E.; Lightner, D.A. Transannular Orbital Interaction in Diketones Detected by C-13 NMR Spectroscopy. Tetrahedron 1993, 49, 9191–9196. [Google Scholar] [CrossRef]
- APEX, 4.1.0; Bruker AXS Inc.: Madison, WI, USA, 2017.
- SAINT, V8.40B; Bruker AXS Inc.: Madison, WI, USA, 2019.
- SADABS, 2016/2; Bruker AXS Inc.: Madison, WI, USA, 2012.
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Kleemiss, F.; Dolomanov, O.V.; Bodensteiner, M.; Peyerimhoff, N.; Midgley, L.; Bourhis, L.J.; Genoni, A.; Malaspina, L.A.; Jayatilaka, D.; Spencer, J.L.; et al. Accurate crystal structures and chemical properties from NoSpherA2. Chem. Sci. 2021, 12, 1675–1692. [Google Scholar] [CrossRef]
- Midgley, L.; Bourhis, L.J.; Dolomanov, O.V.; Grabowsky, S.; Kleemiss, F.; Puschmann, H.; Peyerimhoff, N. Vanishing of the atomic form factor derivatives in non-spherical structural refinement—A key approximation scrutinized in the case of Hirshfeld atom refinement. Acta Crystallogr. A 2021, 77, 519–533. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Bourhis, L.J.; Dolomanov, O.V.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. The anatomy of a comprehensive constrained, restrained refinement program for the modern computing environment—Olex2 dissected. Acta Crystallogr. A 2015, 71, 59–75. [Google Scholar] [CrossRef]
- Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Jayatilaka, D.; Grimwood, D.J. Tonto: A Fortran Based Object-Oriented System for Quantum Chemistry and Crystallography. In Lecture Notes in Computer Science, Computational Science—ICCS 2003; Sloot, P.M.A., Abramson, D., Bogdanov, A.V., Gorbachev, Y.E., Dongarra, J.J., Zomaya, A.Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 142–151. [Google Scholar]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. D 2009, 65, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Hertwig, R.H.; Koch, W. On the parameterization of the local correlation functional. What is Becke-3-LYP? Chem. Phys. Lett. 1997, 268, 345–351. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley & Sons: Chichester, UK, 1987. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).