Abstract
Protein-protein interactions are important for biochemical processes in biological systems. The 3D structure of the macromolecular complex resulting from the protein-protein association is a very useful source to understand its specific functions. This work focuses on computational study for protein-protein docking, where the individually crystallized structures of interacting proteins are treated as rigid, and the conformational space generated by the two interacting proteins is explored extensively. The energy function consists of intermolecular electrostatic potential, desolvation free energy represented by empirical contact potential, and simple repulsive energy terms. The conformational space is six dimensional, represented by translational vectors and rotational angles formed between two interacting proteins. The conformational sampling is carried out by the search algorithms such as simulated annealing (SA), conformational space annealing (CSA), and CSA combined with SA simulations (combined CSA/SA). Benchmark tests are performed on a set of 18 protein-protein complexes selected from various protein families to examine feasibility of these search methods coupled with the energy function above for protein docking study.
1. Introduction
Most biological processes are known to take place through protein-protein interactions. The three-dimensional structure of a protein-protein complex could be a crucial clue to understand the way proteins interact with each other and their functions. Therefore, knowing the detailed structure of protein-protein complexes at the atomic level has been very important issues in biological sciences. Experimental determination of three-dimensional structure of the complexes is not an easy task. In the protein data bank [1], where experimentally determined 3D structures of proteins are stored, most of the protein structures are a singe protein chain and only a small fraction (about 10 %) of the structures correspond to protein-protein complexes. The goal of protein-protein docking is to determine the molecular structure of the protein-protein complex formed by interaction of two or more proteins without the need for experimental measurement. It is important to develop reliable protein-protein docking methods which can predict the structures of complexes with reasonable accuracies from given unbound structures of protein components. Various methods have been developed for the protein-protein docking studies over the years and many review articles are available in the literature [2–9].
Protein-protein docking can be divided into rigid and flexible dockings. In the rigid docking, interacting proteins are treated as rigid bodies without any conformational changes as they interact with each other, while, in the flexible docking, the conformational flexibility of the protein molecules upon protein association is taken into account. Total conformational space in the rigid docking is represented by six variables, consisting of relative translational vectors (x,y,z) and rotational angles (φθψ) of the protein components. On the other hand, for the flexible docking, torsional angle changes of each protein are added to the conformational space. However, the docking procedure that fully considers the conformational flexibilities of the proteins is computationally prohibiting, since the enormous number of degrees of freedom should be included. Therefore, a complete procedure [3] for protein-protein docking study usually follows two separate steps where the rigid docking is first performed, and then the flexible docking is carried out for the refinement of protein-protein complex structure obtained from the previous rigid docking step.
Two key elements are generally required for carrying out a protein-protein docking; an efficient conformational search algorithm and an accurate free energy function. The free energy function should be reasonably accurate so that it can discriminate the native-like association of two component molecules from a variety of non-native associations. The search algorithm should explore the huge conformational space extensively, so that it can find conformations with free energy values close to the global minimum. There is always some inaccuracy in a free energy function, and in order to take this into account, the search algorithm usually generates multiple low-energy conformations in the final stage of a docking procedure, instead of producing the one conformation with the lowest energy. Several structures are then selected from the final conformations based on an appropriate scoring function, and proposed as candidates for the native-like structures for the complex.
Many docking programs [10–13] employ the fast Fourier transformation (FFT) algorithm [14] to carry out the global search by extensively exploring the entire search space. FFT generates too many structures that are often difficult to manage, so a top fraction of energy-ranked structures are selected to be considered as prediction candidates. However, since the conformational diversity among the structures is not guaranteed, it is possible for all the selected structures to be distant from the native one when the free energy function is inaccurate. Therefore, it is meaningful to devise a search algorithm having an ability of achieving both diversity and efficacy in a conformational search. One of the most well-known search algorithms is “Simulated Annealing (SA)” [15,16]. The major advantage of SA is its ability to avoid becoming trapped at local minima. The SA algorithm employs a stochastic move which is accepted or rejected based on an acceptance probability. SA has been applied to various combinatorial problems and many other global optimization problems [17–19]. However, since this method generates only one conformation at a time, the conformational diversity cannot be directly implemented. Another powerful search algorithm is “Conformational Space Annealing (CSA)” [20]. The CSA is based on the genetic algorithms (GA). The major advantage of the CSA is that it can generate diverse low-energy solutions. The CSA method has been applied to small-molecule docking [21] and protein-protein docking [22] for the CAPRI experiment [23], showing a promising potential of the CSA algorithm for the docking study. A new search method is introduced in this work, named “CSA combined with SA (combined CSA/SA)”. The combined CSA/SA adapts the genetic operations of CSA for a global search and the stochastic search of SA for a local search to maximize the effectiveness of conformational search. The combined CSA/SA carries out a rigorous conformational search by taking an advantage of the CSA and the SA methods.
The free energy function used in this work consists of electrostatic, desolvation and repulsive energy terms. The electrostatic energy corresponds to the standard Coulombic electrostatic potential and the desolvation energy features the desolvation free energy of proteins calculated by an empirical atomic contact potential. These two energy terms have been practically used in the FastContact server [24,25] which provides a fast computational estimate of the binding free energy of proteins. The third term is a simple repulsive term, similar to the steric energy used in the SCWRL side-chain prediction program [26].
In this work, three conformational search algorithms, CSA, SA, and combined CSA/SA, are incorporated with the energy function consisting of the three energy terms to carry out rigid protein-protein docking. Instead of explicitly taking into account the flexibility of the interacting protein molecules, they are treated as a rigid object allowing small clashes. In order to investigate the feasibility of three docking methods, benchmark tests are performed for a set consisting of 18 unbound protein-protein pairs selected from the benchmark2.0 developed by Mintseris et al [27]. The rest of this article contains details on computational methods including algorithms and implementations followed by results. Analysis and discussions are provided at the end by highlighting key findings and suggestions for further improvements.
2. Computational Method
2.1. Conformational Searches
Three types of conformational search algorithms are used in this work. They are CSA, SA and combined CSA/SA. Details of each method are explained below.
2.1.1 Conformational space annealing (CSA)
The CSA unifies the essential ingredients of two optimization methods, GA [28] and Monte Carlo with minimization (MCM) [29]. First, as in MCM, the CSA consider only the phase space of local minima; that is, all conformations are energy-minimized by a local minimizer. Second, as in GA, it deals with a population of conformations, called a bank. The initial bank is constructed by randomly generating a given number (500 in this work) of conformations. This initial bank is copied as the first bank, which is kept unchanged throughout the procedure. The number of conformations in the bank is also kept constants, but the bank conformations are updated by using new trial conformations obtained by procedures similar to genetic operations in GA. Seeds are randomly selected from the bank conformations, which are perturbed by replacing its small portion with the corresponding parts of a conformation randomly selected from the bank or the first bank. The perturbed conformation is then subsequently energy-minimized to generate a new trial conformation. Uniquely in CSA, an annealing parameter Dcut is introduced as a cutoff distance reflecting the structural difference between the conformations in the phase space of local minima. The major advantage of CSA is that it can maintain the structural diversity of conformations generated during the docking procedure for a given energy function. The sampling diversity is directly controlled by measuring a distance judging the structural difference between two conformations and comparing it with Dcut. To elaborate, a trial conformation a is compared with the bank conformations, and the conformation A is selected from the bank, which is the closest to the conformation a with respect to a suitable distance measure D(a,A) which can be calculated using eq (2). If D(a,A) < Dcut, the conformation a is considered as being more or less similar to the conformation A. The conformation with the lower energy between a and A is kept in the bank, and the other one is discarded. However, if D(a,A) > Dcut, the conformation a is regarded as being distinct from any other conformation in the bank. Therefore, a is compared with the bank conformation with the highest energy, and again, the conformation with the lower energy is kept in the bank, and the other one is discarded. The diversity of the bank is maintained for a large value of Dcut, and the low-energy properties of the conformations are emphasized for a small value of Dcut. Dcut is gradually decreased as the algorithm proceeds. Through this annealing procedure, the CSA narrows down the search space to a smaller region with low energy values. This implies that there is high probability of having a native-like structure in the set of conformations found by the CSA operations.
The random conformations are generated by assigning random translational vectors (x,y,z) and rotational Euler angles (φ,θ,ψ) between two interacting proteins. The initial value of Dcut is set as Dave/2, where Dave is the average pairwise distance between the conformations in the first bank and defined as follows:
where D(i,j) is the distance between the conformations i and j, N is the number of the conformations in the bank, ΔTij(x,y,z) is the translation vector from i to j, and Θij(φ,θ,ψ) is the angle between two Euler vectors of i and j. The weight factor ωΘ is determined following the reference [21]. The value of Dcut, which is initially set to Dave/2, is gradually reduced to a smaller value each iteration until its final value reaches Dave/5 through 200,000 steps according to the annealing scheme.
When all conformations in the bank are used as seeds, one round of iterations is completed. Another round of iterations then is initiated by deleting the information regarding to the usage of seeds. The CSA run is arbitrarily terminated after three rounds because the value of the global minimum energy is not known. Finally, 500 low-energy and diverse conformations survive in the bank.
In this work, the number of bank conformations is 500 and 100 bank conformations among 500 are selected as seeds. Each seed conformation produces 5 conformations by replacing a part of the seed variables with the corresponding ones of a randomly selected bank conformation. Total 500 perturbed conformations are generated from 100 seed conformations and energy-minimized to become trial conformations, which are used to update the bank.
As already mentioned, all conformers generated during the CSA search are energy-minimized by a quench method. In this minimization process, the energy is quenched by small random-moves combined of translation (up to ±2 Å) and rotation (up to ±5°). The moves that lower the energy are only accepted and the others are rejected. The quench-minimization process stops either when 100 unsuccessful trials occur in a row or when the total number of trials becomes 500. Details of the CSA algorithm and its successful applications can be found in the references [21,22,30,31].
2.1.2 Simulated Annealing (SA)
SA is a stochastic global optimization method which is able to avoid being trapped in local minima. The SA search is carried out by random moves that can cause the increase or the decrease of an objective function, an energy function in this work. A random move that decreases the energy is always accepted, and the one that increase it is accepted with a finite probability [16]. The acceptance probability is defined as
where ΔE is the change in the energy function, Enew – Eold, T is an absolute temperature, and k is the Boltzmann constant. In practice, when ΔE ≥ 0, a random number R between 0 and 1 is generated and the move is accepted only if p ≤ R(0,1)
Each of 500 parallel runs using SA begins at 300 K and with a randomly generated conformation for a protein-protein complex. Total 80,000 moves for each are attempted with up to ±3 Å for translation and ±8° for rotation. The temperature decreases by 10 % upon acceptance and increases by 3 % upon rejection. The possible lowest temperature is set to be 1.0 K. In the final stage, 500 conformations are collected from all SA runs.
2.1.3 Combined CSA/SA
The combined CSA/SA is based on the CSA and the SA algorithms. Instead of performing local minimization of conformations by the quench method, the SA technique is used in a local minimization to enforce more effective conformational search. Since SA accepts some moves that increase the energy function, in contrast to the quench method that accepts only the moves that decrease the energy function, small local energy barriers can be overcome.
The parameters used for CSA and SA are the same as those described in the sub-sections 2.1.1 and 2.1.2, respectively.
2.2. Energy Function
The energy function consists of three terms; electrostatic potentials, desolvation contact energy and repulsive energy.
The first two terms are based on the binding free potentials from the FastContact server [24,25] and defined as
where qi and qj is atomic charge of atoms i and j taken from CHARMM19 [32]; ε(r) (=4r) is the distance-dependent dielectric constant; rij is the distance between atoms i and j; eij is the atomic contact potential (ACP), which is determined empirically, between atoms i and j. g(rij) is 0 for atoms that are more than 7 Å apart and 1 if less than 5 Å apart. It is a smoothly linear function varying between these two limits. The last term represents the simple repulsive interaction between atoms of two interacting proteins defined as
where Dijvdw is the sum of the hard-sphere radii for atoms i and j. The values for the hard-radii are van der Waals parameters taken from CHARMM19.
The FastContact server provides a service that estimates the binding free energy between two proteins by calculating the intermolecular electrostatic potential and the desolvation free energy represented by empirical contact potential. In addition, it supplies the residue contact free energies of interacting proteins. Determination of ACP was done using 18 atomic types from statistical analysis of diverse set of 90 protein structures by converting frequencies of structural factors into atom-atom contacts. The ACP is similar to Miyazawa-Jernigan residue contact potential [33,34], but is more specific since it is an atom-based contact potential. This server has been successfully tested and validated for scoring refined complex structures and blind sets of docking protein decoys. The repulsive energy has been modified from the simple steric energy used in the SCWRL program [26]. Since the flexibility of proteins is not explicitly taken into account, some softness is added to the atomic hard-sphere so that only the interaction between two atoms being within 80 % of the sum of their hard-sphere radii is considered repulsive. This term is especially needed since the repulsive energy such as that used in the van der Waals interaction is too strict to allow a small clash between two atoms. The resulting energy function seems reasonable to describe the protein-protein interaction, and it is implemented to this docking study.
2.3. Benchmark Test Set
The protein test set contains total 18 protein-protein complexes which are of 100~400 residues in chain-length selected from the benchmark2.0 developed by Mintseris et al [27].
3. Results and Discussion
Three optimization methods (SA, CSA and combined CSA/SA) are incorporated into protein-protein docking. The results obtained from these methods are compared in terms of the effectiveness of conformational search and the ability of finding the native-like conformations among the final set of 500 conformations. Furthermore, the feasibility of the energy function is validated for scoring the protein-protein interaction. The docking results are summarized in Table 1.

Table 1.
Performance of the protein-protein dockings using SA, CSA and combined CSA/SA.
The aim of the rigid-body docking is to produce many conformations of a protein-protein complex, among which at least one native-like conformation is expected to be found. The evaluation [35] for prediction can be made using the RMSD (root-mean-square deviation). The RMSD is defined as the RMSD of Cα atoms at the interface calculated after the receptor part of the predicted structure is superimposed using Cα atoms on the receptor part of the bound experimental structure. The interface is defined as any residue in one component having at least one atom within 10 Å of an atom in the other component in the native structure of the bound complex. According to the evaluation criteria [35], a predicted model is considered being acceptable if the RMSD ≤ 4.0 Å. The prediction accuracy is considered high if the RMSD ≤ 0.1 Å and medium if 1.0 Å < the RMSD ≤ 2.0 Å. The RMSD is calculated for 500 conformations in the final set for each of 18 complexes. The acceptable native-like conformations are found for the 6 complexes (1ACB, 1CGI, 1CSE, 1TGS, 1UDI and 2TEC) when the SA method is used. They are found for the 7 complexes (1ACB, 1CGI, 1CHO, 1CSE, 1MEL, 1PPE and 2TEC) and for the 9 complexes (1A0O, 1ACB, 1CGI, 1CHO, 1CSE, 1PPE, 1UDI, 2TEC and 4HTC), when the CSA and the combined CSA/SA methods are used, respectively. The result shows that the combined CSA/SA demonstrates the ability of finding the most acceptable structures. The acceptable native-like structures of 1ACB, 1CGI, 1CSE and 2TEC are found using all three methods. However, none of these three methods can find the acceptable ones for the 7 complexes (1AVZ, 1BRC, 1BRS, 1STF, 1TAB, 2KAI and 2PTC). This failure can be explained by the following possible reasons. One reason is that conformational changes of side-chains and/or backbone occur upon binding. This docking study is basically carried out based on the rigid-body docking so it is hard to reproduce a native-binding mode involving noticeable conformational changes, although small softness effect is added to the energy function. To observe the overall conformation changes of the complexes upon binding, the RMSD values between the bound and the unbound structures of each protein component were calculated over the side-chains at the binding interface after the Cα atoms at the interfaces of the two structures were superimposed. The sum of the RMSD values of the interface side-chains of receptor and ligand proteins for each complex are varied from 0.7 to 3.5 Å. The smallest summed RMSD, 0.7 Å, corresponds to the complex 2TEC for which all three algorithms found the acceptable native-like conformations. The largest RMSD, 3.5 Å, is observed for 2KAI whose native-like conformation was not found using three search methods. The calculated RMSD values are 3.2, 2.9, 2.9, 1.6, 1.2, 3.5 and 2.2 Å for seven complexes (1AVZ, 1BRC, 1BRS, 1STF, 1TAB, 2KAI and 2PTC), for which a native-like conformation was not found, and only two complexes out of seven give the RMSD less than 2.0 Å. The RMSD values for eleven complexes having a least one native-like structure using three methods are also varied from 0.7 to 3.2 Å, and five among them show the RMSD less than 2.0 Å. The RMSD comparison between the bound and the unbound structures of component molecules shows that there is higher probability of finding a native-like structure by conformational searches for complexes showing smaller RMSD between the bound and the unbound states, i.e. smaller conformational changes upon binding. Another possible, yet critical, reason is originated from incomplete PDB structures. Some protein structures, for example, 1TGS, have missing atoms and/or residues, which produces a sequence discrepancy between bound and unbound protein components.
This hampers an accurate calculation of the binding free energy. Other reason might be that the energy function used in this study is not accurate enough. The performance of the energy function can be evaluated by observing the relation of the RMSD and the energy values. The binding free energy landscape in protein-protein interaction is known to have a quite rugged and funnel-like shape [36, 37]. If the energy function is reasonably correct, the energy values are supposed to increase with the RMSD values, which would results in a positive correlation. The native structure should correspond to the global minimum in the energy landscape and the energies of native-like conformations should be relatively low since the landscape looks funnel-like. The figure 1 shows the scatter plot of the RMSD versus the energy values for the complex, 1ACB, one of the targets in which all three methods are able to find the native-like conformations. The conformations having unrealistic interactions including no residue-residue contacts and too much penetration are excluded from the plot. In fact, a good correlation is not observed in all three cases (SA, CSA and combined CSA/SA) in Figure 1. Three plots show a similar phenomenon that the conformations seem to be largely grouped into two clusters. This figure also shows that the methods adapting the CSA algorithm, CSA and combined CSA/SA, search the conformational space more broadly than that using SA. This validates that CSA rigorously explores the search space by maintaining the conformational diversity in the final set. This diversity allows the CSA search to have more possibility of keeping a native-like conformation. The results also demonstrate that the combined CSA/SA method enforces the local search by utilizing the SA algorithm. It is promising that the combined CSA/SA method shows the best performance of docking even though the energy function is not too good.
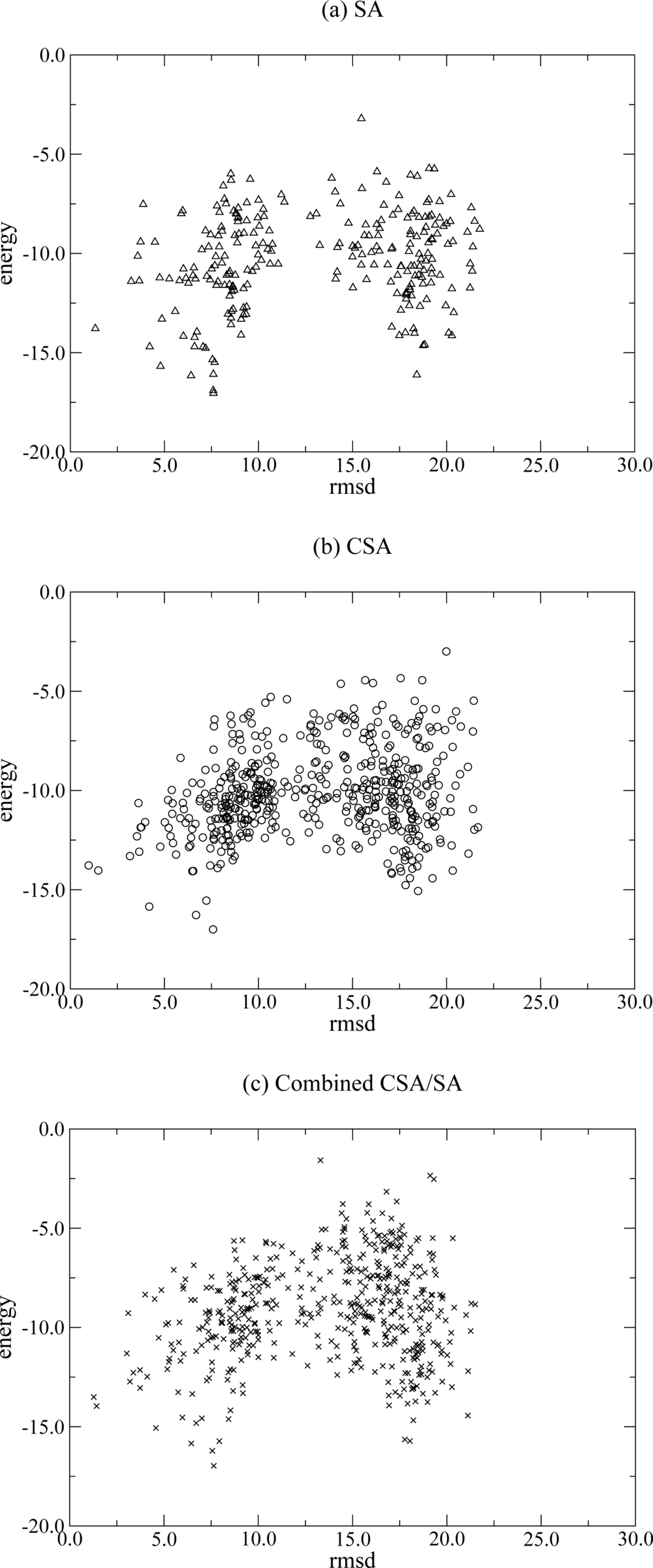
Figure 1.
Scatter plots of RMSD (Å) versus energy for the complex, 1ACB, for (a) SA, (b) CSA, and (c) combined CSA/SA.
The limitation of this study is in the absence of explicit treatment of protein flexibility although softness effect is added to the energy function. Since it is computationally too expensive to conduct a rigorous conformational search while fully allowing the conformational changes, the generally accepted procedure in docking involves rigid docking followed by the refinement for flexibility. The rigid-body docking should be performed with a reasonable and efficient global search algorithm, so that it is highly likely that at least one native-like conformation is included in the set of conformations, which will be the initial set for the next refinement. The flexibility will be considered in the next work for more complete docking study. An additional work will be left to develop the energy function for better native-recognition. Use of the biological information of interest will be also included in the future work since the biological information plays an important role in greatly reducing the search space. This will make the conformational search more efficient.
Acknowledgements
This work was supported by Brain Korea 21 BT-IT Integrationist Program, Dept. of Bioinformatics and Life Science, Soongsil University.
References and Notes
- Berman, HM; Westbrook, J; Feng, Z; Gilliland, G; Bhat, TN; Weissig, H; Shindyalov, IN; Bourne, PE. The Protein Data Bank. Nucleic Acids Research 2000, 28, 235–242, DOI 10.1093/nar/28.1.235; PubMed 10592235. [Google Scholar]
- Jones, S; Thornton, JM. Principles of protein-protein interactions. Proc Natl Acad Sci USA 1996, 93, 13–20, DOI 10.1073/pnas.93.1.13. [Google Scholar]
- Smith, GR; Sternberg, MJE. Prediction of protein-protein interactions by docking methods. Curr Opin Struct Biol 2002, 12, 28–35, DOI 10.1016/S0959-440X(02)00285-3; PubMed 11839486. [Google Scholar]
- Elcock, AH; Sept, D; McCammon, JA. Computer simulation of protein–protein interactions. J Phys Chem B 2001, 105, 1504–1518, DOI 10.1021/jp003602d. [Google Scholar]
- Bonvin, AM. Flexible protein-protein docking. Curr Opin Struct Biol 2006, 16, 194–200, DOI 10.1016/j.sbi.2006.02.002; PubMed 16488145. [Google Scholar]
- Gary, JJ. High-resolution protein-protein docking. Curr Opin Struct Biol 2006, 16, 183–193, DOI 10.1016/j.sbi.2006.03.003; PubMed 16546374. [Google Scholar]
- Sternberg, MJE; Gabb, HA; Jackson, RM. Predictive docking of protein-protein and protein-DNA complexes. Curr Opin Struct Biol 1998, 8, 250–256, DOI 10.1016/S0959-440X(98)80047-X; PubMed 9631301. [Google Scholar]
- Halperin, I; Ma, B; Wolfson, H; Nussinov, R. Principles of docking: an overview of search algorithms and a guide to scoring functions. Proteins 2002, 47, 409–443, DOI 10.1002/prot.10115; PubMed 12001221. [Google Scholar]
- Russell, RB; Alber, F; Aloyl, P; Davis, FP; Korkin, D; Pichaud, M; Topf, M; Sali, A. A structural perspective on protein–protein interactions. Curr Opin Struct Biol 2004, 14, 313–324, DOI 10.1016/j.sbi.2004.04.006; PubMed 15193311. [Google Scholar]
- Vakser, IA. Protein docking for low-resolution structures. Protein Eng 1995, 8, 371–377, DOI 10.1093/protein/8.4.371; PubMed 7567922. [Google Scholar]
- Gabb, HA; Jackson, RM; Sternberg, MJE. Modeling protein docking using shape complementarity, electrostatics and biochemical information. J Mol Biol 1997, 272, 106–120, DOI 10.1006/jmbi.1997.1203; PubMed 9299341. [Google Scholar]
- Chen, R; Weng, Z. Docking unbound proteins using shape complementarity desolvation, and electrostatics. Proteins 2002, 47, 281–294, DOI 10.1002/prot.10092; PubMed 11948782. [Google Scholar]
- Mandell, JG; Roberts, VA; Pique, ME; Kotlovyi, V; Mitchell, JC; Nelson, E; Tsigelny, I; Eyck, TLF. Protein docking using continuum electrostatics and geometric fit. Protein Eng 2001, 14, 105–113, DOI 10.1093/protein/14.2.105; PubMed 11297668. [Google Scholar]
- Harrison, RW; Kourinov, IV; Andrews, LC. The Fourier-Greens function and the rapid evaluation of molecular potentials. Protein Eng 1994, 7, 359–369, DOI 10.1093/protein/7.3.359; PubMed 8177885. [Google Scholar]
- Metropolis, N; Rosenbluth, AW; Rosenbluth, MN; Teller, AH; Teller, E. Equation of state calculations by fast computing machines. J Chem Phys 1953, 21, 1087–1092, DOI 10.1063/1.1699114. [Google Scholar]
- Kirkpatrick, S; Gelatt, CD; Vecchi, MP. Optimization by simulated annealing. Science 1983, 220, 671–680, PubMed 17813860. [Google Scholar]
- Hwang, J; Liao, W. Side-chain prediction by neural networks and simulated annealing optimization. Protein Eng 1995, 8, 363–370, DOI 10.1093/protein/8.4.363; PubMed 7567921. [Google Scholar]
- Cerny, V. Thermodynamical approach to the traveling salesman problem: an efficient simulation algorithm. J Optim Theory Appl 1985, 45, 41–51, DOI 10.1007/BF00940812. [Google Scholar]
- de Vicente, J; Lanchares, J; Hermida, R. Placement by thermodynamic simulated annealing. Phys Lett A 2003, 317, 415–423, DOI 10.1016/j.physleta.2003.08.070. [Google Scholar]
- Lee, J; Scheraga, HA; Rackovsky, S. New optimization method for conformational energy calculations on polypeptide: conformational space annealing. J Comput Chem 1997, 18, 1222–1232, DOI 10.1002/(SICI)1096-987X(19970715)18:9<1222::AID-JCC10>3.0.CO;2–7. [Google Scholar]
- Lee, K; Czaplewski, C; Kim, S-Y; Lee, J. An efficient molecular docking using conformational space annealing. J Comput Chem 2005, 26, 78–87, PubMed 15538770. [Google Scholar]
- Lee, K; Sim, J; Lee, J. Study of protein-protein interaction using conformational space annealing. Proteins 2005, 60, 257–262, DOI 10.1002/prot.20567; PubMed 15981254. [Google Scholar]
- Janin, J; Hendrick, K; Moult, J; Eyck, LT; Sternberg, MJE; Vajda, S; Vakser, IA; Wodak, SJ. CAPRI: A Critical Assessment of PRedicted Interactions. Proteins 2003, 52, 2–9, DOI 10.1002/prot.10381; PubMed 12784359. [Google Scholar]
- Camacho, CJ; Zhang, C. FastContact: rapid estimate of contact and binding free energies. Bioinformatics 2005, 21, 2534–2536, DOI 10.1093/bioinformatics/bti322; PubMed 15713734. [Google Scholar]
- Champ, PC; Camacho, CJ. FastContact: a free energy scoring tool for protein–protein complex structures. Nucleic Acids Research 2007, 35, W556–W560, PubMed 17537824. [Google Scholar]
- Dunbrack, RL; Cohen, FE. Bayesian statistical analysis of protein side-chain rotamer preferences. Protein Sci 1997, 6, 1661–1681, PubMed 9260279. [Google Scholar]
- Mintseris, J; Wiehe, K; Pierce, B; Anderson, R; Chen, R; Janin, J; Weng, Z. Protein-protein docking benchmark 20: an update. Proteins 2005, 60, 214–216. [Google Scholar]
- Goldberg, DE. Genetic Algorithms in Search, Optimization and Machine Learning; Kluwer Academic Publishers: Boston, MA, 1989. [Google Scholar]
- Nayeem, A; Vila, J; Scheraga, HA. A comparative study of the simulated annealing and Monte Carlo-with-minimization approaches to the minimum-energy structures of polypeptides: [met]-enkephalin. J Comput Chem 1991, 12, 594–605, DOI 10.1002/jcc.540120509. [Google Scholar]
- Lee, J; Liwo, A; Ripoll, DR; Pillardy, J; Scheraga, HA. Calculation of protein conformation by global optimization of a potential energy function. Proteins Suppl 1999, 3, 204–208, DOI 10.1002/(SICI)1097-0134(1999)37:3+<204::AID-PROT26>3.0.CO;2-F. [Google Scholar]
- Lee, J; Kim, S-Y; Joo, K; Kim, I; Lee, J. Prediction of protein tertiary structure using profesy, a novel method based on fragment assembly and conformational space annealing. Proteins 2004, 56, 704–714, PubMed 15281124. [Google Scholar]
- Brooks, BR; Bruccoleri, RE; Olafson, BD; States, DJ; Karplus, M. CHARMM: a program for macromolecular energy, minimization, and molecular dynamics calculations. J Comput Chem 1983, 4, 187–217, DOI 10.1002/jcc.540040211. [Google Scholar]
- Miyazawa, S; Jernigan, RL. Estimation of effective interresidue contact energies from protein crystal structures: quasi-chemical approximation. Macromolecules 1985, 18, 534–552, DOI 10.1021/ma00145a039. [Google Scholar]
- Miyazawa, S; Jernigan, RL. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J Mol Biol 1996, 256, 623–644, DOI 10.1006/jmbi.1996.0114; PubMed 8604144. [Google Scholar]
- Mendez, R; Leplae, R; de Maria, L; Wodak, S. Assessment of blind predictions of protein-protein interactions: current status of docking methods. Proteins 2003, 52, 51–67, PubMed 12784368. [Google Scholar]
- Ma, B; Kumar, S; Tsai, CJ; Nussinov, R. Folding funnels and binding mechanisms. Protein Eng 1999, 12, 713–720, PubMed 10506280. [Google Scholar]
- Tovchigrechko, A; Vakser, IA. How common is the funnel-like energy landscape in protein-protein interactions. Protein Science 2001, 10, 1572–1583, PubMed 11468354. [Google Scholar]