Chromatographic Retention Times of Polychlorinated Biphenyls: from Structural Information to Property Characterization
Abstract
:1. Introduction
2. Materials and Methods
2.1 Polychlorinated Biphenyls (PCBs)
2.2 Methodology of using Molecular Descriptors Family in QSPR/QSAR
- (a)
- A minimal fragment is that one containing only the atom i, while a maximal fragment will contain all the atoms connected to i, excluding the atom j.
- (b)
- A Szeged fragment is the set of vertices located closer to i than j (a distance-based criterion), the distance d(i, k) being lesser than d(k, j), and
- (c)
- A Cluj fragment is generated by excluding the path from i to j (except its terminal points) and then applying the above Szeged criterion.
- – Step 1 (implies inheritance and mutation). To the solution domain (2×6×24×6×4×19 MDF members) having the genetic representation with six letters words) are applied the linearization procedure from above, when every descendent is obtained from a parent (inheritance) through a transformation (mutation). Six times more (than parents) descendants are obtained. In this step, the fitness function is defined as “have real and distinct values”. A number of 490030 descendants dye due to mutation on PCB data set (remaining 297938 descendants, having genetic representation with seven letters words now).
- – Step 2 (implies selection). To the solution domain (MDF descendants from Step 1) a bias procedure (selection) is applied. In this step, the fitness function is defined as “have distinct first nine digits of determination coefficient with measured property”. For PCBs data set, only 99806 members pass selection. From this solution domain another selection is made: best descriptor (which correlates the best with measured property (for PCBs result being presented in Eq(1)).
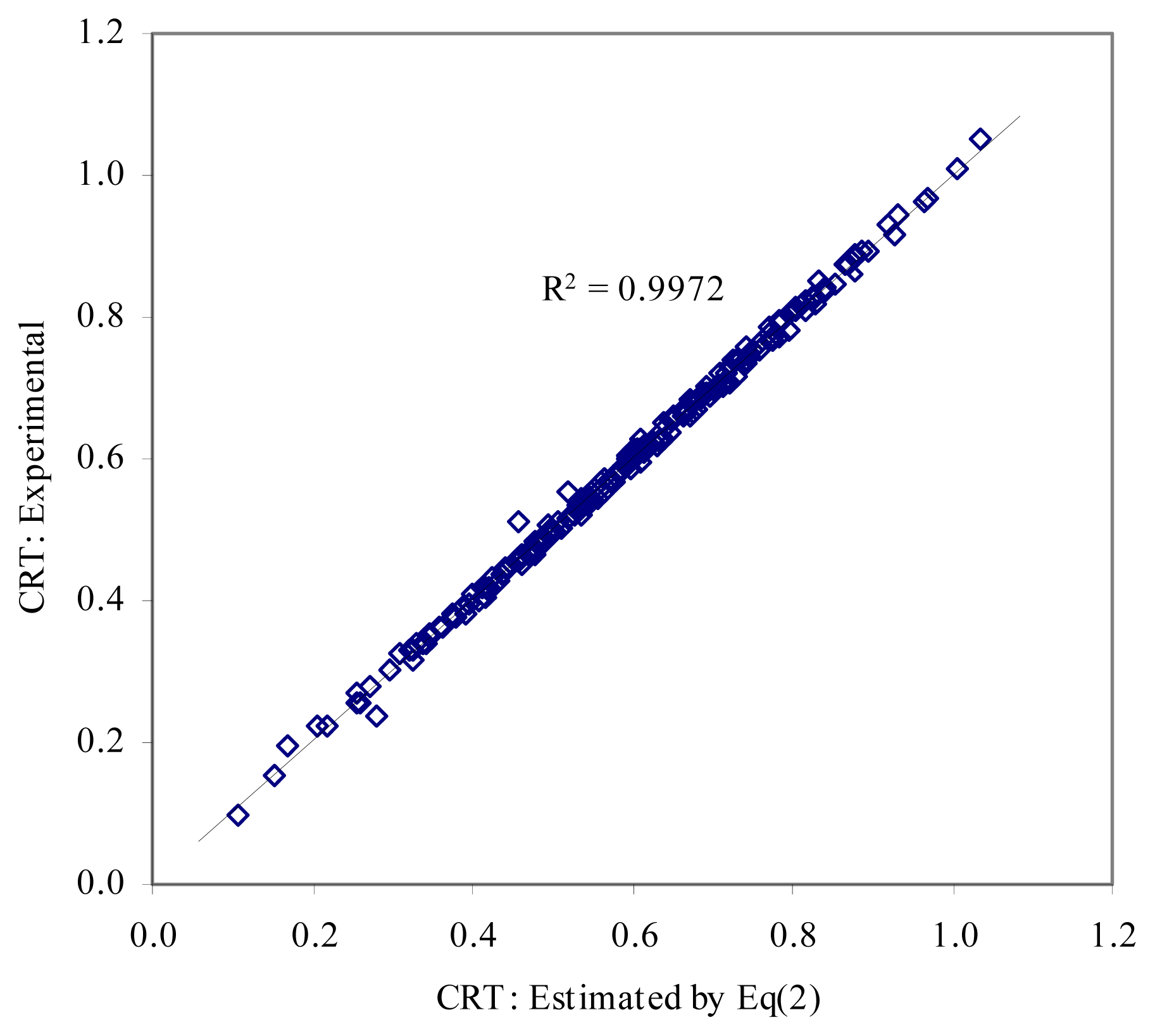
- – Step 3 (implies crossover). Pairs of MDF members are crossover in order to obtain models with two descriptors. Two fitness functions are used here: “have better determination coefficient” and “have better cross-validation leave-one-out score”. The result for PCBs data set is given in Eq(2).
2.3 Computational Details
3. Results and Discussion
- ○ The MDF model obtained by Eq(2) is significantly better models comparing with models reported in [24] and [25] in terms of correlation coefficients. Moreover, it is a better model comparing with model reported in [22] in terms of number of variables used (two descriptors used by the Eq(2), and five descriptors used by the model reported in [22]).
4. Conclusions
- ○ http://l.academicdirect.org/Chemistry/SARs/MDF_SARs/sar/ Training and test analysis:

| Mol | PCB structure | Y | iIDRwHg | Ŷ1d | Y-Ŷ1d | ISDmsHt | lADrtHg | Ŷ2d | Y-Ŷ2d |
|---|---|---|---|---|---|---|---|---|---|
| PCB001 |  | 0.0997 | 10.02 | −0.0122 | −0.5363 | 133.20 | −3.42 | 0.1119 | −0.0122 |
| PCB002 |  | 0.1544 | 10.60 | 0.0041 | 0.1800 | 134.27 | −3.47 | 0.1503 | 0.0041 |
| PCB003 |  | 0.1937 | 9.96 | 0.0376 | 1.6541 | 135.23 | −3.40 | 0.1561 | 0.0376 |
| PCB004 |  | 0.2245 | 10.14 | 0.0054 | 0.2377 | 134.89 | −3.42 | 0.2191 | 0.0054 |
| PCB005 |  | 0.2785 | 9.75 | 0.0251 | 1.1035 | 133.36 | −3.41 | 0.2534 | 0.0251 |
| PCB006 |  | 0.2709 | 10.15 | −0.0193 | −0.8496 | 136.72 | −3.38 | 0.2902 | −0.0193 |
| PCB007 |  | 0.2566 | 10.72 | 0.0028 | 0.1234 | 134.60 | −3.48 | 0.2538 | 0.0028 |
| PCB008 |  | 0.2783 | 10.27 | −0.0048 | −0.2094 | 133.35 | −3.43 | 0.2831 | −0.0048 |
| PCB009 |  | 0.2570 | 11.12 | 0.0348 | 1.5315 | 134.95 | −3.55 | 0.2222 | 0.0348 |
| PCB010 |  | 0.2243 | 11.75 | 0.0333 | 1.4623 | 133.57 | −3.57 | 0.1910 | 0.0333 |
| PCB011 |  | 0.3238 | 11.26 | 0.0168 | 0.7378 | 133.12 | −3.52 | 0.3070 | 0.0168 |
| PCB012 |  | 0.3298 | 11.52 | 0.0442 | 1.9425 | 132.24 | −3.57 | 0.2856 | 0.0442 |
| PCB013 |  | 0.3315 | 11.09 | 0.0065 | 0.2857 | 134.24 | −3.49 | 0.3250 | 0.0065 |
| PCB014 |  | 0.2373 | 10.98 | −0.0393 | −1.7268 | 133.10 | −3.50 | 0.2766 | −0.0393 |
| PCB015 | 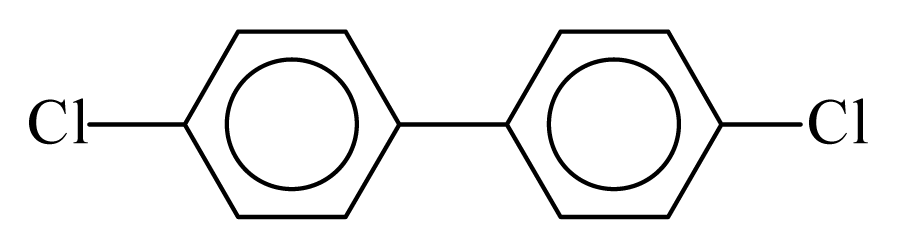 | 0.3387 | 10.98 | 0.0036 | 0.1567 | 131.58 | −3.51 | 0.3351 | 0.0036 |
| PCB016 | 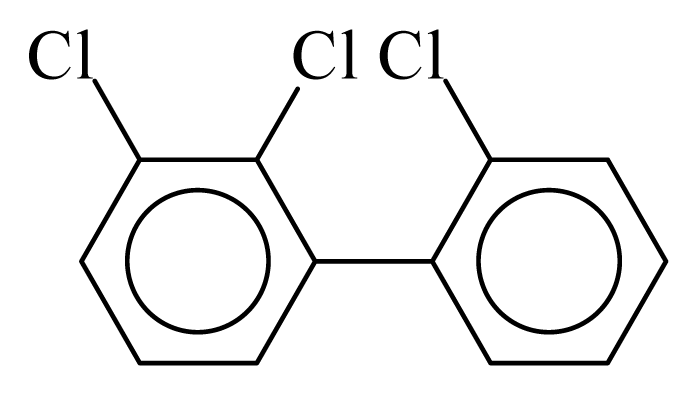 | 0.3625 | 10.45 | 0.0193 | 0.8481 | 132.74 | −3.45 | 0.3432 | 0.0193 |
| PCB017 | 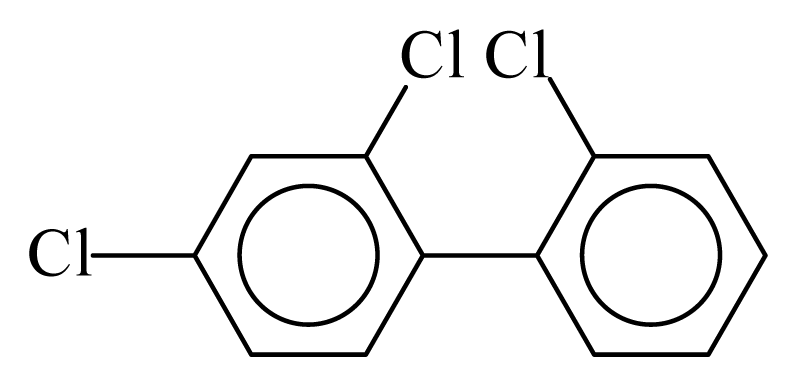 | 0.3398 | 10.97 | −0.0184 | −0.8086 | 133.06 | −3.51 | 0.3582 | −0.0184 |
| PCB018 | 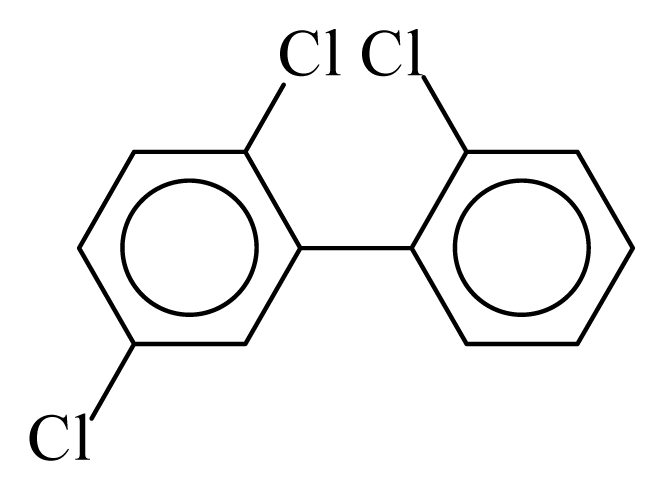 | 0.3378 | 10.72 | −0.0125 | −0.5510 | 131.64 | −3.50 | 0.3503 | −0.0125 |
| PCB019 | 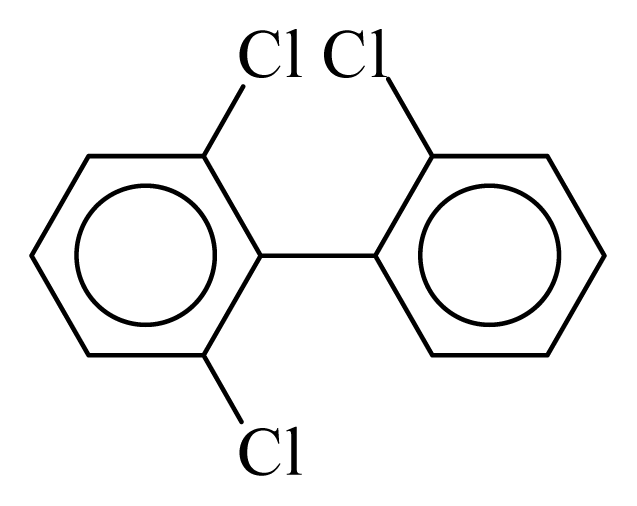 | 0.3045 | 10.16 | 0.0042 | 0.1849 | 132.62 | −3.44 | 0.3003 | 0.0042 |
| PCB020 |  | 0.4170 | 11.56 | 0.0015 | 0.0644 | 132.66 | −3.57 | 0.4155 | 0.0015 |
| PCB021 |  | 0.4135 | 11.09 | −0.0179 | −0.7855 | 133.32 | −3.50 | 0.4314 | −0.0179 |
| PCB022 | 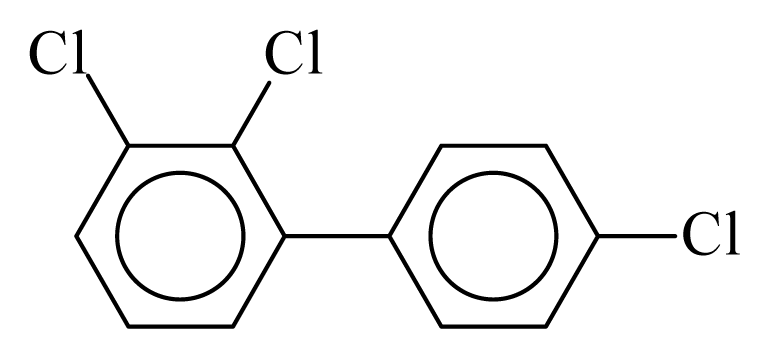 | 0.4267 | 11.05 | 0.0005 | 0.0212 | 131.66 | −3.52 | 0.4262 | 0.0005 |
| PCB023 |  | 0.3770 | 11.05 | −0.0239 | −1.0517 | 132.19 | −3.51 | 0.4009 | −0.0239 |
| PCB024 | 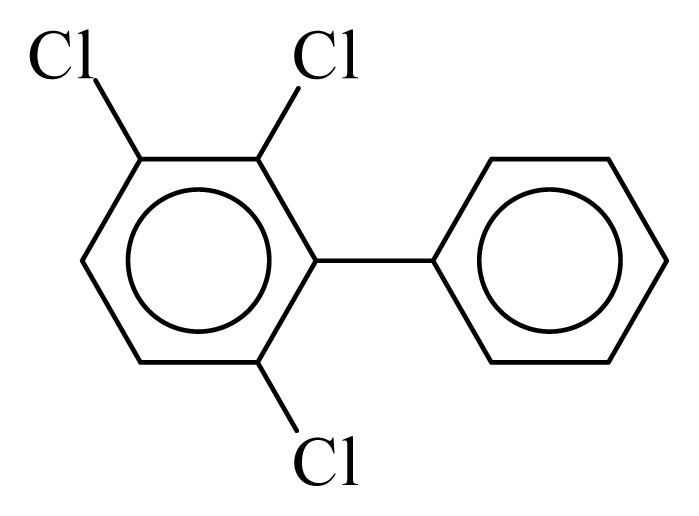 | 0.3508 | 10.52 | 0.0042 | 0.1838 | 131.49 | −3.46 | 0.3466 | 0.0042 |
| PCB025 | 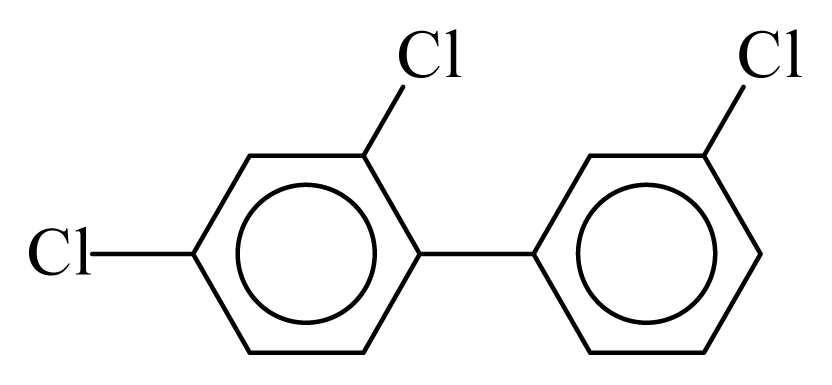 | 0.3937 | 10.80 | −0.0283 | −1.2445 | 133.28 | −3.48 | 0.4220 | −0.0283 |
| PCB026 |  | 0.3911 | 10.24 | −0.0015 | −0.0653 | 133.94 | −3.42 | 0.3926 | −0.0015 |
| PCB027 | 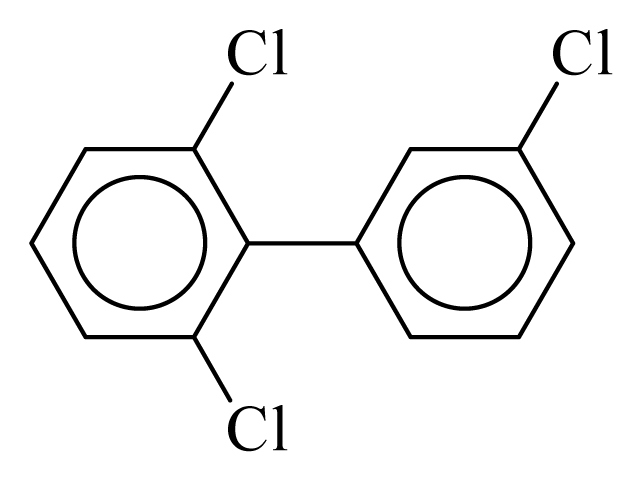 | 0.3521 | 10.75 | 0.0056 | 0.2482 | 132.13 | −3.50 | 0.3465 | 0.0056 |
| PCB028 | 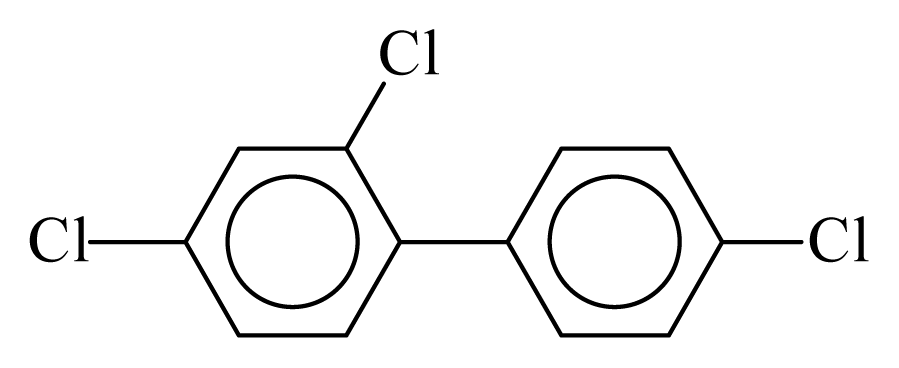 | 0.4031 | 10.23 | −0.0294 | −1.2916 | 131.25 | −3.45 | 0.4325 | −0.0294 |
| PCB029 |  | 0.3820 | 12.03 | −0.0161 | −0.7060 | 132.78 | −3.65 | 0.3981 | −0.0161 |
| PCB030 |  | 0.3165 | 11.48 | −0.0323 | −1.4195 | 133.66 | −3.57 | 0.3488 | −0.0323 |
| PCB031 |  | 0.4094 | 11.55 | 0.0086 | 0.3793 | 132.00 | −3.60 | 0.4008 | 0.0086 |
| PCB032 | 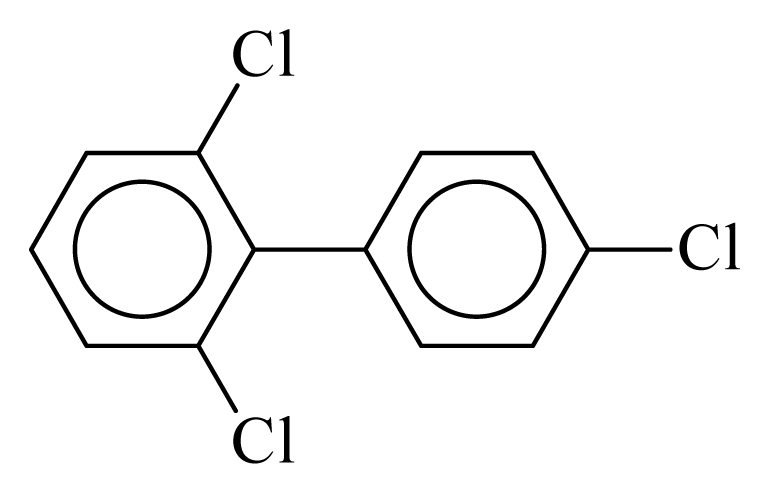 | 0.3636 | 11.22 | 0.0089 | 0.3932 | 131.75 | −3.57 | 0.3547 | 0.0089 |
| PCB033 |  | 0.4163 | 11.25 | 0.0057 | 0.2490 | 132.12 | −3.58 | 0.4106 | 0.0057 |
| PCB034 |  | 0.3782 | 12.89 | −0.0103 | −0.4521 | 130.80 | −3.73 | 0.3885 | −0.0103 |
| PCB035 | 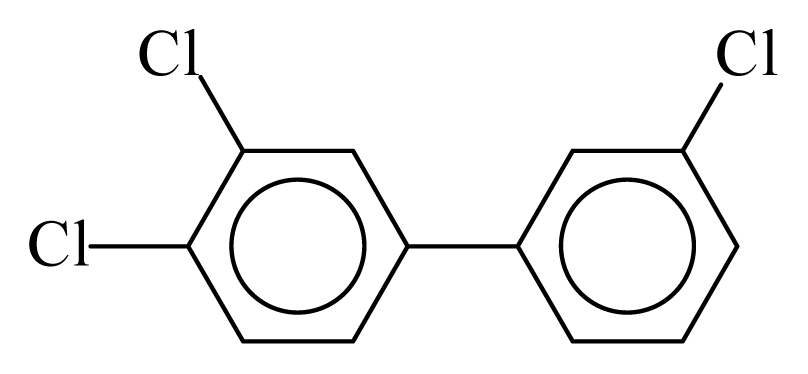 | 0.4738 | 12.32 | 0.0138 | 0.6063 | 131.52 | −3.67 | 0.4600 | 0.0138 |
| PCB036 |  | 0.4375 | 12.42 | 0.0027 | 0.1167 | 130.24 | −3.68 | 0.4348 | 0.0027 |
| PCB037 | 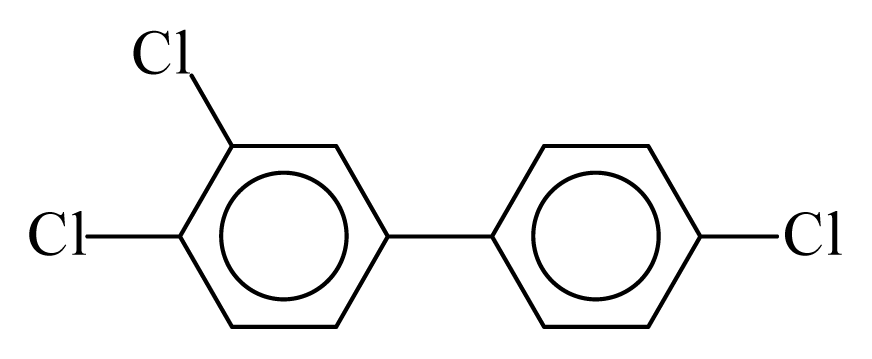 | 0.4858 | 11.87 | 0.0184 | 0.8096 | 129.97 | −3.61 | 0.4674 | 0.0184 |
| PCB038 | 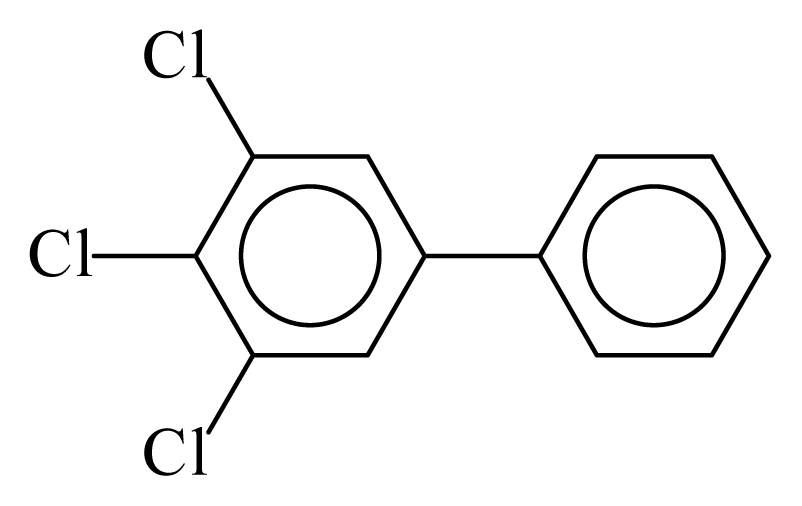 | 0.5102 | 12.09 | 0.0635 | 2.7897 | 130.07 | −3.66 | 0.4467 | 0.0635 |
| PCB039 |  | 0.4488 | 11.53 | 0.0041 | 0.1782 | 131.14 | −3.59 | 0.4447 | 0.0041 |
| PCB040 | 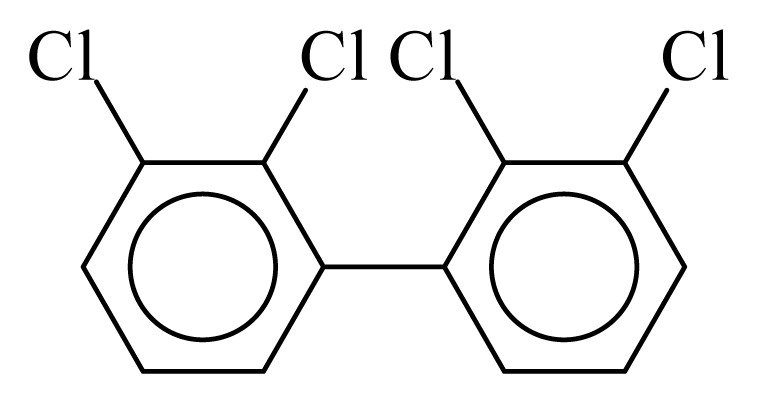 | 0.5102 | 11.58 | 0.0012 | 0.0545 | 129.81 | −3.60 | 0.5090 | 0.0012 |
| PCB041 | 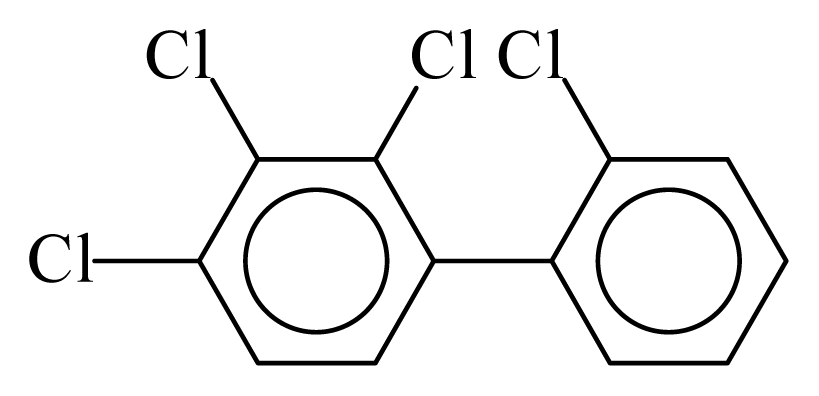 | 0.4990 | 12.15 | −0.0127 | −0.5568 | 130.26 | −3.67 | 0.5117 | −0.0127 |
| PCB042 | 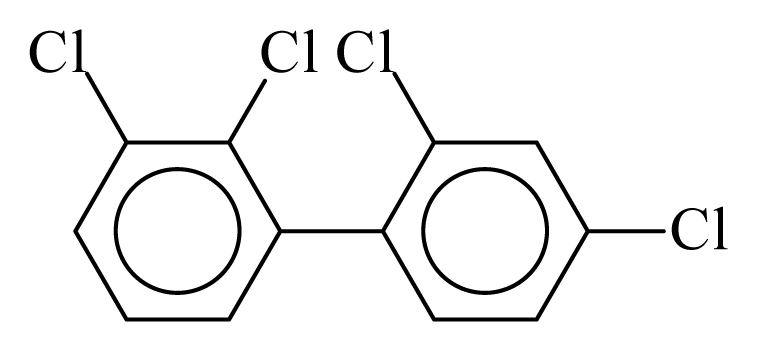 | 0.4870 | 11.30 | −0.0324 | −1.4222 | 129.77 | −3.59 | 0.5194 | −0.0324 |
| PCB043 | 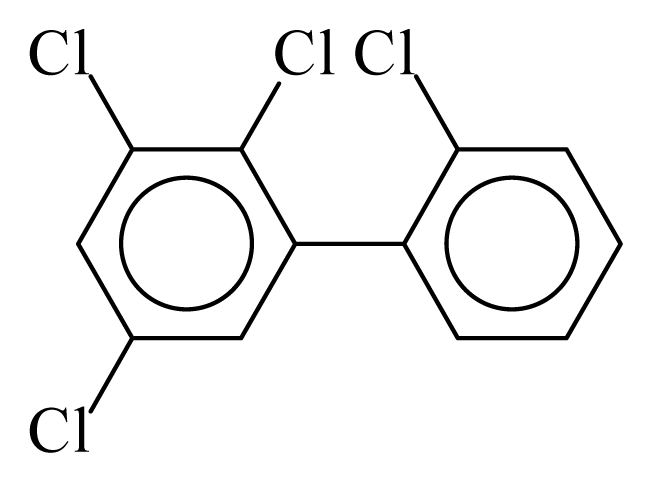 | 0.4587 | 12.11 | −0.0267 | −1.1744 | 130.59 | −3.66 | 0.4854 | −0.0267 |
| PCB044 | 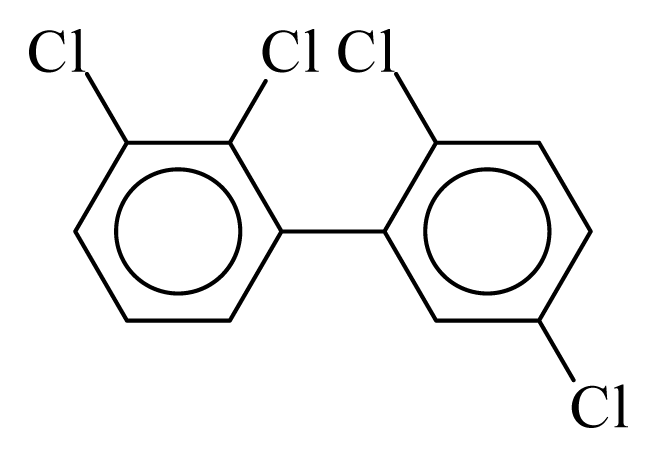 | 0.4832 | 11.60 | −0.0088 | −0.3869 | 129.80 | −3.61 | 0.4920 | −0.0088 |
| PCB045 | 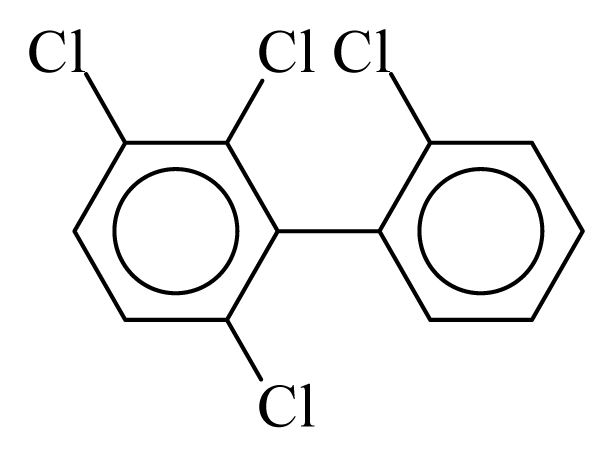 | 0.4334 | 12.57 | 0.0004 | 0.0168 | 130.50 | −3.74 | 0.4330 | 0.0004 |
| PCB046 |  | 0.4450 | 13.43 | 0.0088 | 0.3881 | 128.67 | −3.82 | 0.4362 | 0.0088 |
| PCB047 |  | 0.4639 | 12.87 | −0.0562 | −2.4723 | 128.32 | −3.76 | 0.5201 | −0.0562 |
| PCB048 | 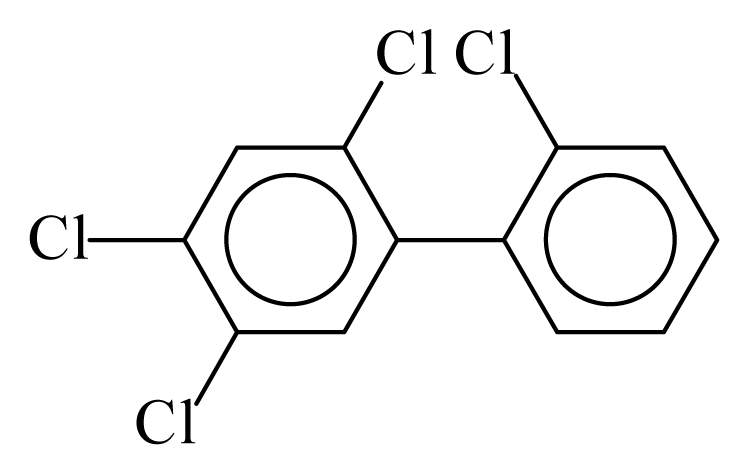 | 0.4651 | 12.62 | −0.0098 | −0.4320 | 128.24 | −3.75 | 0.4749 | −0.0098 |
| PCB049 | 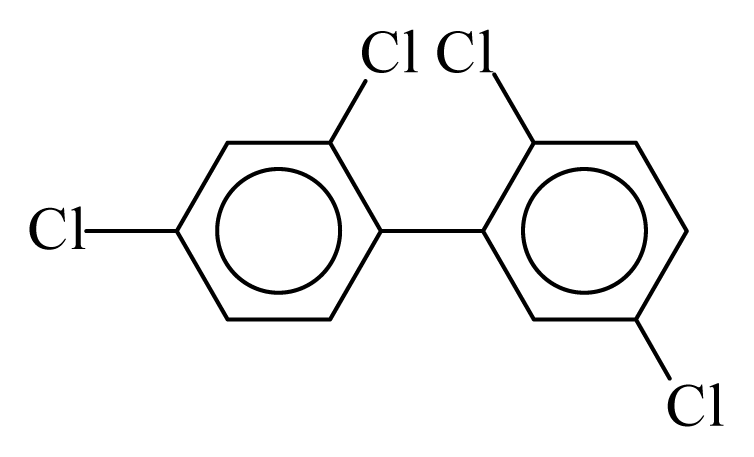 | 0.4610 | 14.04 | −0.0314 | −1.3821 | 126.70 | −3.90 | 0.4924 | −0.0314 |
| PCB050 |  | 0.4007 | 10.02 | −0.0122 | −0.5363 | 133.20 | −3.42 | 0.1119 | −0.0122 |
| PCB051 | 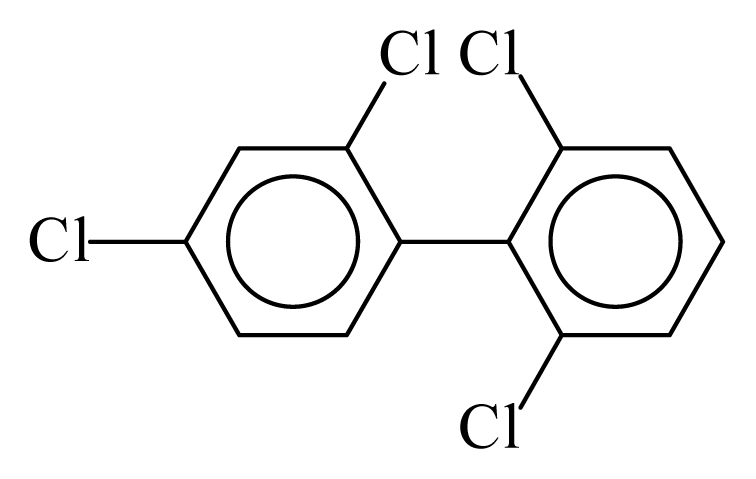 | 0.4242 | 10.60 | 0.0041 | 0.1800 | 134.27 | −3.47 | 0.1503 | 0.0041 |
| PCB052 | 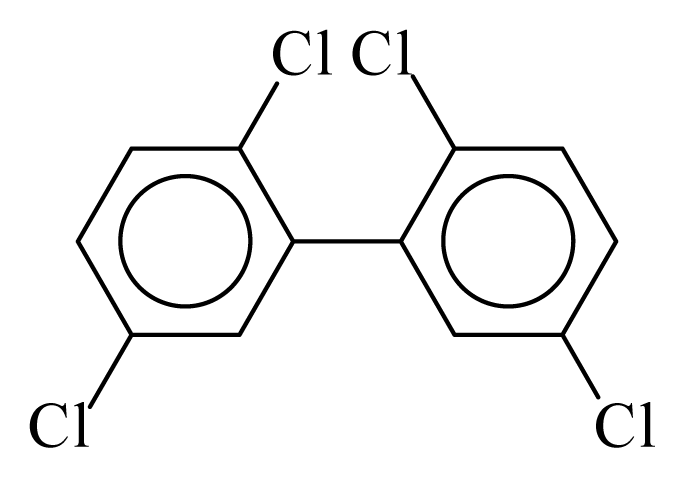 | 0.4557 | 9.96 | 0.0376 | 1.6541 | 135.23 | −3.40 | 0.1561 | 0.0376 |
| PCB053 | 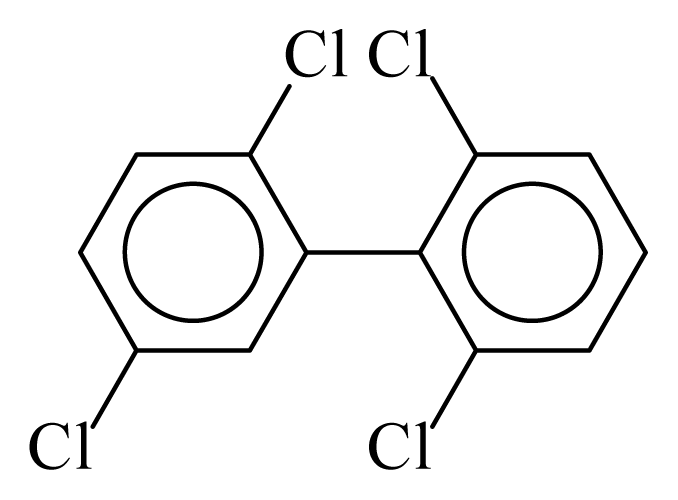 | 0.4187 | 10.14 | 0.0054 | 0.2377 | 134.89 | −3.42 | 0.2191 | 0.0054 |
| PCB054 | 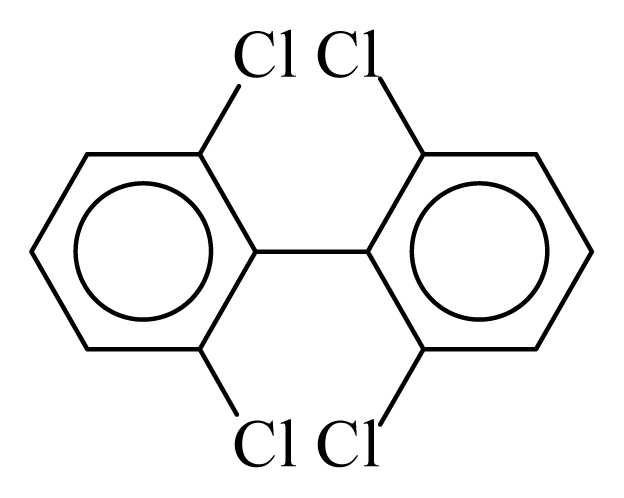 | 0.3800 | 9.75 | 0.0251 | 1.1035 | 133.36 | −3.41 | 0.2534 | 0.0251 |
| PCB055 | 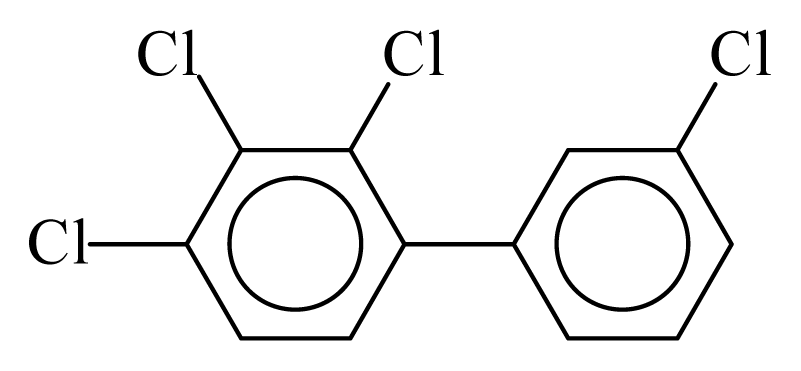 | 0.5562 | 10.15 | −0.0193 | −0.8496 | 136.72 | −3.38 | 0.2902 | −0.0193 |
| PCB056 | 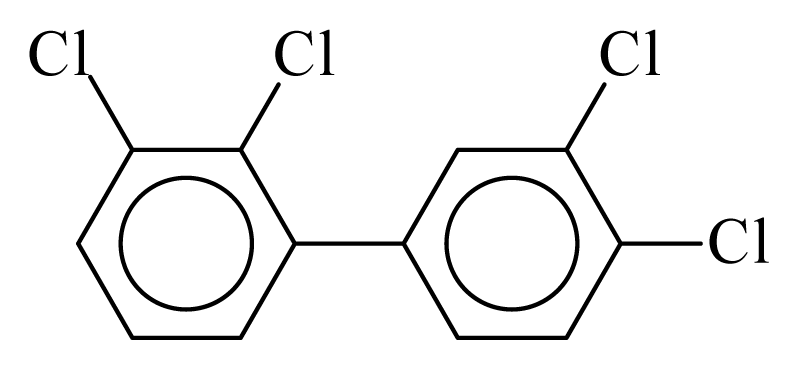 | 0.5676 | 10.72 | 0.0028 | 0.1234 | 134.60 | −3.48 | 0.2538 | 0.0028 |
| PCB057 | 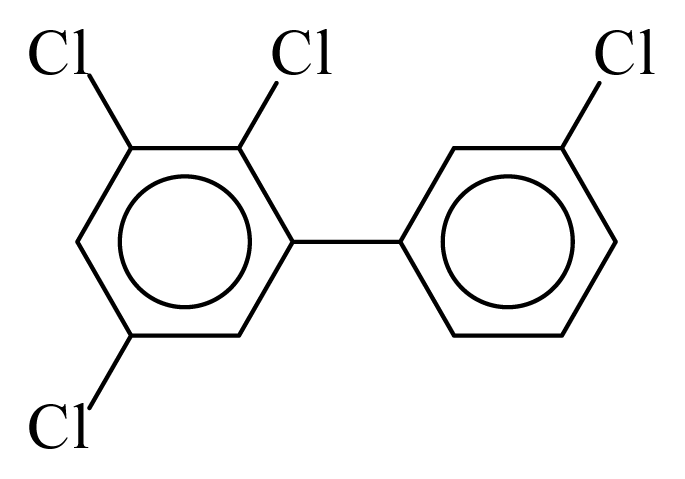 | 0.5515 | 10.27 | −0.0048 | −0.2094 | 133.35 | −3.43 | 0.2831 | −0.0048 |
| PCB058 |  | 0.5267 | 11.12 | 0.0348 | 1.5315 | 134.95 | −3.55 | 0.2222 | 0.0348 |
| PCB059 | 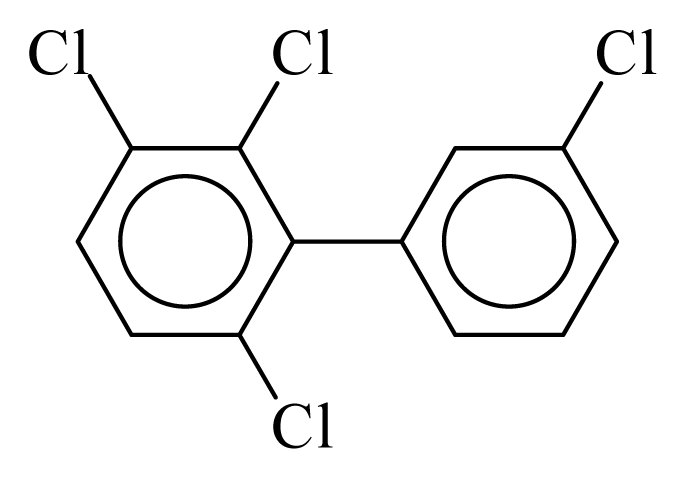 | 0.4860 | 11.75 | 0.0333 | 1.4623 | 133.57 | −3.57 | 0.1910 | 0.0333 |
| PCB060 | 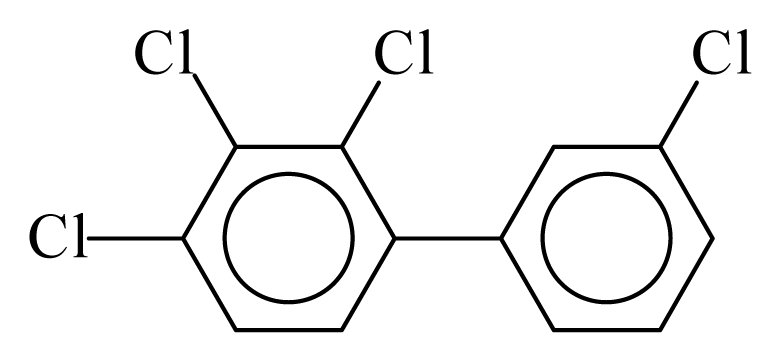 | 0.5676 | 11.26 | 0.0168 | 0.7378 | 133.12 | −3.52 | 0.3070 | 0.0168 |
| PCB061 |  | 0.5331 | 11.52 | 0.0442 | 1.9425 | 132.24 | −3.57 | 0.2856 | 0.0442 |
| PCB062 | 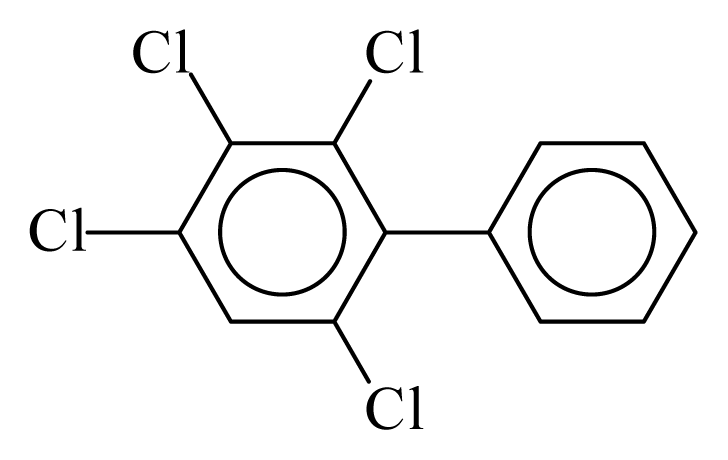 | 0.4685 | 11.09 | 0.0065 | 0.2857 | 134.24 | −3.49 | 0.3250 | 0.0065 |
| PCB063 | 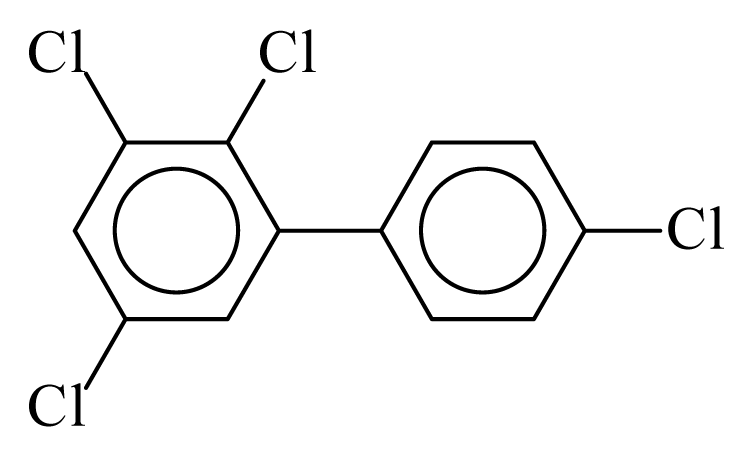 | 0.5290 | 10.98 | −0.0393 | −1.7268 | 133.10 | −3.50 | 0.2766 | −0.0393 |
| PCB064 | 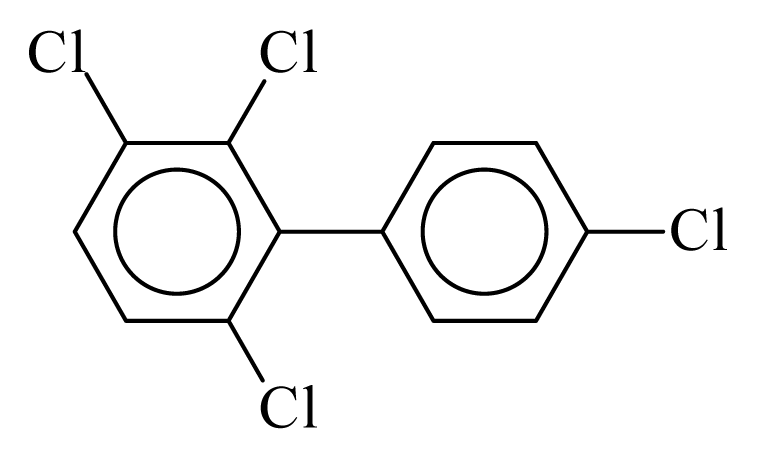 | 0.4999 | 10.98 | 0.0036 | 0.1567 | 131.58 | −3.51 | 0.3351 | 0.0036 |
| PCB065 |  | 0.4671 | 10.45 | 0.0193 | 0.8481 | 132.74 | −3.45 | 0.3432 | 0.0193 |
| PCB066 | 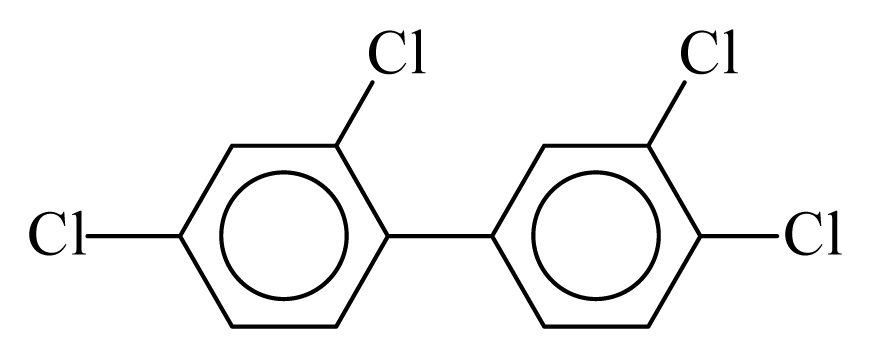 | 0.5447 | 10.97 | −0.0184 | −0.8086 | 133.06 | −3.51 | 0.3582 | −0.0184 |
| PCB067 | 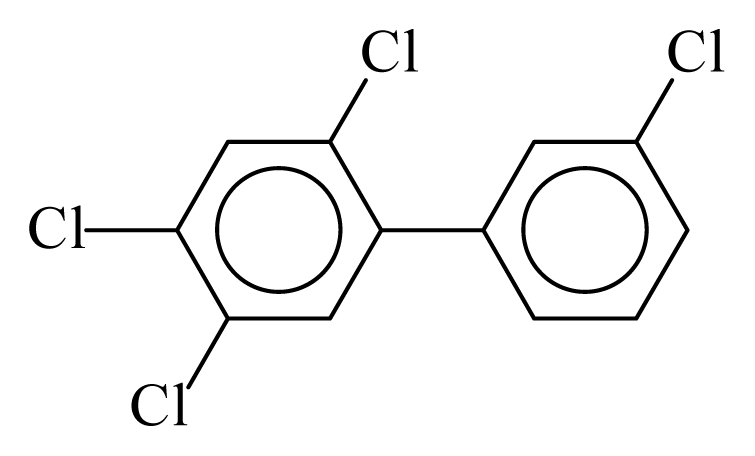 | 0.5214 | 10.72 | −0.0125 | −0.5510 | 131.64 | −3.50 | 0.3503 | −0.0125 |
| PCB068 | 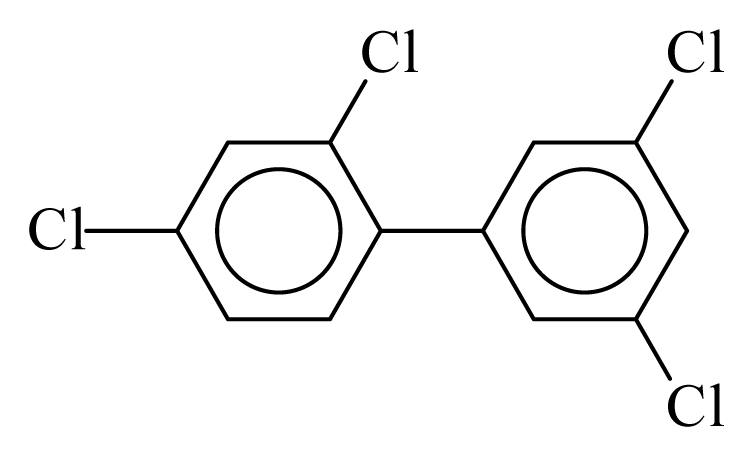 | 0.5040 | 10.16 | 0.0042 | 0.1849 | 132.62 | −3.44 | 0.3003 | 0.0042 |
| PCB069 | 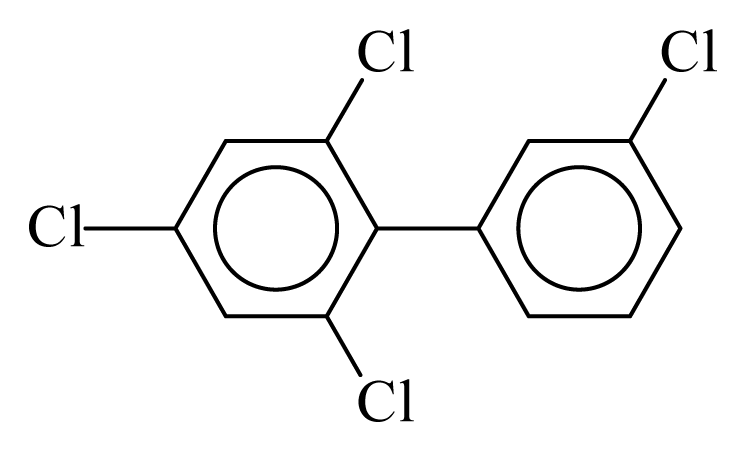 | 0.4510 | 11.56 | 0.0015 | 0.0644 | 132.66 | −3.57 | 0.4155 | 0.0015 |
| PCB070 | 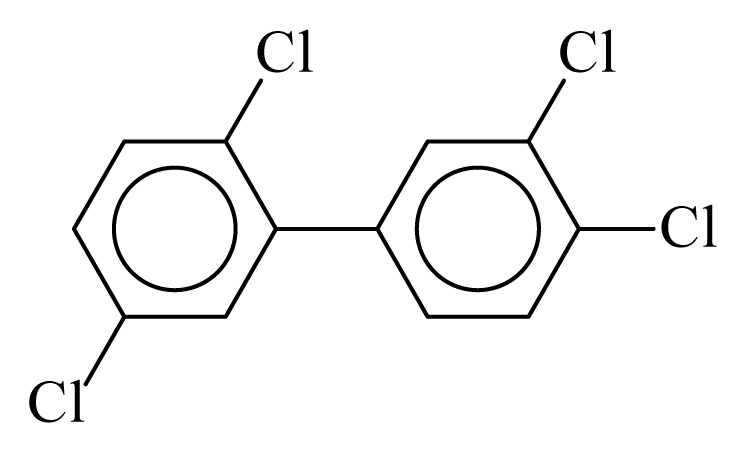 | 0.5407 | 11.09 | −0.0179 | −0.7855 | 133.32 | −3.50 | 0.4314 | −0.0179 |
| PCB071 |  | 0.4989 | 11.05 | 0.0005 | 0.0212 | 131.66 | −3.52 | 0.4262 | 0.0005 |
| PCB072 | 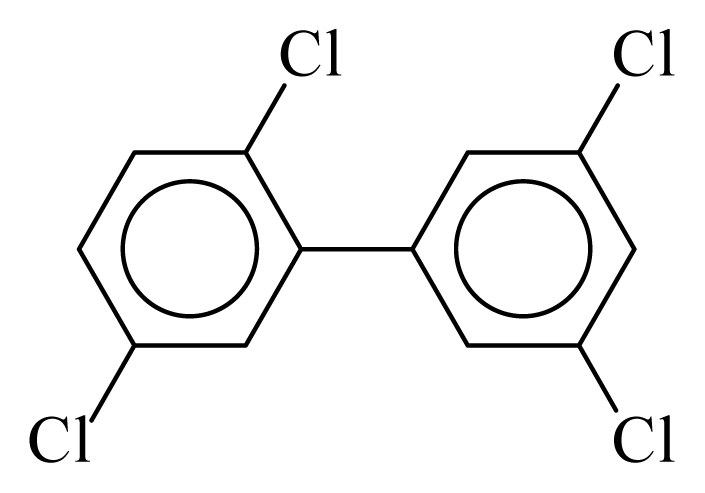 | 0.4984 | 11.05 | −0.0239 | −1.0517 | 132.19 | −3.51 | 0.4009 | −0.0239 |
| PCB073 |  | 0.4554 | 10.52 | 0.0042 | 0.1838 | 131.49 | −3.46 | 0.3466 | 0.0042 |
| PCB074 |  | 0.5341 | 10.80 | −0.0283 | −1.2445 | 133.28 | −3.48 | 0.4220 | −0.0283 |
| PCB075 |  | 0.4643 | 10.24 | −0.0015 | −0.0653 | 133.94 | −3.42 | 0.3926 | −0.0015 |
| PCB076 |  | 0.5408 | 10.75 | 0.0056 | 0.2482 | 132.13 | −3.50 | 0.3465 | 0.0056 |
| PCB077 |  | 0.6295 | 10.23 | −0.0294 | −1.2916 | 131.25 | −3.45 | 0.4325 | −0.0294 |
| PCB078 |  | 0.6024 | 12.03 | −0.0161 | −0.7060 | 132.78 | −3.65 | 0.3981 | −0.0161 |
| PCB079 |  | 0.5894 | 11.48 | −0.0323 | −1.4195 | 133.66 | −3.57 | 0.3488 | −0.0323 |
| PCB080 |  | 0.5464 | 11.55 | 0.0086 | 0.3793 | 132.00 | −3.60 | 0.4008 | 0.0086 |
| PCB081 |  | 0.6149 | 11.22 | 0.0089 | 0.3932 | 131.75 | −3.57 | 0.3547 | 0.0089 |
| PCB082 |  | 0.6453 | 11.25 | 0.0057 | 0.2490 | 132.12 | −3.58 | 0.4106 | 0.0057 |
| PCB083 |  | 0.6029 | 12.89 | −0.0103 | −0.4521 | 130.80 | −3.73 | 0.3885 | −0.0103 |
| PCB084 | 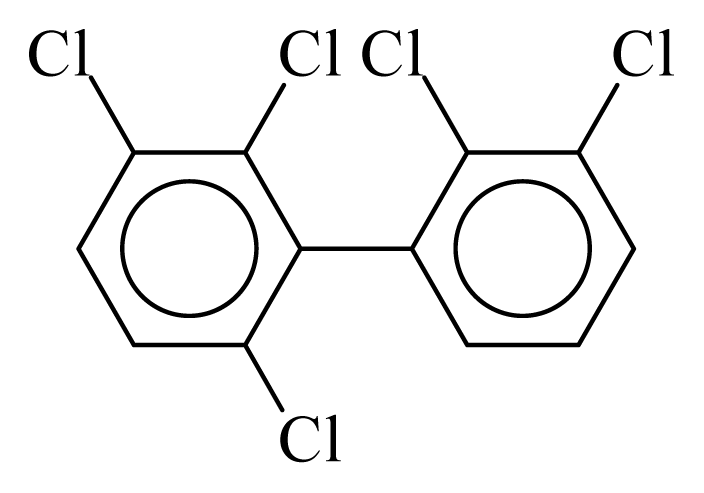 | 0.5744 | 12.32 | 0.0138 | 0.6063 | 131.52 | −3.67 | 0.4600 | 0.0138 |
| PCB085 | 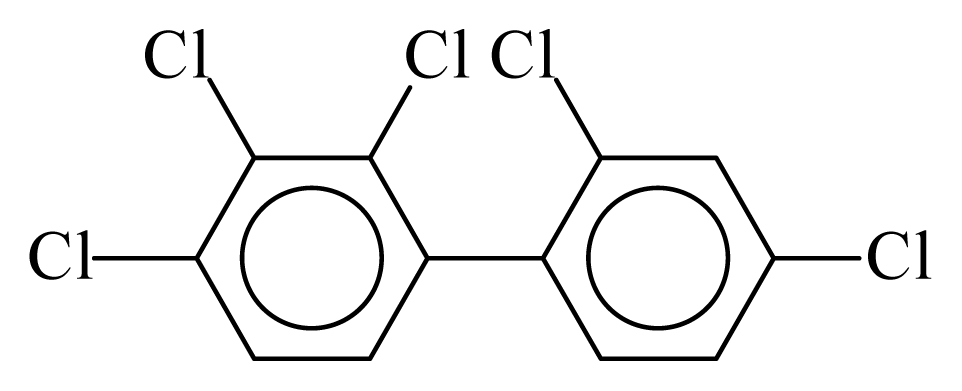 | 0.6224 | 12.42 | 0.0027 | 0.1167 | 130.24 | −3.68 | 0.4348 | 0.0027 |
| PCB086 |  | 0.6105 | 11.87 | 0.0184 | 0.8096 | 129.97 | −3.61 | 0.4674 | 0.0184 |
| PCB087 | 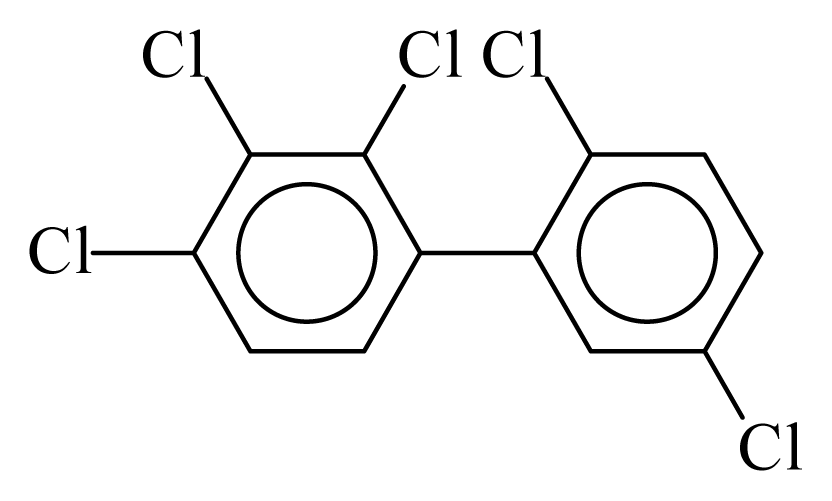 | 0.6175 | 12.09 | 0.0635 | 2.7897 | 130.07 | −3.66 | 0.4467 | 0.0635 |
| PCB088 | 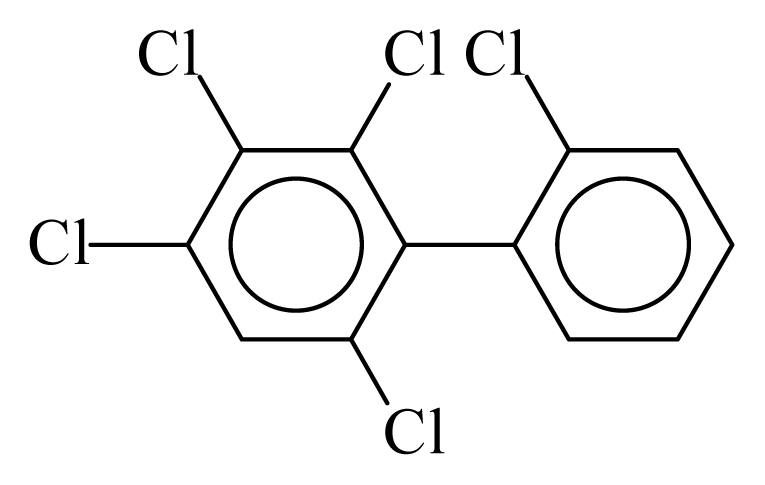 | 0.5486 | 11.53 | 0.0041 | 0.1782 | 131.14 | −3.59 | 0.4447 | 0.0041 |
| PCB089 | 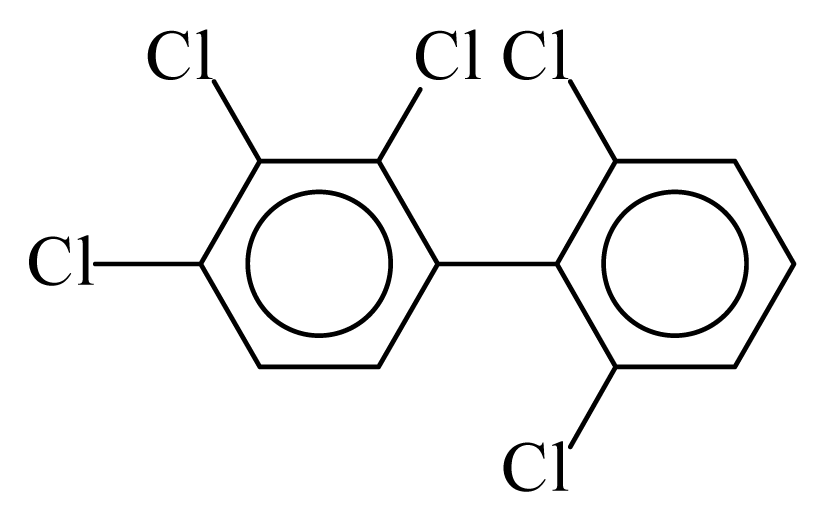 | 0.5779 | 11.58 | 0.0012 | 0.0545 | 129.81 | −3.60 | 0.5090 | 0.0012 |
| PCB090 | 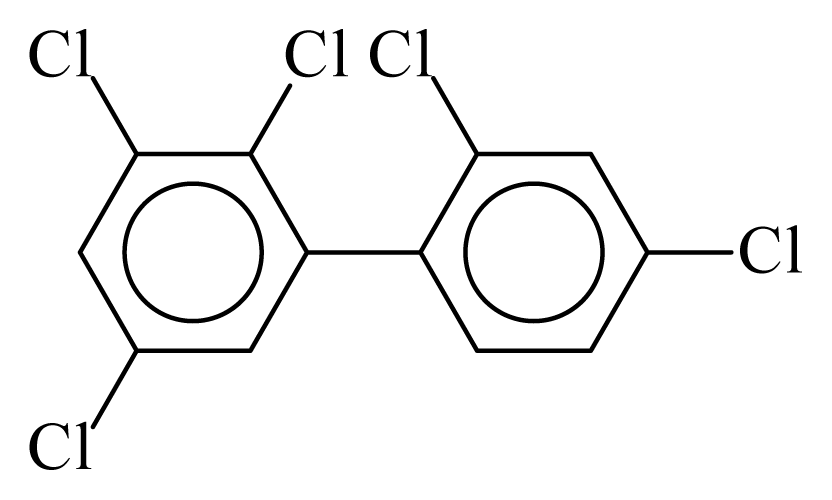 | 0.5814 | 12.15 | −0.0127 | −0.5568 | 130.26 | −3.67 | 0.5117 | −0.0127 |
| PCB091 | 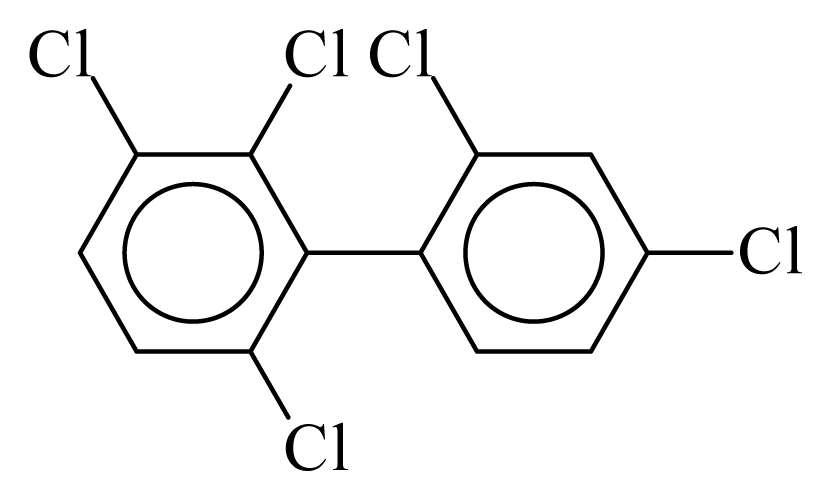 | 0.5549 | 11.30 | −0.0324 | −1.4222 | 129.77 | −3.59 | 0.5194 | −0.0324 |
| PCB092 | 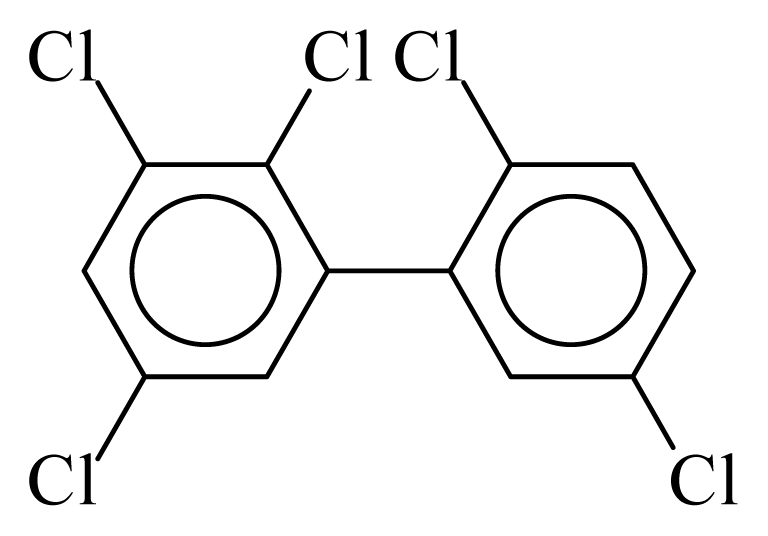 | 0.5742 | 12.11 | −0.0267 | −1.1744 | 130.59 | −3.66 | 0.4854 | −0.0267 |
| PCB093 |  | 0.5437 | 11.60 | −0.0088 | −0.3869 | 129.80 | −3.61 | 0.4920 | −0.0088 |
| PCB094 |  | 0.5331 | 12.57 | 0.0004 | 0.0168 | 130.50 | −3.74 | 0.4330 | 0.0004 |
| PCB095 | 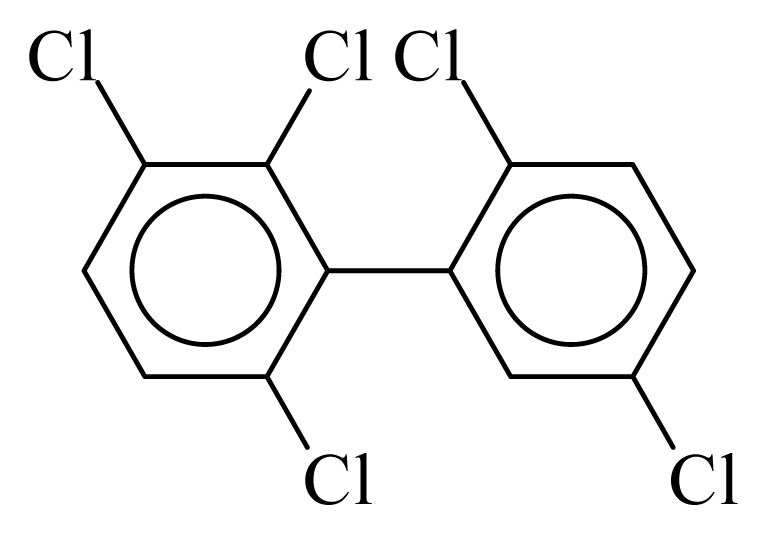 | 0.5464 | 13.43 | 0.0088 | 0.3881 | 128.67 | −3.82 | 0.4362 | 0.0088 |
| PCB096 |  | 0.5057 | 12.87 | −0.0562 | −2.4723 | 128.32 | −3.76 | 0.5201 | −0.0562 |
| PCB097 | 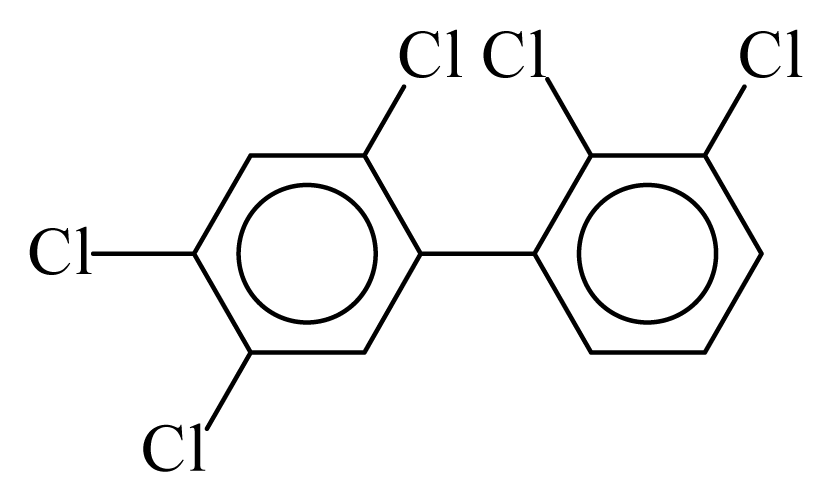 | 0.6100 | 12.62 | −0.0098 | −0.4320 | 128.24 | −3.75 | 0.4749 | −0.0098 |
| PCB098 | 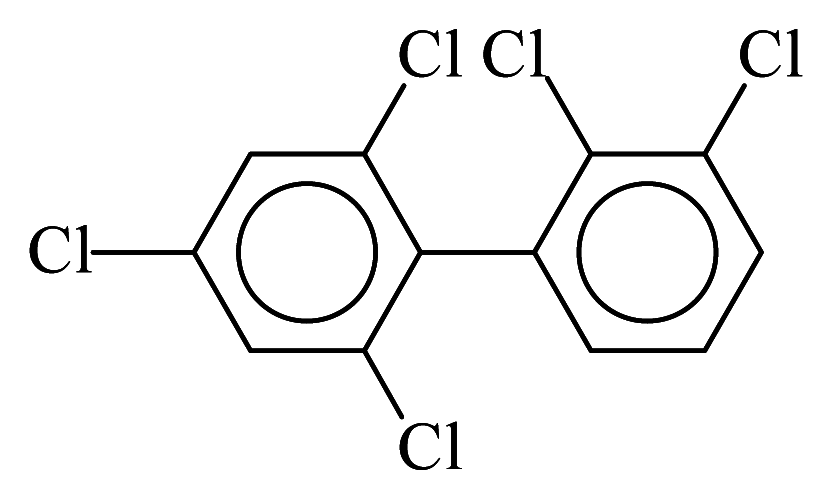 | 0.5415 | 14.04 | −0.0314 | −1.3821 | 126.70 | −3.90 | 0.4924 | −0.0314 |
| PCB099 |  | 0.5880 | 10.02 | −0.0122 | −0.5363 | 133.20 | −3.42 | 0.1119 | −0.0122 |
| PCB100 |  | 0.5212 | 10.60 | 0.0041 | 0.1800 | 134.27 | −3.47 | 0.1503 | 0.0041 |
| PCB101 | 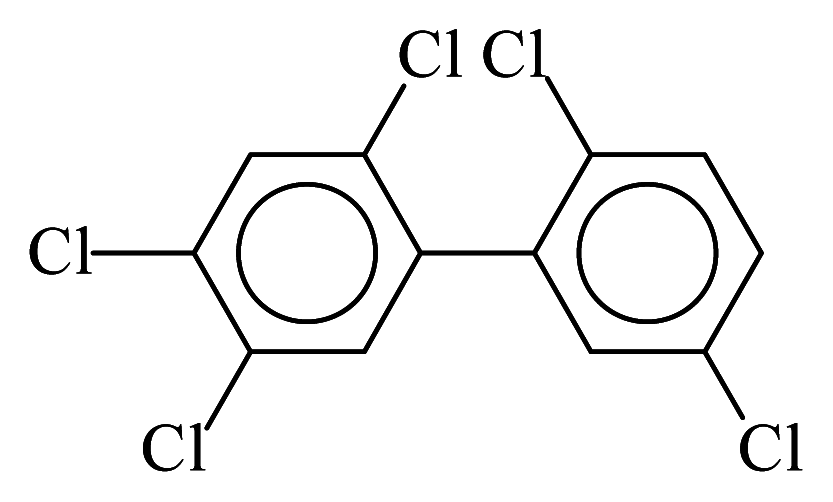 | 0.5816 | 9.96 | 0.0376 | 1.6541 | 135.23 | −3.40 | 0.1561 | 0.0376 |
| PCB102 | 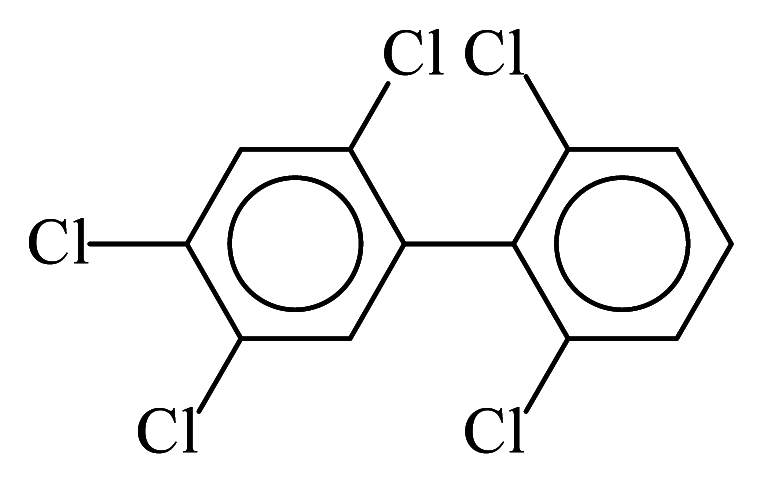 | 0.5431 | 10.14 | 0.0054 | 0.2377 | 134.89 | −3.42 | 0.2191 | 0.0054 |
| PCB103 | 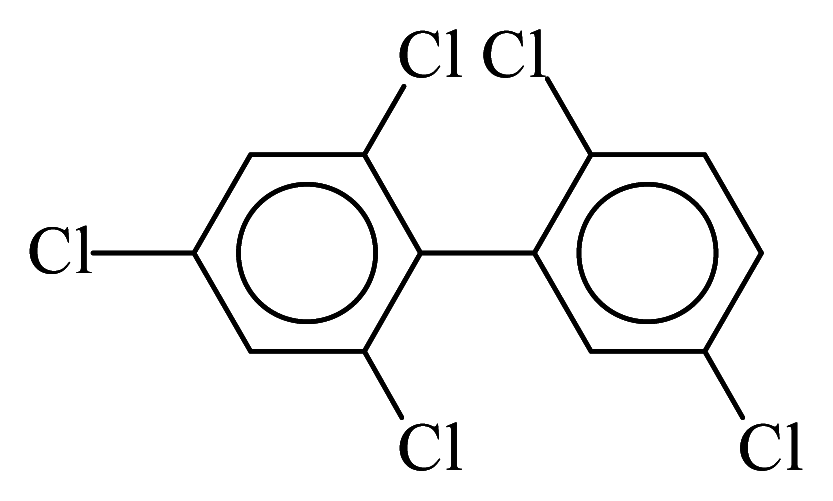 | 0.5142 | 9.75 | 0.0251 | 1.1035 | 133.36 | −3.41 | 0.2534 | 0.0251 |
| PCB104 | 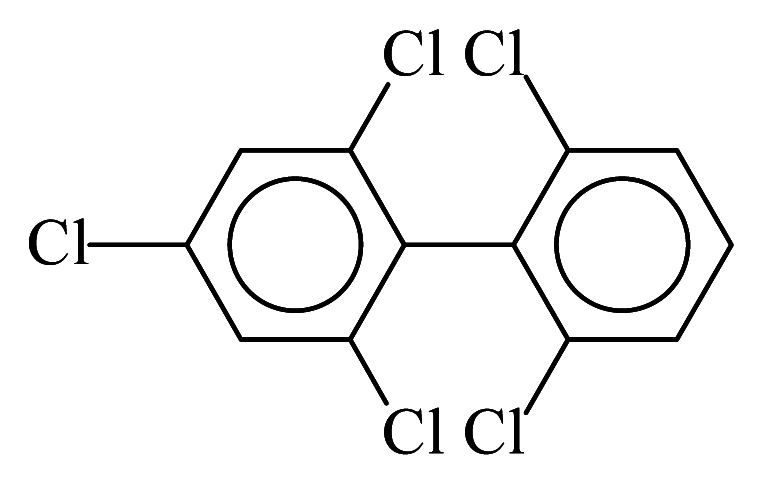 | 0.4757 | 10.15 | −0.0193 | −0.8496 | 136.72 | −3.38 | 0.2902 | −0.0193 |
| PCB105 | 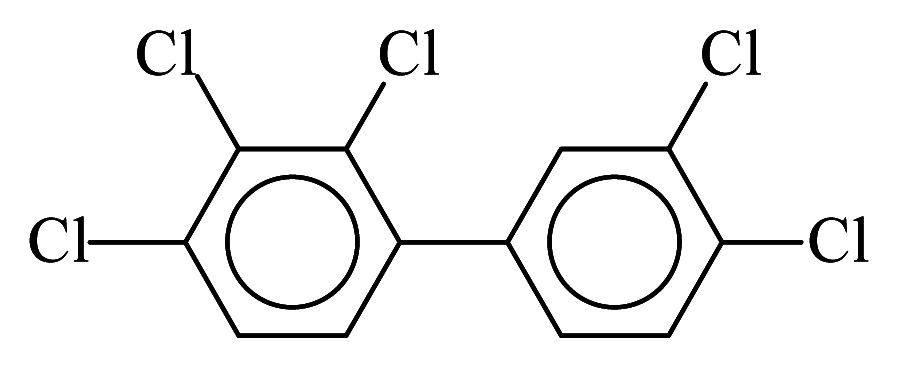 | 0.7049 | 10.72 | 0.0028 | 0.1234 | 134.60 | −3.48 | 0.2538 | 0.0028 |
| PCB106 |  | 0.6680 | 10.27 | −0.0048 | −0.2094 | 133.35 | −3.43 | 0.2831 | −0.0048 |
| PCB107 | 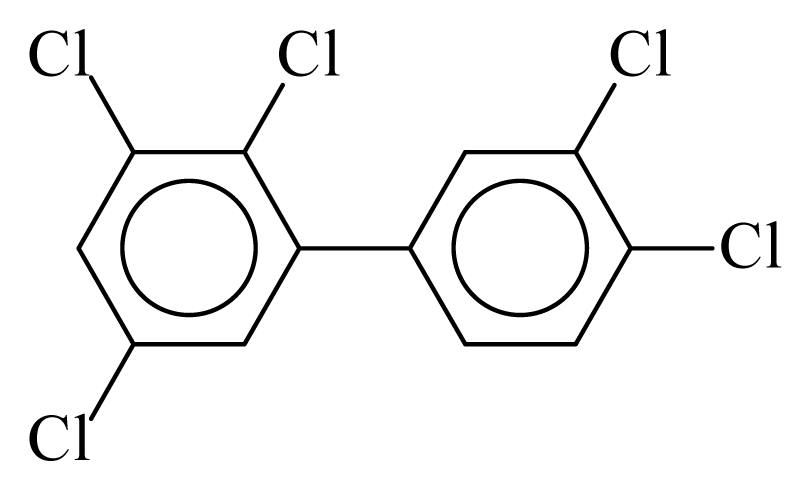 | 0.6628 | 11.12 | 0.0348 | 1.5315 | 134.95 | −3.55 | 0.2222 | 0.0348 |
| PCB108 |  | 0.6626 | 11.75 | 0.0333 | 1.4623 | 133.57 | −3.57 | 0.1910 | 0.0333 |
| PCB109 | 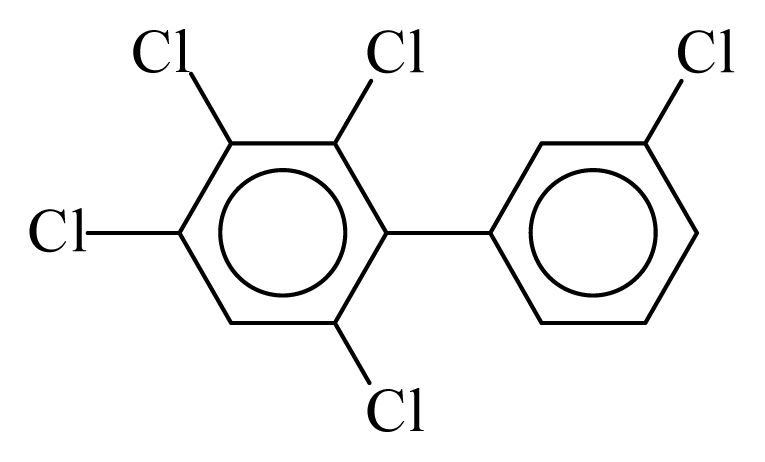 | 0.6016 | 11.26 | 0.0168 | 0.7378 | 133.12 | −3.52 | 0.3070 | 0.0168 |
| PCB110 | 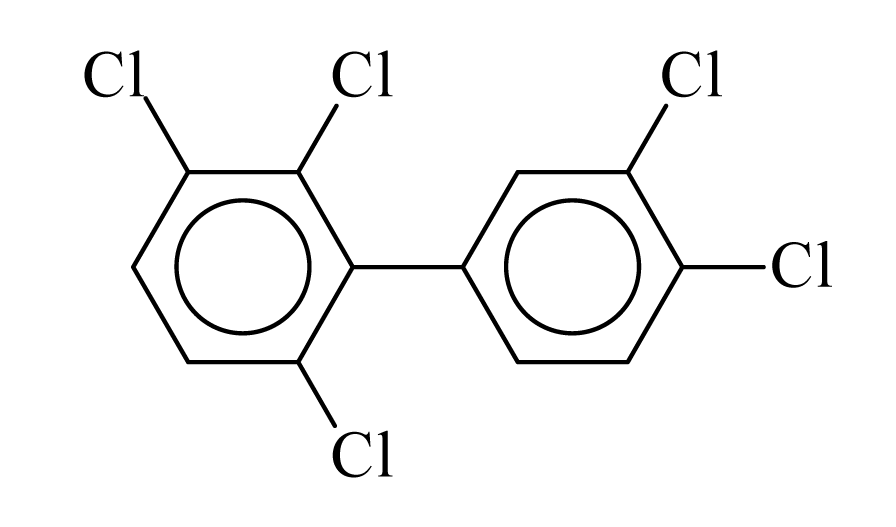 | 0.6314 | 11.52 | 0.0442 | 1.9425 | 132.24 | −3.57 | 0.2856 | 0.0442 |
| PCB111 | 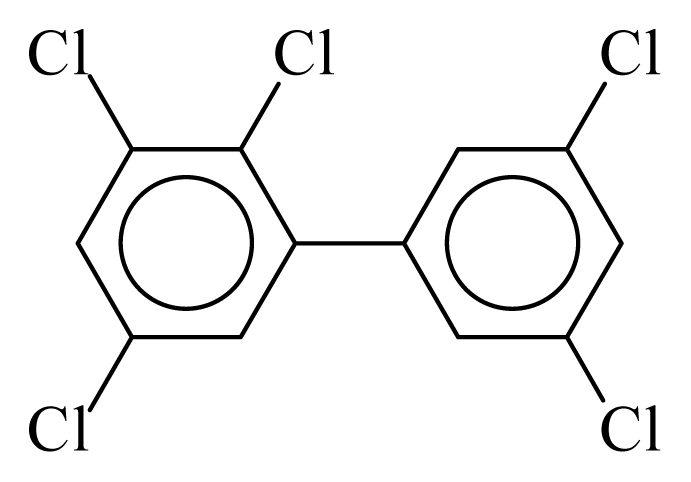 | 0.6183 | 11.09 | 0.0065 | 0.2857 | 134.24 | −3.49 | 0.3250 | 0.0065 |
| PCB112 |  | 0.5986 | 10.98 | −0.0393 | −1.7268 | 133.10 | −3.50 | 0.2766 | −0.0393 |
| PCB113 |  | 0.5862 | 10.98 | 0.0036 | 0.1567 | 131.58 | −3.51 | 0.3351 | 0.0036 |
| PCB114 |  | 0.6828 | 10.45 | 0.0193 | 0.8481 | 132.74 | −3.45 | 0.3432 | 0.0193 |
| PCB115 | 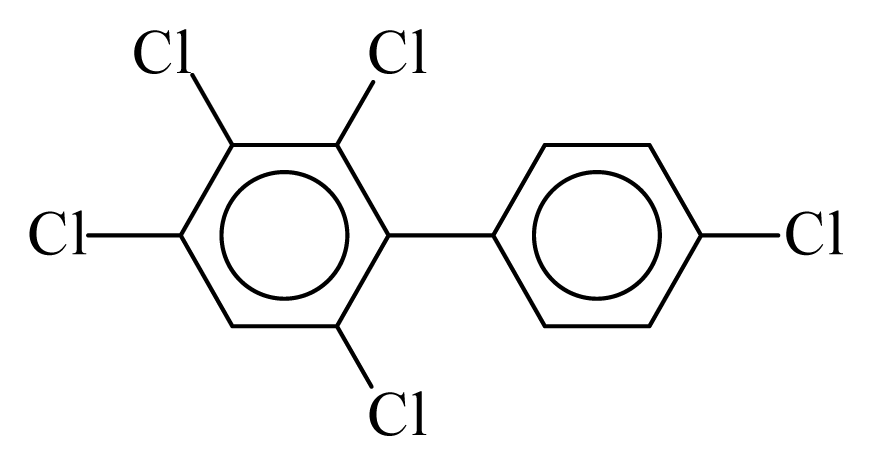 | 0.6171 | 10.97 | −0.0184 | −0.8086 | 133.06 | −3.51 | 0.3582 | −0.0184 |
| PCB116 | 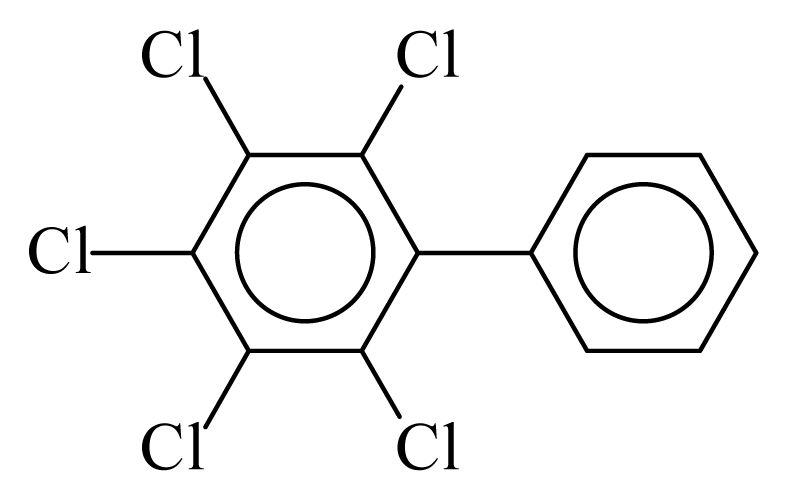 | 0.6132 | 10.72 | −0.0125 | −0.5510 | 131.64 | −3.50 | 0.3503 | −0.0125 |
| PCB117 | 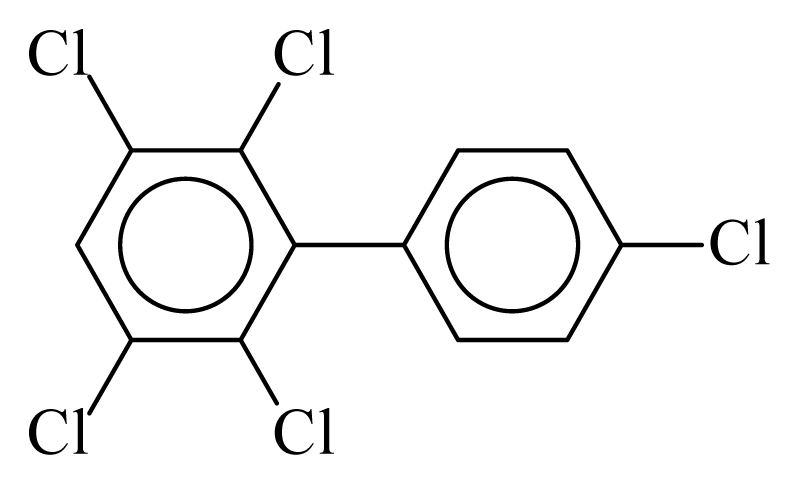 | 0.6150 | 10.16 | 0.0042 | 0.1849 | 132.62 | −3.44 | 0.3003 | 0.0042 |
| PCB118 | 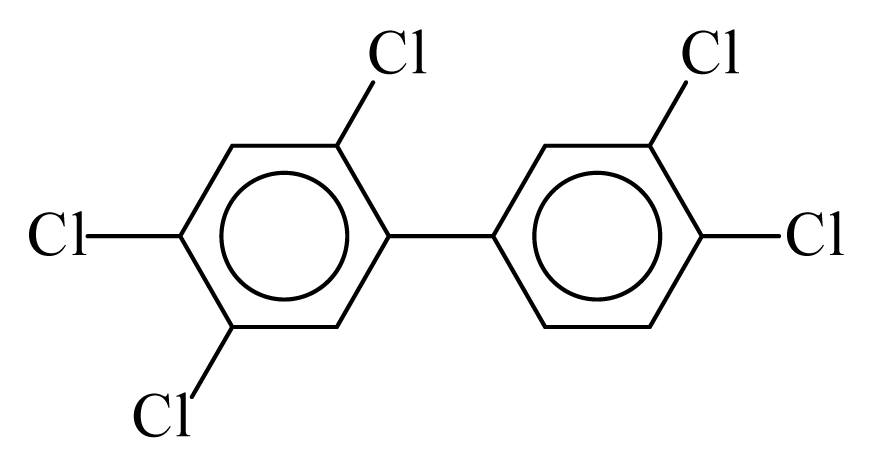 | 0.6693 | 11.56 | 0.0015 | 0.0644 | 132.66 | −3.57 | 0.4155 | 0.0015 |
| PCB119 |  | 0.5968 | 11.09 | −0.0179 | −0.7855 | 133.32 | −3.50 | 0.4314 | −0.0179 |
| PCB120 | 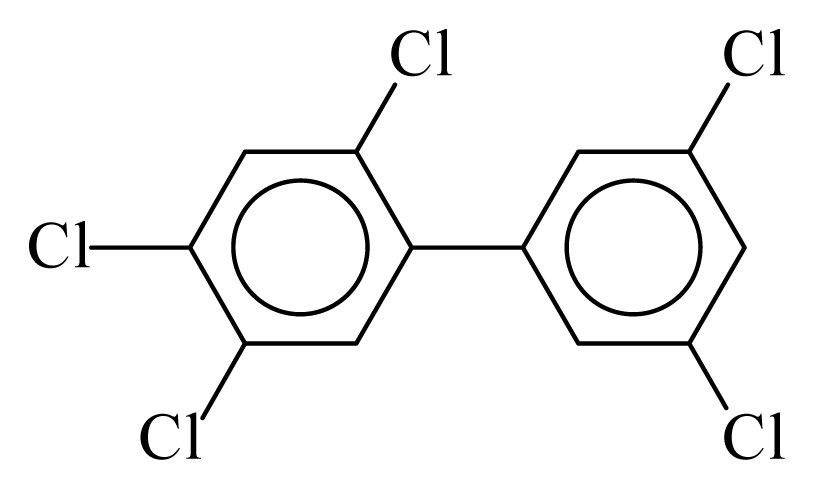 | 0.6256 | 11.05 | 0.0005 | 0.0212 | 131.66 | −3.52 | 0.4262 | 0.0005 |
| PCB121 |  | 0.5518 | 11.05 | −0.0239 | −1.0517 | 132.19 | −3.51 | 0.4009 | −0.0239 |
| PCB122 | 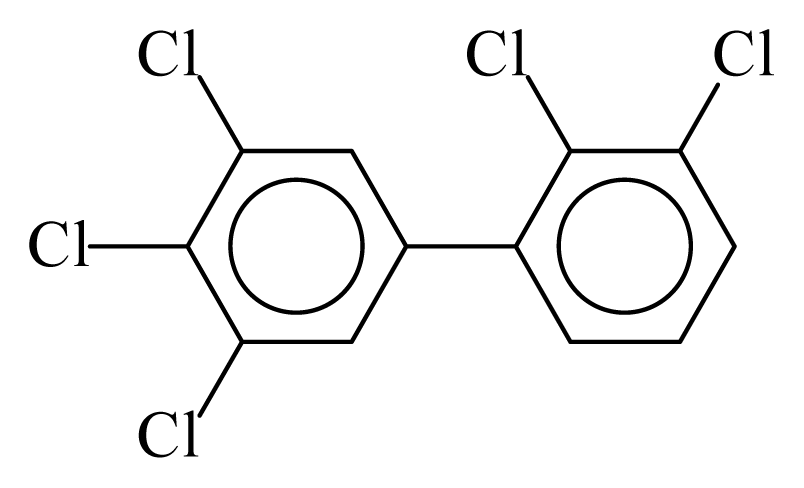 | 0.6871 | 10.52 | 0.0042 | 0.1838 | 131.49 | −3.46 | 0.3466 | 0.0042 |
| PCB123 | 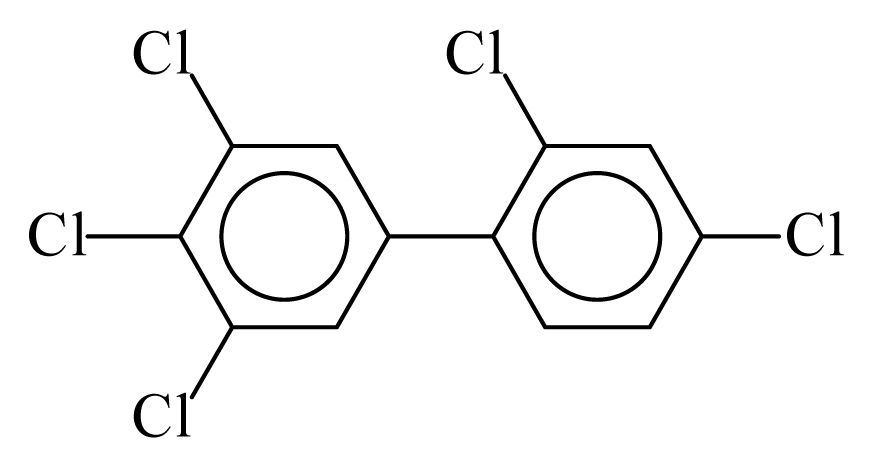 | 0.6658 | 10.80 | −0.0283 | −1.2445 | 133.28 | −3.48 | 0.4220 | −0.0283 |
| PCB124 | 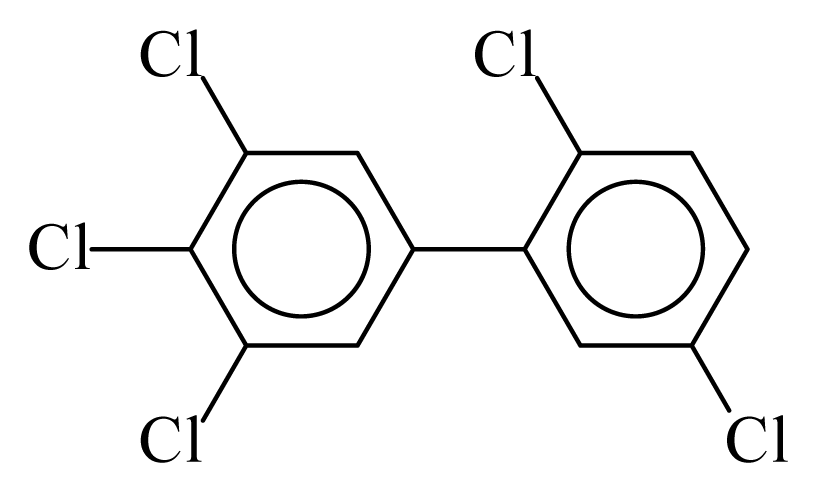 | 0.6584 | 10.24 | −0.0015 | −0.0653 | 133.94 | −3.42 | 0.3926 | −0.0015 |
| PCB125 |  | 0.6142 | 10.75 | 0.0056 | 0.2482 | 132.13 | −3.50 | 0.3465 | 0.0056 |
| PCB126 | 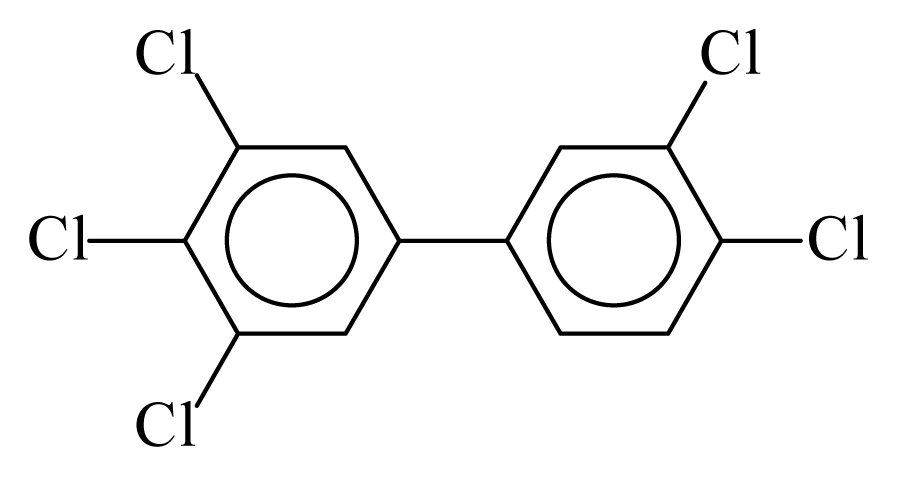 | 0.7512 | 10.23 | −0.0294 | −1.2916 | 131.25 | −3.45 | 0.4325 | −0.0294 |
| PCB127 | 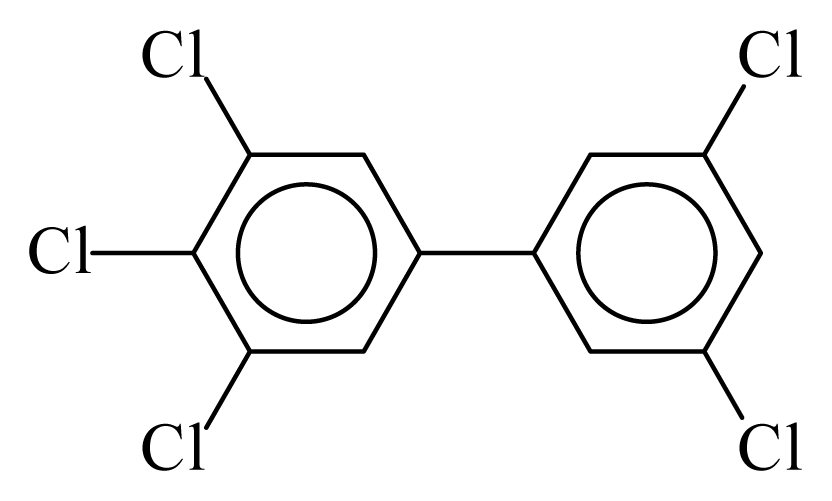 | 0.7078 | 12.03 | −0.0161 | −0.7060 | 132.78 | −3.65 | 0.3981 | −0.0161 |
| PCB128 | 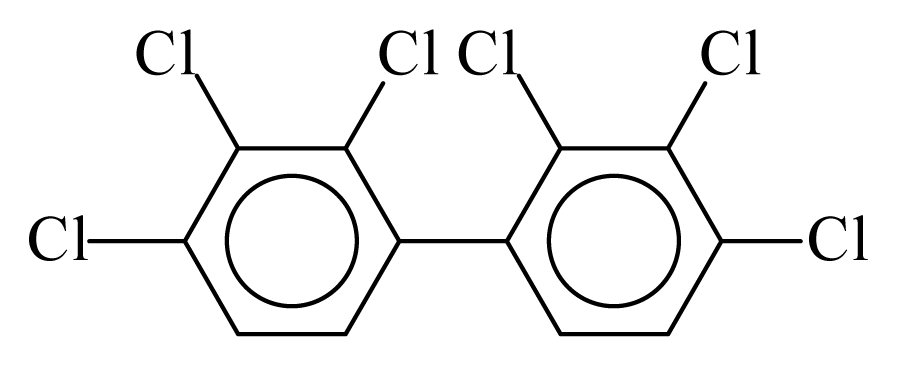 | 0.7761 | 11.48 | −0.0323 | −1.4195 | 133.66 | −3.57 | 0.3488 | −0.0323 |
| PCB129 | 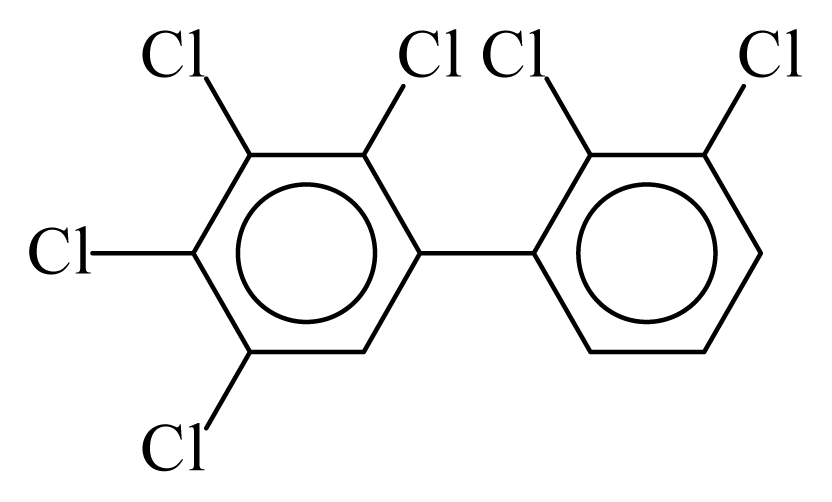 | 0.7501 | 11.55 | 0.0086 | 0.3793 | 132.00 | −3.60 | 0.4008 | 0.0086 |
| PCB130 |  | 0.7184 | 11.22 | 0.0089 | 0.3932 | 131.75 | −3.57 | 0.3547 | 0.0089 |
| PCB131 |  | 0.6853 | 11.25 | 0.0057 | 0.2490 | 132.12 | −3.58 | 0.4106 | 0.0057 |
| PCB132 | 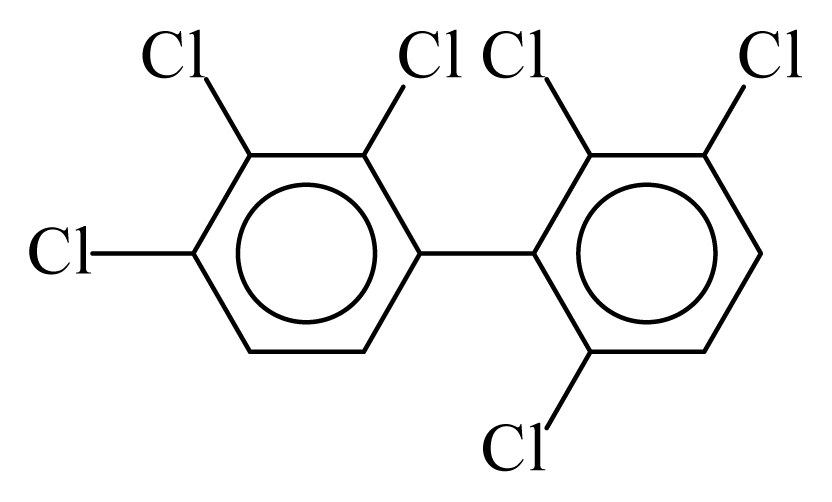 | 0.7035 | 12.89 | −0.0103 | −0.4521 | 130.80 | −3.73 | 0.3885 | −0.0103 |
| PCB133 |  | 0.6871 | 12.32 | 0.0138 | 0.6063 | 131.52 | −3.67 | 0.4600 | 0.0138 |
| PCB134 | 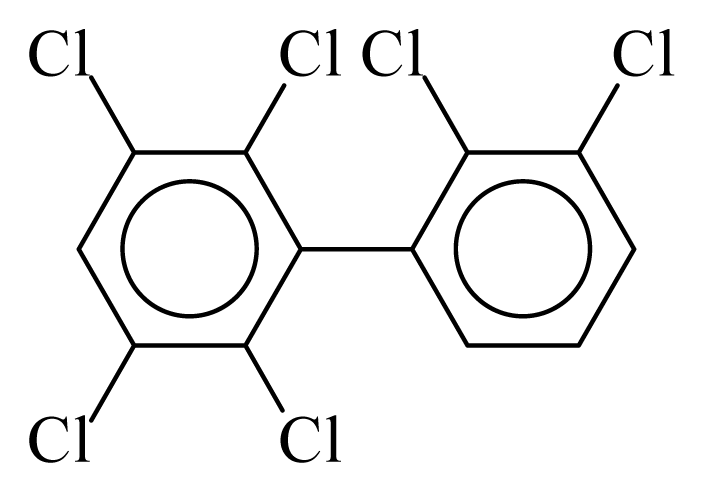 | 0.6796 | 12.42 | 0.0027 | 0.1167 | 130.24 | −3.68 | 0.4348 | 0.0027 |
| PCB135 | 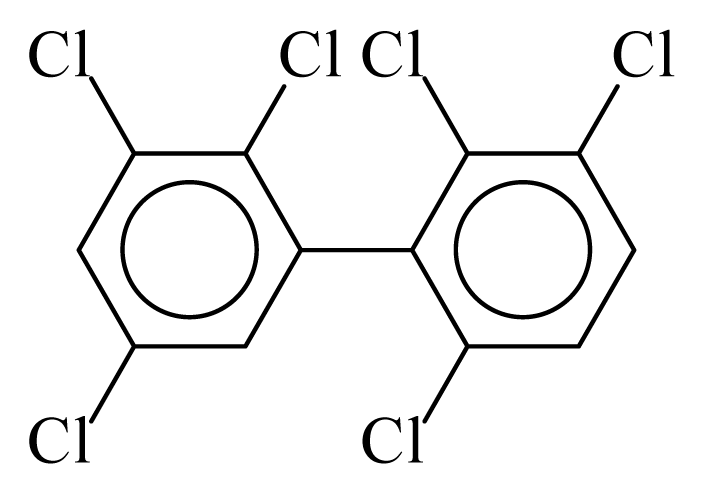 | 0.6563 | 11.87 | 0.0184 | 0.8096 | 129.97 | −3.61 | 0.4674 | 0.0184 |
| PCB136 |  | 0.6257 | 12.09 | 0.0635 | 2.7897 | 130.07 | −3.66 | 0.4467 | 0.0635 |
| PCB137 | 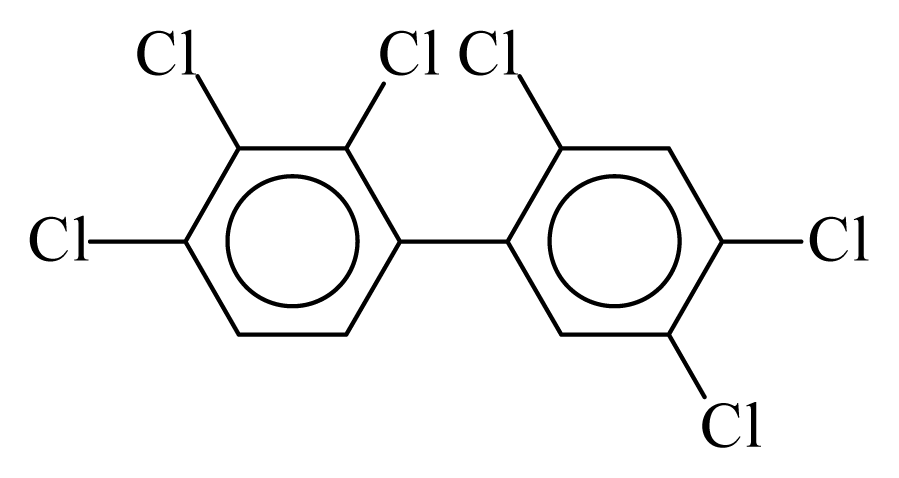 | 0.7329 | 11.53 | 0.0041 | 0.1782 | 131.14 | −3.59 | 0.4447 | 0.0041 |
| PCB138 |  | 0.7403 | 11.58 | 0.0012 | 0.0545 | 129.81 | −3.60 | 0.5090 | 0.0012 |
| PCB139 |  | 0.6707 | 12.15 | −0.0127 | −0.5568 | 130.26 | −3.67 | 0.5117 | −0.0127 |
| PCB140 |  | 0.6707 | 11.30 | −0.0324 | −1.4222 | 129.77 | −3.59 | 0.5194 | −0.0324 |
| PCB141 | 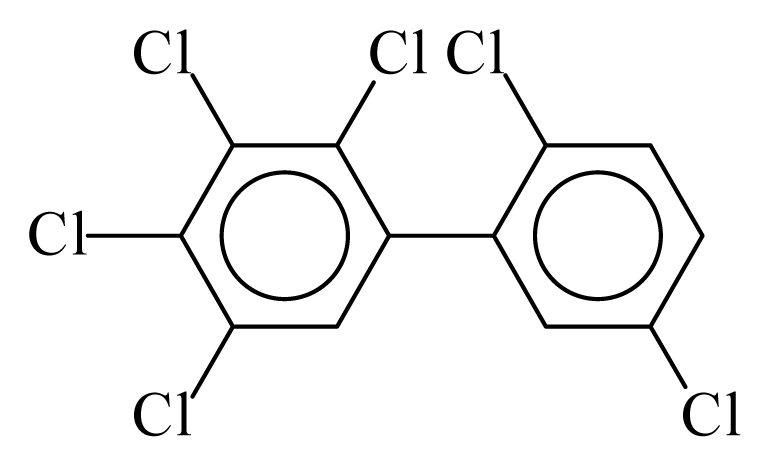 | 0.7200 | 12.11 | −0.0267 | −1.1744 | 130.59 | −3.66 | 0.4854 | −0.0267 |
| PCB142 | 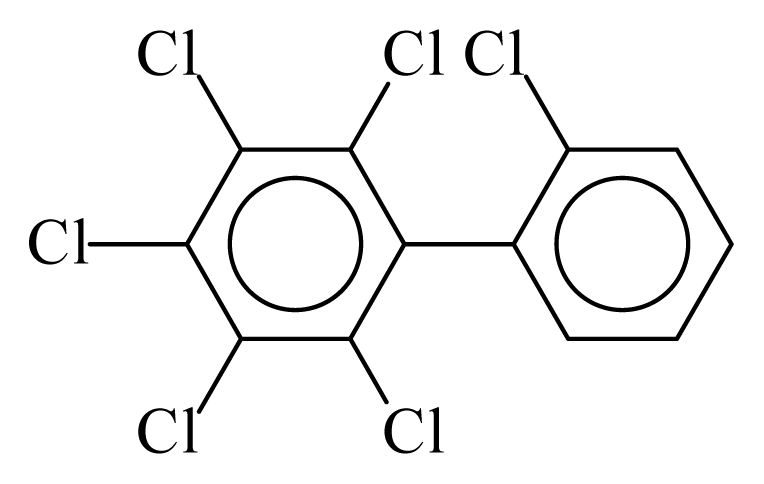 | 0.6848 | 11.60 | −0.0088 | −0.3869 | 129.80 | −3.61 | 0.4920 | −0.0088 |
| PCB143 | 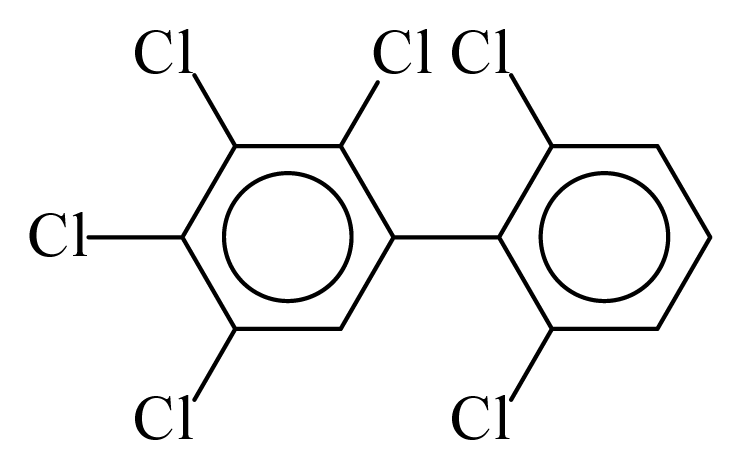 | 0.6789 | 12.57 | 0.0004 | 0.0168 | 130.50 | −3.74 | 0.4330 | 0.0004 |
| PCB144 | 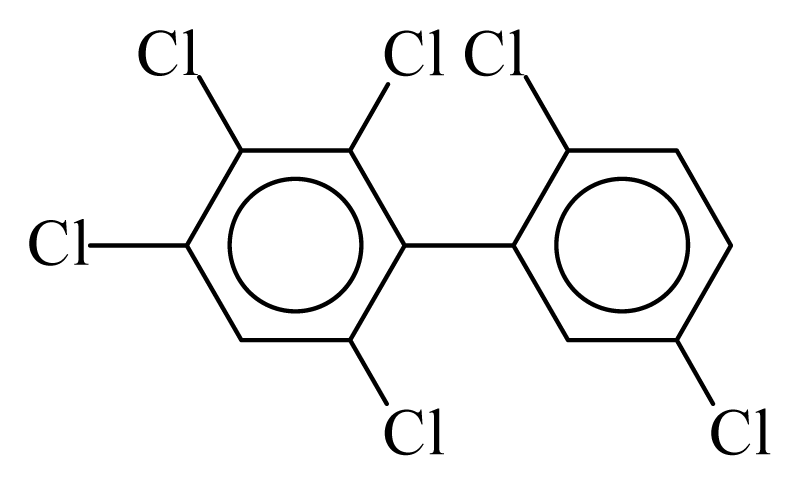 | 0.6563 | 13.43 | 0.0088 | 0.3881 | 128.67 | −3.82 | 0.4362 | 0.0088 |
| PCB145 | 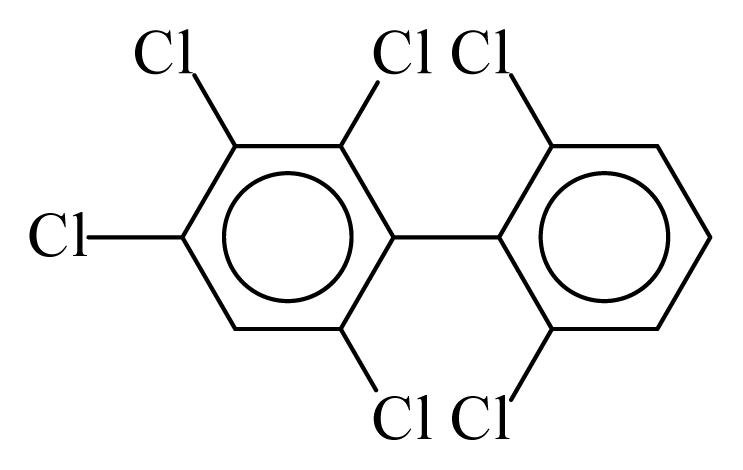 | 0.6149 | 12.87 | −0.0562 | −2.4723 | 128.32 | −3.76 | 0.5201 | −0.0562 |
| PCB146 |  | 0.6955 | 12.62 | −0.0098 | −0.4320 | 128.24 | −3.75 | 0.4749 | −0.0098 |
| PCB147 |  | 0.6608 | 14.04 | −0.0314 | −1.3821 | 126.70 | −3.90 | 0.4924 | −0.0314 |
| PCB148 |  | 0.6243 | 10.02 | −0.0122 | −0.5363 | 133.20 | −3.42 | 0.1119 | −0.0122 |
| PCB149 | 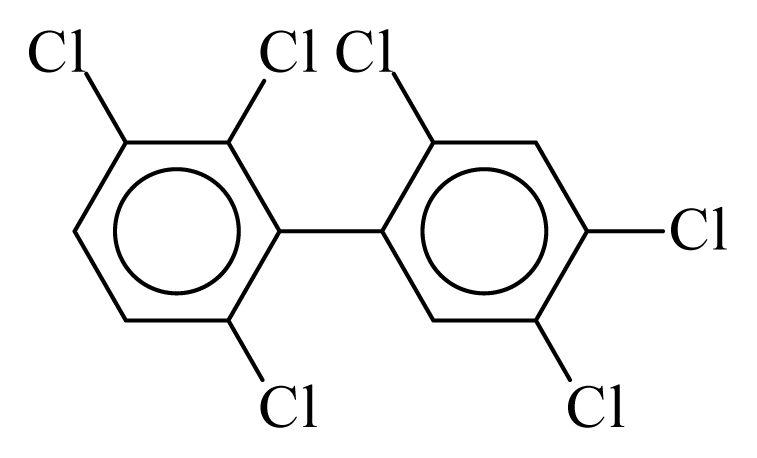 | 0.6672 | 10.60 | 0.0041 | 0.1800 | 134.27 | −3.47 | 0.1503 | 0.0041 |
| PCB150 | 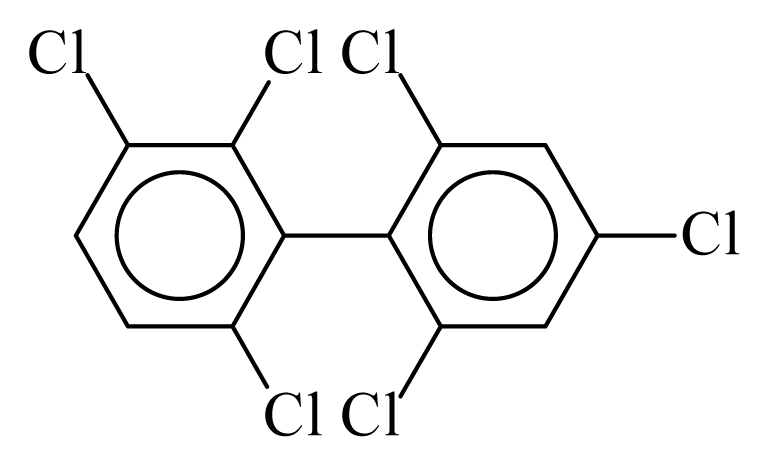 | 0.5969 | 9.96 | 0.0376 | 1.6541 | 135.23 | −3.40 | 0.1561 | 0.0376 |
| PCB151 |  | 0.6499 | 10.14 | 0.0054 | 0.2377 | 134.89 | −3.42 | 0.2191 | 0.0054 |
| PCB152 | 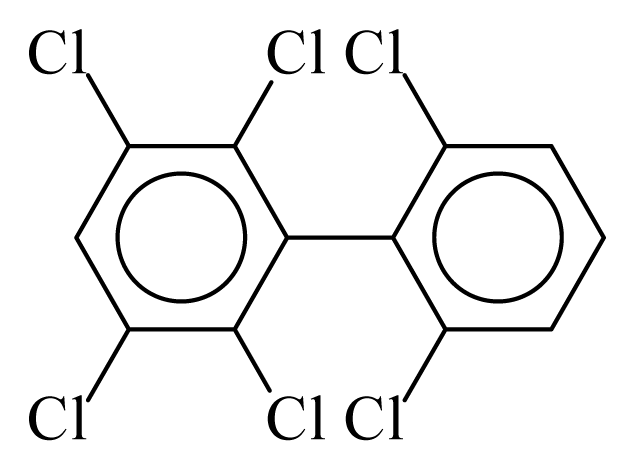 | 0.6062 | 9.75 | 0.0251 | 1.1035 | 133.36 | −3.41 | 0.2534 | 0.0251 |
| PCB153 | 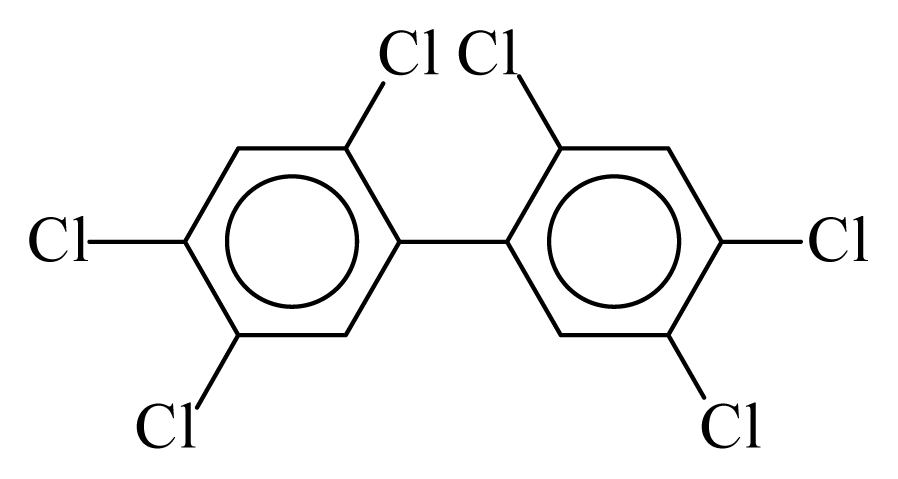 | 0.7036 | 10.15 | −0.0193 | −0.8496 | 136.72 | −3.38 | 0.2902 | −0.0193 |
| PCB154 |  | 0.6349 | 10.72 | 0.0028 | 0.1234 | 134.60 | −3.48 | 0.2538 | 0.0028 |
| PCB155 | 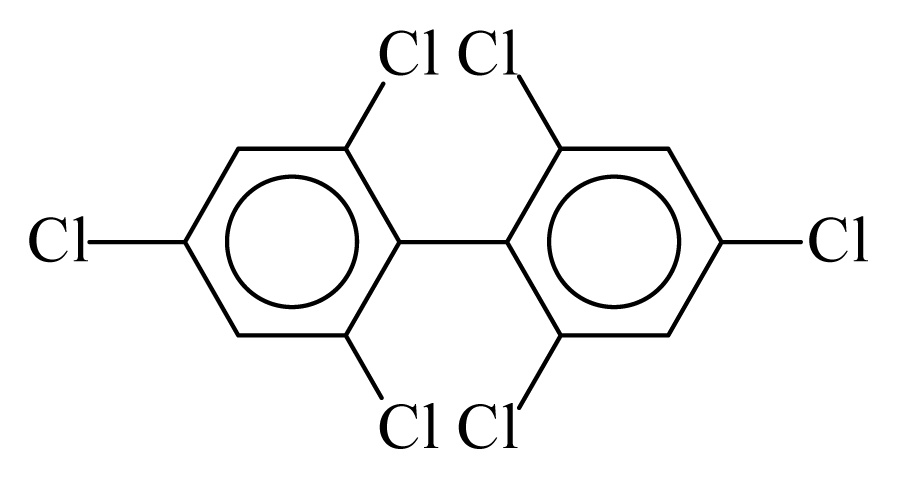 | 0.5666 | 10.27 | −0.0048 | −0.2094 | 133.35 | −3.43 | 0.2831 | −0.0048 |
| PCB156 |  | 0.8105 | 11.12 | 0.0348 | 1.5315 | 134.95 | −3.55 | 0.2222 | 0.0348 |
| PCB157 | 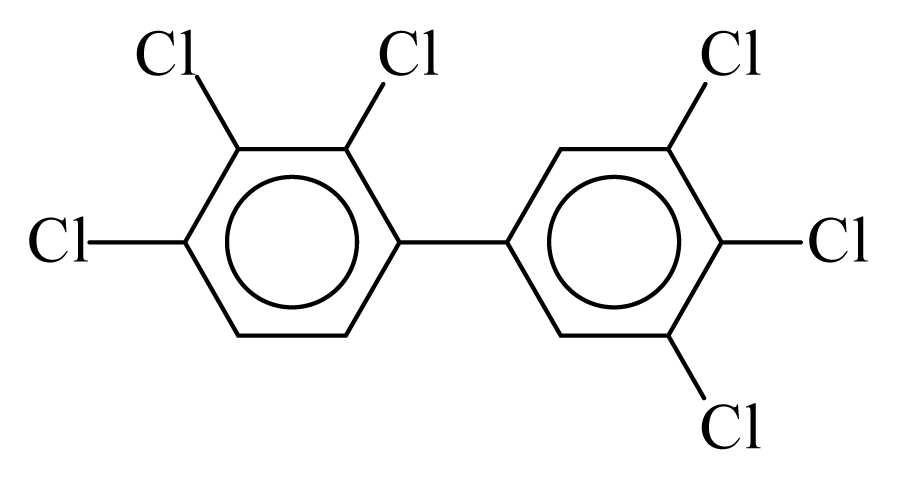 | 0.8184 | 11.75 | 0.0333 | 1.4623 | 133.57 | −3.57 | 0.1910 | 0.0333 |
| PCB158 |  | 0.7429 | 11.26 | 0.0168 | 0.7378 | 133.12 | −3.52 | 0.3070 | 0.0168 |
| PCB159 |  | 0.7655 | 11.52 | 0.0442 | 1.9425 | 132.24 | −3.57 | 0.2856 | 0.0442 |
| PCB160 | 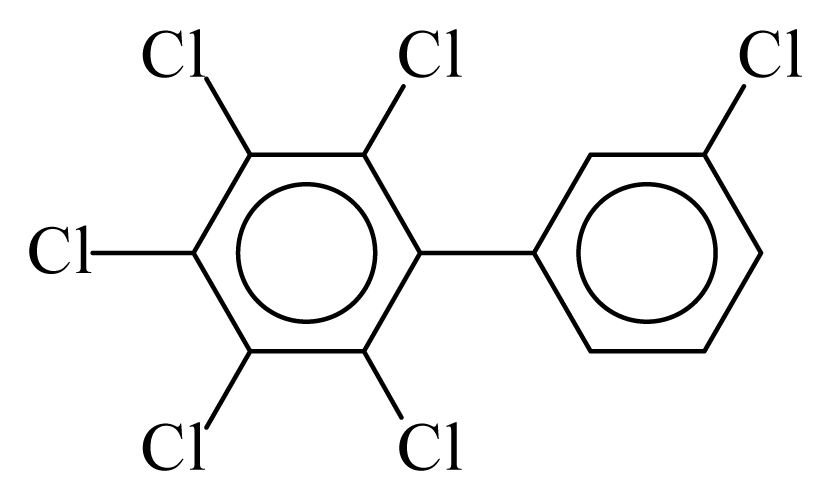 | 0.7396 | 11.09 | 0.0065 | 0.2857 | 134.24 | −3.49 | 0.3250 | 0.0065 |
| PCB161 | 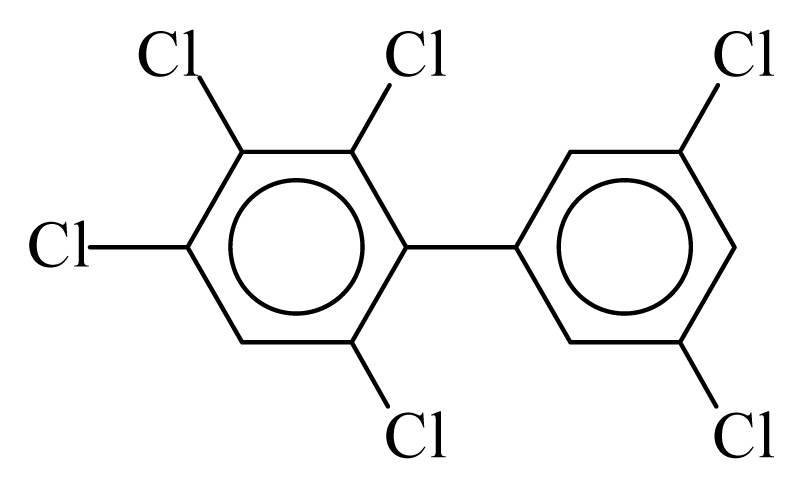 | 0.6968 | 10.98 | −0.0393 | −1.7268 | 133.10 | −3.50 | 0.2766 | −0.0393 |
| PCB162 | 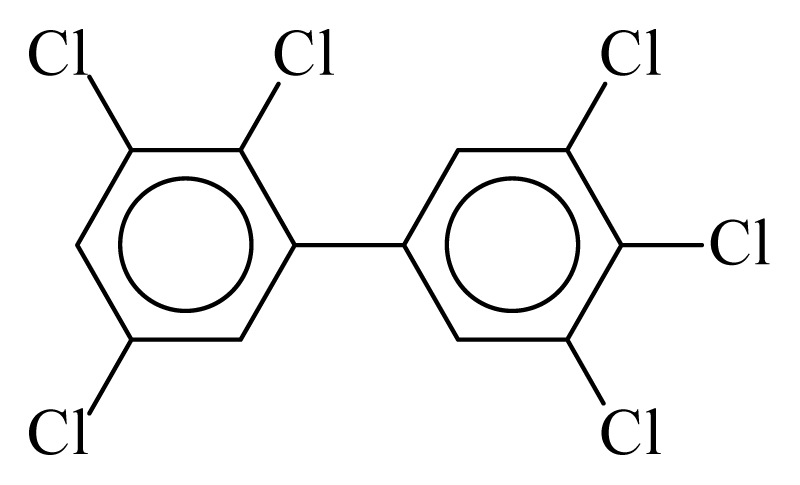 | 0.7737 | 10.98 | 0.0036 | 0.1567 | 131.58 | −3.51 | 0.3351 | 0.0036 |
| PCB163 | 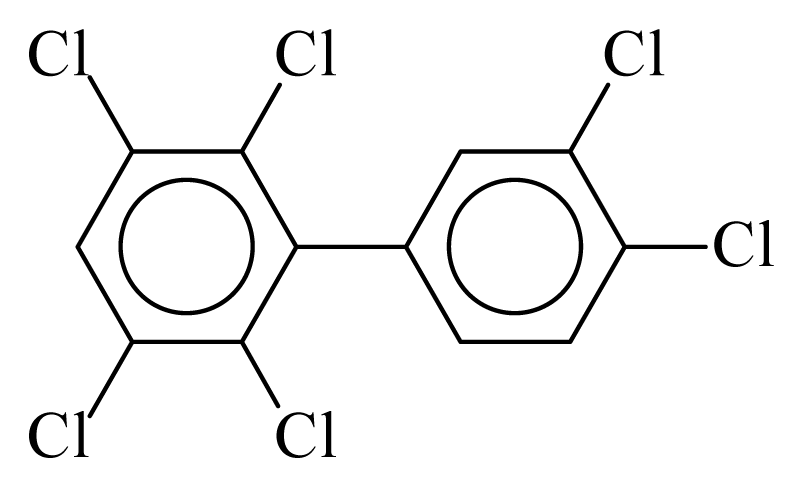 | 0.7396 | 10.45 | 0.0193 | 0.8481 | 132.74 | −3.45 | 0.3432 | 0.0193 |
| PCB164 |  | 0.7399 | 10.97 | −0.0184 | −0.8086 | 133.06 | −3.51 | 0.3582 | −0.0184 |
| PCB165 |  | 0.6920 | 10.72 | −0.0125 | −0.5510 | 131.64 | −3.50 | 0.3503 | −0.0125 |
| PCB166 | 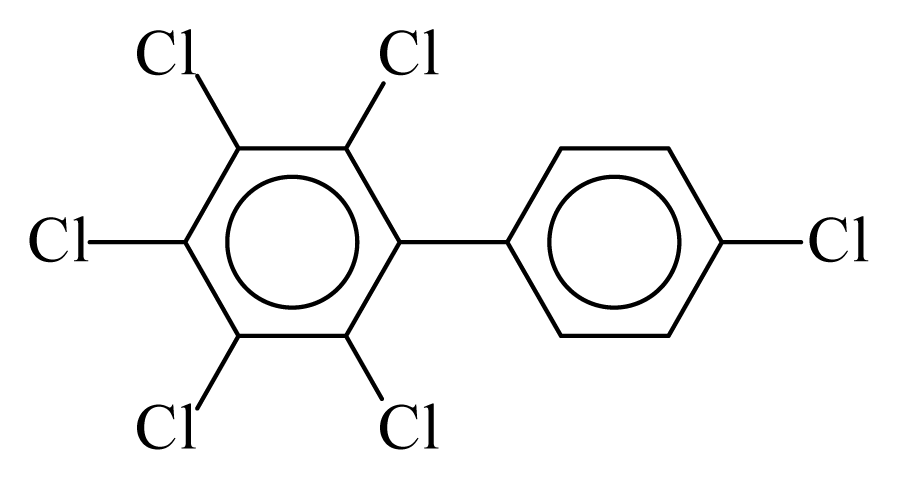 | 0.7572 | 10.16 | 0.0042 | 0.1849 | 132.62 | −3.44 | 0.3003 | 0.0042 |
| PCB167 |  | 0.7814 | 11.56 | 0.0015 | 0.0644 | 132.66 | −3.57 | 0.4155 | 0.0015 |
| PCB168 | 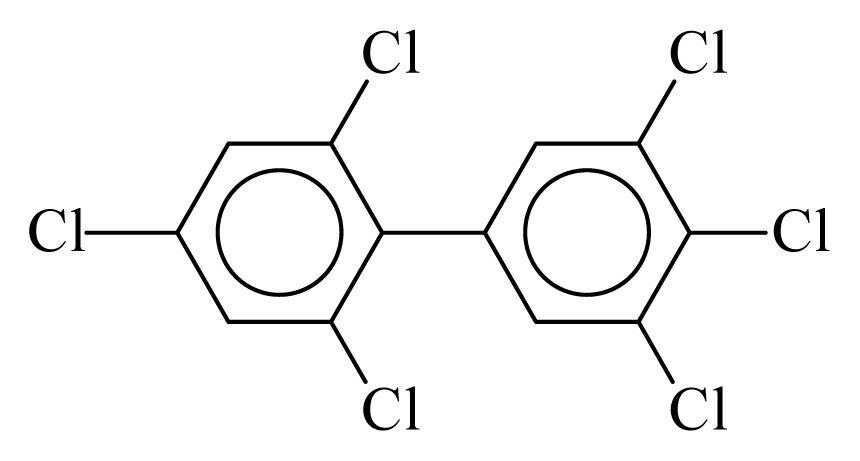 | 0.7068 | 11.09 | −0.0179 | −0.7855 | 133.32 | −3.50 | 0.4314 | −0.0179 |
| PCB169 | 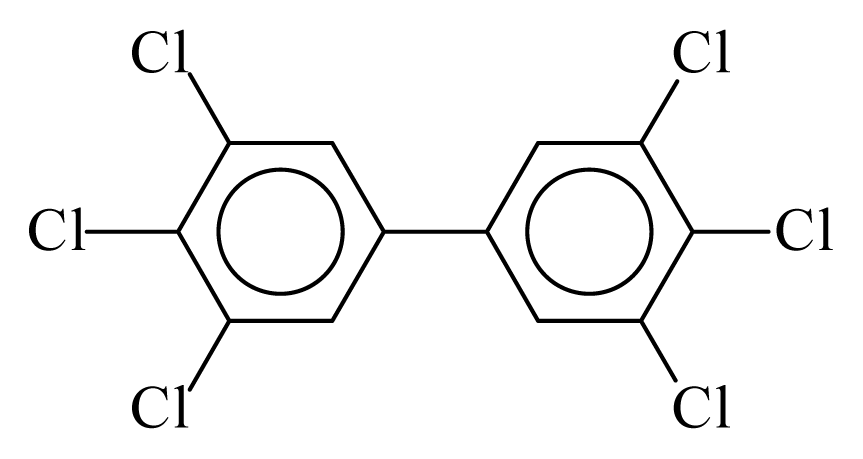 | 0.8625 | 11.05 | 0.0005 | 0.0212 | 131.66 | −3.52 | 0.4262 | 0.0005 |
| PCB170 | 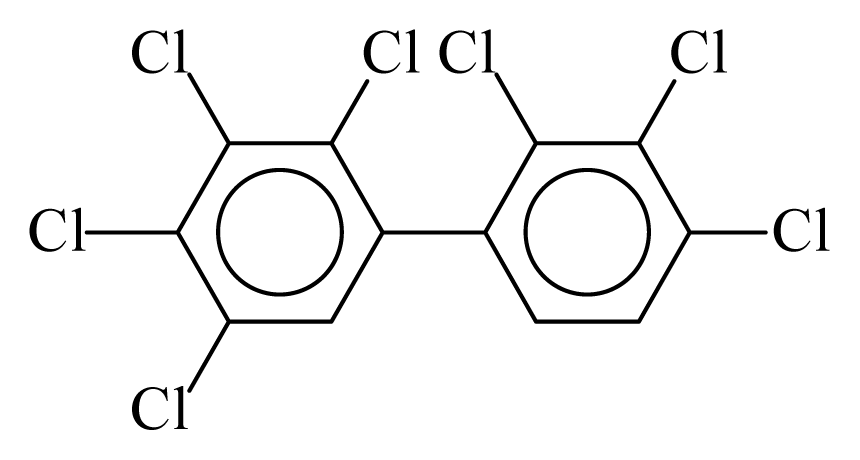 | 0.8740 | 11.05 | −0.0239 | −1.0517 | 132.19 | −3.51 | 0.4009 | −0.0239 |
| PCB171 | 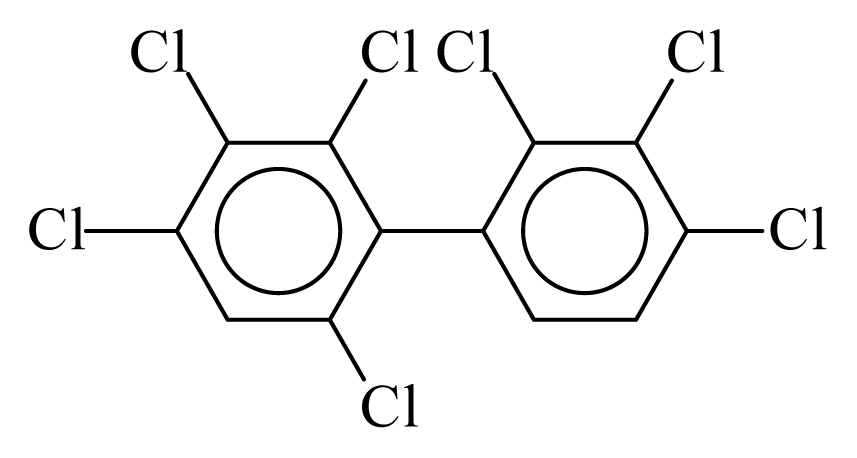 | 0.8089 | 10.52 | 0.0042 | 0.1838 | 131.49 | −3.46 | 0.3466 | 0.0042 |
| PCB172 | 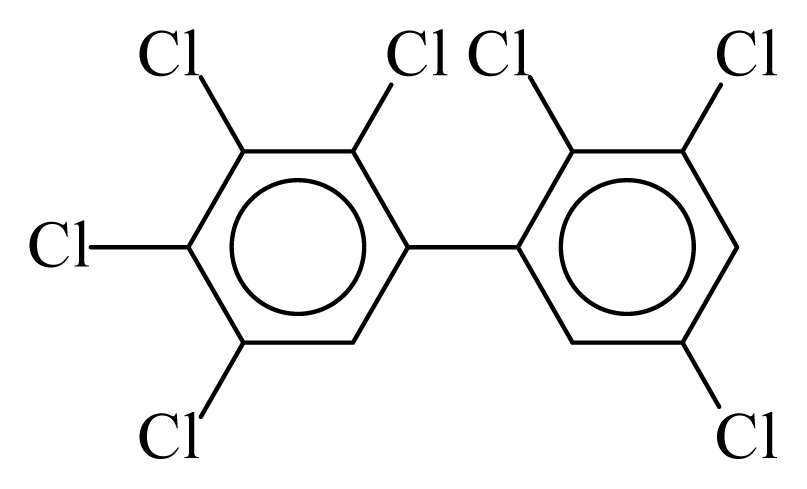 | 0.8278 | 10.80 | −0.0283 | −1.2445 | 133.28 | −3.48 | 0.4220 | −0.0283 |
| PCB173 | 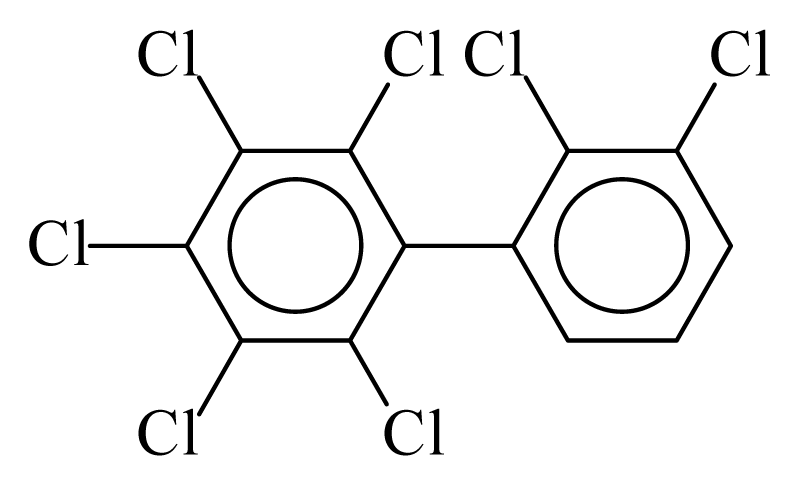 | 0.8152 | 10.24 | −0.0015 | −0.0653 | 133.94 | −3.42 | 0.3926 | −0.0015 |
| PCB174 | 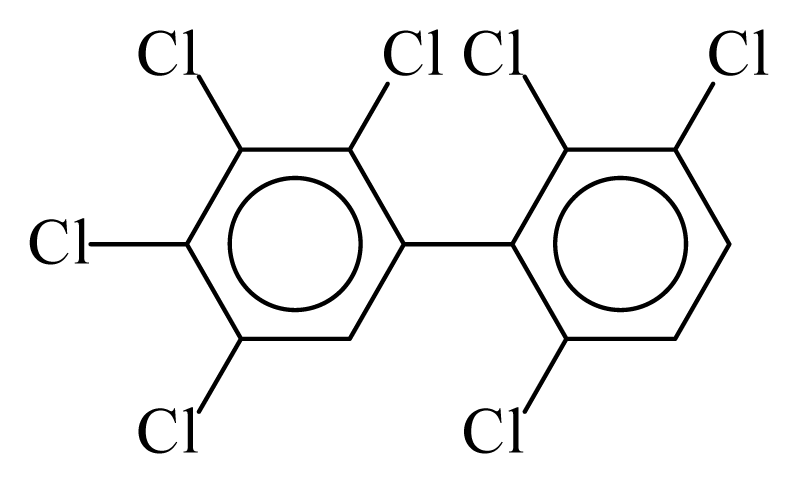 | 0.7965 | 10.75 | 0.0056 | 0.2482 | 132.13 | −3.50 | 0.3465 | 0.0056 |
| PCB175 |  | 0.7611 | 10.23 | −0.0294 | −1.2916 | 131.25 | −3.45 | 0.4325 | −0.0294 |
| PCB176 |  | 0.7305 | 12.03 | −0.0161 | −0.7060 | 132.78 | −3.65 | 0.3981 | −0.0161 |
| PCB177 |  | 0.8031 | 11.48 | −0.0323 | −1.4195 | 133.66 | −3.57 | 0.3488 | −0.0323 |
| PCB178 | 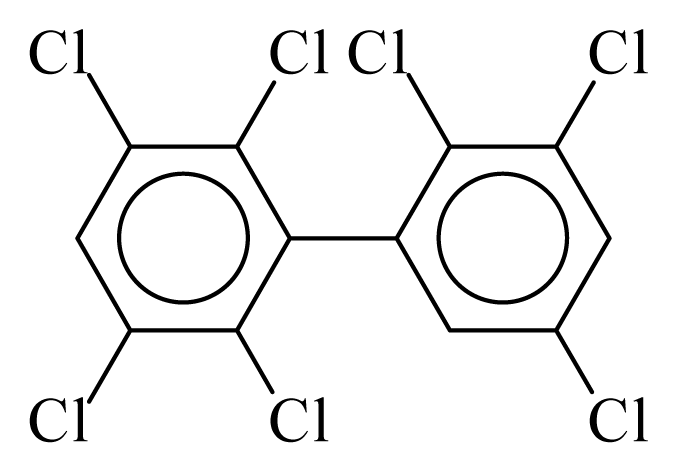 | 0.7537 | 11.55 | 0.0086 | 0.3793 | 132.00 | −3.60 | 0.4008 | 0.0086 |
| PCB179 |  | 0.7205 | 11.22 | 0.0089 | 0.3932 | 131.75 | −3.57 | 0.3547 | 0.0089 |
| PCB180 |  | 0.8362 | 11.25 | 0.0057 | 0.2490 | 132.12 | −3.58 | 0.4106 | 0.0057 |
| PCB181 | 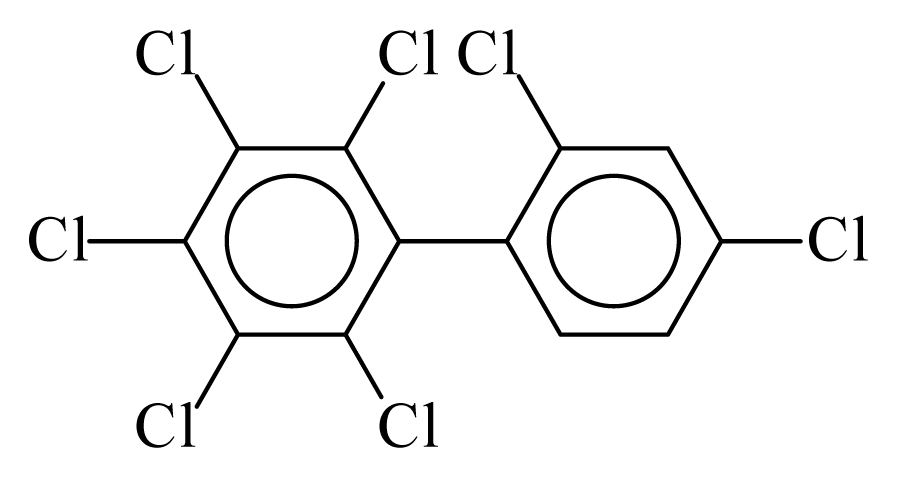 | 0.7968 | 12.89 | −0.0103 | −0.4521 | 130.80 | −3.73 | 0.3885 | −0.0103 |
| PCB182 | 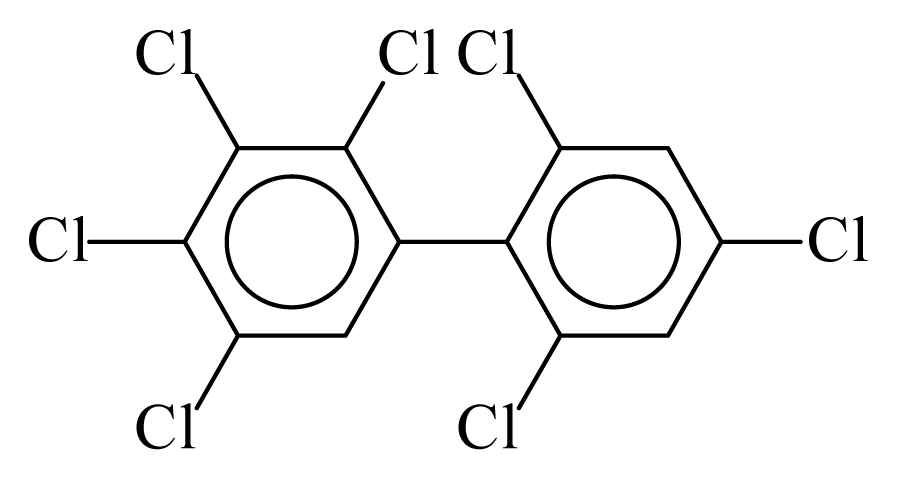 | 0.7653 | 12.32 | 0.0138 | 0.6063 | 131.52 | −3.67 | 0.4600 | 0.0138 |
| PCB183 |  | 0.7720 | 12.42 | 0.0027 | 0.1167 | 130.24 | −3.68 | 0.4348 | 0.0027 |
| PCB184 |  | 0.7016 | 11.87 | 0.0184 | 0.8096 | 129.97 | −3.61 | 0.4674 | 0.0184 |
| PCB185 | 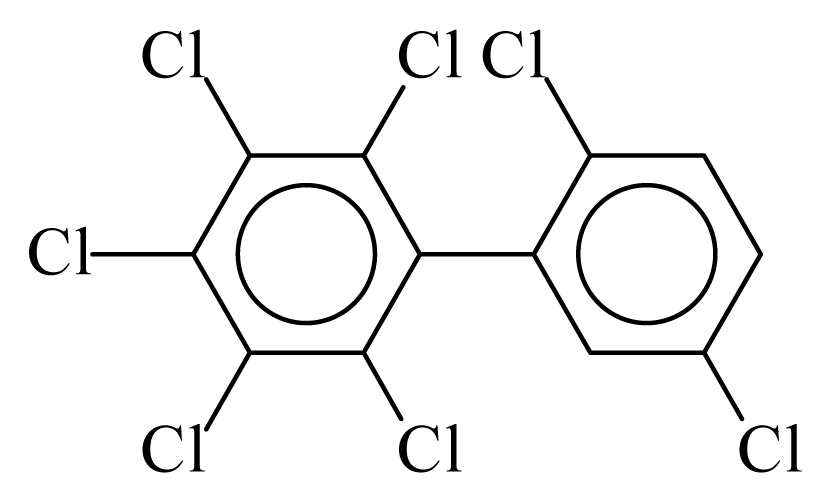 | 0.7848 | 12.09 | 0.0635 | 2.7897 | 130.07 | −3.66 | 0.4467 | 0.0635 |
| PCB186 | 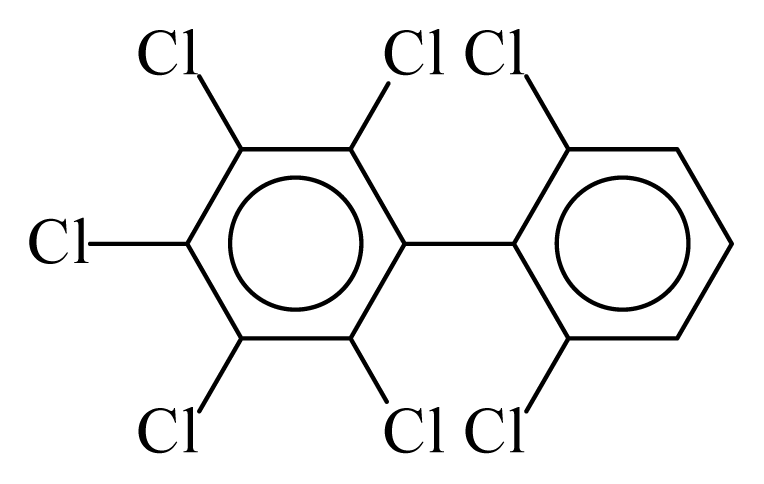 | 0.7416 | 11.53 | 0.0041 | 0.1782 | 131.14 | −3.59 | 0.4447 | 0.0041 |
| PCB187 | 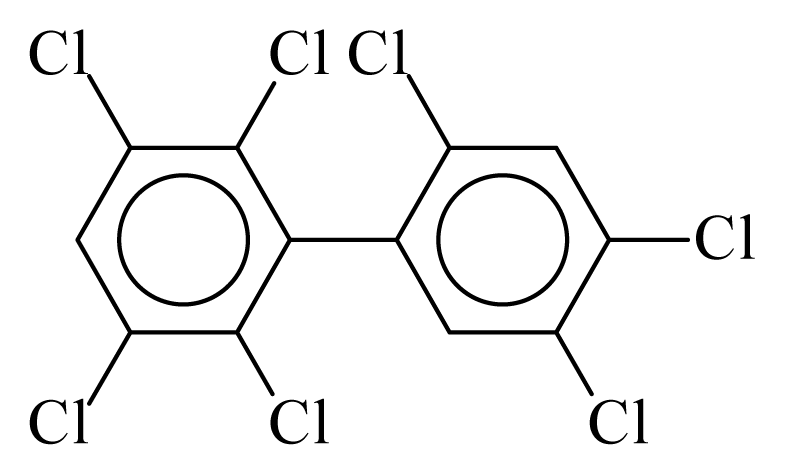 | 0.7654 | 11.58 | 0.0012 | 0.0545 | 129.81 | −3.60 | 0.5090 | 0.0012 |
| PCB188 |  | 0.6920 | 12.15 | −0.0127 | −0.5568 | 130.26 | −3.67 | 0.5117 | −0.0127 |
| PCB189 | 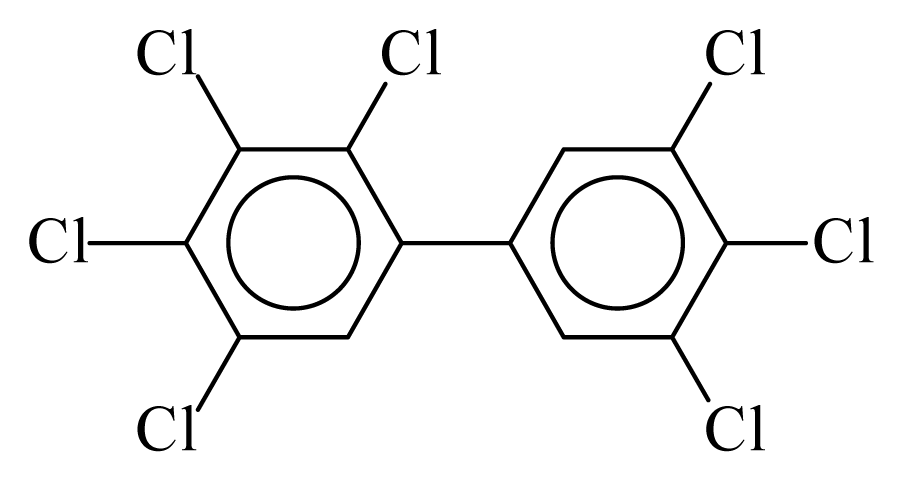 | 0.9142 | 11.30 | −0.0324 | −1.4222 | 129.77 | −3.59 | 0.5194 | −0.0324 |
| PCB190 |  | 0.8740 | 12.11 | −0.0267 | −1.1744 | 130.59 | −3.66 | 0.4854 | −0.0267 |
| PCB191 | 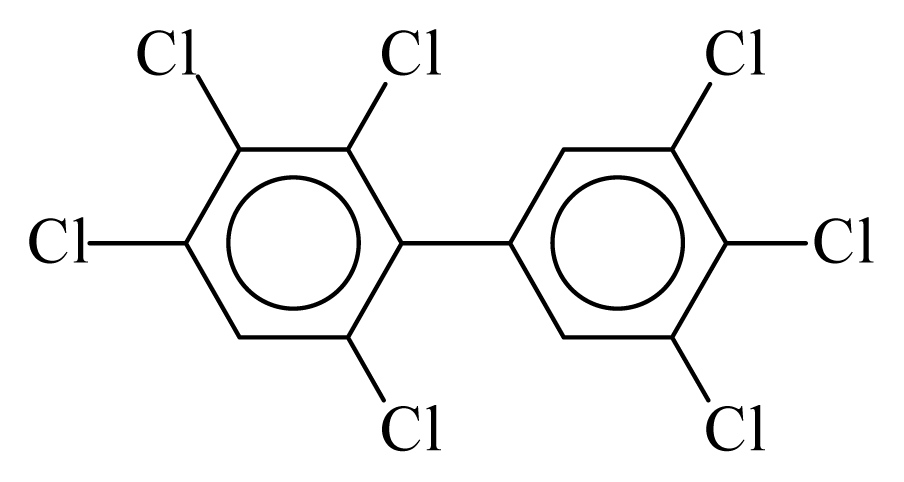 | 0.8447 | 11.60 | −0.0088 | −0.3869 | 129.80 | −3.61 | 0.4920 | −0.0088 |
| PCB192 |  | 0.8269 | 12.57 | 0.0004 | 0.0168 | 130.50 | −3.74 | 0.4330 | 0.0004 |
| PCB193 | 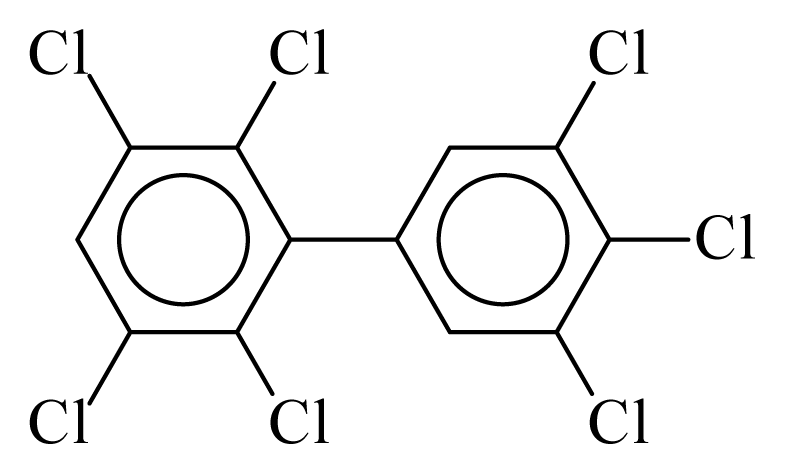 | 0.8397 | 13.43 | 0.0088 | 0.3881 | 128.67 | −3.82 | 0.4362 | 0.0088 |
| PCB194 | 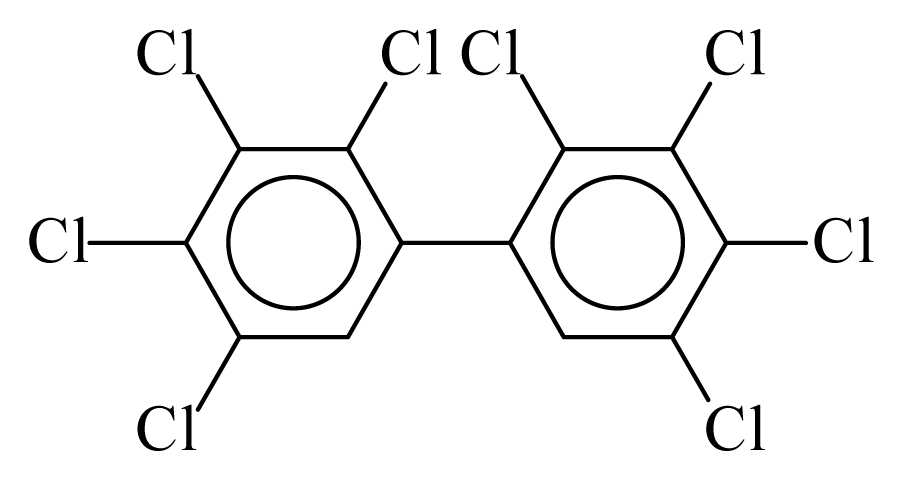 | 0.9620 | 12.87 | −0.0562 | −2.4723 | 128.32 | −3.76 | 0.5201 | −0.0562 |
| PCB195 | 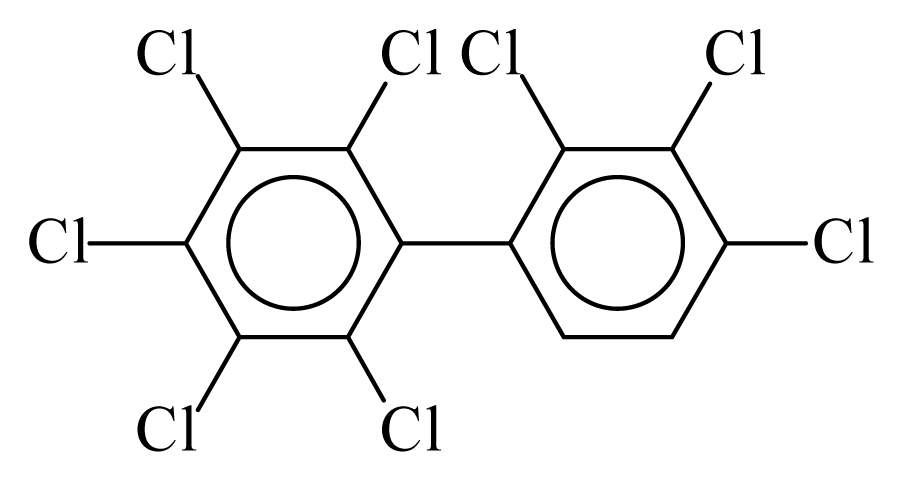 | 0.9321 | 12.62 | −0.0098 | −0.4320 | 128.24 | −3.75 | 0.4749 | −0.0098 |
| PCB196 | 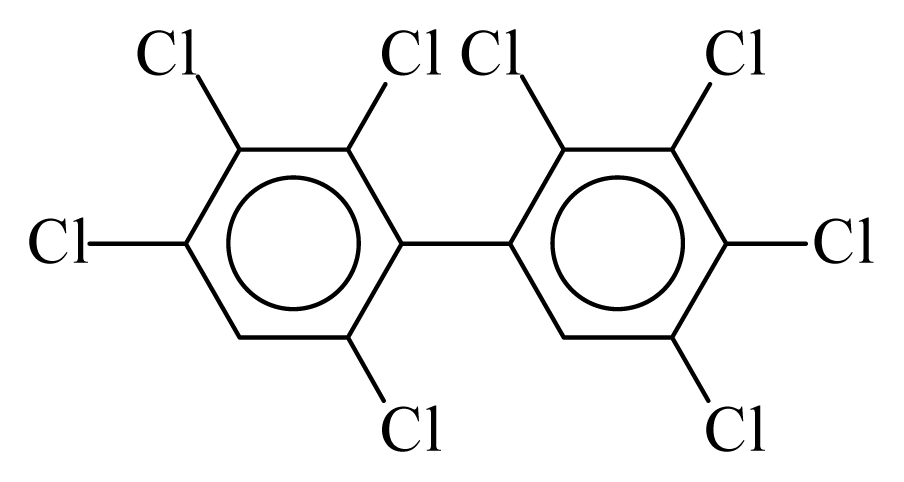 | 0.8938 | 14.04 | −0.0314 | −1.3821 | 126.70 | −3.90 | 0.4924 | −0.0314 |
| PCB197 | 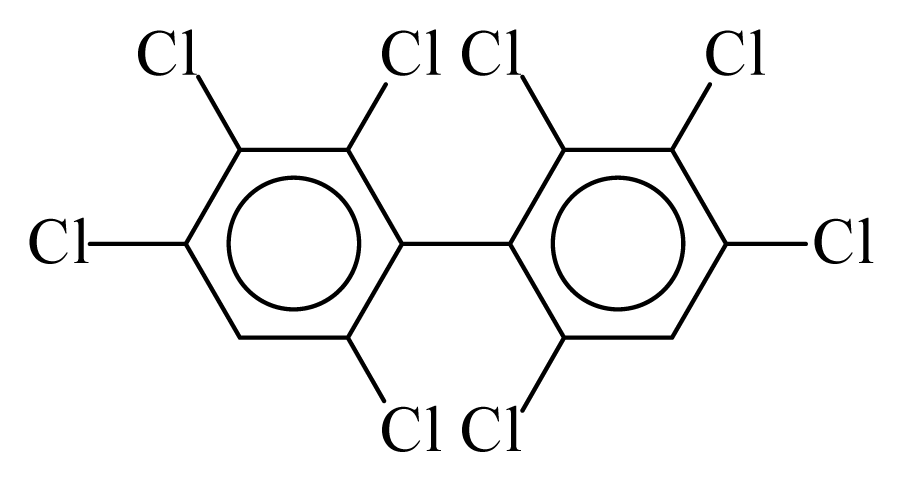 | 0.8293 | 10.02 | −0.0122 | −0.5363 | 133.20 | −3.42 | 0.1119 | −0.0122 |
| PCB198 |  | 0.8845 | 10.60 | 0.0041 | 0.1800 | 134.27 | −3.47 | 0.1503 | 0.0041 |
| PCB199 | 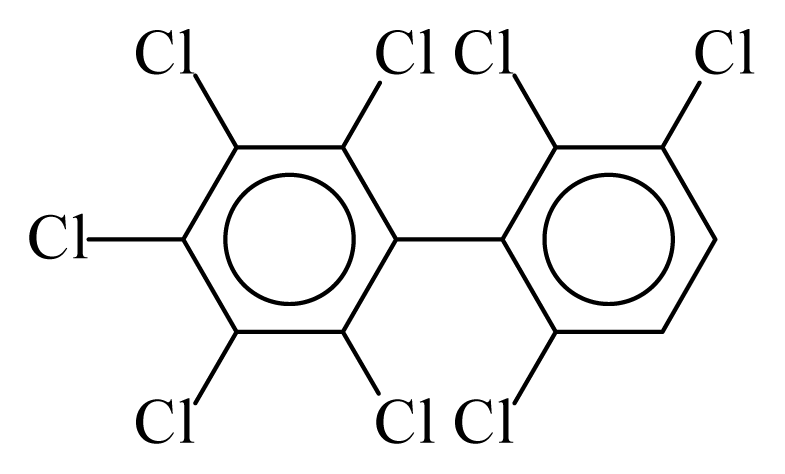 | 0.8494 | 9.96 | 0.0376 | 1.6541 | 135.23 | −3.40 | 0.1561 | 0.0376 |
| PCB200 | 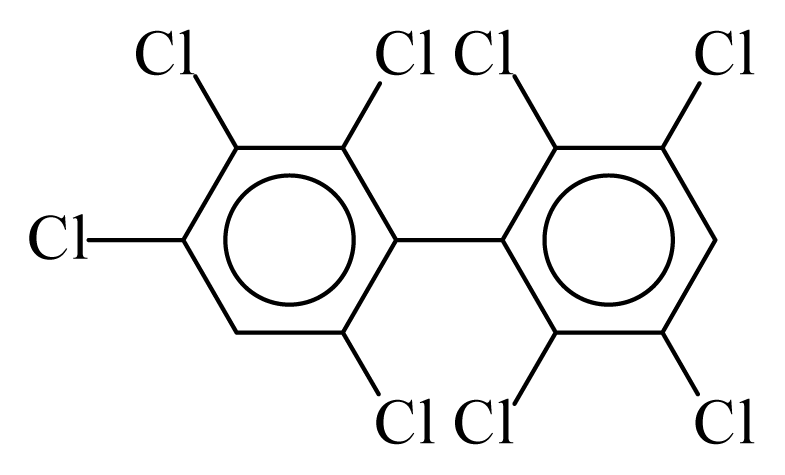 | 0.8197 | 10.14 | 0.0054 | 0.2377 | 134.89 | −3.42 | 0.2191 | 0.0054 |
| PCB201 | 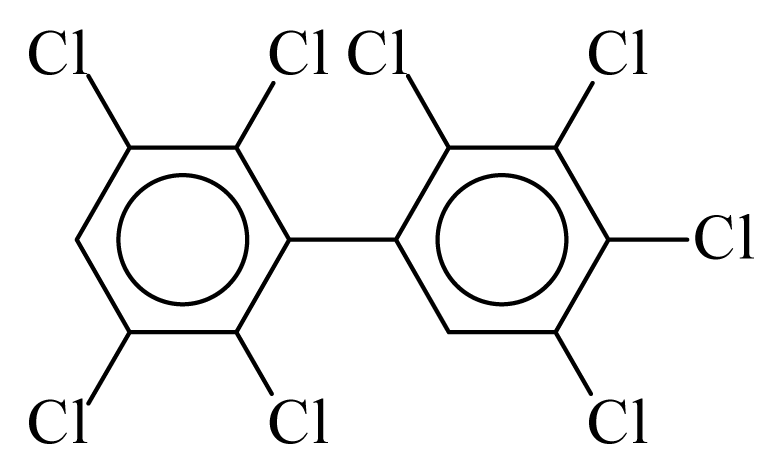 | 0.8875 | 9.75 | 0.0251 | 1.1035 | 133.36 | −3.41 | 0.2534 | 0.0251 |
| PCB202 |  | 0.8089 | 10.15 | −0.0193 | −0.8496 | 136.72 | −3.38 | 0.2902 | −0.0193 |
| PCB203 | 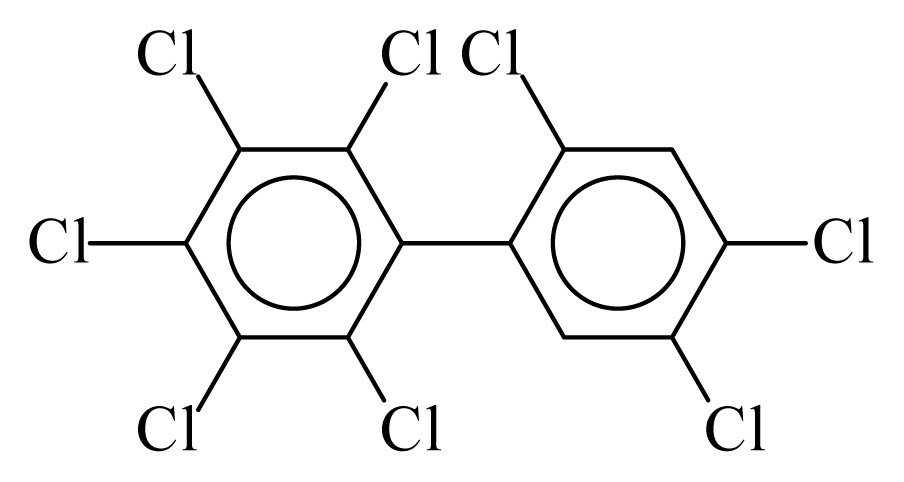 | 0.8938 | 10.72 | 0.0028 | 0.1234 | 134.60 | −3.48 | 0.2538 | 0.0028 |
| PCB204 |  | 0.8217 | 10.27 | −0.0048 | −0.2094 | 133.35 | −3.43 | 0.2831 | −0.0048 |
| PCB205 | 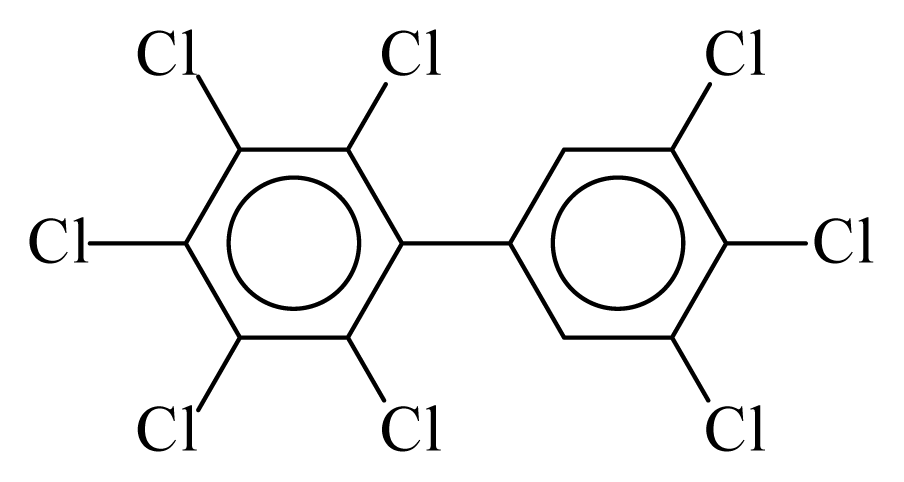 | 0.9678 | 11.12 | 0.0348 | 1.5315 | 134.95 | −3.55 | 0.2222 | 0.0348 |
| PCB206 | 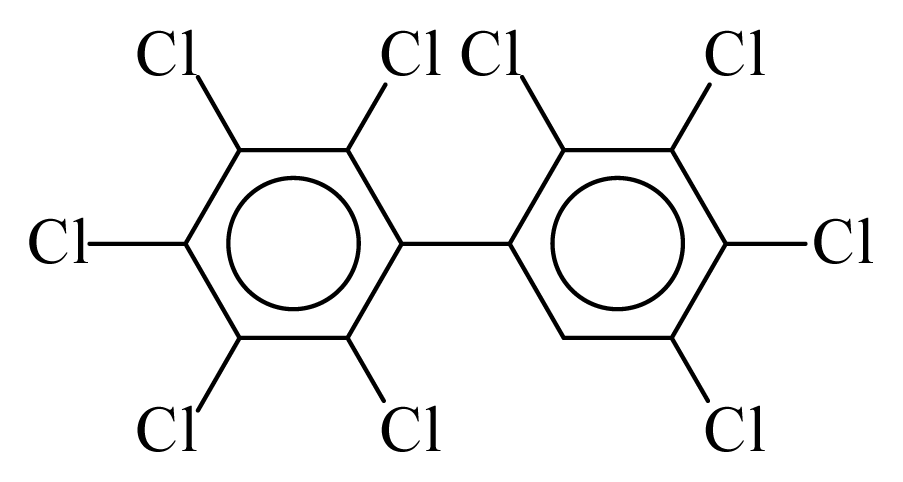 | 1.0103 | 11.75 | 0.0333 | 1.4623 | 133.57 | −3.57 | 0.1910 | 0.0333 |
| PCB207 | 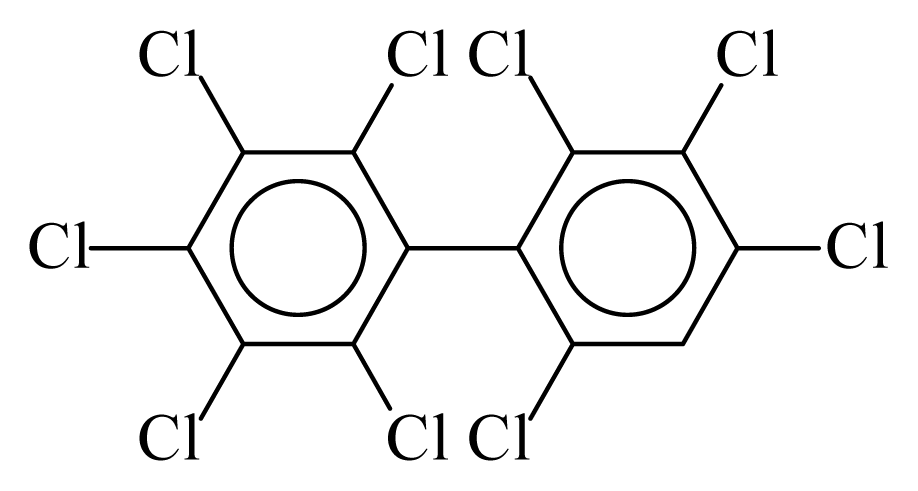 | 0.9423 | 11.26 | 0.0168 | 0.7378 | 133.12 | −3.52 | 0.3070 | 0.0168 |
| PCB208 |  | 0.9320 | 11.52 | 0.0442 | 1.9425 | 132.24 | −3.57 | 0.2856 | 0.0442 |
| PCB209 |  | 1.0496 | 11.09 | 0.0065 | 0.2857 | 134.24 | −3.49 | 0.3250 | 0.0065 |
| Training set | Test set | |||||||
|---|---|---|---|---|---|---|---|---|
| No PCBs | Coefficients | Statistics | No PCBs | Statistics | ||||
| Intercept | ISDmsHt | lADrtHg | R2 | F | Q2 | F | ||
| 9 | −6.06 | 0.0243 | −1.0294 | 0.999 | 2640† | 200 | 0.997 | 32807† |
| 19 | −6.18 | 0.0248 | −1.0442 | 0.998 | 4827† | 190 | 0.997 | 28567† |
| 29 | −5.94 | 0.0237 | −1.0195 | 0.996 | 3342† | 180 | 0.997 | 32047† |
| 39 | −5.80 | 0.0230 | −1.0040 | 0.998 | 8406† | 170 | 0.997 | 27678† |
| 49 | −5.89 | 0.0234 | −1.0172 | 0.998 | 9608† | 160 | 0.997 | 25667† |
| 59 | −6.30 | 0.0257 | −1.0448 | 0.996 | 6924† | 150 | 0.998 | 27578† |
| 69 | −6.21 | 0.0251 | −1.0440 | 0.996 | 7641† | 140 | 0.998 | 29667† |
| 79 | −5.95 | 0.0238 | −1.0170 | 0.996 | 9186† | 130 | 0.998 | 29915† |
| 89 | −6.12 | 0.0246 | −1.0348 | 0.997 | 16315† | 120 | 0.997 | 19049† |
| 99 | −6.06 | 0.0244 | −1.0278 | 0.997 | 15763† | 110 | 0.997 | 20314† |
| 109 | −6.07 | 0.0244 | −1.0304 | 0.996 | 13489† | 100 | 0.998 | 26764† |
| 119 | −6.10 | 0.0245 | −1.0361 | 0.997 | 19333† | 90 | 0.997 | 14990† |
| 129 | −6.07 | 0.0245 | −1.0284 | 0.997 | 19823† | 80 | 0.998 | 17306† |
| 139 | −5.98 | 0.0240 | −1.0219 | 0.997 | 21316† | 70 | 0.997 | 11610† |
| 149 | −6.07 | 0.0244 | −1.0297 | 0.997 | 25972† | 60 | 0.997 | 10077† |
| 159 | −6.03 | 0.0241 | −1.0287 | 0.997 | 31071† | 50 | 0.997 | 5692† |
| 169 | −6.03 | 0.0242 | −1.0258 | 0.997 | 25723† | 40 | 0.998 | 12671† |
| 179 | −5.97 | 0.0239 | −1.0203 | 0.997 | 30942† | 30 | 0.997 | 4938† |
| 189 | −6.02 | 0.0242 | −1.0247 | 0.997 | 31570† | 20 | 0.998 | 3383† |
| 199 | −6.01 | 0.0241 | −1.0243 | 0.997 | 34566† | 10 | 0.998 | 1450† |
Acknowledgements
References
- National Research Council (U.S.), Committee on the Assessment of Polychlorinated Biphenyls in the Environment. In Polychlorinated biphenyls: a report; National Academy of Sciences: Washington, 1979.
- Angulo Lucena, R.; Farouk Allam, M.; Serrano Jiménez, S.; Luisa, Jodral; Villarejo, M. A review of environmental exposure to persistent organochlorine residuals during the last fifty years. Curr. Drug Safety 2007, 2(2), 163–172. [Google Scholar]
- Roveda, A. M.; Veronesi, L.; Zoni, R.; Colucci, M. E.; Sansebastiano, G. Exposure to polychlorinated biphenyls (PCBs) in food and cancer risk: recent advances. Igiene e sanità pubblica 2006, 62(6), 677–696. [Google Scholar]
- Lundqvist, C.; Zuurbier, M.; Leijs, M.; Johansson, C.; Ceccatelli, S.; Saunders, M.; Schoeters, G.; Ten Tusscher, G.; Koppe, J. G. The effects of PCBs and dioxins on child health. Acta. Paediatr 2006, 95(453), 55–64. [Google Scholar]
- Poppenga, R. H. Current environmental threats to animal health and productivity. Vet. Clin. N. Am.-Food A 2000, 16(3), 545–558. [Google Scholar]
- Bren, U.; Zupan, M.; Guengerich, F. P.; Mavri, J. Chemical Reactivity as a Tool to Study Carcinogenicity: Reaction between Chloroethylene Oxide and Guanine. J. Org. Chem 2006, 71(11), 4078–4084. [Google Scholar]
- Lebeuf, M.; Noël, M.; Trottier, S.; Measures, L. Temporal trends (1987–2002) of persistent, bioaccumulative and toxic (PBT) chemicals in beluga whales (Delphinapterus leucas) from the St. Lawrence Estuary, Canada. Sci. Total Environ 2007, 383(1–3), 216–231. [Google Scholar]
- Tan, J.; Cheng, S. M.; Loganath, A.; Chong, Y. S.; Obbard, J. P. Selected organochlorine pesticide and polychlorinated biphenyl residues in house dust in Singapore. Chemosphere 2007, 68(9), 1675–1682. [Google Scholar]
- Borrell, A.; Cantos, G.; Aguilar, A.; Androukaki, E.; Dendrinos, P. Concentrations and patterns of organochlorine pesticides and PCBs in Mediterranean monk seals (Monachus monachus) from Western Sahara and Greece. Sci. Total Environ 2007, 381(1–3), 316–325. [Google Scholar]
- Klánová, J.; Kohoutek, J.; Kostrhounová, R.; Holoubek, I. Are the residents of former Yugoslavia still exposed to elevated PCB levels due to the Balkan wars?. Part 1: air sampling in Croatia, Serbia, Bosnia and Herzegovina. Environ. Int 2007, 33(6), 719–726. [Google Scholar]
- Hansch, C. Quantitative approach to biochemical structure-activity relationships. Acc. Chem. Res 1969, 2(8), 232–239. [Google Scholar]
- Hansch, C.; Leo, A. Substituent Constants for Correlation Analysis in Chemistry and Biology; John Wiley & Sons: New York, 1979. [Google Scholar]
- Castro, E. A.; Toropov, A. A.; Nesterova, A.I.; Nabiev, O. M. QSPR modeling aqueous solubility of polychlorinated biphenyls by optimization of correlation weights of local and global graph invariants. Central European Journal of Chemistry 2004, 2(3), 500–523. [Google Scholar]
- Wei, B.; Xie, S.; Yu, M.; Wu, L. QSPR-based prediction of gas/particle partitioning of polychlorinated biphenyls in the atmosphere. Chemosphere 2007, 66(10), 1807–1820. [Google Scholar]
- Niu, J. F.; Yang, Z. F.; Shen, Z. Y.; Wang, L. L. QSPRs for the prediction of photodegradation half-life of PCBs in n-hexane. SAR QSAR Environ. Res 2006, 17(2), 173–182. [Google Scholar]
- Padmanabhan, J.; Parthasarathi, R.; Subramanian, V.; Chattaraj, P. K. QSPR models for polychlorinated biphenyls: n-Octanol/water partition coefficient. Bioorg. Med. Chem. Lett 2006, 14(4), 1021–1028. [Google Scholar]
- Jäntschi, L.; Bolboacă, S. Molecular Descriptors Family on Structure Activity Relationships 6. Octanol-Water Partition Coefficient of Polychlorinated Biphenyls. Leonardo El. J. Pract. Technol 2006, 8, 71–86. [Google Scholar]
- Puri, S.; Chickos, J. S.; Welsh, W. J. Three-dimensional quantitative structure - Property relationship (3D-QSPR) models for prediction of thermodynamic properties of polychlorinated biphenyls (PCBs): Enthalpy of vaporization. J. Chem. Inf. Comp. Sci 2002, 42(2), 299–304. [Google Scholar]
- Padmanabhan, J.; Parthasarathi, R.; Subramanian, V.; Chattaraj, P. K. Using QSPR models to predict the enthalpy of vaporization of 209 polychlorinated biphenyl congeners. QSAR Comb. Sci 2007, 26(2), 227–237. [Google Scholar]
- Puri, S.; Chickos, J. S.; Welsh, W. J. Three-dimensional quantitative structure - Property relationship (3D-QSPR) models for prediction of thermodynamic properties of polychlorinated biphenyls (PCBs): Enthalpy of sublimation. J. Chem. Inf. Comp. Sci 2002, 42(1), 109–116. [Google Scholar]
- Devillers, J. A simple method for the prediction of the GLC retention times of all the 209 PCB congeners. Fresenius Z. Anal. Chem 1988, 332(1), 61–62. [Google Scholar]
- Hasan, M.N.; Jurs, P.C. Computer-assisted prediction of gas chromatographic retention times of polychlorinated biphenyls. Anal. Chem 1988, 60(10), 978–982. [Google Scholar]
- Makino, M. Novel classification to predict relative gas chromatographic retention times and noctanol/water partition coefficients of polychlorinated biphenyls. Chemosphere 1999, 39(6), 893–903. [Google Scholar]
- Liu, S.-S.; Liu, Y.; Yin, D.-Q.; Wang, X.-D.; Wang, L.-S. Prediction of chromatographic relative retention time of polychlorinated biphenyls from the molecular electronegativity distance vector. J. Sep. Sci 2006, 29(2), 296–301. [Google Scholar]
- Ren, Y.; Liu, H.; Yao, X.; Liu, M. An accurate QSRR model for the prediction of the GC×GCTOFMS retention time of polychlorinated biphenyl (PCB) congeners. Anal. Bioanal. Chem 2007, 388(1), 165–172. [Google Scholar]
- Jäntschi, L.; Katona, G.; Diudea, M. Modeling Molecular Properties by Cluj Indices. MATCH Commun. Math. Comput. Chem 2000, 41, 151–188. [Google Scholar]
- Jäntschi, L. MDF - A New QSPR/QSAR Molecular Descriptors Family. Leonardo J. Sci 2004, 4, 68–85. [Google Scholar]
- Jäntschi, L. Molecular Descriptors Family on Structure Activity Relationships 1. Review of the Methodology. Leonardo El. J. Pract. Technol 2005, 6, 76–98. [Google Scholar]
- Jäntschi, L.; Bolboacă, S. Results from the Use of Molecular Descriptors Family on Structure Property/Activity Relationships. Int. J. Mol. Sci 2007, 8(3), 189–203. [Google Scholar]
- Mullin, M. D.; Pochini, C. M.; McCrindle, S.; Romkes, M.; Safe, S. H.; Safe, L. M. High resolution PCB analysis: synthesis and chromatographic properties of all 209 PCB congeners. Environ. Sci. Technol 1984, 18, 468–476. [Google Scholar]
- HyperChem, Molecular Modelling System; [software]; ©2003. Hypercube. [cited 2007 June]. Available from: URL: http://hyper.com/products/.
- Chambers, D.L. The practical handbook of genetic algorithms; Chapman & Hall: Boca Raton, 2001. [Google Scholar]
- The PHP Group. [online]; ©2001–2007. The PHP Group. [cited 2007 June]. Available from: URL: http://php.net.
- MySQL AB. [online]; ©1995–2007. MySQL AB. [cited 2007 June]. Available from: URL: http://mysql.com.
- The FreeBSD Project. [online]; ©1995–2007. The FreeBSD Project. [cited 2007 June]. Available from: URL: http://freebsd.org.
- Borland Software Corporation. [online]; ©1994–2007. Borland Software Corporation. [cited 2007 June]. Available from: URL: http://borland.com.
© 2007 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Jäntschi, L.; Bolboaca, S.D.; Diudea, M.V. Chromatographic Retention Times of Polychlorinated Biphenyls: from Structural Information to Property Characterization. Int. J. Mol. Sci. 2007, 8, 1125-1157. https://doi.org/10.3390/i8111125
Jäntschi L, Bolboaca SD, Diudea MV. Chromatographic Retention Times of Polychlorinated Biphenyls: from Structural Information to Property Characterization. International Journal of Molecular Sciences. 2007; 8(11):1125-1157. https://doi.org/10.3390/i8111125
Chicago/Turabian StyleJäntschi, Lorentz, Sorana D. Bolboaca, and Mircea V. Diudea. 2007. "Chromatographic Retention Times of Polychlorinated Biphenyls: from Structural Information to Property Characterization" International Journal of Molecular Sciences 8, no. 11: 1125-1157. https://doi.org/10.3390/i8111125
APA StyleJäntschi, L., Bolboaca, S. D., & Diudea, M. V. (2007). Chromatographic Retention Times of Polychlorinated Biphenyls: from Structural Information to Property Characterization. International Journal of Molecular Sciences, 8(11), 1125-1157. https://doi.org/10.3390/i8111125







