QSAR of Some N1-Aryl/Heteroarylaminomethyl/ethyl-1,2,4-Triazoles Part II: Antimicrobial Activity Against BacillusSubtilis

Vesna Dimova; Katica Colanceska Ragenovic; Vladimir Kakurinov

doi:10.3390/i7040119

,

and

¹

Faculty of Technology and Metallurgy, The “Sv. Kiril & Metodij” University, Ruger Boskovic 16, 1000 Skopje, Macedonia

²

Faculty of Agriculture, Department of Microbiology, The “Sv. Kiril & Metodij” University, bul. Aleksandar Makedonski, bb, 1000 Skopje, Macedonia

^*

Author to whom correspondence should be addressed.

Int. J. Mol. Sci.2006, 7(4), 119-129;https://doi.org/10.3390/i7040119

Version Notes

Order Reprints

Abstract

QSAR analysis of a series of previously synthesized N¹-aryl-amino/methyl/ethyl-1,2,4-triazole and N¹-heteroarylamino/methyl/ethyl-1,2,4-triazole derivatives tested for growth inhibitory activity against Bacillus subtilis, was performed using the computer-assisted multiple regression procedure. Using the Hansch and Free Wilson approaches the activity contribution for either the aminomethyl/aminoethyl unit or the aromatic/heteroaromatic ring was determined from the correlation equation.

Keywords:

QSAR/QSPR; N1-heteroarylamino/methyl/ethyl-1; 2; 4-triazole; physico- chemical parameters

1. Introduction

Our society is faced with several challenges that may have a chemical solution. Examples include bacterial drug resistance, new diseases like AIDS, and agricultural pest control. Characterizing the biological activity and properties of all the known compounds is impossible so it is necessary to develop predictive tools for molecular properties and environmental behaviour. Quantitative structure activity relationships (QSAR) and quantitative structure properties relationships (QSPR) play a central role in this effort, so these methods are unquestionably of great importance in modern chemistry and biochemistry [1,2,3]. The concept of QSAR/QSPR is to transform searches for compounds with desired properties using chemical intuition and experience into a mathematically quantified and computerized form. Once a correlation between structure and activity/property is found, any number of compounds, including those not yet synthesized, can be readily screened on the computer in order to select structure with the properties desired. It is then possible to select the most promising compounds to be synthesized and tested in the laboratory.

1,2,4-Triazole and its derivatives represent one of the most biologically active classes of compounds, possessing a wide spectrum of activities. The 1,2,4-triazole nucleus is associated with diverse pharmacological activities such as antibacterial, antifungal, hypoglycemic, antihypertensive and analgesic properties [4,5,6,7]. Consequently, spurred by the need for new antimicrobial agents and the fact that many new effective antimicrobial drugs possess heterocyclic rings in their structure, such as a 1,2,4-triazole ring, over the last few years we have synthesized some novel 1,2,4-triazole derivatives and tested them for antibacterial and antifungal effects against Escherichia coli, Bacillus subtilis, Salmonella enteritidis, Staphylococcus aureus, Aspergillus niger and Candida albicans [8,9,10,11]. The antibacterial activity of synthesized N¹-aryl/heteroarylamino/methyl/ethyl-1,2,4-triazole derivatives against Bacillus subtilis were used in this QSAR analysis.

2. Results and Discussion

In our work, the chosen model is based on the in vitro antimicrobial activity of certain N¹-aryl- and N¹-heteroarylaminoaminomethyl/ethyl-1,2,4-triazole derivatives 1-18, (Table 1 and Table 2; Figure 1 and Figure 2), against Bacillus subtilis.

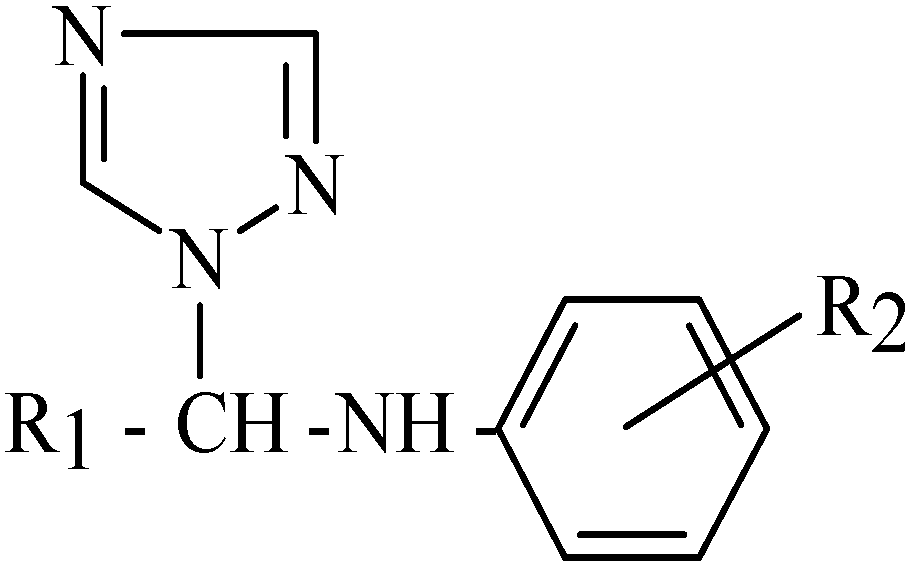
Figure 1.

Table 1. N¹-arylaminomethyl/ethyl-1,2,4-triazole derivatives (1-10) used in the present study.

**Table 1.** N¹-arylaminomethyl/ethyl-1,2,4-triazole derivatives (**1-10**) used in the present study.
Comp. No:	R₁	R₂
1	H	p-COOC₂H₅
2	H	p-COOH
3	H	o-COOH
4	H	p-Cl
5	H	p-Br
6	H	p-CH₃
7	H	p-C₆H₅
8	H	p-C₆H₄-CH₂-NH-
9	CH₃	p-COOC₂H₅
10	CH₃	p-NO₂

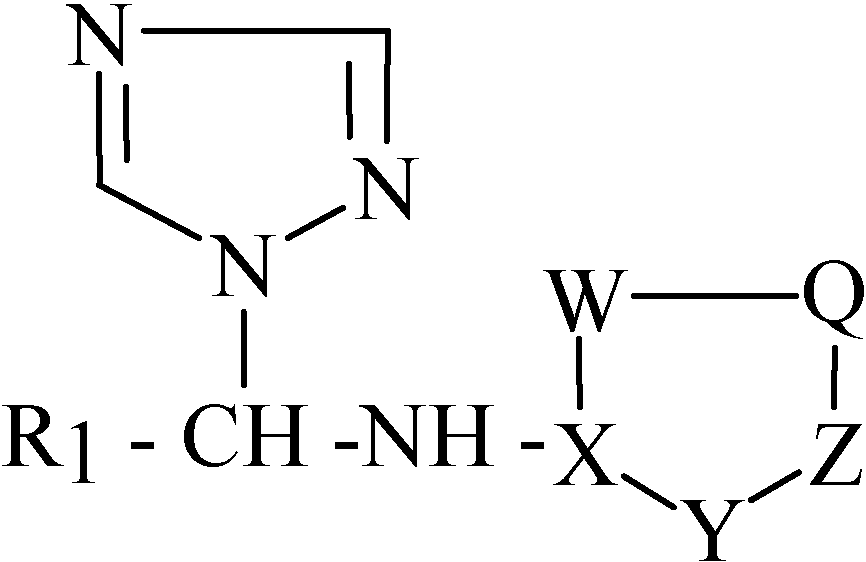
Figure 2.

Table 2. N¹-heteroarylaminomethyl/ethyl-1,2,4-triazole derivatives (11-18) used in the present study.

**Table 2.** N¹-heteroarylaminomethyl/ethyl-1,2,4-triazole derivatives (**11-18**) used in the present study.
Comp. No:	R₁	X	Y	Z	Q	W
11	H	-C=	=N-	-CH=	=CH-	-CH=CH-
12	H	-C=	=N-	-CH=	=CH-	-C(CH₃)=CH-
13	H	-C=	=N-	=C(CH₃)-	=CH-	-CH=CH-
14	H	-C=	=N-	-CH=	=C(Cl)-	-CH=CH-
15	H	-C=	=N-	-CH=	=N-	-CH=CH-
16	H	-N-	-CH=	=N-	-N=	=CH-
17	CH₃	-C=	=N-	=C(CH3)-	=CH-	-CH=CH-
18	CH₃	-C=	=N-	-CH=	=CH-	-S-

The results of antimicrobial tests indicated that not all compounds exhibited antibacterial and antifungal activities. It must also be noted that compounds 17 and 18 do not inhibit the growth of the selected microorganisms. The inhibitory effects of compounds 1-18, against B. subtilis, expressed as minimum inhibition concentration (MIC), are given in Table 3, where C is the MIC value expressed in molar concentration units (Table 3).

Table 3. Experimentally obtained MIC values, calculated log 1/C and log P.

**Table 3.** Experimentally obtained MIC values, calculated log 1/C and log P.
Compound No:	MIC^a	log 1/ C	log P^b	MR^c
1	4.061 x 10^-6	5.3914	1.2981	17.47
2	2.291 x 10^-5	4.6399	0.4579	6.93
3	-	-	1.4690	6.93
4	4.793 x 10^-5	4.3194	1.2210	6.03
5	1.975 x 10^-5	4.7044	1.4665	8.88
6	2.656 x 10^-5	4.5757	1.1238	5.65
7	3.995 x 10^-6	5.3984	2.3405	25.36
8	-	-	-1.6900	-
9	3.842 x 10^-5	4.4154	1.7157	17.47
10	4.287 x 10^-5	4.3678	1.3895	0.67
11	5.708 x 10^-5	4.2435	0.0301	-
12	-	-	0.5774	-
13	5.399 x 10^-5	4.2676	0.5774	-
16	6.055 x 10^-5	4.2178	-2.1800	-

^a minimum inhibition concentration expressed in molar concentration; ^b Ref. [12]; ^c Ref. [1].

Using the filter paper disc method [13] compounds 3, 8, 12, 14 and 15 do not inhibit the growth of the chosen microorganism [10]. From the data obtained, first MIC values were calculated and then the log 1/C values (Table 3). It was important for further analysis to find the correlation matrix for the descriptors used (Table 4).

Table 4. Correlation matrix for the chosen electronic, steric and hydrophobic parameters.

**Table 4.** Correlation matrix for the chosen electronic, steric and hydrophobic parameters.
	σ	π	logP	MR	F	R	L
σ	1.0000
π	-0.8861	1.0000
logP	-0.4792	0.8180	1.0000
MR	-0.4751	0.7235	0.7732	1.0000
F	0.2547	-0.1186	0.6125	-0.2499	1.0000
R	0.6327	-0.7356	0.0348	-0.5815	0.3997	1.0000
L	0.1416	-0.0128	0.4108	0.4519	-0.2317	0.1457	1.0000

In our work, attempts were made to establish a correlation between selected physicochemical properties and experimental values for antimicrobial activities against B. subtilis, in three ways:

➢: applying the general Hansch equation for structurally identical compounds (1-8);
➢: using the Free Wilson approach which included derivatives with some structural changes (aminomethyl unit has been replaced with aminoethyl group), compounds (1-10);
➢: extend the Free Wilson equation, for determination of the influence of heterocyclic ring, substituted on the amino group, compounds (1-18).

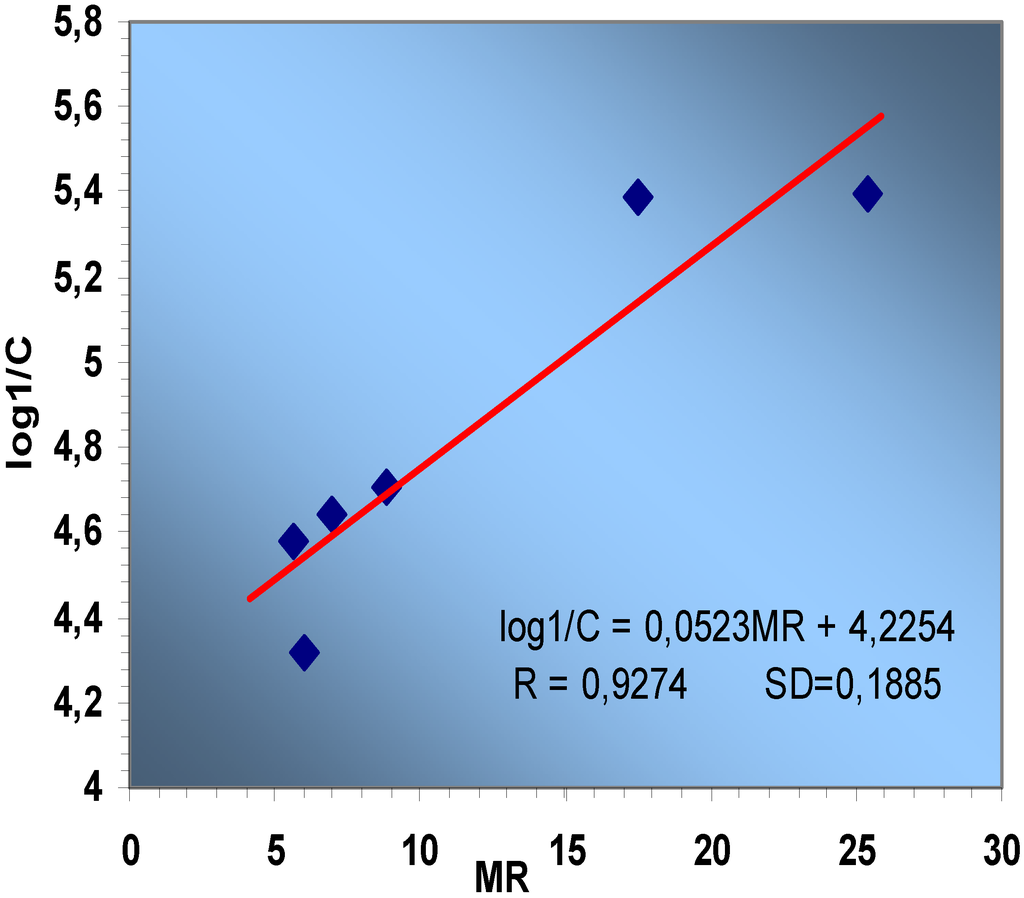
Figure 3. Linear correlation between log 1/C and MR

When the data in Table 3 and Table 7 were submitted to linear regression (Figure 3) the resulting QSAR equation is:

log1/C = 0.0523MR + 4.2254
R = 0.9274 SD=0.1885

where R is correlation coefficients and SD is the standard deviation.

The data for the chosen compounds were reasonably well correlated with a regression coefficient of 0.9274, indicating a relatively good fit.

However, moderate linear collinearities exist between log1/C and other selected descriptors (σ, π, logP, F, R and L) where R is below 0.7. This weak correlation is unable to describe the biological activities of the selected set of compounds. Addition of some other groups to the parent triazole ring would certainly improve those linear fittings.

An attempt was also made to find the parabolic correlation. Parabolic relationships between biological response (log1/C) and logP term, can be explained by the fact that many membranes must be traversed for compounds to get to the target site, and those with greatest hydrophobicity will become localized in the membranes they encounter initially. Thus, an optimum hydrophobicity may be found in some test systems.

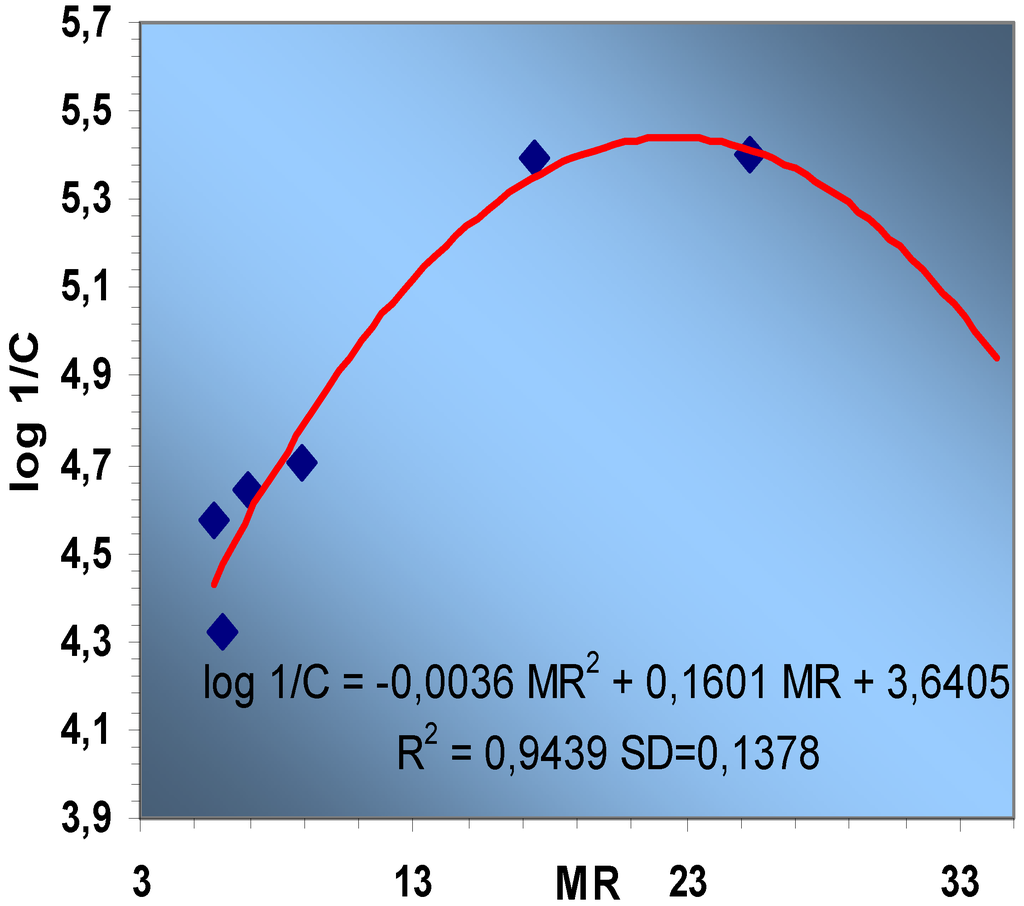
Figure 4. Parabolic correlation between log 1/C and MR.

Knowing this fact, we tried to find parabolic correlations and thus an excellent correlation is obtained between log1/C and MR, (Figure 4):

log 1/C = - 0.0036 MR² + 0.1601 MR + 3.6405
R² = 0.9439 SD=0.1378

For many QSAR studies many descriptors are needed. Addition of more then one descriptor would certainly improve the QSAR model.

Several multivariate correlations between the structural parameters mentioned above and log1/C are presented in Table 5, together with correlation coefficients (R) and standard deviations (SD).

In bivariate correlation analysis also, the correlations involving π, logP and σ are found to be good (Table 5, correlation No 1-13; R=0.91-0.96). Excellent correlation (0.9679) is obtained when in bivariate correlation logP and R were used. The correlation is expressed as:

log1/C = 0.7156logP + 2.5765R + 3.9939
R=0.9679 SD=0.1462

It is interesting to note that an excellent correlation is also obtained in tervariate correlation involving the same parameters (correlation No 14-18, Table 5). The correlation coefficients in all the cases were found to be approximately the same (0.97-0.98), and the standard deviation below 0.16.

Table 5. Regression parameters and the quality of correlation of log 1/C with σ, π, log P, MR, F, R and L, multivariate regressions for substituted 1,2,4-triazoles.

**Table 5.** Regression parameters and the quality of correlation of log 1/C with σ, π, log P, MR, F, R and L, multivariate regressions for substituted 1,2,4-triazoles.
Correlation No	Correlation parameters used ^a	Slope Ai i=1-2		Intercept B	R	SD
1	σ	A₁=	0.2668	4.1667	0.9389	0.2002
1	MR	A₂=	0.0528	4.1667	0.9389	0.2002
2	σ	A₁=	-0.2059	3.4557	0.9565	0.1697
2	L	A₂=	0.3222	3.4557	0.9565	0.1697
3	π	A₁=	-3.0467	1.6286	0.9130	0.2373
3	logP	A₂=	4.0843	1.6286	0.9130	0.2373
4	π	A₁=	-0.2347	4.2092	0.9647	0.1542
4	MR	A₂=	0.0679	4.2092	0.9647	0.1542
5	π	A₁=	0.6084	4.5146	0.9452	0.1899
5	R	A₂=	2.8805	4.5146	0.9452	0.1899
6	π	A₁=	-0.0131	3.4419	0.9502	0.1812
6	L	A₂=	0.3182	3.4419	0.9502	0.1812
7	logP	A₁=	-0.2789	4.3958	0.9556	0.1714
7	MR	A₂=	0.0691	4.3958	0.9556	0.1714
8	logP	A₁=	0.7156	3.9939	0.9679	0.1462
8	R	A₂=	2.5765	3.9939	0.9679	0.1462
9	logP	A₁=	0.0007	3.4492	0.9500	0.1815
9	L	A₂=	003143	3.4492	0.9500	0.1815
10	MR	A₁=	0.0495	4.2878	0.9599	0.1630
10	R	A₂=	0.7650	4.2878	0.9599	0.1630
11	MR	A₁=	0.0120	3.6068	0.9519	0.1780
11	L	A₂=	0.2469	3.6068	0.9519	0.1780
12	F	A₁=	-0.4005	3.5676	0.9654	0.1517
12	L	A₂=	0.3111	3.5676	0.9654	0.1517
13	R	A₁=	0.1041	3.4743	0.9505	0.1807
13	L	A₂=	0.3097	3.4743	0.9505	0.1807
14	σ	A₁=	-0.6667	3.3456	0.9736	0.1625
	π	A₂=	-0.2226
	L	A₃=	0.4036
15	π	A₁=	-1.4854	3.0706	0.9866	0.1165
	logP	A₂=	1.7219
	MR	A₃=	0.0476
16	π	A₁=	-1.2182	3.0139	0.9853	0.1217
	logP	A₂=	2.0982
	R	A₃=	1.8779
17	π	A₁=	-1.7249	3.6820	0.9771	0.1513
	MR	A₂=	0.1866
	R	A₃=	-5.1995
18	logP	A₁=	1.8755	3.5299	0.9728	0.1649
	MR	A₂=	-0.0812
	R	A₃=	5.5237

^a x, y, z from the Eqn. 1; R - correlation coefficient; SD - standard deviation

After including the compounds with little structural modification (compounds 9 and 10) the following correlations were obtained (Table 6):

Table 6. Regression parameters and the quality of correlation of log 1/C with σ, π, log P, MR, F, R and L; (log1/C = ΣAi x Ii + B).

**Table 6.** Regression parameters and the quality of correlation of log 1/C with σ, π, log P, MR, F, R and L; (log1/C = ΣAi x Ii + B).
Correlation No	Correlation parameters used^a	Slope Ai i=1-4		Intercept B	R	SD
1.	I_H	A₁=	0.4783	3.8239	0.9034	0.2199
1.	MR	A₂=	0.0457	3.8239	0.9034	0.2199
2.	I_H	A₁=	0.6556	3.5334	0.9289	0.2124
	σ	A₂=	0.4197
	MR	A₃=	0.0483
3.	I_H	A₁=	0.6410	3.6390	0.9373	0.1998
	π	A₂=	-0.2520
	MR	A₃=	0.0629
4.	I_H	A₁=	0.442	3.9815	0.9138	0.2328
	logP	A₂=	-0.1849
	MR	A₃=	0.0562
5.	I_H	A₁=	0.6674	3.5784	0.9387	0.2282
	σ	A₂=	0.1454
	π	A₃=	-0.1976
	MR	A₄=	0.0600
6.	I _H	A₁=	0.6394	3.5760	0.9290	0.2449
	σ	A₂=	0.3951
	logP	A₃=	-0.0300
	MR	A₄=	0.0499
7.	I_H	A₁=	1.5164	1.8039	0.9885	0.0909
	π	A₂=	-1.2034
	logP	A₃=	1.3356
	MR	A₄=	0.0525

R - correlation coefficient; SD - standard deviation

As it can be seen from Table 6, an excellent correlation was obtained when π, logP and MR were used:

log 1/C = 1.5164 I_H - 1.2034 π + 1.3356 log P + 0.0525MR + 1.8039

where I_H is structural indicator parameter representing –CH₂- group as 1 and CH₃-CH- group as 0. From the value of R (0.9885) can be seen that a relatively good model was chosen.

The last step was determination of the influence of heterocyclic ring by using the extend Free – Wilson equation. The following equation was obtained:

log1/C = 0.3094 I_H + 0.3712 I_=CH- - 0.2104 logP + 4.6375
R = 0.7171 SD = 0.3567

Extending the investigation system may lead to developing the better QSAR system when another heterocyclic nucleus, besides triazole, is included in the chosen substituted 1,2,4-triazoles.

3. Conclusions

Spurred by the need for new antimicrobial agents and the fact that many effective drugs, insecticides and fungicides possess heterocyclic systems in their structure, such as the triazole ring, we synthesized some new 1,2,4-triazole derivatives. Analysis of this limited set of substituted 1,2,4-triazole molecules allowed us to build a QSAR model of their antimicrobial activity against B. subtilis in which π, logP and σ are important factors. When we summarized the results derived from this limited set of triazole derivatives we came to the conclusion that the QSAR results don’t really explain anything, but rather the QSAR equations just point to correlations. On the other hand, QSAR is a very important and routine method for many areas of chemistry. QSAR is best appreciated as a guide for our chemical intuition and QSAR models may guide us to what to synthesize next in our search for more effective solutions to our problems. This, in turn, will help medical as well as agriculture chemist in their prediction of increasing activity and thus the synthesis of new triazoles exhibiting better activities then those reported in this paper.

4. Experimental

4.1 Microbiology

The filter paper disc method [13] was performed in Sabouraud dextrose broth and Mueller Hinton broth. These agar media were inoculated with 24 h liquid cultures containing 10⁷ microorganisms/mL (0.5 mL). Filter paper discs (5 mm diameter) saturated with each compound solution (1 mg/mL; 5 mg/mL and 10 mg/mL in DMSO) were placed on the indicated agar mediums. The incubation time was 24 h at 37 ºC for bacterial and 48 h at 30 ºC for Candida sp. Discs with DMSO were used as control. The diameter of zone inhibition (mm) was measured. The tests were repeated 3 times to confirm the findings.

4.2 QSAR analysis

The MVA (multi variable analysis) approach in QSAR analysis has been most widely and effectively used for theoretical drug design due to various physicochemical (electronic, steric and hydrophobic) parameters and structural indicator parameters used together (Hansch and Free Wilson approaches) [1,2].

The assumption can be formulated as given in Eqn. 1, (Hansch approach):

log1/C = A₁ x + A₂ y + A₃ z+ B

Eqn. 1

where x, y and z are molecular properties, and log1/C is the desired biological activities. From the values of linear slopes A₁, A₂, A₃ we can see the correlation of the particular molecular properties with the activity of the investigated compounds.

Applying the same chosen descriptors in Free Wilson analysis (Eqn. 2) the activity contributions of either methyl- or substituted heterocyclic ring systems were determined from the correlation equation:

log1/C = Σa_i I_i + Σb_i x_i + B

Eqn. 2

where I_i is the structural indicator parameter; x_i and log1/C had the same meaning as in Eqn.1.

The variables used as descriptors in the analysis are electronic, steric and structural parameters (Table 3 and Table 7). Physicochemical parameters taken into consideration in QSAR study are σ electronic parameter of substituents, π hydrophobic parameter, F (field effect) as electronic influences, Verloop’s STERIMOL parameter L for the steric interactions of the substituents R₂. L is defined as the length of a substituent along the axis of its substitution to the parent skeleton. Electronic effect of the substituents, expressed in term of F, is found to be important in determining the activity, as it is predictive in electrophilic reactions of bimolecules. The classical Hammett σ parameters and MR value were used (Table 3 and Table 7). For each compound the partition coefficient logP has been calculated [12] (Table 3).

Table 7. Physicochemical parameters of the triazole derivatives studied

**Table 7.** Physicochemical parameters of the triazole derivatives studied
R	σ^a	π ^a	F ^a	R ^a	L ^a
p-COOC₂H₅	0.45	0.51	0.33	0.15	5.96
p-COOH	0.45	-0.32	0.33	0.15	3.91
o-COOH	1.2	-0.32	0.33	0.15	3.91
p-Cl	0.23	0.71	0.41	-0.15	3.52
p-Br	0.23	0.86	0.44	-0.17	3.83
p-CH₃	-0.17	0.56	-0.04	-0.13	3.00
p-C₆H₅	-0.01	1.96	0.08	-0.08	6.28
p-NO₂	0.78	-0.28	0.67	0.16	3.44

^a Ref. [1]

Applying the Free Wilson analysis, in first step, the structural variable indicator I_H expresses the replacement of hydrogen atom by the methyl group in the aminomethyl unit. I_H is defined as 1 for the N¹-aryl/heteroarylaminomethyl-1,2,4-triazoles (1-8, 11-16), and 0 for N¹-aryl/heteroarylaminoethyl-1,2,4-triazole derivatives (9,10,17,18). In second step, the other indicator I_=CH- is defined as 1 for compounds with =CH- in the six membered ring (1-10), and 0 for compound with –N= group in the six membered ring (11-18) (Table 8).

Table 8. Matrix for Free Wilson approach.

**Table 8.** Matrix for Free Wilson approach.
Compound	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
I_H	1	1	1	1	1	1	1	1	0	0	1	1	1	1	1	1
I_=CH-	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0

References

Available online: http://www.chem.swin.edu.au/modules/mod4/index.html.
Hansch, C.; Leo, A. Exploring QSAR: Fundamentals and Applications in Chemistry and Biology; American Chemical Society: Washington, DC, 1995. [Google Scholar]
Karelson, M.; Lobanov, V.; Katritzky, A. Chem. Rev. 1996, 96, 1027–1043. [CrossRef]
Jones, D.H.; Slack, R.; Squires, S.; Woolridge, K.R.H. J. Med. Chem. 1965, 8, 676–680. [CrossRef]
Goswami, B.N.; Kataky, J.C.S.; Baruah, J.N. J. Heterocyclic Chem. 1984, 21, 1225–1229. [CrossRef]
Holla, B.S.; Kalluraya, B.; Sridhar, K.R. Curr. Sci. 1987, 56, 236–239.
Mishra, R.K.; Tewari, R.K.; Srivastava, S.K.; Bahel, S.C. J. Indian Chem. Soc. 1991, 68, 1.
Colanceska, K.; Dimova, V.; Kakurinov, V.; Molnar-Gabor, D.; Buzarovska, A. Molecules 2001, 6, 815–824. [CrossRef]
Perisic-Janjic, N.; Acinski, M.; Janjic, N.; Lazarevic, M.; Dimova, V. J. Planar Chromatogr. 2000, 13, 281–284.
Lazarevic, M.; Dimova, V.; Molnar Gabor, D.; Kakurinov, V.; Colanceska Ragenovic, K. Heterocycl. Comm. 2001, 7, 577–582.
Spasovska-Gerasimova, B.; Ilievska, S.; Colanceska Ragenovic, K.; Lazarevic, M.; Dimova, V. Vlákna a textil 2002, 9, 46–49.
Available online: http://esc.syrres.com/interkow/kowdemo.htm.
Rollas, S.; Kalyoncuoglu, N.; Sür-Altiner, D.; Yegenoglu, Y. Pharmazie 1993, 48, 308–309.

QSAR of Some N¹-Aryl/Heteroarylaminomethyl/ethyl-1,2,4-Triazoles Part II: Antimicrobial Activity Against BacillusSubtilis