The Quantitative Structure-Mutagenicity Relationship of Polycylic Aromatic Hydrocarbon Metabolites
Abstract
:1. Introduction
2. Methods
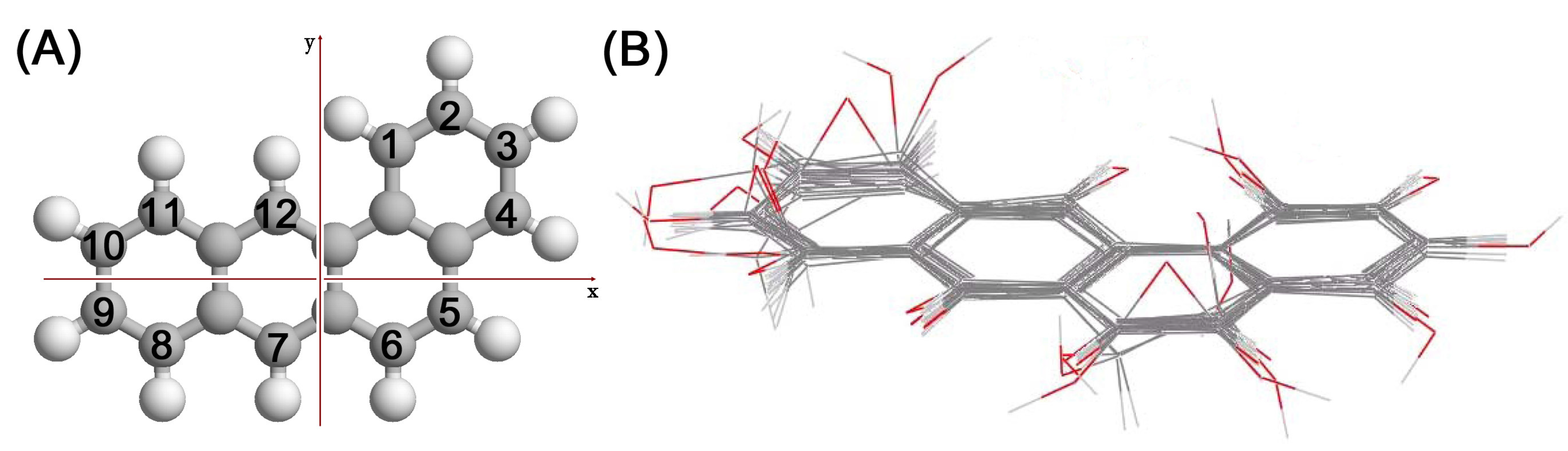
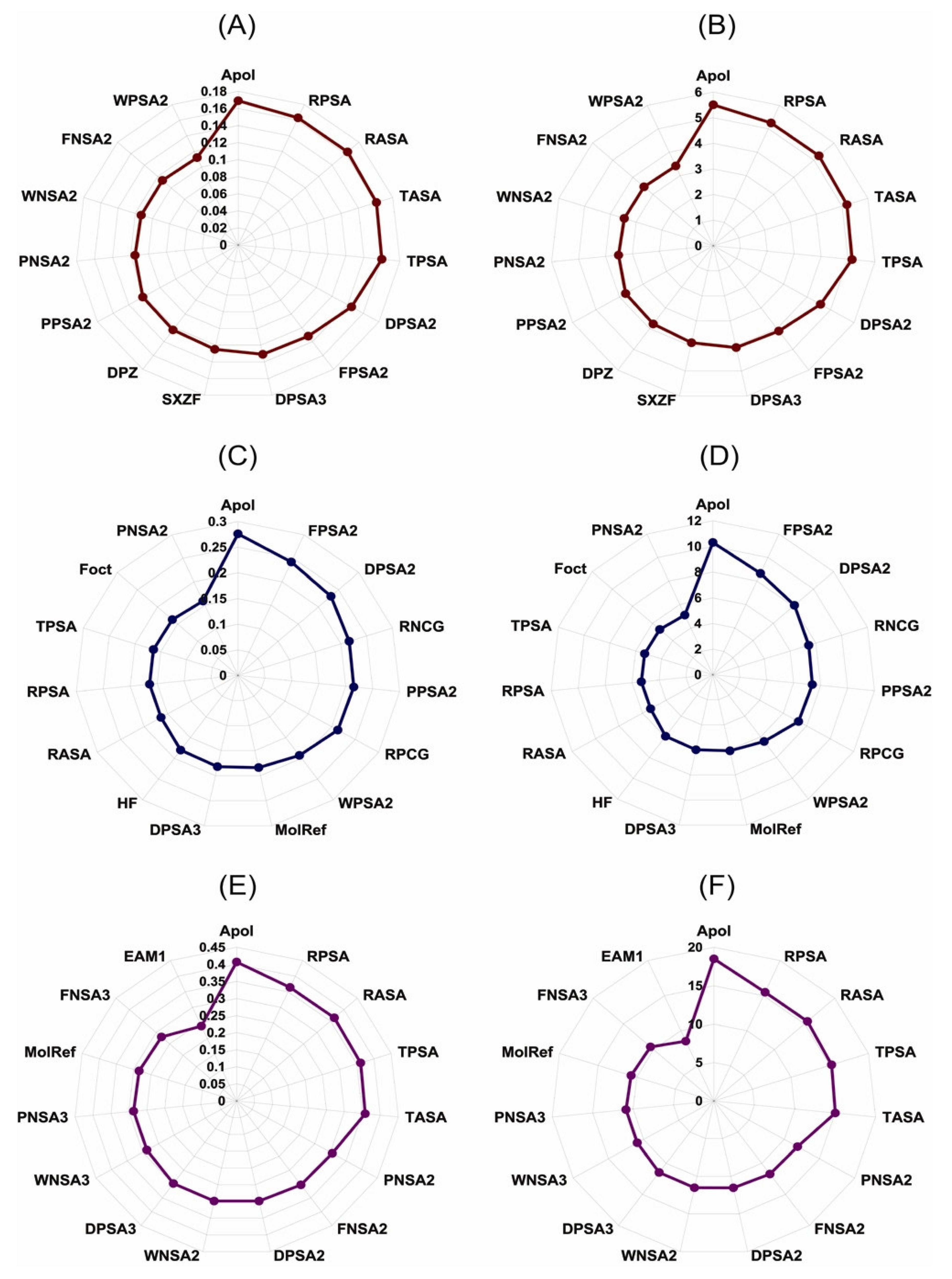
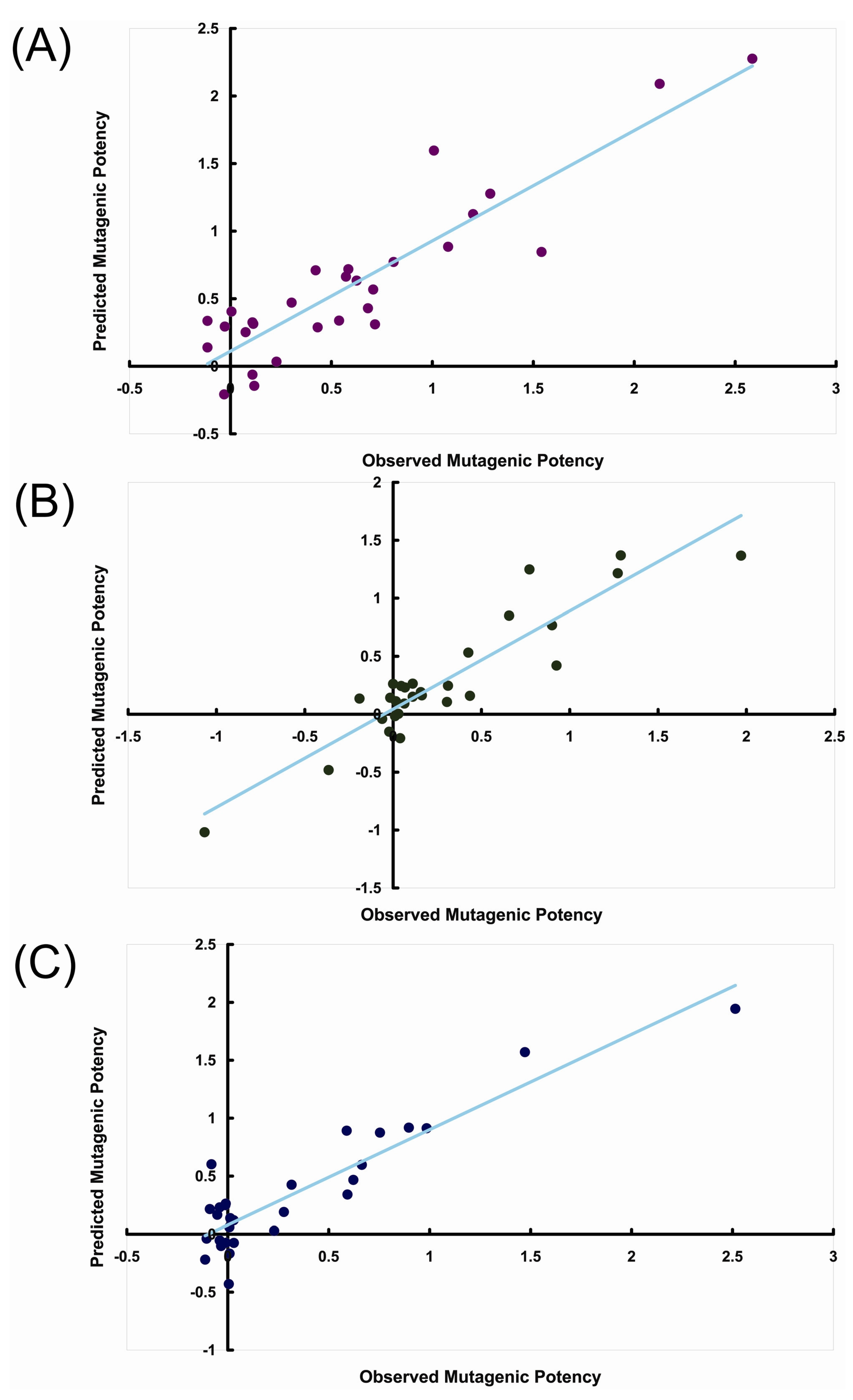
3. Results and Discussion
| no | compound | MPmv | MPmg | MPmf |
|---|---|---|---|---|
| 1 | 1-Hydroxy BA | 1.2181 | 0.1841 | 1.0136 |
| 2 | 2-Hydroxy BA | 0.1276 | -0.214 | 0.0090 |
| 3 | 3-Hydroxy BA | 0.8090 | 0.1774 | 0.6701 |
| 4 | 4-Hydroxy BA | -0.1288 | 0.0519 | -0.0915 |
| 5 | 5-Hydroxy BA | -0.0316 | 0.1254 | -0.0452 |
| 6 | 6-Hydroxy BA | 2.4023 | 1.0452 | 1.6634 |
| 7 | 7-Hydroxy BA | 0.7989 | 1.0170 | 0.7029 |
| 8 | 8-Hydroxy BA | 0.0847 | -0.4124 | 0.0136 |
| 9 | 9-Hydroxy BA | 0.1231 | 0.7424 | 0.3141 |
| 10 | 10-Hydroxy BA | -0.1288 | -1.2057 | -0.0102 |
| 11 | 11-Hydroxy BA | -0.0350 | -0.0180 | 0.0328 |
| 12 | 12-Hydroxy BA | 1.7413 | 0.3446 | 0.7503 |
| 13 | BA 4,5-oxide | 2.9210 | 2.2261 | 2.8408 |
| 14 | BA 7,8-oxide | 1.3582 | 1.4565 | 1.1131 |
| 15 | BA 9,10-oxide | 1.4543 | 1.4373 | 0.8520 |
| 16 | BA 11,12-oxide | 1.1390 | 0.8723 | 0.6656 |
| 17 | BA-1,6-quinone | 0.6599 | 0.4915 | -0.0113 |
| 18 | BA 3,6-quinone | 0.7695 | 0.0757 | 0.0339 |
| 19 | BA 4,5-quinone | 0.4768 | 0.4813 | -0.0588 |
| 20 | BA 6,12-quinone | 0.6463 | -0.0701 | 0.0102 |
| 21 | BA 11,12-quinone | 0.1231 | 0.3514 | -0.1187 |
| 22 | BA-cis-4,5-dihydrodiol | 0.2576 | 0.0339 | -0.1266 |
| 23 | BA-trans-4,5-dihydrodiol | 0.6079 | 0.0181 | -0.1006 |
| 24 | BA-cis-7,8- dihydrodiol | 0.1333 | 0.0723 | 0.0057 |
| 25 | BA-trans-7,8-dihydrodiol | 0.9130 | 0.1254 | -0.0373 |
| 26 | BA-cis-9,10-dihydrodiol | 0.7062 | -0.0249 | -0.0452 |
| 27 | BA-trans-9,10-dihydrodiol | 0.4881 | 0.0000 | 0.3571 |
| 28 | BA-cis-11,12-dihydrodiol | 0.3423 | 0.0452 | 0.2599 |
| 29 | BA-trans-11,12-dihydrodiol | 0.0056 | 0.0124 | -0.0136 |
| #terms | MV | MG | MF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r2 | rcv2 | F | r2 | rcv2 | F | r2 | rcv2 | F | |||
| 2 | 0.4531 | 0.2882 | 9.8321 | 0.6735 | 0.4983 | 21.6813 | 0.6226 | 0.4002 | 18.0054 | ||
| 3 | 0.6452 | 0.4927 | 12.5079 | 0.8498 | 0.6780 | 28.5687 | 0.6622 | 0.4305 | 13.3509 | ||
| 4 | 0.7989 | 0.6565 | 16.3567 | 0.8893 | 0.5695 | 25.0317 | 0.8136 | 0.5345 | 17.4562 | ||
| 5 | 0.8814 | 0.7492 | 18.4133 | 0.9571 | 0.8520 | 28.8207 | 0.8735 | 0.5526 | 17.6845 | ||
| 6 | 0.9391 | 0.7729 | 20.3106 | 0.9854 | 0.8238 | 28.2466 | 0.9299 | 0.7062 | 19.3196 | ||
| compd | Q5 | Q6 | Q7 | Q8 | Q10 | PNSA1 | FPSA3 | WPSA2 | RPCG | SXL | SYL | SXYF | Area | ELUMO | Fh2o |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.1491 | -0.1254 | -0.1356 | -0.1424 | -0.1311 | 229.5878 | 0.0858 | 235.1733 | 0.1389 | 13.7679 | 9.9044 | 0.9142 | 315.0700 | -1.5842 | -20.8971 |
| 2 | -0.1231 | -0.1062 | -0.1299 | -0.1469 | -0.1367 | 221.4845 | 0.0858 | 252.4443 | 0.1389 | 15.0979 | 9.4061 | 0.8712 | 315.2406 | -1.6554 | -20.8971 |
| 3 | -0.1367 | -0.1276 | -0.1367 | -0.1412 | -0.1299 | 235.8921 | 0.0847 | 235.5531 | 0.1389 | 14.5363 | 10.8378 | 0.8068 | 317.7797 | -1.6057 | -20.8971 |
| 4 | -0.1785 | -0.1243 | -0.1345 | -0.1423 | -0.1310 | 235.8965 | 0.0836 | 233.2377 | 0.1389 | 14.5080 | 10.8581 | 0.8113 | 314.9355 | -1.6136 | -20.8971 |
| 5 | 0.0949 | -0.1265 | -0.1345 | -0.1423 | -0.1322 | 236.2311 | 0.0836 | 230.4635 | 0.1401 | 14.5453 | 9.0162 | 0.9130 | 317.1458 | -1.6452 | -20.8971 |
| 6 | -0.1367 | 0.1378 | -0.1017 | -0.1615 | -0.1480 | 214.5938 | 0.0881 | 245.7413 | 0.1389 | 14.4854 | 9.6051 | 0.8949 | 313.6791 | -1.5605 | -20.8971 |
| 7 | -0.1378 | -0.1254 | 0.1062 | -0.1762 | -0.1695 | 231.2251 | 0.0847 | 232.2152 | 0.1389 | 14.4391 | 10.0705 | 0.8633 | 313.9253 | -1.6452 | -20.8971 |
| 8 | -0.1378 | -0.1288 | -0.1752 | 0.1017 | -0.0904 | 234.8886 | 0.0858 | 232.6568 | 0.1389 | 16.2471 | 9.8298 | 0.7977 | 320.6997 | -1.6136 | -20.8971 |
| 9 | -0.1310 | -0.1028 | -0.0949 | -0.1649 | -0.2395 | 227.0046 | 0.0870 | 244.9354 | 0.1378 | 14.5137 | 10.8525 | 0.8068 | 315.9751 | -1.5763 | -20.8971 |
| 10 | -0.1378 | -0.1231 | -0.1672 | -0.1132 | 0.1017 | 224.8677 | 0.0892 | 236.7316 | 0.1401 | 14.5771 | 10.0298 | 0.8522 | 318.9956 | -1.6633 | -20.8971 |
| 11 | -0.1378 | -0.1107 | -0.1311 | -0.1469 | -0.1536 | 219.7138 | 0.0892 | 242.4539 | 0.1412 | 14.5408 | 8.9349 | 0.9096 | 320.1910 | -1.6554 | -20.8971 |
| 12 | -0.1276 | -0.1276 | -0.1379 | -0.1401 | -0.1265 | 230.2533 | 0.0836 | 237.7893 | 0.1401 | 14.4821 | 9.6795 | 0.8723 | 314.4078 | -1.5910 | -20.8971 |
| 13 | -0.0067 | -0.1096 | -0.1311 | -0.1435 | -0.1322 | 239.5555 | 0.0824 | 213.1961 | 0.0971 | 14.5544 | 9.6829 | 0.8588 | 306.9769 | -1.1492 | -15.2844 |
| 14 | -0.1356 | -0.1131 | -0.0094 | -0.0203 | -0.1131 | 230.6985 | 0.0836 | 208.9912 | 0.0971 | 14.4742 | 9.6569 | 0.8712 | 316.8452 | -1.5062 | -15.0606 |
| 15 | -0.1367 | -0.1186 | -0.1186 | -0.1695 | -0.0067 | 228.2148 | 0.0847 | 210.5529 | 0.0960 | 14.6618 | 9.7552 | 0.8463 | 317.8882 | -1.4136 | -15.0606 |
| 16 | -0.1333 | -0.1132 | -0.1333 | -0.1435 | -0.1356 | 221.4541 | 0.0847 | 213.5474 | 0.0971 | 14.5759 | 9.9530 | 0.8384 | 314.1999 | -1.3232 | -15.2844 |
| 17 | -0.0644 | 0.3503 | -0.0666 | -0.1570 | -0.1412 | 264.7059 | 0.0836 | 250.5007 | 0.1638 | 13.7182 | 9.7067 | 0.9424 | 308.8934 | -2.6656 | -11.4356 |
| 18 | -0.0757 | 0.3480 | -0.0644 | -0.1593 | -0.1446 | 263.3149 | 0.0847 | 238.6266 | 0.1638 | 14.5883 | 9.7236 | 0.8859 | 308.0301 | -2.6634 | -11.5915 |
| 19 | 0.2644 | -0.0192 | -0.1131 | -0.1491 | -0.1424 | 255.5156 | 0.0791 | 234.5394 | 0.1367 | 14.5171 | 11.4231 | 0.7774 | 312.5625 | -1.5797 | -11.5915 |
| 20 | -0.0983 | 0.3492 | -0.0678 | -0.1548 | -0.1345 | 253.0364 | 0.0858 | 264.4754 | 0.1638 | 14.4662 | 10.0671 | 0.8701 | 310.5761 | -2.5820 | -11.5915 |
| 21 | -0.1276 | -0.0644 | -0.1345 | -0.1435 | -0.1299 | 252.1911 | 0.0802 | 242.2675 | 0.1356 | 14.5916 | 9.4727 | 0.8802 | 318.5922 | -2.0893 | -11.5915 |
| 22 | 0.0440 | -0.1051 | -0.1299 | -0.1446 | -0.1333 | 231.7393 | 0.0926 | 314.1141 | 0.1186 | 14.5205 | 11.5406 | 0.757 | 341.2679 | -1.1785 | -30.2772 |
| 23 | 0.0587 | -0.0961 | -0.1276 | -0.1457 | -0.1345 | 230.7132 | 0.0926 | 308.9974 | 0.1175 | 14.4685 | 11.5666 | 0.7876 | 337.9344 | -1.0881 | -30.2772 |
| 24 | -0.1344 | -0.1017 | 0.0474 | 0.0282 | -0.1457 | 232.5721 | 0.0926 | 311.7173 | 0.1186 | 16.3183 | 9.8954 | 0.7864 | 343.6861 | -1.5752 | -30.2231 |
| 25 | -0.1310 | -0.0994 | 0.0553 | 0.0237 | -0.1231 | 237.3091 | 0.0915 | 310.4981 | 0.1152 | 16.3239 | 10.0084 | 0.8034 | 370.8242 | -1.2882 | -30.2231 |
| 26 | -0.1378 | -0.1224 | -0.1288 | -0.2135 | 0.1062 | 230.1324 | 0.0904 | 304.8706 | 0.1231 | 16.0979 | 9.7394 | 0.8102 | 343.3721 | -1.3356 | -29.8841 |
| 27 | -0.1412 | -0.1224 | -0.1322 | -0.2282 | 0.0418 | 234.7473 | 0.0938 | 318.6419 | 0.1131 | 14.4515 | 9.7191 | 0.8621 | 340.4012 | -1.4836 | -29.8841 |
| 28 | -0.1344 | -0.1085 | -0.1356 | -0.1423 | -0.1333 | 216.3973 | 0.0961 | 319.1381 | 0.1186 | 14.5092 | 9.6547 | 0.8689 | 339.3932 | -1.3819 | -30.2772 |
| 29 | -0.1333 | -0.1096 | -0.1379 | -0.1401 | -0.1299 | 228.1753 | 0.0949 | 319.0668 | 0.1118 | 14.5487 | 9.4072 | 0.8791 | 349.1621 | -1.4034 | -30.2771 |
| ave | -0.0915 | -0.0531 | -0.0994 | -0.1276 | -0.1107 | 234.2106 | 0.0871 | 256.6603 | 0.1299 | 14.7284 | 9.9993 | 0.8497 | 323.4015 | -1.6249 | -21.0551 |
| std dev | 0.09605 | 0.1480 | 0.0678 | 0.0711 | 0.0757 | 12.6797 | 0.0045 | 37.6764 | 0.0192 | 0.6633 | 0.6847 | 0.0474 | 15.3691 | 0.4011 | 6.6918 |
Acknowledgements
References
- Anstead, G.M.; Kym, P.R. Benz[a]anthracene diols: Predicted carcinogenicity and structure-estrogen receptor binding affinity relationships. Steroids 1995, 60, 383–394. [Google Scholar] [CrossRef]
- Ito, Y.; Ueda, N.; Maeda, S.; Murao, S.I.; Sugiyama, T.; Lee, H.; Harvey, R.G. Induction of chromosomal aberrations in rat bone marrow cells and mutations in Salmonella typhimurium by benz[a]anthracene derivatives. Mutation Res. 1988, 206, 55–63. [Google Scholar] [CrossRef]
- Wood, A.W.; Chang, R.L.; Levin, W. Mutagenicity of the enantiomers of the diastereomeric bay-region benz(a)anthracene 3,4-diol-1,2-epoxides in bacterial and mammalian cells. Cancer Res. 1983, 43, 5821–5825. [Google Scholar]
- Nordling, M.M.; Nygren, J.; Bergman, J.; Sundberg, K.; Rafter, J.J. Toxicological characterization of a novel in vivo benzo[a]pyrene metabolite, 7-oxo-benz[d]anthracene-3,4-dicarboxylic acid anhydride. Chem. Res. Toxicol. 2002, 15, 1274–1280. [Google Scholar] [CrossRef]
- Morreal, C.E.; Sinha, D.K.; Schneider, S.L. Antiestrogenic properties of substituted benz[a]anthracene-3,9-diols. J. Med. Chem. 1982, 25, 323–326. [Google Scholar] [CrossRef]
- Nashed, N.T.; Balani, S.K.; Loncharich, R.J.; Sayer, J.M.; Shipley, D.Y.; Mohan, R.S.; Whalen, D.L.; Jerina, D.M. Solvolysis of K-region arene oxides: Substituent effects on reactions of benz[a]anthracene 5,6-oxide. J. Am. Chem. Soc. 1991, 113, 3910–3919. [Google Scholar] [CrossRef]
- Mushtaq, M.; Weems, H.B.; Yang, S.K. Metabolic and stereoselective formations of non-K-region benz[a]anthracene 8,9- and 10,11-epoxides. Arch. Biochem. Biophys. 1986, 246, 478–487. [Google Scholar] [CrossRef]
- Urano, S.; Price, H.L.; Fetzer, S.M.; Briedis, A.V.; Milliman, A.; LeBreton, P.R. Photoemission probes of hydrocarbon-DNA interactions: A comparison of DNA influences on the reactivities of (±)-trans-7,8-dihydroxy-anti-9,10-epoxy-7,8,9,10-tetrahydrobenzo[a]pyrene, benzo[a]pyrene 4,5-oxide, and benz[a]anthracene 5,6-oxide. J. Am. Chem. Soc. 1991, 113, 3881–3893. [Google Scholar] [CrossRef]
- Smithgall, T.E.; Harvey, R.G.; Penning, T.M. Oxidation of the trans-3,4-dihydrodiol metabolites of the potent carcinogen 7,12-dimethylbenz(a)anthracene and other benz(a)anthracene derivatives by 3α-hydroxysteroid-dihydrodiol dehydrogenase: Effects of methyl substitution on velocity and stereochemical course of trans-dihydrodiol oxidation. Cancer Res. 1988, 48, 1227–1232. [Google Scholar]
- Wettstein, J.G.; Chien, M.T.; Flesher, J.W. DNA binding and mutagenicity of 7-substituted derivatives of benz[a]anthracene. Drug Chem. Toxicol. 1979, 2, 383–396. [Google Scholar] [CrossRef]
- Slaga, T.J.; Huberman, E.; Selkirk, J.K. Carcinogenicity and mutagenicity of benz(a)anthracene diols and diol-epoxides. Cancer Res. 1978, 38, 1699–1704. [Google Scholar]
- Booth, J.; Sims, P. Metabolism of benz[a]anthracene epoxides by rat liver. Biochem. Pharm. 1974, 23, 2547–2555. [Google Scholar] [CrossRef]
- Roe, F.J.; Dipple, A.; Mitchley, B.C. Carcinogenic activity of some benz(a)anthracene derivatives in newborn mice. Br. J. Cancer 1972, 26, 461–465. [Google Scholar] [CrossRef]
- Pataki, J.; Huggins, C. Molecular site of substituents of benz(a)anthracene related to carcinogenicity. Cancer Res. 1969, 29, 506–509. [Google Scholar]
- Boyland, E.; Sims, P. The carcinogenic activities in mice of compounds related to benz[a]anthracene. Int. J. Cancer 1967, 2, 500–504. [Google Scholar] [CrossRef]
- Stevenson, J.L.; Von Haam, E. Carcinogenicity of benzo(a)anthracene and benz(c)phenanthrene derivatives. Am. Ind. Hygiene Ass. J. 1965, 26, 475–478. [Google Scholar] [CrossRef]
- Aoki, T.; Ohshima, S.; Sakamoto, Y. Structure-carcinogenicity studies for Benz[a]anthracenes by13C NMR spectroscopy and molecular orbital calculation. Polycyclic Aromatic Compounds 1996, 11, 245–252. [Google Scholar] [CrossRef]
- Cajthaml, T.; Erbanova, P.; Sasek, V.; Moeder, M. Breakdown products on metabolic pathway of degradation of benz[a]anthracene by a ligninolytic fungus. Chemosphere 2006, 64, 560–564. [Google Scholar] [CrossRef]
- Moody, J.D.; Freeman, J.P.; Cerniglia, C.E. Degradation of benz[a]anthracene by Mycobacterium vanbaalenii strain PYR-1. Biodegrad. 2005, 16, 513–526. [Google Scholar]
- Schneider, J.; Grosser, R.; Jayasimhulu, K.; Xue, W.; Warshawsky, D. Degradation of pyrene, benz[a]anthracene, and benzo[a]pyrene by Mycobacterium sp. strain RJGII-135, isolated from a former coal gasification site. Appl. Env. Microbiol. 1996, 62, 13–19. [Google Scholar]
- Juhasz, A.L.; Britz, M.L.; Stanley, G.A. Degradation of fluoranthene, pyrene, benz[a]anthracene and dibenz[a,h]anthracene by Burkholderia cepacia. J. Appl. Microbiol. 1997, 83, 189–198. [Google Scholar]
- Veille, M.; Kuroki, T.; Sims, P. Mutagenicity of isomeric diol-epoxides of benzo[a]pyrene and benz[a]anthracene in S. typhimurium TA98 and TA100 and in V79 Chinese hamster cells. Mutation Res. 1977, 44, 313–325. [Google Scholar] [CrossRef]
- Malaveille, C.; Bartsch, H.; Grover, P.L.; Sims, P. Mutagenicity of non K region diols and diol epoxides of benz(a)anthracene and benzo(a)pyrene in S. typhimurium TA 100. Biochem. Biophy. Res. Comm. 1975, 66, 693–700. [Google Scholar] [CrossRef]
- Boyle, S.P.; Craft, J.A. Gender-specific metabolism of benz[a]anthracene in hepatic microsomes from Long-Evans and Hooded Lister rats. Chem.-Biol. Interact. 2000, 125, 209–220. [Google Scholar] [CrossRef]
- McCord, A.; Boyle, S.P.; Knowler, J.T.; Burnett, A.K.; Craft, J. A. Metabolism of benz[a]anthracene by human bone marrow in vitro. Chem.-Biol. Interact. 1996, 99, 29–40. [Google Scholar] [CrossRef]
- Sahali, Y.; Kidd La, C.R.; Skipper, P.L.; Tannenbaum, S.R. Metabolism of benz[a]anthracene by human liver microsomes. Cancer Lett. 1994, 83, 299–303. [Google Scholar] [CrossRef]
- Cerniglia, C.E.; Gibson, D.T.; Dodge, R.H. Metabolism of benz[a]anthracene by the filamentous fungus Cunninghamella elegans. Appl. Environ. Microbiol. 1994, 60, 3931–3938. [Google Scholar]
- Sims, P.; Grover, P.L.; Kuroki, T.; Huberman, E.; Marquardt, H.; Selkirk, J.K.; Heidelberger, C. The metabolism of benz(a)anthracene and dibenz(a,h)anthracene and their related "K-region" epoxides, cis-dihydrodiols and phenols by hamster embryo cells. Bioche. Pharm. 1973, 22, 1–8. [Google Scholar] [CrossRef]
- Geancintov, N.E.; Cosman, M.; Hingerty, B.E.; Amin, S.; Broyde, S.; Patel, D.J. NMRsolutionstructures of stereoisomericcovalentpolycyclicaromaticcarcinogen-DNAadducts: Principles, patterns, and diversity. Chem. Res. Toxicol. 1997, 10, 111–146. [Google Scholar] [CrossRef]
- Heidelberger, C. Chemical oncogenesis in culture. Advan. Cancer. Res. 1973, 18, 317–366. [Google Scholar] [CrossRef]
- Glatt, H.; Vogel, K.; Bentley, P. Large differences in metabolic activation and inactivation of chemically closely related compounds: Effects of pure enzymes end enzyme induction on the mutagenicity of the twelve monomethylated benz[a]anthracenes, 7,12-dimethylbenz[a]anthracene and benz[a]anthracene in the Ames test. Carcinogenesis 1981, 2, 813–821. [Google Scholar] [CrossRef]
- Coombs, M.M.; Dixon, C.; Kissonerghis, A.M. Evaluation of the mutagenicity of compounds of known carcinogenicity, belonging to the benz[a]anthracene, chrysene, and cyclopenta[a]phenanthrene series, using Ames's test. Cancer Res. 1976, 36, 4525–4529. [Google Scholar]
- Norpoth, K.; Kemena, A.; Jacob, J.; Schumann, C. The influence of 18 environmentally relevant polycyclic aromatic hydrocarbons and Clophen A50, as liver monooxygenase inducers, on the mutagenic activity of benz[a]anthracene in the Ames test. Carcinogenesis 1984, 5, 747–752. [Google Scholar] [CrossRef]
- MacNicoll, A.D.; Cooper, C.S.; Ribeiro, O. The metabolic activation of benz[a]anthracene in three biological systems. Cancer Lett. 1981, 11, 243–249. [Google Scholar] [CrossRef]
- Seike, K.; Murata, M.; Oikawa, S.; Hiraku, Y.; Hirakawa, K.; Kawanishi, S. Oxidative DNA Damage Induced by Benz[a]anthracene Metabolites via Redox Cycles of Quinone and Unique Non-Quinone. Chem. Res. Toxicol. 2003, 16, 1470–1476. [Google Scholar] [CrossRef]
- Devillers, J. J. Genetic algorithms in molecular modeling. Academic Press, 1996. [Google Scholar]
- Rogers, D.; Hopfinger, A.J. Application of genetic function approximation to quantitative structure-activity relationships and quantitative structure-property relationships. J. Chem. Inf. Comput. Sci. 1994, 34, 854–866. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in artificial and natural systems. University of Michigan Press, 1975. [Google Scholar]
- Friedman, J. Multivariate adaptive regression splines. Technical Report 102. Laboratory for Computational Statistics, Department of Statistics, Stanford University: Stanford, CA, 1988; revised 1990. [Google Scholar]
- Myers, L.E.; Sexton, N.H.; Southerland, L.I.; Wolff, T.J. Regression analysis of Ames test data. Environ. Mutagen. 1981, 3, 575–586. [Google Scholar] [CrossRef]
- Smith, C.J.; Hansch, C.; Morton, M.J. QSAR treatment of multiple toxicities: the mutagenicity and cytotoxicity of quinolines. Mutation Res. 1997, 379, 167–175. [Google Scholar] [CrossRef]
- Cerius2, Version 3.5. Molecular Simulations Inc.: San Diego, CA.
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, afullperiodictable force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Rappé, K.; Goddard III, W.A. Charge equilibration for molecular dynamics simulation. J. Phys. Chem. 1991, 95, 3358–3363. [Google Scholar] [CrossRef]
- Hansch, C.; Fujita, T. ρ-σ-π analysis. A method for the correlation of biological activity and chemical structure. J. Am. Chem. Soc. 1964, 86, 1616–1626. [Google Scholar] [CrossRef]
- Kubinyi, H. QSAR: Hansch analysis and related approaches, VCH. 1993. [Google Scholar]
- Stanton, T.; Jurs, P.C. Development and use of charged partial surface area structural descripters in computer-assisted quantitative structure-property relationship studies. Anal. Chem. 1990, 62, 2323–2329. [Google Scholar] [CrossRef]
- Ghose, A.; Crippen, G. Atomic physicochemical parameters for three-dimensional structure directed quantitative structure-activity relationships I. Partition coefficients as a measure of hydrophobicity. J. Comp. Chem. 1986, 7, 565–577. [Google Scholar] [CrossRef]
- Hopfinger, J. Polymer-Solvent Interactions for Homopolypeptides in Aqueous Solution. Macromolecules 1971, 4, 731–737. [Google Scholar] [CrossRef]
© 2006 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kim, D.; Hong, S.-I.; Lee, D.-S. The Quantitative Structure-Mutagenicity Relationship of Polycylic Aromatic Hydrocarbon Metabolites. Int. J. Mol. Sci. 2006, 7, 556-570. https://doi.org/10.3390/i7120556
Kim D, Hong S-I, Lee D-S. The Quantitative Structure-Mutagenicity Relationship of Polycylic Aromatic Hydrocarbon Metabolites. International Journal of Molecular Sciences. 2006; 7(12):556-570. https://doi.org/10.3390/i7120556
Chicago/Turabian StyleKim, Dooil, Suk-In Hong, and Dae-Sil Lee. 2006. "The Quantitative Structure-Mutagenicity Relationship of Polycylic Aromatic Hydrocarbon Metabolites" International Journal of Molecular Sciences 7, no. 12: 556-570. https://doi.org/10.3390/i7120556
APA StyleKim, D., Hong, S.-I., & Lee, D.-S. (2006). The Quantitative Structure-Mutagenicity Relationship of Polycylic Aromatic Hydrocarbon Metabolites. International Journal of Molecular Sciences, 7(12), 556-570. https://doi.org/10.3390/i7120556



