Abstract
Molecular modeling and MTD methods are useful tools to assess both qualitative (SAR) and quantitative (QSAR) chemical structure-biological activity relationships. The 1-[(2-hydroxiethoxi)-methyl]-6-(phenylthio)thymine congeners (HEPT ligands) show in vitro anti-viral activity against the type-1 human immunodeficiency virus (HIV-1), which is the etiologic agent of AIDS. This work shows an extensive QSAR study performed upon a large series of 79 HEPT ligands using the MTD and HyperChem molecular modeling methods. The studied HEPT ligands are HIV reverse-transcriptase inhibitors. Their geometries were optimized and conformational analysis was carried out to build the hypermolecule, which allowed applying the MTD method. The hypermolecule was used for space mapping of the receptor’s interaction site. The obtained results show that there are three 3D molecular zones important for the anti-HIV biological activity of the HEPT ligands under study.
1. Introduction
The acquired immunodeficiency syndrome (AIDS) appears due to an infection process with viral agents belonging to the retrovirus family: human immunodeficiency viruses 1 (HIV-1) and 2 (HIV-2) [1,2]. HIV-1 is the main etiological agent of the disease. It attacks lymphocytes expressing CD4 molecules affecting profoundly the cellular mediated immunity [3]. Thus, in time, the HIV-1 infection leads to the clearance of T-CD4 lymphocytes (T helper lymphocytes) allowing the appearance of several potential lethal complications: infections with opportunistic agents, carcinomas. The HIV virus contains a single RNA chain being limited by an envelope. There are genetic differences between the two types [4,5]. Actually, the research by means of discovering new pharmacological anti-HIV agents is oriented towards identifying the essential critical steps of viral replication. The most studied is the reverse enzymatic transcription of genomic viral RNA (implying the reverse-transcriptase RT pathway) into double chained DNA. The new formed DNA migrates into the host cell nucleus and it is integrated into its genome by the viral integrase. Most anti-HIV agents approved by the FDA (Food and Drug Administration, USA) are RT-inhibitors [6] and they are 2’,3’-dideoxynucleosidic substrate analogs (ddN), like zidovudine (AZT). Other studies proved the anti-HIV inhibition capacity of other pharmacological agents with a different chemical structure. Thus, new drugs have been developed, belonging to non-nucleoside congeners, NN (nevirapine). ddN ligands are analogs of the natural substrate, the triphosphate of dezoxynucleoside. They interact with a binding site at the level of RT. This interaction is possible in vivo when ddN compounds are phosphorilated resulting dezoxynucleosidic 5’-phosphorilated derivatives. Only in this way it is possible these compounds to inhibit competitively the natural substrates (dTTP, dCTP, dATP and dGTP) [7].
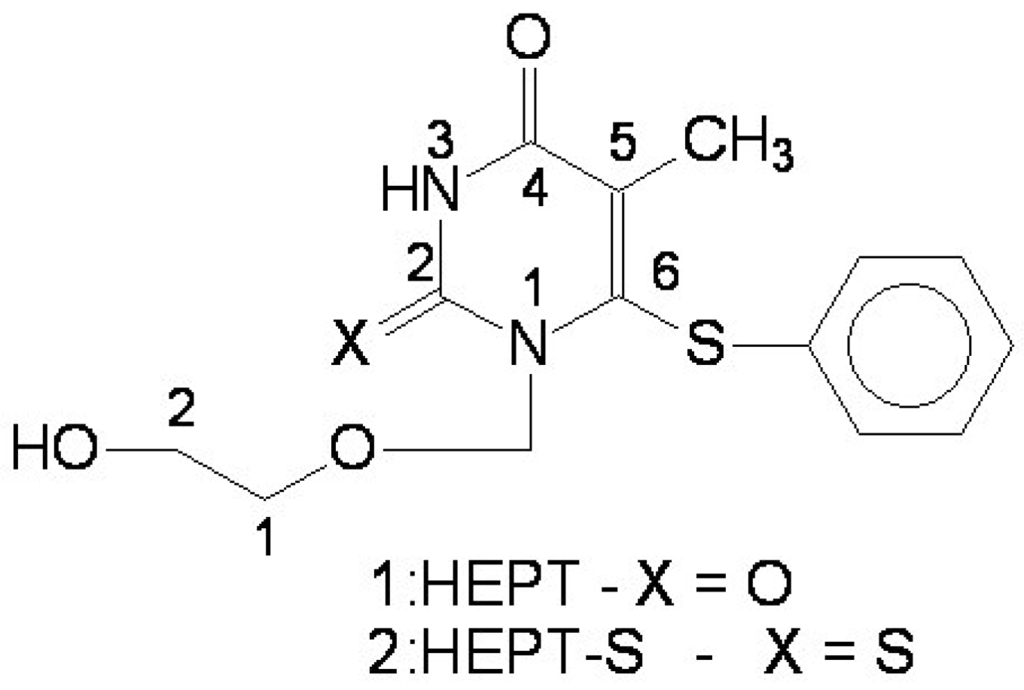
Figure 1.
The structure of HEPT: 1-[(2-hydroxiethoxi)-methyl]-6-(phenylthio) thymine.
The 1-[(2-hydroxiethoxi)-methyl]-6-(phenylthio) thymine congeners (HEPT ligands) [8] – see Figure 1 – show in vitro antiviral activity against HIV-1. HEPT ligands inhibit exclusively HIV-1 replication, showing no effect upon other retroviruses including HIV-2. Extensive studies [9] upon synthesis and biological activity of HEPT derivatives showed that methyl in position 5, a cyclic structure in position 6 and a two-atoms HN-3 constellation are essential elements to promote the anti-HIV activity. Tanaka et al. [10] concluded that also derivatives 2: HEPT-S have an improved antiviral activity. This is why studies upon HEPT ligands that inhibit the viral reverse-transcriptase (RT) were structurally extended and major interest was shown to analyze the anti-HIV activity depending on the variation of substituents on the phenyl ring and upon C-5 as well [10]. Experimental biological activities led to structure-activity studies, yet only concerning qualitative aspects (SAR), by means of presence or absence of atomic groups in certain positions on the HEPT general structure shown in Figure 1.
Our research is focused on quantitative chemical structure – biologic activity studies based on a 3D method, the Minimal Topological Difference method (MTD). This method, beyond the improved correlation equation delivers also a structural stereochemical requirement necessary for an optimal HEPT ligand attack estimation on the HIV-1 virus.
2. The MTD (Minimal Topological Difference) Method
Following the Fisher’s old “key-into-lock” idea [11], the main premise of the MTD approach is that each potential ligand Li should fit at the best into the binding site of the receptor and that the larger the ligand-binding site misfit, the lower affinity, i.e. the biologic activity Ai, would be [12]. For quantifying of this steric assumption the QSAR group of Timişoara developed through years the MTD method among the consecrated 3D-QSAR techniques [13,14].
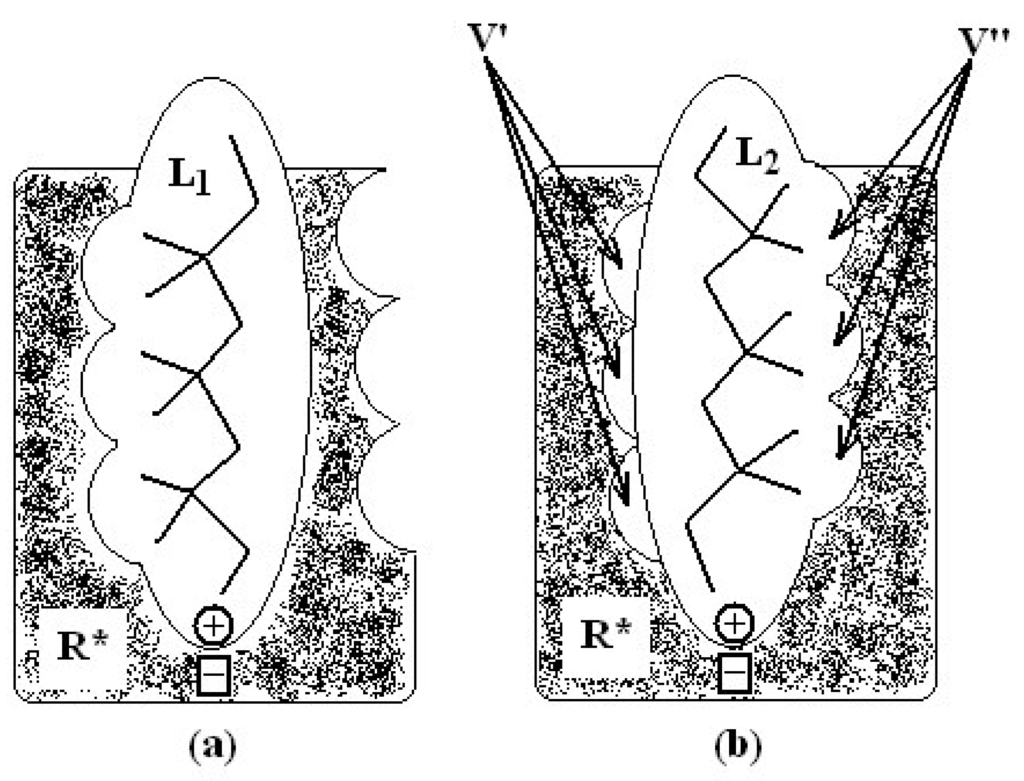
Figure 2.
Schematic illustration of the MTD principle, namely the biological activity is proportional with the binding degree between the ligands (L1, L2) and the receptor R: in (a) as perfect matching and in (b) as the misfit relating the total volume V’+V’’.
Basically, the analytical formulation of MTD can be understood in terms of volume effective picture. In such, the decrease of the ligand affinity to the biologic receptor parallels the increase of their un-overlapped volumes. To better sustain this idea, in Figure 2 there are illustrated two ligand molecules: L1 that perfectly matches with the binding site of the receptor R, and other, say L2, which do not cover the volume V’ and additionally producing the V’’ volume deformation in the cavity of the binding site receptor R, in (a) and (b), respectively. Since the total steric misfit of the ligand L2 is proportional with the volume V’+V’’ a viable way of quantifying this property of the ligand-receptor interaction provides a steric parameter to be accounted of in a QSAR correlation equation.
To achieve the MTD steric parameters, firstly, worth recalling that, in general, two operation types are used to compare the molecular stereochemistry:
- molecular superposition, based on certain common molecular elements or on a “pharmacophoral” constellation” of the atoms, and
- defining equivalent positions.
These positions, together with the bonds between them, form a so called “hyperstructure” with both topological and geometrical connotations.
In this context, let’s consider N molecules Li (I=1, 2,…, N) with known activities Ai for which we wish to obtain a structure-activity correlation equation so that to pose minimum steric/topologic differences MTDi as a quantitative degree of their misfit with the receptor’s cavity [15]. In short, the MTD method implies the construction and optimization of the so called hypermolecule (H) from where the QSAR equation follows. However, the construction stage requires the superposition of the second or higher period atoms X or XHn, being the hydrogen atoms “contracted” within their bond atoms X. The molecules with fixed orientation are superimposed as atom-over-atom. As a base, an active rigid molecule S will be considered over which all other molecules are superimposed in a maximum way; that is, whenever atoms of different Li give out inter-distances less than 0.5Ǻ, when superimposed or respecting the atoms of the benchmark S molecule, they are considered as belonging to the same vertex j of the hypermolecule H. The resulting vertices j, j = 1,M, represent the approximate positions of the atoms in the R*Li complex, while edges embody the valence bonds between atoms. The activated R*Li complex results from the receptor-ligand interaction:
where R* is the active conformation of the receptor, induced by the Li ligand binding.
R(aq) + Li (aq) → R*Li(aq) + nH2O,
Since hydrogen atoms are neglected in the obtained hypermolecule each ligand Li is described by a “vector” {Xij} with binary components (xij=0, 1). If the vertex j from Li is not occupied, then xij = 0 otherwise xij=1. The minimal topological difference MTDi of molecule “i” with respect to the receptor is calculated according to the following formula [11,12,13,14,15,16,17,18]:
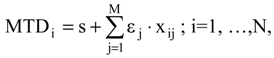 where εj = -1, 0 or +1 for vertices attributed to the receptor cavity (beneficial for the biological activity), to the exterior (irrelevant) and to the receptor walls (detrimental), respectively, while s is the total number of cavity vertices (with εj = -1). In these condition, the term
where εj = -1, 0 or +1 for vertices attributed to the receptor cavity (beneficial for the biological activity), to the exterior (irrelevant) and to the receptor walls (detrimental), respectively, while s is the total number of cavity vertices (with εj = -1). In these condition, the term 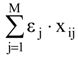 in (2) represents the summation over both the vertices of cavity of R that are not occupied by the ligand Li as well as of those from the wall of R being occupied by the atoms of Li, unless the hydrogen atoms, in equation (1), respectively. As a consequence, the key relation (2) gives the analytical quantification of the steric relation between each ligand „i” of the total tested N respecting the available M vertices of receptor R in the course of bonding. Thus, the degree of steric misfit for the molecule Li with respect to the receptor, i.e. MTDi, is defined as the sum of the number of unoccupied cavity vertices of H and the number of occupied wall vertices of H. If Li shows more low energy conformations, k = 1,…,Ci (Ci is the number of conformations of molecule I), the conformation that fits best in the receptor site will be retained through the modified version of equation (2):
in (2) represents the summation over both the vertices of cavity of R that are not occupied by the ligand Li as well as of those from the wall of R being occupied by the atoms of Li, unless the hydrogen atoms, in equation (1), respectively. As a consequence, the key relation (2) gives the analytical quantification of the steric relation between each ligand „i” of the total tested N respecting the available M vertices of receptor R in the course of bonding. Thus, the degree of steric misfit for the molecule Li with respect to the receptor, i.e. MTDi, is defined as the sum of the number of unoccupied cavity vertices of H and the number of occupied wall vertices of H. If Li shows more low energy conformations, k = 1,…,Ci (Ci is the number of conformations of molecule I), the conformation that fits best in the receptor site will be retained through the modified version of equation (2):
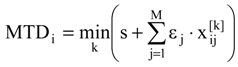
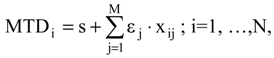
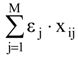 in (2) represents the summation over both the vertices of cavity of R that are not occupied by the ligand Li as well as of those from the wall of R being occupied by the atoms of Li, unless the hydrogen atoms, in equation (1), respectively. As a consequence, the key relation (2) gives the analytical quantification of the steric relation between each ligand „i” of the total tested N respecting the available M vertices of receptor R in the course of bonding. Thus, the degree of steric misfit for the molecule Li with respect to the receptor, i.e. MTDi, is defined as the sum of the number of unoccupied cavity vertices of H and the number of occupied wall vertices of H. If Li shows more low energy conformations, k = 1,…,Ci (Ci is the number of conformations of molecule I), the conformation that fits best in the receptor site will be retained through the modified version of equation (2):
in (2) represents the summation over both the vertices of cavity of R that are not occupied by the ligand Li as well as of those from the wall of R being occupied by the atoms of Li, unless the hydrogen atoms, in equation (1), respectively. As a consequence, the key relation (2) gives the analytical quantification of the steric relation between each ligand „i” of the total tested N respecting the available M vertices of receptor R in the course of bonding. Thus, the degree of steric misfit for the molecule Li with respect to the receptor, i.e. MTDi, is defined as the sum of the number of unoccupied cavity vertices of H and the number of occupied wall vertices of H. If Li shows more low energy conformations, k = 1,…,Ci (Ci is the number of conformations of molecule I), the conformation that fits best in the receptor site will be retained through the modified version of equation (2):
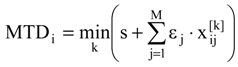
In these conditions, the regression equation type of the MTD method looks like:
where Pi, i= 1,2,…, represent other structural parameters that can be used during the optimization process or after obtaining the optimized receptor chart, say S*, using the corresponding optimized MTD* values.
A = α0 + α1·P1 + α2·P2 +…−β·MTD,
However, the present picture holds under the assumption that the necessary energy to correct the steric misfit shows a linear variation with the corresponding volume misfit. The minus sign in (4) is in agreement with the fact that the biological activity decreases with the ligand steric misfit degree.
The optimization procedure starts from an initial 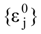 attribution set, the beginning chart S0. Then, one has to calculate the
attribution set, the beginning chart S0. Then, one has to calculate the 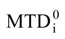 values and, by employing the multi-linear regression analysis, the regression coefficients in the above equation (4) and the associate correlation coefficient are computed. The algorithm continues with one by one modification of εj attributions resulting in a number of 2M mono-substituted charts, with the respective MTDi values together with 2M correlation equations of type (4) and their correlation coefficients. The mono-substituted chart with the highest correlation coefficient r from all 2M outputs is taken as starting point for the next cycle. The process continues until the regression coefficient r doesn’t increase anymore. The final increase anymore. The final {εj} set of values, j = 1,M, represents the optimized receptor chart, S*, and provides through their employment in equation (2) the optimized predictor variables MTD* for the QSAR problem [18].
values and, by employing the multi-linear regression analysis, the regression coefficients in the above equation (4) and the associate correlation coefficient are computed. The algorithm continues with one by one modification of εj attributions resulting in a number of 2M mono-substituted charts, with the respective MTDi values together with 2M correlation equations of type (4) and their correlation coefficients. The mono-substituted chart with the highest correlation coefficient r from all 2M outputs is taken as starting point for the next cycle. The process continues until the regression coefficient r doesn’t increase anymore. The final increase anymore. The final {εj} set of values, j = 1,M, represents the optimized receptor chart, S*, and provides through their employment in equation (2) the optimized predictor variables MTD* for the QSAR problem [18].
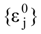 attribution set, the beginning chart S0. Then, one has to calculate the
attribution set, the beginning chart S0. Then, one has to calculate the 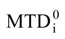 values and, by employing the multi-linear regression analysis, the regression coefficients in the above equation (4) and the associate correlation coefficient are computed. The algorithm continues with one by one modification of εj attributions resulting in a number of 2M mono-substituted charts, with the respective MTDi values together with 2M correlation equations of type (4) and their correlation coefficients. The mono-substituted chart with the highest correlation coefficient r from all 2M outputs is taken as starting point for the next cycle. The process continues until the regression coefficient r doesn’t increase anymore. The final increase anymore. The final {εj} set of values, j = 1,M, represents the optimized receptor chart, S*, and provides through their employment in equation (2) the optimized predictor variables MTD* for the QSAR problem [18].
values and, by employing the multi-linear regression analysis, the regression coefficients in the above equation (4) and the associate correlation coefficient are computed. The algorithm continues with one by one modification of εj attributions resulting in a number of 2M mono-substituted charts, with the respective MTDi values together with 2M correlation equations of type (4) and their correlation coefficients. The mono-substituted chart with the highest correlation coefficient r from all 2M outputs is taken as starting point for the next cycle. The process continues until the regression coefficient r doesn’t increase anymore. The final increase anymore. The final {εj} set of values, j = 1,M, represents the optimized receptor chart, S*, and provides through their employment in equation (2) the optimized predictor variables MTD* for the QSAR problem [18]. 3. Computational Details
Most actual molecular modeling strategies provide computable data about the analyzed molecular systems, and, also, 3D extended data. The current work summarizes the studies [19] performed upon a series of HEPT derivatives with structural variations in available positions of the uracyl ring, Figure 3.
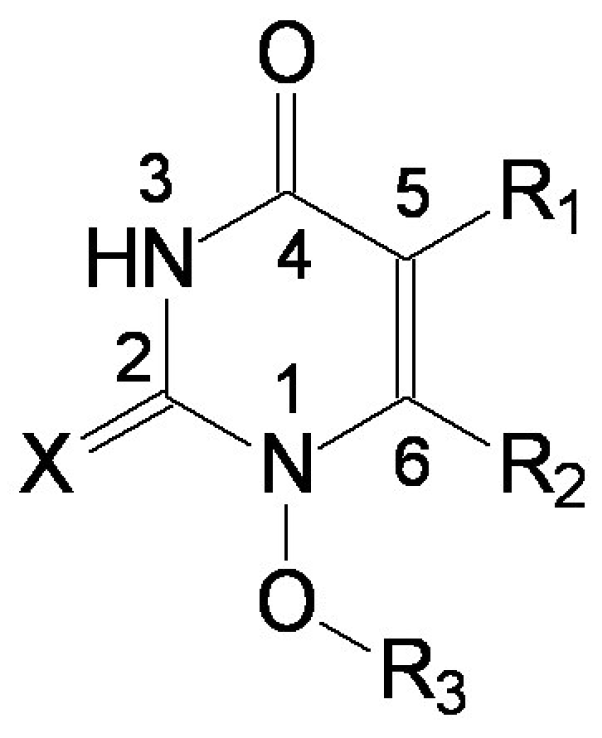
Figure 3.
The envisaged positions for substituents of the uracyl ring.
Different substituents in C-5 and C-6 positions on the phenyl ring (bounded by oxygen or a sulphur bridge at C-6) allow for HEPT series to be studied [8,20,21]. The recorded effects of various substituents, different from 1-[(2-hydroxiethoxy)-methyl], correlates with the capacity to inhibit the enzyme implied in the inverse transcription of RNA into DNA – reverse-transcriptase (RT) enzyme, of which the observed biologic effect stands as the anti-HIV activity. Table I shows the structures of the 79 HEPT derivatives [21] under actual study.

Table I.
The series of structures of the studied HEPT ligand molecules of types of Figure 3.
| i/Li | R1 | R2 | R3 | X |
|---|---|---|---|---|
| 1 | methyl | 2-methylphenylthio | 2-hidroxyethyl | O |
| 2 | methyl | 2-nitrophenhylthio | 2-hidroxyethyl | O |
| 3 | methyl | 2-methoxyphenylthio | 2-hidroxyethyl | O |
| 4 | methyl | 3-metilfeniltio | 2-hidroxietil | O |
| 5 | methyl | 3-ethylphenylthio | 2-hidroxyethyl | O |
| 6 | methyl | 3- tertbuthylphenylthio | 2-hidroxyethyl | O |
| 7 | methyl | 3-trifluoromethylphenylthio | 2-hidroxyethyl | O |
| 8 | methyl | 3-fluorophenylthio | 2-hidroxyethyl | O |
| 9 | methyl | 3-clorophenylthio | 2-hidroxyethyl | O |
| 10 | methyl | 3-bromophenylthio | 2-hidroxyethyl | O |
| 11 | methyl | 3-iodophenylthio | 2-hidroxyethyl | O |
| 12 | methyl | 3-nitrophenylthio | 2-hidroxyethyl | O |
| 13 | methyl | 3-hidroxyphenylthio | 2-hidroxyethyl | O |
| 14 | methyl | 3-metoxyphenylthio | 2-hidroxyethyl | O |
| 15 | methyl | 3,5-dimetilphenylthio | 2-hidroxyethyl | O |
| 16 | methyl | 3,5-diclorophenylthio | 2-hidroxyethyl | O |
| 17 | methyl | 3,5-dimethylphenylthio | 2-hidroxyethyl | S |
| 18 | methyl | 3-metoxycarbonylphenylthio | 2-hidroxyethyl | O |
| 19 | methyl | 3-acetylphenylthio | 2-hidroxyethyl | O |
| 20 | methyl | 3-cyanophenylthio | 2-hidroxyethyl | O |
| 21 | allyl | phenylthio | 2-hidroxyethyl | O |
| 22 | ethyl | phenylthio | 2-hidroxyethyl | S |
| 23 | propyl | phenylthio | 2-hidroxyethyl | S |
| 24 | isopropyl | phenylthio | 2-hidroxyethyl | S |
| 25 | ethyl | 3,5-dimethylphenylthio | 2-hidroxyethyl | S |
| 26 | isopropyl | 3,5-dimethylphenylthio | 2-hidroxyethyl | S |
| 27 | ethyl | 3,5-diclorophenylthio | 2-hidroxyethyl | S |
| 28 | ethyl | phenylthio | 2-hidroxyethyl | O |
| 29 | propyl | phenylthio | 2-hidroxyethyl | O |
| 30 | isopropyl | phenylthio | 2-hidroxyethyl | O |
| 31 | ethyl | 3,5-dimetylphenylthio | 2-hidroxyethyl | O |
| 32 | isopropyl | 3,5-dimetylphenylthio | 2-hidroxyethyl | O |
| 33 | ethyl | 3,5-diclorophenylthio | 2-hidroxyethyl | O |
| 34 | methyl | 4-metylphenylthio | 2-hidroxyethyl | O |
| 35 | methyl | phenylthio | 2-hidroxyethyl | O |
| 36 | methyl | phenylthio | 2-hidroxyethyl | S |
| 37 | iodo | phenylthio | 2-hidroxyethyl | O |
| 38 | ethenyl | phenylthio | 2-hidroxyethyl | O |
| 39 | 2-phenylethenyl | phenylthio | 2-hidroxyethyl | O |
| 40 | benzyl | phenylthio | 2-hidroxyethyl | O |
| 41 | methyl | phenylthio | 2-metoxyethyl | O |
| 42 | methyl | phenylthio | 2-acetyloxyethyl | O |
| 43 | methyl | phenylthio | 2-benzoyloxyethyl | O |
| 44 | methyl | phenylthio | ethyl | O |
| 45 | methyl | phenylthio | 2-cloroethyl | O |
| 46 | methyl | phenylthio | 2-azidoethyl | O |
| 47 | methyl | phenylthio | 2-fluoroethyl | O |
| 48 | methyl | phenylthio | propyl | O |
| 49 | methyl | phenylthio | benzyl | O |
| 50 | ethyl | phenylthio | ethyl | O |
| 51 | ethyl | phenylthio | ethyl | S |
| 52 | ethyl | 3,5-dimethylphenylthio | ethyl | O |
| 53 | ethyl | 3,5-dimethylphenhylthio | ethyl | S |
| 54 | ethyl | phenylthio | benzyl | O |
| 55 | ethyl | 3,5-dimethylphenylthio | benzyl | O |
| 56 | ethyl | phenylthio | benzyl | S |
| 57 | ethyl | 3,5-dimethylphenylthio | benzyl | S |
| 58 | isopropyl | phenylthio | ethyl | O |
| 59 | isopropyl | phenylthio | benzyl | O |
| 60 | isopropyl | phenylthio | ethyl | S |
| 61 | isopropyl | phenylthio | benzyl | S |
| 62 | methyl | phenylthio | methyl | O |
| 63 | methyl | phenylthio | butyl | O |
| 64 | methyl | phenylthio | methyl | S |
| 65 | methyl | phenylthio | propyl | S |
| 66 | ethyl | 3,5-diclorophenylthio | ethyl | S |
| 67 | ethyl | phenylthio | isopropyl | S |
| 68 | ethyl | phenylthio | cyclohexyl | S |
| 69 | ethyl | phenylthio | cyclohexylmethyl | S |
| 70 | ethyl | phenylthio | 4-methylbenzyl | S |
| 71 | ethyl | phenylthio | 4-clorobenzyl | S |
| 72 | ethyl | phenylthio | 2-phenylethyl | S |
| 73 | ethyl | 3,5-diclorophenylthio | ethyl | O |
| 74 | ethyl | phenylthio | isopropyl | O |
| 75 | ethyl | phenylthio | cyclohexyl | O |
| 76 | ethyl | phenylthio | cyclohexylmethyl | O |
| 77 | ethyl | phenylthio | 2-ciclohexylethyl | O |
| 78 | cyclopropyl | phenylthio | ethyl | S |
| 79 | cyclopropyl | phenylthio | ethyl | O |
Molecular modeling and conformational analysis were performed using the HyperChem 7.01 program package (MM+ program) [22] with conjugated gradient was employed for the optimization of geometries of the ligands Li of the Table I.
The work conditions are the following:
- flexible torsion angles variation: ±60º - ±180º;
- energetic criteria to accept a conformation: 4 kcal/mol above the minimum;
- conformation cancellation: for atoms with distances less than 0.5 Å and torsion angles differences less than 15º;
- duplicate conformations: energy differences less than 0.05 kcal/mol;
- optimization program: MM+;
- optimization algorithm: Polak-Ribiere;
- optimization RMS (root mean square value) gradient: 0.05 kcal/mol;
- maximum iterations: 250;
- maximum optimizations: 250;
- maximum retained conformations: 20.
Conformational analysis allowed the most stable conformations (with the lowest energy level) for each of the 79 HEPT ligands of Table I. The 79 minimal energy conformations optimized with the MM+ program were superposed on the cyclic structure: pyrimidine-2,4(1H,3H)-dione.
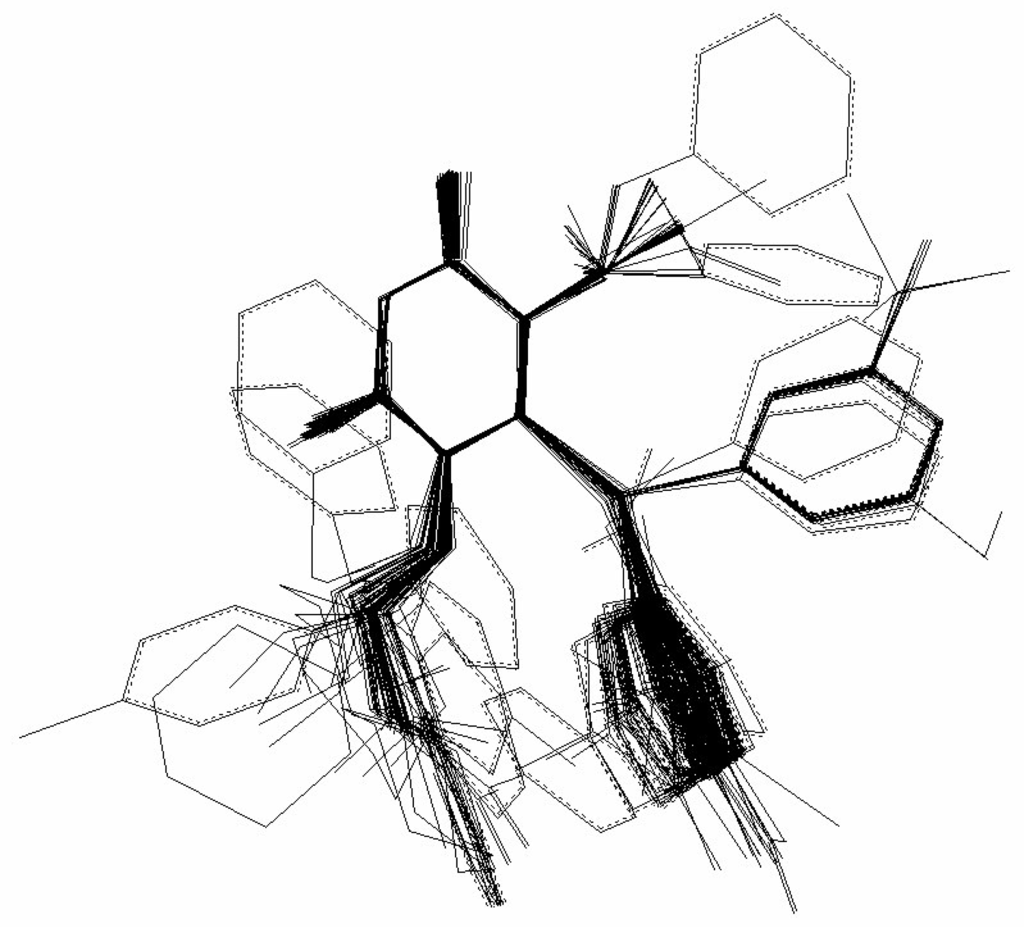
Figure 4.
Superposition of the minimum energy conformations of the 79 ligands from Table I.
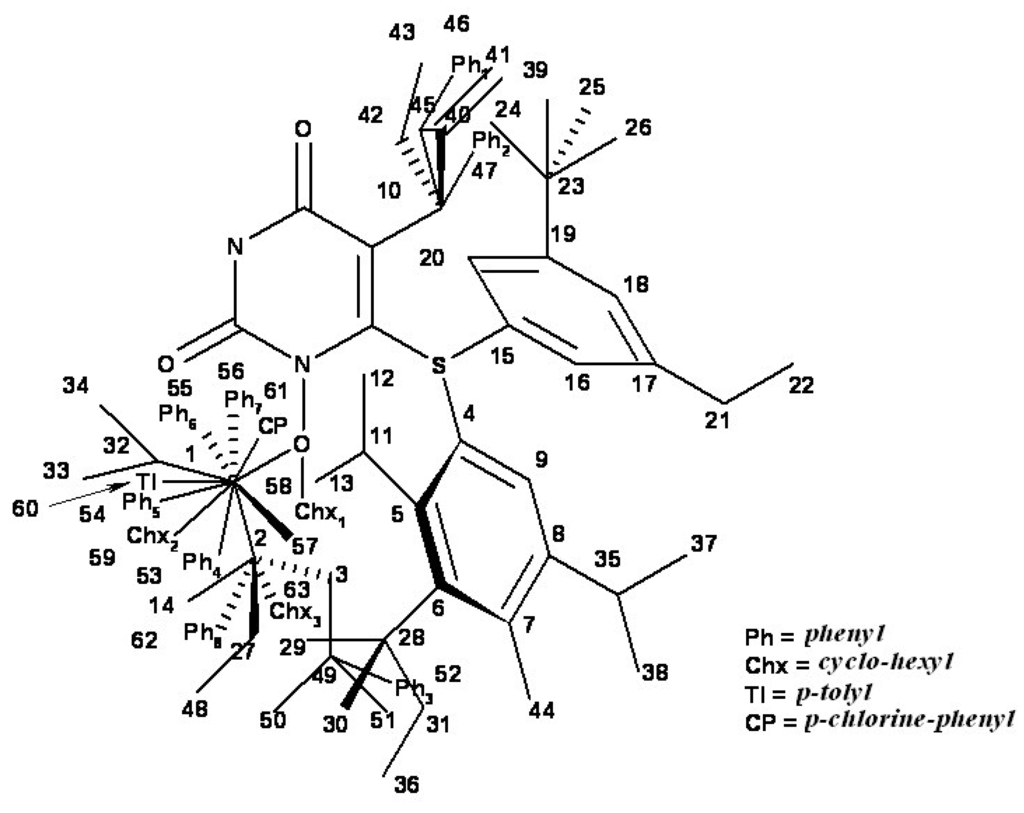
Figure 5.
Hypermolecule H obtained by superposition of the minimum energy conformations of the 79 HEPT derivatives (M = 63 vertices).
The superposition of conformers was performed using the HyperChem 7.01 program in order to minimize the sum of square distances between equivalent atoms. As stated before, when the distances between the atoms, after the superposing procedure, were above than 0.5 Å, a new vertex was created.
| i/Li | Vertices occupancy in hypermolecule | i/Li | Vertices occupancy in hypermolecule |
|---|---|---|---|
| 1 | 1,2,3,4,5,6,7,8,9,10,11 | 41 | 1,2,4,5,6,7,8,9,10,27,48 |
| 2 | 1,2,3,4,5,6,7,8,9,10,11,12,13 | 42 | 1,2,3,4,5,6,7,8,9,10,49,50,51 |
| 3 | 1,2,4,5,6,7,8,9,10,11,12,14 | 43 | 1,2,3,4,5,6,7,8,9,10,49,50,51,52 |
| 4 | 1,2,3,4,5,6,7,8,9,10,11 | 44 | 1,2,4,5,6,7,8,9,10 |
| 5 | 1,2,3,10,15,16,17,18,19,20,21,22 | 45 | 1,2,3,4,5,6,7,8,9,10 |
| 6 | 1,2,10,14,15,16,17,18,19,20,23,24,25,26 | 46 | 1,2,3,4,5,6,7,8,9,10,49,50 |
| 7 | 1,2,4,5,6,7,8,9,10,27,28,29,30,31 | 47 | 1,2,3,4,5,6,7,8,9,10 |
| 8 | 1,4,5,6,7,8,9,10,28,32,33 | 48 | 1,2,3,4,5,6,7,8,9,10 |
| 9 | 1,2,3,10,15,16,17,18,19,20,23 | 49 | 1,4,5,6,7,8,9,10,53 |
| 10 | 1,2,3,10,15,16,17,18,19,20,23 | 50 | 1,2,4,5,6,7,8,9,10,40 |
| 11 | 1,2,3,10,15,16,17,18,19,20,23 | 51 | 1,2,3,4,5,6,7,8,9,10,42 |
| 12 | 1,2,3,4,5,6,7,8,9,10,28,29,31 | 52 | 1,2,3,4,5,6,7,8,9,10,28,35,40 |
| 13 | 1,2,3,10,15,16,17,18,19,20,23 | 53 | 1,2,3,4,5,6,7,8,9,10,28,35,42 |
| 14 | 1,10,15,16,17,18,19,20,23,26,32,34 | 54 | 1,4,5,6,7,8,9,10,40,53 |
| 15 | 1,2,3,10,15,16,17,18,19,20,21,23 | 55 | 1,4,5,6,7,8,9,10,28,35,40,53 |
| 16 | 1,2,3,4,5,6,7,8,9,10,28,35 | 56 | 1,4,5,6,7,8,9,10,42,54 |
| 17 | 1,2,3,4,5,6,7,8,9,10,28,35 | 57 | 1,4,5,6,7,8,9,10,28,35,42,55 |
| 18 | 1,2,3,4,5,6,7,8,9,10,28,29,31,36 | 58 | 1,2,3,4,5,6,7,8,9,10,40,42 |
| 19 | 1,2,3,4,5,6,7,8,9,10,35,37,38 | 59 | 1,4,5,6,7,8,9,10,40,42,53 |
| 20 | 1,2,10,15,16,17,18,19,20,23,27,39 | 60 | 1,2,3,4,5,6,7,8,9,10,40,42 |
| 21 | 1,2,3,4,5,6,7,8,9,10,40,41 | 61 | 1,4,5,6,7,8,9,10,40,42,56 |
| 22 | 1,4,5,6,7,8,9,10,32,34,42 | 62 | 1,4,5,6,7,8,9,10 |
| 23 | 1,4,5,6,7,8,9,10,32,34,42,43 | 63 | 1,2,3,4,5,6,7,8,9,10,49 |
| 24 | 1,10,15,16,17,18,19,20,32,34,40,42 | 64 | 1,4,5,6,7,8,9,10 |
| 25 | 1,4,5,6,7,8,9,10,28,32,34,35,40 | 65 | 1,2,3,4,5,6,7,8,9,10 |
| 26 | 1,4,5,6,7,8,9,10,28,32,34,35,40,42 | 66 | 1,2,4,5,6,7,8,9,10,28,35,40 |
| 27 | 1,4,5,6,7,8,9,10,28,32,34,35,40 | 67 | 1,2,4,5,6,7,8,9,10,40,57 |
| 28 | 1,2,3,4,5,6,7,8,9,10,40 | 68 | 4,5,6,7,8,9,10,40,58 |
| 29 | 1,2,3,4,5,6,7,8,9,10,40,41 | 69 | 1,4,5,6,7,8,9,10,40,59 |
| 30 | 1,2,3,4,5,6,7,8,9,10,40,42 | 70 | 1,4,5,6,7,8,9,10,40,60 |
| 31 | 1,2,3,4,5,6,7,8,9,10,28,35,40 | 71 | 1,4,5,6,7,8,9,10,41,61 |
| 32 | 1,2,3,4,5,6,7,8,9,10,28,35,40,42 | 72 | 1,2,4,5,6,7,8,9,10,40,62 |
| 33 | 1,2,4,5,6,7,8,9,10,27,28,35,40 | 73 | 1,4,5,6,7,8,9,10,28,35,42,57 |
| 34 | 1,4,5,6,7,8,9,10,32,34,44 | 74 | 1,2,4,5,6,7,8,9,10,40 |
| 35 | 1,4,5,6,7,8,9,10,32,33 | 75 | 4,5,6,7,8,9,10,40,58 |
| 36 | 1,4,5,6,7,8,9,10,32,34 | 76 | 1,4,5,6,7,8,9,10,42,59 |
| 37 | 1,2,10,14,15,16,17,18,19,20 | 77 | 1,2,4,5,6,7,8,9,10,40,63 |
| 38 | 1,2,3,4,5,6,7,8,9,10,45 | 78 | 1,2,3,4,5,6,7,8,9,10,40,45 |
| 39 | 1,2,3,4,5,6,7,8,9,10,45,46 | 79 | 1,2,4,5,6,7,8,9,10,40,45 |
| 40 | 1,2,4,5,6,7,8,9,10,27,47 |
Figure 4 show the superposition of the minimum energy conformations. The obtained hypermolecule has 63 vertices and it is represented in Figure 5.
The beginning chart (S0) was automatically generated with an in house program, considering the weight of “local” molecular activity depending on the occupancy degree of each vertex as in the Table II.
It has the form:


A few molecules have voluminous radicals (phenyl – Ph; cyclo-hexyl – Chx; p-tolyl – Tl; p-chlorine-phenyl – CP) in various positions of the hypermolecule. These radicals occupy singular vertices in the hypermolecule and they were reduced to a single vertex each (Ph1-8 – vertices 46, 47, 52, 53, 54, 55, 56 and 62, respectively; Chx1-3– vertices 58, 59 and 63, respectively; Tl – vertex 60; CP – vertex 61).
However, the relatively high number of (flexible) torsion angles did not allow applying this method in the multi-conformational variant. Thus, the hypermolecule H was obtained by the superposition of the minimal energy conformations – resulted from the conformational HyperChem analysis – upon the primary heterocyclic common structure of Figure 3 with the result presented in Figure 4 and Figure 5.
The validation of QSAR model was realized using the cross-validation (cv) method. This procedure implies that the series of N ligands Li with the determined activities Ai is firstly divided into two sub-series, odd and even, corresponding to the successions L1, L3, L5, …, and L2, L4, L6, …, respectively. Then, while the optimized chart S* and the correlation equation is obtained from the odd sub-series the parameters MTDi and the associated activities Ai* are evaluated for the molecules of the even sub-series. The procedure is completed through the reciprocal consideration, i.e. starting from the even sub-series the odd sub-series activities are obtained. Finally, the cross validation correlation index,
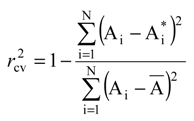 through its
through its 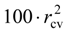 value, approximate the percent from the (experimental) biological activity variance around the average A that can be predicted with the help of the correlation equation (4) and of the optimized chart.
value, approximate the percent from the (experimental) biological activity variance around the average A that can be predicted with the help of the correlation equation (4) and of the optimized chart.
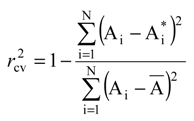
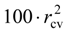 value, approximate the percent from the (experimental) biological activity variance around the average A that can be predicted with the help of the correlation equation (4) and of the optimized chart.
value, approximate the percent from the (experimental) biological activity variance around the average A that can be predicted with the help of the correlation equation (4) and of the optimized chart. 4. Results and Discussions
To analyze QSAR relations of HEPT derivatives with anti-HIV activity, experimental biological activities from Table III were used. The experimental biologic activity is Aexp = log (1/ EC50), where EC50 stands as the level that produces a 50% protection of MT-4 cells against HIV-1 cytopathic effect [8,20,21].
Three type of QSAR are here considered, namely:
- the mono-parametric model of hidrophobicity:
Ai = α0 + α1log Pi,
- the case of linear mono-parametric model where MTD is the steric parameter:
Ai = α0 − β · MTDi
- and the combined correlation
Ai = α0 + α1log Pi − βMTDi
In equations (7) and (9), hydrophobicity parameters are calculated using the „QSAR Properties” from the HyperChem [22] program package and they are listed in Table III. MTDi parameters represent the MTD* corresponding to the S* optimized chart of the receptor; α0, α1 and β express the regression parameters corresponding to the obtained QSAR studies. Ai is the calculated value of Aexp,i.
The optimization process of the hypermolecule allows to optimize the beginning chart of the receptor, S0={εj}j=1,..., M, using a subsequent changing process of vertices attribution (εj) in H, starting with the initial correlation coefficient, r0 (corresponding to the S0 beginning chart), until obtaining of a maximal correlation coefficient, rmax, corresponding to the receptor’s optimized chart, S*; the r correlation coefficient, on every step of the optimization process, is obtained by minimizing the sum of the squares of differences between experimental Aexp,i and calculated Acalc,i biological activities:
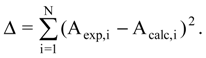
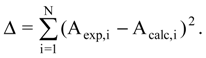
The receptor chart is considered optimized (S*) when any single new modification εj does not reduce the value of (10). S* represents a simplified image of R interacting with Li ligands.

Table III.
The structural parameters of the HEPT ligands of Table I and their biological activities against binding with HIV-1 receptor. The hydrophobicities (logP) are derived with the help of HyperChem program [22], while parameters MTD* and MTD*logP are computed with relation (3) upon the optimized charts (13) and (15), respectively. The associated calculated activities AlogP, AMTD and AMTD+logP are derived from the equations (11), (12) and (14), respectively. The experimental biologic activities (Aexp) are taken from ref. [21].
| i/Li | logP | MTD* | MTD*logP | AlogP | AMTD | AMTD+LogP | Aexp |
|---|---|---|---|---|---|---|---|
| 1 | 2.14 | 13 | 15 | 5.529 | 5.052 | 4.778 | 4.15 |
| 2 | 1.62 | 14 | 16 | 5.118 | 4.218 | 3.851 | 3.85 |
| 3 | 1.42 | 13 | 14 | 4.960 | 5.052 | 5.101 | 4.72 |
| 4 | 2.14 | 13 | 15 | 5.529 | 5.052 | 4.778 | 5.59 |
| 5 | 2.53 | 12 | 14 | 5.837 | 5.886 | 5.643 | 5.57 |
| 6 | 3.3 | 13 | 16 | 6.445 | 5.052 | 4.670 | 4.92 |
| 7 | 2.55 | 14 | 16 | 5.853 | 4.218 | 4.304 | 4.35 |
| 8 | 1.81 | 12 | 13 | 5.268 | 5.886 | 5.965 | 5.48 |
| 9 | 2.19 | 13 | 15 | 5.568 | 5.052 | 4.803 | 4.89 |
| 10 | 2.46 | 13 | 15 | 5.781 | 5.052 | 4.934 | 5.24 |
| 11 | 2.93 | 13 | 15 | 6.153 | 5.052 | 5.164 | 5,00 |
| 12 | 1.62 | 13 | 15 | 5.118 | 5.052 | 4.525 | 4.47 |
| 13 | 1.39 | 13 | 15 | 4.936 | 5.052 | 4.412 | 4.09 |
| 14 | 1.42 | 14 | 15 | 4.960 | 4.218 | 4.427 | 4.66 |
| 15 | 2.61 | 12 | 14 | 5.900 | 5.886 | 5.682 | 6.59 |
| 16 | 2.71 | 11 | 13 | 5.979 | 6.720 | 6.404 | 5.89 |
| 17 | 3.25 | 11 | 13 | 6.406 | 6.720 | 6.668 | 6.66 |
| 18 | 1.4 | 13 | 14 | 4.944 | 5.052 | 5.091 | 5.10 |
| 19 | 0.98 | 13 | 14 | 4.612 | 5.052 | 4.886 | 5.14 |
| 20 | 1.71 | 13 | 14 | 5.189 | 5.052 | 5.242 | 5,00 |
| 21 | 2.25 | 12 | 14 | 5.616 | 5.886 | 5.506 | 5.60 |
| 22 | 2.72 | 11 | 13 | 5.987 | 6.720 | 6.409 | 6.96 |
| 23 | 3.11 | 12 | 14 | 6.295 | 5.886 | 5.926 | 5,00 |
| 24 | 3.05 | 10 | 12 | 6.248 | 7.554 | 7.244 | 7.23 |
| 25 | 3.65 | 10 | 12 | 6.722 | 7.554 | 7.537 | 8.11 |
| 26 | 3.98 | 9 | 11 | 6.982 | 8.388 | 8.372 | 8.30 |
| 27 | 3.75 | 10 | 12 | 6.801 | 7.554 | 7.586 | 7.37 |
| 28 | 2.07 | 11 | 13 | 5.473 | 6.720 | 6.092 | 6.92 |
| 29 | 2.46 | 12 | 14 | 5.781 | 5.886 | 5.608 | 5.47 |
| 30 | 2.4 | 10 | 12 | 5.734 | 7.554 | 6.927 | 7.20 |
| 31 | 3 | 10 | 12 | 6.208 | 7.554 | 7.220 | 7.89 |
| 32 | 3.33 | 9 | 11 | 6.469 | 8.388 | 8.055 | 8.57 |
| 33 | 3.1 | 10 | 12 | 6.287 | 7.554 | 7.269 | 7.85 |
| 34 | 2.14 | 13 | 15 | 5.529 | 5.052 | 4.778 | 3.66 |
| 35 | 1.67 | 13 | 14 | 5.157 | 5.052 | 5.223 | 5.15 |
| 36 | 2.32 | 12 | 14 | 5.671 | 5.886 | 5.540 | 6.01 |
| 37 | 2.03 | 12 | 13 | 5.442 | 5.886 | 6.073 | 5.44 |
| 38 | 1.85 | 12 | 14 | 5.300 | 5.886 | 5.311 | 5.69 |
| 39 | 3.42 | 13 | 15 | 6.540 | 5.052 | 5.403 | 5.22 |
| 40 | 3.28 | 13 | 15 | 6.429 | 5.052 | 5.335 | 4.37 |
| 41 | 1.95 | 13 | 14 | 5.379 | 5.052 | 5.360 | 5.06 |
| 42 | 1.8 | 12 | 14 | 5.260 | 5.886 | 5.286 | 5.17 |
| 43 | 3.71 | 13 | 15 | 6.769 | 5.052 | 5.544 | 5.12 |
| 44 | 2.46 | 12 | 14 | 5.781 | 5.886 | 5.608 | 6.48 |
| 45 | 2.82 | 12 | 14 | 6.066 | 5.886 | 5.784 | 5.82 |
| 46 | 3.15 | 12 | 14 | 6.327 | 5.886 | 5.945 | 5.24 |
| 47 | 2.27 | 12 | 14 | 5.631 | 5.886 | 5.516 | 5.96 |
| 48 | 2.93 | 12 | 14 | 6.153 | 5.886 | 5.838 | 5.48 |
| 49 | 3.89 | 11 | 14 | 6.911 | 6.720 | 6.306 | 7.06 |
| 50 | 2.85 | 9 | 11 | 6.090 | 8.388 | 7.821 | 7.72 |
| 51 | 3.5 | 9 | 11 | 6.603 | 8.388 | 8.138 | 7.58 |
| 52 | 3.79 | 10 | 12 | 6.832 | 7.554 | 7.606 | 8.24 |
| 53 | 4.44 | 9 | 11 | 7.346 | 8.388 | 8.597 | 8.30 |
| 54 | 4.29 | 10 | 12 | 7.227 | 7.554 | 7.850 | 8.23 |
| 55 | 5.22 | 9 | 11 | 7.962 | 8.388 | 8.977 | 8.55 |
| 56 | 4.94 | 10 | 12 | 7.741 | 7.554 | 8.167 | 8.09 |
| 57 | 5.87 | 9 | 13 | 8.475 | 8.388 | 7.947 | 8.14 |
| 58 | 3.18 | 12 | 14 | 6.350 | 5.886 | 5.960 | 7.99 |
| 59 | 4.62 | 12 | 13 | 7.488 | 5.886 | 7.337 | 8.51 |
| 60 | 3.83 | 12 | 14 | 6.864 | 5.886 | 6.277 | 7.89 |
| 61 | 5.27 | 12 | 14 | 8.001 | 5.886 | 6.980 | 8.14 |
| 62 | 2.11 | 10 | 12 | 5.505 | 7.554 | 6.786 | 5.68 |
| 63 | 3.32 | 12 | 14 | 6.461 | 5.886 | 6.028 | 5.33 |
| 64 | 2.11 | 11 | 13 | 5.505 | 6.720 | 6.112 | 5.66 |
| 65 | 2.93 | 11 | 14 | 6.153 | 6.720 | 5.838 | 5.92 |
| 66 | 4.54 | 10 | 12 | 7.425 | 7.554 | 7.972 | 7.89 |
| 67 | 3.91 | 12 | 14 | 6.927 | 5.886 | 6.316 | 6.66 |
| 68 | 4.74 | 12 | 14 | 7.583 | 5.886 | 6.721 | 5.79 |
| 69 | 5.06 | 11 | 13 | 7.835 | 6.720 | 7.551 | 6.45 |
| 70 | 5.4 | 11 | 13 | 8.104 | 6.720 | 7.717 | 7.11 |
| 71 | 5.45 | 11 | 13 | 8.144 | 6.720 | 7.742 | 7.92 |
| 72 | 5.19 | 11 | 14 | 7.938 | 6.720 | 6.941 | 7.04 |
| 73 | 3.89 | 10 | 12 | 6.911 | 7.554 | 7.654 | 8.13 |
| 74 | 3.27 | 11 | 13 | 6.421 | 6.720 | 6.678 | 6.47 |
| 75 | 4.1 | 11 | 13 | 7.077 | 6.720 | 7.083 | 5.40 |
| 76 | 4.41 | 11 | 13 | 7.322 | 6.720 | 7.234 | 6.35 |
| 77 | 4.17 | 11 | 13 | 7.132 | 6.720 | 7.117 | 7.02 |
| 78 | 3.33 | 11 | 13 | 6.469 | 6.720 | 6.707 | 7.02 |
| 79 | 2.68 | 11 | 13 | 5.955 | 6.720 | 6.390 | 7.00 |
The regression equation regarding the hydrophobicity aspect,
shows that biological activity increases while the partition octanol/water coefficient increases, indicating that in the studied series the transport of the bioactive compound to the target (receptor site) is important. Still, the corelation coefficient, although significant from the statistical point of view, display a rather modest value. However, this is the indication that steric effects have to be further taken into account either by replacing the hydrofobicity with MTD parameters or by adding them to the correlation equation (11) as will be in next exposed.
Ai = 3.838(±0.327) + 0.790(±0.099)·logPi
(N = 79; r = 0.673; F = 63.85)
(N = 79; r = 0.673; F = 63.85)
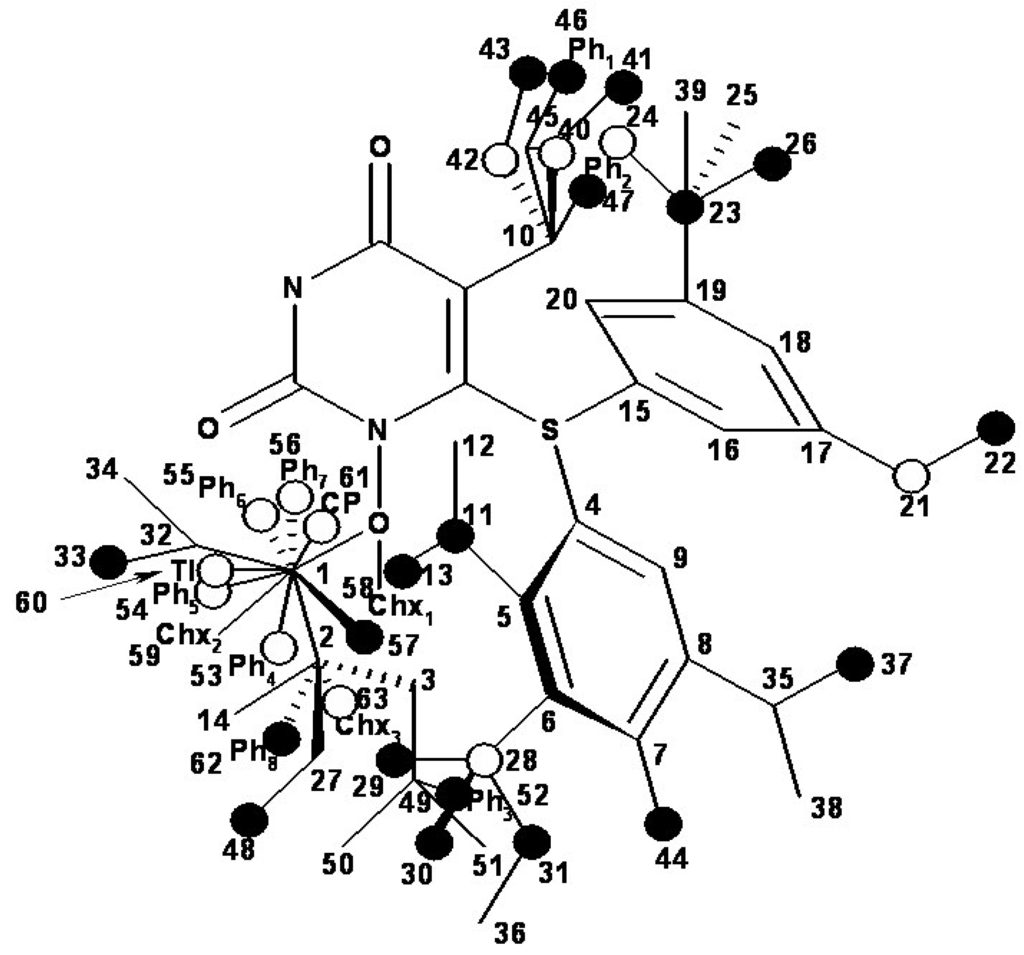
Figure 6.
The occupancy of the hypermolecule vertices within the linear mono-parametric MTD model given by equation (12) and the optimized chart (13).
As a direct comparison, by applying the mono-linear MTD method (8) on the studied series of 79 HEPT anti-HIV derivatives the following statistically validated model was obtained, now with a fine correlation coefficient (r = 0.830):
Ai = 15.894(±0.742) − 0.834(±0.064) · MTDi
(N = 79; r = 0.830; F = 169.9; r2cv = 0.685)
(N = 79; r = 0.830; F = 169.9; r2cv = 0.685)
The optimized chart and the vertices attribution of the hypermolecule are shown in Figure 6: white circles represent vertices attributed to the receptor cavity (beneficial), black circles correspond to vertices attributed to receptor walls (detrimental) and the numbered vertices represent those attributed to the exterior (irrelevant). The optimized chart, S*, derived from equation (12) employing the above minimization procedure, see equation (10), looks like:


Chart (13) gives information about the stability of vertices attribution in the H hypermolecule and quantifies the place of ligand-receptor binding as (-1) inside the cavity, (+1) inside the walls and (0) corresponding to the steric irrelevant region.
The obtained results using the mono-parametric MTD method (12) prove that the presence of substituents in the R1 region (C-5 of Figure 3) is proper for interaction only when substituents are of relatively low dimension (methyl, ethyl, isopropyl, cyclopropyl). More voluminous substituents (allyl, propyl, phenethyl, and benzyl) determine the appearance of detrimental vertices influencing negatively the anti-HIV activity.
In the R2 substituents region (C-6 of Figure 3), phenyl rests interact positively with the receptor site if they are substituted with small radicals in meta positions; methoxi, methoxicarbonyl, nitro and cyano radicals have a detrimental effect.
The most favorable region to interact with the receptor is the R3 region (N-1 of Figure 3). Single and voluminous substituents bound to the 2-hydroxiethyl rest have a benefic effect on the anti-HIV activity. These substituents, mostly aromatic, interact with a relatively large receptor cavity through hydrophobic (van der Waals) [23] bonds. Radicals in “extreme” regions of the mentioned hydroxiethylic rest lead to detrimental vertices in the region.
Finally, by considering both the hydrophobicity parameter (logP) and the minimal topological difference, a bilinear statistically validated equation is obtained:
with a correlation coefficient, r=0.882, significantly improved compared to the simple case of the mono-hydrophobic model (11). This way, the fundamental feature of MTD-QSAR contribution, as enhancing the degree of correlation through accounting of the steric effects, is computationally proved.
Ai = 13.844(±0.972) + 0.488(±0.070)·logPi − 0.674(±0.064)·MTDi
(N = 79; r = 0.882; F = 133.2; r2cv = 0.774)
(N = 79; r = 0.882; F = 133.2; r2cv = 0.774)
From equation (14) there is observed that since high values of the MTD parameters characterize the structural and bonding symetries that lead with a dimishment of the biological activity, an opposite situation is met when the parameters are associated with the complementary symetry, see Figure 2 and the relating MTD principle. Therefore, higher biological activity relates with the asymetry degree of the hypermolecule, a feature properly described by the MTD steric quantifications as next discussed.
Using equation (14), like before, the optimized MTD parameters chart can be obtained also in this case as:


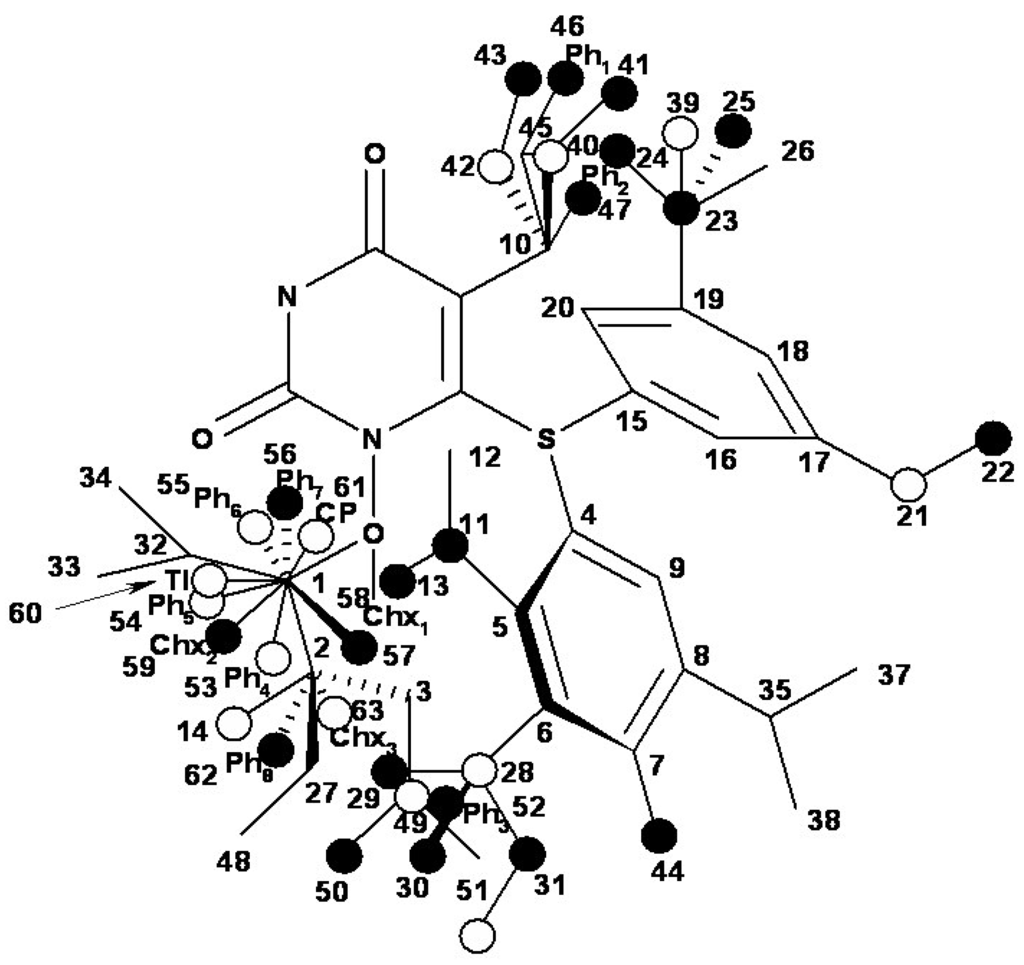
Figure 7.
The occupancy of the hypermolecule vertices within the bilinear MTD model given by equation (14) and the optimized chart (15).
Now, the vertices attribution in the hypermolecule has been changed, especially in the R3 substituents region, see Figure 7. Part of the “extreme” vertices of the hydroxiethyl rest became benefic (vertices 14 and 49), while some vertices corresponding to voluminous rests became detrimental (vertices 56 and 59, corresponding to phenyl and cyclohexyl rests). In the mentioned positions it is possible that hydrophobic interactions (which appear when other voluminous rests in the same region are considered) do not exist, whereas hydrophobic interaction favor van der Walls interactions (vertices 53-55, 60 and 61). Most probably, the increase of biological activity simultaneously with the octanol/water partition coefficient increase is due to an improved transport of ligands to the receptor site since the ligand-receptor interaction is characterized through the MTD parameter.
Comprising the hydrophobicity and topological parameters in the MTD analysis it improves significantly the correlation equations qualities, but it does not significantly modify the hypermolecule vertices attribution. The most important change is shown in the R3 substituents region, where vertices corresponding to voluminous rests close to R2 region (including those corresponding to substituents in o, m, p of phenyl in R2 region) become detrimental for interaction.
Multi-parametric models, with structural descriptors of different classes, may lead to correlation coefficients close to 0.9, especially when topological parameters are analyzed with the hydrophobicity parameter; constitutive parameters seem not to improve significantly statistical data [17].
5. Conclusions
Molecular modeling systems deliver powerful tools in order to build, to observe, to analyze and to keep the obtained molecular systems, from the most simple to the extremely complex biological macromolecules with thousands of atoms. These “tools” are very effective in qualitative (SAR) and quantitative (QSAR) studies. The goal of molecular modeling is not only to explain physical and chemical phenomenon and/or properties, but also to suggest new experiments (meaning in this context new molecular structures). Yet, molecular modeling is not able to give a quantitative prediction upon biological activity (unless few exceptions); however, it can deliver very useful data in order to design new molecular structures with increased bioactive potential [24].
Molecular modeling techniques can be used as well as in direct and indirect drug design (differences are strictly due to scientific knowledge at a given time). Direct drug design implies to know the three-dimensional (3D) receptor properties and their direct employment. Indirect drug design is used when the 3D geometry of the receptor is not known or when the ligand action is not specific or when there is not clear which is the target receptor of a ligand. The method analyses comparatively structural features of known active and inactive compounds, data being integrated in terms of complementarity with a hypothetical model of the biological receptor’s site (unknown or with uncertain 3D structure). The first way of SAR and/or QSAR seems more exact but things get more complicated in practice because the receptor topography is determined in other conditions than those in the live body; this means that there appear severe approximations in calculations reducing the value of the obtained conclusions, in many situations after long and expensive studies. The above second method is paradoxically closer to biological realities of receptor-ligand (R-L) interactions, especially when in vivo ligand biological activities are known because they contain all data regarding the interaction process at a molecular level. Therefore, indirect drug design shows an acceptable level of confidence, corresponding to experimental data.
In this context, MTD method is simple and effective to use by allowing quantitative appreciations of chemical structure – biological activity studies and through delivering QSAR models with explanatory and predictive power. This method successfully accompanies the need to have a reliable computational tool to optimize the process of developing new prototype structures (leading compound) and to reduce the necessary costs for a new drug to evolve from a theoretical conception to its appliance in clinical practice. In such, the MTD method consent to identify and to separate the effects that appear in a given biological interaction, to quantify them independently as steric, electronic, hydrophobic, etc. factors and to measure quantitatively biological activity by means of steric correlation analysis.
Since HIV infection still remains a public health issue at a global level, the application of the MTD methods to elucidate the chemical features of the anti-HIV ligand congeners appears as a preeminent actual challenge. This because, unfortunately, the most chemical structure – biological activity studies have been performed only at a qualitative level (SAR) which explains the absence on the market of an “ideal” anti-HIV drug, effective and with less toxic effects. The interaction between bioactive molecules and the RT receptor site was analyzed using the mono- and bi- dimensional MTD method considering only the minimal energy conformations. These conformations were used to obtain the hypermolecule which represents a topological network able to describe the interaction site of the biological receptor with the 79 HEPT ligands. The results through the 79 bioactive compounds indicated the presence of three important regions in order to have biological activity:
- the region of R1 substitute (see Table I) in the common pirymidin-2,4(1H,3H)-dione structure (corresponding to position 5 on this structure) with generally substitutes of small volume (alkyl, arylalkyl);
- the region of R2 substitute in the common structure (position 6) with phenyl-thyo rests un-substituted or substituted;
- the region of R3 substitute in the common structure (position N-1 in the primary structure of Figure 3) with the highest structural variation.
Most of the obtained stable conformations (by means conformational analysis) showed an orientation towards R3 region of the R2 radicals; voluminous substituents in the R3 (phenyl, chlorine-phenyl, tolyl, cyclohexyl) indicated an orientation towards R2, parallel with the phenyl nucleus from this region, or towards the primary structure in a pseudo-parallel way; this behavior indicates a possible van der Waals interaction between these more or less aromatic rests. There was also concluded that the transport of molecules to the receptor site seems to be very important in the studied series; this is demonstrated via the mono-parametric model, statistically significant, which is obtained using the hydrophobicity (transport) parameter, logP.
Biological activity increases significantly when the logarithm of the octanol/water partition coefficient increases (i.e. the activity increases by almost 1 logarithmic unit when this parameter increases by 1).
Afterall, through considering the MTD method leaves with the possibility of obtaining essential stereochemical data upon the structure of bioactive ligands, pointing out structural requirements necessary to have an improved and significant biological activity. Further 3D-QSAR studies are envisaged targeting the possibility to know the structural requirements for a compound to have an increased anti-HIV activity.
Acknowledgements
Special thanks of Corina Duda-Seiman are addressed to the Romanian National Council of Scientific Research in Universities – CNCSIS for the Grant TD/275/2003-2005. As well, Mihai V. Putz kindly appreciates the financial assistance of the Romanian National Council of Scientific Research in Universities – CNCSIS through the Grant AT/54/2006-2007.
References
- Clavel, F.; Guyader, M.; Guetard, M.; Salle, M.; Montagnier, L.; Alizon, M. Molecular cloning and polymorphism of the human immune deficiency virus type 2. Nature 1986, 324, 691–695. [Google Scholar] [CrossRef]
- Guyader, M.; Emerman, M.; Sonigo, P.; Clavel, F.; Montagnier, M.; Alizon, M. Genome organization and transactivation of the human immunodeficiency virus type 2. Nature 1987, 326, 662–669. [Google Scholar] [CrossRef]
- Fauci, A.S. The human immunodeficiency virus: infectivity and mechanisms of pathogenesis. Science 1988, 239, 617–622. [Google Scholar]
- Barre-Sinoussi, F.; Chermann, J.-C.; Rey, F.; Nugeyre, M.T.; Chamaret, S.; Gruest, J.; Dauguet, C.; Axler-Blin, C.; Vezinet-Brun, F.; Rouzioux, C.; Rozenbaum, W.; Montagnier, L. Isolation of a T-lymphotropic retrovirus from a patient at risk for acquired immune deficiency syndrome (AIDS). Science 1983, 220, 868–871. [Google Scholar]
- Popovic, M.; Sarngadharan, M.G.; Read, E.; Gallo, R.C. Detection, isolation, and continuous production of cytopathic retroviruses (HTLV-III) from patients with AIDS and pre-AIDS. Science 1984, 224, 497–500. [Google Scholar]Gallo, R.C.; Salahuddin, S.Z.; Popovic, M.; Shearer, G.M.; Kaplan, M.; Haynes, B.F.; Palker, T.J.; Redfield, R.; Oleske, J.; Safai, B.; White, G.; Foster, P.; Markham, P.D. Frequent detection and isolation of cytopathic retroviruses (HTLV-III) from patients with AIDS and at risk for AIDS. Science 1984, 224, 500–503. [Google Scholar]
- Fauci, A.S.; Lane, H.C. Human Immunodeficiency virus disease: AIDS and related disorders. In Harrison’s Principles of Internal Medicine, 16th ed.; Kasper, D. L., Braunwald, E., Fauci, A. S., Hauser, S. L., Longo, D. L., Jameson, J. L., Eds.; McGraw-Hill Companies Inc., 2005; pp. 1076–1139. [Google Scholar]
- De Clercq, E. HIV-1-specific RT inhibitors: highly selective inhibitors of human immunodeficiency virus type 1 that are specifically targeted at the viral reverse transcriptase. Med. Res. Rev. 1993, 13, 229–258. [Google Scholar] [CrossRef]
- Miyasaka, T.; Tanaka, H.; Baba, M.; Hayakawa, H.; Walker, R.T.; Balzarini, J.; De Clercq, E. A novel lead for specific anti-HIV-1 agents: 1-[(2-hydroxyethoxy)methyl]-6-(phenylthio)thymine. J. Med. Chem. 1989, 32, 2507–2509. [Google Scholar]Baba, M.; Tanaka, H.; De Clercq, E.; Pauwels, R.; Balzarini, J.; Schols, D.; Nakashima, H.; Perno, C.F.; Walker, R.T.; Miyasaka, T. Highly specific inhibition of human immunodeficiency virus type 1 by a novel 6-substituted acyclouridine derivative. Biochem. Biophys. Res. Commun. 1989, 165, 1375–1381. [Google Scholar]
- Tanaka, H.; Hirayama, M.; Suzuki, M.; Miyasaka, T.; Matsuda, A.; Ueda, T. A lithiation route to c-5 substitution of an imidazole nucleoside and its application to the synthesis of 3-deazaguanosine. Tetrahedron 1986, 42, 1971–1980. [Google Scholar] [CrossRef]
- Tanaka, H.; Takashima, H.; Ubasawa, M.; Sekiya, K.; Nitta, I.; Baba, M.; Shigeta, S.; Walker, R.T.; De Clerq, E. Structure-activity relationships of 1-[(2-hydroxyethoxy)methyl]-6-(phenylthio)thymine analogues: effect of substitutions at the C-6 phenyl ring and at the C-5 position on anti-HIV-1 activity. J. Med. Chem. 1992, 35, 337–345. [Google Scholar]
- Balaban, A. T.; Chiriac, A.; Motoc, I; Simon, Z. Steric Fit in QSAR; Springer: Berlin, (Lecture Notes in Chemistry Series); 1980. [Google Scholar]
- Simon, Z; Chiriac, A.; Holban, S.; Ciubotariu, D.; Mihalas, G. I. Minimum Steric Difference. The MTD Method for QSAR Studies; Res. Studies Press (Wiley): Letchworth, 1984. [Google Scholar]
- Ciubotariu, D.; Deretey, E.; Oprea, T. I.; Sulea, T.; Simon, Z.; Kurunczi, L.; Chiriac, A. Multiconformational Minimal Steric Difference. Structure-Acetylcholinesterase Hydrolysis Rates Relations for Acetic Acid Esters. Quant. Struct. Act. Relat. 1993, 12, 367–372. [Google Scholar] [CrossRef]
- Simon, Z.; Chiriac, A.; Ciubotariu, D.; Mureşan, S.; Bologa, C.; Sulea, T.; Kurunczi, L. Metoda MTD (The MTD method). In Relaţii cantitative structură chimică – activitate biologică (QSAR). Metoda MTD (Quantitative chemical structure – biological activity relationships studies (QSAR). The MTD method); Chiriac, A., Ciubotariu, D., Simon, Z., Eds.; Mirton Publishing House: Timişoara, Romania, 1996; Chapter 5. [Google Scholar]
- Ciubotariu, D.; Gogonea, V.; Medeleanu, M. QSAR Studies by Molecular Descriptions; Diudea, M. V., Ed.; Nova Science Publ. Inc.: Huntington New York, 2001; Chapter 10. [Google Scholar]
- Ciubotariu, D.; Medeleanu, M.; Vlaia, V.; Olariu, T.; Ciubotariu, C.; Dragoş, D.; Seiman, C. Molecular van der Waals Space and Topological Indices from the Distance Matrix. Molecules 2004, 9, 1053–1078. [Google Scholar]
- Duda-Seiman, C. Doctoral Thesis: QSAR Studies of Pyrimidinic Compounds with Anti-HIV Activity; West University of Timişoara, 2005. [Google Scholar]
- Chiriac, A; Ciubotariu, D.; Funar-Timoftei, S.; Kurunczi, L.; Mracec, M.; Mracec, M.; Szabadai, Z.; Seclaman, E.; Simon, Z. QSAR and 3D-QSAR in Timişoara. 1972-2005. Rev. Roum. Chim. 2006, 51, 79–99. [Google Scholar]
- Duda-Seiman, C.; Duda-Seiman, D.; Hegheş, A.; Nuţiu, R.; Ciubotariu, D.; Suceveanu, N. Modelarea compuSilor pirimidinici cu activitate anti-HIV (Molecular modeling of pyrimidinic compounds with anti-HIV activity). Revista de Medicină şi Farmacie (Journal of Medicine and Pharmacy ) 2004, 50 (Supl. II), 144–149, ISSN 1221-2229. [Google Scholar]
- Tanaka, H.; Baba, M.; Ubasawa, M.; Takashima, H.; Sekiya, K.; Nitta, I.; Shigeta, S.; Walker, R.T.; De Clercq, E.; Miyasaka, T. Synthesis and anti-HIV activity of 2-, 3-, and 4-substituted analogues of 1-[(2-hydroxyethoxy)methyl]-6-(phenylthio)thymine (HEPT). J. Med. Chem. 1991, 34, 1394–1399. [Google Scholar] [CrossRef]
- Tanaka, H.; Baba, M.; Saito, S.; Miyasaka, T.; Takashima, H.; Sekiya, K.; Ubasawa, M.; Nitta, I.; Walker, R.T.; Nakashima, H.; De Clercq, E. Specific anti-HIV-1 "acyclonucleosides" which cannot be phosphorylated: synthesis of some deoxy analogues of 1-[(2-hydroxyethoxy)methyl]-6-(phenylthio)thymine. J. Med. Chem. 1991, 34, 1508–1511. [Google Scholar] [CrossRef]
- HyperChem 7.01, Program package. Hypercube Inc., 2002.
- Olah, M.; Ciubotariu, D.; Ciubotariu, C.; Seiman, C.; Dragoş, D.; Pasere, M.; Medeleanu, M. Quantitative treatment of steric effects with the aid of molecular van der Waals descriptors for size and shape of substituents. In International Course & Conference on the Interface among Mathematics, Chemistry and Computer Sciences; Book of Abstracts; Ante, Graovac, Biserka, Pokrič, Vilko, Smrečky, Eds.; Inter University Centre: Dubrovnik, Croatia, June 24–29th; 2002; p. 55, ISBN 953-6690-22-5. [Google Scholar]
- Dean, P.M. Molecular Foundations of Drug-Receptor Interactions, 1st ed.; Vol. 1, Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
© 2006 by MDPI, (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.