Abstract
Assuming the in vitro conditions for the enzyme-catalyzed reactions, the basic Michaelis-Menten description is modified in a logistic (mathematical) manner such that the inherent limitations that appear in the previous method are removed. Beside its generality, the reliability of the present approach is proved through applications on the competitive multi- and bi- substrate enzyme catalyses.
1. Introduction
According to Charles Darwin’s famous paradigm of evolution, the principle of natural selection prescribes “the survival of the fittest” [1].
With the advent of the general theory of models in biology [2], as genomic, proteomic, and metabolomic scales are approached, the fitting concept resembles the equation of the net production of the species “i” [3]:
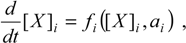 whose solution, i.e. the time-dependent concentrations [X]i=[X]i(t), depends on the particular parameters ai specific for the particular processes considered.
whose solution, i.e. the time-dependent concentrations [X]i=[X]i(t), depends on the particular parameters ai specific for the particular processes considered.
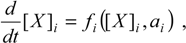
However, even displaying the temporal character, the master equation (1) differs at the micro-scale from the consecrated Hamilton-Jacobi ( 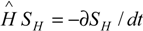 ) or Schrödinger (
) or Schrödinger ( 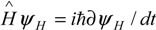 ) ones that drive the atomic and molecular quantum evolutions. While the equations of quantum mechanics pose the feature of being linear to superposition [4], the function fi in (1) has to be non-linear in variable [X]i due to the complexity of the structure of the bio-systems and of the biochemical kinetics.
) ones that drive the atomic and molecular quantum evolutions. While the equations of quantum mechanics pose the feature of being linear to superposition [4], the function fi in (1) has to be non-linear in variable [X]i due to the complexity of the structure of the bio-systems and of the biochemical kinetics.
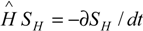 ) or Schrödinger (
) or Schrödinger ( 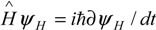 ) ones that drive the atomic and molecular quantum evolutions. While the equations of quantum mechanics pose the feature of being linear to superposition [4], the function fi in (1) has to be non-linear in variable [X]i due to the complexity of the structure of the bio-systems and of the biochemical kinetics.
) ones that drive the atomic and molecular quantum evolutions. While the equations of quantum mechanics pose the feature of being linear to superposition [4], the function fi in (1) has to be non-linear in variable [X]i due to the complexity of the structure of the bio-systems and of the biochemical kinetics.Still, a mechanistic study of a biochemical network can be performed by a two-folded analysis. First, a “wiring diagram” of intermediates is proposed and then, by considering the individual interactions, a certain kinetic model is proposed [3].
With these principles, the most elementary biochemical model can be understood in the world of the almost mystic field of enzymatic reactions – notoriously complex in mechanism and kinetics. It is well known that the rate of an enzyme-catalyzed reaction in which a substrate S is converted into product P is found to depend on the concentration of enzyme E even though the enzyme undergoes no net change [5]. As a mechanism, it is assumed that the substrate enzyme forms an intermediate ES, with the rates k1 and k–1, which then irreversibly breaks down into the product and the enzyme [6,7,8,9]:
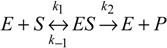
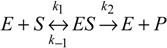
So far, kinetic studies for the reaction in (2) have been conducted in the context (or with the help) of the Michaelis-Menten model, due to this model’s flexibility in characterizing complex mechanisms derived from this type of reaction. For instance, when an analogue substrate blocks the action of a specific enzyme the so-called inhibited reaction takes place, with a major function in chemotherapeutic trainings [10,11]. On the other side, when an enzyme catalyzes the transfer of a specific functional group from one substrate to another in a many-substrate environment, the multiple alternative substrate type of reactions occur, highlighting the economical industrial synthesis of the enantiomerically pure compounds as well as the environmental issues [12]. Therefore, having a complete analytical picture of the elementary Michaelis-Menten reaction (2) becomes crucial in treating the more complex enzymic reactions derived from it.
The mechanism (2) is solved when the involved concentrations, i.e. [E](t), [S](t), [ES](t), and [P](t), are analytically known from the nonlinear differential equations of type (1) [13,14]. However, beyond approaching the progress curves of species in (2) through graphical methods [15] or by powerful computers [16], the analytical solutions have to be shaped in such a manner as to be further compatible with the temporal non-linear fitting when assaying experimental data [17,18,19].
The present work proposes the way in which the basic Michaelis-Menten kinetics is modified under logistic form when in vitro conditions are assumed, i.e. when the reaction parameters (temperature, solvent, pH, etc.) are held constant, as it can often be assumed in the laboratory [18]. The proposed logistic ansatz is then applied to real enzymic systems governed by competitive alternative substrates [12], with a particular emphasis on inhibitive bi-substrate enzyme-catalyzed reactions [11]. This way, it follows that the present approach is a two-fold one viz. both through its logistic (mathematical) analysis and due to its applications to real systems.
2. Method
When the law of mass action is considered for the reaction (2), the time evolution scheme can be draw as the system of the coupled nonlinear differential equations [20]:
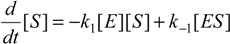
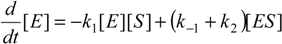
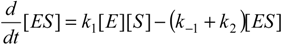
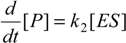 with initial conditions ([S],[E],[ES],[P]) = ([S0],[E0],0,0) at the time t=0.
with initial conditions ([S],[E],[ES],[P]) = ([S0],[E0],0,0) at the time t=0.
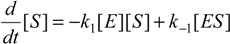
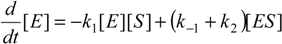
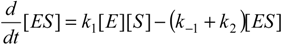
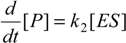
The set of equations (3) can be simplified in three steps.
First, it can be seen that when the equations (3b) and (3c) are added, the conservation law for enzyme is obtained:
while the combination of equations (3a), (3c) and (3d) leads to the conservation law for the substrate:
[E](t) + [ES](t) = [E0]
[S](t) + [ES](t) + [P](t) = [S0]
With the help of identities (4), the system of differential equations (3) takes the reduced form:
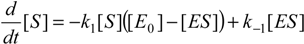
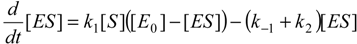 in terms of substrate and substrate enzyme concentrations only, [S] and [ES], respectively.
in terms of substrate and substrate enzyme concentrations only, [S] and [ES], respectively.
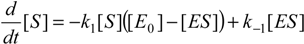
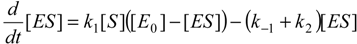
Then, employing the in vitro conditions, the enzyme can always be saturated with the substrate, so that the quasi-steady-state (or equilibrium) approximation (QSSA) may apply to the intermediate formed complex in (2). It implies imposing on (5b) the mathematical constrain [14,21,22]:
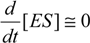 yielding with its equivalent form:
yielding with its equivalent form:
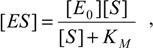 where the reaction parameter
where the reaction parameter
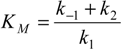 is known as the Michaelis-Menten constant [9].
is known as the Michaelis-Menten constant [9].
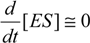
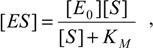
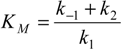
Now, plugging relation (7) into the equation (5a), we get the decoupled differential equation for the substrate consumption rate:
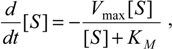 where
has been set as the maximum velocity of reaction.
where
has been set as the maximum velocity of reaction.
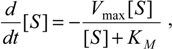
Vmax = k2[E0]
At this point, the system (3) achieves its minimum dimension consisting in one equation for the substrate concentration. However, by combining the equations (3d) and (7), the velocity of the product formation also comes out,
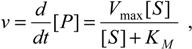 as the famous Michaelis-Menten equation [8,9].
as the famous Michaelis-Menten equation [8,9].
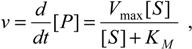
However, equation (11) reveals the first shortcoming of the Michaelis-Menten kinetic: when used without explicit temporal dependency of concentrations, it accounts only for the velocity of the initial instants of the reaction. In other words, the information outside the first moments of the progress curve [S](t) is virtually lost or neglected as long as its analytical form is not known for any moments of time [23,24].
Therefore, the necessity of a fully temporal analysis for the enzymatic processes stands as a natural imperative when further fitting with experiment is envisaged.
The temporal problem is to formulate a viable analytical solution [S](t) for the differential equation (9). Once that has been done, the progress curves of the rest of species in (2) can be accordingly formulated employing the conservation laws (4) together with the relation (7) for the substrate enzyme complex.
However, it is worth noting that, for the expression (7), a more general temporal formulation can be cast as [25]:
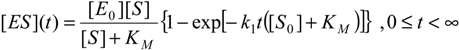 becoming identically zero at initial time, t→0, and recovering the former expression (7) in the long range regime, t→∞, respectively.
becoming identically zero at initial time, t→0, and recovering the former expression (7) in the long range regime, t→∞, respectively.
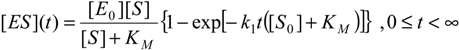
Going to analytically solve equation (9) it is firstly rearranged as
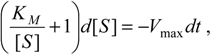 and then integrated to give [26]:
and then integrated to give [26]:
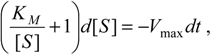
[S] + KM ln[S] = [S0] − Vmaxt + KM ln[S0]
Unfortunately, the equation (14) shows another limitation of the Michaelis-Menten enzymic description. Having a transcendental form, equation (14) does not allow for explicitly writing the dependency [S](t). In these conditions, many biochemists prefer to rearrange equation (14) under a sort of double plot equation [27,28,29], for instance:
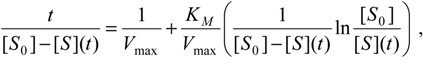 from where an intercept of 1/Vmax and a slope of KM/Vmax provide the kinetic parameters Vmax and KM, respectively. Still, this approach has been criticized [5,18], and it is worthwhile investigating whether the exact solution of (14) can be obtained for fitting a non-linear progress curve.
from where an intercept of 1/Vmax and a slope of KM/Vmax provide the kinetic parameters Vmax and KM, respectively. Still, this approach has been criticized [5,18], and it is worthwhile investigating whether the exact solution of (14) can be obtained for fitting a non-linear progress curve.
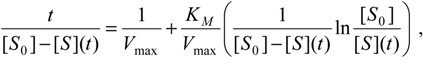
In this respect, once the substitution
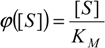 is performed in (14), it leads to the equivalent equation:
is performed in (14), it leads to the equivalent equation:
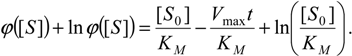
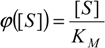
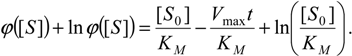
The closed-form solution of equation (17) was recognized by Schnell and Mendoza through the analogy with the famous Lambert type equation [30]:
W(x) + lnW(x) = ln x, x ≥ −1/e.
By comparing equations (17) and (18), the formal temporal solution for the substrate concentration can be achieved as [5,25]:
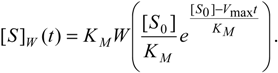
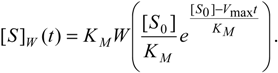
With the W-Lambert dependence (19) of the kinetic solution of the reaction (2), we arrive at the mathematical disadvantages of the traditional Michaelis-Menten analysis. For example, it can return multiple values for the same argument or result in an infinitely iterated exponential function [31].
The fundamental contribution of the present venture regards the discovery of the explicit time-dependent solution of [S](t) under an elementary form so that it does not depend on other unknown function, as is the case of the W-Lambert related solution (19). However, the present attempt comes in middle of enmities regarding the admittance or not of the W-Lambert function as an elementary one, there being no analytical replacement available so far [31]. Aiming to find a suitable substitute for W-Lambert solution (19), we found that the suggested associate logistic form [32],
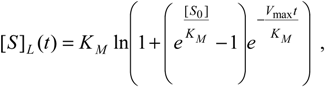 fulfils the main requirements of an enzymic kinetic through the limits:
fulfils the main requirements of an enzymic kinetic through the limits:
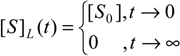
However, attempting for a closer comparison, the W-Lambert and the logistic progress curves of the substrate concentration, (19) and (20), are together plotted in Figure 1 under their scaled forms, [S]W(τ)/[S0] and [S]L(τ)/[S0], against the scaled time [25]
 for a working case in which the parametric values were chosen as k-1 = k2 = 102s-1, k1 = 106M-1s-1, while the initial conditions are set to [S0] = 10-4M and [E0] = 10-6M, respectively. As seen in Figure 1, the qualitative and quantitative behaviors of the substrate concentration in both W-Lambert and logistic cases are striking similar.
for a working case in which the parametric values were chosen as k-1 = k2 = 102s-1, k1 = 106M-1s-1, while the initial conditions are set to [S0] = 10-4M and [E0] = 10-6M, respectively. As seen in Figure 1, the qualitative and quantitative behaviors of the substrate concentration in both W-Lambert and logistic cases are striking similar.
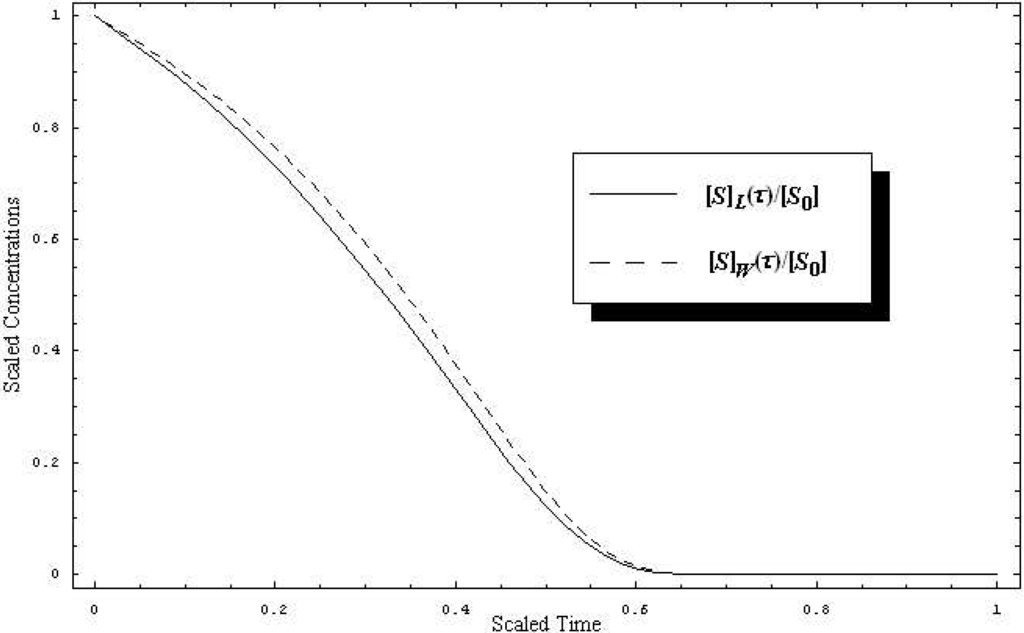
Figure 1.
Time-dependent behavior of the substrate scaled concentration for the paradigmatic enzyme-substrate reaction (2) when the W-Lambert (dashed line) and logistic (solid line), (19) and (20) versions of the Michaelis-Menten kinetics, are employed, respectively, with the parametric values k-1 = k2 = 102s-1, k1 = 106M-1s-1, [S0] = 10-4M, and [E0] = 10-6M, against the scaled time (22).
Therefore, this is the opportunity to answer on the issue whether is possible to replace the transcendent W-Lambert function with an analytical elementary one in the positive. It assumes the general logistic transformation:
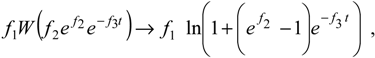 while maintaining untouched the specific (kinetic) parameters of a particular reaction, comprised in the functions f1, f2, and f3.
while maintaining untouched the specific (kinetic) parameters of a particular reaction, comprised in the functions f1, f2, and f3.
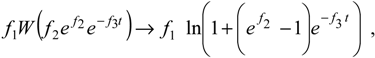
With the logistic ansatz (23), we now have a consistent recipe for temporal modeling of, in principle, any scheme of enzymatic reactions in vitro. This algorithm consists of two steps: first, the associated kinetics is solved within basic Michaelis-Menten picture until the W-Lambert solution is achieved; then, the logistic transformation (23) is performed leading with an elementary analytical form that can be further used for theoretical predictions and numerical fitting of the experimental assays. However, to emphasize the reliability of the logistic transformation (23) for complex enzymatic reactions as well, the case of the enzyme kinetic of the multiple alternative substrates will be presented next and then particularized to the fully competitive enzyme catalysis.
3. Multiple Alternative Enzyme-Substrate Reactions
After a century of supremacy, the central dogma of biology, i.e. the fact that the genotype can not be in any way affected through protein supply and interaction [33,34], is currently being taken under discussion [35]. It started with the landmark contributions of the 1950s and 1960s scientists Koshland, Monod, Wyman, and Changeux proposing the “induced fit” model with the help of which they rationalized the competing needs of substrate binding affinity. It was concluded that the metabolic protein, in general, and enzymatic, in particular, activities can be regulated by small molecules other than the substrates, the inhibitors or activators [36,37].
As a consequence, the developed theory of allosteric regulation (from Greek: allos, other + stereos, space) prescribes that, within a cooperative interaction, the binding of one ligand (substrate) at a specific site is influenced by the binding of another ligand (inhibitor) at a different or allosteric site on the protein (or enzyme). However, actually, such behaviour is generalized at the level of organismal and cellular regulation in which the cell converts the comparison of the proteins with organisms needs into metabolic process. It follows that the proteins and gene expression, far from being the endpoint, are rather a bridge from where begin the process of editing RNA transcripts, altering and maintaining the genome, over and over again by signalling other cells or bio-inspired nano-implants [38]. In this process of cell differentiation, proliferation and programming, the receptors (substrates and inhibitors) and enzymes perform the task of molecular messengers. Therefore, studying the cooperative effects of the inhibitors on the enzymatic reactions, here at the theoretical level, should be most valuable for the forefront of biomedical researches.
Basically, an alternative n-substrate system consists of n-reactions of the Michaelis-Menten type (2),
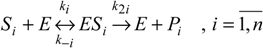 which, nevertheless, generate a system with 3n+1 differential equations, viewed as the direct expansion of the single-substrate one (3), with the initial temporal constraints:
which, nevertheless, generate a system with 3n+1 differential equations, viewed as the direct expansion of the single-substrate one (3), with the initial temporal constraints:
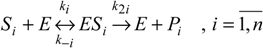
([S]i),[E],[ES]i,[P]i) t=0 = ([S0]i,[E0],0,0).
The associated conservation laws now look as generalizations of the basic ones given in (4):
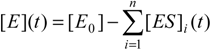
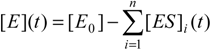
[P]i(t) = [S0]i − [S]i(t) − [ES]i(t).
Following the deduction line of the foreground enzymic kinetic, the specific Michaelis-Menten i-constants
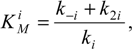 and the maximum velocity for the i-reaction
and the maximum velocity for the i-reaction
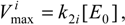 are firstly introduced.
are firstly introduced.
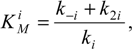
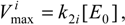
Additionally, a few new notations are considered here [12], namely the first order rate i-constants,
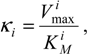 and the reduced i-concentrations,
and the reduced i-concentrations,
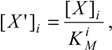 in order to shortcut the script of further emerging equations.
in order to shortcut the script of further emerging equations.
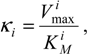
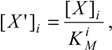
With these amendments, the above temporal equations are accompanied by the actual form of the enzyme-substrate i-complex concentration [12]:
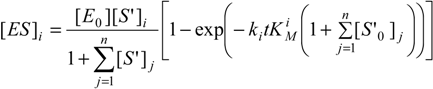 from which its simple form (12) can be recovered, since only one substrate reaction is retained from the scheme (24).
from which its simple form (12) can be recovered, since only one substrate reaction is retained from the scheme (24).
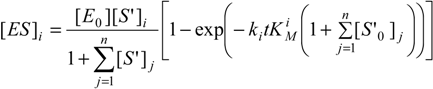
Certainly, as before, the kinetics is not solved until temporal analytical solution for the i-substrate concentration is derived. To achieve this goal, in this particular case, we first need to solve the generalized system of coupled equations for the alternative substrates in reaction (24) [12,39]:
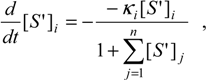
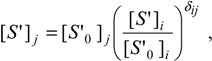 when the participating substrates are interrelated through the parameter
when the participating substrates are interrelated through the parameter
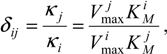 also referred to as the competition matrix, due to its ability to measure the degree of competition among the substrates involved in the reaction with the enzyme.
also referred to as the competition matrix, due to its ability to measure the degree of competition among the substrates involved in the reaction with the enzyme.
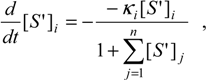
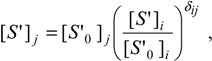
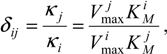
As a note, one can easily check that relations (28) become the basic Michaelis-Menten equation (9) when dealing with single-substrate reaction. Unfortunately, the general system (28) has no explicit solution unless the competition matrix is specified in some particular cases.
As such, a first case assumes the so-called even competition when δij ≅ 1. In this frame, the system (28) can be integrated and the result rearranged so that the proper comparison with the W-Lambert equation (18) to be employed. This causes the W-Lambert transcendent solutions for the system (28) to take the closed forms [12]:
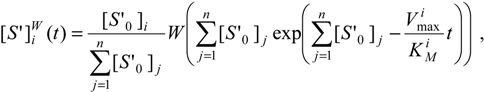 as a direct generalization of the mono-substrate Michaelis-Menten temporal solution (19). Finally, the logistic transformation (23) can be directly applied on (29a) leading to the elementary analytic expressions:
as a direct generalization of the mono-substrate Michaelis-Menten temporal solution (19). Finally, the logistic transformation (23) can be directly applied on (29a) leading to the elementary analytic expressions:
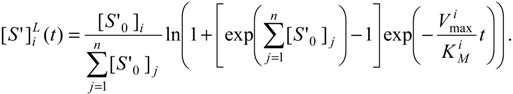
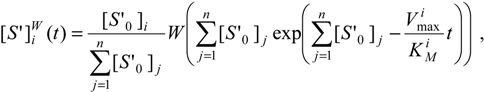
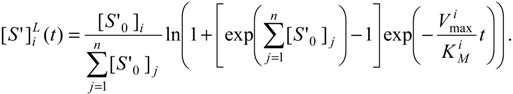
Looking at the mathematical form of even competition solutions (29), observing the benchmark single-substrate ones, (19) and (20), it appears that at any time the reduced substrate concentrations keep the proportion determined from their initial reduced concentrations.
Consequently, the time evolutions of the set of alternative reactants are very similar to those considered in the mono-substrate reaction.
A more interesting case regards the so-called weak competition when the reactants are not catalyzed with the same efficiency from the enzyme. In this situation, the competition matrix (28c) ranges as 0 < δij <<1. However, in this case the first order of the Taylor expansion of (28b) in (28a) can be retained and, by repeating the previous integration and rearrangement procedure the W-Lambert closed form solution can be cast as [12]:
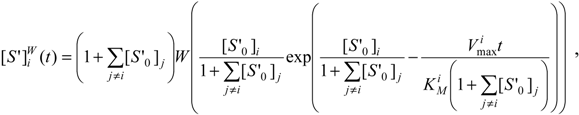 which, in turn, allows its transcription under an elementary analytical form through performing the logistic transformation (23):
which, in turn, allows its transcription under an elementary analytical form through performing the logistic transformation (23):
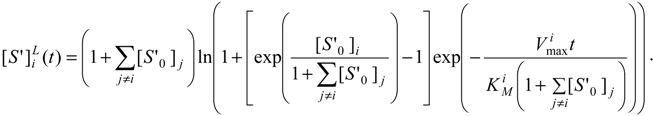
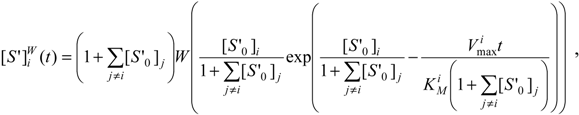
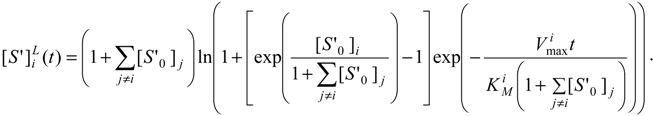
Certainly, similar mathematical analyses and logistic transformations can be considered for various types of enzymatic reactions, no matter how complex the biochemical network may be. However, in order to prove that the logistic ansatz closely follows the W-Lambert implicit solutions for all species when a complex kinetics is under study, the special bi-substrate case of weak competition, i.e. the case of competitive inhibition, will be presented in detail next.
4. Application on Competitive Inhibition
When an inhibitor acts to reduce the concentration of the available fee enzyme for the substrate binding, it is said that competitive inhibition takes place. An eminent example is that of succinate dehydrogenase, which is competitively inhibited by malonate to convert succinate to fumarate within the citric acid cycle [10,40].
With fully competitive interaction, the associate network model is particularized from the scheme (24) by retaining two channels of alternative enzyme-substrate reactions only:
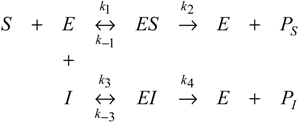

It is worth noting that the present assumed model for competitive inhibition represents an improved version of the commonly accepted one, in which the inhibitor-enzyme complex EI of (31) undergoes no further reaction or specific product formation [10].
To set the competitive inhibition’s characteristics, the general alternative substrate kinetic parameters (26a) and (26b) now become:
- the respective Michaelis-Menten constants for the substrate and inhibitor branches of (31):
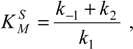
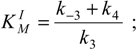
- the respective maximum velocities for the substrate and inhibitor branches of (31):
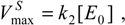
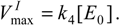
Nevertheless, the kinetic information comprised in the parameters (32) can be combined in a single quantity through the competition matrix (28c), which now takes the specialized form
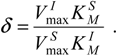
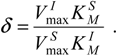
Focusing in what follows on the case of weak competition exclusively, in which the competition index fulfills the kinetic condition δ <<1, the respective reduced initial and instantaneous concentrations of the substrate and inhibitor, particularizing the general definition (26d) for the reaction channels of (31),
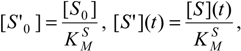
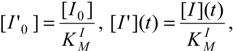 provide the keys with which the overall bi-substrate kinetic is solved.
provide the keys with which the overall bi-substrate kinetic is solved.
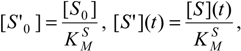
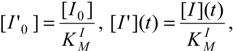
This way, the W-Lambert time dependent closed solutions for the substrate and inhibition progress curves unfold with the respective forms [11]:
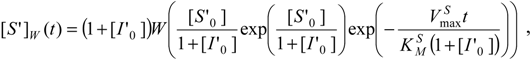
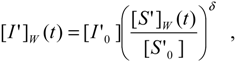 by specializing the general multi-substrate formulas (30a) and (28b) to the present analysis.
by specializing the general multi-substrate formulas (30a) and (28b) to the present analysis.
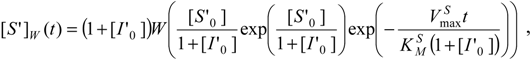
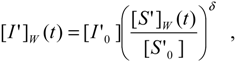
In order to get the analytical counterparts of (35a) and (35b), actually, two-folded methods can be considered. One is to particularize the already obtained generalized logistic form (30b) to the actual bi-substrate alternative scheme; equally, one can directly apply the logistic transformation (23) to the specific W-Lambert solution of the weakly competitive inhibition of the substrate progress curve (35a).
Using either of these two methodologies, the logistic expression that shapes the decrease (or consumption) in substrate concentration in reaction (31) can be obtained with the elementary form:
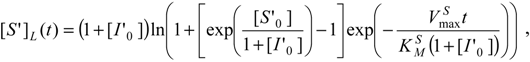 being as well accompanied by the logistic version of the inhibitor progress curve of (35b):
being as well accompanied by the logistic version of the inhibitor progress curve of (35b):
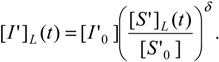
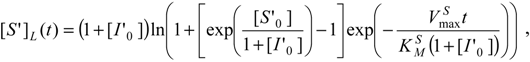
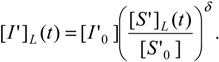
Having formulated the W-Lambert and logistic functions of substrate and inhibitor progress curve for the enzymic processes of (31), the complete kinetic picture can be revealed for all the species.
For instance, the progress curves for the substrate-enzyme and inhibitor-enzyme complexes of (31) can be obtained by means of adapting the general formula (27), respectively as [11]:
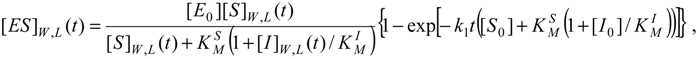
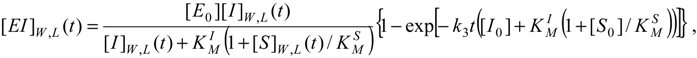 written compactly for both the W-Lambert and logistic temporal solutions.
written compactly for both the W-Lambert and logistic temporal solutions.
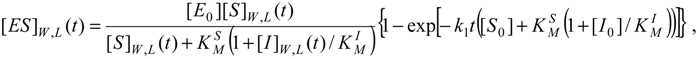
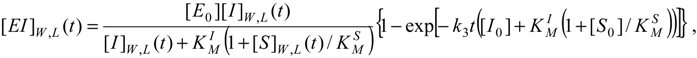
With expressions (37), the conservation laws (25) can be further employed with their actual particular progress curves:
for the product from substrate, product from inhibitor and for the enzyme, respectively.
[PS]W,L(t) = [S0]−[S]W,L(t)−[ES]W,L(t),
[PI]W,L(t) = [I0]−[I]W,L(t)−[EI]W,L(t),
[E]W,L(t) = [E0]−[ES]W,L(t)−[EI]W,L(t),
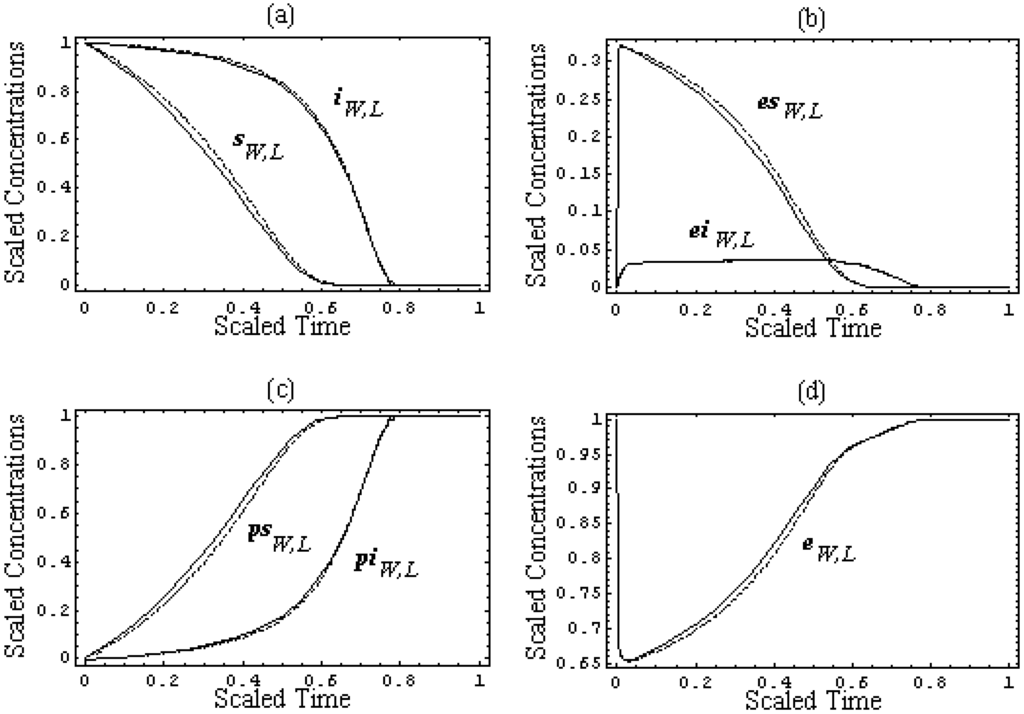
Figure 2.
The scaled progress curves (39) of the species concentrations involved in competitive reaction (31) for the pilot test with k-1 = k2 = 102s-1, k1 = 106M-1s-1, k-3 = k4 = 10s-1, k3 = 105M-1s-1, [S0] = 10-4M, [I0] = 10-5M, and [E0] = 10-6M, arranged as follows: (a) for the leading and inhibitory substrates concentrations, according to (39a), (b) for the substrate-enzyme and inhibitor-enzyme complexes concentrations, according to (39b), (c) for the products of the leading and inhibitory substrates concentrations, according to (39c), and (d) for the enzyme concentration, according to (39d), within the W-Lambert (dashed lines) and logistic (solid lines) Michaelis-Menten kinetics against the scaled time (22), respectively.
However, in order to underline the equivalence of the W-Lambert and logistic at all levels of an enzymic kinetic in vitro, within the present weak competition conditions, Figure 2 shows the scaled shapes of the progress curves (35) – (38) of all species of the biochemical network (31):
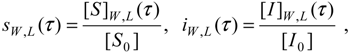
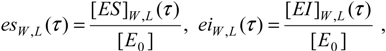
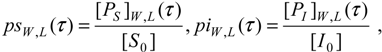
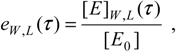 against the scaled time (22) for a pilot computational test in which the parametric values were chosen as k-1 = k2 = 102s-1, k1 = 106M-1s-1, k-3 = k4 = 10s-1, k3 = 105M-1s-1, while the initial condition have been set to [S0] = 10-4M, [I0] = 10-5M, and [E0] = 10-6M, respectively.
against the scaled time (22) for a pilot computational test in which the parametric values were chosen as k-1 = k2 = 102s-1, k1 = 106M-1s-1, k-3 = k4 = 10s-1, k3 = 105M-1s-1, while the initial condition have been set to [S0] = 10-4M, [I0] = 10-5M, and [E0] = 10-6M, respectively.
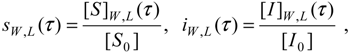
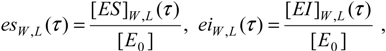
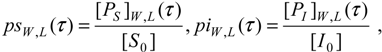
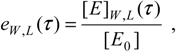
From the plots in Figure 2, it is clear that for each envisaged species of (31), the W-Lambert and logistic progress curves display outstanding similar, or almost coincident, shapes.
We have thus formulated and illustrated all the analytic steps for achieving the complete temporal picture of enzymatic catalyzed reactions in vitro, leading to the framework in which the experimental assay can be fitted to obtain the characteristic parameters, the algorithm presented being applicable, in principle, at any level of biochemical network complexity [41,42,43,44].
Moreover, the present approach may be found useful in predicting or validating the assumed kinetic schemes by employing the logistic progress curves to the non-linear fitting of the experimentally recorded data. Such studies are currently in progress and will be reported in subsequent communications.
5. Conclusions
Enzymes and their activity are known, in various forms, from the ancient history. In short, from a description of wine making in the Codex of Hammurabi (Babylon, cca. 2100 B.C.) to the early civilizations of India, China, Egypt, Greece, and Rome the use of microorganisms as enzyme supply for fermentation was a common practice among antique people. However, early enzymology started with the studies of Réaumur (1683-1757) and Spallanzani (1729-1799), who performed the first experimental demonstration of enzyme specificity to show that digestion, is a chemical process rather than a physical one. Later, thanks to Emil Fischer works, modern enzymology was developed with the cornerstone 1890 discovery of the “lock and key” mechanistic model for the stereochemical relationship between enzymes and their substrate. Soon after, in 1902, Brown made the insightful observation that enzyme-catalysis is not a simple diffusion-limited reaction, but that it is governed by the formation of an enzyme-substrate complex. His remark is still most valuable for the present study: “it is quite conceivable…that the time elapsing during molecular union and transformation may be sufficiently prolonged to influence the general course of the action” [7]. Following this line, in 1903 Victor Henry reported the first successful mathematical description of enzyme kinetics, expanded ten years later by the Michaelis and Menten, to get the enzyme rate equation based on their yet paradigmatic scheme of reaction [8,9]. Despite many practical applications of the Michaelis-Menten mechanism, its complete temporal solution was not achieved until Schnell and Mendoza formulated the closed form solution as the transcendent W-Lambert function [25]. The final analytical step in the sense of a fully mathematical formulation of the progress curves of a general in vitro enzymic reaction was undertaken in this study with the help of elementary logistic transformation (23).
Due to its analytical logarithmic structure, the actual mathematical analysis may be extended to also cover the time derivatives of reactant progress curves making it possible to fit the reaction parameters from experimental data assays. Nonetheless, the link with the experiment can also be made by straight employment of the present logistic curves to fit with the data series in a single in vitro experiment since the enzymatic activity is recorded, thus suggesting another truthful and swift method for estimating the enzymic kinetic parameters.
However, the present logistic method has been tested for its reliable application to real systems. In this respect, cooperative substrate-enzyme reactions as well as particular bi-substrate competitive inhibition kinetic were illustrated in this work. It follows that the logistic ansatz can be adopted as an adequate analytical tool for describing the full temporal course of enzymic reactions at whatever level of complexity. Further applications of the present method should be considered in the fields of biochemistry, biotechnology, and genomics.
Acknowledgements
We would like to thank Prof. Dr. Ecaterina Putz from Economics Faculty of West University of Timişoara for the enlightening discussions on the logistic functions and methods. Authors are indebted to the anonymous referee for the very instructive and constructive remarks on the intermediate form of manuscript, many of the actual statements having been inspired by his insight. We also thank our colleague Cristian Chiş from the “Dimitrie Cantemir” Christian University of Timişoara for the careful reading of the manuscript. The financial support from the Romanian National Council of Scientific Research in Universities – CNCSIS (by Grant AT/54/2006) is kindly appreciated.
References
- Mayr, E. What evolution is? The Orion Publishing Group Ltd., “Science Masters” Brockmann Inc., 2001. [Google Scholar]
- Thom, R. Structural Stability and Morphogenesis – An Outline of a General Theory of Models; W. I. Benjamin, Inc.: Reading, Massachusetts , 1975. [Google Scholar]
- Crampin, E. J.; Schnell, S.; McSharry, P. E. Mathematical and Computational Techniques to Deduce Complex Biochemical Reaction Mechanisms. Prog. Biophys. Mol. Biol. 2004, 86, 77–112. [Google Scholar]
- Mandl, F. Quantum mechanics; John Wiley & Sons: Chichester, 1992. [Google Scholar]
- Schnell, S.; Maini, P. K. A Century of Enzyme Kinetics: Reliability of the KM and Vmax Estimates. Comm. Theor. Biol. 2003, 8, 169–187. [Google Scholar]
- Brown, A. J. Influence of Oxygen and Concentration on Alcohol Fermentation. J. Chem. Soc. Trans. 1892, 61, 369–385. [Google Scholar]
- Brown, A. J. Enzyme Action. J. Chem. Soc. Trans. 1902, 81, 373–388. [Google Scholar]
- Henri, V. Über das gesetz der wirkung des invertins. Z. Phys. Chem. 1901, 39, 194–216. [Google Scholar]
- Michaelis, L.; Menten, M. L. Die kinetik der invertinwirkung. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Voet, D.; Voet, J. G. Biochemistry, (second edition); John Wiley & Sons, Inc.: New York, 1995; Chapter 13. [Google Scholar]
- Schnell, S.; Mendoza, C. Time-Dependent Closed Form Solution for Fully Competitive Enzyme Reactions. Bull. Math. Biol. 2000, 62, 321–336. [Google Scholar]
- Schnell, S.; Mendoza, C. Enzyme Kinetics of Multiple Alternative Substrates. J. Math. Chem. 2000, 27, 155–170. [Google Scholar]
- Cornish-Bowden, A. Fundamentals of Enzyme Kinetics; Butterworths: London, 1979. [Google Scholar]
- Segel, I. H. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Systems; Wiley: New York, 1975. [Google Scholar]
- Ritchie, R. J.; Prvan, T. A Simulation Study on Designing Experiments to Measure the Km of Michaelis-Menten Kinetics Curves. J. Theor. Biol. 1996, 178, 239–254. [Google Scholar]
- Zimmerle, C. T.; Frieden, C. Analysis of Progress Curves by Simulations Generated by Numerical Integration. Biochem. J. 1989, 258, 381–387. [Google Scholar]
- Szedlacsek, S. E.; Ostafe, V.; Duggleby, R. G.; Serban, M.; Vlad, M. O. Progress-Curve Equations for Reversible Enzyme-Catalysed Reactions Inhibited by Tight-Binding Inhibitors. Biochem. J. 1990, 265, 647–653. [Google Scholar]
- Goudar, C. T.; Sonnad, J. R.; Duggleby, R. G. Parameter Estimation Using a Direct Solution of the Integrated Michaelis-Menten Equation. Biochim. Biophys. Acta 1999, 1429, 377–383. [Google Scholar]
- Câteau, H.; Tanaka, S. Kinetic Analysis of Multisite Phosphorylation Using Analytic Solutions to Michaelis-Menten Equation. J. Theor. Biol. 2002, 217, 1–14. [Google Scholar]
- Gray, P; Scott, S. K. Chemical Oscillations and Instabilities. Non-linear Chemical Kinetics; Clarendon Press: Oxford, 1990. [Google Scholar]
- Segel, L. A. On the Validity of the Steady State Assumption of Enzyme Kinetics. Bull. Math. Biol. 1988, 50, 579–593. [Google Scholar]
- Segel, L. A.; Slemrod, M. The Quasi-Steady-State Assumption: A Case Study in Perturbation. SIAM Rev. 1989, 31, 446–477. [Google Scholar]
- Duggleby, R. G.; Morrison, J. F. The Analysis of Progress Curves for Enzyme-Catalysed Reactions by Non-Linear Regression. Biochim. Biophys. Acta 1977, 481, 297–312. [Google Scholar]
- Duggleby, R. G. Quantitative Analysis of the Time Courses of Enzyme-Catalyzed Reactions. Methods 2001, 24, 168–174. [Google Scholar]
- Schnell, S.; Mendoza, C. Closed Form Solution for Time-Dependent Enzyme Kinetics. J. Theor. Biol. 1997, 187, 207–212. [Google Scholar]
- Rubinow, S. I. Introduction to Mathematical Biology; Wiley: New York, 1975. [Google Scholar]
- Haldane, J. B. S.; Stern, K. G. Allgemeine Chemie der Enzyme; Dresden: Verlag von Steinkopff, 1932. [Google Scholar]
- Lineweaver, H.; Burk, D. The Determination of the Enzyme Dissociation Constants. J. Am. Chem. Soc. 1934, 56, 658–666. [Google Scholar]
- Cornish-Bowden, A. The Use of the Direct Linear Plot for Determining Initial Velocities. Biochem. J. 1975, 149, 305–312. [Google Scholar]
- Barry, D. A.; Parlange, J. –Y; Li, L.; Prommer, H.; Cunningham, C. J.; Stagnitti, F. Analytical Approximations for Real Values of Lambert W-function. Math. Comp. Simulation 2000, 53, 95–103. [Google Scholar]
- Hayes, B. Why W? American Scientist 2005, 93, 104–108. [Google Scholar]
- Lacrămă, A. -M.; Putz, M. V.; Ostafe, V. New Enzymatic Kinetic Relating Michaelis-Menten Mechanisms. Annals of West University of Timisoara-Series of Chemistry 2005, 14(2), 179–190. [Google Scholar]
- Mattick, J. S. The Hidden Genetic Program of Complex Organisms. Sci. Am. 2004, 291, 60–7. [Google Scholar] [CrossRef]
- Silverman, P. H. Rethinking Genetic Determinism. The Scientist 2004, 18(10), 32–3. [Google Scholar]
- Goodman, A. F.; Bellato, C. M.; Khidr, L. The Uncertain Future for Central Dogma. The Scientist 2005, 19(12), 20–1. [Google Scholar]
- Cantor, C. R.; Schimmel, P. R. Biophysical Chemistry. Part III. The Behavior of Biological Macromolecules; W.H. Freeman and Company: San Francisco, 1980. [Google Scholar]
- Copeland, R. A. Enzymes-A Practical Introduction to Structure, Mechanism, and Data Analysis; Wiley-VCH: New York, 2000. [Google Scholar]
- Curran, J. M.; Gallagher, J. A.; Hunt, J. A. The Inflammatory Potential of Biphasic Calcium Phosphate Granules in Osteoblasts/Macrophage Co-Culture. Biomaterials 2005, 26, 5313–5320. [Google Scholar] [CrossRef]
- Rubinow, S. I; Lebowitz, J. L. Time-Dependent Michaelis-Menten Kinetics for an Enzyme-Substrate-Inhibitor System. J. Am. Chem. Soc. 1970, 92, 3888–3893. [Google Scholar] [CrossRef]
- Walsh, C. Enzymatic reaction mechanisms; W.H. Freeman and Company: San Francisco, 1979. [Google Scholar]
- Duggleby, R. G.; Wood, C. Analysis of Progress Curves for Enzyme-Catalysed Reactions. Automatic Construction of Computer Programs for Fitting Integrated Rate Equations. J. Biochem. 1989, 258, 397–402. [Google Scholar]
- Duggleby, R. G. Analysis of Enzyme Progress Curves by Nonlinear Regression. Methods Enzymol. 1995, 249, 61–90. [Google Scholar] [CrossRef]
- Duggleby, R. G. Progress Curves of Reactions Catalyzed by Unstable Enzymes. A Theoretical Approach. J. Theor. Biol. 1986, 123, 67–80. [Google Scholar] [CrossRef]
- Ross, J.; Schreiber, I.; Vlad, M. O. Determination of Complex Reaction Mechanisms: Analysis of Chemical, Biological and Genetic Networks; Oxford University Press, 2006. [Google Scholar]
© 2006 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.