Molecular Orbital and Density Functional Study of the Formation, Charge Transfer, Bonding and the Conformational Isomerism of the Boron Trifluoride (BF3) and Ammonia (NH3) Donor-Acceptor Complex
Abstract
:Introduction
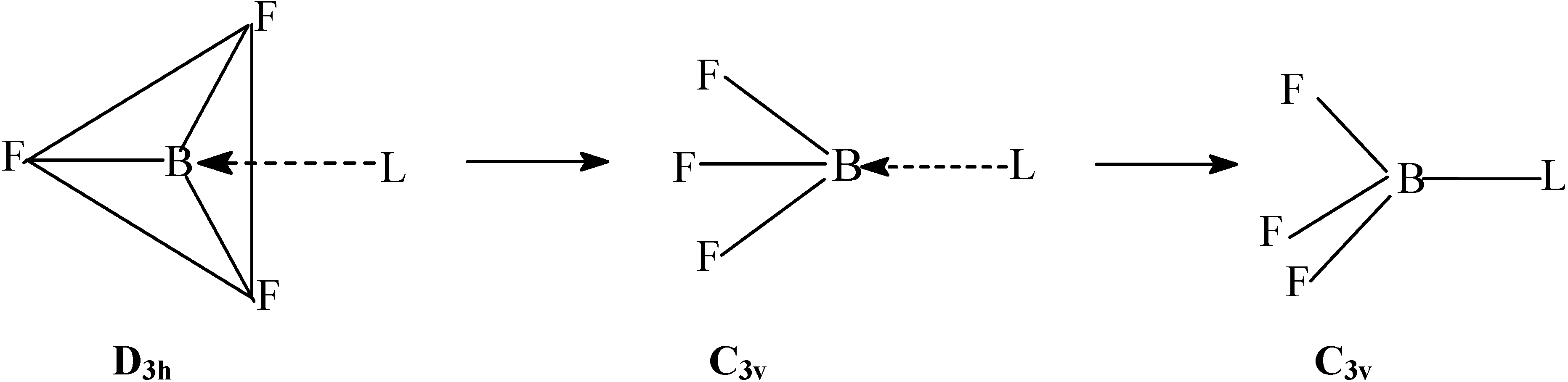
Method of Computation
1. The Density Functional parameters.
2. Calculation of occupation numbers of the MO’s of the interacting fragments after the chemical interaction.
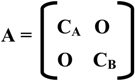
νi = 2 ∑ ∑ (di(g) )2 + 2 ∑ ∑ di(g) dk(g) Sik
g=1 g=1 k=1
3. Calculation of charge transfer and heat of reaction and estimation of the chemical potential and global hardness of the adduct super molecules from the fragments.
μ n =−( Π| μi| ) 1/n .
i
1/ ηng = 1/n Σ 1/ ηi
i
ηnd =−( Π ηi|) 1/n
i
4. Partitioning of total energy into one- and two-center physical components
Results and Discussion
| Angle of torsion | ∠FBF angle | ∠HNH angle | N-H length |
| (Degrees) | (Degrees) | (Degrees) | ( A0) |
| 0 | 111 | 109.9 | 1.072 |
| 10 | 111 | 109.9 | 1.071 |
| 20 | 111.1 | 110 | 1.071 |
| 30 | 111.1 | 110.1 | 1.069 |
| 40 | 111.1 | 110.1 | 1.068 |
| 50 | 111.2 | 110.1 | 1.068 |
| 60 | 111.3 | 110.1 | 1.068 |
| BF3 | NH3 | ||||
| ΔE | Δ(Δε) | Δμ | ΔE | Δ(Δε) | Δμ |
| 0.12742 | -0.18166 | -0.07667 | 0.00244 | -0.02464 | 0.00077 |
The density functional study of the effect of structural reorganization of the acceptor and donor moieties; activation in BF3 due to structural reorganization.
Effect of Reorganization in NH3.
The Density Functional Correlation of the process of adduct formation
| Species | η | μ | ΔN= (μB- μA)/ ( ηB+ηA) | ηAB – ηA –ηB | ΔEreac = -½ (ηAB – ηA –ηB) |
| BF3 | 0.35741 | -0.36137 | (-0.15257+0.36137)/ | (0.35506 – 0.35741 | 0.21764 |
| NH3 | 0.43293 | -0.15257 | (0.43293+0.35741) | – 0.43293) | |
| F3B– NH3 | 0.35506 | -0.25105 | = 0.264178 | = – 0.43528 |
Charge transfer and binding
| BF3 | NH3 | ||||
| MO’s | Eigen value | νi | MO’s | Eigen value | νi |
| 1a1 | -1.75077 | 1.9970 | 1a1 | -1.30916 | 1.9399 |
| 1e | -1.67425 | 1.9997 | 1e | -0.73008 | 1.9791 |
| 2e | -1.67425 | 1.9997 | 2e | -0.73008 | 1.9791 |
| 2a1 | -0.90879 | 1.9998 | 2a1 | -0.58551 | 1.7394 |
| 3e | -0.87371 | 1.9989 | 3a1* | 0.28036 | 0.0128 |
| 4e | -0.87371 | 1.9989 | 3e* | 0.32922 | 0.0102 |
| 3a1 | -0.83915 | 1.9355 | 4e* | 0.32922 | 0.0102 |
| 4a1 | -0.77162 | 1.9999 | |||
| 5e | -0.75533 | 1.9992 | |||
| 6e | -0.75533 | 1.9992 | |||
| 7e | -0.71878 | 1.9988 | |||
| 8e | -0.71878 | 1.9988 | |||
| 5a1* | -0.00395 | 0.3688 | |||
| 6a1* | 0.21206 | 0.0068 | |||
| 9e* | 0.27557 | 0.0141 | |||
| 10e* | 0.27557 | 0.0141 | |||
| Total | 24.3292 | Total | 7.6707 | ||
| (+0.3292) | (–0.3293) | ||||
Correlation of charge transfer and bond formation in terms of DFT parameters
Conformational analysis of F3B–NH3
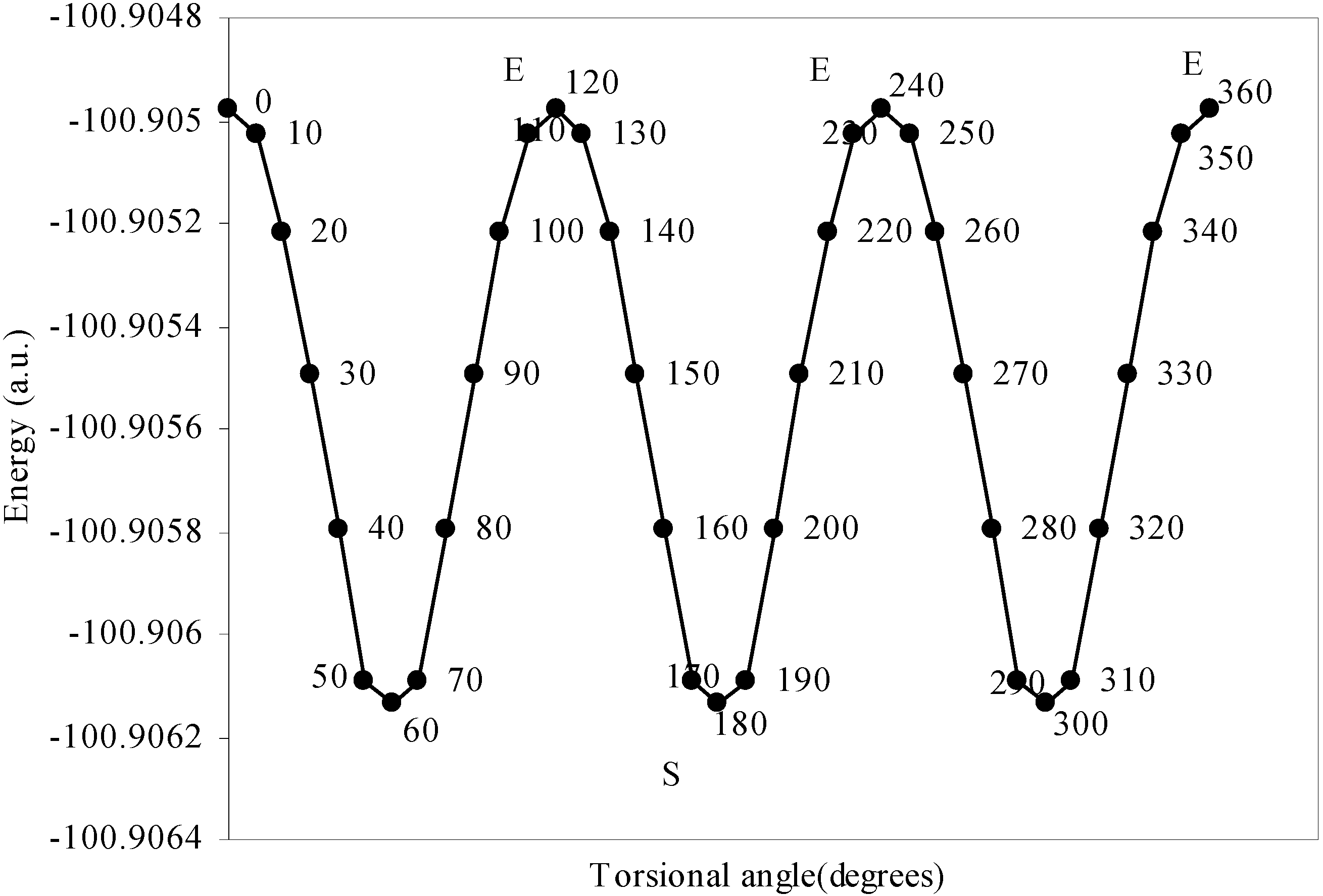
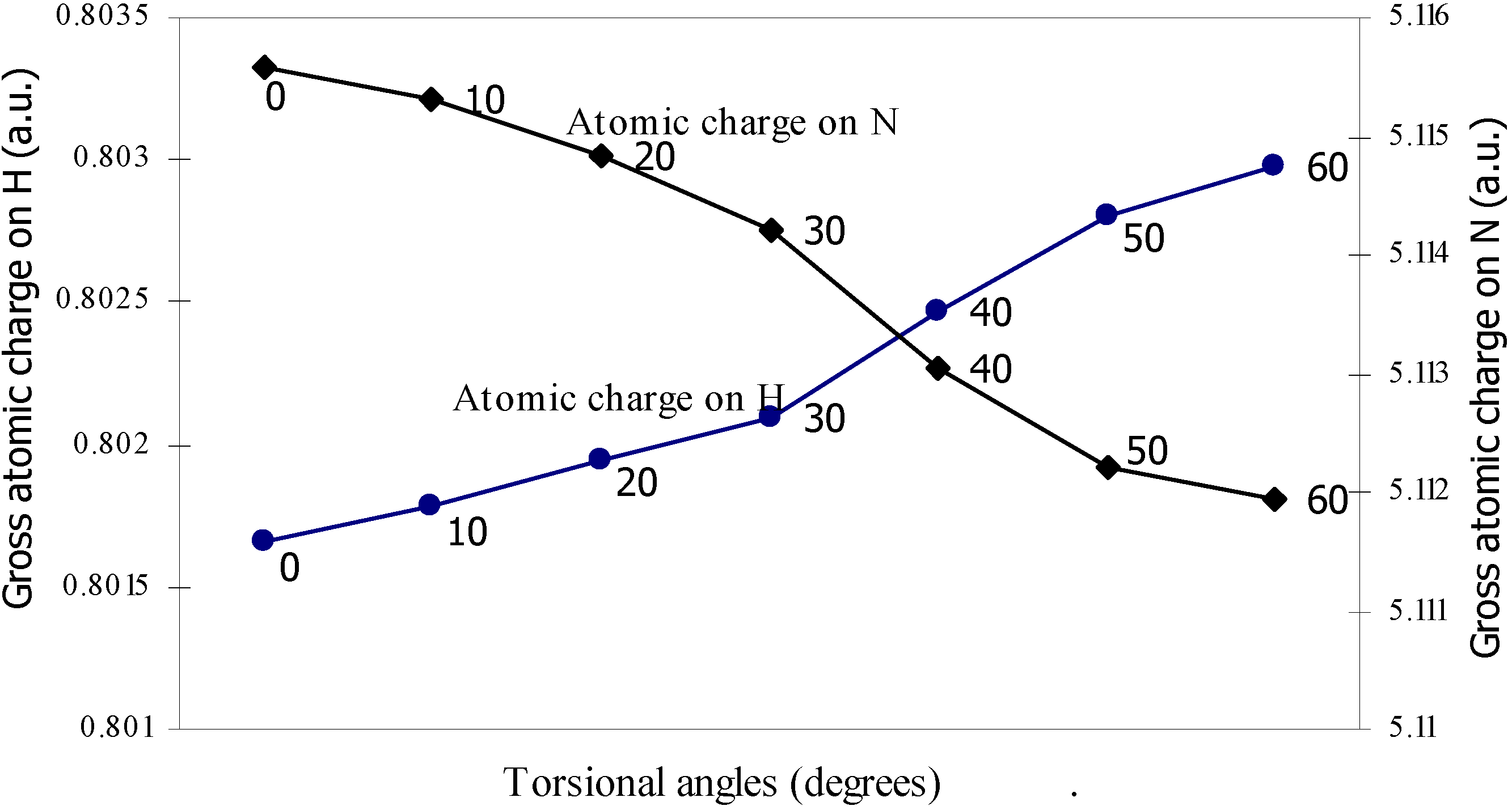
| Angle of torsion | Total Energy | Charge density on B atom | Charge density on N atom | Charge density on H atom | Charge density on F atom |
| (degrees) | |||||
| 0 | -100.90498 | 2.47328 | 5.11559 | 0.80166 | 7.3353 |
| 10 | -100.905 | 2.47337 | 5.1153 | 0.80178 | 7.3353 |
| 20 | -100.9052 | 2.47367 | 5.11483 | 0.80194 | 7.33519 |
| 30 | -100.9055 | 2.47408 | 5.11420 | 0.80210 | 7.33511 |
| 40 | -100.9058 | 2.47418 | 5.11305 | 0.80247 | 7.33500 |
| 50 | -100.9061 | 2.47433 | 5.11222 | 0.80280 | 7.33492 |
| 60 | -100.9061 | 2.47441 | 5.11194 | 0.80298 | 7.33487 |
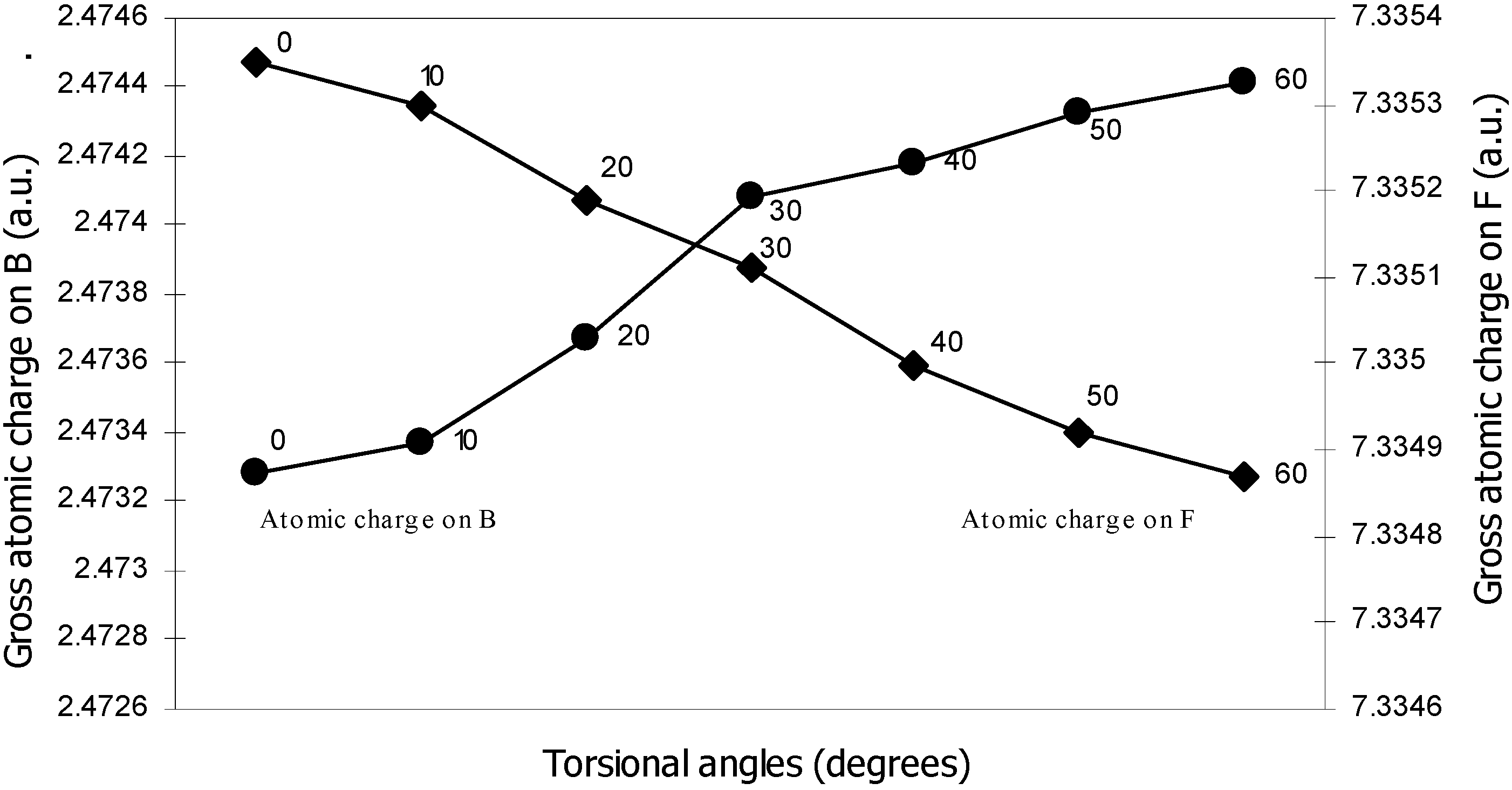
Density Functional study of conformational isomerism
| Angle of torsion | Global hardness | Chemical |
| (degrees) | potential | |
| 0 | 0.3544 | -0.25084 |
| 10 | 0.35456 | -0.25067 |
| 20 | 0.35466 | -0.25094 |
| 0 | 0.35476 | -0.25081 |
| 40 | 0.35484 | -0.25079 |
| 50 | 0.35493 | -0.25096 |
| 60 | 0.35506 | -0.25105 |
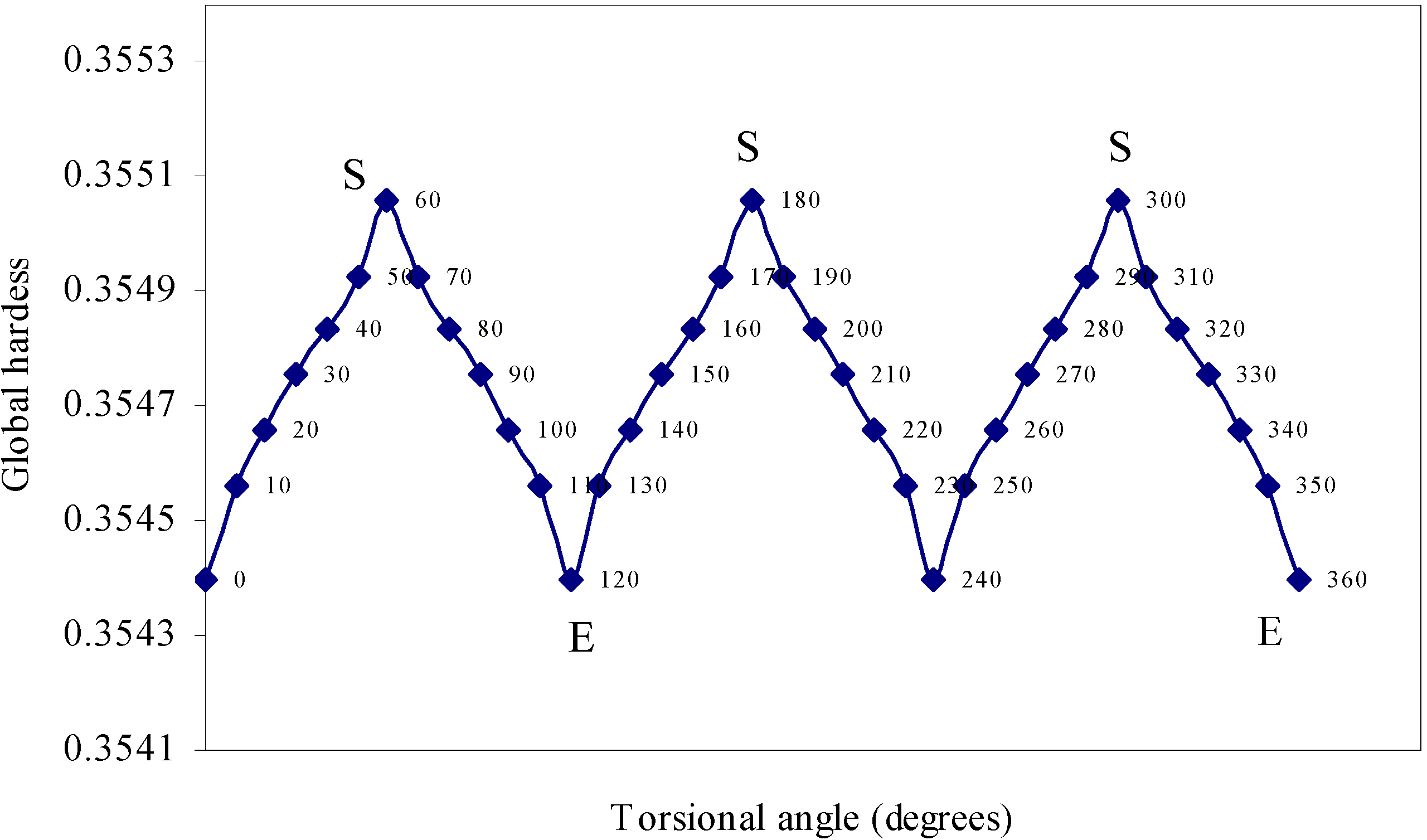
The quest of locating the origin and development of the barrier.
| Angle of torsion | E(B-F) | E(N-H) | E(B-N) |
| (degrees) | |||
| 0 | -0.90155 | -0.73435 | -0.7858 |
| 10 | -0.901558 | -0.73445 | -0.7856 |
| 20 | -0.90158 | -0.73453 | -0.78509 |
| 30 | -0.90164 | -0.7348 | -0.78454 |
| 40 | -0.90168 | -0.73491 | -0.78429 |
| 50 | -0.90179 | -0.73493 | -0.78397 |
| 60 | -0.90184 | -0.73494 | -0.78367 |
| Angle of torsion | (EJ) | (EN) | (EV) | (EK) | (ER) | E (B-N) |
| (degrees) | ||||||
| 0 | 4.05983 | 5.02692 | -8.89252 | -0.11023 | -0.86979 | -0.7858 |
| 10 | 4.05975 | 5.02692 | -8.89238 | -0.1102 | -0.86968 | -0.7856 |
| 20 | 4.05986 | 5.02692 | -8.89241 | -0.11013 | -0.86933 | -0.78509 |
| 30 | 4.06004 | 5.02692 | -8.89246 | -0.11005 | -0.86899 | -0.78454 |
| 40 | 4.05979 | 5.02692 | -8.892 | -0.11001 | -0.86898 | -0.78429 |
| 50 | 4.0592 | 5.02692 | -8.89127 | -0.10996 | -0.86886 | -0.78397 |
| 60 | 4.05879 | 5.02692 | -8.89082 | -0.10991 | -0.86864 | -0.78367 |
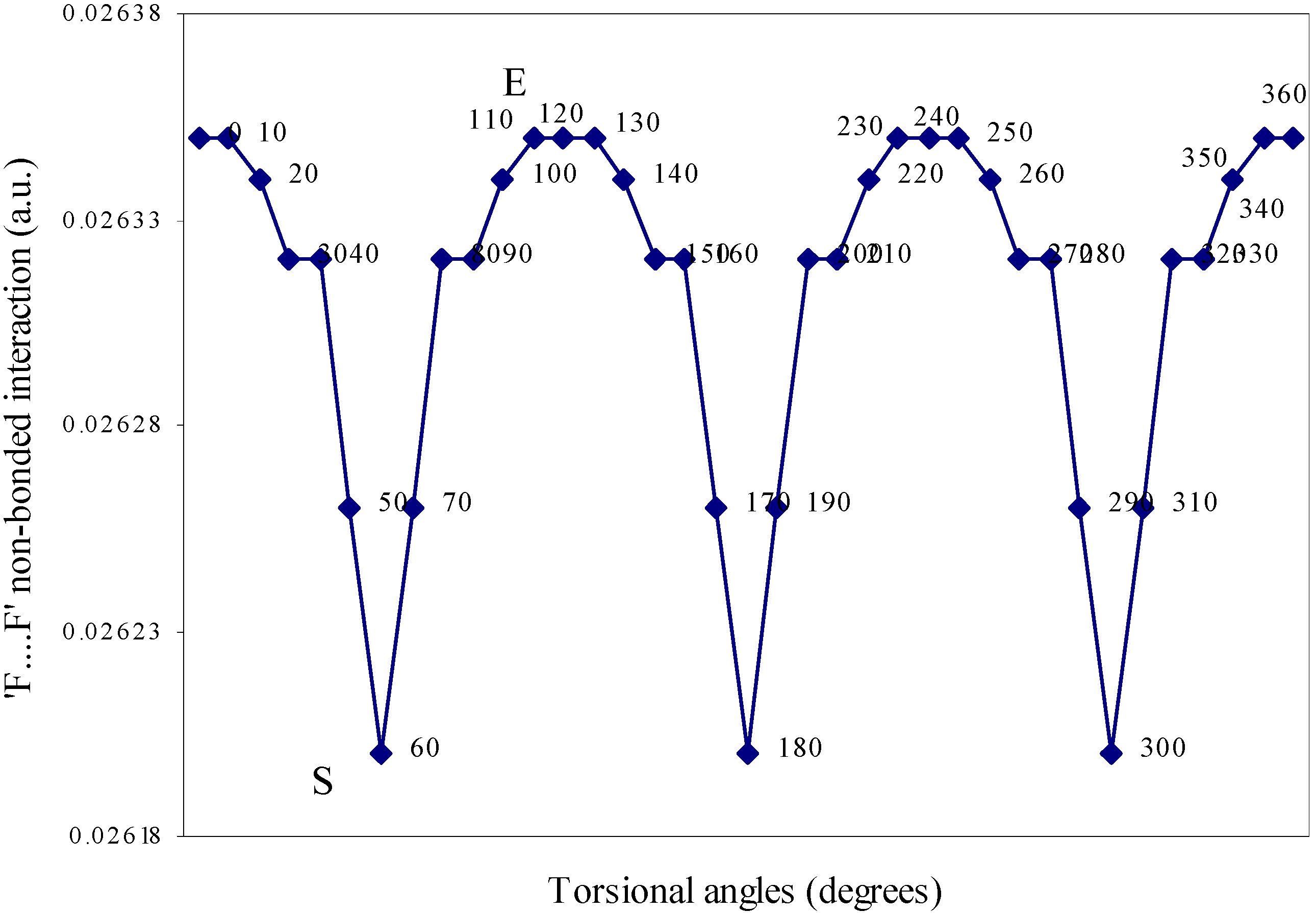
| Angle of torsion | E(N···F) | E(B···H) | E(H···F) | E(F···F) | E(H···H) |
| ( degrees) | |||||
| 0 | 0.01642 | 0.00710 | -0.01293 | 0.02635 | 0.01701 |
| 10 | 0.01638 | 0.00710 | -0.01287 | 0.02634 | 0.01701 |
| 20 | 0.01633 | 0.00692 | -0.01279 | 0.02634 | 0.01704 |
| 30 | 0.01622 | 0.0067 | -0.01265 | 0.02632 | 0.01701 |
| 40 | 0.01605 | 0.0066 | -0.01247 | 0.02632 | 0.0171 |
| 50 | 0.01598 | 0.00656 | -0.01236 | 0.02626 | 0.01708 |
| 60 | 0.01549 | 0.00655 | -0.01224 | 0.0262 | 0.01707 |
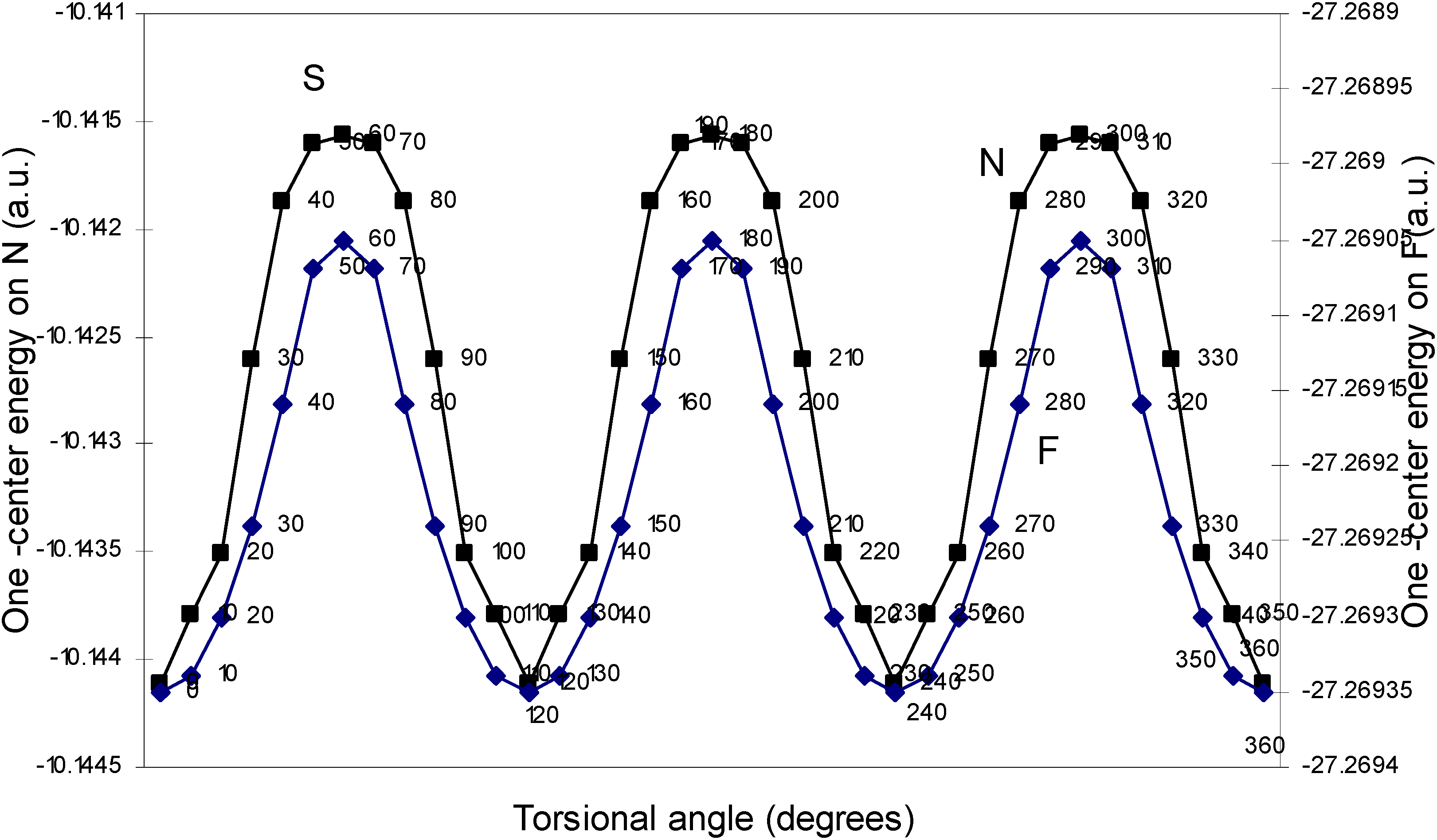
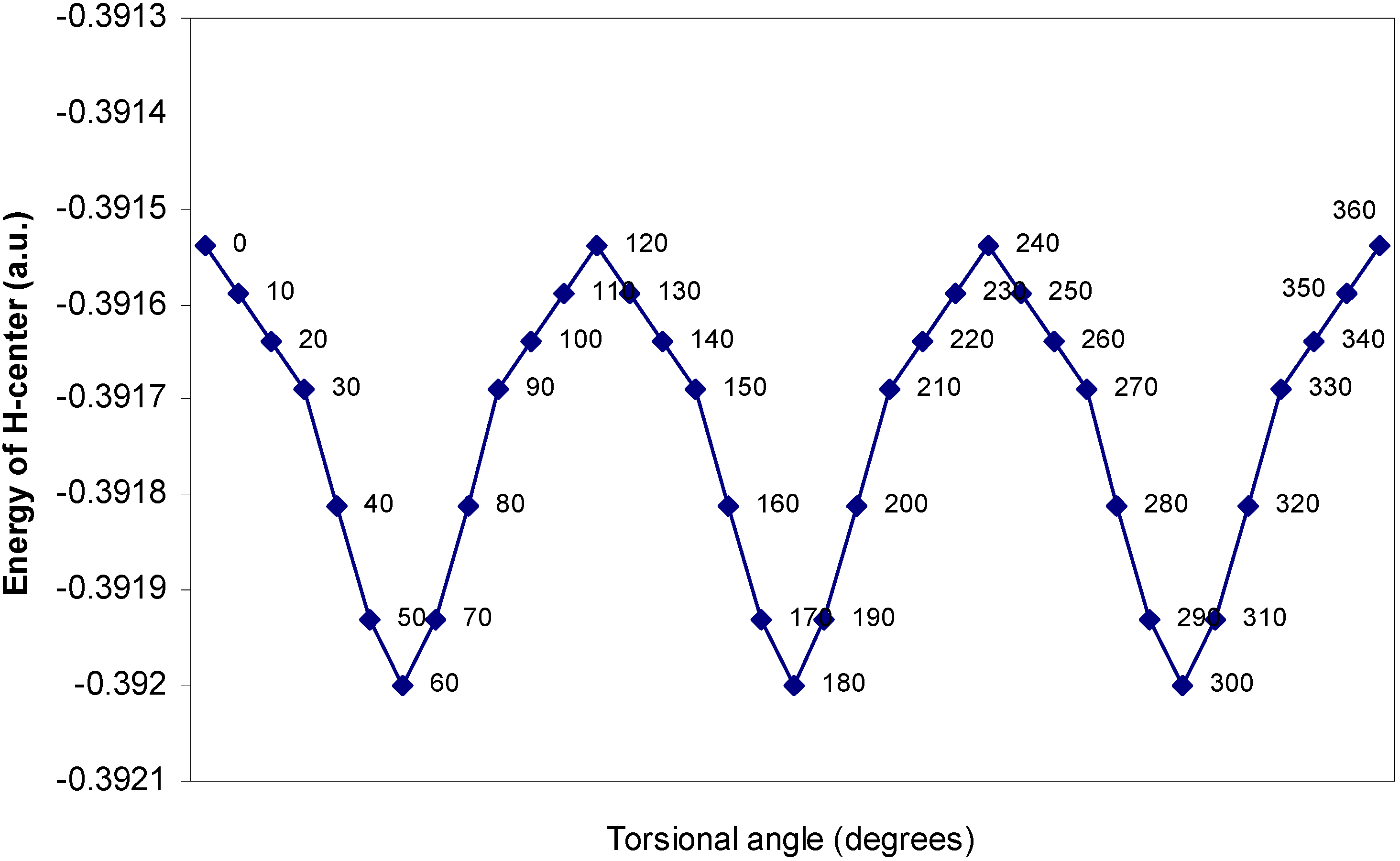
| Angle of torsion | E (B) | E (N) | E (H) | E (F) |
| (degrees) | ||||
| 0 | -2.17600 | -10.14411 | -0.39154 | -27.26935 |
| 10 | -2.17604 | -10.14379 | -0.39159 | -27.26934 |
| 20 | -2.17688 | -10.14351 | -0.39164 | -27.2693 |
| 30 | -2.17633 | -10.14261 | -0.39169 | -27.26924 |
| 40 | -2.17649 | -10.14188 | -0.39181 | -27.26916 |
| 50 | -2.17652 | -10.1416 | -0.39193 | -27.26907 |
| 60 | -2.17651 | -10.14156 | -0.392 | -27.26905 |
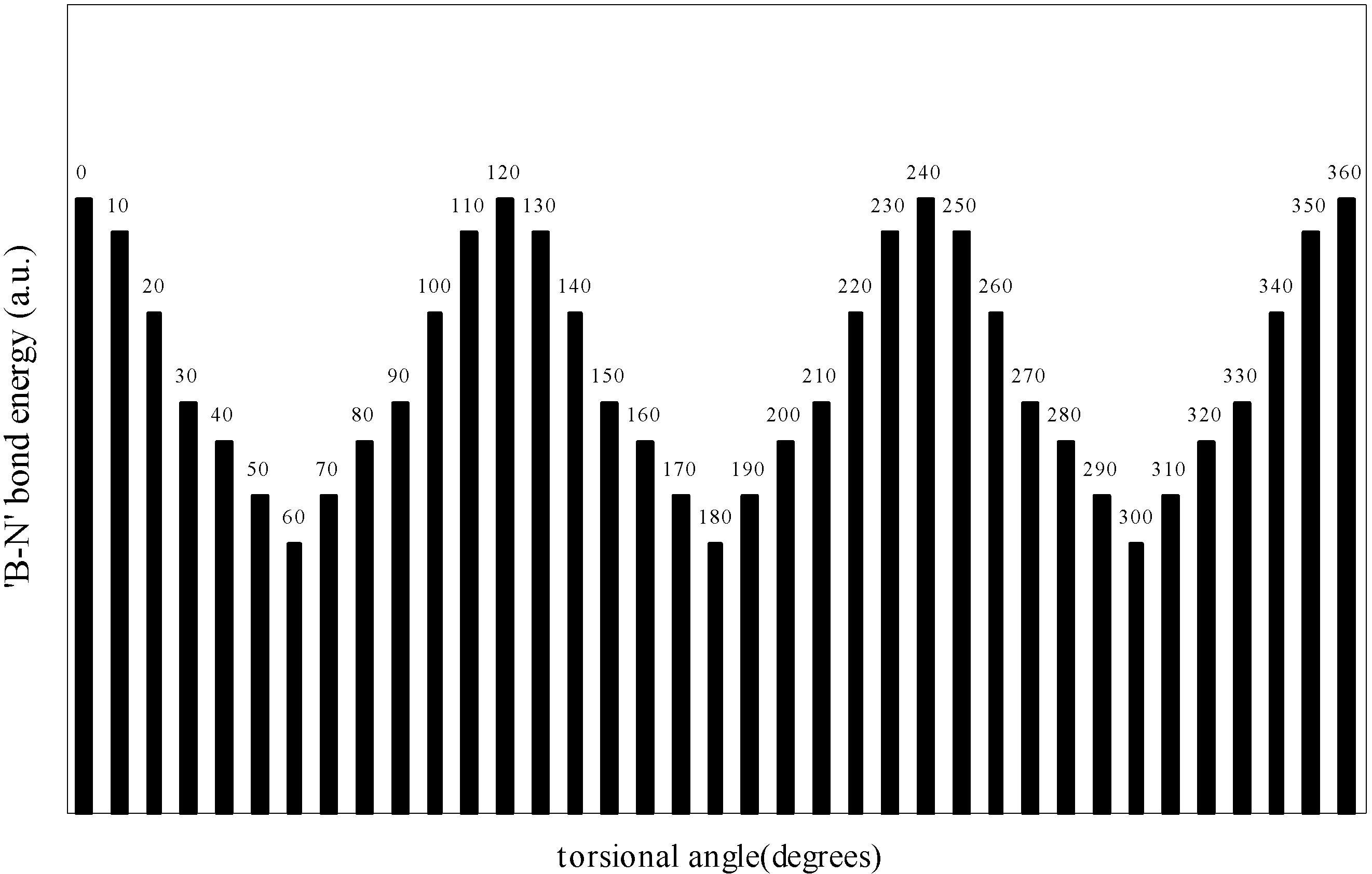
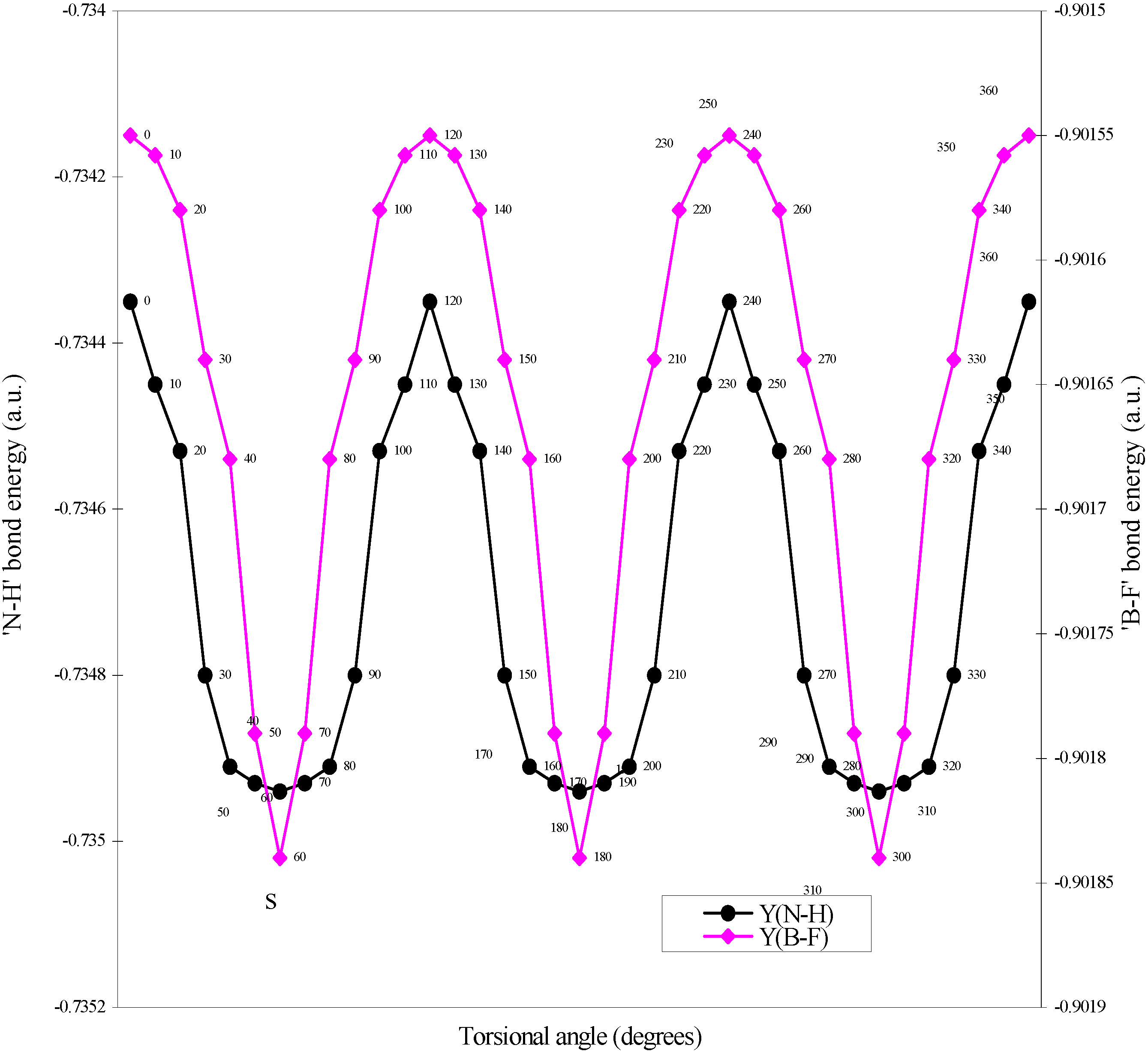

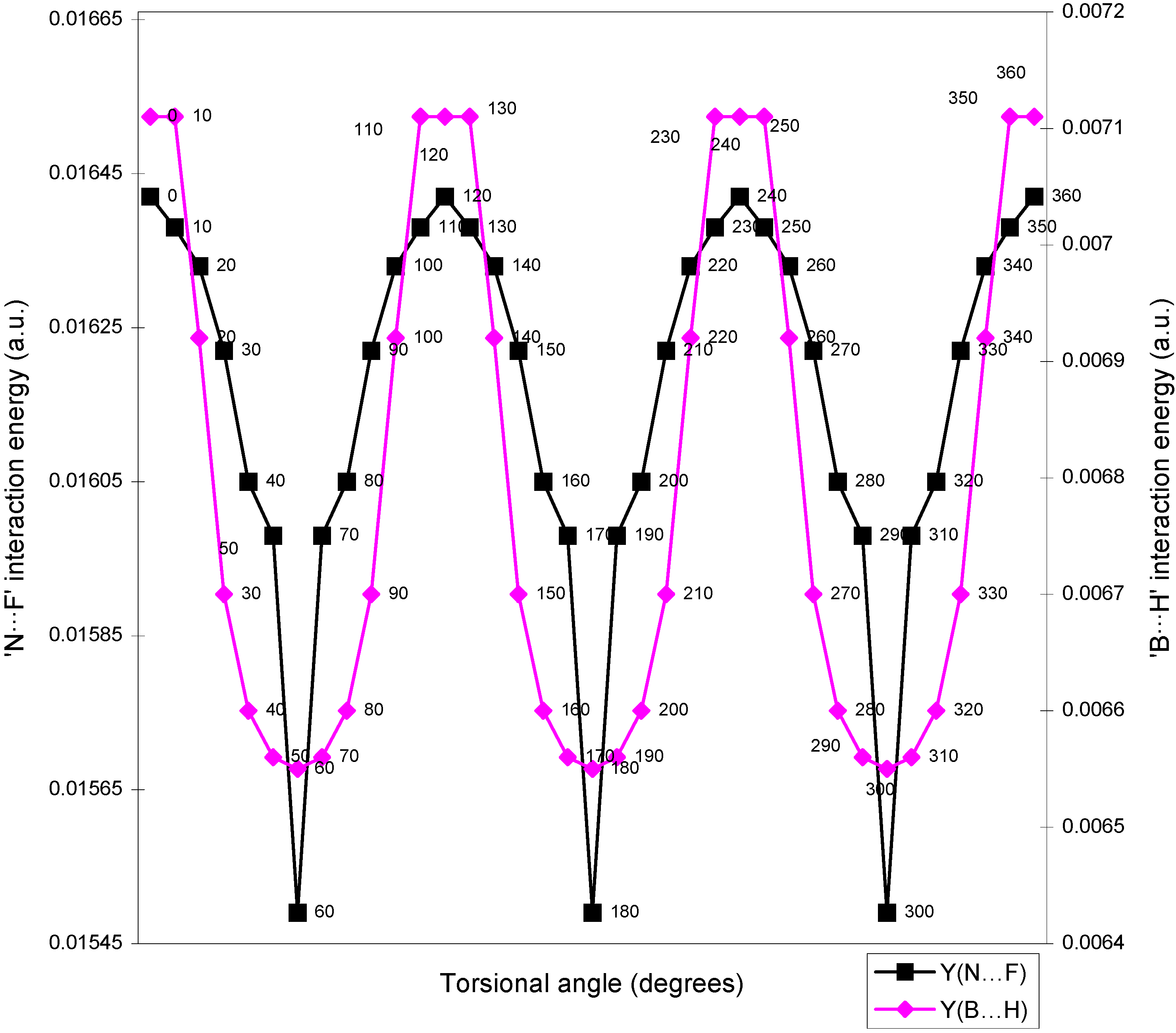
Two-center bonded interactions.
Two-center nonbonded interactions.
One–center energy terms.
The rationale for the small height of the barrier to internal rotation.
Conclusions
References
- Lewis, G.N. Valence and the Structure of Atoms and Molecules; The Chemical Catalog Company: New York, 1923. [Google Scholar]
- Pearson, R.G. J. Am. Chem. Soc. 1963, 85, 3533.idem. Science 1966, 151, 172.
- Labarre, J.F. Struct. Bond. 1978, 35, 1.
- Gay-Lussac, J.L.; Thenard, J.L. Mem. Phys. Chim. Soc. d’Arcueil 1809, 2, 210.Davy, H. Phil Trans. 1812, 102, 365.
- Haaland, A. Angew. Chem. 1989, 101, 1017.idem. Angew. Chem., Int. Ed. Engl. 1989, 28, 992.
- Ghosh, D.C.; Jana, J.; Chakraborty, A. Ind. J. Chem. Soc. 2002, 41A, 462.
- Ghosh, D.C.; Jana, J. Int. J. Quant. Chem. 2003, 92, 484. [CrossRef]
- Fujimoto, H.; Kato, S.; Yamabe, S.; Fukui, K. J. Chem. Phys. 1974, 60, 572.idem. J. Am. Chem. Soc. 1974, 96, 2024.
- Sanderson, R.T. Science 1951, 114, 670.idem. ibid 1952, 116, 41.idem. ibid 1955, 121, 207.idem. J. Chem Ed. 1952, 29, 539.idem. ibid 1954, 31, 238.(f)idem. In Chemical Periodicity; Reinhold Publishing Corporation: New York, 1960.
- Ghosh, D.C. Indian J. Pure Appl. Phys. 1984, 22, 346.idem. Indian J. Pure Appl. Phys. 1989, 27, 160.
- Mulliken, R. S. J. Am. Chem. Soc. 1952, 64, 811. [CrossRef]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. J. Chem. Phys. 1978, 68, 3801.
- Parr, R.G.; Pearson, R.G. J. Am. Chem. Soc. 1983, 105, 7512. [CrossRef]
- Hohenberg, P.; Kohn, H. Phys. Rev. 1964, 136, B864. [CrossRef]
- Cedillo, A.; Chattaraj, P.K.; Parr, R.G. Int. J. Quan. Chem. 2000, 77, 403.
- Chattaraj, P.K.; Nath, S.; Sannigrahi, A.B. J. Phys. Chem. 1994, 98, 9143.Sannigrahi, A.B.; Nandi, P.K. J Mol Struc (THEOCHEM) 1994, 307, 99.
- Pearson, R.G. J. Chem. Ed. 1987, 64, 562. [CrossRef]
- Parr, R.G.; Chattaraj, P.K. J. Am. Chem. Soc. 1991, 113, 1854. [CrossRef]
- Pearson, R.G. Acc. Chem. Res. 1993, 26, 250.Chattaraj, P.K.; Liu, G.H.; Parr, R.G. Chem. Phys. Lett. 1995, 237, 171.Ayers, P.W.; Parr, R.G. J. Am. Chem. Soc. 2000, 122, 2010.
- Chattaraj, P.K.; Sengupta, S. J. Phys. Chem. 1999, 103, 6122. [CrossRef]
- Pearson, R.G.; Palke, W.E. J. Phys. Chem. 1992, 96, 3283. [CrossRef]
- Yang, W.; Lee, C.; Ghosh, S.K. J. Phys. Chem. 1985, 89, 5413.
- Datta, D. J. Phys. Chem. A 1986, 90, 4216. [CrossRef]
- Gázquez, J.L. J. Phys. Chem. 1997, 101, 9464. [CrossRef]
- Freeman, F.; Tsegai, Z.M.; Kasner, M.L.; Hehre, W.J. J. Chem. Ed. 2000, 77, 661. [CrossRef]
- Ghosh, D.C. J. Indian Chem. Soc. 2002, 79, 240.
- Chattaraj, P.K.; Fuentealba, P.; Jaque, P.; Toro, A. J. Phys. Chem. A 1999, 103, 9307. [CrossRef]
- Schleyer, P.v.R.; Kaup, M.; Hampel, F.; Bremer, M.; Mislow, K. J. Am. Chem. Soc. 1992, 114, 6791.
- Ghosh, D.C.; Jana, J.; Biswas, R. Int. J. Quantum. Chem. 2000, 80, 1.
- Ghosh, D.C.; Jana, J.; Bhattacharyya, S. Int. J. Quantum Chem. 2002, 87, 111. [CrossRef]
- Fischer, H.; Kollmar, H. Theoret. Chim. Acta., 1970, 16, 163. [CrossRef]
- Jonas, V.; Frenking, G.; Reetz, M.T. J. Am. Chem. Soc. 1994, 116, 8741. [CrossRef]
- Legon, A.C.; Warner, H.E. J. Chem. Soc. Chem. Commun. 1991, 1397.
- Dvorak, A.; Ford, R.S.; Suenran, R.D.; Levas, F.J.; Leopold., K.R. J. Am. Chem. Soc. 1992, 114, 108.
- Hoard, J.L.; Geller, S.; Cashin, W.M. Acta. Cryst. 1951, 4, 396.
- Ray, R.K.; Chandra, A. K.; Pal, S. J. Phys. Chem. 1994, 98, 1047. [CrossRef]
- Cederbaum, L.S.; Domeke, W. Adv. Chem. Phys. 1977, 36, 205.
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, 1989. [Google Scholar]
- Ghosh, D.C. Proc. Indian. Acad. Sci. 1984, 93, 33.
- Gordon, M.S. J. Am. Chem. Soc. 1969, 91, 3122. [CrossRef]
- Pople, J.A.; Beveridge, D.L. Approximate Molecular Orbital Theory; McGraw-Hill: New York, 1970. [Google Scholar]
- Löwdin, P.O. Adv. Phys. (USA) 1956, 5, 111.
- Roothaan, C.C.J. J. Chem. Phys. 1951, 19, 1445.
- Janda, K.C.; Bernstein, S.S.; Steed, J. M.; Novick, S.E.; Klemperer, W. J. Am. Chem. Soc. 1978, 100, 8074.
- Pearson, R.G. Inorg. Chem. 1988, 27, 734.
- Zhou, Z.; Parr, R.G. G. J. Am. Chem. Soc. 1990, 112, 5720. [CrossRef]
- Parr, R.G.; Zhou, Z. Acc. Chem. Res. 1993, 26, 256. [CrossRef]
- Eliel, E.L.; Wilen, S.H.; Mander, L.N. ‘Stereochemistry of Organic Compounds’; Wiley: New York, 1994. [Google Scholar]
- Nasipuri, D. Stereochemistry of Organic Compounds; Wiley Eastern Ltd.: New Delhi, 1994. [Google Scholar]
© 2004 by MDPI (http://www.mdpi.org).
Share and Cite
Ghosh, D.C.; Bhattacharyya, S. Molecular Orbital and Density Functional Study of the Formation, Charge Transfer, Bonding and the Conformational Isomerism of the Boron Trifluoride (BF3) and Ammonia (NH3) Donor-Acceptor Complex. Int. J. Mol. Sci. 2004, 5, 239-264. https://doi.org/10.3390/i5050239
Ghosh DC, Bhattacharyya S. Molecular Orbital and Density Functional Study of the Formation, Charge Transfer, Bonding and the Conformational Isomerism of the Boron Trifluoride (BF3) and Ammonia (NH3) Donor-Acceptor Complex. International Journal of Molecular Sciences. 2004; 5(8):239-264. https://doi.org/10.3390/i5050239
Chicago/Turabian StyleGhosh, Dulal C., and Soma Bhattacharyya. 2004. "Molecular Orbital and Density Functional Study of the Formation, Charge Transfer, Bonding and the Conformational Isomerism of the Boron Trifluoride (BF3) and Ammonia (NH3) Donor-Acceptor Complex" International Journal of Molecular Sciences 5, no. 8: 239-264. https://doi.org/10.3390/i5050239
APA StyleGhosh, D. C., & Bhattacharyya, S. (2004). Molecular Orbital and Density Functional Study of the Formation, Charge Transfer, Bonding and the Conformational Isomerism of the Boron Trifluoride (BF3) and Ammonia (NH3) Donor-Acceptor Complex. International Journal of Molecular Sciences, 5(8), 239-264. https://doi.org/10.3390/i5050239




