On the Use of Connected Moments Expansion with Coupled Cluster Reference
Abstract
:1 Introduction
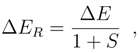
2 The Connected Moments Expansion
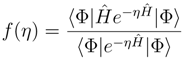
- i)
- f(0) is the expectation value of
with the reference function
- ii)
- it is monotonically decreasing
- iii)
- its Taylor expansion coefficients are the connected moments of
- iv)
- f(∞) is the exact ground state energy.
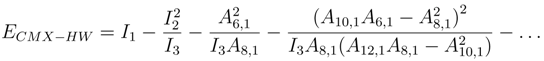
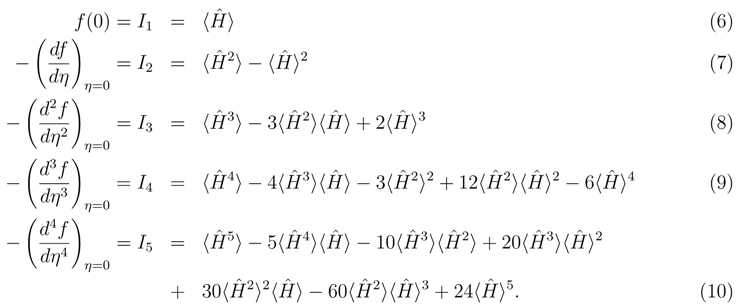
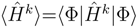 . One easily recognizes that
. One easily recognizes that
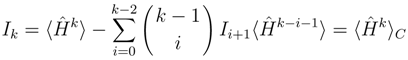

- i)
- whether the above expansion of the true energy is feasible if Φ is an approximate CC wave function, say CCSD; and
- ii)
- whether a modification of the original Horn-Weinstein function, replacing the expectation values by non-symmetric matrix elements in the spirit of CC theory, provides meaningful results.
3 CMX Using a Coupled Cluster Reference State
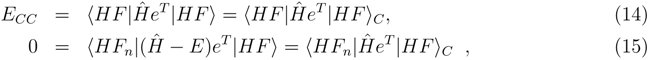
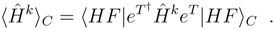
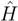 〉 is not a coupled cluster energy calculated in a traditional way. Though already in the original coupled cluster papers it is proven that an expectation value of the Hamiltonian (or any nelectron operator) in terms of the CC wave function is a connected expansion [3], such an approach is not widely used. The reason is simply that evaluation of such matrix elements is substantially complicated due to the occurrence of the (deexcitation) operator eT† in the bra functions. This results in a non-terminating, though factorizable, expansion of the expectation value. Thinking in this way, one meets the problem of determining where to terminate this expansion, since unfortunately, it consists of many mutually (almost) canceling terms [52]. An alternative way is to compute these matrix elements by determining the CC wave function, converting the CC amplitudes to CI-type coefficients. In principle the procedure involves letting the Hamiltonian act on the eT |HF〉, and taking the scalar product of the two vectors. This is certainly very demanding computationally, but easy to apply as soon as a general CI program is available. We used the latter approach in obtaining the testing numerical examples reported below.
〉 is not a coupled cluster energy calculated in a traditional way. Though already in the original coupled cluster papers it is proven that an expectation value of the Hamiltonian (or any nelectron operator) in terms of the CC wave function is a connected expansion [3], such an approach is not widely used. The reason is simply that evaluation of such matrix elements is substantially complicated due to the occurrence of the (deexcitation) operator eT† in the bra functions. This results in a non-terminating, though factorizable, expansion of the expectation value. Thinking in this way, one meets the problem of determining where to terminate this expansion, since unfortunately, it consists of many mutually (almost) canceling terms [52]. An alternative way is to compute these matrix elements by determining the CC wave function, converting the CC amplitudes to CI-type coefficients. In principle the procedure involves letting the Hamiltonian act on the eT |HF〉, and taking the scalar product of the two vectors. This is certainly very demanding computationally, but easy to apply as soon as a general CI program is available. We used the latter approach in obtaining the testing numerical examples reported below.3.1 Modified CC-CMX formulas
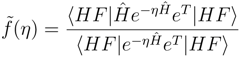
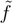 (0) = 〈HF|HeT |HF〉 = ECC is the coupled cluster energy, and
(0) = 〈HF|HeT |HF〉 = ECC is the coupled cluster energy, and 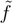 (∞) = E0 is the exact (full CI) eigenvalue. To prove the latter statement, consider the spectral resolution of
(∞) = E0 is the exact (full CI) eigenvalue. To prove the latter statement, consider the spectral resolution of 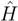 and insert it into (17):
and insert it into (17):
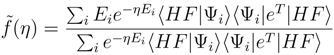
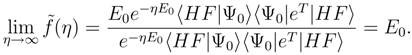
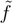 (η) with respect to η and taking the derivatives at η = 0 we obtain
(η) with respect to η and taking the derivatives at η = 0 we obtain
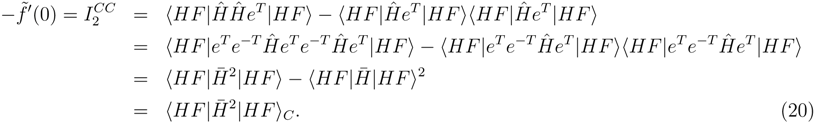
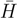 for the similarity transformed Hamiltonian:
for the similarity transformed Hamiltonian:
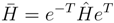
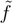 (η) by parenthesized superscripts,
(η) by parenthesized superscripts,
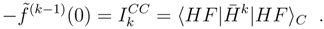
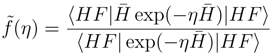
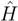 replaced by
replaced by 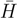 . Accordingly, now one has connected moments of
. Accordingly, now one has connected moments of 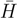 defined by Eq. (23), and the CMX expansion may proceed along the same line as with the symmetric formulas. Although the similarity transformed Hamiltonian
defined by Eq. (23), and the CMX expansion may proceed along the same line as with the symmetric formulas. Although the similarity transformed Hamiltonian 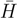 is more than a mere two-particle operator, evaluation of the non-symmetric connected moments is, nevertheless, substantially simpler than (16). The reason is that, in opposite to (16),
is more than a mere two-particle operator, evaluation of the non-symmetric connected moments is, nevertheless, substantially simpler than (16). The reason is that, in opposite to (16), 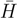 k always consists of finite number of terms, for finite k.
k always consists of finite number of terms, for finite k.| Reference function | ||||||
| CCSD | CISDc | CCSDT | CISDTc | |||
| CCa | XCCb | CCa | XCC | |||
| 3-21G (-14.531444 Eh) | ||||||
| CMX-HW(1) | 0.028 | 0.028 | 0.048 | 0.002 | 0.000 | 0.023 |
| CMX-HW(2) | 0.028 | 0.003 | 0.005 | 0.002 | 0.000 | 0.000 |
| CMX-HW(3) | 0.032 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 |
| CMX-HW(4) | 0.024 | 0.000 | 0.000 | -0.001 | 0.000 | 0.000 |
| CMX-LT(4) | 0.018 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 6-311G (-14.632864 Eh) | ||||||
| CMX-HW(1) | 0.189 | 0.190 | 1.492 | 0.004 | 0.001 | 1.312 |
| CMX-HW(2) | 0.189 | 0.023 | 0.129 | 0.004 | 0.000 | 0.083 |
| CMX-HW(3) | 0.150 | 0.003 | 0.054 | 0.003 | 0.000 | 0.036 |
| CMX-HW(4) | -0.234 | 0.001 | -0.010 | 0.002 | 0.000 | 0.038 |
| CMX-LT(4) | -0.197 | 0.001 | -0.012 | 0.003 | 0.000 | 0.038 |
| 6-311G** (-14.633376 Eh) | ||||||
| CMX-HW(1) | 0.274 | 0.274 | 1.528 | 0.004 | 0.002 | 1.265 |
| CMX-HW(2) | 0.274 | 0.052 | 0.175 | 0.004 | 0.000 | 0.082 |
| CMX-HW(3) | -0.049 | 0.005 | 0.069 | 0.004 | 0.000 | 0.036 |
| CMX-HW(4) | -0.210 | 0.001 | 0.032 | 0.001 | 0.000 | 0.040 |
| CMX-LT(4) | -0.207 | 0.002 | 0.031 | 0.002 | 0.001 | 0.040 |
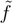 (η). It may happen therefore, that estimating
(η). It may happen therefore, that estimating 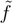 (∞) with low order derivatives does not improve the energy. Another interesting difference is that while the symmetric second moment, f′(0), being the distribution of the Hamiltonian, vanishes if and only if Φ is an exact eigenfunction,
(∞) with low order derivatives does not improve the energy. Another interesting difference is that while the symmetric second moment, f′(0), being the distribution of the Hamiltonian, vanishes if and only if Φ is an exact eigenfunction, 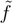 ′(0) may be zero due to several reasons. In particular, one may easily prove that it vanishes for a CCSD wave function provided that the amplitude equations have been exactly solved. Coming back to Eq. (20) we can write:
′(0) may be zero due to several reasons. In particular, one may easily prove that it vanishes for a CCSD wave function provided that the amplitude equations have been exactly solved. Coming back to Eq. (20) we can write:
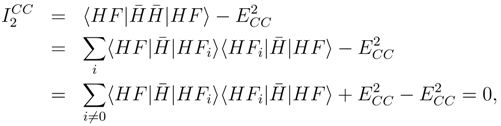
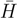 |HFi〉 vanish as well.
|HFi〉 vanish as well.4 Test Results
| Ref. | R=1.01 Å | R=1.5 Å | R=2.0 Å | ||||||
| CCSD | CISD | CCSD | CISD | CCSD | CISD | ||||
| CC | XCC | CC | XCC | CC | XCC | ||||
| STO-3G/FCIa | -83.736245 Eh | -82.218671 Eh | -81.401484 Eh | ||||||
| CMX-HW(1) | 0.145 | 0.117 | 0.990 | 0.378 | 0.175 | 4.045 | 0.417 | 0.119 | 9.354 |
| CMX-HW(2) | 0.145 | 0.029 | 0.167 | 0.378 | 0.066 | 0.831 | 0.417 | 0.073 | 2.411 |
| CMX-HW(3) | 0.146 | 0.029 | 0.071 | 0.383 | 0.040 | 0.319 | 0.423 | 0.060 | 0.922 |
| CMX-HW(4) | 0.158 | 0.030 | 0.066 | 0.409 | 0.034 | 0.321 | 0.452 | 0.063 | 0.935 |
| CMX-LT(4) | 0.189 | 0.009 | 0.050 | 0.505 | 0.017 | 0.327 | 0.565 | 0.071 | 0.963 |
| 3-21G/FCIa | -84.434106 Eh | -82.923660 Eh | -82.112076 Eh | ||||||
| CMX-HW(1) | 1.886 | 1.670 | 6.372 | 3.953 | 3.511 | 12.422 | 7.552 | 6.584 | 25.057 |
| CMX-HW(2) | 1.886 | 0.483 | 1.705 | 3.953 | 1.062 | 4.527 | 7.552 | 2.145 | 10.997 |
| CMX-HW(3) | 2.071 | 0.195 | 0.813 | 4.250 | 0.495 | 2.519 | 7.996 | 1.137 | 6.209 |
| CMX-HW(4) | 1.448 | 0.168 | 0.601 | 2.777 | 0.463 | 2.009 | 5.620 | 0.975 | 5.130 |
| CMX-LT(4) | 1.034 | 0.142 | 0.436 | 1.694 | 0.431 | 1.591 | 3.853 | 0.791 | 4.259 |
| Ref. | R=1.0 Å | R=1.5 Å | R=2.0 Å | ||||||
| CCSD | CISD | CCSD | CISD | CCSD | CISD | ||||
| CC | XCC | CC | XCC | CC | XCC | ||||
| 6-31G/FCIa | -104.877215 Eh | -103.201083 Eh | -102.348497 Eh | ||||||
| CMX-HW(1) | 1.233 | 0.958 | 5.865 | 3.379 | 2.861 | 11.730 | 7.545 | 5.809 | 24.322 |
| CMX-HW(2) | 1.233 | 0.386 | 1.234 | 3.379 | 1.120 | 3.610 | 7.545 | 2.572 | 9.615 |
| CMX-HW(3) | 1.296 | 0.110 | 0.520 | 3.480 | 0.477 | 1.859 | 7.695 | 1.745 | 5.117 |
| CMX-HW(4) | 0.933 | 0.092 | 0.383 | 2.287 | 0.419 | 1.545 | 5.620 | 0.497 | 4.508 |
| CMX-LT(4) | 0.610 | 0.077 | 0.231 | 0.925 | 0.352 | 1.179 | 3.002 | -1.941 | 3.827 |
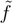 (η) (24) may not be monotonic as one would like to have. This most probably explains the “worst” performance of the CC moments, from the three investigated approaches for beryllium. As soon as we start from CCSDT wave function —which is almost “exact”— CMX through CC moments outperforms the CISDT based CMX.
(η) (24) may not be monotonic as one would like to have. This most probably explains the “worst” performance of the CC moments, from the three investigated approaches for beryllium. As soon as we start from CCSDT wave function —which is almost “exact”— CMX through CC moments outperforms the CISDT based CMX.Acknowledgments
References
- Coester, F. Nucl. Phys. 1958, 7, 421.Coester, F.; Kümmel, H. Nucl. Phys. 1960, 17, 477.
- Čížzek, J. J. Chem. Phys. 1966, 45, 4256.
- Čížzek, J. Adv. Chem. Phys. 1969, 14, 35.
- Purvis, G. D.; Bartlett, R. J. J. Chem. Phys. 1982, 76, 1910.
- Noga, J.; Bartlett, R. J. J. Chem. Phys. 1987, 86, 7071.1988, 89, 3401 (E).
- Scuseria, G. E.; Schaefer III, H. F. Chem. Phys. Lett. 1988, 152, 382.
- Oliphant, N.; Adamowicz, L. J. Chem. Phys. 1991, 95, 6645.
- Kucharski, S. A.; Bartlett, R. J. Theor. Chim. Acta 1991, 80, 387.J. Chem. Phys. 1992, 97, 4282.
- Kállay, M.; Surján, P. J. Chem. Phys. 2000, 113, 1359.
- Kállay, M.; Surján, P. J. Chem. Phys. 2001, 115, 2945.
- Olsen, J. J. Chem. Phys. 2000, 113, 7140.
- Hirata, S.; Nooijen, M.; Grabowski, I.; Bartlett, R. J. J. Chem. Phys. 2001, 114, 3919.2001, 115, 3967 (E).
- Lee, Y. S.; Kucharski, S. A.; Bartlett, R. J. J. Chem. Phys. 1984, 81, 5906.
- Urban, M.; Noga, J.; Cole, S. J.; Bartlett, R. J. J. Chem. Phys. 1985, 83, 404.
- Noga, J.; Bartlett, R. J.; Urban, M. Chem. Phys. Lett. 1987, 134, 126.
- Kucharski, S. A.; Bartlett, R. J. Chem. Phys. Lett. 1989, 158, 550.
- Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. Chem. Phys. Lett. 1989, 157, 479.
- Noga, J.; Kutzelnigg, W.; Klopper, W. Chem. Phys. Lett. 1992, 199, 497.
- Raghavachari, K. J. Chem. Phys. 1985, 82, 5761.
- Raghavachari, K.; Pople, J. A.; Replogle, E. S.; Head-Gordon, M. J. Phys. Chem. 1990, 94, 5579.
- Bartlett, R. J.; Watts, J. D.; Kucharski, S. A.; Noga, J. Chem. Phys. Lett. 1990, 165, 513.
- Piecuch, P.; Paldus, J. Theor. Chim. Acta 1990, 78, 65.Piecuch, P.; Tobola, R.; Paldus, J. Int. J. Quantum Chem. 1995, 55, 133.
- Kucharski, S. A.; Bartlett, R. J. Chem. Phys. Lett. 1993, 206, 574.
- Deegan, M. J. O.; Knowles, P. J. Chem. Phys. Lett. 1994, 227, 321.
- Stanton, J.; Gauss, J. J. Chem. Phys. 1995, 103, 1064.Theor. Chim. Acta 1996, 93, 303.1997, 95, 97 (E).Crawford, T. D.; Stanton, J. F. Int. J. Quantum Chem. 1998, 70, 601.
- Christiansen, O.; Koch, H.; Jørgensen, P. J. Chem. Phys. 1996, 105, 1451.
- Crawford, T. D.; Lee, T. J.; Schaefer III, H. F. J. Chem. Phys. 1997, 107, 7943.
- Kucharski, S. A.; Bartlett, R. J. J. Chem. Phys. 1998, 108, 5243.
- Kucharski, S. A.; Bartlett, R. J. J. Chem. Phys. 1998, 108, 5255.
- Kowalski, K.; Piecuch, P. Computational Chemistry: Reviews of Current Trends; Lesz-cynski, J., Ed.; World Scientific: Singapore, 2000; Vol 5. p. 1. [Google Scholar]
- Kowalski, K.; Piecuch, P. J. Chem. Phys. 2000, 113, 18.
- Kowalski, K.; Piecuch, P. J. Chem. Phys. 2001, 115, 2966.
- Kowalski, K.; Piecuch, P. J. Molec. Struct. (THEOCHEM). 2001, 547, 191.
- Gwaltney, S. R.; Head-Gordon, M. Chem. Phys. Lett. 2000, 323, 21.Gwaltney, S. R.; Sherrill, C. D.; Head-Gordon, M.; Krylov, A. I. J. Chem. Phys. 2000, 113, 3548.Gwaltney, S. R.; Head-Gordon, M. J. Chem. Phys. 2001, 115, 2014.
- Meissner, L.; Bartlett, R. J. J. Chem. Phys. 2001, 115, 50.
- Kucharski, S. A.; Noga, J.; Bartlett, R. J. J. Chem. Phys. 1989, 90, 7282.
- Noga, J.; Pluta, T. Chem. Phys. Lett. 1997, 264, 101.
- Olsen, J.; Christiansen, O.; Koch, H.; Jorgensen, P. J. Chem. Phys. 1996, 105, 5082.
- Jankowski, K.; Kowalski, K. J. Chem. Phys. 1999, 111, 2952.
- Kowalski, K.; Piecuch, P. J. Chem. Phys. 2000, 113, 5644.Piecuch, P.; Kucharski, S. A.; Špirko, V.; Kowalski, K. J. Chem. Phys. 2001, 115, 5796.Kowalski, K.; Piecuch, P. Chem. Phys. Lett. 2001, 344, 165.Piecuch, P.; Kucharski, S. A.; Kowalski, K. Chem. Phys. Lett. 2001, 344, 176.
- Stanton, J. F. Chem. Phys. Lett. 1997, 281, 130.
- Cioslowski, J. Phys. Rev. Lett. 1987, 58, 83. [PubMed]
- Cioslowski, J.; Kertéesz, M.; Surján, P.; Poirier, R. A. Chem. Phys. Lett. 1987, 138, 516.
- Cioslowski, J. Int. J. Quantum Chem. 1987, S21, 563.
- Knowles, P. Chem. Phys. Lett. 1987, 134, 512.
- Mancini, J. D.; Zhou, Y.; Meier, P. F. Int. J. Quantum Chem. 1994, 50, 101.
- Yoshida, T.; Iguchi, K. Chem. Phys. Lett. 1988, 143, 329.J. Chem. Phys. 1989, 91, 4249.
- Wolinski, K.; Pulay, P. J. Chem. Phys. 1989, 90, 3647.
- Surján, P.; Szabados, Á. to be published.
- Horn, D.; Weinstein, M. Phys. Rev. D 1984, 30, 1256.
- Lanczos, C. J. J. Res. Natl. Bur. Std. 1950, 45, 55.
- Bartlett, R. J.; Noga, J. Chem. Phys. Lett. 1988, 150, 29.
- 1Originally denoted as CCSD+T(CCSD). Abbreviation CCSD[T] was introduced for simplicity in [18].
© 2002 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Noga, J.; Szabados, A.; Surján, P.R. On the Use of Connected Moments Expansion with Coupled Cluster Reference. Int. J. Mol. Sci. 2002, 3, 508-521. https://doi.org/10.3390/i3050508
Noga J, Szabados A, Surján PR. On the Use of Connected Moments Expansion with Coupled Cluster Reference. International Journal of Molecular Sciences. 2002; 3(5):508-521. https://doi.org/10.3390/i3050508
Chicago/Turabian StyleNoga, Jozef, Agnes Szabados, and Péter R. Surján. 2002. "On the Use of Connected Moments Expansion with Coupled Cluster Reference" International Journal of Molecular Sciences 3, no. 5: 508-521. https://doi.org/10.3390/i3050508
APA StyleNoga, J., Szabados, A., & Surján, P. R. (2002). On the Use of Connected Moments Expansion with Coupled Cluster Reference. International Journal of Molecular Sciences, 3(5), 508-521. https://doi.org/10.3390/i3050508




