Theoretical Calculation of Absolute Radii of Atoms and Ions. Part 1. The Atomic Radii

Abstract

A set of theoretical atomic radii corresponding to the principal maximum in the radial distribution function, 4πr²_R² for the outermost orbital has been calculated for the ground state of 103 elements of the periodic table using Slater orbitals. The set of theoretical radii are found to reproduce the periodic law and the Lother Meyer’s atomic volume curve and reproduce the expected vertical and horizontal trend of variation in atomic size in the periodic table. The d-block and f-block contractions are distinct in the calculated sizes. The computed sizes qualitatively correlate with the absolute size dependent properties like ionization potentials and electronegativity of elements. The radii are used to calculate a number of size dependent periodic physical properties of isolated atoms viz., the diamagnetic part of the atomic susceptibility, atomic polarizability and the chemical hardness. The calculated global hardness and atomic polarizability of a number of atoms are found to be close to the available experimental values and the profiles of the physical properties computed in terms of the theoretical atomic radii exhibit their inherent periodicity. A simple method of computing the absolute size of atoms has been explored and a large body of known material has been brought together to reveal how many different properties correlate with atomic size.

Introduction

The concept of atomic and ionic radii has been found to be very useful in understanding, explaining, correlating and even predicting many physico-chemical properties of atoms, ions and molecules. The periodicity of chemical and physical properties of the elements has been recognized from the date of early history of chemistry. The atomic volume curve of Lother Meyer was a striking example of periodicity of physical properties of elements. The atomic size has been also an important periodic property of the elements. The atomic and ionic radii values are important input in many calculations of size dependent physico–chemical properties of isolated atoms. The crystal chemists have tried for many years to treat atoms and ions as hard spheres and published series of atomic and ionic radii with the only significance that such atomic and ionic radii, when added, reproduce the minimum distance of separation between atoms and ions respectively in crystal lattices. Approximate additivity of atomic and ionic radii were noted by early investigators like Goldschmidt et al [1], Pauling [2], Zachariasen [3], and Bragg [4]. However, the inter atomic or inter ionic distance depend upon the crystal type, its allotropic modification, co-ordination number, temperature etc. Unfortunately this very important property –– the size concept of atoms and ions is heavily underplayed. The text books dealing with this size aspects of atoms or ions never make the position distinctly clear as to the meaning and purport of the terms ‘atomic’ or ‘ionic’ radii and the term ‘radii’ is kept vague. But invariably the text books display one or the other chart of atomic and ionic radii and recently there has been a proliferation of the tables and data of atomic and ionic radii with bewildering array of terms including bonded, non-bonded, ionic, covalent and van der Waals radii [5]. But such radii data though useful in reproducing the inter atomic/ionic distances for the particular purposes but not useful in computing the radial dependent absolute properties of atoms. Also, there is no means of verifying the merit of a set of radii determined experimentally or calculated theoretically because, there is no experimental value of the sizes of atoms and ions [6].

According to quantum mechanical view, the atoms and the ions do not have any rigid shape or size and hence the question of atomic and ionic radii simply does not arise in the true sense of the term. However, chemical experience suggests that the atoms and ions do have an effective size because, the atoms and ions cannot approach each other beyond certain limiting distance under the influence of forces encountered in chemical interactions. The determination of the empirical atomic and ionic radii, on the basis of hard sphere approximation model, has a history stretching back to the work of Bragg⁴ in 1920’s to the work of Slater [7] in the year 1964. Attempts of computing theoretical atomic and ionic radii within the scope of Self Consistent Field (SCF) theory are also reported [7,8].

The inherent approximation of the SCF method suggests that each electron have its own one-electron function or orbital in many–electron situation. The fact that each electron in a many electron system should have one-electron function is a pre-quantum mechanical thinking [9] when it was pointed out that many spectroscopic facts could be rationalized if energy levels were identified with those of a single electron moving in a central field. Slater [7] argued that there must be a connection between empirically determined atomic and ionic size with the wave functions of atoms and ions and pointed out a good correlation between the atomic radii and the distance of maximum charge density in the outermost electron shell of the atom. To be more precise, according to the suggestion of Slater, the principal maxima of the radial charge density distribution function of the outermost orbital of the atom may be considered as its theoretical atomic radius. Slater [7] published a set of atomic radii computed through comparison of a large number of crystal data and it is claimed that such crystal radii are very close to the theoretical atomic radii calculated by Liberman, Waber and Cromer through self–consistent field wave functions for all the atoms with relativistic correlations according to the Dirac equations. Waber and Cromer [8] calculated the theoretical atomic radii of a number of atoms through relativistic Hartree–Fock method. In absence of any experimental data [6] regarding the absolute size of atoms and ions the question of accuracy of any theoretical or experimental method of computing atomic or ionic size cannot be just tested. Sporadic informations of calculations of atomic size by sophisticated theoretical methods are found to appear in the literature but such data are mostly unpublished. Also it appears that such data has never been applied to compute any property of isolated atom or ion. In the premises, we propose a less sophisticated simple technique of computing theoretical or absolute radii of atoms and ions. The level of theory is semi-empirical. Slater [10] suggested an analytical form of the radial part of one-electron function that provides with a scope of computing a number of one–electron and radial properties including the scope of computation of theoretical atomic and ionic radii. The computation of theoretical atomic and ionic radii becomes tremendously simplified if Slater Orbitals are used in such calculation.

Slater [10] proposed a much simpler analytical form for the radial part of the one-electron function or orbital now widely known as Slater–type orbitals, STO’s. The analytical form of normalized radial part of atomic orbital R_nl(r) is given by,

R_nl(r) = (2ξ)^n+1/2[(2n)!]^-1/2r^n-1exp(−ξr)

(1)

Where,

n = the principal quantum number of the electron

r = distance from the nucleus

ξ is the orbital exponent and is given by

ξ = (Z–S)/n^*

(2)

Where, Z= atomic number and S is the screening constant and n^* is the effective principal quantum number. The quantity, (Z–S) is further identified as effective nuclear charge, Z^*.

In terms of Slater orbitals the theoretical atomic or ionic radii,

r_max = n / ξ

(3)

The eqn. (3) is the formula of computation of theoretical atomic and ionic radii in terms of Slater orbital. This shows that theoretical radii of atoms and ions can be easily computed only if ξ is known and one can know ξ, if the effective principal quantum number of the outermost shell of the atom (n^*) and the screening constant (S) are known. Although the SCF ξ is also available [11], Slater [10] laid down a set of empirical rules for calculating S and n^* to give good approximations to the best atomic orbitals of this type. The goal of this work has been to explore the possibility of developing a simple but effective method of computing the absolute radii atoms and ions relying upon Slater’s definition of absolute radii and using Slater’s orbitals. It is well known that orbital exponent, ξ obtained by Slater’s empirical rules are found useful in SCF calculation giving satisfactory results although use of SCF optimized ξ is simultaneously in use [11].

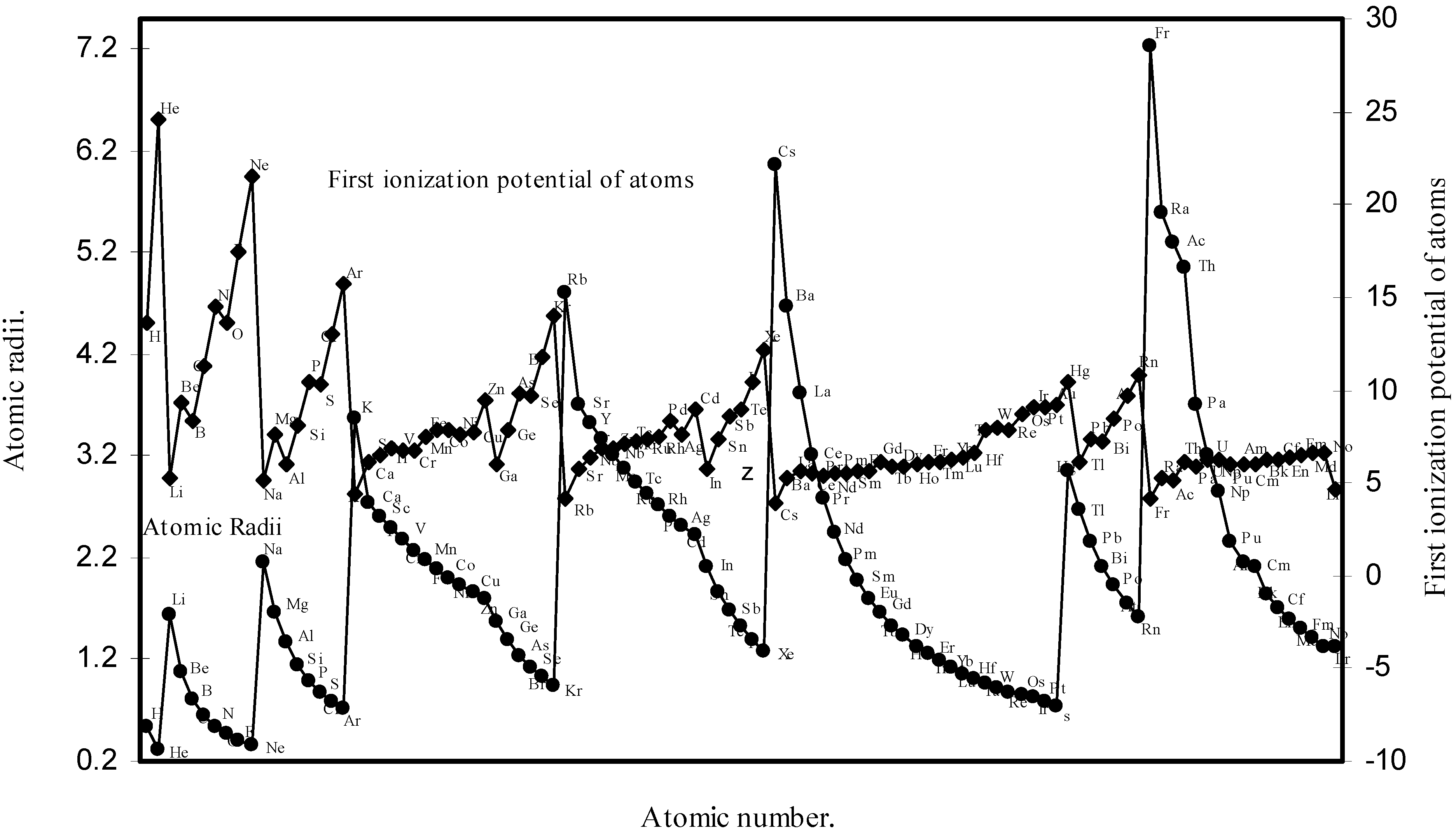
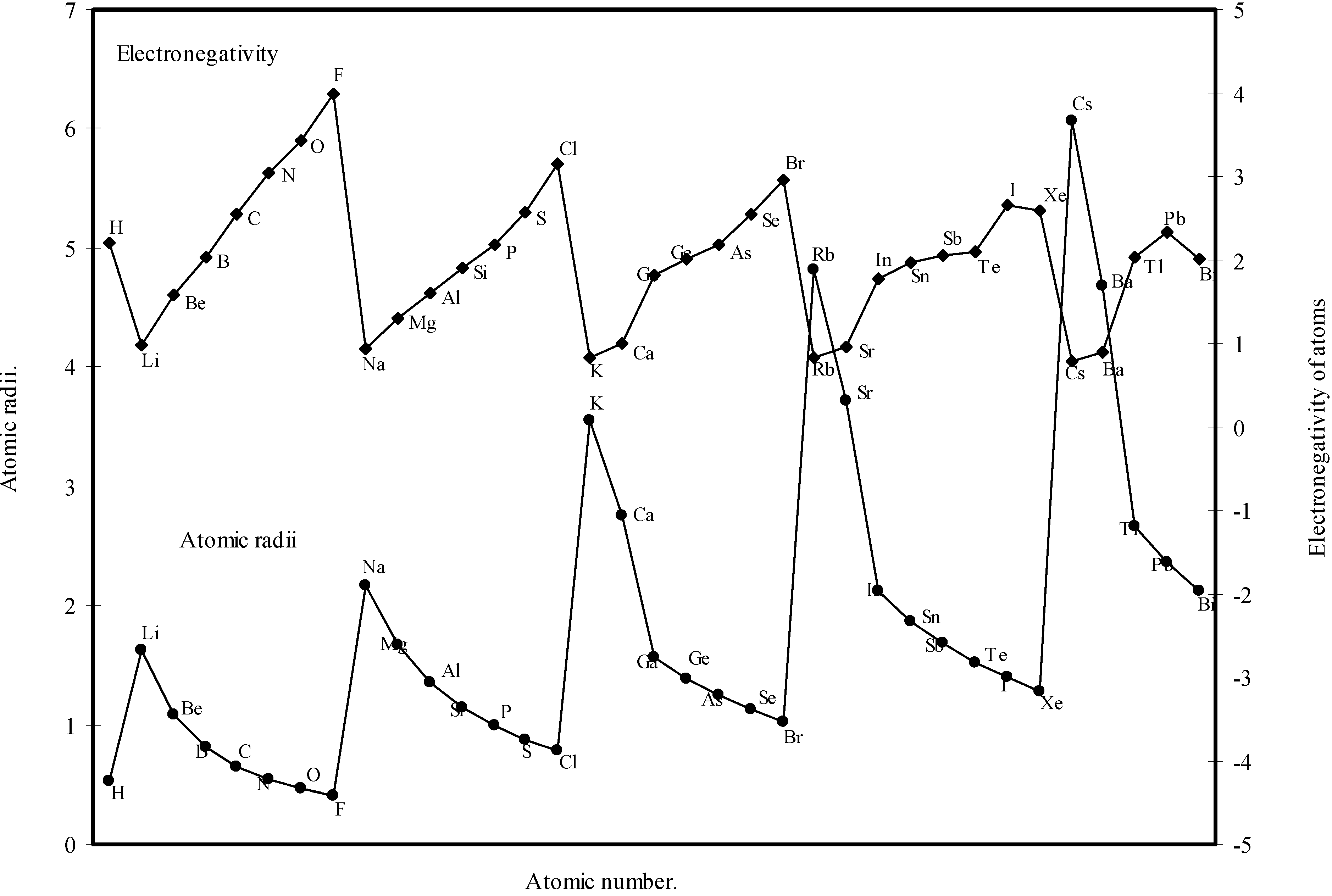
In the present venture we have computed the theoretical atomic radii of as many as 103 elements of the periodic table by semi-empirical method using Slater’s orbital and involving Slater’s empirical rule for the computation of ξ. Since there is no scope of comparing the atomic and ionic radii with the experimental values, we have tested the range of validity of calculated sizes in a number of ways. The periodicity exhibited by the computed radii is compared with the periodicity inherent in the periodic table. In order to explore the internal consistency between the calculated sizes and the size dependent properties of the atoms, a comparative study of size vis-a-vis the electronegativity and the experimental quantity like first ionization potential of the atoms is made. A comparative study of the relative magnitudes of the sizes of the atoms of present calculation and the radii published by other workers – both theoretical and experimental is also made. The computed theoretical radii are used to calculate a number of size dependent intrinsic physical properties of isolated atoms viz., (1) the diamagnetic part of magnetic susceptibility (χ_dia) of 54 elements, and (2) the atomic polarizability (α), and (3) the global hardness (η) of as many as 103 elements of the periodic table. We have compared such computed size dependent properties of the atoms with available results of such quantities.

Method of Computation

The radial charge density distribution function is defined [5,12,13] as 4πr² R² or simply r²R² where R is the radial function. According to Slater [7], theoretical atomic radius is the maximum of the radial charge density distribution function of the topmost electron of the atom or ion.

Radial charge density distribution function ρ(r) is given by

ρ (r) = 4πr²R²

(4)

Now, putting the normalized form of the R from the eqn.(1) into eqn.(4) we get

ρ (r) = 4πr²(2ξ)²ⁿ⁺¹[(2n)!]^-1r^2n-2exp(-2ξr)
  = 4πr²ⁿ(2ξ)²ⁿ⁺¹[(2n)!]^-1exp(-2ξr)

(5)

The parameters n and ξ are explained above.

Differentiating the left-hand side with respect to r, and equating the result with zero, we get the maximum of the radial charge density distribution function, the theoretical atomic radii,

dρ(r)/dr = [4π(2ξ)²ⁿ⁺¹[(2n)!]^-1exp(-2ξr)][2nr^2n-1-2ξr²ⁿ]

(6)

Equating the right hand side of the eqn. (6) equal to zero and replacing r by r_max, we obtain,

( nr_max^2n-1 – ξr_max²ⁿ) = 0

(7)

From which it follows that

n r_max ^–1 = ξ

From this relation we obtain the formula for computing the theoretical atomic or ionic radii already noted in eqn (3) above, i.e. the theoretical atomic or ionic radii r = r_max

r = n/ξ

(3)

the relevant quantities and parameters are defined above.

The screening constant (S) may be calculated from Slater’s rule and are profusely available in any standard textbook of physical and inorganic chemistry. The values of n^* for principal quantum number n up to 6 and Z^* for about 26 elements are published by Pople [14]. For the rest of the atoms, n^* are calculated by simple extrapolation. and we have got the extrapolated value of n^* = 4.3 for principal quantum number 7. The Z^* and ξ for required atoms are calculated and for that matter we have relied upon the ground state electron–configuration published by Shriver and Atkins [15]. In this work we report the theoretical radii of atoms only. 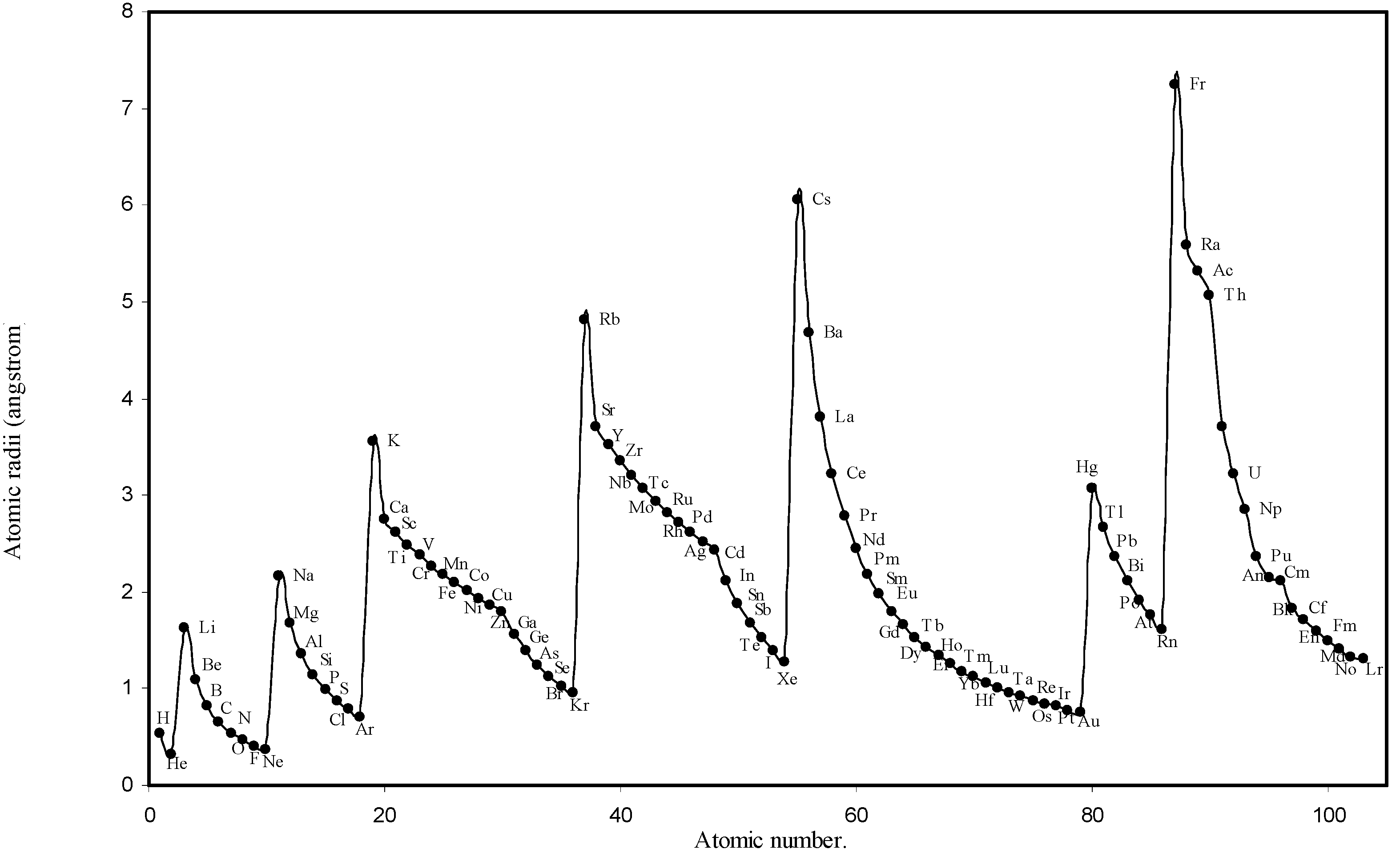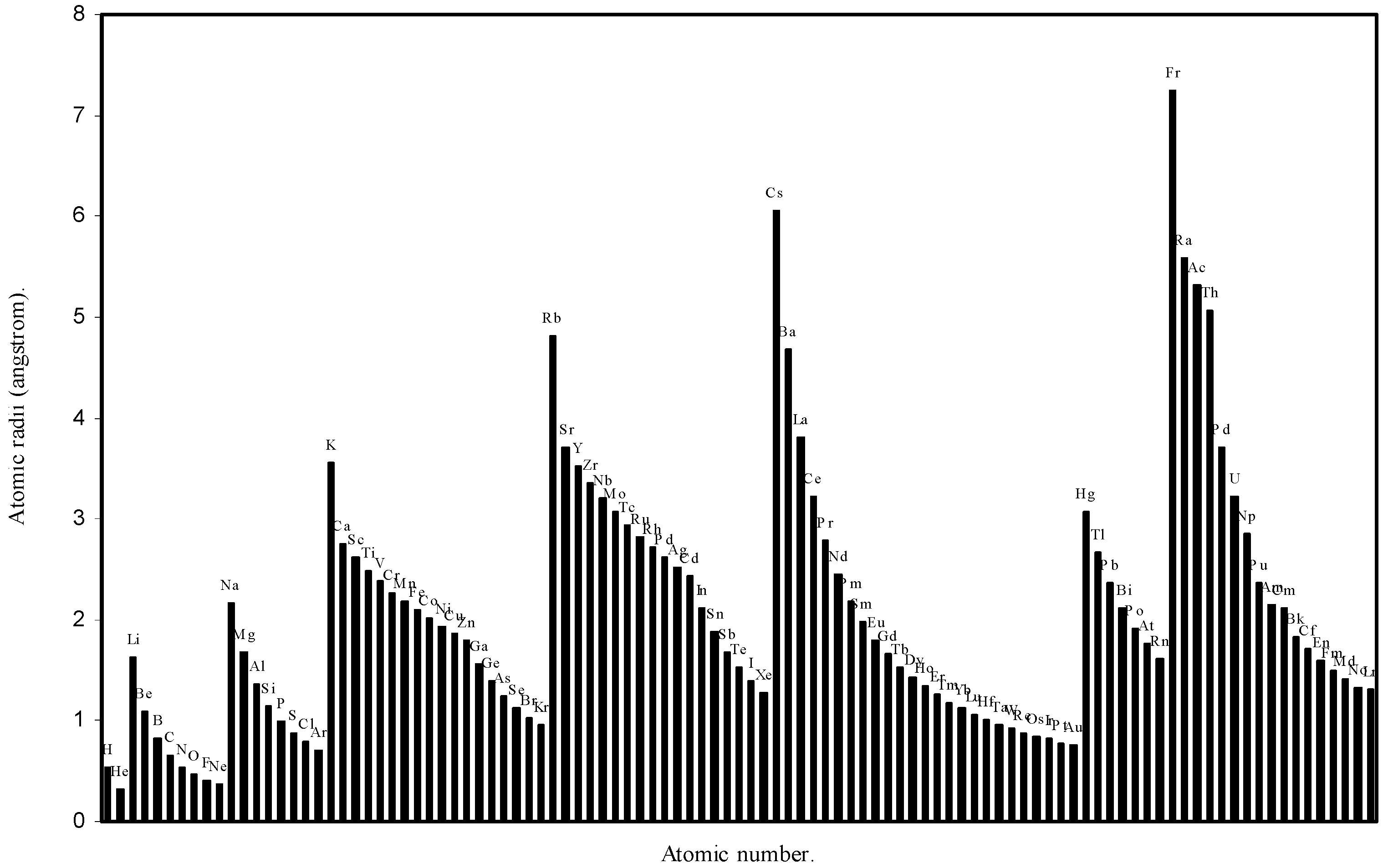The calculated orbital exponents and atomic radii are shown in Table 1. The computed theoretical atomic radii are plotted as a function of atomic number in Figure 1 and Figure 2. To explore the effectiveness of the present method in exhibiting the well known

Figure 1. Plot of atomic radii (angstrom) as a function of atomic number.

Figure 1. Plot of atomic radii (angstrom) as a function of atomic number.

Figure 2. Plot of atomic radii (angstrom) as a function of atomic number.

Figure 2. Plot of atomic radii (angstrom) as a function of atomic number.

Table 1. Calculated orbital exponents (ξ) and radii of atoms.

Atoms	Orbital Exponent	Atomic Radii (Å)	Atoms	Orbital Exponent	Atomic Radii (Å)	Atoms	Orbital Exponent	Atomic Radii (Å)
H	1	0.5292	Kr	2.2297	0.9493	Lu	3	1.0583
He	1.7	0.3113	Rb	0.55	4.8106	Hf	3.15	1.0079
Li	0.65	1.6282	Sr	0.7125	3.7135	Ta	3.3095	0.9594
Be	0.975	1.0855	Y	0.75	3.5278	W	3.4643	0.9165
B	1.3	0.8141	Zr	0.7875	3.3598	Re	3.619	0.8773
C	1.625	0.6513	Nb	0.825	3.2071	Os	3.7738	0.8413
N	1.95	0.5427	Mo	0.8625	3.0677	Ir	3.9286	0.8182
O	2.275	0.4652	Tc	0.9	2.9398	Pt	4.0833	0.7776
F	2.6	0.4071	Ru	0.9375	2.8222	Au	4.2381	0.7492
Ne	2.925	0.3618	Rh	0.975	2.7137	Hg	4.3929	3.0636
Na	0.7333	2.1649	Pd	1.0125	2.6132	Tl	1.1905	2.667
Mg	0.95	1.6711	Ag	1.05	2.5199	Pb	1.3452	2.3603
Al	1.1667	1.3607	Cd	1.0875	2.433	Bi	1.5	2.1167
Si	1.3833	1.1476	In	1.25	2.1167	Po	1.6548	1.9187
P	1.6	0.9922	Sn	1.4125	1.8732	At	1.8095	1.7546
S	1.8167	0.8738	Sb	1.575	1.6799	Rn	1.9643	1.6164
Cl	2.0333	0.7807	Te	1.7375	1.5228	Fr	0.5116	7.2404
Ar	2.25	0.7056	I	1.9	1.3926	Ra	0.6628	5.5887
K	0.5946	3.5598	Xe	2.0625	1.2828	Ac	0.6977	5.3091
Ca	0.7703	2.7479	Cs	0.5238	6.0615	Th	0.7326	5.0569
Sc	0.8108	2.6106	Ba	0.6786	4.6788	Pa	1	3.7042
Ti	0.8514	2.4861	La	0.8333	3.8102	U	1.1512	3.2177
V	0.8919	2.3732	Ce	0.9881	3.2133	Np	1.3023	2.8443
Cr	0.9324	2.2701	Pr	1.1429	2.778	Pu	1.5698	2.3596
Mn	0.973	2.1754	Nd	1.2976	2.4468	Am	1.7209	2.1525
Fe	1.0135	2.0885	Pm	1.4524	2.1861	Cm	1.7558	2.1097
Co	1.0541	2.008	Sm	1.6071	1.9756	Bk	2.0233	1.8308
Ni	1.0946	1.9337	Eu	1.7619	1.802	Cf	2.1744	1.7035
Cu	1.1351	1.8648	Gd	1.9167	1.6565	En	2.3256	1.5928
Zn	1.1757	1.8004	Tb	2.0714	1.5328	Fm	2.4767	1.4956
Ga	1.3514	1.5663	Dy	2.2262	1.4262	Md	2.6279	1.4096
Ge	1.527	1.3862	Ho	2.381	1.3335	No	2.7791	1.3329
As	1.7027	1.2431	Er	2.5357	1.2521	Lr	2.814	1.3164
Se	1.8784	1.1269	Tm	2.6905	1.1801
Br	2.0541	1.0305	Yb	2.8452	1.1159

Table 1. Calculated orbital exponents (ξ) and radii of atoms.

Atoms	Orbital Exponent	Atomic Radii (Å)	Atoms	Orbital Exponent	Atomic Radii (Å)	Atoms	Orbital Exponent	Atomic Radii (Å)
H	1	0.5292	Kr	2.2297	0.9493	Lu	3	1.0583
He	1.7	0.3113	Rb	0.55	4.8106	Hf	3.15	1.0079
Li	0.65	1.6282	Sr	0.7125	3.7135	Ta	3.3095	0.9594
Be	0.975	1.0855	Y	0.75	3.5278	W	3.4643	0.9165
B	1.3	0.8141	Zr	0.7875	3.3598	Re	3.619	0.8773
C	1.625	0.6513	Nb	0.825	3.2071	Os	3.7738	0.8413
N	1.95	0.5427	Mo	0.8625	3.0677	Ir	3.9286	0.8182
O	2.275	0.4652	Tc	0.9	2.9398	Pt	4.0833	0.7776
F	2.6	0.4071	Ru	0.9375	2.8222	Au	4.2381	0.7492
Ne	2.925	0.3618	Rh	0.975	2.7137	Hg	4.3929	3.0636
Na	0.7333	2.1649	Pd	1.0125	2.6132	Tl	1.1905	2.667
Mg	0.95	1.6711	Ag	1.05	2.5199	Pb	1.3452	2.3603
Al	1.1667	1.3607	Cd	1.0875	2.433	Bi	1.5	2.1167
Si	1.3833	1.1476	In	1.25	2.1167	Po	1.6548	1.9187
P	1.6	0.9922	Sn	1.4125	1.8732	At	1.8095	1.7546
S	1.8167	0.8738	Sb	1.575	1.6799	Rn	1.9643	1.6164
Cl	2.0333	0.7807	Te	1.7375	1.5228	Fr	0.5116	7.2404
Ar	2.25	0.7056	I	1.9	1.3926	Ra	0.6628	5.5887
K	0.5946	3.5598	Xe	2.0625	1.2828	Ac	0.6977	5.3091
Ca	0.7703	2.7479	Cs	0.5238	6.0615	Th	0.7326	5.0569
Sc	0.8108	2.6106	Ba	0.6786	4.6788	Pa	1	3.7042
Ti	0.8514	2.4861	La	0.8333	3.8102	U	1.1512	3.2177
V	0.8919	2.3732	Ce	0.9881	3.2133	Np	1.3023	2.8443
Cr	0.9324	2.2701	Pr	1.1429	2.778	Pu	1.5698	2.3596
Mn	0.973	2.1754	Nd	1.2976	2.4468	Am	1.7209	2.1525
Fe	1.0135	2.0885	Pm	1.4524	2.1861	Cm	1.7558	2.1097
Co	1.0541	2.008	Sm	1.6071	1.9756	Bk	2.0233	1.8308
Ni	1.0946	1.9337	Eu	1.7619	1.802	Cf	2.1744	1.7035
Cu	1.1351	1.8648	Gd	1.9167	1.6565	En	2.3256	1.5928
Zn	1.1757	1.8004	Tb	2.0714	1.5328	Fm	2.4767	1.4956
Ga	1.3514	1.5663	Dy	2.2262	1.4262	Md	2.6279	1.4096
Ge	1.527	1.3862	Ho	2.381	1.3335	No	2.7791	1.3329
As	1.7027	1.2431	Er	2.5357	1.2521	Lr	2.814	1.3164
Se	1.8784	1.1269	Tm	2.6905	1.1801
Br	2.0541	1.0305	Yb	2.8452	1.1159

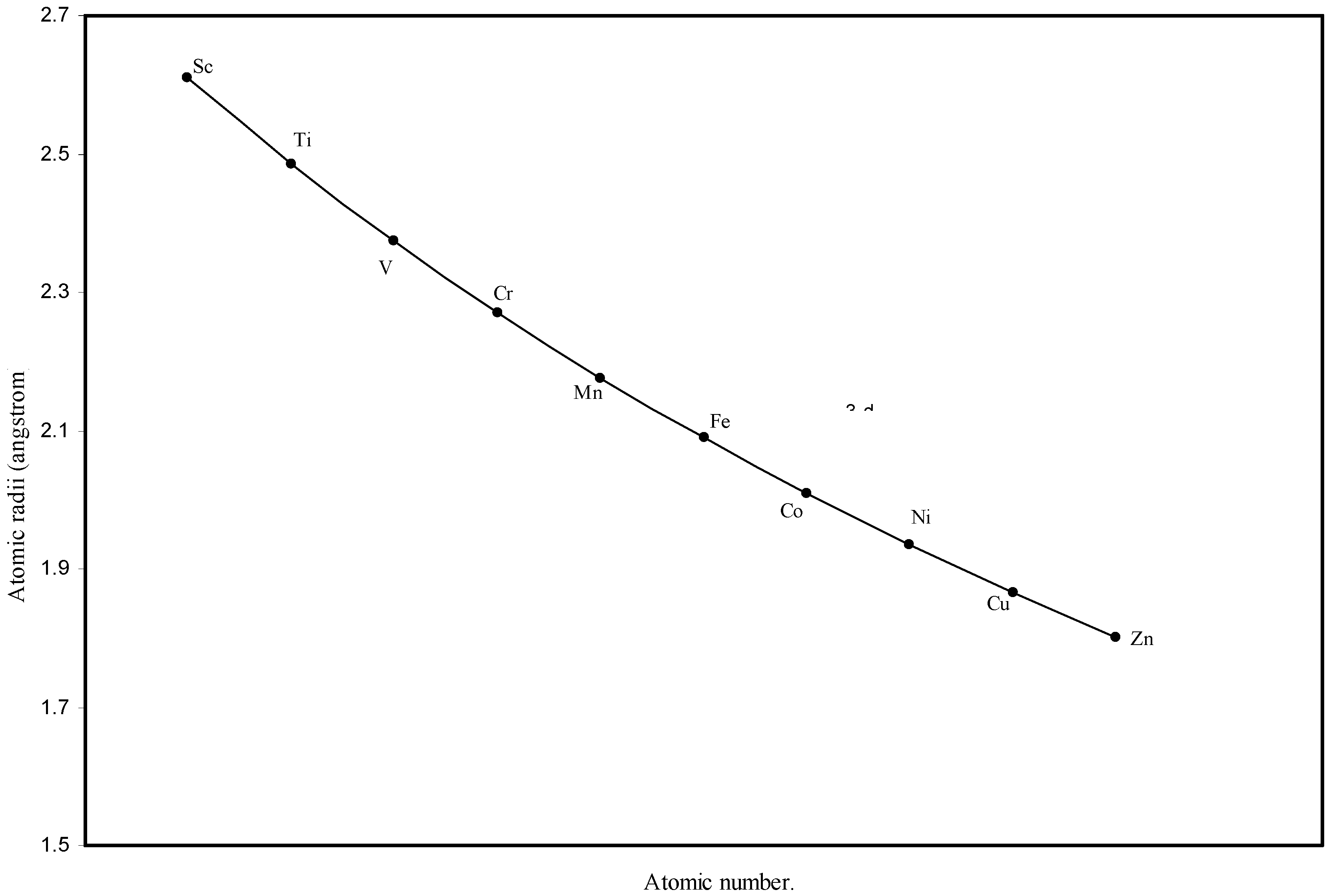
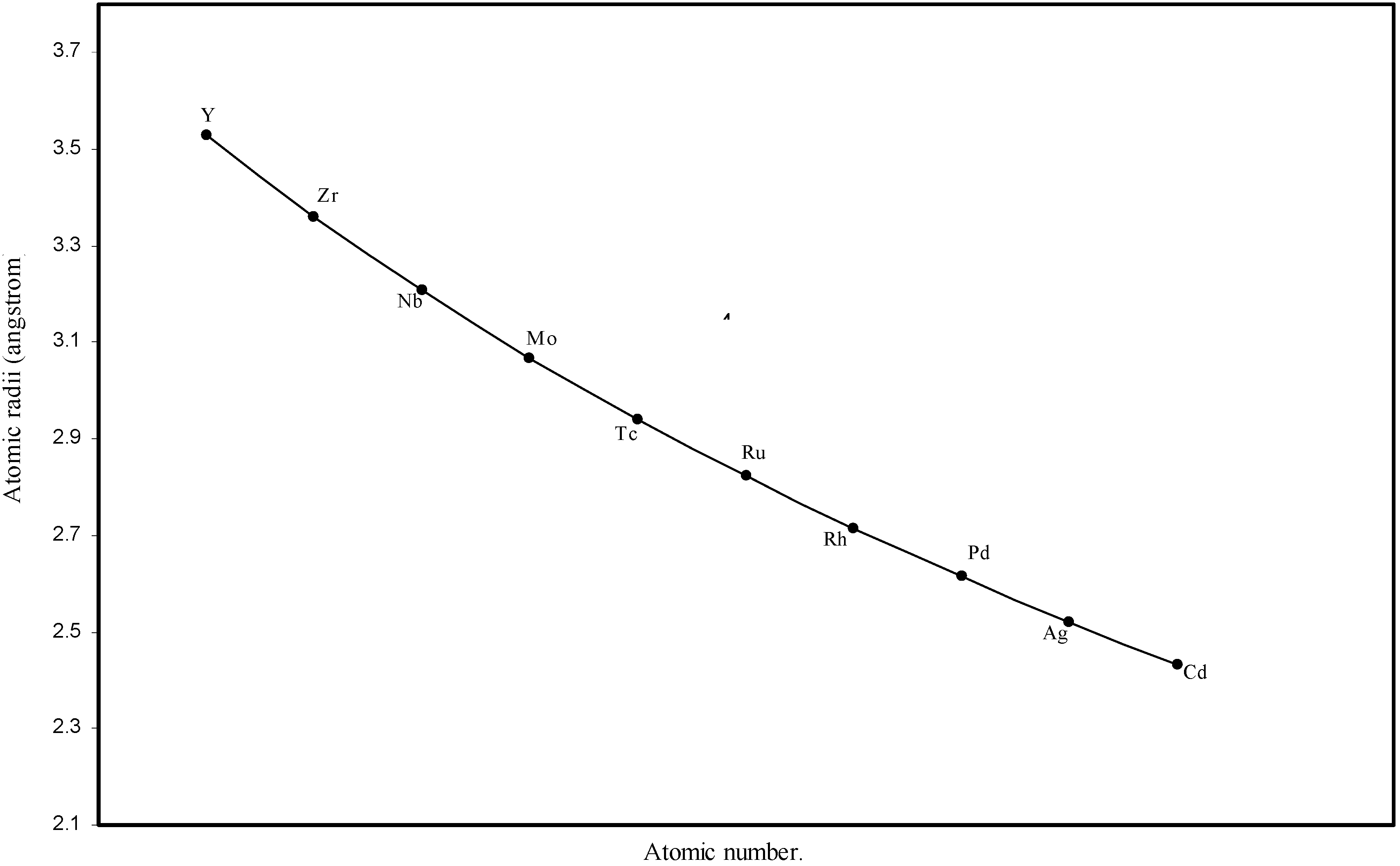
d-block and f-block contractions in the periodic table, the computed radii of 3d, 4d, 4f and 5f elements are separately plotted as a function of the atomic numbers in Figs. 3, Figs. 4, Figs. 5, and Figs. 6, respectively. The methods of computation of absolute size dependent physical properties like (A) the diamagnetic part of magnetic susceptibilities (χ_dia), (B) atomic polarizabilities (α), and (C) the global hardness (η) are stated below.

Figure 3. Plot of atomic radii of first transition sereis (3-d block) elements in angstrom unit as a function of atomic number.

Figure 3. Plot of atomic radii of first transition sereis (3-d block) elements in angstrom unit as a function of atomic number.

Figure 4. Plot of atomic radii of second transition series (4-d block) elements in angstrom unit as a function of atomic number.

Figure 4. Plot of atomic radii of second transition series (4-d block) elements in angstrom unit as a function of atomic number.

Figure 5. Plot of atomic radii of lanthanides in angstrom unit as function of atomic number.

Figure 5. Plot of atomic radii of lanthanides in angstrom unit as function of atomic number.

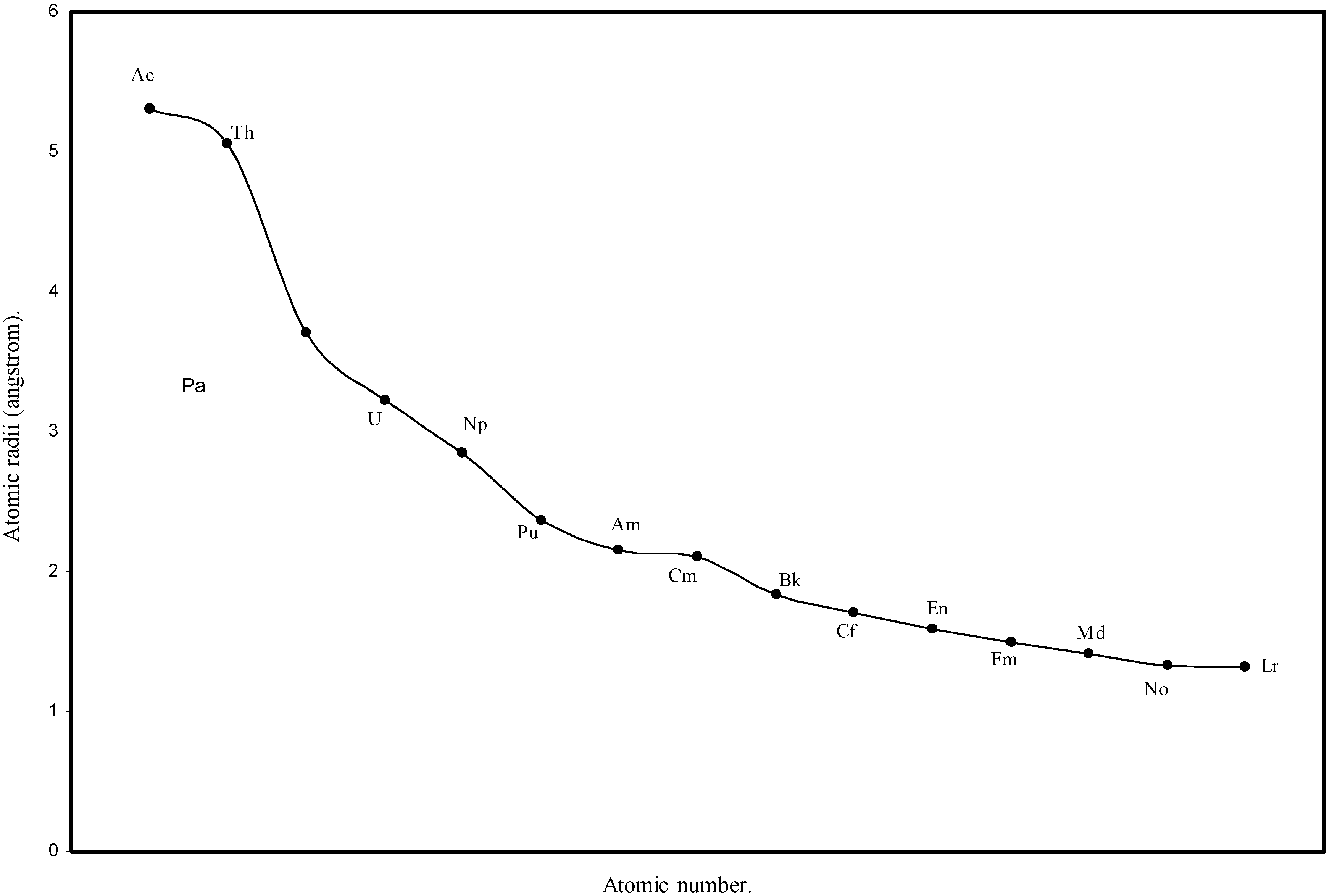
Figure 6. Plot of atomic radii of actinides in angstrom unit as a function of Atomic number.

Figure 6. Plot of atomic radii of actinides in angstrom unit as a function of Atomic number.

(A) Diamagnetic part of magnetic susceptibility, χ_dia.

The theoretical determination of atomic and ionic radii provides with a scope of a theoretical calculation of the diamagnetic part of the atomic susceptibility, which occurs even when an atom already has a permanent moment. We have computed the diamagnetic susceptibility of as many as 54 elements starting from hydrogen. Since atoms after element with atomic number 54 are strongly paramagnetic due to L-S coupling, the computation of diamagnetic susceptibility of atoms of such elements is not taken up.

The induced diamagnetic moment of an atom is opposite to the applied field and is proportional to the square of the orbit radius. The classical equation of diamagnetic susceptibility of atom [16,17] per mole is given by

χ_dia = – 2.84 × 10^-10 Σ_n <r²>_av

(8)

Where, <r²>_av is the mean square of the actual orbital radius or the average of the square of all the orbit radii and Σ implies the summation of <r²>_av for all n electrons in atom as the total moment is given by the sum over all the electrons in the atom.

There can not be any experimental value for Σ_n <r²>_av of an atom as such and quantum mechanics can compute it and it is interpreted as the average of the square of the distance from the center for the probability distribution [18]. However, it is mentioned that a slight modification of the formula (8) by replacing the pre-factor of the RHS by 1.888 in place of 2.84 gives better result [19]. The modified formula is

χ_dia = – 1.888 × 10^–10 Σ_n <r²>_av

(9)

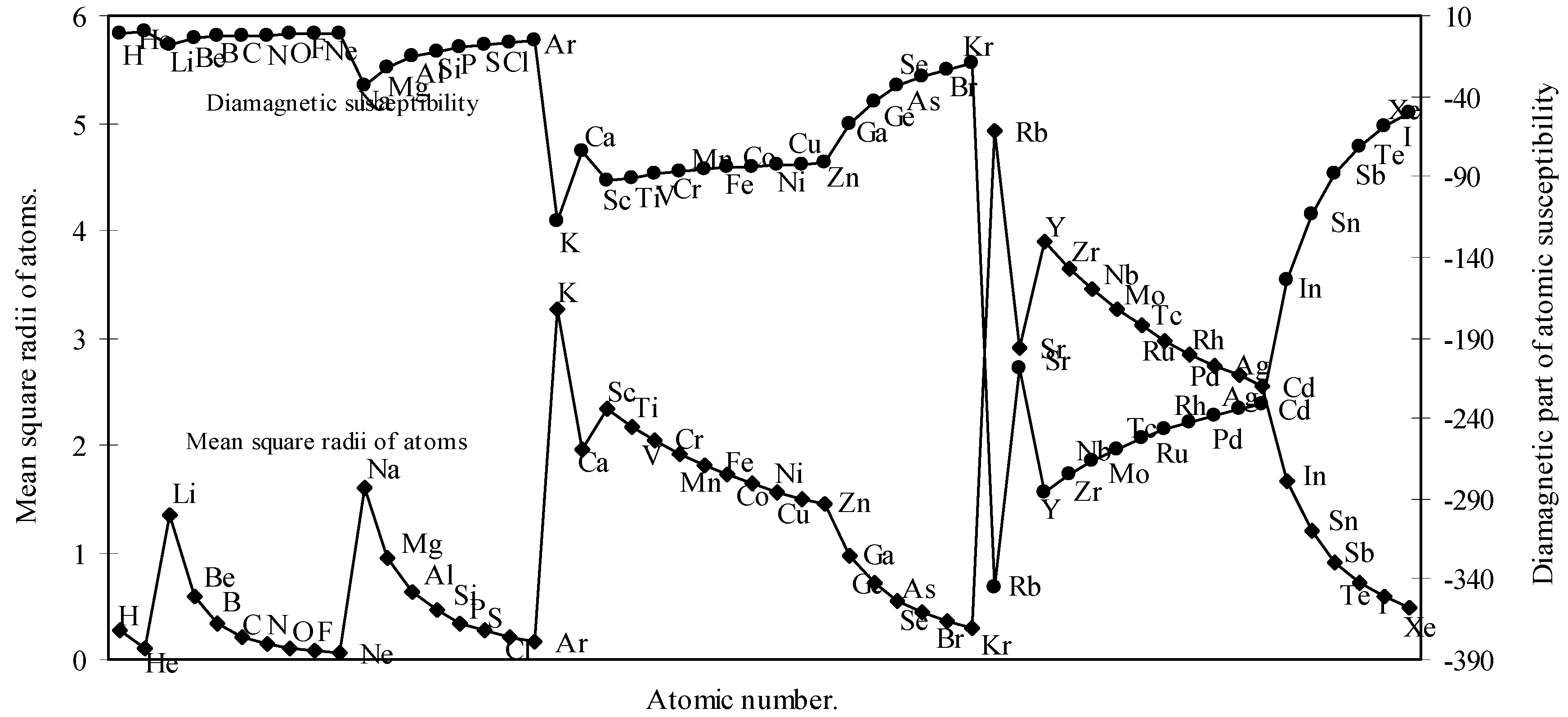
We have calculated the <r²>_av of each atom by calculating the radii of each orbital. We have computed the <r²>_av for all the 54 elements. With these values of <r²>_av, the molar diamagnetic susceptibility is computed through eqn.(9). The calculated <r²>_av and χ_dia are shown in Table 2. The computed values of <r²>_av and χ_dia are plotted as a function of atomic number in Fig.7.

Figure 7. Plot of mean square radii and diamagnetic part of magnetic susceptibility of atoms as a function of atomic number.

Figure 7. Plot of mean square radii and diamagnetic part of magnetic susceptibility of atoms as a function of atomic number.

(B) Atomic polarizability, α.

One more important size dependent physical property of the atoms is the atomic polarizability, α. By polarizability, Pearson [20] meant the ease of deforming the valance electron cloud of a chemical species. A closely related experimental quantity is electric dipole polarizability, α, which actually

Table 2. Computed mean square radii, < r² > and diamagnetic part of atomic susceptibility, (χ_dia) of atoms.

Atom	< r2 > X 10–16 sq.cm	χdia x 10–6 c.c	Atoms	< r2 > X 10–16 sq.cm	χdia x 10–6 c.c
H	0.2801	-0.5287	Ni	1.5669	-82.8339
He	0.0969	-0.3659	Cu	1.5013	-82.2003
Li	1.3447	-7.6165	Zn	1.4422	-81.6834
Be	0.5994	-4.5267	Ga	0.9694	-56.7355
B	0.3377	-3.1882	Ge	0.7087	-42.8176
C	0.2164	-2.4513	As	0.5452	-33.912
N	0.1504	-1.9872	Se	0.4345	-27.8915
O	0.1106	-1.6698	Br	0.3553	-23.4787
F	0.0847	-1.4395	Kr	0.2965	-20.1491
Ne	0.0669	-1.264	Rb	4.9346	-344.7138
Na	1.5972	-33.1713	Sr	2.9131	-208.9958
Mg	0.9558	-21.6546	Y	3.8844	-286.0142
Al	0.6368	-15.6297	Zr	3.6483	-275.519
Si	0.4549	-12.0238	Nb	3.444	-266.593
P	0.3413	-9.6652	Mo	3.266	-258.9836
S	0.2655	-8.0205	Tc	3.1099	-252.4745
Cl	0.2125	-6.8214	Ru	2.9723	-246.9151
Ar	0.1741	-5.915	Rh	2.8505	-242.1745
K	3.2677	-117.2196	Pd	2.7419	-238.1305
Ca	1.9664	-74.2518	Ag	2.6448	-234.6907
Sc	2.338	-92.6958	Cd	2.5577	-231.7906
Ti	2.1789	-90.5027	In	1.6726	-154.7359
V	2.0413	-88.6433	Sn	1.2015	-113.4178
Cr	1.9214	-87.0608	Sb	0.9035	-87.9572
Mn	1.8158	-85.7077	Te	0.7218	-70.8638
Fe	1.723	-84.5766	I	0.5866	-58.7022
Co	1.6403	-83.6167	Xe	0.4872	-49.6685

Table 2. Computed mean square radii, < r² > and diamagnetic part of atomic susceptibility, (χ_dia) of atoms.

Atom	< r2 > X 10–16 sq.cm	χdia x 10–6 c.c	Atoms	< r2 > X 10–16 sq.cm	χdia x 10–6 c.c
H	0.2801	-0.5287	Ni	1.5669	-82.8339
He	0.0969	-0.3659	Cu	1.5013	-82.2003
Li	1.3447	-7.6165	Zn	1.4422	-81.6834
Be	0.5994	-4.5267	Ga	0.9694	-56.7355
B	0.3377	-3.1882	Ge	0.7087	-42.8176
C	0.2164	-2.4513	As	0.5452	-33.912
N	0.1504	-1.9872	Se	0.4345	-27.8915
O	0.1106	-1.6698	Br	0.3553	-23.4787
F	0.0847	-1.4395	Kr	0.2965	-20.1491
Ne	0.0669	-1.264	Rb	4.9346	-344.7138
Na	1.5972	-33.1713	Sr	2.9131	-208.9958
Mg	0.9558	-21.6546	Y	3.8844	-286.0142
Al	0.6368	-15.6297	Zr	3.6483	-275.519
Si	0.4549	-12.0238	Nb	3.444	-266.593
P	0.3413	-9.6652	Mo	3.266	-258.9836
S	0.2655	-8.0205	Tc	3.1099	-252.4745
Cl	0.2125	-6.8214	Ru	2.9723	-246.9151
Ar	0.1741	-5.915	Rh	2.8505	-242.1745
K	3.2677	-117.2196	Pd	2.7419	-238.1305
Ca	1.9664	-74.2518	Ag	2.6448	-234.6907
Sc	2.338	-92.6958	Cd	2.5577	-231.7906
Ti	2.1789	-90.5027	In	1.6726	-154.7359
V	2.0413	-88.6433	Sn	1.2015	-113.4178
Cr	1.9214	-87.0608	Sb	0.9035	-87.9572
Mn	1.8158	-85.7077	Te	0.7218	-70.8638
Fe	1.723	-84.5766	I	0.5866	-58.7022
Co	1.6403	-83.6167	Xe	0.4872	-49.6685

describes the linear response of the electron cloud of a chemical species to an external field much lower than what would be needed to ionize the system. The static electric dipole polarizability α can be determined theoretically and experimentally in various ways.

The induced dipole moment in an atom or molecule is proportional to the applied electric field [13] and the necessary formula can be written as

d = α F

(10)

where, F = the applied electric field, d = induced dipole moment, and α is the constant of proportionality and is called polarizability.

It has been shown [21] that the polarizability α of a conducting sphere of radius r is equal to r³.

α = r³

(11)

And in terms of its volume V, the same formula looks like

α = 3V/4π

(12)

where

V = 4/3 π r³

(13)

The generality of linear volume–polarizability has been assessed [21] quantum mechanically in case of atoms. Although the formula for the polarizability has been laid down in eqn (11), it is suggested that, due to inhomogeneity of the electron cloud, the actual formula [22] should be

α = Kr³

(14)

where, K is the proportionality constant.

For atoms, the value of ‘K’ was determined by Dimitrieva and Plindov [23] by ‘Atomic Oscillation Theory’ as 0.585. Dutta and Hati [22] used the value of K= 0.792 which is the arithmetic average of 1 and the value of Dimitrieva and Plindov [23]. But the exact quantum mechanical calculation [19] of polarizability of hydrogen atom derives the formula

α = (9/2) a₀³

(15)

where a₀ is the Bohr radius.

Comparing eqns. (14) and (15) we see that K = 4.5

Relying more upon the quantum mechanical derivation [19] of the atomic polarizability, we see that, the proportional constant K in eqn.(14) is neither 1 nor less than 1, but it is equal to 4.5 for hydrogen atom. In absence of any other reliable value of ‘K’, the proportionality constant, we have first tried to obtain an optimized the proportionality constant K. We first computed the atomic polarizability of as much as 8 elements whose experimental polarizabilities are quoted by Purcell in reference [19] using the above quantum mechanical value of K = 4.5. We find that the calculated values of atomic polarizability of eight elements with K = 4.5 through the theoretical atomic radii are close to the experimental values quoted by Purcell [19]. We have, therefore, computed the atomic polarizabilities of the rest of the elements with the same value of the proportionality constant K=4.5. 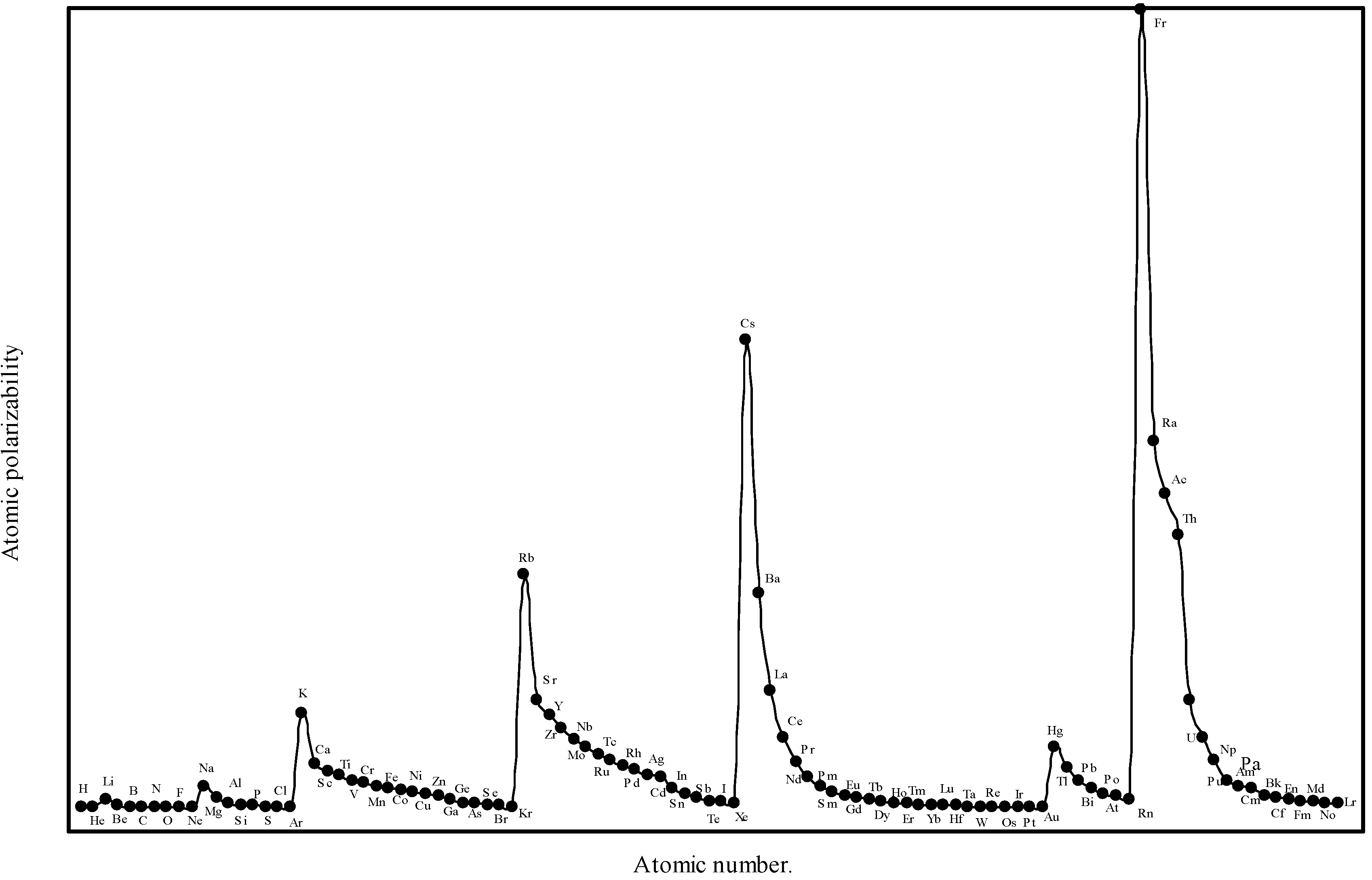The computed atomic polarizability of all the 103 elements are shown in Table 3. We have plotted the theoretically computed atomic polarizability as a function of atomic number in Figure 8.

Figure 8. Plot of atomic polarizability (c.c) as a function of atomic number.

Figure 8. Plot of atomic polarizability (c.c) as a function of atomic number.

Table 3. Computed atomic polarizability ( α) and global hardness (η) of atoms.

Atoms	α x 10–24 c.c	η (ev)	Atoms	α x 10–24 c.c	η (ev)	Atoms	α x 10–24 c.c	η (ev)
H	0.6669	13.588	Kr	3.8497	7.5748	Lu	5.3338	6.7947
He	0.1358	22.383	Rb	500.9683	1.4948	Hf	4.6075	7.1344
Li	19.4239	4.4164	Sr	230.4462	1.9364	Ta	3.9739	7.4951
Be	5.7558	6.6244	Y	197.5715	2.0383	W	3.4643	7.8459
B	2.428	8.8328	Zr	170.6683	2.1402	Re	3.0385	8.1965
C	1.2432	11.0407	Nb	148.4397	2.2422	Os	2.6796	8.5472
N	0.7193	13.25	Mo	129.9126	2.344	Ir	2.3756	8.8973
O	0.453	15.4574	Tc	114.3315	2.446	Pt	2.1175	9.2474
F	0.3034	17.6634	Ru	101.1523	2.5479	Au	1.8924	9.598
Ne	0.2131	19.875	Rh	89.9286	2.6498	Hg	129.646	2.3456
Na	45.659	3.3215	Pd	80.3028	2.7517	Tl	85.3653	2.6962
Mg	21	4.303	Ag	72.005	2.8536	Pb	59.1717	3.0466
Al	11.337	5.2846	Cd	64.8095	2.9555	Bi	42.6767	3.3972
Si	6.8011	6.2659	In	42.6767	3.3972	Po	31.7858	3.7477
P	4.3955	7.2473	Sn	29.5777	3.8388	At	24.3079	4.0983
S	3.0023	8.2293	Sb	21.3335	4.2805	Rn	19.0046	4.4487
Cl	2.1412	9.2107	Te	15.8906	4.7221	Fr	1705	0.9913
Ar	1.5808	10.191	I	12.1532	5.0636	Ra	785.4977	1.2867
K	202.9969	2.02	Xe	9.4993	5.6056	Ac	673.4033	1.3544
Ca	93.3717	2.6162	Cs	1002.1964	1.1863	Th	581.6815	1.4222
Sc	80.0633	2.7545	Ba	460.9098	1.5369	Pa	228.7156	1.9413
Ti	69.1712	2.8924	La	248.9177	1.8873	U	149.9164	2.2348
V	60.1472	3.03	Ce	149.2883	2.2378	Np	103.5473	2.5281
Cr	52.6438	3.1676	Pr	96.4738	2.5885	Pu	59.1266	3.0473
Mn	46.3265	3.3055	Nd	65.9186	2.9389	Am	44.8789	3.3407
Fe	40.9939	3.443	Pm	47.0135	3.2893	Cm	42.2547	3.4084
Co	36.4555	3.5811	Sm	34.6984	3.6398	Bk	27.5918	3.9277
Ni	32.5372	3.7187	Eu	26.3316	3.9905	Cf	22.2453	4.2212
Cu	29.1769	3.8561	Gd	20.4544	4.341	En	18.1843	4.5146
Zn	26.2615	3.994	Tb	16.2057	4.6913	Fm	15.0542	4.808
Ga	17.2917	4.5909	Dy	13.0543	5.0419	Md	12.6038	5.1013
Ge	11.9864	5.1874	Ho	10.6707	5.3924	No	10.6563	5.3949
As	8.6443	5.7846	Er	8.8334	5.743	Lr	10.2631	5.4629
Se	6.4397	6.381	Tm	7.3955	6.0934
Br	4.9244	6.978	Yb	6.253	6.4439

Table 3. Computed atomic polarizability ( α) and global hardness (η) of atoms.

Atoms	α x 10–24 c.c	η (ev)	Atoms	α x 10–24 c.c	η (ev)	Atoms	α x 10–24 c.c	η (ev)
H	0.6669	13.588	Kr	3.8497	7.5748	Lu	5.3338	6.7947
He	0.1358	22.383	Rb	500.9683	1.4948	Hf	4.6075	7.1344
Li	19.4239	4.4164	Sr	230.4462	1.9364	Ta	3.9739	7.4951
Be	5.7558	6.6244	Y	197.5715	2.0383	W	3.4643	7.8459
B	2.428	8.8328	Zr	170.6683	2.1402	Re	3.0385	8.1965
C	1.2432	11.0407	Nb	148.4397	2.2422	Os	2.6796	8.5472
N	0.7193	13.25	Mo	129.9126	2.344	Ir	2.3756	8.8973
O	0.453	15.4574	Tc	114.3315	2.446	Pt	2.1175	9.2474
F	0.3034	17.6634	Ru	101.1523	2.5479	Au	1.8924	9.598
Ne	0.2131	19.875	Rh	89.9286	2.6498	Hg	129.646	2.3456
Na	45.659	3.3215	Pd	80.3028	2.7517	Tl	85.3653	2.6962
Mg	21	4.303	Ag	72.005	2.8536	Pb	59.1717	3.0466
Al	11.337	5.2846	Cd	64.8095	2.9555	Bi	42.6767	3.3972
Si	6.8011	6.2659	In	42.6767	3.3972	Po	31.7858	3.7477
P	4.3955	7.2473	Sn	29.5777	3.8388	At	24.3079	4.0983
S	3.0023	8.2293	Sb	21.3335	4.2805	Rn	19.0046	4.4487
Cl	2.1412	9.2107	Te	15.8906	4.7221	Fr	1705	0.9913
Ar	1.5808	10.191	I	12.1532	5.0636	Ra	785.4977	1.2867
K	202.9969	2.02	Xe	9.4993	5.6056	Ac	673.4033	1.3544
Ca	93.3717	2.6162	Cs	1002.1964	1.1863	Th	581.6815	1.4222
Sc	80.0633	2.7545	Ba	460.9098	1.5369	Pa	228.7156	1.9413
Ti	69.1712	2.8924	La	248.9177	1.8873	U	149.9164	2.2348
V	60.1472	3.03	Ce	149.2883	2.2378	Np	103.5473	2.5281
Cr	52.6438	3.1676	Pr	96.4738	2.5885	Pu	59.1266	3.0473
Mn	46.3265	3.3055	Nd	65.9186	2.9389	Am	44.8789	3.3407
Fe	40.9939	3.443	Pm	47.0135	3.2893	Cm	42.2547	3.4084
Co	36.4555	3.5811	Sm	34.6984	3.6398	Bk	27.5918	3.9277
Ni	32.5372	3.7187	Eu	26.3316	3.9905	Cf	22.2453	4.2212
Cu	29.1769	3.8561	Gd	20.4544	4.341	En	18.1843	4.5146
Zn	26.2615	3.994	Tb	16.2057	4.6913	Fm	15.0542	4.808
Ga	17.2917	4.5909	Dy	13.0543	5.0419	Md	12.6038	5.1013
Ge	11.9864	5.1874	Ho	10.6707	5.3924	No	10.6563	5.3949
As	8.6443	5.7846	Er	8.8334	5.743	Lr	10.2631	5.4629
Se	6.4397	6.381	Tm	7.3955	6.0934
Br	4.9244	6.978	Yb	6.253	6.4439

(C) Global Hardness, η.

The term hardness,η, as applied to atoms and molecules has no reference to its mechanical physical hardness [24]. We are concerned here about the chemical hardness of atoms. The definition of hardness has evolved with time from qualitative concept to the rigorous quantum mechanical definition [20]. The concept of hardness was first introduced by Mulliken [25] and formalized as a qualitative thumb rule of chemical reactivity known as HSAB principle by Pearson [20]. Using the Density Functional Theory (DFT) as basis, the qualitative HSAB principle of Pearson [20] was placed on a quantum mechanical basis by Parr, Pearson and others [26,27,28,29,30]. In terms of Density Functional Theory, the qualitative idea of hardness and softness was quantified and the terms ‘hardness’ and ‘softness’ were identified as fundamental theoretical parameters. Although the hardness was rigorously defined in terms of the Density Functional Theory, the operational and approximate definition for the purpose of computation was also suggested as follows [27,28,30].

The operational definition of hardness, η

η = (I – A)/2

(16)

where,

η = the global hardness of atoms or molecules

I = the ionization potential of atoms or molecules.

A = the electron affinity of atoms or molecules.

But in case of atoms, Pearson [31] pointed out that a simple formula of computing hardness of atoms could be derived from simple electrostatic considerations using atomic size. Dutta and Hati [22] have used the formula derived by Pearson to calculate the global hardness of a series of atoms. The only needed quantity for computing global hardness of atoms is the atomic radius. We therefore venture to use the atomic radii for the instant calculation to compute the global hardness η of atoms. We have derived the formula for computing the global hardness of atoms as follows:

The energy, E (q) of charging a conducting sphere of radius R with charge q is classically given by [18]

E (q) = q²/(4πε₀) 2R

(17) (S. I. Unit).

= q²/2R

(18) ( C. G. S. Unit).

where, q = charge and R = radius.

The implication of the eqn (18) is that the E(q) is the energy in ergs, q is the charge in electrostatic unit and R should be measured in cm. Now increasing q by one unit and decreasing q by one unit, we get the changes in energy which are I and A, the ionization potential and electron affinity of atom respectively.

Now in e.s.u, the one unit of charge, which is associated with the process of ionization I, and the electron affinity A, should be e, the electronic charge. Hence,

I = (q + e) ²/2R – q²/2R

A = q²/2R – (q – e) ²/2R

Since, the global hardness of atoms η = 1/2 (I – A)

Or,

η = e²/ 2R

(19)

where, e = the electronic charge in e.s.u.

But the formula derived by Pearson [31] looks a bit different from the formula in eqn. (19).

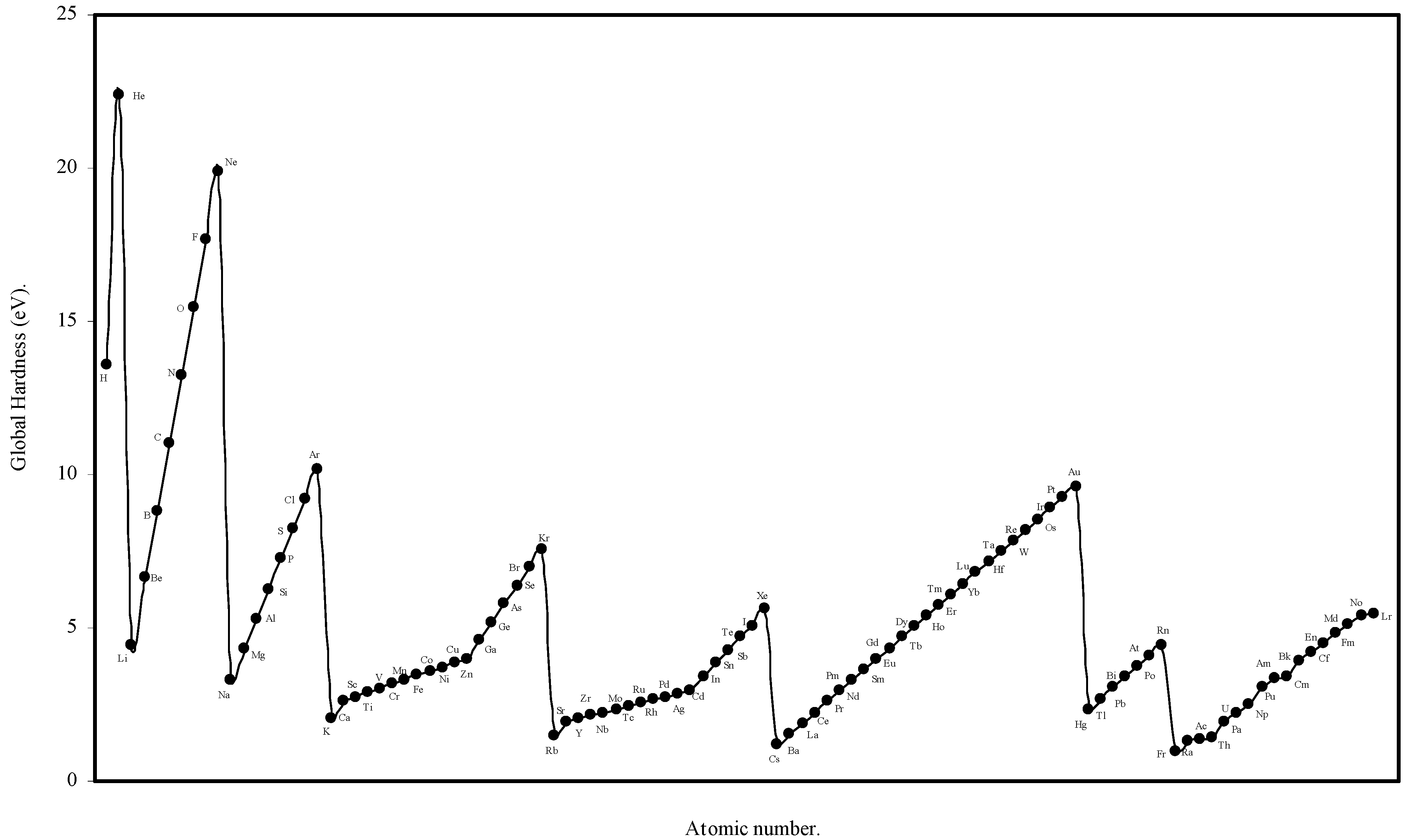
We have computed the global hardness of atoms, η, through eqn (19) and ultimately it is converted to electron volt (eV). The theoretically computed values of global hardness of as many as 103 atoms are tabulated in Table 3. We have plotted the global hardness of atoms as a function of atomic number in Figure 9.

Figure 9. Plot of Global hardness (eV) of atoms as a function of atomic number.

Figure 9. Plot of Global hardness (eV) of atoms as a function of atomic number.

Results and Discussions.

The test of Periodicity of the sizes, and a comparative study of the radii of present calculation vis-a-vis other available data on the sizes of atoms.

The periodicity of elements, along with Darwin’s theory of evolution and Planck’s quantum theory, ranks as one of the greatest generalizations in Science [32,33]. Periodicity of atomic and ionic size is of utmost importance in chemistry. The phenomenon of contraction of the atomic size among the transition metals, lanthanides and actinides are some important periodic relationship of chemistry. However, a general trend of atomic size that has to be followed in a row and group of periodic table is already laid down [34] and stated as follows:

i)

Atomic and ionic size decreases along the row.

ii)

Atomic and ionic size increases down the main group.

iii)

There is d–block contraction.

iv)

There is f–block contraction.

v)

The periodicity of atomic size should be isomorphic with the periodicity of ionization potential.

vi)

The periodicity of size should be matched with the periodicity of electronegativity

The size relationship as a function of vertically downward or horizontally rightward movement will be straightforward if the sizes of the atoms are extrapolated as a function of atomic number. We have drawn the sizes of atoms as a function of atomic numbers in two different fashions in Fig. 1 and Fig. 2. It is distinctly evident that the curve 1 is isomorphic with the periodic curve of Lother Meyer. The general features of vertically downward expansion of size in a group and the horizontal contraction along a period is more distinct in Fig. 2. From a close examination of the nature of the profiles in Fig. 1 and Fig. 2 it is evident that the general pattern of size variation exhibited by the computed atomic radii as a function of atomic number conform to the basic demand of periodic law regarding the periodicity of atomic volumes. The general appearance of curves in Fig 3 and Fig 4 show that the d-block contraction is distinct in the computed atomic radii. A close looks at the Fig. 5 and Fig. 6 reveals that the f-block contraction is distinctly manifest in the computed sizes of the atoms of lanthanides and actinides. Thus we see that the calculated sizes of atoms faithfully observe the periodic law and reproduce the periodic table.

Thereafter, in order to explore a correlation between the computed atomic size with the absolute periodic properties of atoms we now examine the nature of the curves of the first ionization potential and the electronegativities drawn as a function of atomic number in Fig. 10 and Fig. 11 respectively. The correlation between the ionization potential and the size of the atoms is so reliable that Arhen’s³⁵ method utilized the regularities of the curve found by plotting radii vs. ionization potential for the determination of atomic radii of elements from graphical extrapolation.

Figure 10. Plot of atomic radii and first ionization potential of atoms as a function of atomic number.

Figure 10. Plot of atomic radii and first ionization potential of atoms as a function of atomic number.

A close look at the figure 10 reveals that the ionization potential profile is just maintaining the inverse periodic relation with the atomic size curve and the two curves are homomorphic. It transpires from the nature of the profiles of the atomic radii and the ionization potential that the calculated atomic radii have a good correlation with the experimentally determined size dependent absolute property, the ionization potential. In Fig.11 the Pauling electronegativity [2,15] of as many as 35 elements and their

Figure 11. Plot of atomic radii and electronegativity of atoms as a function of atomic number.

Figure 11. Plot of atomic radii and electronegativity of atoms as a function of atomic number.

theoretical atomic radii are plotted as function of atomic number. Although the electronegativity is an atomic property and depends upon the atomic radii [36], it is not a directly measurable experimental quantity of an isolated atom and it has no quantum mechanical operator [6,37]. But the inverse relationship between the polarizability and hardness is well established [38]. The inverse relationship between the polarizability and the electronagativity is also suggested [6]. From an analysis of the evident mutual inter-relationship between η, α and electronegativity and their relation with atomic radii, the inverse relationship between electronegativity and atomic size is self-evident. It is evident from Fig.11 that the profile for atomic size and the profile for electronegativity are both periodic and mutually homomorphic. Thus it is evident that the calculated sizes of the atoms have a good correlation with the electronegativity, and the experimental quantity like ionization potential.

To make a comparative study of the theoretical radii vis-à-vis the so called experimental radii, we have chosen the experimental values of Pauling [2] and have tabulated the radii of as many as 47 atoms forming crystalline metallic solids in Table 4, the covalent radii of 15 atoms in Table 5, and the van der Waal radii of 13 atoms in Table 6.

The following general observations transpire from a comparative study of the sizes of atoms.

(i) From Table 4 it is distinct that the Pauling’s radii of the atoms forming the crystalline solids are systematically smaller in size than the radii of such atoms of the present calculation. This trend in size in the two methods is perfectly justified. The rationale may be as follows: In the crystalline solids, metal atoms do not remain as undistorted atoms rather the valence electrons of the metal atoms form a completely delocalized band and the lattice is a giant molecule. The metal ions and not the metal atoms

Table 4. Comparative study of theoretical radii and Pauling’s experimental metallic radii of atoms.

Atoms	Theoretical atomic radii (Å)	Single bond metallic radii (Å)	Atoms	Theoretical atomic radii (Å)	Single bond metallic radii (Å)
Li	1.6282	1.225	Mo	3.0677	1.296
Be	1.0855	0.889	Tc	2.9398	1.271
Na	2.1649	1.572	Ru	2.8222	1.246
Mg	1.6711	1.364	Rh	2.7137	1.252
Al	1.3607	1.248	Pd	2.6132	1.283
K	3.5598	2.025	Ag	2.5199	1.339
Ca	2.7479	1.736	Cd	2.433	1.413
Sc	2.6106	1.439	In	2.1167	1.497
Ti	2.4861	1.324	Sn	1.8732	1.399
V	2.3732	1.224	Cs	6.0615	2.35
Cr	2.2701	1.176	Ba	4.6788	1.981
Mn	2.1754	1.171	La	3.8102	1.69
Fe	2.0885	1.165	Hf	1.0079	1.442
Co	2.008	1.162	Ta	0.9594	1.343
NI	1.9337	1.154	W	0.9165	1.304
Cu	1.8648	1.173	Re	0.8773	1.283
Zn	1.8004	1.249	Os	0.8413	1.26
Ga	1.5663	1.245	Ir	0.8082	1.265
Ge	1.3862	1.223	Pt	0.7776	1.295
Rb	4.8106	2.16	Au	0.7492	1.336
Sr	3.7135	1.914	Hg	3.0656	1.44
Y	3.5278	1.616	Tl	2.667	1.549
Zr	3.3598	1.454	Pb	2.3603	1.539
Nb	3.2071	1.342

Table 4. Comparative study of theoretical radii and Pauling’s experimental metallic radii of atoms.

Atoms	Theoretical atomic radii (Å)	Single bond metallic radii (Å)	Atoms	Theoretical atomic radii (Å)	Single bond metallic radii (Å)
Li	1.6282	1.225	Mo	3.0677	1.296
Be	1.0855	0.889	Tc	2.9398	1.271
Na	2.1649	1.572	Ru	2.8222	1.246
Mg	1.6711	1.364	Rh	2.7137	1.252
Al	1.3607	1.248	Pd	2.6132	1.283
K	3.5598	2.025	Ag	2.5199	1.339
Ca	2.7479	1.736	Cd	2.433	1.413
Sc	2.6106	1.439	In	2.1167	1.497
Ti	2.4861	1.324	Sn	1.8732	1.399
V	2.3732	1.224	Cs	6.0615	2.35
Cr	2.2701	1.176	Ba	4.6788	1.981
Mn	2.1754	1.171	La	3.8102	1.69
Fe	2.0885	1.165	Hf	1.0079	1.442
Co	2.008	1.162	Ta	0.9594	1.343
NI	1.9337	1.154	W	0.9165	1.304
Cu	1.8648	1.173	Re	0.8773	1.283
Zn	1.8004	1.249	Os	0.8413	1.26
Ga	1.5663	1.245	Ir	0.8082	1.265
Ge	1.3862	1.223	Pt	0.7776	1.295
Rb	4.8106	2.16	Au	0.7492	1.336
Sr	3.7135	1.914	Hg	3.0656	1.44
Y	3.5278	1.616	Tl	2.667	1.549
Zr	3.3598	1.454	Pb	2.3603	1.539
Nb	3.2071	1.342

Table 5. Comparative study of theoretical radii and Pauling’s experimental covalent radii of atoms.

Atoms	Theoretical atomic radii (Å)	Experimental covalent radii (Å)	Atoms	Theoretical atomic radii (Å)	Experimental covalent radii (Å)
B	0.8141	0.88	Cl	0.7807	0.99
C	0.6531	0.77	As	1.2431	1.18
N	0.5427	0.7	Se	1.1269	1.14
O	0.4652	0.66	Br	1.0305	1.11
F	0.4071	0.64	Sb	1.6799	1.36
Si	1.1476	1.17	Te	1.5228	1.32
P	0.9922	1.1	I	1.3926	1.28
S	0.8738	1.04

Table 5. Comparative study of theoretical radii and Pauling’s experimental covalent radii of atoms.

Atoms	Theoretical atomic radii (Å)	Experimental covalent radii (Å)	Atoms	Theoretical atomic radii (Å)	Experimental covalent radii (Å)
B	0.8141	0.88	Cl	0.7807	0.99
C	0.6531	0.77	As	1.2431	1.18
N	0.5427	0.7	Se	1.1269	1.14
O	0.4652	0.66	Br	1.0305	1.11
F	0.4071	0.64	Sb	1.6799	1.36
Si	1.1476	1.17	Te	1.5228	1.32
P	0.9922	1.1	I	1.3926	1.28
S	0.8738	1.04

Table 6. Comparative study of absolute radii and covalent radii of Politzer-Parr-Murphy.

Atoms	Covalent radii (Å)	Absolute radii (Å)
Li	1.357	1.6282
Na	1.463	2.1649
Al	1.487	1.3607
K	1.802	3.5598
Cr	1.494	2.2701
Ni	1.3	1.9337
Cu	1.166	1.8648
Rb	1.924	4.8106
Ag	1.28	2.5199
Sn	1.492	1.8732
Te	1.381	1.5228
B	1.091	0.8141
C	0.912	0.6513
N	0.814	0.5427
O	0.764	0.4652
F	0.671	0.4071
Si	1.296	1.1476
P	1.185	0.9922
S	1.12	0.8738
Cl	0.999	0.7807
As	1.258	1.2431
Se	1.209	1.1269
Br	1.116	1.0305
Sb	1.433	1.6799
I	1.299	1.3926

Table 6. Comparative study of absolute radii and covalent radii of Politzer-Parr-Murphy.

Atoms	Covalent radii (Å)	Absolute radii (Å)
Li	1.357	1.6282
Na	1.463	2.1649
Al	1.487	1.3607
K	1.802	3.5598
Cr	1.494	2.2701
Ni	1.3	1.9337
Cu	1.166	1.8648
Rb	1.924	4.8106
Ag	1.28	2.5199
Sn	1.492	1.8732
Te	1.381	1.5228
B	1.091	0.8141
C	0.912	0.6513
N	0.814	0.5427
O	0.764	0.4652
F	0.671	0.4071
Si	1.296	1.1476
P	1.185	0.9922
S	1.12	0.8738
Cl	0.999	0.7807
As	1.258	1.2431
Se	1.209	1.1269
Br	1.116	1.0305
Sb	1.433	1.6799
I	1.299	1.3926

occupy the positions of atoms and held by strong cohesive force. Therefore, because of the strong cohesive force of metallic bonding in the lattice, the metal ions become very close and the inter nuclear distance between two immediate neighbours must be considerably smaller compared to a sum of the absolute radii of two atoms. Hence Pauling’s determination of atomic radii by the apportionment of the distance of inter nuclear separation to the atoms in crystalline lattice does not refer to the absolute size of the atoms at all. Thus the smaller magnitude of Pauling’s radii, compared to the absolute radii of present calculation is quite justified. We have one more precedent example [39] where theoretical absolute radii of atoms are greater than the so-called experimental radii. Waber and Larson [39] independently used the principal maximum of the charge densities as the orbital radii of the rare earth atoms and they used the nonrelativistic Hartree- Fock eigen functions to compute the orbital radii of free lanthanide atoms. They also concluded that the radii corresponding to these outer orbitals were significantly larger than the atomic or metallic radii. The Pauling’s radii do not really represent the absolute radii of atoms rather such radii should be used to reproduce the distance of closest approach of two atoms in crystalline solid.

(ii) From Table 5 we see that, out of 15 elements, the covalent radii of as many as 6 elements are very close in both methods. The rest of the elements cited in Table 5 have radii both smaller and larger than the absolute radii of the present calculation. The covalent radii depend upon the force of covalent binding and the bond order. Since the type of covalent bonding is not uniform rather atoms may be bonded by single, double and triple bond depending upon the chemical situation, no general trend of correlation of theoretical absolute radii and covalent radii of atoms can be predicted.

(iii) A comparative study is also made between theoretical covalent radii of atoms of Politzer, Parr and Murphy [40] and the corresponding absolute radii of present calculation. Based on density functional theory, DFT, Politzer, Parr and Murphy [40] enquired into the relationship between atomic chemical potentials, electrostatic potentials and covalent radii and observed that the points at a certain radial distance at which electrostatic potential is equal to the chemical potential corresponds to the covalent radii. These covalent radii may be defined as theoretical covalent radii. Politzer et al [40] published the theoretical covalent radii of atoms of as many as 25 elements. We have arranged the theoretical radii and the corresponding absolute radii in the Table 6. A close look at the Table 6 reveals a strange behavior of the absolute radii vis-à-vis the theoretical covalent radii of atoms of corresponding elements. Absolute radii of the metallic atoms are consistently larger while the absolute radii of the non-metallic atoms are consistently smaller than the theoretical covalent radii of the atoms. However, the absolute radii of a few elements are also close to the theoretical covalent radii. This strange pattern of variation of the two sets of radii cannot be correlated unless the fundamental relationship between the covalent radii and the absolute radii is explored.

(iv) The van der Waal’s radii.

It is sporadically sprinkled impression in the chemical literature that the inert gas atoms are unusually big in size. The published data very often shows that radii of the inert gas atoms is the biggest in the row where it occurs and that too, in violation of periodic law. Looking at the Table 7 we see that the van der Waal’s radii in Pauling’s determination are considerably larger than the absolute radii of the present calculation. In this connection we feel pertinent to make a more critical survey and study of the van der Waal radii of inert gas elements. The periodic law demands that the atomic size should be a monotone decreasing function of atomic number in a horizontal row and the size of the end element, the inert gas atom, must be smallest in the row. The formula of computing the theoretical radii shows that the absolute size of the atoms of the inert gas elements must be smallest in the row.

Table 7. Comparative study of theoretical radii and Pauling’s experimental van der Waal’s radii of atoms.

Atoms	Theoretical atomic radii (Å)	Experimental van der Waal's radii (Å)	Atoms	Theoretical atomic radii (Å)	Experimental van der Waal's radii (Å)
N	0.5427	1.5	Se	1.1269	2
P	0.9922	1.9	Te	1.5228	2.2
As	1.2431	2	F	0.4071	1.35
Sb	1.6799	2.2	Cl	0.7807	1.8
H	0.5292	1.2	Br	1.0305	1.95
O	0.4652	1.4	I	1.3926	2.15
S	0.8738	1.85

Table 7. Comparative study of theoretical radii and Pauling’s experimental van der Waal’s radii of atoms.

Atoms	Theoretical atomic radii (Å)	Experimental van der Waal's radii (Å)	Atoms	Theoretical atomic radii (Å)	Experimental van der Waal's radii (Å)
N	0.5427	1.5	Se	1.1269	2
P	0.9922	1.9	Te	1.5228	2.2
As	1.2431	2	F	0.4071	1.35
Sb	1.6799	2.2	Cl	0.7807	1.8
H	0.5292	1.2	Br	1.0305	1.95
O	0.4652	1.4	I	1.3926	2.15
S	0.8738	1.85

The available data regarding the size of the inert gas atoms in the chemical literature are all van der Waal radii. Since the van der Waal force of attraction is very weak, the gap between the atoms bonded by van der Waal bond is large and the van der Waal radii so computed must be very large. Thus, there is no reason of mysterious swelling of size of inert gas atoms as implied by their experimental radii. Justifiably, the absolute sizes of such atoms must be considerably smaller than their van der Waals radii. The radii of inert gas atoms in the present calculation are in conformity with the periodic law.

Lanthanide Contraction.

From the Table 1 and Fig. 1 and Fig. 2 we see that the present method of atomic radii calculation reproduces the “lanthanide contraction”. To make the position more distinct and self-evident we have plotted the radii of atoms of 14 elements after lanthanum as a function of atomic number in Fig. 5. Fig. 5 demonstrates that the size of the lanthanide atoms decreases fairly regularly and steadily. Most of the textbooks speak about the sharp rise of the atomic radii of Eu and Yb. Instead of being contracted, atomic radii of these two elements are reported to be extremely large compared with other atoms of the series. The stated situation is self-evident in the curve reproduced in figure 14.4 at page 601 of the reference [5]. However, no rationale of abrupt increase in size of these two elements is put forward. The sharp increase in atomic size of Eu and Yb is missing in the curve of the calculated radii (Fig 5) and Table 1 shows that the orbital exponents of the outermost orbital of the atoms of the elements of lanthanide series steadily increase and as a consequence, the sizes of the atoms are bound to decrease steadily. Therefore, there is no scope of sudden increase in the size of Eu and Yb. However, we may try to rationalize the mystery of sudden increase in the reported crystal radii of Eu and Yb. These two metal atoms form metallic bonds with two ‘s’ electrons compared to the other lanthanides, which form metallic bonds with more than two electrons. Hence lanthanides other than Eu and Yb have more valance electrons for metallic binding and as a result such atoms become closer by stronger force of attraction reducing the inter nuclear distance and hence their smaller size. But Eu and Yb with fewer numbers of valence electrons form solids with relatively weaker force of attraction and hence the inter-atomic distance between two similar atoms in metallic state should be comparatively large. The fault lies in the method of determination of radii of atoms of such elements. So the apparent difference in the general appearance of atomic radii curve of lanthanides of the present calculation and that in reference [5] is rationalized. Thus the present theoretical determination of the sizes of the lanthanide elements is internally consistent and physically justified.

Actinide Contraction.

We know that according to the suggestion of Seaborg [41], known as actinide hypothesis, the elements following Ac form a new inner transition series analogous to the lanthanide elements. The Fig. 1 and Fig. 2 reveal that there is a steady decrease in sizes of the atoms of elements after actinium and the Table 1 shows that the orbital exponents of the outermost orbital of all such elements increase monotonically. To have a clearer view of the matter of actinide contraction in the present calculation, the radii of all 14 elements from Th to Lr are plotted as function of atomic number in Fig.6. The Fig.6 demonstrates distinctly the actinide contraction where the atoms of actinide elements undergo slow but steady decrease in size. Thus the physical reality of periodic size contraction among the lanthanide and actinide elements of the periodic table is realistically reproduced in the present set of theoretical atomic radii.

Waber and Cromer [8] calculated the theoretical radii of a number of atoms through the same formalism of radial charge density function but the orbitals are computed by the relativistic Hartree-Fock method. The trend of regular variation of atomic size in the d-block contraction, lanthanide contraction was reproduced in their work.

Diamagnetic part of the atomic susceptibility.

Partington [42] remarked that the Lother Meyer’s atomic volume curve shows the periodicity of a number of physico-chemical properties including magnetic susceptibility. The diamagnetic part of magnetic susceptibility of as many as 54 elements is computed through the eqn. (9) and the computed values of <r²>_av and χ_dia are shown in Table 2 and plotted in Fig. 7 as a function of atomic number. A comparison of the Fig.7 and Fig.1 reveals that the nature of the curve for <r²>_av is quite periodic in nature and mimics pattern of the atomic size curve and it further transpires that the diamagnetic part of magnetic susceptibility of the atoms, χ_dia, basically a size property, varies periodically like other periodic properties of elements. The study of the nature of the profiles of the two curves in Fig. 7 reveals that the curve of χ_dia, and the curve of <r²>_av are homomorphic to each other. Now comparing the pattern of the profile of the diamagnetic susceptibility of atoms in Fig.7 with the pattern of the curve of the magnetic susceptibilities of atoms published in American Institute of Physics Handbook [43], it is apparent that the general appearance of the two curves have some resemblance. We further note that the position of occurrence of the inert gas elements in the curve of Figure 7 and the curve of the American Institute of Physics Handbook [43] are similar. It is also apparent from a comparative study of the values of the χ_dia of the present calculation (Table 2) and that published in CRC Handbook [44] that the trend of variation of the magnitude of the values of χ_dia, of inert gas atoms as calculated by the present method and that published in the CRC Handbook [44] is similar in nature.

The Periodicity of Atomic Polarizability (α) and Global Hardness (η)

Chattaraj and Maity [45] have recently pointed out that the hardness and polarizability of atoms are periodic properties of the elements and the periodicity of these properties can be justified and formulated on the basis of maximum hardness principle, MHP [24,28,46] and the minimum polarizability principle, MPP [47]. It follows from MHP and MPP that an atom with a closed-shell structure is the most stable, hardest,and least polarizable among all the atoms in a given period and in general, the polarizabilty decreases along a period and increses along a group while the hardness has the reverse trend. The hardness increases along a period and decreases along a group. Thus, like other periodic physico-chemical properties, the global hardness and polarizability of elements are the periodic functions of the atomic number. The trend of variation of atomic polarizability in groups and periods set in this work was also predicted earlier [19].

Atomic polarizability (α).

From the eqn.14 we find that the atomic polarizability,α is directly proportional to the size of the atoms. Comparing the experimental [19] atomic polarizability of as many as nine elements with the corresponding theoretical polarizability in Table 8 we see that the theoretical values are close to the experimental results of as many as eight elements. The Fig. 8 reveals that the polarizability profile mimics the atomic size curve of Fig.1. Thus the computed atomic polarizability is a perfect periodic physical property having the nature of variation similar to the atomic volume curve of Lother Meyer. A close look at Fig.8 shows the set trend of variation of the atomic polarizability, α. The polarizability increases steadily with increasing atomic number in a group, and it gradually decreases and ends at the atom of inert gas element in a period. But the trend of polarizability of the inert gases within the family must be increasing with increasing atomic number [45]. It is distinct from the Fig.8 that the alkali metal atoms appear at the top and the inert gas atoms occur at the bottom of the polarizability curve. Apparently, the alkali metal atoms, as a class, can be easily deformed by an electric field. The easy polarizability of the alkali metal atoms is due to the loosely bound outer or valance electrons in its structure. But the electronic structures of the noble gas atoms are much stiffer or hard. The expected pattern of variation of polarizability of the inert gas atoms within the group is also reproduced in the polarizabilities of atoms calculated in terms of theoretical atomic radii. From the above it transpires that the polarizabilities atoms computed in terms of the theoretical radii is quantitatively close to the experimental values and qualitatively reproduce the expected periodicity. Therefore, we can say that the theoretical atomic radii of the present calculation can be used to effectively compute the periodic physical property of atoms of the elements – the atomic polarizability.

Table 8. Comparative study of theoretical and experimental atomic polarizability of some elements.

Atoms	Theoretical Atomic Polarizability (x 10–24 cc.)	Experimental Atomic Polarizability (x 10–24 cc.)
H	0.6669	0.66
He	0.1358	0.21
Li	19.4239	12
Be	5.7558	9.3
C	2.4279	1.5
Ne	1.2432	0.4
Na	45.659	27
Ar	1.5808	1.6
K	202.9969	34

Table 8. Comparative study of theoretical and experimental atomic polarizability of some elements.

Atoms	Theoretical Atomic Polarizability (x 10–24 cc.)	Experimental Atomic Polarizability (x 10–24 cc.)
H	0.6669	0.66
He	0.1358	0.21
Li	19.4239	12
Be	5.7558	9.3
C	2.4279	1.5
Ne	1.2432	0.4
Na	45.659	27
Ar	1.5808	1.6
K	202.9969	34

Global Hardness (η).

The hardness is an intrinsic periodic physical property of atoms [45]. The global hardness of 103 elements is computed through eqn.(19) using the values of theoretical atomic radii and shown in Table 3. Pearson [31] correlated the global hardness, η, with the polarizability of the atoms. Although the global hardness has been rigorously defined by Density Functional Theory, the qualitative idea is still a valuable guide. We see from eqn.19 that, since e, the electronic charge is constant, the global hardness of the atoms, η is inversely proportional to R, the radius of the atoms. Thus the hardness is determined by the size factor of atoms only. We have plotted the computed global hardness of atoms as a function of atomic number in Figure 9. The general appearance of the profile of global hardness of atoms as revealed in Fig. 9 is periodic in nature and has resemblance to the atomic volume curve of Lother Meyer in Fig. 1. The alkali metals have the smallest hardness and the inert gas atoms have the largest hardness and the hardness increases monotonically horizontally in a period. The hardness decreases vertically in a group. The same pattern is repeated in all the periods and groups. Thus, it is transparent that the hardness values of atoms computed in terms of the atomic radii of the present work meaningfully exhibit its qualitative periodic nature. Now we seek a quantitative correlation of the computed hardness of the atoms. A number of informations have appeared regarding the numerical values of global hardness of atoms [6,22,27,31,48] of which the hardness values of Parr and Pearson [27], and Pearson [31] were calculated from the experimental ionization potential and electron affinity. It appears that the values of hardness of atoms calculated by Pearson [31] are absolute. In the Table 9 we have tabulated, side by side, the hardness values of atoms of 63 elements calculated by Pearson [31] and the hardness values of the corresponding atoms calculated through eqn.19. A close look at the values of the hardness calculated by Pearson [31] on the basis of experimental ionization potential and electron affinity reveals that in a significant number of cases the expected relative order of the hardness and radii are inverted and the atoms of smaller radii has smaller hardness and the atoms of larger radii has larger hardness in violation of periodic law. However, comparing the values of hardness of present calculation vis-à-vis and those published by Pearson [31], we find that the theoretically computed values of global hardness of as many as 26 of atoms are close (within 0.1 to1.0 eV) to that of Pearson’s values. Thus we conclude that the result is encouraging both qualitatively and quantitatively.

Conclusion.

The terms atomic and ionic radii are very popular in chemical literature and the concept has been largely employed in rationalizing various physico-chemical properties of atoms and molecules and is a useful parameter of electronic structure theory. We have explored a simple method of computing the absolute size of atoms and brought together a large body of known material to reveal how many different properties correlate with atomic size. Although a large body of scattered information on sizes of atoms and ions has appeared in the literature, a critical analysis of the status of a reported set of radii

Table 9. Comparative study of theoretical and absolute global hardness (atoms having theoretical hardness close within 0.1–1.0 eV to the experimental are given asterisks).

Atoms	Theoretical Global hardness of atoms (eV)	Absolute Global hardness of atoms (eV)	Atoms	Theoretical Global hardness of atoms (eV)	Absolute Global hardness of atoms (eV)
H	13.588	6.43	Rb*	1.4948	1.85
Li	4.4164	2.39	Sr	1.9364	3.7
Be	6.6244	4.5	Yb	2.0383	3.19
B	8.8328	4.01	Zr	2.1402	3.21
C	11.0407	5	Nb*	2.2422	3
N	13.25	7.23	Mo*	2.344	3.1
O	15.4574	6.08	Ru*	2.5479	3
F	17.6634	7.01	Rh*	2.6498	3.16
Na*	3.3215	2.3	Pd	2.7517	3.89
Mg*	4.303	3.9	Ag*	2.8536	3.14
Al	5.2846	2.77	Cd	2.9555	4.66
Si	6.2659	3.38	In*	3.3972	2.8
P	7.2473	4.88	Sn*	3.8388	3.05
S	8.2293	4.14	Sb*	4.2805	3.8
Cl	9.2107	4.68	Te	4.7221	3.52
K*	2.02	1.92	I	5.1636	3.69
Ca	2.6168	4	Cs*	1.1863	1.71
Sc*	2.7545	3.2	Ba	1.5369	2.9
Ti*	2.8924	3.37	La*	1.8873	2.6
V*	3.03	3.1	Hf	7.1344	3
Cr*	3.0676	3.06	Ta	7.4951	3.79
Mn*	3.3055	3.72	W	7.8459	3.58
Fe*	3.443	3.81	Re	8.1965	3.87
Co*	3.5811	3.6	Os	8.5472	3.8
Ni*	3.7187	3.25	Ir	8.8973	3.8
Cu	3.8561	3.25	Pt	9.2474	3.5
Zn*	3.994	4.94	Au	9.598	3.46
Ga	4.5909	2.9	Hg	2.3456	5.54
Ge	5.1874	3.4	Tl*	2.6962	2.9
As	5.7846	4.5	Pb*	3.0466	3.53
Se	6.381	3.87	Bi*	3.3972	3.74
Br	6.978	4.22

Table 9. Comparative study of theoretical and absolute global hardness (atoms having theoretical hardness close within 0.1–1.0 eV to the experimental are given asterisks).

Atoms	Theoretical Global hardness of atoms (eV)	Absolute Global hardness of atoms (eV)	Atoms	Theoretical Global hardness of atoms (eV)	Absolute Global hardness of atoms (eV)
H	13.588	6.43	Rb*	1.4948	1.85
Li	4.4164	2.39	Sr	1.9364	3.7
Be	6.6244	4.5	Yb	2.0383	3.19
B	8.8328	4.01	Zr	2.1402	3.21
C	11.0407	5	Nb*	2.2422	3
N	13.25	7.23	Mo*	2.344	3.1
O	15.4574	6.08	Ru*	2.5479	3
F	17.6634	7.01	Rh*	2.6498	3.16
Na*	3.3215	2.3	Pd	2.7517	3.89
Mg*	4.303	3.9	Ag*	2.8536	3.14
Al	5.2846	2.77	Cd	2.9555	4.66
Si	6.2659	3.38	In*	3.3972	2.8
P	7.2473	4.88	Sn*	3.8388	3.05
S	8.2293	4.14	Sb*	4.2805	3.8
Cl	9.2107	4.68	Te	4.7221	3.52
K*	2.02	1.92	I	5.1636	3.69
Ca	2.6168	4	Cs*	1.1863	1.71
Sc*	2.7545	3.2	Ba	1.5369	2.9
Ti*	2.8924	3.37	La*	1.8873	2.6
V*	3.03	3.1	Hf	7.1344	3
Cr*	3.0676	3.06	Ta	7.4951	3.79
Mn*	3.3055	3.72	W	7.8459	3.58
Fe*	3.443	3.81	Re	8.1965	3.87
Co*	3.5811	3.6	Os	8.5472	3.8
Ni*	3.7187	3.25	Ir	8.8973	3.8
Cu	3.8561	3.25	Pt	9.2474	3.5
Zn*	3.994	4.94	Au	9.598	3.46
Ga	4.5909	2.9	Hg	2.3456	5.54
Ge	5.1874	3.4	Tl*	2.6962	2.9
As	5.7846	4.5	Pb*	3.0466	3.53
Se	6.381	3.87	Bi*	3.3972	3.74
Br	6.978	4.22

and inter-relationship between various sets of radii seems to have not been taken up. The scientific workers often feel the need of more representative atomic and ionic radii than that available in chemical literature. Powell [49] has stated that the structure, stability and reactivity of organo–lanthanide compounds seem to be largely determined by electrostatic and steric effects and by selecting a metal of appropriate size it may in future be possible to tailor the steric effect so as to provide just right environment to bring about a desired reaction. The present theoretical investigation of physical problem of atomic size has been found largely successful in providing with an unambiguous concept of the absolute size of atoms and rationalizing the range of validity and status of various sets of reported atomic radii by a qualitative and quantitative study. The computed theoretical radii qualitatively reproduce the periodic table and the atomic volume curve of Lother Meyer. A comparative study of the relative sizes of the atoms in groups and periods reveals that the expected vertical trend of variation in a group and the horizontal trend in a period in atomic size are nicely reproduced by the theoretical atomic radii. The d-block and f-block contractions are also distinct in the calculated sizes. The atomic radii of present calculation are found to have a good correlation with other available so called experimental radii and theoretical radii computed through more sophisticated method. The computed size is applied to calculate the periodic size dependent physical properties of distinct and isolated atoms: the diamagnetic part of the atomic susceptibility, the atomic polarizability and the global hardness. The computed theoretical results have a good resemblance with experimental data. In a significant number of cases the theoretically computed physical properties in terms of the absolute radii calculated by the present method are quantitatively close to their experimental values. The atomic radii of present calculation are found to have a good correlation with other available theoretical radii computed through more sophisticated method. Thus, the present approach of computing the absolute size of atoms in a simple way seems to be a successful venture and should be exploited as fully as possible.