Fluorescence Resonance Energy Transfer for Drug Loading Assessment in Reconstituted High-Density Lipoprotein Nanoparticles
Abstract
1. Introduction
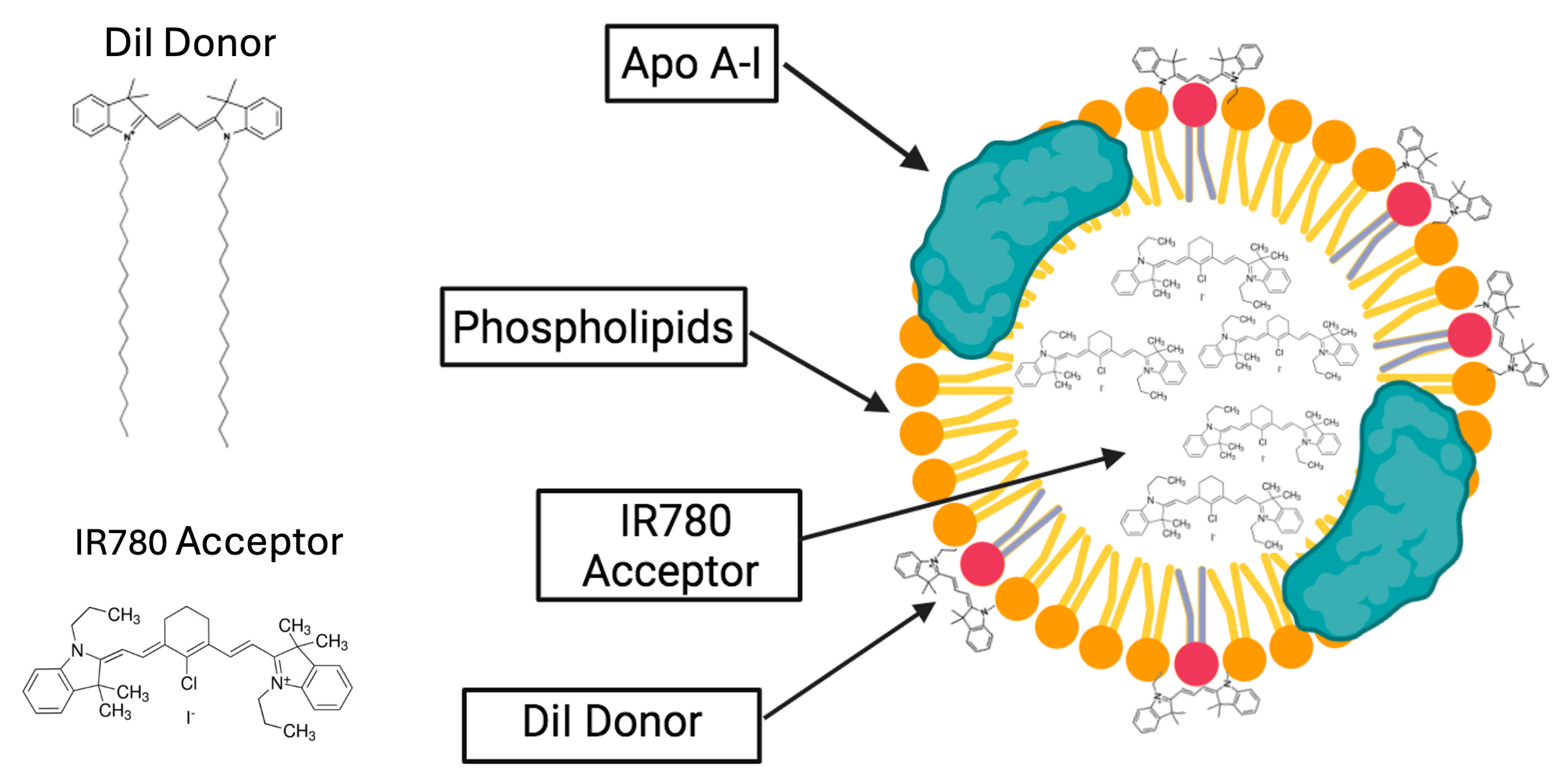
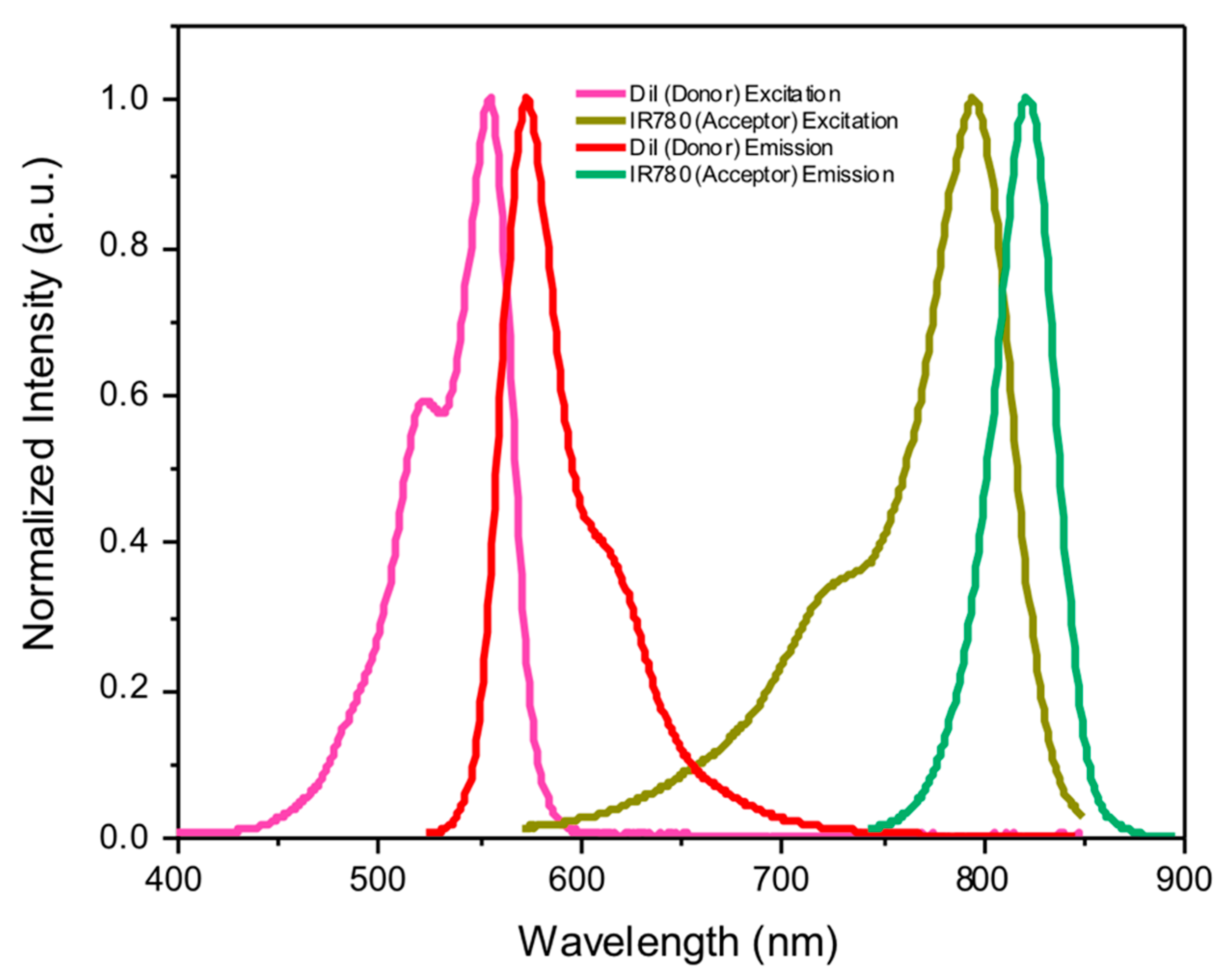
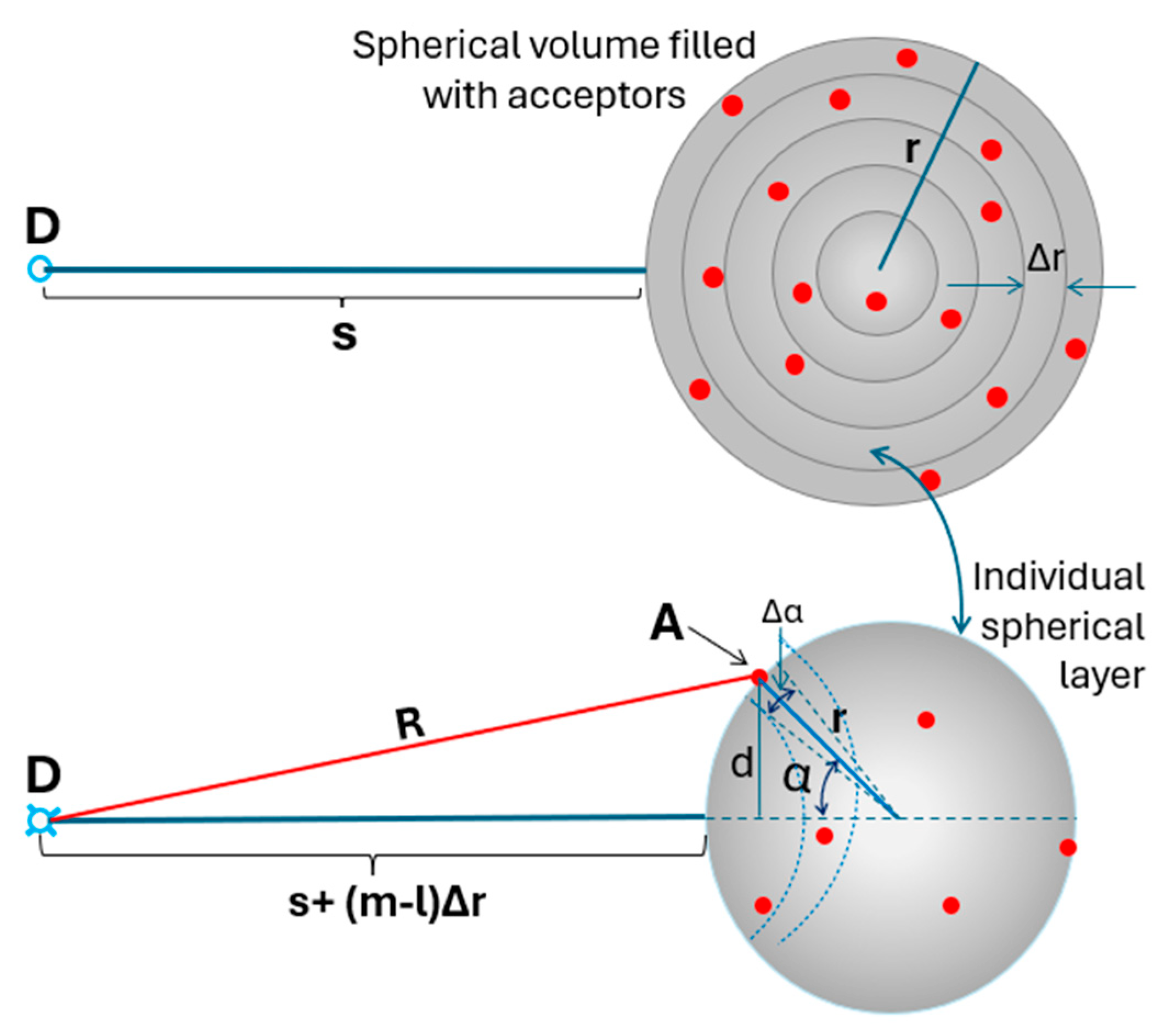
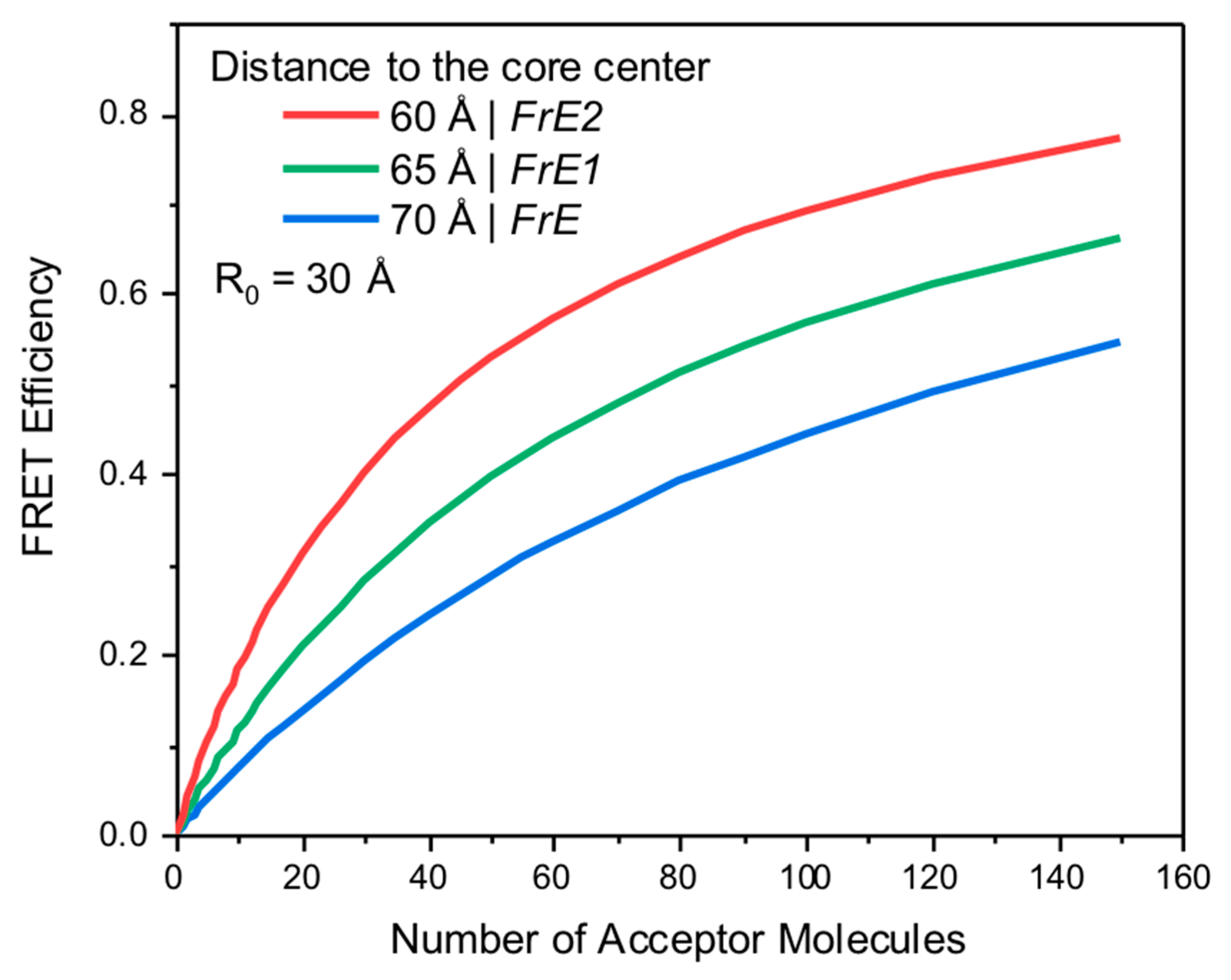
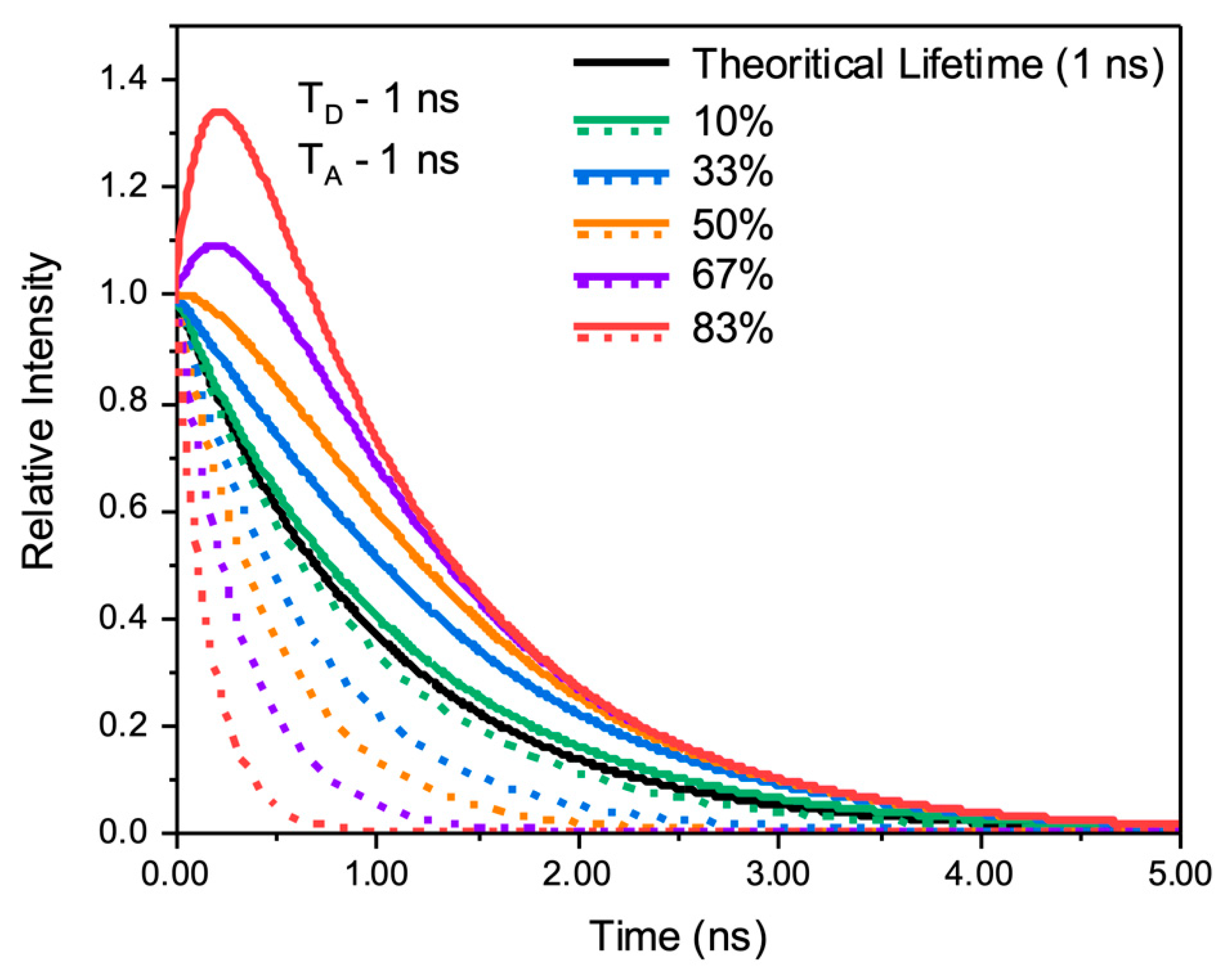
Theoretical Considerations
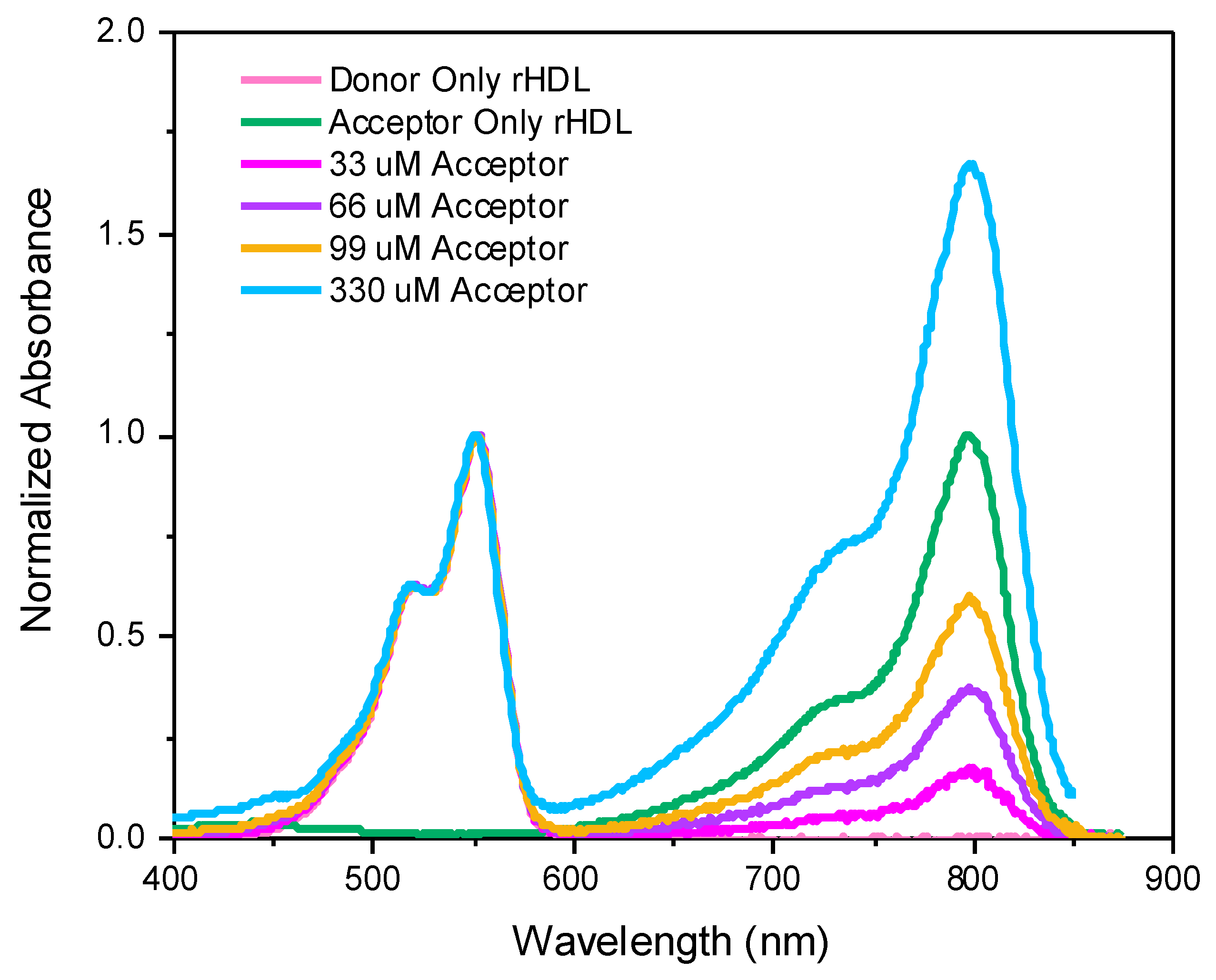
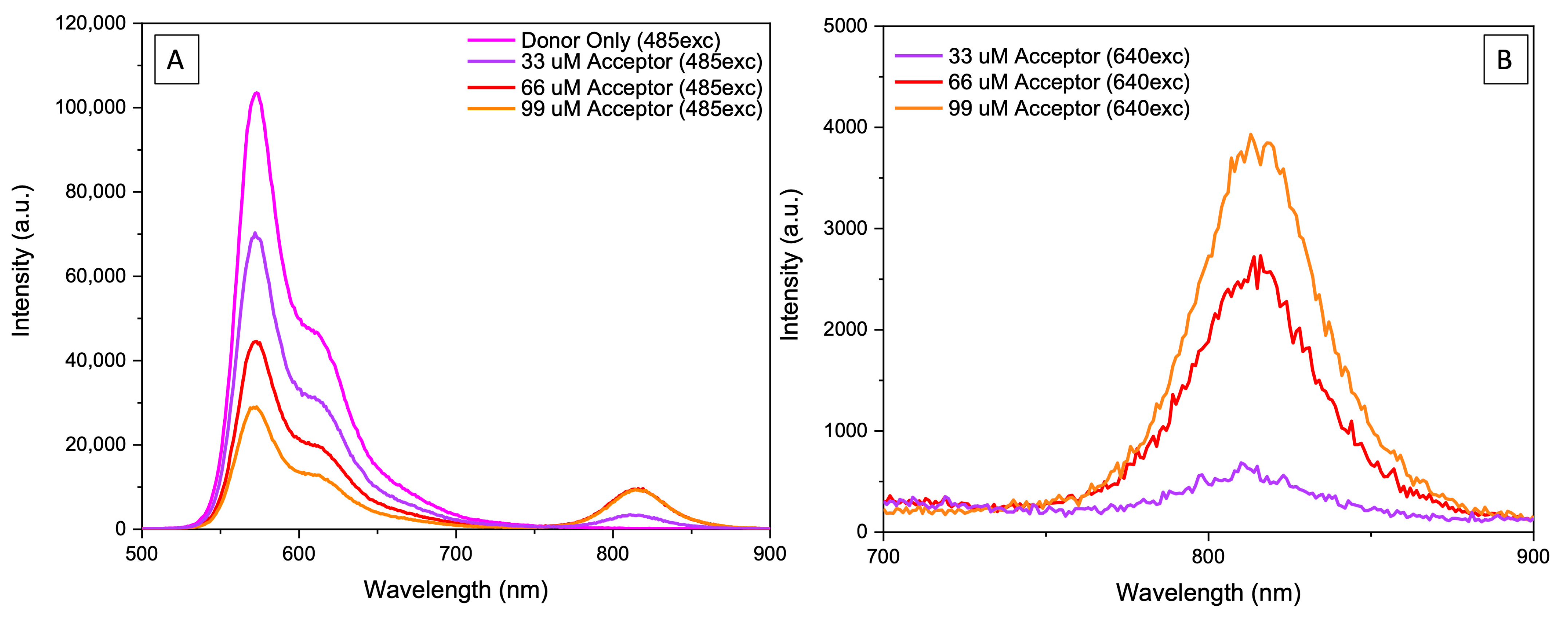
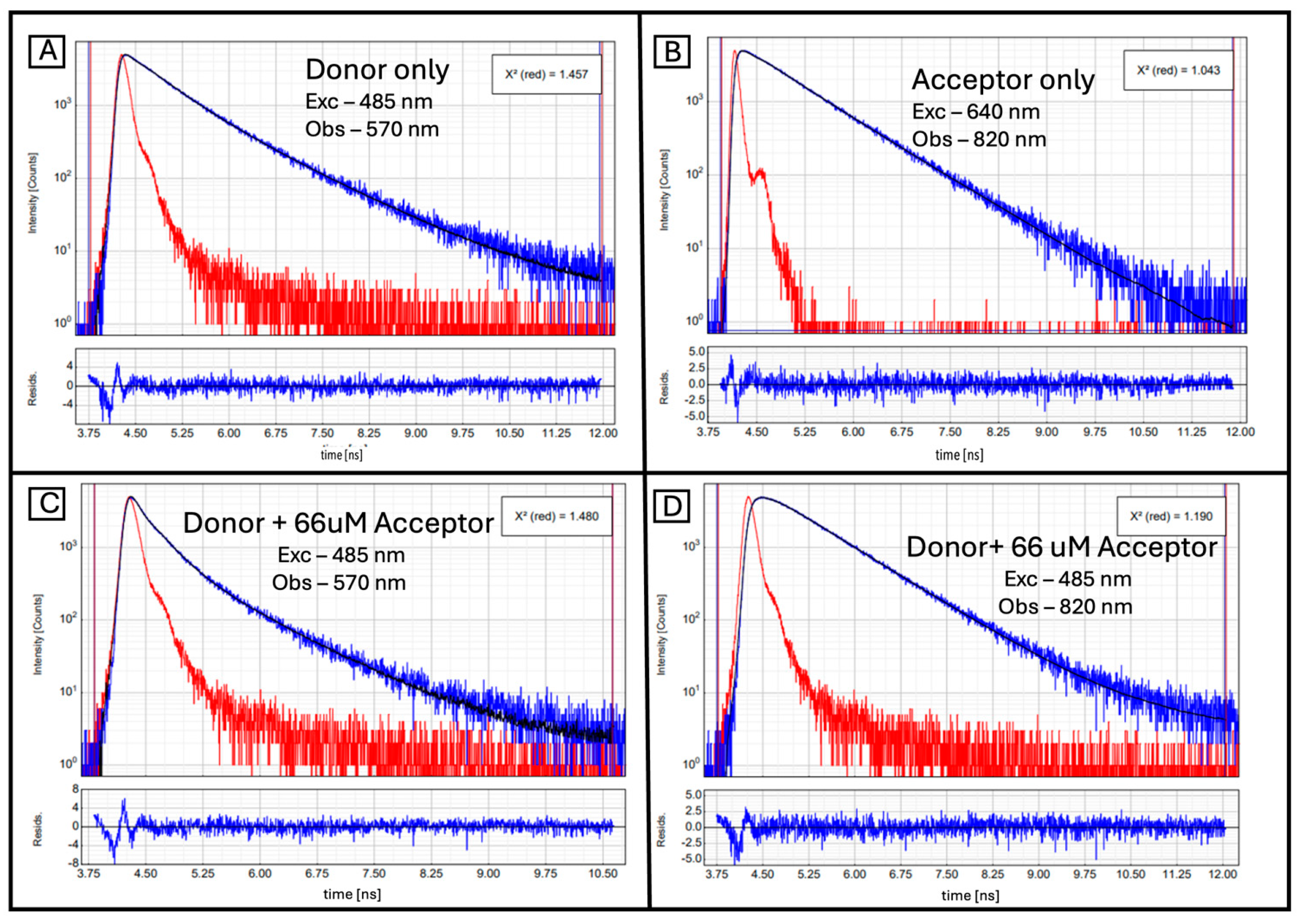
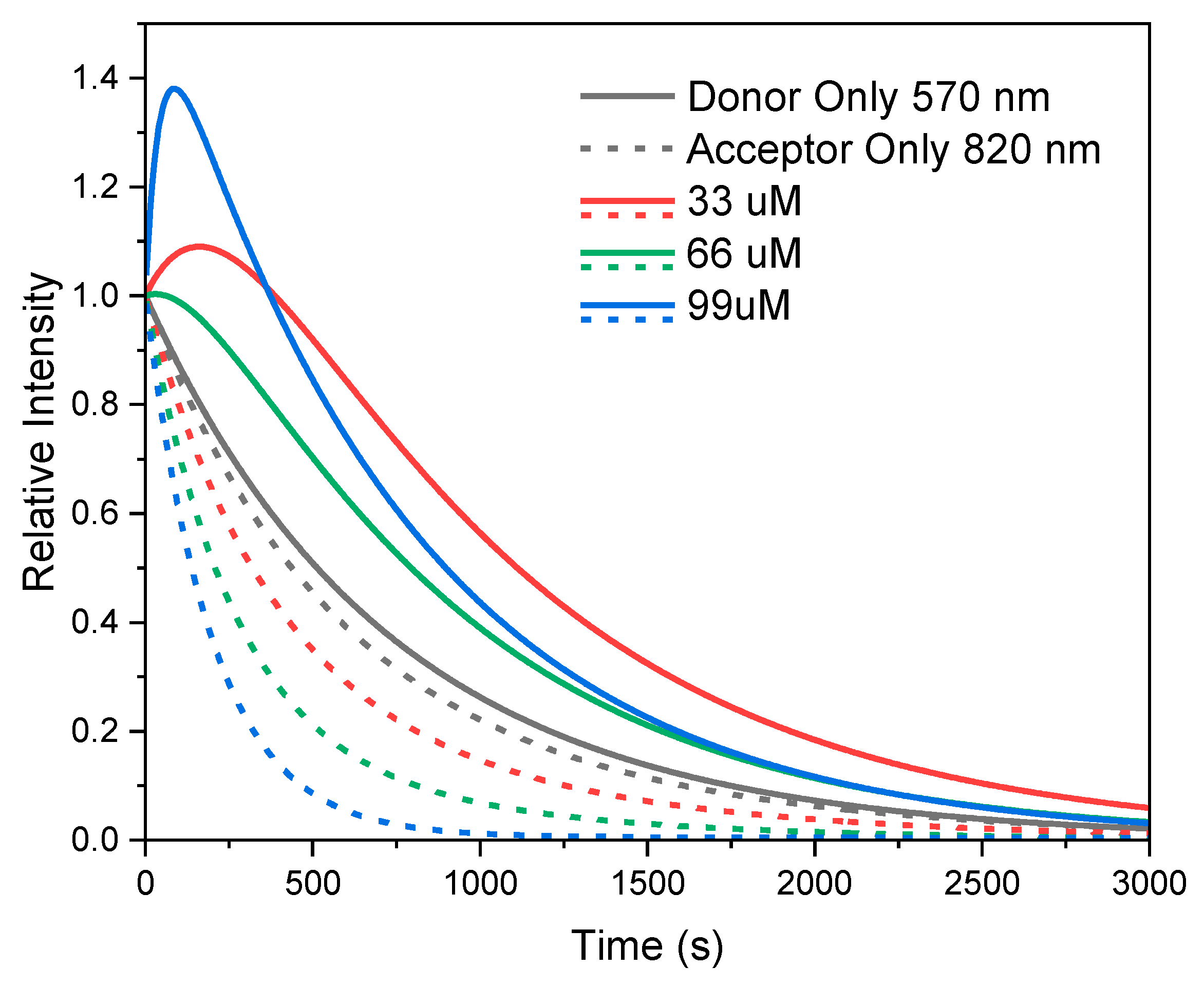
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Counsell, R.E.; Pohland, R.C. Lipoproteins as potential site-specific delivery systems for diagnostic and therapeutic agents. J. Med. Chem. 1982, 25, 1115–1120. [Google Scholar] [PubMed]
- Lacko, A.G.; Nair, M.; Paranjape, S.; Mooberry, L.; McConathy, W.J. Trojan horse meets magic bullet to spawn a novel, highly effective drug delivery model. Chemotherapy 2006, 52, 171–173. [Google Scholar] [CrossRef] [PubMed]
- Lacko, A.G.; Nair, M.; Paranjape, S.; Johnson, S.; McConathy, W.J. High density lipoprotein complexes as delivery vehicles for anticancer drugs. Anticancer Res. 2002, 22, 2045–2050. [Google Scholar] [PubMed]
- McConathy, W.J.; Nair, M.P.; Paranjape, S.; Mooberry, L.; Lacko, A.G. Evaluation of synthetic/reconstituted high-density lipoproteins as delivery vehicles for paclitaxel. Anti-Cancer Drugs 2008, 19, 183–188. [Google Scholar]
- McConathy, W.J.; Paranjape, S.; Mooberry, L.; Buttreddy, S.; Nair, M.; Lacko, A.G. Validation of the reconstituted high-density lipoprotein (rHDL) drug delivery platform using dilauryl fluorescein (DLF). Drug Deliv. Transl. Res. 2011, 1, 113–120. [Google Scholar]
- Ryan, R.O.; Forte, T.M.; Oda, M.N. Optimized bacterial expression of human apolipoprotein AI. Protein Expr. Purif. 2003, 27, 98–103. [Google Scholar]
- Remaley, A.T.; Thomas, F.; Stonik, J.A.; Demosky, S.J.; Bark, S.E.; Neufeld, E.B.; Bocharov, A.V.; Vishnyakova, T.G.; Patterson, A.P.; Eggerman, T.L. Synthetic amphipathic helical peptides promote lipid efflux from cells by an ABCA1-dependent and an ABCA1-independent pathway. J. Lipid Res. 2003, 44, 828–836. [Google Scholar]
- Zhang, Z.; Chen, J.; Ding, L.; Jin, H.; Lovell, J.F.; Corbin, I.R.; Cao, W.; Lo, P.C.; Yang, M.; Tsao, M.S. HDL-mimicking peptide–lipid nanoparticles with improved tumor targeting. Small 2010, 6, 430–437. [Google Scholar]
- Richards-Kortum, R.; Sevick-Muraca, E. Quantitative optical spectroscopy for tissue diagnosis. Annu. Rev. Phys. Chem. 1996, 47, 555–606. [Google Scholar]
- Contag, C.H.; Jenkins, D.; Contag, P.R.; Negrin, R.S. Use of reporter genes for optical measurements of neoplastic disease in vivo. Neoplasia 2000, 2, 41–52. [Google Scholar]
- Bhaumik, S.; Gambhir, S. Optical imaging of Renilla luciferase reporter gene expression in living mice. Proc. Natl. Acad. Sci. USA 2002, 99, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Elson, D.; Requejo-Isidro, J.; Munro, I.; Reavell, F.; Siegel, J.; Suhling, K.; Tadrous, P.; Benninger, R.; Lanigan, P.; McGinty, J. Time-domain fluorescence lifetime imaging applied to biological tissue. Photochem. Photobiol. Sci. 2004, 3, 795–801. [Google Scholar] [CrossRef] [PubMed]
- Jaffer, F.A.; Weissleder, R. Molecular imaging in the clinical arena. JAMA 2005, 293, 855–862. [Google Scholar] [CrossRef] [PubMed]
- Soubret, A.; Ntziachristos, V. Fluorescence molecular tomography in the presence of background fluorescence. Phys. Med. Biol. 2006, 51, 3983. [Google Scholar] [CrossRef]
- May, A.; Bhaumik, S.; Gambhir, S.S.; Zhan, C.; Yazdanfar, S. Whole-body, real-time preclinical imaging of quantum dot fluorescence with time-gated detection. J. Biomed. Opt. 2009, 14, 060504. [Google Scholar] [CrossRef]
- Levitt, J.A.; Matthews, D.R.; Ameer-Beg, S.M.; Suhling, K. Fluorescence lifetime and polarization-resolved imaging in cell biology. Curr. Opin. Biotechnol. 2009, 20, 28–36. [Google Scholar] [CrossRef]
- Vahrmeijer, A.L.; Hutteman, M.; Van Der Vorst, J.R.; Van De Velde, C.J.; Frangioni, J.V. Image-guided cancer surgery using near-infrared fluorescence. Nat. Rev. Clin. Oncol. 2013, 10, 507–518. [Google Scholar] [CrossRef]
- Rich, R.M.; Stankowska, D.L.; Maliwal, B.P.; Sørensen, T.J.; Laursen, B.W.; Krishnamoorthy, R.R.; Gryczynski, Z.; Borejdo, J.; Gryczynski, I.; Fudala, R. Elimination of autofluorescence background from fluorescence tissue images by use of time-gated detection and the AzaDiOxaTriAngulenium (ADOTA) fluorophore. Anal. Bioanal. Chem. 2013, 405, 2065–2075. [Google Scholar] [CrossRef]
- Jenkins, R.; Burdette, M.K.; Foulger, S.H. Mini-review: Fluorescence imaging in cancer cells using dye-doped nanoparticles. Rsc Adv. 2016, 6, 65459–65474. [Google Scholar] [CrossRef]
- Forster, T. Delocalization excitation and excitation transfer. Mod. Quantum Chem. 1965, III, 93–137. [Google Scholar]
- Förster, T. Experimentelle und theoretische Untersuchung des zwischenmolekularen Übergangs von Elektronenanregungsenergie. Z. Naturforschung A 1949, 4, 321–327. [Google Scholar]
- Stryer, L. Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 1978, 47, 819–846. [Google Scholar] [PubMed]
- Gryczynski, Z.; Fronticelli, C.; Tenenholz, T.; Bucci, E. Effect of disordered hemes on energy transfer rates between tryptophans and heme in myoglobin. Biophys. J. 1993, 65, 1951–1958. [Google Scholar]
- Gryczynski, Z.; Gryczynski, I.; Lakowicz, J.R. Basics of fluorescence and FRET. In Molecular Imaging; Elsevier: Amsterdam, The Netherlands, 2005; pp. 21–56. [Google Scholar]
- Hell, S.W. Toward fluorescence nanoscopy. Nat. Biotechnol. 2003, 21, 1347–1355. [Google Scholar]
- Rittweger, E.; Han, K.Y.; Irvine, S.E.; Eggeling, C.; Hell, S.W. STED microscopy reveals crystal colour centres with nanometric resolution. Nat. Photonics 2009, 3, 144–147. [Google Scholar]
- Maliwal, B.P.; Raut, S.; Fudala, R.; D’Auria, S.; Marzullo, V.M.; Luini, A.; Gryczynski, I.; Gryczynski, Z. Extending Förster resonance energy transfer measurements beyond 100 Å using common organic fluorophores: Enhanced transfer in the presence of multiple acceptors. J. Biomed. Opt. 2012, 17, 011006. [Google Scholar]
- Gryczynski, Z.; Lubkowski, J.; Bucci, E. [28] Intrinsic fluorescence of hemoglobins and myoglobins. Methods Enzymol. 1997, 278, 538–569. [Google Scholar]
- Laws, W.R.; Brand, L. Analysis of two-state excited-state reactions. The fluorescence decay of 2-naphthol. J. Phys. Chem. 1979, 83, 795–802. [Google Scholar] [CrossRef]
- Zelent, B.; Vanderkooi, J.M.; Coleman, R.G.; Gryczynski, I.; Gryczynski, Z. Protonation of excited state pyrene-1-carboxylate by phosphate and organic acids in aqueous solution studied by fluorescence spectroscopy. Biophys. J. 2006, 91, 3864–3871. [Google Scholar]
| M) | Total Diameter Size (nm) | Core Size (nm) Approx. | Zeta Potential (mV) | Polydispersity Index |
|---|---|---|---|---|
| 33 | 9.72 ± 0.74 | 3.22 | −4.32 ± 0.718 | 0.336 ± 0.165 |
| 66 | 10.03 ± 1.17 | 3.53 | −11.32 ± 0.58 | 0.256 ± 0.004 |
| 99 | 9.77 ± 0.58 | 3.27 | −10.53 ± 1.02 | 0.328 ± 0.207 |
| 330 | 11.29 ± 0.82 | 4.79 | −11.04 ± 3.70 | 0.290 ± 0.024 |
| A1 [Cnts] | 1 [ns] | A2 [Cnts] | 2 [ns] | Av 1 [ns] | Av 2 [ns] | ||
|---|---|---|---|---|---|---|---|
| Formulation | Ex/Em | ||||||
| Donor Only | 485/570 | 3865.5 | 0.496 | 2196.4 | 1.022 | 0.780 | 0.687 |
| Acceptor Only | 640/820 | 2490.5 | 0.595 | 3988.1 | 0.855 | 0.776 | 0.755 |
| 33 M Acceptor | 485/570 | 4044.1 | 0.354 | 1786.0 | 0.916 | 0.654 | 0.526 |
| 485/820 | 9201.2 | 0.877 | −4100 | 0.240 | 0.965 | 1.388 | |
| 640/820 | 740.0 | 0.788 | --- | --- | 0.788 | 0.788 | |
| 66 M Acceptor | 485/570 | 3936.1 | 0.251 | 959.8 | 0.770 | 0.473 | 0.353 |
| 485/820 | 7944.3 | 0.810 | -2038 | 0.183 | 0.849 | 1.027 | |
| 640/820 | 3790.9 | 0.636 | 2630.3 | 0.901 | 0.767 | 0.744 | |
| 99 M Acceptor | 485/570 | 3168.2 | 0.198 | 78.64 | 0.991 | 0.286 | 0.217 |
| 485/820 | 6958.0 | 0.756 | −2713 | 0.042 | 0.772 | 1.212 | |
| 640/820 | 3277.9 | 0.565 | 3172.4 | 0.839 | 0.727 | 0.699 | |
| 330 M Acceptor | 485/570 | 424510 | 0.009 | 49.73 | 1.069 | 0.024 | 0.009 |
| 485/820 | 15226 | 0.168 | 3880.3 | 0.642 | 0.341 | 0.067 | |
| 640/820 | 18483 | 0.146 | 3896.6 | 0.628 | 0.375 | 0.230 |
| rHDL Formulation | Average Lifetime (ns) Ex485 Em570 | Average Lifetime (ns) Ex485 Em820 | Average Lifetime (ns) Ex640 Em820 |
|---|---|---|---|
| Donor Only | 0.685 | --- | --- |
| Acceptor Only | --- | --- | 0.746 |
| Donor + 66 M Acceptor | 0.447 | 0.947 | 0.762 |
| PBS Resuspension (66 M Acceptor) | 0.485 | 0.952 | 0.805 |
| DMSO Resuspension (66 M Acceptor) | 0.541 | --- | 0.845 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petty, R.M.; Ceresa, L.; Alexander, E.; Pham, D.; Sabnis, N.; Fudala, R.; Lacko, A.G.; Krishnamoorthy, R.R.; Gryczynski, Z.; Gryczynski, I. Fluorescence Resonance Energy Transfer for Drug Loading Assessment in Reconstituted High-Density Lipoprotein Nanoparticles. Int. J. Mol. Sci. 2025, 26, 3276. https://doi.org/10.3390/ijms26073276
Petty RM, Ceresa L, Alexander E, Pham D, Sabnis N, Fudala R, Lacko AG, Krishnamoorthy RR, Gryczynski Z, Gryczynski I. Fluorescence Resonance Energy Transfer for Drug Loading Assessment in Reconstituted High-Density Lipoprotein Nanoparticles. International Journal of Molecular Sciences. 2025; 26(7):3276. https://doi.org/10.3390/ijms26073276
Chicago/Turabian StylePetty, R. Max, Luca Ceresa, Emma Alexander, Danh Pham, Nirupama Sabnis, Rafal Fudala, Andras G. Lacko, Raghu R. Krishnamoorthy, Zygmunt Gryczynski, and Ignacy Gryczynski. 2025. "Fluorescence Resonance Energy Transfer for Drug Loading Assessment in Reconstituted High-Density Lipoprotein Nanoparticles" International Journal of Molecular Sciences 26, no. 7: 3276. https://doi.org/10.3390/ijms26073276
APA StylePetty, R. M., Ceresa, L., Alexander, E., Pham, D., Sabnis, N., Fudala, R., Lacko, A. G., Krishnamoorthy, R. R., Gryczynski, Z., & Gryczynski, I. (2025). Fluorescence Resonance Energy Transfer for Drug Loading Assessment in Reconstituted High-Density Lipoprotein Nanoparticles. International Journal of Molecular Sciences, 26(7), 3276. https://doi.org/10.3390/ijms26073276







