Purinergic Receptor Activation Protects Glomerular Microvasculature from Increased Mechanical Stress in Angiotensin II-Induced Hypertension: A Modeling Study †
Abstract
1. Introduction
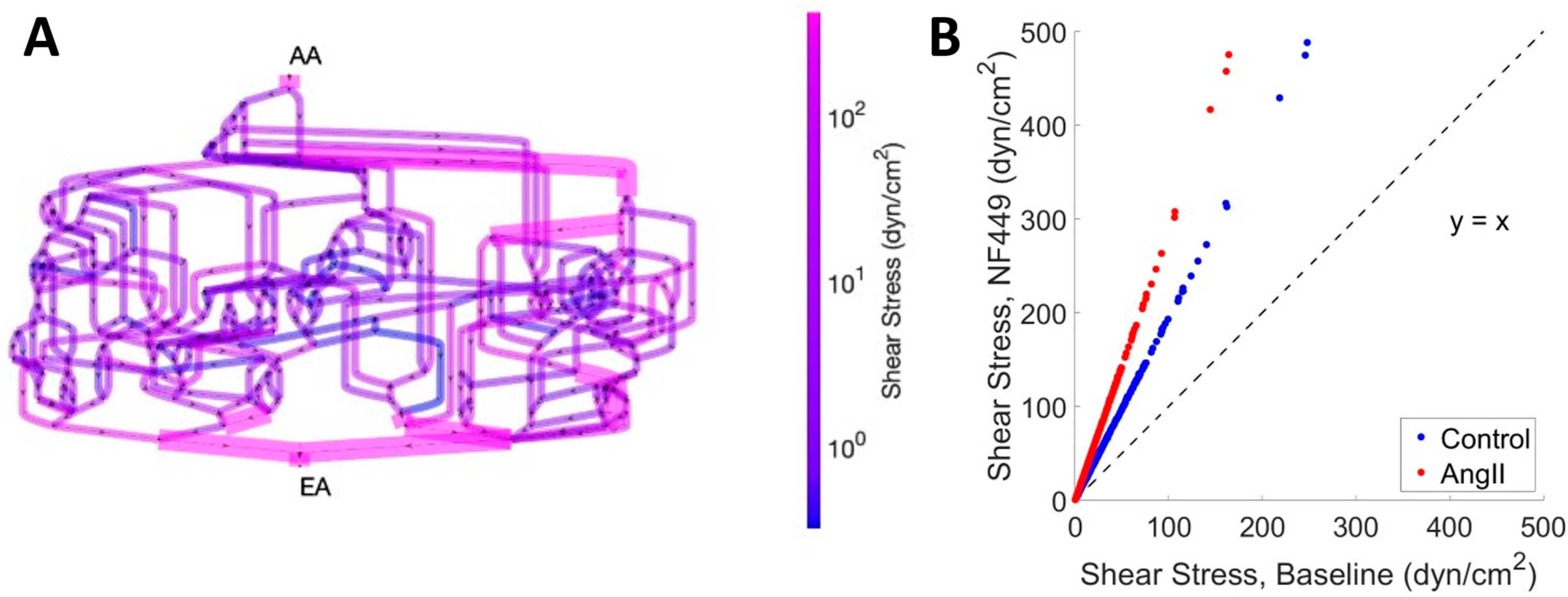
2. Results
3. Discussion
4. Materials and Methods
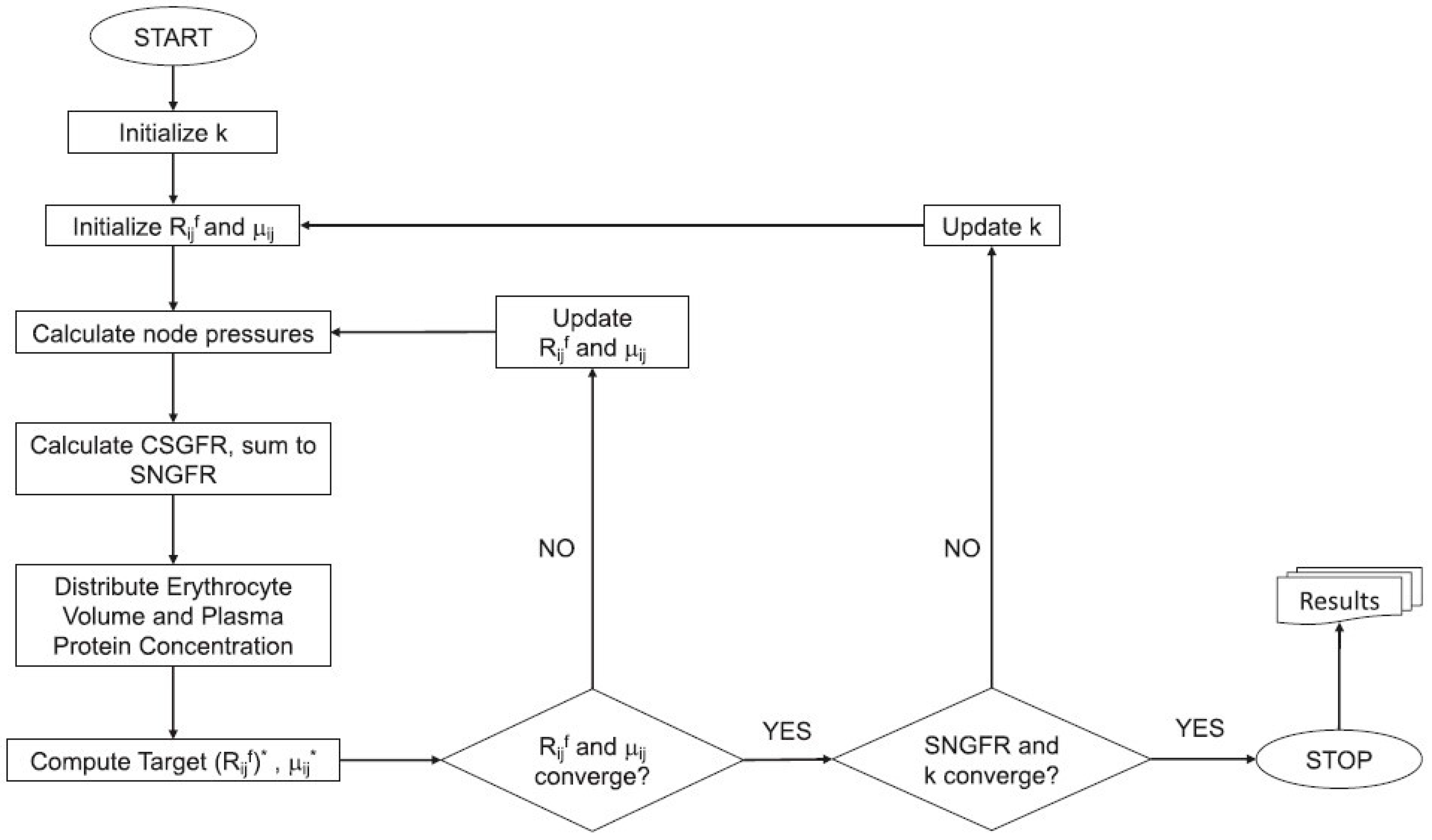
4.1. Model Formulation
| Variable | Reported Units | Symbolic Units (M, T, L) | Conversion to Working Units (µg, s, µm) |
|---|---|---|---|
| Diameter, D | µm | L | 1 µm |
| Length, L | µm | L | 1 µm |
| Pressure, p | mmHg | M T−2 L−1 | 133,322 µg s−2 µm−1 |
| Flow, Q | nL/min | L3 T−1 | 16,666.67 µm3 s−1 |
| Resistance, R | mmHg/nL/min | M T−3 L−4 | 8 µg s−3 µm−4 |
| Shear Stress, τ | dynes/cm2 | M T−2 L−1 | 100 µg s−2 µm−1 |
| Hoop Stress, σ | kPa | M T−2 L−1 | 1,000,000 µg s−2 µm−1 |
| Viscosity, µ | cP | M T−1 L−1 | 1 µg s−1 µm−1 |
| CSGFR | nL/min | L3 T−1 | 16,666.67 µm3 s−1 |
| Hydraulic Conductivity, k | nL/min/mmHg/ µm2 | M−1 T3 L2 | 0.125 µg−1 s3 µm2 |
4.2. Simulating AA and EA Purinergic Receptor Blockade
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeng, X.; Zeng, Q.; Zhou, L.; Zhu, H.; Luo, J. Prevalence of Chronic Kidney Disease Among US Adults With Hypertension, 1999 to 2018. Hypertension 2023, 80, 2149–2158. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Zou, M.; Young, C.A.; Zhu, W.; Chiu, H.C.; Jin, G.; Tian, L. Disease Burden of Chronic Kidney Disease Due to Hypertension From 1990 to 2019: A Global Analysis. Front. Med. 2021, 8, 690487. [Google Scholar] [CrossRef] [PubMed]
- Navar, L.G. Intrarenal renin–angiotensin system in regulation of glomerular function. Curr. Opin. Nephrol. Hypertens. 2014, 23, 38–45. [Google Scholar] [CrossRef] [PubMed]
- Sorensen, C.M.; Cupples, W.A. Myoendothelial communication in the renal vasculature and the impact of drugs used clinically to treat hypertension. Curr. Opin. Pharmacol. 2019, 45, 49–56. [Google Scholar] [CrossRef]
- Inscho, E.W.; Cook, A.K. P2 receptor-mediated afferent arteriolar vasoconstriction during calcium blockade. Am. J. Physiol. Ren. Physiol. 2002, 282, F245–F255. [Google Scholar] [CrossRef] [PubMed]
- Inscho, E.W.; Cook, A.K.; Imig, J.D.; Vial, C.; Evans, R.J. Physiological role for P2X1 receptors in renal microvascular autoregulatory behavior. J. Clin. Invest. 2003, 112, 1895–1905. [Google Scholar] [CrossRef] [PubMed]
- Inscho, E.W.; LeBlanc, E.A.; Pham, B.T.; White, S.M.; Imig, J.D. Purinoceptor-mediated calcium signaling in preglomerular smooth muscle cells. Hypertension 1999, 33, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Franco, M.; Bautista, R.; Tapia, E.; Soto, V.; Santamaria, J.; Osorio, H.; Pacheco, U.; Sanchez-Lozada, L.G.; Kobori, H.; Navar, L.G. Contribution of renal purinergic receptors to renal vasoconstriction in angiotensin II-induced hypertensive rats. Am. J. Physiol. Ren. Physiol. 2011, 300, F1301–F1309. [Google Scholar] [CrossRef]
- Franco, M.; Bautista-Perez, R.; Cano-Martinez, A.; Pacheco, U.; Santamaria, J.; Del Valle Mondragon, L.; Perez-Mendez, O.; Navar, L.G. Physiopathological implications of P2X(1) and P2X(7) receptors in regulation of glomerular hemodynamics in angiotensin II-induced hypertension. Am. J. Physiol. Ren. Physiol. 2017, 313, F9–F19. [Google Scholar] [CrossRef]
- Kulthinee, S.; Shao, W.; Franco, M.; Navar, L.G. Purinergic P2X1receptor, purinergic P2X7receptor, and angiotensin II type 1 receptor interactions in the regulation of renal afferent arterioles in angiotensin II-dependent hypertension. Am. J. Physiol. Ren. Physiol. 2020, 318, F1400–F1408. [Google Scholar] [CrossRef]
- Oken, A.C.; Krishnamurthy, I.; Savage, J.C.; Lisi, N.E.; Godsey, M.H.; Mansoor, S.E. Molecular Pharmacology of P2X Receptors: Exploring Druggable Domains Revealed by Structural Biology. Front. Pharmacol. 2022, 13, 925880. [Google Scholar] [CrossRef]
- Bailey, M.A.; Unwin, R.J.; Shirley, D.G. P2X receptors and kidney function. Wiley Interdiscip. Rev. Membr. Transp. Signal. 2012, 1, 503–511. [Google Scholar] [CrossRef]
- Endlich, K.; Kliewe, F.; Endlich, N. Stressed podocytes-mechanical forces, sensors, signaling and response. Pflug. Arch. 2017, 469, 937–949. [Google Scholar] [CrossRef] [PubMed]
- Endlich, N.; Endlich, K. The challenge and response of podocytes to glomerular hypertension. Semin. Nephrol. 2012, 32, 327–341. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, C.; Endlich, N.; Kriz, W.; Endlich, K. Podocytes are sensitive to fluid shear stress in vitro. Am. J. Physiol. Ren. Physiol. 2006, 291, F856–F865. [Google Scholar] [CrossRef] [PubMed]
- Fuhrmann, A.; Pritz, B.; Endlich, K.; Kriz, W. Numerical Flow Simulations of the Shear Stress Forces Arising in Filtration Slits during Glomerular Filtration in Rat Kidney. J. Am. Soc. Nephrol. 2025, 36, 219–230. [Google Scholar] [CrossRef] [PubMed]
- Kriz, W.; Lemley, K.V. A potential role for mechanical forces in the detachment of podocytes and the progression of CKD. J. Am. Soc. Nephrol. 2015, 26, 258–269. [Google Scholar] [CrossRef] [PubMed]
- Kriz, W.; Lemley, K.V. Mechanical challenges to the glomerular filtration barrier: Adaptations and pathway to sclerosis. Pediatr. Nephrol. 2017, 32, 405–417. [Google Scholar] [CrossRef] [PubMed]
- Petrosyan, A.; Cravedi, P.; Villani, V.; Angeletti, A.; Manrique, J.; Renieri, A.; De Filippo, R.E.; Perin, L.; Da Sacco, S. A glomerulus-on-a-chip to recapitulate the human glomerular filtration barrier. Nat. Commun. 2019, 10, 3656. [Google Scholar] [CrossRef]
- Musah, S.; Mammoto, A.; Ferrante, T.C.; Jeanty, S.S.F.; Hirano-Kobayashi, M.; Mammoto, T.; Roberts, K.; Chung, S.; Novak, R.; Ingram, M.; et al. Mature induced-pluripotent-stem-cell-derived human podocytes reconstitute kidney glomerular-capillary-wall function on a chip. Nat. Biomed. Eng. 2017, 1, 0069. [Google Scholar] [CrossRef]
- Richfield, O.; Cortez, R.; Navar, L.G. Simulations of Glomerular Shear and Hoop Stresses in Diabetes, Hypertension, and Reduced Renal Mass using a Network Model of a Rat Glomerulus. Physiol. Rep. 2020, 8, e14577. [Google Scholar] [CrossRef]
- Richfield, O.; Cortez, R.; Navar, L.G. Modeling the interaction between tubuloglomerular feedback and myogenic mechanisms in the control of glomerular mechanics. Front. Physiol. 2024, 15, 1410764. [Google Scholar] [CrossRef] [PubMed]
- Richfield, O.; Cortez, R.; Navar, L.G. Simulations of increased glomerular capillary wall strain in the 5/6-nephrectomized rat. Microcirculation 2021, 28, e12721. [Google Scholar] [CrossRef]
- Fogo, A.B. Causes and pathogenesis of focal segmental glomerulosclerosis. Nat. Rev. Nephrol. 2015, 11, 76–87. [Google Scholar] [CrossRef]
- Lim, B.J.; Yang, J.W.; Do, W.S.; Fogo, A.B. Pathogenesis of Focal Segmental Glomerulosclerosis. J. Pathol. Transl. Med. 2016, 50, 405–410. [Google Scholar] [CrossRef] [PubMed]
- Dessapt, C.; Baradez, M.O.; Hayward, A.; Dei Cas, A.; Thomas, S.M.; Viberti, G.; Gnudi, L. Mechanical forces and TGFbeta1 reduce podocyte adhesion through alpha3beta1 integrin downregulation. Nephrol. Dial. Transpl. 2009, 24, 2645–2655. [Google Scholar] [CrossRef] [PubMed]
- Ohno, M.; Cooke, J.P.; Dzau, V.J.; Gibbons, G.H. Fluid shear stress induces endothelial transforming growth factor beta-1 transcription and production. Modulation by potassium channel blockade. J. Clin. Investig. 1995, 95, 1363–1369. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, B.K.; Moon, K.C.; Hong, H.K.; Lee, H.S. Activation of the TGF-beta/Smad signaling pathway in focal segmental glomerulosclerosis. Kidney Int. 2003, 64, 1715–1721. [Google Scholar] [CrossRef]
- Graciano, M.L.; Nishiyama, A.; Jackson, K.; Seth, D.M.; Ortiz, R.M.; Prieto-Carrasquero, M.C.; Kobori, H.; Navar, L.G. Purinergic receptors contribute to early mesangial cell transformation and renal vessel hypertrophy during angiotensin II-induced hypertension. Am. J. Physiol. Ren. Physiol. 2008, 294, F161–F169. [Google Scholar] [CrossRef] [PubMed]
- Vargas-Martínez, E.M.; Gómez-Coronado, K.S.; Espinosa-Luna, R.; Valdez-Morales, E.E.; Barrios-García, T.; Barajas-Espinosa, A.; Ochoa-Cortes, F.; Montaño, L.M.; Barajas-López, C.; Guerrero-Alba, R. Functional expression of P2X1, P2X4 and P2X7 purinergic receptors in human monocyte-derived macrophages. Eur. J. Pharmacol. 2020, 888, 173460. [Google Scholar] [CrossRef]
- Bautista-Pérez, R.; Pérez-Méndez, O.; Cano-Martínez, A.; Pacheco, U.; Santamaría, J.; Rodríguez-Iturbe, F.R.B.; Navar, L.G.; Franco, M. The Role of P2X7 Purinergic Receptors in the Renal Inflammation Associated with Angiotensin II-induced Hypertension. Int. J. Mol. Sci. 2020, 21, 4041. [Google Scholar] [CrossRef] [PubMed]
- Ciocanel, M.-V.; Stepien, T.L.; Sgouralis, I.; Layton, A.T. A Multicellular Vascular Model of the Renal Myogenic Response. Processes 2018, 6, 89. [Google Scholar] [CrossRef]
- Sgouralis, I.; Evans, R.G.; Gardiner, B.S.; Smith, J.A.; Fry, B.C.; Layton, A.T. Renal hemodynamics, function, and oxygenation during cardiac surgery performed on cardiopulmonary bypass: A modeling study. Physiol. Rep. 2015, 3, e12260. [Google Scholar] [CrossRef] [PubMed]
- Sgouralis, I.; Layton, A.T. Autoregulation and conduction of vasomotor responses in a mathematical model of the rat afferent arteriole. Am. J. Physiol. Ren. Physiol. 2012, 303, F229–F239. [Google Scholar] [CrossRef]
- Sgouralis, I.; Layton, A.T. Theoretical assessment of renal autoregulatory mechanisms. Am. J. Physiol. Ren. Physiol. 2014, 306, F1357–F1371. [Google Scholar] [CrossRef] [PubMed]
- Sgouralis, I.; Layton, A.T. Mathematical modeling of renal hemodynamics in physiology and pathophysiology. Math. Biosci. 2015, 264, 8–20. [Google Scholar] [CrossRef]
- Sgouralis, I.; Maroulas, V.; Layton, A.T. Transfer Function Analysis of Dynamic Blood Flow Control in the Rat Kidney. Bull. Math. Biol. 2016, 78, 923–960. [Google Scholar] [CrossRef] [PubMed]
- Soni, S.; Lukhey, M.S.; Thawkar, B.S.; Chintamaneni, M.; Kaur, G.; Joshi, H.; Ramniwas, S.; Tuli, H.S. A current review on P2X7 receptor antagonist patents in the treatment of neuroinflammatory disorders: A patent review on antagonists. Naunyn Schmiedebergs Arch. Pharmacol. 2024, 397, 4643–4656. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Xie, N.; Illes, P.; Di Virgilio, F.; Ulrich, H.; Semyanov, A.; Verkhratsky, A.; Sperlagh, B.; Yu, S.-G.; Huang, C.; et al. From purines to purinergic signalling: Molecular functions and human diseases. Signal Transduct. Target. Ther. 2021, 6, 162. [Google Scholar] [CrossRef] [PubMed]
- Remuzzi, A.; Brenner, B.M.; Pata, V.; Tebaldi, G.; Mariano, R.; Belloro, A.; Remuzzi, G. Three-dimensional reconstructed glomerular capillary network: Blood flow distribution and local filtration. Am. J. Physiol. Ren. Physiol. 1992, 263, F562–F572. [Google Scholar] [CrossRef]
- Shea, S.M. Glomerular hemodynamics and vascular structure. The pattern and dimensions of a single rat glomerular capillary network reconstructed from Ultrathin sections. Microvasc. Res. 1979, 18, 129–143. [Google Scholar] [CrossRef] [PubMed]
- Papenfuss, H.D.; Gross, J.F. Analytic study of the influence of capillary pressure drop and permeability on glomerular ultrafiltration. Microvasc. Res. 1978, 16, 59–72. [Google Scholar] [CrossRef] [PubMed]
- Pries, A.R.; Secomb, T.W.; Gessner, T.; Sperandio, M.B.; Gross, J.F.; Gaehtgens, P. Resistance to blood flow in microvessels in vivo. Circ. Res. 1994, 75, 904–915. [Google Scholar] [CrossRef] [PubMed]
- Pries, A.R.; Secomb, T.W.; Gaehtgens, P. Biophysical aspects of blood flow in the microvasculature. Cardiovasc. Res. 1996, 32, 654–667. [Google Scholar] [CrossRef]
- Richfield, O.; Cortez, R.; Franco, M.; Navar, L.G.G. Abstract P006: Purinergic Receptor Activation Protects Glomerular Microvasculature From Increased Mechanical Stress In Angiotensin Ii-induced Hypertension: A Modeling Study. Hypertension 2020, 76 (Suppl. S1), AP006. [Google Scholar] [CrossRef]
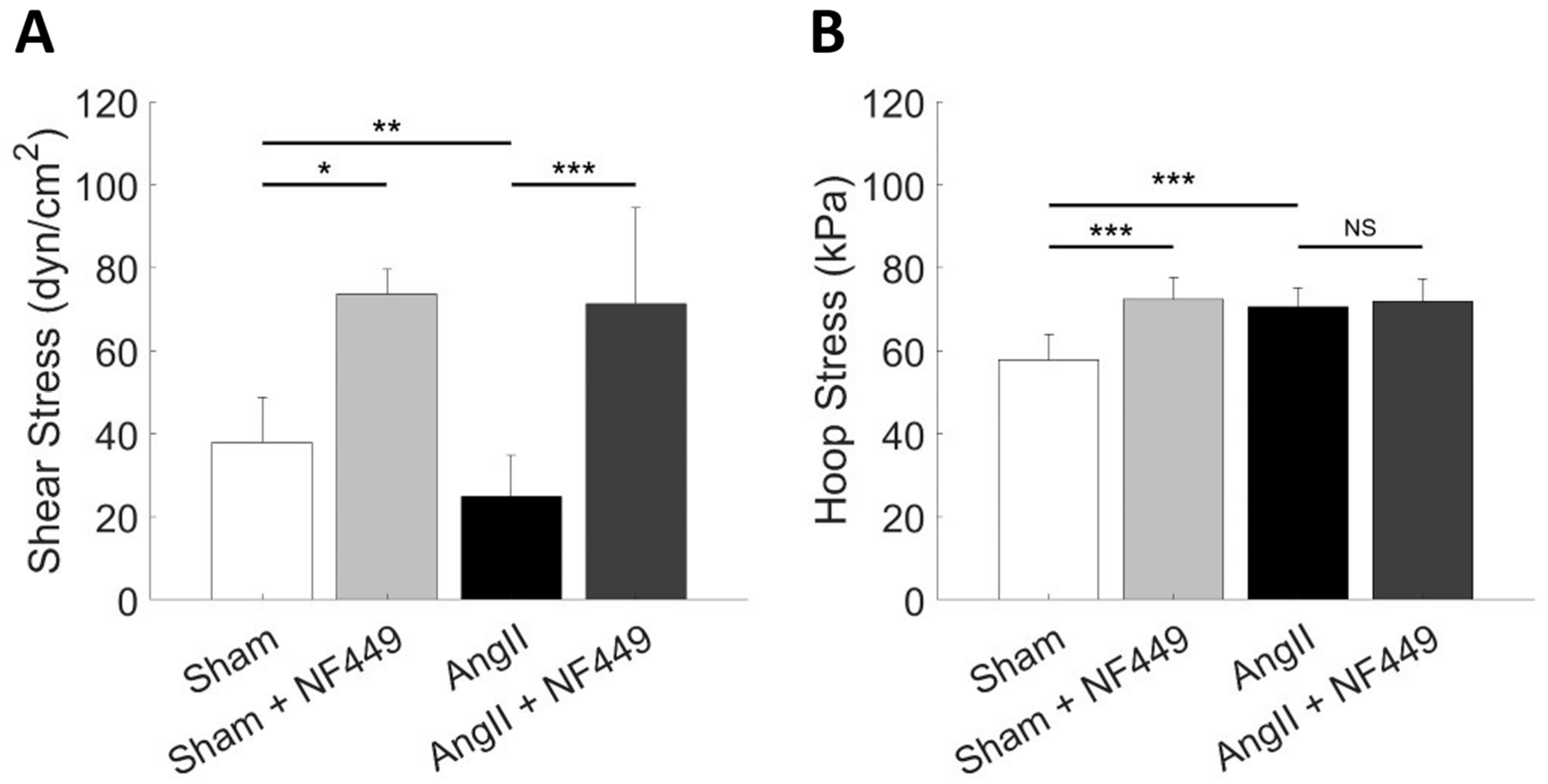
| Condition | PGC (mmHg) | QA (nL/min) | SNGFR (nL/min) | MAP (mmHg) | RA (mmHg min/nL) | RE (mmHg min/nL) | k (×10−5 nL/min/µm2/mmHg) |
|---|---|---|---|---|---|---|---|
| Sham | 46.9 | 125.8 | 38.8 | 119.7 | 2.9 | 1.3 | 1.83 |
| Sham + NF449 | 56.2 | 215.6 | 53.7 | 122.8 | 1.5 | 0.9 | 1.82 |
| AngII | 55.8 | 76.1 | 21.3 | 162.8 | 6.6 | 3.0 | 0.71 |
| AngII + NF449 | 56.6 | 213.1 | 48.8 | 171.6 | 2.5 | 1.0 | 1.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richfield, O.; Cortez, R.; Kulthinee, S.; Franco, M.; Navar, L.G. Purinergic Receptor Activation Protects Glomerular Microvasculature from Increased Mechanical Stress in Angiotensin II-Induced Hypertension: A Modeling Study. Int. J. Mol. Sci. 2025, 26, 1928. https://doi.org/10.3390/ijms26051928
Richfield O, Cortez R, Kulthinee S, Franco M, Navar LG. Purinergic Receptor Activation Protects Glomerular Microvasculature from Increased Mechanical Stress in Angiotensin II-Induced Hypertension: A Modeling Study. International Journal of Molecular Sciences. 2025; 26(5):1928. https://doi.org/10.3390/ijms26051928
Chicago/Turabian StyleRichfield, Owen, Ricardo Cortez, Supaporn Kulthinee, Martha Franco, and L. Gabriel Navar. 2025. "Purinergic Receptor Activation Protects Glomerular Microvasculature from Increased Mechanical Stress in Angiotensin II-Induced Hypertension: A Modeling Study" International Journal of Molecular Sciences 26, no. 5: 1928. https://doi.org/10.3390/ijms26051928
APA StyleRichfield, O., Cortez, R., Kulthinee, S., Franco, M., & Navar, L. G. (2025). Purinergic Receptor Activation Protects Glomerular Microvasculature from Increased Mechanical Stress in Angiotensin II-Induced Hypertension: A Modeling Study. International Journal of Molecular Sciences, 26(5), 1928. https://doi.org/10.3390/ijms26051928







