Localization of Potential Energy in Hydrogen Bonds of the ATXN2 Gene
Abstract
1. Introduction
2. Results and Discussion
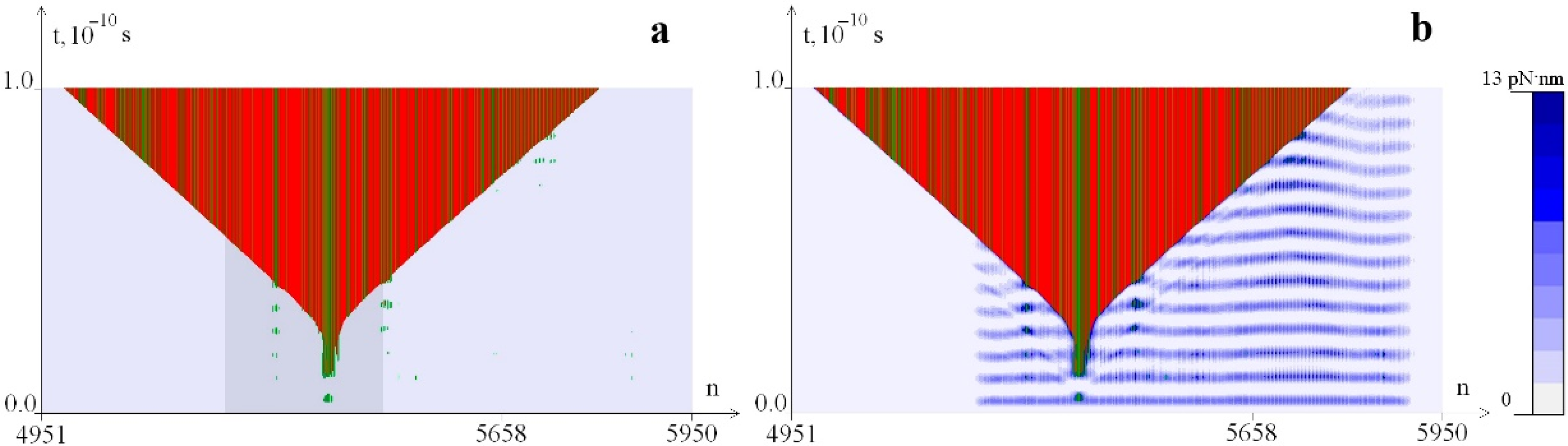
2.1. Distribution of Potential Energy of Hydrogen Bonds with a Change in the Magnitude of the Torque M0
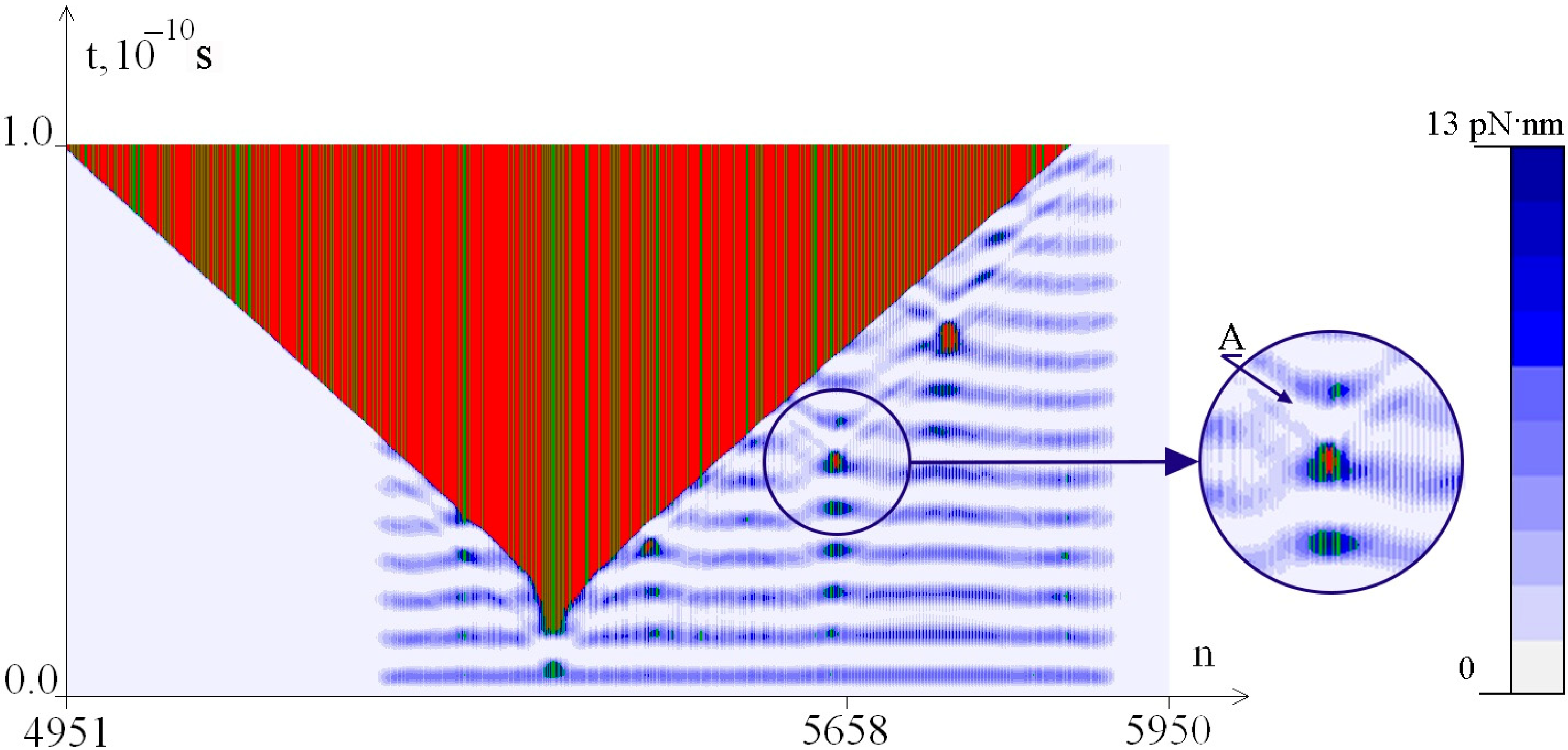
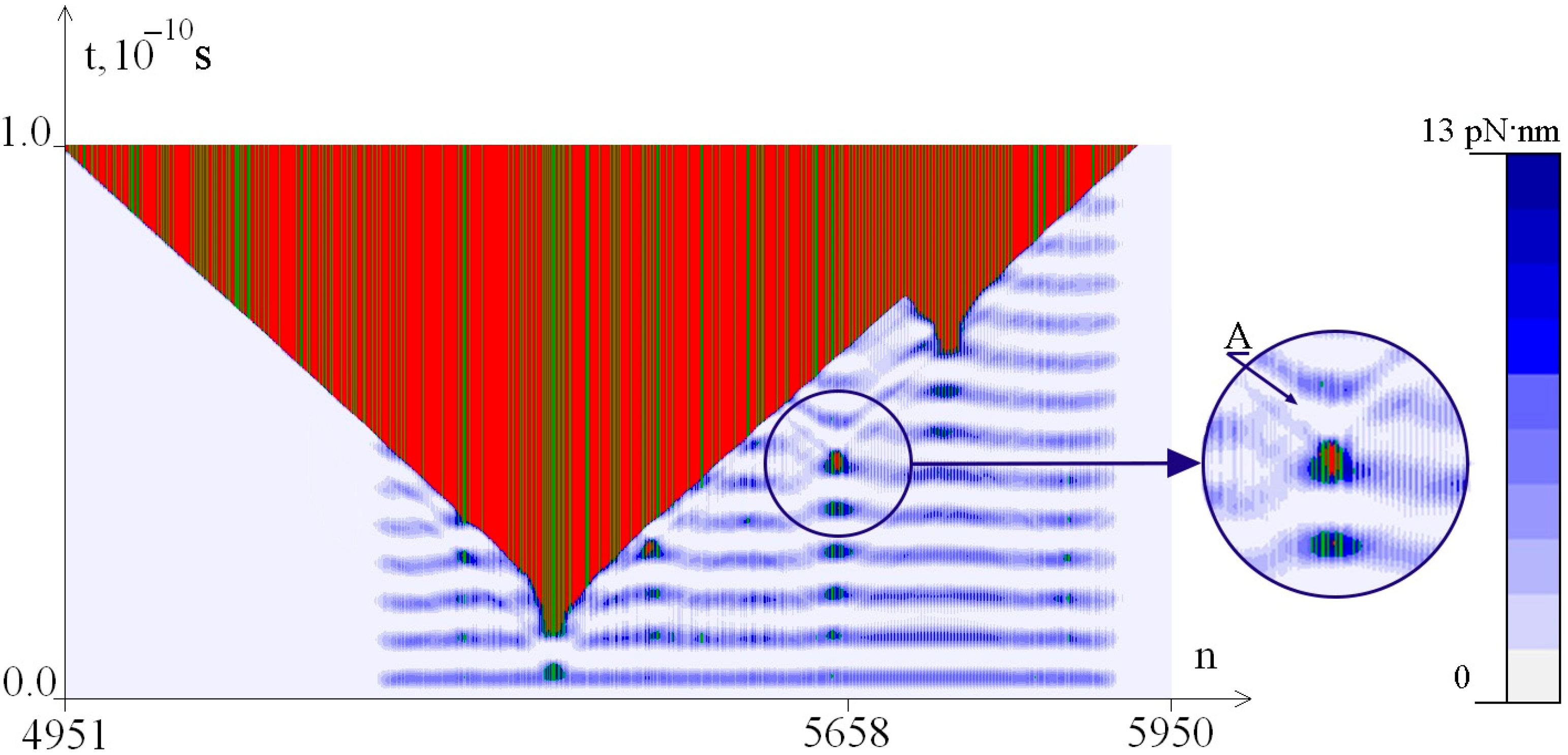
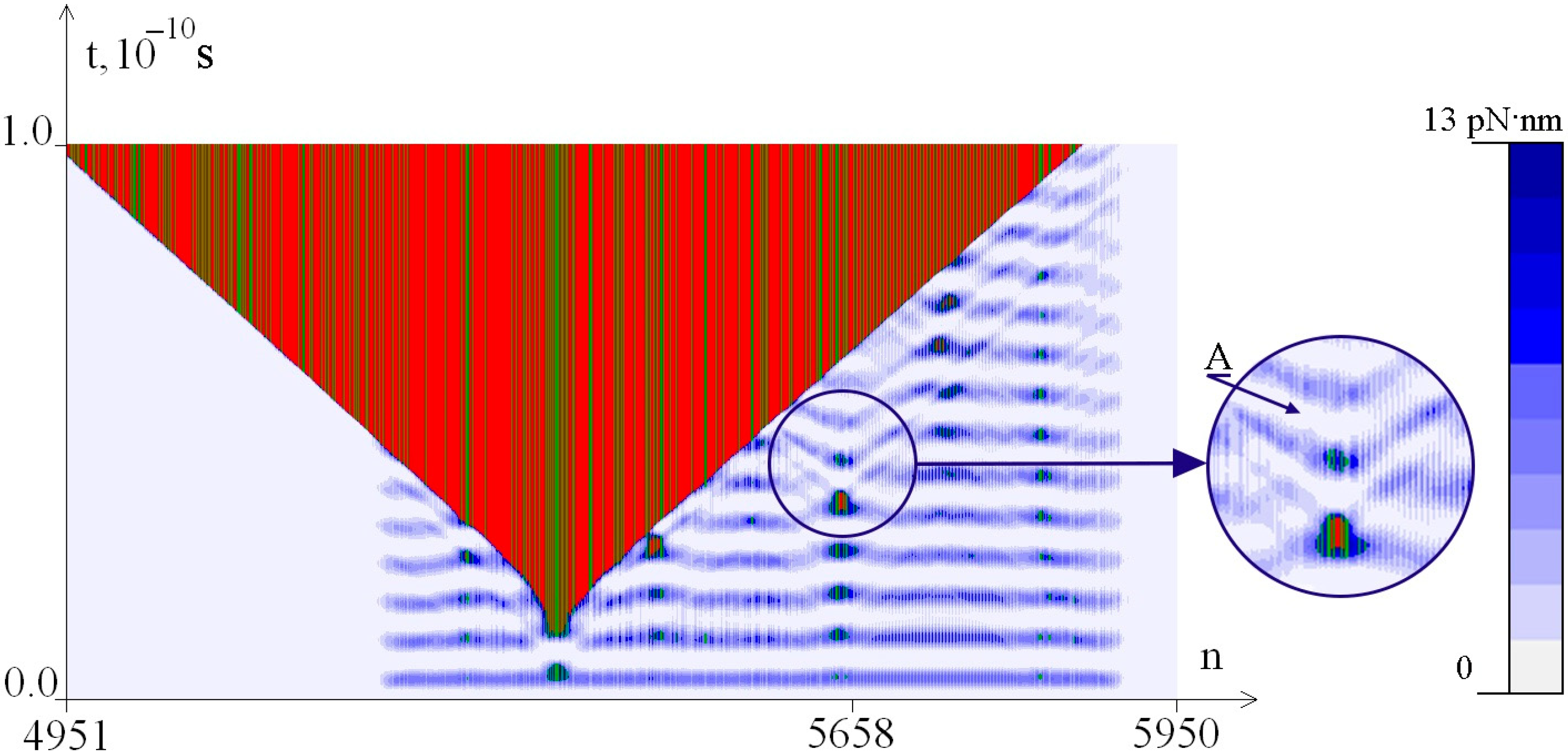
2.2. The Influence of the Environment Viscosity on the Distribution of Hydrogen Bonds Potential Energy
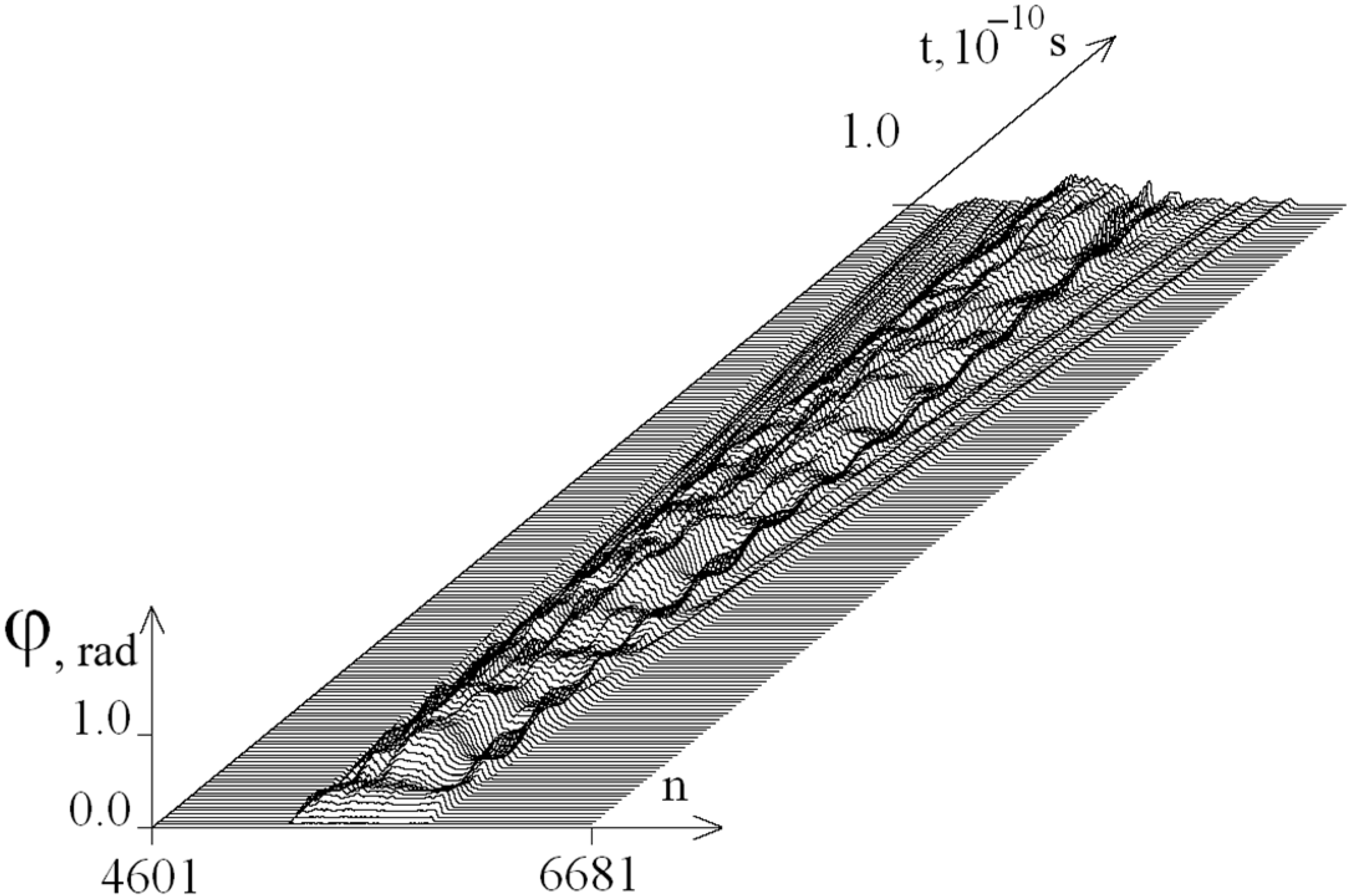
2.3. The Influence of CAA Interruptions on the Distribution of Hydrogen Bonds Potential Energy
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Costa, R.G.; Conceição, A.; Matos, C.A.; Nóbrega, C. The polyglutamine protein ATXN2: From its molecular functions to its involvement in disease. Cell Death Dis. 2024, 15, 415. [Google Scholar] [CrossRef] [PubMed]
- Carmo-Silva, S.; Nobrega, C.; Pereira de Almeida, L.; Cavadas, C. Unraveling the role of ataxin-2 in metabolism. Trends Endocrinol. Metab. 2017, 28, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Sonakar, A.K.; Shamim, U.; Srivastava, M.P.; Faruq, M.; Srivastava, A.K. SCA2 in the Indian population: Unified haplotype and variable phenotypic patterns in a large case series. Parkinsonism Relat. Disord. 2021, 89, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Borrego-Hernández, D.; Vázquez-Costa, J.F.; Domínguez-Rubio, R.; Expósito-Blázquez, L.; Aller, E.; Padró-Miquel, A.; García-Casanova, P.; Colomina, M.J.; Martín-Arriscado, C.; Osta, R.; et al. Intermediate Repeat Expansion in the ATXN2 Gene as a Risk Factor in the ALS and FTD Spanish Population. Biomedicines 2024, 12, 356. [Google Scholar] [CrossRef]
- Iyer, R.R.; Pluciennik, A.; Napierala, M.; Wells, R.D. DNA triplet repeat expansion and mismatch repair. Annu. Rev. Biochem. 2015, 84, 199–226. [Google Scholar] [CrossRef]
- Polleys, E.J.; Del Priore, I.; Haber, J.E.; Freudenreich, C.H. Structure-forming CAG/CTG repeats interfere with gap repair to cause repeat expansions and chromosome breaks. Nat. Commun. 2023, 14, 2469. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, Z.; Hou, X.; Chen, Z.; Shen, L.; Xia, K.; Tang, B.; Jiang, H.; Wang, J. Effect of CAG repeats on the age at onset of patients with spinocerebellar ataxia type 2 in China. J. Cent. South Univ. Med. Sci. 2021, 46, 793–799. [Google Scholar] [CrossRef]
- Hu, T.; Morten, M.J.; Magennis, S.W. Conformational and migrational dynamics of slipped-strand DNA three-way junctions containing trinucleotide repeats. Nat. Commun. 2021, 12, 204. [Google Scholar] [CrossRef]
- Glass, J.D.; Dewan, R.; Ding, J.; Gibbs, J.R.; Dalgard, C.; Keagle, P.J.; Shankaracharya García-Redondo, A.; Traynor, B.J.; Chia, R.; Landers, J.E. ATXN2 intermediate expansions in amyotrophic lateral sclerosis. Brain 2022, 145, 2671–2676. [Google Scholar] [CrossRef]
- Pan, F.; Zhang, Y.; Xu, P.; Man, V.H.; Roland, C.; Weninger, K.; Sagui, C. Molecular conformations and dynamics of nucleotide repeats associated with neurodegenerative diseases: Double helices and CAG hairpin loops. Comput. Struct. Biotechnol. J. 2021, 19, 2819–2832. [Google Scholar] [CrossRef] [PubMed]
- Magaña, J.J.; Tapia-Guerrero, Y.S.; Velázquez-Pérez, L.; Cerecedo-Zapata, C.M.; Maldonado-Rodríguez, M.; Jano-Ito, J.S.; Leyva-García, N.; González-Piña, R.; Martínez-Cruz, E.; Hernández-Hernández, O.; et al. Analysis of CAG repeats in five SCA loci in Mexican population: Epidemiological evidence of a SCA7 founder effect. Clin. Genet. 2014, 85, 159–165. [Google Scholar] [CrossRef]
- Velázquez-Pérez, L.; Tünnerhoff, J.; Rodríguez-Labrada, R.; Torres-Vega, R.; Ruiz-Gonzalez, Y.; Belardinelli, P.; Medrano-Montero, J.; Canales-Ochoa, N.; González-Zaldivar, Y.; Vazquez-Mojena, Y.; et al. Early corticospinal tract damage in prodromal SCA2 revealed by EEG-EMG and EMG-EMG coherence. Clin. Neurophysiol. 2017, 128, 2493–2502. [Google Scholar] [CrossRef]
- Yokoshi, M.; Li, Q.; Yamamoto, M.; Okada, H.; Suzuki, Y.; Kawahara, Y. Direct binding of Ataxin-2 to distinct elements in 3’ UTRs promotes mRNA stability and protein expression. Mol. Cell 2014, 55, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Orr, H.T.; Zoghbi, H.Y. Trinucleotide repeat disorders. Annu. Rev. Neurosci. 2007, 30, 575–621. [Google Scholar] [CrossRef] [PubMed]
- Choudhry, S.; Mukerji, M.; Srivastava, A.K.; Jain, S.; Brahmachari, S.K. CAG repeat instability at SCA2 locus: Anchoring CAA interruptions and linked single nucleotide polymorphisms. Hum. Mol. Genet. 2001, 10, 2437–2446. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Labrada, R.; Ortega-Sanchez, R.; Hernández Casaña, P.; Santos Morales, O.; Padrón-Estupiñan, M.D.C.; Batista-Nuñez, M.; Jiménez Rodríguez, D.; Canales-Ochoa, N.; Peña Acosta, A.; Medrano Montero, J.; et al. Erythropoietin in Spinocerebellar Ataxia Type 2: Feasibility and Proof-of-Principle Issues from a Randomized Controlled Study. Mov. Disord. 2022, 37, 1516–1525. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Liu, C.; Shen, L.; Dai, H.; Pan, Q.; Jing, L.; Ouyang, S.; Xia, J. Frequency of SCA1, SCA2, SCA3/MJD, SCA6, SCA7, and DRPLA CAG trinucleotide repeat expansion in patients with hereditary spinocerebellar ataxia from Chinese kindreds. Arch. Neurol. 2000, 57, 540–544. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Mojena, Y.; Rodríguez-Córdova, Y.; Dominguez-Barrios, Y.; León-Arcia, K.; Miranda-Becerra, D.; Gonzalez-Zaldivar, Y.; Guerra-Bustillos, G.; Ziemann, U.; Auburger, G.; Rodríguez-Labrada, R.; et al. Peripheral Inflammation Links with the Severity of Clinical Phenotype in Spinocerebellar Ataxia 2. Mov. Disord. 2023, 38, 880–885. [Google Scholar] [CrossRef]
- Wang, J.L.; Xiao, B.; Cui, X.X.; Guo, J.F.; Lei, L.F.; Song, X.W.; Shen, L.; Jiang, H.; Yan, X.X.; Pan, Q.; et al. Analysis of SCA2 and SCA3/MJD repeats in Parkinson’s disease in mainland China: Genetic, clinical, and positron emission tomography findings. Mov. Disord. 2009, 24, 2007–2011. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.; Li, W.; Liu, P.; Liu, Z.; Yuan, Y.; Ni, J.; Shen, L.; Tang, B.; Wang, J. The Clinical and Polynucleotide Repeat Expansion Analysis of ATXN2, NOP56, AR and C9orf72 in Patients With ALS From Mainland China. Front. Neurol. 2022, 3, 811202. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Zhu, Y.; Chen-Plotkin, A.S.; Clay-Falcone, D.; McCluskey, L.; Elman, L.; Kalb, R.G.; Trojanowski, J.Q.; Lee, V.M.; Van Deerlin, V.M.; et al. PolyQ repeat expansions in ATXN2 associated with ALS are CAA interrupted repeats. PLoS ONE 2011, 6, e17951. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yuan, Y.; Wang, M.; Ni, J.; Li, W.; Huang, L.; Hu, Y.; Liu, P.; Hou, X.; Hou, X.; et al. Mutation spectrum of amyotrophic lateral sclerosis in Central South China. Neurobiol. Aging 2021, 107, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Salmon, K.; Ross, J.P.; Bertone, V.; Gobbo, M.; Anoja, N.; Karamchandani, J.; Dion, P.A.; Rouleau, G.A.; Genge, A. The value of testing for ATXN2 intermediate repeat expansions in routine clinical practice for amyotrophic lateral sclerosis. Eur. J. Hum. Genet. 2022, 30, 1205–1207. [Google Scholar] [CrossRef]
- Scoles, D.R.; Gandelman, M.; Paul, S.; Dexheimer, T.; Dansithong, W.; Figueroa, K.P.; Pflieger, L.T.; Redlin, S.; Kales, S.C.; Sun, H.; et al. A quantitative high-throughput screen identifies compounds that lower expression of the SCA2-and ALS-associated gene ATXN2. J. Biol. Chem. 2022, 298, 102228. [Google Scholar] [CrossRef] [PubMed]
- Monte, T.L.; Reckziegel, E.D.R.; Augustin, M.C.; Locks-Coelho, L.D.; Santos, A.S.P.; Furtado, G.V.; de Mattos, E.P.; Pedroso, J.L.; Barsottini, O.P.; Vargas, F.R.; et al. The progression rate of spinocerebellar ataxia type 2 changes with stage of disease. Orphanet. J. Rare. Dis. 2018, 13, 20. [Google Scholar] [CrossRef] [PubMed]
- Blazek, A.M.; Meade, G.; Jackson, L.M.; Gavrilova, R.; Stierwalt, J.; Martinez-Thompson, J.M.; Duffy, J.R.; Clark, H.; Machulda, M.M.; Whitwell, J.L.; et al. Progressive Apraxia of Speech as a Manifestation of Spinocerebellar Ataxia 2 Case Report. Neurol. Genet. 2024, 10, e200202. [Google Scholar] [CrossRef] [PubMed]
- Vieira de Sá, R.; Sudria-Lopez, E.; Cañizares Luna, M.; Harschnitz, O.; van den Heuvel, D.M.A.; Kling, S.; Vonk, D.; Westeneng, H.J.; Karst, H.; Bloemenkamp, L.; et al. ATAXIN-2 intermediate-length polyglutamine expansions elicit ALS-associated metabolic and immune phenotypes. Nat. Commun. 2024, 15, 7484. [Google Scholar] [CrossRef] [PubMed]
- Ghahremani Nezhad, H.; Franklin, J.P.; Alix, J.J.P.; Moll, T.; Pattrick, M.; Cooper-Knock, J.; Shanmugarajah, P.; Beauchamp, N.J.; Hadjivissiliou, M.; Paling, D.; et al. Simultaneous ALS and SCA2 associated with an intermediate-length ATXN2 CAG-repeat expansion. Amyotroph. Lateral Scler. Front. Degener. 2021, 22, 579–582. [Google Scholar] [CrossRef]
- Charles, P.; Camuzat, A.; Benammar, N.; Sellal, F.; Destée, A.; Bonnet, A.M.; Lesage, S.; Le Ber, I.; Stevanin, G.; Dürr, A.; et al. French Parkinson’s Disease Genetic Study Group. Are interrupted SCA2 CAG repeat expansions responsible for parkinsonism? Neurology 2007, 69, 1970–1975. [Google Scholar] [CrossRef] [PubMed]
- Tan, D.; Wei, C.; Chen, Z.; Huang, Y.; Deng, J.; Li, J.; Liu, Y.; Bao, X.; Xu, J.; Hu, Z.; et al. CAG Repeat Expansion in THAP11 Is Associated with a Novel Spinocerebellar Ataxia. Mov. Disord. 2023, 38, 1282–1293. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, V.; Conti, M.; Bovenzi, R.; Cerroni, R.; Pierantozzi, M.; Mercuri, N.B.; Stefani, A. Rare association between spinocerebellar ataxia and amyotrophic lateral sclerosis: A case series. Neurol. Sci. 2024, 45, 4367–4371. [Google Scholar] [CrossRef] [PubMed]
- Niewiadomska-Cimicka, A.; Fievet, L.; Surdyka, M.; Jesion, E.; Keime, C.; Singer, E.; Eisenmann, A.; Kalinowska-Poska, Z.; Nguyen, H.H.P.; Fiszer, A.; et al. AAV-Mediated CAG-Targeting Selectively Reduces Polyglutamine-Expanded Protein and Attenuates Disease Phenotypes in a Spinocerebellar Ataxia Mouse Model. Int. J. Mol. Sci. 2024, 25, 4354. [Google Scholar] [CrossRef]
- Paul, S.; Dansithong, W.; Gandelman, M.; Figueroa, K.P.; Scoles, D.R.; Pulst, S.M. Cerebellar Micro-RNA Profile in a Mouse Model of Spinocerebellar Ataxia Type 2. Neurol. Genet. 2024, 10, e200144. [Google Scholar] [CrossRef] [PubMed]
- Scoles, D.R.; Dansithong, W.; Pflieger, L.T.; Paul, S.; Gandelman, M.; Figueroa, K.P.; Rigo, F.; Bennett, C.F.; Pulst, S.M. ALS-associated genes in SCA2 mouse spinal cord transcriptomes. Hum. Mol. Genet. 2020, 29, 1658–1672. [Google Scholar] [CrossRef] [PubMed]
- Nikitiuk, A.S.; Burmistrova, O.S.; Naimark, O.B. Study of the DNA denaturation based on the Peyrard-Bishop-Dauxois model and recurrence quantification analysis. Rus. J. Biomech. 2022, 26, 34–44. [Google Scholar] [CrossRef]
- Manghi, M.; Destainville, N. Physics of base-pairing dynamics in DNA. Phys. Rep. 2016, 631, 1–41. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Zakarya, M.; Nisar Sooppy, K.; Abdel-Aty, A.H. Dynamics and stability analysis of nonlinear DNA molecules: Insights from the Peyrard-Bishop model. AIMS Math. 2024, 9, 23449–23467. [Google Scholar] [CrossRef]
- Tantawy, M.; Abdel-Gawad, H.I. Dynamics of molecules in torsional DNA exposed to microwave and possible impact on its deformation: Stability analysis. Eur. Phys. J. Plus 2024, 139, 312. [Google Scholar] [CrossRef]
- Chevizovich, D.; Michieletto, D.; Mvogo, A.; Zakiryanov, F.; Zdravković, S. A review on nonlinear DNA physics. R. Soc. Open Sci. 2020, 7, 200774. [Google Scholar] [CrossRef] [PubMed]
- Sobczak, K.; Krzyzosiak, W.J. CAG Repeats Containing CAA Interruptions Form Branched Hairpin Structures in Spinocerebellar Ataxia Type 2 Transcripts. J. Biol. Chem. 2005, 280, 3898–3910. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Liu, Y.J.; Zhang, X.L.; Liu, Y.H.; Jiang, L.L.; Hu, H.Y. PolyQ-expanded ataxin-2 aggregation impairs cellular processing-body homeostasis via sequestering the RNA helicase DDX6. J. Biol. Chem. 2024, 300, 107413. [Google Scholar] [CrossRef] [PubMed]
- Stezin, A.; Sathe, G.J.; Gajbhiye, A.; Bharadwaj, S.; Ghose, V.; Bellad, A.; Malo, P.K.; Holla, V.; Hegde, S.; Bharath, R.D.; et al. Dysregulated Cerebrospinal Fluid Proteome of Spinocerebellar Ataxia Type 2 and its Clinical Implications. Mov. Disord. 2024, 39, 1418–1423. [Google Scholar] [CrossRef]
- Xu, Y.D.; Zhou, X.Y.; Wei, S.D.; Liu, F.T.; Zhao, J.; Tang, Y.L.; Shen, B.; Ding, Z.T.; Wu, J.J.; Sun, Y.M.; et al. Clinical features, disease progression, and nuclear imaging in ATXN2-related parkinsonism in a longitudinal cohort. Neurol. Sci. 2024, 45, 3191–3200. [Google Scholar] [CrossRef] [PubMed]
- Lyasota, O.; Dorohova, A.; Hernandez-Caceres, J.L.; Svidlov, A.; Tekutskaya, E.; Drobotenko, M.; Dzhimak, S. Stability of the CAG Tract in the ATXN2 Gene Depends on the Localization of CAA Interruptions. Biomedicines 2024, 12, 1648. [Google Scholar] [CrossRef]
- Matos-Rodrigues, G.; Hisey, J.A.; Nussenzweig, A.; Mirkin, S.M. Detection of alternative DNA structures and its implications for human disease. Mol. Cell 2023, 83, 3622–3641. [Google Scholar] [CrossRef]
- Ni, C.W.; Wei, Y.J.; Shen, Y.I.; Lee, I.R. Long-Range Hairpin Slippage Reconfiguration Dynamics in Trinucleotide Repeat Sequences. J. Phys. Chem. Lett. 2019, 10, 3985–3990. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Pan, F.; Roland, C.; Sagui, C.; Weninger, K. Dynamics of strand slippage in DNA hairpins formed by CAG repeats: Role of sequence parity and trinucleotide interrupts. Nucl. Acids Res. 2020, 48, 2232. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, J.; Pan, F.; Mahn, C.; Roland, C.; Sagui, C.; Weninger, K. Frustration Between Preferred States of Complementary Trinucleotide Repeat DNA Hairpins Anticorrelates with Expansion Disease Propensity. J. Mol. Biol. 2023, 435, 168086. [Google Scholar] [CrossRef] [PubMed]
- Belotserkovskii, B.P.; Hanawalt, P.C. Topology and kinetics of R-loop formation. Biophys. J. 2022, 121, 3345–3357. [Google Scholar] [CrossRef] [PubMed]
- Murmann, A.E.; Patel, M.; Jeong, S.Y.; Bartom, E.T.; Jennifer Morton, A.; Peter, M.E. The length of uninterrupted CAG repeats in stem regions of repeat disease associated hairpins determines the amount of short CAG oligonucleotides that are toxic to cells through RNA interference. Cell Death Dis. 2022, 13, 1078. [Google Scholar] [CrossRef]
- Tevonyan, L.L.; Beniaminov, A.D.; Kaluzhny, D.N. Quenching of G4-DNA intrinsic fluorescence by ligands. Eur. Biophys. J. 2024, 53, 47–56. [Google Scholar] [CrossRef]
- Belotserkovskii, B.P.; Hanawalt, P.C. Mechanism for R-loop formation remote from the transcription start site: Topological issues and possible facilitation by dissociation of RNA polymerase. DNA Repair. 2022, 110, 103275. [Google Scholar] [CrossRef]
- Crossley, M.P.; Bocek, M.; Cimprich, K.A. R-Loops as Cellular Regulators and Genomic Threats. Mol. Cell 2019, 73, 398–411. [Google Scholar] [CrossRef] [PubMed]
- Drobotenko, M.I.; Lyasota, O.M.; Hernandez-Caceres, J.L.; Rodriguez-Labrada, R.; Svidlov, A.A.; Dorohova, A.A.; Baryshev, M.G.; Nechipurenko, Y.D.; Velázquez-Pérez, L.; Dzhimak, S.S. Abnormal open states patterns in the ATXN2 DNA sequence depends on the CAG repeats length. Intl. J. Biol. Macromol. 2024, 276, 133849. [Google Scholar] [CrossRef] [PubMed]
- Dorohova, A.; Lyasota, O.; Dzhimak, S.; Svidlov, A.; Leontyeva, O.; Drobotenko, M. Fluctuations in Medium Viscosity May Affect the Stability of the CAG Tract in the ATXN2 Gene. Biomedicines 2024, 12, 2396. [Google Scholar] [CrossRef] [PubMed]
- Dorohova, A.; Lyasota, O.; Svidlov, A.; Anashkina, A.; Tekutskaya, E.; Dzhimak, S.; Drobotenko, M. Ratio of AT and GC pairs in the zones of open states genesis in DNA molecules. Front. Biosci. (Landmark Ed.) 2024, 29, 381. [Google Scholar] [CrossRef]
- Drobotenko, M.; Svidlov, A.; Dorohova, A.; Baryshev, M.; Dzhimak, S. Medium viscosity influence on the open states genesis in a DNA molecule. J. Biomolec. Struc. Dyn. 2023, 1–9. [Google Scholar] [CrossRef]
- Dzhimak, S.; Svidlov, A.; Elkina, A.; Gerasimenko, E.; Baryshev, M.; Drobotenko, M. Genesis of Open States Zones in a DNA Molecule Depends on the Localization and Value of the Torque. Int. J. Mol. Sci. 2022, 23, 4428. [Google Scholar] [CrossRef] [PubMed]
- Tabi, C.B.; Bineli, G.; Mohamadou, A. Energy patterns in twist-opening models of DNA with solvent interactions. J. Biol. Phys. 2015, 41, 391–408. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, R.; Mak, C.H. A Deep Dive into DNA Base Pairing Interactions under Water. J. Phys. Chem. B 2020, 124, 5559–55709. [Google Scholar] [CrossRef]
- Kannan, S.; Zacharias, M. Folding of a DNA hairpin loop structure in explicit solvent using replica-exchange molecular dynamics simulations. Biophys. J. 2007, 93, 3218–3228. [Google Scholar] [CrossRef]
- Völker, J.; Eric Plum, G.; Gindikin, V.; Breslauer, K.J. Dynamic DNA energy landscapes and substrate complexity in triplet repeat expansion and DNA repair. Biomolecules 2019, 9, 709. [Google Scholar] [CrossRef] [PubMed]
- Zdravković, S.; Satarić, M.V.; Hadžievski, L.J. DNA-RNA transcription as an impact of viscosity. Chaos 2010, 20, 043141. [Google Scholar] [CrossRef] [PubMed]
- Svidlov, A.; Drobotenko, M.; Basov, A.; Gerasimenko, E.; Elkina, A.; Baryshev, M.; Nechipurenko, Y.; Dzhimak, S. Influence of Environmental Parameters on the Stability of the DNA Molecule. Entropy 2021, 23, 1446. [Google Scholar] [CrossRef] [PubMed]
- Tabi, C.B.; Mohamadou, A.; Kofané, T.C. Modulated wave packets in DNA and impact of viscosity. Chin. Phys. Lett. 2009, 26, 068703. [Google Scholar] [CrossRef]
- Tabi, C.B.; Mohamadou, A.; Kofané, T.C. Modulational instability and pattern formation on DNA dynamics with viscosity. J. Comp. Theor. Nanosci. 2008, 5, 647–654. [Google Scholar] [CrossRef]
- Saha, M.; Kofané, T.C. DNA base pairs openings perturbed by the surrounding medium. Comm. Non. Sci. Num. Sim. 2015, 23, 1–9. [Google Scholar] [CrossRef]
- Dornberger, U.; Leijon, M.; Fritzsche, H. High base pair opening rates in tracts of GC base pairs. J. Biol. Chem. 1999, 274, 6957–6962. [Google Scholar] [CrossRef]
- Choi, C.H.; Kalosakas, G.; Rasmussen, K.O.; Hiromura, M.; Bishop, A.R.; Usheva, A. DNA dynamically directs its own transcription initiation. Nucleic Acids Res. 2004, 32, 1584–1590. [Google Scholar] [CrossRef] [PubMed]
- Kalosakas, G.; Rasmussen, K.O.; Bishop, A.R.; Choi, C.H.; Usheva, A. Sequence-specific thermal fluctuations identify start sites for DNA transcription. Europhys. Lett. 2004, 68, 127–133. [Google Scholar] [CrossRef][Green Version]
- Yakushevich, L.V. Nonlinear Physics of DNA.; John Wiley & Sons: Hoboken, HJ, USA, 2007; p. 252. [Google Scholar] [CrossRef]
- Drobotenko, M.I.; Dzhimak, S.S.; Svidlov, A.A.; Basov, A.A.; Lyasota, O.M.; Baryshev, M.G. A mathematical model for basepair opening in a DNA double helix. Biophysics 2018, 63, 177–182. [Google Scholar] [CrossRef]
- Englander, S.W.; Kallenbach, N.R.; Heeger, A.J.; Krumhansl, J.A.; Litwin, S. Nature of the open state in long polynucleotide double helices: Possibility of soliton excitations. Proc. Natl. Acad. Sci. USA 1980, 77, 7222–7226. [Google Scholar] [CrossRef]
- Krasnobaeva, L.A.; Yakushevich, L.V. The dynamic and statistical properties of DNA kinks. Biophysics 2020, 65, 22–27. [Google Scholar] [CrossRef]
- Masulis, I.; Grinevich, A.; Yakushevich, L. Dynamics of Open States and Promoter Functioning in the appY_red and appY_green Genetic Constructions Based on the pPF1 Plasmid. Front. Biosci. (Landmark Ed.) 2024, 29, 155. [Google Scholar] [CrossRef] [PubMed]
- Yakushevich, L.V.; Krasnobaeva, L.A. Trajectories of solitons movement in the potential field of pPF1 plasmid with non-zero initial velocity. Math. Biol. Bioinform. 2024, 19, 232–247. [Google Scholar] [CrossRef]
- Svidlov, A.A.; Drobotenko, M.I.; Basov, A.A.; Elkina, A.A.; Gerasimenko, E.O.; Malyshko, V.V.; Baryshev, M.G.; Dzhimak, S.S. Influence of the 2H/1H isotope composition of the water environment on the probability of denaturation bubble formation in a DNA molecule. Phys. Wave Phen. 2021, 29, 180–185. [Google Scholar] [CrossRef]
- Drobotenko, M.I.; Svidlov, A.A.; Baryshev, M.G.; Dzhimak, S.S. Calculation of Rotational Motions in a Double-Stranded DNA Molecule, Computer Program Registration Certificate RU 2017660682. Available online: https://new.fips.ru/registers-doc-view/fips_servlet?DB=EVM&DocNumber=2017660682&TypeFile=html (accessed on 27 November 2024).



| Type of Base | ||||
| 7.61 | 4.86 | 8.22 | 4.11 | |
| Å | 5.80 | 4.80 | 5.70 | 4.70 |
| , N·m | 2.35 | 1.61 | 2.27 | 1.54 |
| 6.20 | 6.20 | 9.60 | 9.60 | |
| 4.25 | 2.91 | 4.10 | 2.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drobotenko, M.; Lyasota, O.; Dzhimak, S.; Svidlov, A.; Baryshev, M.; Leontyeva, O.; Dorohova, A. Localization of Potential Energy in Hydrogen Bonds of the ATXN2 Gene. Int. J. Mol. Sci. 2025, 26, 933. https://doi.org/10.3390/ijms26030933
Drobotenko M, Lyasota O, Dzhimak S, Svidlov A, Baryshev M, Leontyeva O, Dorohova A. Localization of Potential Energy in Hydrogen Bonds of the ATXN2 Gene. International Journal of Molecular Sciences. 2025; 26(3):933. https://doi.org/10.3390/ijms26030933
Chicago/Turabian StyleDrobotenko, Mikhail, Oksana Lyasota, Stepan Dzhimak, Alexandr Svidlov, Mikhail Baryshev, Olga Leontyeva, and Anna Dorohova. 2025. "Localization of Potential Energy in Hydrogen Bonds of the ATXN2 Gene" International Journal of Molecular Sciences 26, no. 3: 933. https://doi.org/10.3390/ijms26030933
APA StyleDrobotenko, M., Lyasota, O., Dzhimak, S., Svidlov, A., Baryshev, M., Leontyeva, O., & Dorohova, A. (2025). Localization of Potential Energy in Hydrogen Bonds of the ATXN2 Gene. International Journal of Molecular Sciences, 26(3), 933. https://doi.org/10.3390/ijms26030933






