Computational Phenotypic Drug Discovery for Anticancer Chemotherapy: PTML Modeling of Multi-Cell Inhibitors of Colorectal Cancer Cell Lines
Abstract
1. Introduction
2. Results and Discussion
2.1. PTML Model: Performance
2.2. Physicochemical Interpretation of the PTML-MLP Through the FBTD Approach
2.3. Designing Novel Molecules Virtually Exhibiting Multi-Cell Anti-CRC Activity
2.4. Druglikeness of the Designed Molecules
3. Materials and Methods
3.1. Data Retrieval and Curation
3.2. Calculation of the Descriptors
3.3. Dataset Splitting and the Box–Jenkins Approach
3.4. Development of the PTML Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Siegel, R.L.; Kratzer, T.B.; Giaquinto, A.N.; Sung, H.; Jemal, A. Cancer statistics, 2025. CA Cancer J. Clin. 2025, 75, 10–45. [Google Scholar] [CrossRef]
- Haynes, J.; Manogaran, P. Mechanisms and Strategies to Overcome Drug Resistance in Colorectal Cancer. Int. J. Mol. Sci. 2025, 26, 1988. [Google Scholar] [CrossRef]
- Oh, J.M.; Kim, S.; Tsung, C.; Kent, E.; Jain, A.; Ruff, S.M.; Zhang, H. Comprehensive review of the resistance mechanisms of colorectal cancer classified by therapy type. Front. Immunol. 2025, 16, 1571731. [Google Scholar] [CrossRef]
- Wang, Z.; Hulikova, A.; Swietach, P. Innovating cancer drug discovery with refined phenotypic screens. Trends Pharmacol. Sci. 2024, 45, 723–738. [Google Scholar] [CrossRef]
- Jiang, C.; Yang, S.; Wang, Y.; Du, L.; Niu, M.M.; Zhang, D. Structure-based design of new potent and highly selective PARP-1 inhibitor for treating colorectal cancer. J. Enzyme Inhib. Med. Chem. 2025, 40, 2542358. [Google Scholar] [CrossRef] [PubMed]
- Sharma, D.; Arumugam, S. A machine learning-Assisted QSAR and integrative computational combined with network pharmacology approach for rational identification of tankyrase inhibitors in colon adenocarcinoma. Comput. Biol. Med. 2025, 197, 111068. [Google Scholar] [CrossRef] [PubMed]
- Pushpaveni, C.; Hemavathi, S.; Kurmi, S.P.C.; Patra, B.R.; Esther, V.A.; Yadav, C.K.; Biradar, M.S.; Thapa, S. Repurposing terfenadine and domperidone for inhibition of apoptotic gene association in colorectal cancer: A system pharmacology approach integrated with molecular docking, MD simulations, and post-MD simulation analysis. Bioinform. Biol. Insights 2025, 19, 11779322251365019. [Google Scholar] [CrossRef] [PubMed]
- Scalvini, L.; Tagliazucchi, L.; Elisi, G.M.; Zappaterra, D.; Moschella, M.G.; Fantini, S.; Aiello, D.; Guerrini, R.; Albanese, V.; Pacifico, S.; et al. Identification of pyrazolo-piperidinone derivatives targeting YAP-TEAD interface 3 as anticancer agents through integrated virtual screening and mass spectrometry proteomics. Eur. J. Med. Chem. 2025, 300, 118056. [Google Scholar] [CrossRef]
- Arooj, M.; Mateen, R.M.; Javed, M.; Ali, M.; Fareed, M.I.; Parveen, R.; Bahadur, A.; Iqbal, S.; Mahmood, S.; Knani, S.; et al. Computational screening of phytochemicals targeting mutant KRAS in colorectal cancer. Sci. Rep. 2025, 15, 28754. [Google Scholar] [CrossRef]
- Khalid, M.; Mateen, R.M.; Javed, M.; Ali, M.; Saqab, M.A.N.; Parveen, R.; Asimov, A.; Bibi, S.; Bahadur, A.; Iqbal, S.; et al. In-silico analysis of potential phytochemicals targeting mitogen activating protein kinase-14 (MAPK14) gene in colorectal cancer. Sci. Rep. 2025, 15, 20361. [Google Scholar] [CrossRef]
- Oladeji, S.M.; Conteh, D.N.; Bello, L.A.; Adegboyega, A.E.; Shokunbi, O.S. Rational Design and Optimization of Novel PDE5 Inhibitors for Targeted Colorectal Cancer Therapy: An In Silico Approach. Int. J. Mol. Sci. 2025, 26, 1937. [Google Scholar] [CrossRef]
- Alshahrani, M.M. Structural stability-guided scaffold hopping and computational modeling of tankyrase inhibitors targeting colorectal cancer. PLoS ONE 2025, 20, e0332798. [Google Scholar] [CrossRef] [PubMed]
- Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. Perturbation-Theory Machine Learning for Multi-Target Drug Discovery in Modern Anticancer Research. Curr. Issues Mol. Biol. 2025, 47, 301. [Google Scholar] [CrossRef]
- Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. Optimizing drug discovery using multitasking models for quantitative structure-biological effect relationships: An update of the literature. Expert Opin. Drug Discov. 2023, 18, 1231–1243. [Google Scholar] [CrossRef] [PubMed]
- Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. In Silico Approach for Antibacterial Discovery: PTML Modeling of Virtual Multi-Strain Inhibitors Against Staphylococcus aureus. Pharmaceuticals 2025, 18, 196. [Google Scholar] [CrossRef]
- Velasquez-Lopez, Y.; Ruiz-Escudero, A.; Arrasate, S.; Gonzalez-Diaz, H. Implementation of IFPTML Computational Models in Drug Discovery Against Flaviviridae Family. J. Chem. Inf. Model. 2024, 64, 1841–1852. [Google Scholar] [CrossRef] [PubMed]
- Santiago, C.; Ortega-Tenezaca, B.; Barbolla, I.; Fundora-Ortiz, B.; Arrasate, S.; Dea-Ayuela, M.A.; Gonzalez-Diaz, H.; Sotomayor, N.; Lete, E. Prediction of Antileishmanial Compounds: General Model, Preparation, and Evaluation of 2-Acylpyrrole Derivatives. J. Chem. Inf. Model. 2022, 62, 3928–3940. [Google Scholar] [CrossRef]
- Dieguez-Santana, K.; Casanola-Martin, G.M.; Torres, R.; Rasulev, B.; Green, J.R.; Gonzalez-Diaz, H. Machine Learning Study of Metabolic Networks vs ChEMBL Data of Antibacterial Compounds. Mol. Pharm. 2022, 19, 2151–2163. [Google Scholar] [CrossRef]
- Vasquez-Dominguez, E.; Armijos-Jaramillo, V.D.; Tejera, E.; Gonzalez-Diaz, H. Multioutput Perturbation-Theory Machine Learning (PTML) Model of ChEMBL Data for Antiretroviral Compounds. Mol. Pharm. 2019, 16, 4200–4212. [Google Scholar] [CrossRef]
- Quevedo-Tumailli, V.; Ortega-Tenezaca, B.; Gonzalez-Diaz, H. IFPTML Mapping of Drug Graphs with Protein and Chromosome Structural Networks vs. Pre-Clinical Assay Information for Discovery of Antimalarial Compounds. Int. J. Mol. Sci. 2021, 22, 13066. [Google Scholar] [CrossRef]
- Barbolla, I.; Hernandez-Suarez, L.; Quevedo-Tumailli, V.; Nocedo-Mena, D.; Arrasate, S.; Dea-Ayuela, M.A.; Gonzalez-Diaz, H.; Sotomayor, N.; Lete, E. Palladium-mediated synthesis and biological evaluation of C-10b substituted Dihydropyrrolo[1,2-b]isoquinolines as antileishmanial agents. Eur. J. Med. Chem. 2021, 220, 113458. [Google Scholar] [CrossRef]
- Kleandrova, V.V.; Speck-Planche, A. PTML Modeling for Alzheimer’s Disease: Design and Prediction of Virtual Multi-Target Inhibitors of GSK3B, HDAC1, and HDAC6. Curr. Top. Med. Chem. 2020, 20, 1661–1676. [Google Scholar] [CrossRef]
- Baltasar-Marchueta, M.; Llona, L.; M.-Alicante, S.; Barbolla, I.; Ibarluzea, M.G.; Ramis, R.; Salomon, A.M.; Fundora, B.; Araujo, A.; Muguruza-Montero, A.; et al. Identification of Riluzole derivatives as novel calmodulin inhibitors with neuroprotective activity by a joint synthesis, biosensor, and computational guided strategy. Biomed. Pharmacother. 2024, 174, 116602. [Google Scholar] [CrossRef]
- Sampaio-Dias, I.E.; Rodriguez-Borges, J.E.; Yanez-Perez, V.; Arrasate, S.; Llorente, J.; Brea, J.M.; Bediaga, H.; Vina, D.; Loza, M.I.; Caamano, O.; et al. Synthesis, Pharmacological, and Biological Evaluation of 2-Furoyl-Based MIF-1 Peptidomimetics and the Development of a General-Purpose Model for Allosteric Modulators (ALLOPTML). ACS Chem. Neurosci. 2021, 12, 203–215. [Google Scholar] [CrossRef] [PubMed]
- Diez-Alarcia, R.; Yanez-Perez, V.; Muneta-Arrate, I.; Arrasate, S.; Lete, E.; Meana, J.J.; Gonzalez-Diaz, H. Big Data Challenges Targeting Proteins in GPCR Signaling Pathways; Combining PTML-ChEMBL Models and [(35)S]GTPgammaS Binding Assays. ACS Chem. Neurosci. 2019, 10, 4476–4491. [Google Scholar] [CrossRef] [PubMed]
- Ferreira da Costa, J.; Silva, D.; Caamano, O.; Brea, J.M.; Loza, M.I.; Munteanu, C.R.; Pazos, A.; Garcia-Mera, X.; Gonzalez-Diaz, H. Perturbation Theory/Machine Learning Model of ChEMBL Data for Dopamine Targets: Docking, Synthesis, and Assay of New l-Prolyl-l-leucyl-glycinamide Peptidomimetics. ACS Chem. Neurosci. 2018, 9, 2572–2587. [Google Scholar] [CrossRef]
- Tenorio-Borroto, E.; Castanedo, N.; Garcia-Mera, X.; Rivadeneira, K.; Vazquez Chagoyan, J.C.; Barbabosa Pliego, A.; Munteanu, C.R.; Gonzalez-Diaz, H. Perturbation Theory Machine Learning Modeling of Immunotoxicity for Drugs Targeting Inflammatory Cytokines and Study of the Antimicrobial G1 Using Cytometric Bead Arrays. Chem. Res. Toxicol. 2019, 32, 1811–1823. [Google Scholar] [CrossRef]
- Vazquez-Prieto, S.; Paniagua, E.; Solana, H.; Ubeira, F.M.; Gonzalez-Diaz, H. A study of the Immune Epitope Database for some fungi species using network topological indices. Mol. Divers. 2017, 21, 713–718. [Google Scholar] [CrossRef]
- He, S.; Segura Abarrategi, J.; Bediaga, H.; Arrasate, S.; Gonzalez-Diaz, H. On the additive artificial intelligence-based discovery of nanoparticle neurodegenerative disease drug delivery systems. Beilstein J. Nanotechnol. 2024, 15, 535–555. [Google Scholar] [CrossRef]
- He, S.; Nader, K.; Abarrategi, J.S.; Bediaga, H.; Nocedo-Mena, D.; Ascencio, E.; Casanola-Martin, G.M.; Castellanos-Rubio, I.; Insausti, M.; Rasulev, B.; et al. NANO.PTML model for read-across prediction of nanosystems in neurosciences. computational model and experimental case of study. J. Nanobiotechnol. 2024, 22, 435. [Google Scholar] [CrossRef]
- Ortega-Tenezaca, B.; Gonzalez-Diaz, H. IFPTML mapping of nanoparticle antibacterial activity vs. pathogen metabolic networks. Nanoscale 2021, 13, 1318–1330. [Google Scholar] [CrossRef]
- Munteanu, C.R.; Gutierrez-Asorey, P.; Blanes-Rodriguez, M.; Hidalgo-Delgado, I.; Blanco Liverio, M.J.; Castineiras Galdo, B.; Porto-Pazos, A.B.; Gestal, M.; Arrasate, S.; Gonzalez-Diaz, H. Prediction of Anti-Glioblastoma Drug-Decorated Nanoparticle Delivery Systems Using Molecular Descriptors and Machine Learning. Int. J. Mol. Sci. 2021, 22, 11519. [Google Scholar] [CrossRef] [PubMed]
- Dieguez-Santana, K.; Gonzalez-Diaz, H. Towards machine learning discovery of dual antibacterial drug-nanoparticle systems. Nanoscale 2021, 13, 17854–17870. [Google Scholar] [CrossRef]
- Urista, D.V.; Carrue, D.B.; Otero, I.; Arrasate, S.; Quevedo-Tumailli, V.F.; Gestal, M.; Gonzalez-Diaz, H.; Munteanu, C.R. Prediction of Antimalarial Drug-Decorated Nanoparticle Delivery Systems with Random Forest Models. Biology 2020, 9, 198. [Google Scholar] [CrossRef]
- Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. Perturbation Theory Machine Learning Model for Phenotypic Early Antineoplastic Drug Discovery: Design of Virtual Anti-Lung-Cancer Agents. Appl. Sci. 2024, 14, 9344. [Google Scholar] [CrossRef]
- Cabrera-Andrade, A.; Lopez-Cortes, A.; Munteanu, C.R.; Pazos, A.; Perez-Castillo, Y.; Tejera, E.; Arrasate, S.; Gonzalez-Diaz, H. Perturbation-Theory Machine Learning (PTML) Multilabel Model of the ChEMBL Dataset of Preclinical Assays for Antisarcoma Compounds. ACS Omega 2020, 5, 27211–27220. [Google Scholar] [CrossRef] [PubMed]
- Cabrera-Andrade, A.; Lopez-Cortes, A.; Jaramillo-Koupermann, G.; Gonzalez-Diaz, H.; Pazos, A.; Munteanu, C.R.; Perez-Castillo, Y.; Tejera, E. A Multi-Objective Approach for Anti-Osteosarcoma Cancer Agents Discovery Through Drug Repurposing. Pharmaceuticals 2020, 13, 409. [Google Scholar] [CrossRef] [PubMed]
- Kleandrova, V.V.; Cordeiro, M.; Speck-Planche, A. Perturbation-theory machine learning for mood disorders: Virtual design of dual inhibitors of NET and SERT proteins. BMC Chem. 2025, 19, 2. [Google Scholar] [CrossRef]
- Tsherniak, A.; Vazquez, F.; Montgomery, P.G.; Weir, B.A.; Kryukov, G.; Cowley, G.S.; Gill, S.; Harrington, W.F.; Pantel, S.; Krill-Burger, J.M.; et al. Defining a Cancer Dependency Map. Cell 2017, 170, 564–576.e16. [Google Scholar] [CrossRef]
- Robin, T.; Capes-Davis, A.; Bairoch, A. CLASTR: The Cellosaurus STR similarity search tool—A precious help for cell line authentication. Int. J. Cancer 2020, 146, 1299–1306. [Google Scholar] [CrossRef]
- van der Meer, D.; Barthorpe, S.; Yang, W.; Lightfoot, H.; Hall, C.; Gilbert, J.; Francies, H.E.; Garnett, M.J. Cell Model Passports-a hub for clinical, genetic and functional datasets of preclinical cancer models. Nucleic Acids Res. 2019, 47, D923–D929. [Google Scholar] [CrossRef]
- Schneider, G.; Wrede, P. Artificial neural networks for computer-based molecular design. Prog. Biophys. Mol. Biol. 1998, 70, 175–222. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification. BioData Min. 2023, 16, 4. [Google Scholar] [CrossRef]
- Kleandrova, V.V.; Cordeiro, M.; Speck-Planche, A. In Silico Approach for Early Antimalarial Drug Discovery: De Novo Design of Virtual Multi-Strain Antiplasmodial Inhibitors. Microorganisms 2025, 13, 1620. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, H.; Lin, H. Global Sensitivity Analysis. In Encyclopedia of GIS; Shekhar, S., Xiong, H., Eds.; Springer: Boston, MA, USA, 2008; pp. 408–409. [Google Scholar]
- Estrada, E. Spectral moments of the edge adjacency matrix in molecular graphs. 1. Definition and applications for the prediction of physical properties of alkanes. J. Chem. Inf. Comput. Sci. 1996, 36, 844–849. [Google Scholar] [CrossRef]
- Estrada, E. Spectral moments of the edge adjacency matrix in molecular graphs. 2. Molecules containing heteroatoms and QSAR applications. J. Chem. Inf. Comput. Sci. 1997, 37, 320–328. [Google Scholar] [CrossRef]
- Estrada, E. Spectral moments of the edge adjacency matrix in molecular graphs. 3. Molecules containing cycles. J. Chem. Inf. Comput. Sci. 1998, 38, 23–27. [Google Scholar] [CrossRef]
- Estrada, E. How the parts organize in the whole? A top-down view of molecular descriptors and properties for QSAR and drug design. Mini Rev. Med. Chem. 2008, 8, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Molina, E. Automatic extraction of structural alerts for predicting chromosome aberrations of organic compounds. J. Mol. Graph. Model. 2006, 25, 275–288. [Google Scholar] [CrossRef] [PubMed]
- Helguera, A.M.; Cabrera Perez, M.A.; Gonzalez, M.P.; Ruiz, R.M.; Gonzalez Diaz, H. A topological substructural approach applied to the computational prediction of rodent carcinogenicity. Bioorg. Med. Chem. 2005, 13, 2477–2488. [Google Scholar] [CrossRef]
- Estrada, E.; Molina, E.; Perdomo-Lopez, I. Can 3D structural parameters be predicted from 2D (topological) molecular descriptors? J. Chem. Inf. Comput. Sci. 2001, 41, 1015–1021. [Google Scholar] [CrossRef]
- Estrada, E. Physicochemical Interpretation of Molecular Connectivity Indices. J. Phys. Chem. A 2002, 106, 9085–9091. [Google Scholar] [CrossRef]
- Kier, L.B.; Murray, W.J.; Hall, L.H. Molecular connectivity. 4. Relationships to biological activities. J. Med. Chem. 1975, 18, 1272–1274. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Hall, L.H. Molecular connectivity VII: Specific treatment of heteroatoms. J. Pharm. Sci. 1976, 65, 1806–1809. [Google Scholar] [CrossRef]
- Hall, L.H.; Kier, L.B. Structure-activity studies using valence molecular connectivity. J. Pharm. Sci. 1977, 66, 642–644. [Google Scholar] [CrossRef]
- Kier, L.B.; Hall, L.H. Derivation and significance of valence molecular connectivity. J. Pharm. Sci. 1981, 70, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Hall, L.H. Intermolecular accessibility: The meaning of molecular connectivity. J. Chem. Inf. Comput. Sci. 2000, 40, 792–795. [Google Scholar] [CrossRef]
- Kier, L.B.; Hall, L.H. Molecular connectivity: Intermolecular accessibility and encounter simulation. J. Mol. Graph. Model. 2001, 20, 76–83. [Google Scholar] [CrossRef]
- Estrada, E. Edge adjacency relationship and a novel topological index related to molecular volume. J. Chem. Inf. Comput. Sci. 1995, 35, 31–33. [Google Scholar] [CrossRef]
- Estrada, E. Edge adjacency relationships in molecular graphs containing heteroatoms: A new topological index related to molar volume. J. Chem. Inf. Comput. Sci. 1995, 35, 701–707. [Google Scholar] [CrossRef]
- Estrada, E.; Rodríguez, L. Edge-Connectivity Indices in QSPR/QSAR Studies. 1. Comparison to Other Topological Indices in QSPR Studies. J. Chem. Inf. Comput. Sci. 1999, 39, 1037–1041. [Google Scholar] [CrossRef]
- Estrada, E. Edge-Connectivity Indices in QSPR/QSAR Studies. 2. Accounting for Long-Range Bond Contributions. J. Chem. Inf. Comput. Sci. 1999, 39, 1042–1048. [Google Scholar] [CrossRef]
- Estrada, E.; Guevara, N.; Gutman, I. Extension of Edge Connectivity Index. Relationships to Line Graph Indices and QSPR Applications. J. Chem. Inf. Comput. Sci. 1998, 38, 428–431. [Google Scholar] [CrossRef]
- Zdrazil, B.; Felix, E.; Hunter, F.; Manners, E.J.; Blackshaw, J.; Corbett, S.; de Veij, M.; Ioannidis, H.; Lopez, D.M.; Mosquera, J.F.; et al. The ChEMBL Database in 2023: A drug discovery platform spanning multiple bioactivity data types and time periods. Nucleic Acids Res. 2024, 52, D1180–D1192. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem 2019 update: Improved access to chemical data. Nucleic Acids Res. 2019, 47, D1102–D1109. [Google Scholar] [CrossRef] [PubMed]
- Lagunin, A.A.; Rudik, A.V.; Pogodin, P.V.; Savosina, P.I.; Tarasova, O.A.; Dmitriev, A.V.; Ivanov, S.M.; Biziukova, N.Y.; Druzhilovskiy, D.S.; Filimonov, D.A.; et al. CLC-Pred 2.0: A Freely Available Web Application for In Silico Prediction of Human Cell Line Cytotoxicity and Molecular Mechanisms of Action for Druglike Compounds. Int. J. Mol. Sci. 2023, 24, 1689. [Google Scholar] [CrossRef] [PubMed]
- Mendez, D.; Gaulton, A.; Bento, A.P.; Chambers, J.; De Veij, M.; Felix, E.; Magarinos, M.P.; Mosquera, J.F.; Mutowo, P.; Nowotka, M.; et al. ChEMBL: Towards direct deposition of bioassay data. Nucleic Acids Res. 2019, 47, D930–D940. [Google Scholar] [CrossRef] [PubMed]
- Papadatos, G.; Davies, M.; Dedman, N.; Chambers, J.; Gaulton, A.; Siddle, J.; Koks, R.; Irvine, S.A.; Pettersson, J.; Goncharoff, N.; et al. SureChEMBL: A large-scale, chemically annotated patent document database. Nucleic Acids Res. 2016, 44, D1220–D1228. [Google Scholar] [CrossRef] [PubMed]
- Gubernator, K.; James, C.A.; Gubernator, N. eMolecules. California, USA. Available online: https://www.emolecules.com/ (accessed on 14 October 2025).
- Irwin, J.J.; Tang, K.G.; Young, J.; Dandarchuluun, C.; Wong, B.R.; Khurelbaatar, M.; Moroz, Y.S.; Mayfield, J.; Sayle, R.A. ZINC20-A Free Ultralarge-Scale Chemical Database for Ligand Discovery. J. Chem. Inf. Model. 2020, 60, 6065–6073. [Google Scholar] [CrossRef]
- Sterling, T.; Irwin, J.J. ZINC 15--Ligand Discovery for Everyone. J. Chem. Inf. Model. 2015, 55, 2324–2337. [Google Scholar] [CrossRef]
- Irwin, J.J.; Sterling, T.; Mysinger, M.M.; Bolstad, E.S.; Coleman, R.G. ZINC: A free tool to discover chemistry for biology. J. Chem. Inf. Model. 2012, 52, 1757–1768. [Google Scholar] [CrossRef]
- Irwin, J.J.; Shoichet, B.K. ZINC– a free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 2005, 45, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Maggiora, G.; Vogt, M.; Stumpfe, D.; Bajorath, J. Molecular similarity in medicinal chemistry. J. Med. Chem. 2014, 57, 3186–3204. [Google Scholar] [CrossRef] [PubMed]
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 2001, 46, 3–26. [Google Scholar] [CrossRef]
- Veber, D.F.; Johnson, S.R.; Cheng, H.Y.; Smith, B.R.; Ward, K.W.; Kopple, K.D. Molecular properties that influence the oral bioavailability of drug candidates. J. Med. Chem. 2002, 45, 2615–2623. [Google Scholar] [CrossRef] [PubMed]
- Mauri, A. alvaDesc: A Tool to Calculate and Analyze Molecular Descriptors and Fingerprints. In Ecotoxicological QSARs; Roy, K., Ed.; Springer: New York, NY, USA, 2020; pp. 801–820. [Google Scholar]
- Pathania, S.; Singh, P.K. Analyzing FDA-approved drugs for compliance of pharmacokinetic principles: Should there be a critical screening parameter in drug designing protocols? Expert Opin. Drug Metab. Toxicol. 2021, 17, 351–354. [Google Scholar] [CrossRef]
- Gaulton, A.; Bellis, L.J.; Bento, A.P.; Chambers, J.; Davies, M.; Hersey, A.; Light, Y.; McGlinchey, S.; Michalovich, D.; Al-Lazikani, B.; et al. ChEMBL: A large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012, 40, D1100–D1107. [Google Scholar] [CrossRef]
- Mok, N.Y.; Brenk, R. Mining the ChEMBL database: An efficient chemoinformatics workflow for assembling an ion channel-focused screening library. J. Chem. Inf. Model. 2011, 51, 2449–2454. [Google Scholar] [CrossRef]
- Holbeck, S.L.; Collins, J.M.; Doroshow, J.H. Analysis of Food and Drug Administration-approved anticancer agents in the NCI60 panel of human tumor cell lines. Mol. Cancer Ther. 2010, 9, 1451–1460, Erratum in Am. J. Psychiatry 2012, 169, 540. [Google Scholar] [CrossRef]
- Johnson, J.I.; Decker, S.; Zaharevitz, D.; Rubinstein, L.V.; Venditti, J.M.; Schepartz, S.; Kalyandrug, S.; Christian, M.; Arbuck, S.; Hollingshead, M.; et al. Relationships between drug activity in NCI preclinical in vitro and in vivo models and early clinical trials. Br. J. Cancer 2001, 84, 1424–1431. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Gutiérrez, Y. MODESLAB, v1.5; Santiago de Compostela, Spain. 2004. Available online: https://insilicomoleculardesign.com/modeslab/ (accessed on 30 September 2025).
- Urias, R.W.; Barigye, S.J.; Marrero-Ponce, Y.; Garcia-Jacas, C.R.; Valdes-Martini, J.R.; Perez-Gimenez, F. IMMAN: Free software for information theory-based chemometric analysis. Mol. Divers. 2015, 19, 305–319. [Google Scholar] [CrossRef]
- Stahura, F.L.; Godden, J.W.; Bajorath, J. Differential Shannon entropy analysis identifies molecular property descriptors that predict aqueous solubility of synthetic compounds with high accuracy in binary QSAR calculations. J. Chem. Inf. Comput. Sci. 2002, 42, 550–558. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C: The Art of Scientific Computing, 1st ed.; Cambridge University Press: New York, NY, USA, 1988. [Google Scholar]
- TIBCO-Software-Inc. STATISTICA (Data Analysis Software System), v13.5.0.17; TIBCO-Software-Inc.: Palo Alto, CA, USA, 2018.
- Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. Perturbation-Theory Machine Learning for Multi-Objective Antibacterial Discovery: Current Status and Future Perspectives. Appl. Sci. 2025, 15, 1166. [Google Scholar] [CrossRef]
- Manallack, D.T.; Livingstone, D.J.; A.-Razzak, M.; Glen, R.C. Neural Networks and Expert Systems in Molecular Design. In Advanced Computer-Assisted Techniques in Drug Discovery; van de Waterbeemd, H., Ed.; Methods and Principles in Medicinal Chemistry; Wiley: Hoboken, NJ, USA, 1994; pp. 293–331. [Google Scholar]
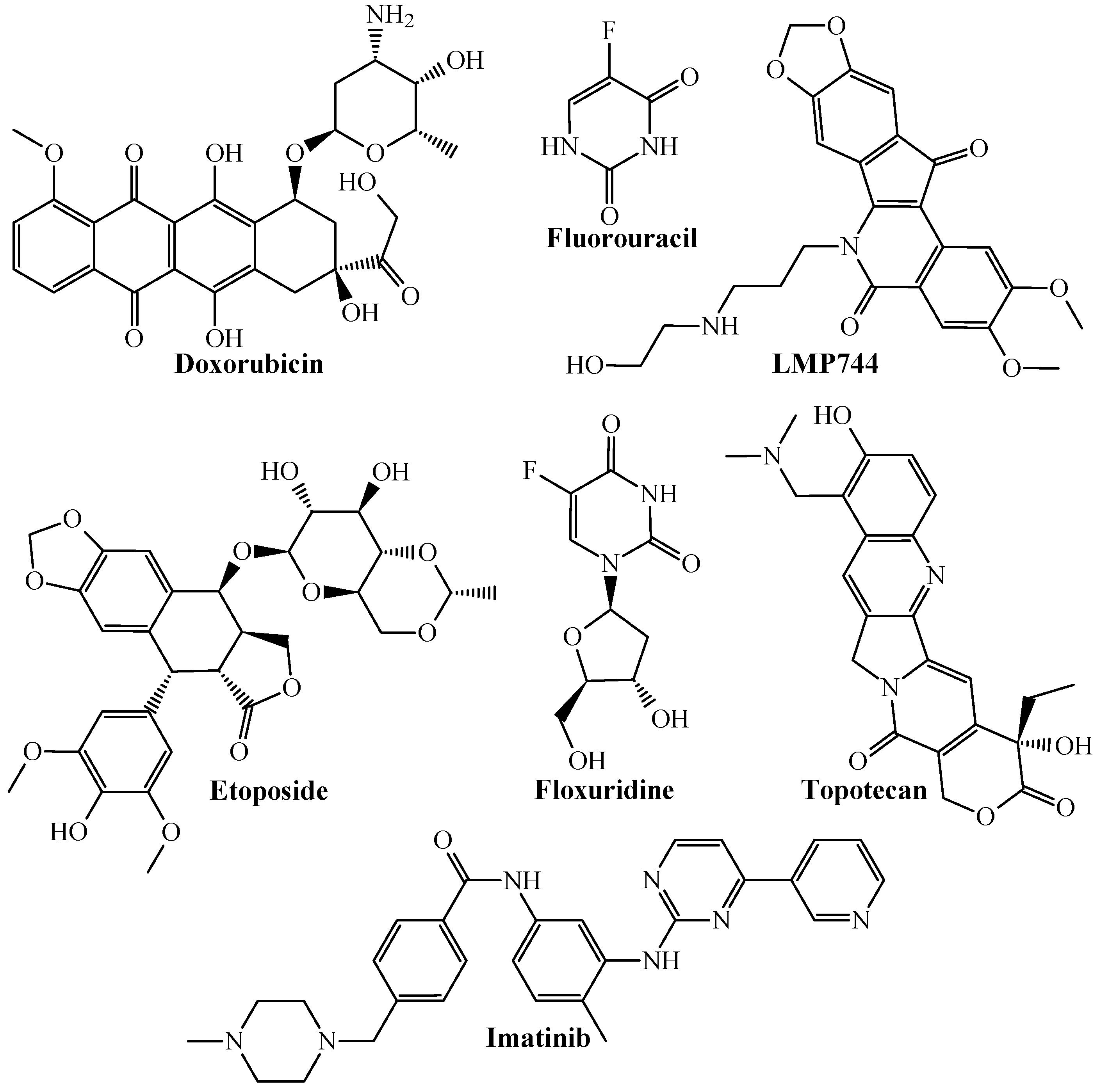


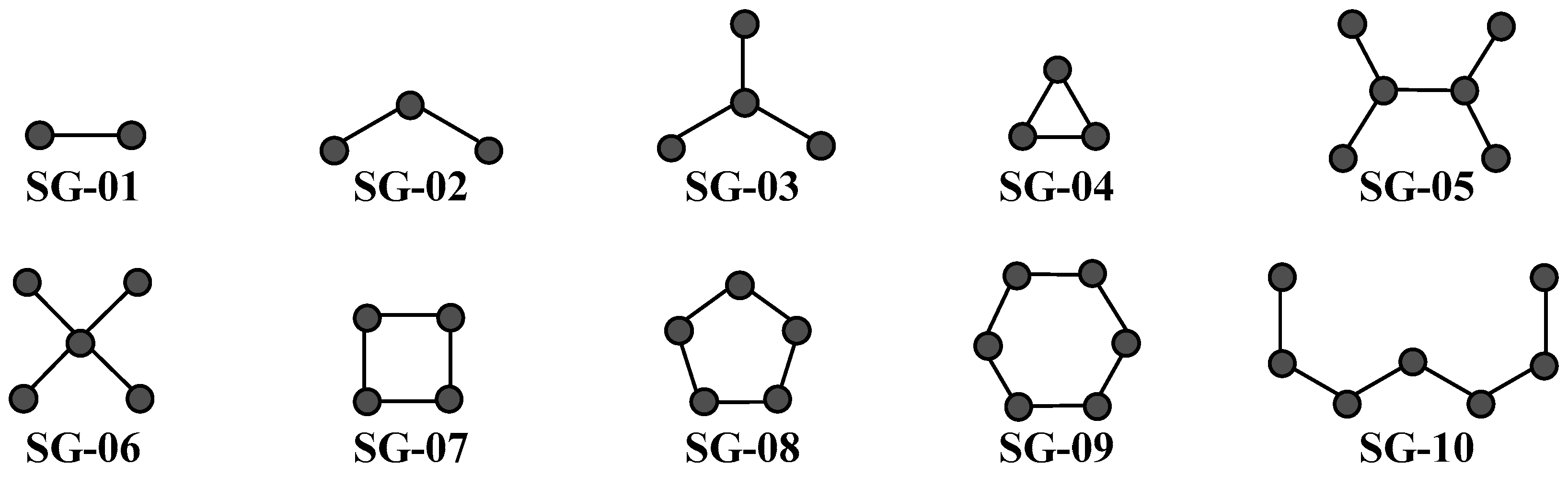
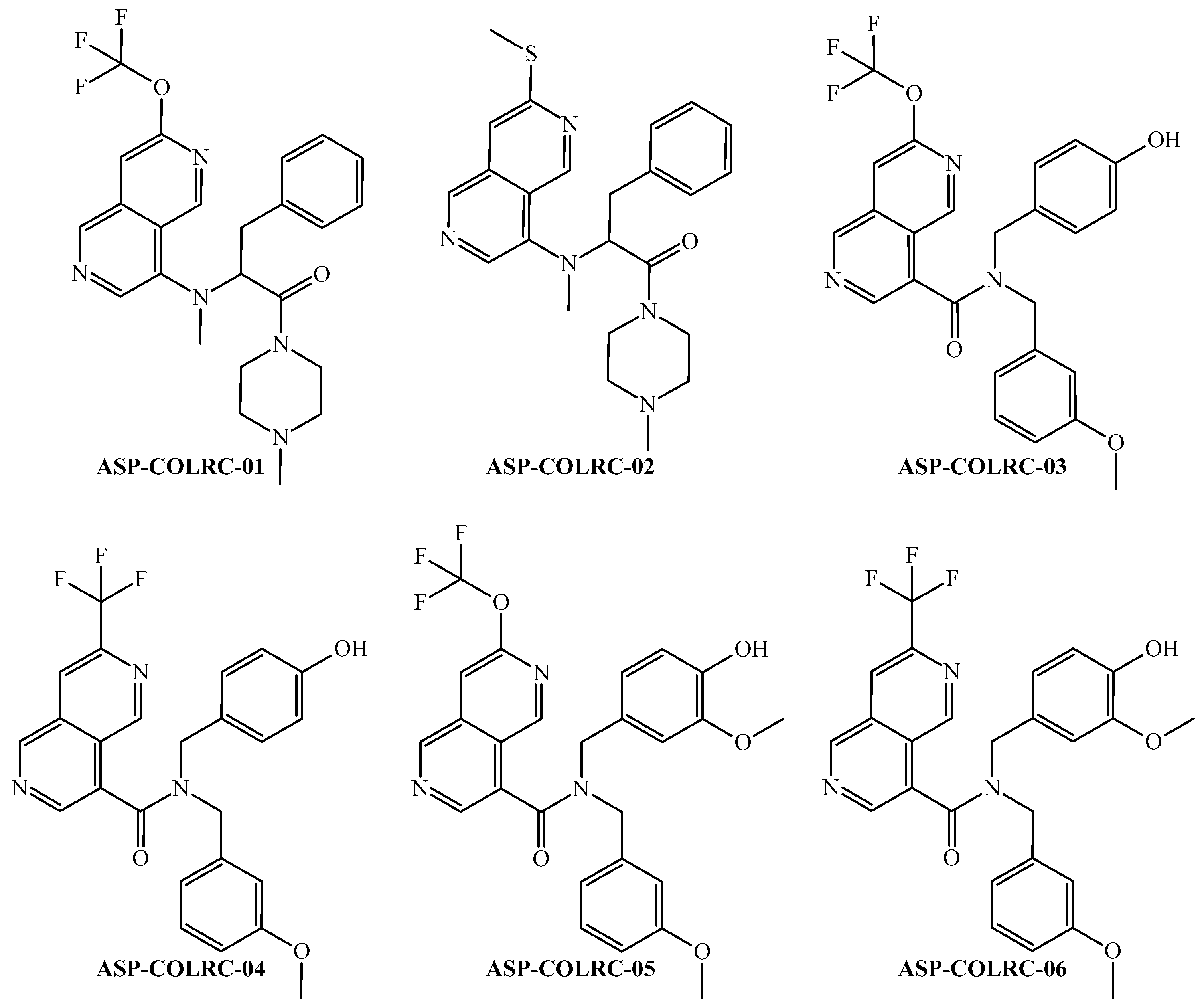
| Codes a,b,c | Symbology | Definition |
|---|---|---|
| DGT01 | D[NSM(Dip)5]dt | Multi-label topological index derived from the normalized bond-based spectral moment of order 5, weighted by the bond dipole moment. |
| DGT02 | D[NSM(Psa)1]dt | Multi-label topological index derived from the normalized bond-based spectral moment of order 1, weighted by the polar surface area. |
| DGT03 | D[NSM(Mol)4]dt | Multi-label topological index derived from the normalized bond-based spectral moment of order 4, weighted by the atomic contributions to the molar refractivity. |
| DGT04 | D[Ne(P)2]dt | Multi-label topological index derived from the normalized bond connectivity of order 2, containing only path subgraphs. |
| DGT05 | D[SM(Psa)1]ct | Multi-label topological index derived from the bond-based spectral moment of order 1, weighted by the atomic contributions to the polar surface area. |
| DGT06 | D[e(C)4]ct | Multi-label topological index derived from the bond connectivity of order 4, containing only cluster subgraphs. |
| DGT07 | D[SM(Hyd)1]mc | Multi-label topological index derived from the bond-based spectral moment of order 1, weighted by the atomic contributions to the hydrophobicity. |
| DGT08 | D[SM(Psa)4]mc | Multi-label topological index derived from the bond-based spectral moment of order 4, weighted by the atomic contributions to the polar surface area. |
| DGT09 | D[SM(Mol)3]mc | Multi-label topological index derived from the bond-based spectral moment of order 3, weighted by the atomic contributions to the molar refractivity. |
| DGT10 | D[SM(Ato)4]mc | Multi-label topological index derived from the bond-based spectral moment of order 4, weighted by the atomic weights. |
| DGT11 | D[Xv(Ch)6]mc | Multi-label topological index derived from the atom-based valence connectivity of order 6, containing only ring (cycle) subgraphs. |
| DGT12 | D[e(P)1]mc | Multi-label topological index derived from the bond connectivity of order 1, containing only path subgraphs. |
| DGT13 | D[e(C)5]mc | Multi-label topological index derived from the bond connectivity of order 5, containing only cluster subgraphs. |
| DGT14 | D[e(Ch)5]mc | Multi-label topological index derived from the bond connectivity of order 5, containing only ring (cycle) subgraphs. |
| DGT15 | D[e(Ch)6]mc | Multi-label topological index derived from the bond connectivity of order 6, containing only ring (cycle) subgraphs. |
| DGT16 | D[NSM(Std)1]mc | Multi-label topological index derived from the normalized bond-based spectral moment of order 1, weighted by the bond standard distance. |
| DGT17 | D[NSM(Mol)1]mc | Multi-label topological index derived from the normalized bond-based spectral moment of order 1, weighted by the atomic contributions to the molar refractivity. |
| DGT18 | D[NXv(P)6]mc | Multi-label topological index derived from the normalized atom-based valence connectivity of order 6, containing only path subgraphs. |
| DGT19 | D[Ne(P)1]mc | Multi-label topological index derived from the normalized bond connectivity of order 1, containing only path subgraphs. |
| DGT20 | D[Ne(P)6]mc | Multi-label topological index derived from the normalized bond connectivity of order 6, containing only path subgraphs. |
| Symbols a | Training Set | Test Set |
|---|---|---|
| NActive | 1846 | 615 |
| CCActive | 1643 | 512 |
| Sn | 89.00% | 83.25% |
| NInactive | 2262 | 755 |
| CCInactive | 2026 | 635 |
| Sp | 89.57% | 84.11% |
| nMCC | 0.892 | 0.836 |
| ej a | dt b | ct c | mc d |
|---|---|---|---|
| ej01 | Slow growth | HCC2998 | MSS |
| ej02 | Fast growth | HT-29 | MSS |
| ej03 | Fast growth | HCT 15 | MSI |
| ej04 | Fast growth | HCT 116 | MSI |
| ej05 | Intermediate growth | KM12 | MSI |
| ej06 | Intermediate growth | SW620 | MSS |
| ej07 | Slow growth | COLO 205 | MSS |
| Codes a | Average Values | Propensity b | |
|---|---|---|---|
| Active | Inactive | ||
| DGT01 | 1.481 × 10−2 | 8.723 × 10−2 | Decrease |
| DGT02 | 5.160 × 10−3 | 1.156 × 10−1 | Decrease |
| DGT03 | 3.545 × 10−3 | 1.048 × 10−1 | Decrease |
| DGT04 | −2.001 × 10−2 | 1.414 × 10−1 | Decrease |
| DGT05 | 2.747 × 10−3 | 4.112 × 10−2 | Decrease |
| DGT06 | 6.336 × 10−3 | 2.913 × 10−2 | Decrease |
| DGT07 | −9.067 × 10−3 | −4.975 × 10−2 | Increase |
| DGT08 | 1.135 × 10−2 | 1.840 × 10−1 | Decrease |
| DGT09 | −1.061 × 10−2 | 8.230 × 10−2 | Decrease |
| DGT10 | 1.251 × 10−2 | −2.358 × 10−2 | Increase |
| DGT11 | −7.321 × 10−3 | −1.911 × 10−3 | Decrease |
| DGT12 | −3.556 × 10−3 | −1.092 × 10−1 | Increase |
| DGT13 | 1.692 × 10−2 | 4.808 × 10−3 | Increase |
| DGT14 | 9.767 × 10−3 | 7.377 × 10−2 | Decrease |
| DGT15 | −2.721 × 10−2 | 2.977 × 10−2 | Decrease |
| DGT16 | −1.179 × 10−2 | −6.458 × 10−2 | Increase |
| DGT17 | −1.816 × 10−2 | 8.865 × 10−2 | Decrease |
| DGT18 | 1.347 × 10−2 | 3.415 × 10−2 | Decrease |
| DGT19 | −7.019 × 10−3 | −6.653 × 10−2 | Increase |
| DGT20 | 2.185 × 10−3 | −1.142 × 10−1 | Increase |
| ID a | ej b | PTML-MLP Model c,d | CLC-Pred 2.0 (GI50 ≤ 100 nM) e | ||
|---|---|---|---|---|---|
| PACRC(ej) | ProbAct (%) | Pa | Pi | ||
| ASP-COLRC-01 | ej01 | −1 | 43.43 | 0.254 | 0.148 |
| ASP-COLRC-01 | ej02 | 1 | 58.41 | 0.266 | 0.124 |
| ASP-COLRC-01 | ej03 | 1 | 55.23 | – | – |
| ASP-COLRC-01 | ej04 | 1 | 66.49 | 0.209 | 0.204 |
| ASP-COLRC-01 | ej05 | 1 | 56.13 | 0.282 | 0.117 |
| ASP-COLRC-01 | ej06 | −1 | 42.44 | – | – |
| ASP-COLRC-01 | ej07 | −1 | 46.02 | 0.337 | 0.098 |
| ASP-COLRC-02 | ej01 | 1 | 55.32 | – | – |
| ASP-COLRC-02 | ej02 | 1 | 59.79 | – | – |
| ASP-COLRC-02 | ej03 | −1 | 39.55 | 0.224 | 0.174 |
| ASP-COLRC-02 | ej04 | −1 | 44.55 | – | – |
| ASP-COLRC-02 | ej05 | −1 | 39.64 | 0.254 | 0.133 |
| ASP-COLRC-02 | ej06 | 1 | 50.60 | – | – |
| ASP-COLRC-02 | ej07 | 1 | 55.38 | – | – |
| ASP-COLRC-03 | ej01 | −1 | 46.75 | 0.336 | 0.097 |
| ASP-COLRC-03 | ej02 | 1 | 59.00 | 0.302 | 0.104 |
| ASP-COLRC-03 | ej03 | 1 | 55.76 | 0.323 | 0.107 |
| ASP-COLRC-03 | ej04 | 1 | 61.67 | 0.361 | 0.097 |
| ASP-COLRC-03 | ej05 | 1 | 55.95 | 0.369 | 0.080 |
| ASP-COLRC-03 | ej06 | −1 | 49.10 | 0.243 | 0.153 |
| ASP-COLRC-03 | ej07 | 1 | 50.88 | 0.353 | 0.091 |
| ASP-COLRC-04 | ej01 | 1 | 66.31 | – | – |
| ASP-COLRC-04 | ej02 | 1 | 74.59 | – | – |
| ASP-COLRC-04 | ej03 | 1 | 72.67 | 0.250 | 0.152 |
| ASP-COLRC-04 | ej04 | 1 | 76.79 | 0.268 | 0.148 |
| ASP-COLRC-04 | ej05 | 1 | 73.99 | 0.204 | 0.171 |
| ASP-COLRC-04 | ej06 | 1 | 67.95 | 0.217 | 0.180 |
| ASP-COLRC-04 | ej07 | 1 | 69.47 | – | – |
| ASP-COLRC-05 | ej01 | 1 | 53.80 | 0.343 | 0.093 |
| ASP-COLRC-05 | ej02 | 1 | 61.15 | 0.302 | 0.104 |
| ASP-COLRC-05 | ej03 | 1 | 58.83 | 0.358 | 0.091 |
| ASP-COLRC-05 | ej04 | 1 | 63.40 | 0.376 | 0.090 |
| ASP-COLRC-05 | ej05 | 1 | 58.85 | 0.397 | 0.072 |
| ASP-COLRC-05 | ej06 | 1 | 54.71 | 0.261 | 0.140 |
| ASP-COLRC-05 | ej07 | 1 | 56.60 | 0.346 | 0.094 |
| ASP-COLRC-06 | ej01 | 1 | 76.95 | – | – |
| ASP-COLRC-06 | ej02 | 1 | 79.13 | 0.189 | 0.188 |
| ASP-COLRC-06 | ej03 | 1 | 76.56 | 0.285 | 0.129 |
| ASP-COLRC-06 | ej04 | 1 | 78.33 | 0.282 | 0.138 |
| ASP-COLRC-06 | ej05 | 1 | 77.20 | 0.228 | 0.152 |
| ASP-COLRC-06 | ej06 | 1 | 77.28 | 0.232 | 0.164 |
| ASP-COLRC-06 | ej07 | 1 | 78.12 | – | – |
| ID | Physicochemical Properties a | |||||||
|---|---|---|---|---|---|---|---|---|
| MW | HBA | HBD | MlogP | AlogP | AvgLogP | RBN | PSA | |
| ASP-COLRC-01 | 473.55 | 10 | 0 | 2.304 | 4.628 | 3.466 | 6 | 61.80 |
| ASP-COLRC-02 | 435.65 | 6 | 0 | 1.941 | 3.050 | 2.496 | 6 | 77.87 |
| ASP-COLRC-03 | 483.48 | 10 | 1 | 2.826 | 5.393 | 4.110 | 7 | 84.78 |
| ASP-COLRC-04 | 467.48 | 9 | 1 | 2.773 | 4.105 | 3.439 | 6 | 75.55 |
| ASP-COLRC-05 | 513.51 | 11 | 1 | 2.277 | 5.377 | 3.827 | 8 | 94.01 |
| ASP-COLRC-06 | 497.51 | 10 | 1 | 2.213 | 4.089 | 3.151 | 7 | 84.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speck-Planche, A.; Cordeiro, M.N.D.S. Computational Phenotypic Drug Discovery for Anticancer Chemotherapy: PTML Modeling of Multi-Cell Inhibitors of Colorectal Cancer Cell Lines. Int. J. Mol. Sci. 2025, 26, 11453. https://doi.org/10.3390/ijms262311453
Speck-Planche A, Cordeiro MNDS. Computational Phenotypic Drug Discovery for Anticancer Chemotherapy: PTML Modeling of Multi-Cell Inhibitors of Colorectal Cancer Cell Lines. International Journal of Molecular Sciences. 2025; 26(23):11453. https://doi.org/10.3390/ijms262311453
Chicago/Turabian StyleSpeck-Planche, Alejandro, and M. Natália D. S. Cordeiro. 2025. "Computational Phenotypic Drug Discovery for Anticancer Chemotherapy: PTML Modeling of Multi-Cell Inhibitors of Colorectal Cancer Cell Lines" International Journal of Molecular Sciences 26, no. 23: 11453. https://doi.org/10.3390/ijms262311453
APA StyleSpeck-Planche, A., & Cordeiro, M. N. D. S. (2025). Computational Phenotypic Drug Discovery for Anticancer Chemotherapy: PTML Modeling of Multi-Cell Inhibitors of Colorectal Cancer Cell Lines. International Journal of Molecular Sciences, 26(23), 11453. https://doi.org/10.3390/ijms262311453







