Establishing a General Atomistic Model for the Stratum Corneum Lipid Matrix Based on Experimental Data for Skin Permeation Studies
Abstract
1. Introduction
2. Results
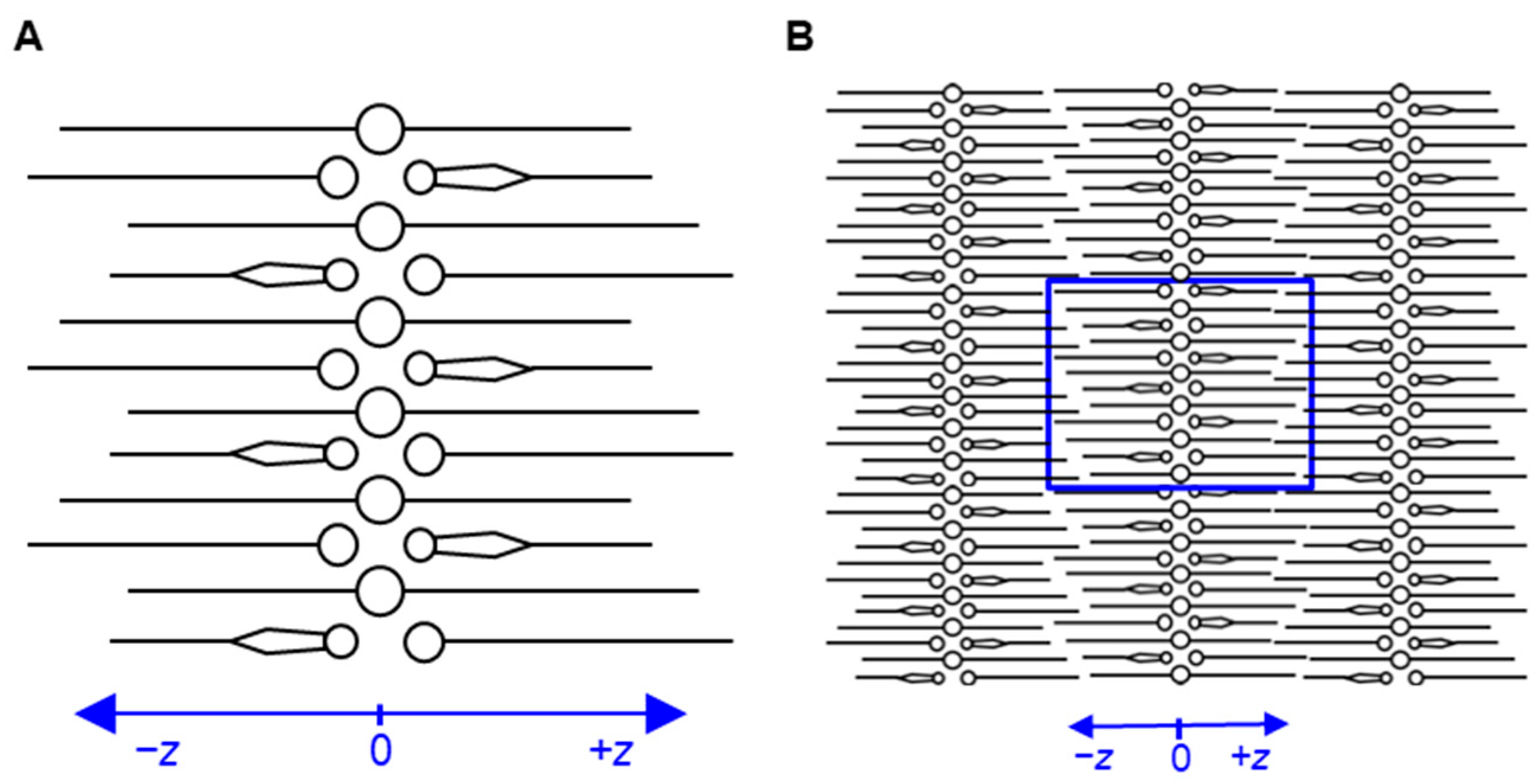
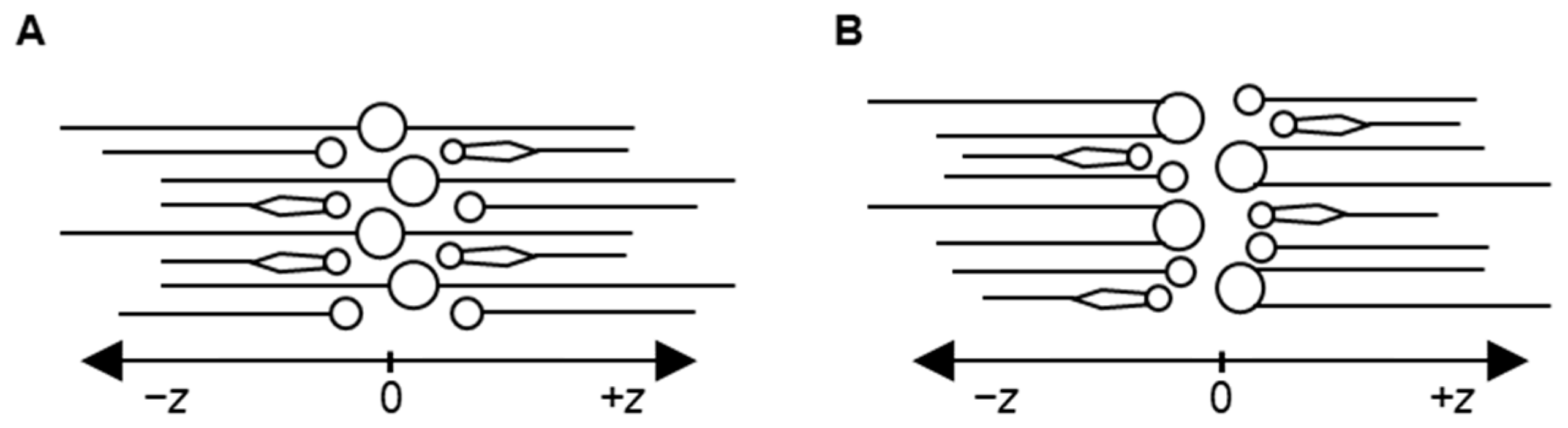
2.1. Developed Molecular Model of Stratum Corneum Lipid Matrix
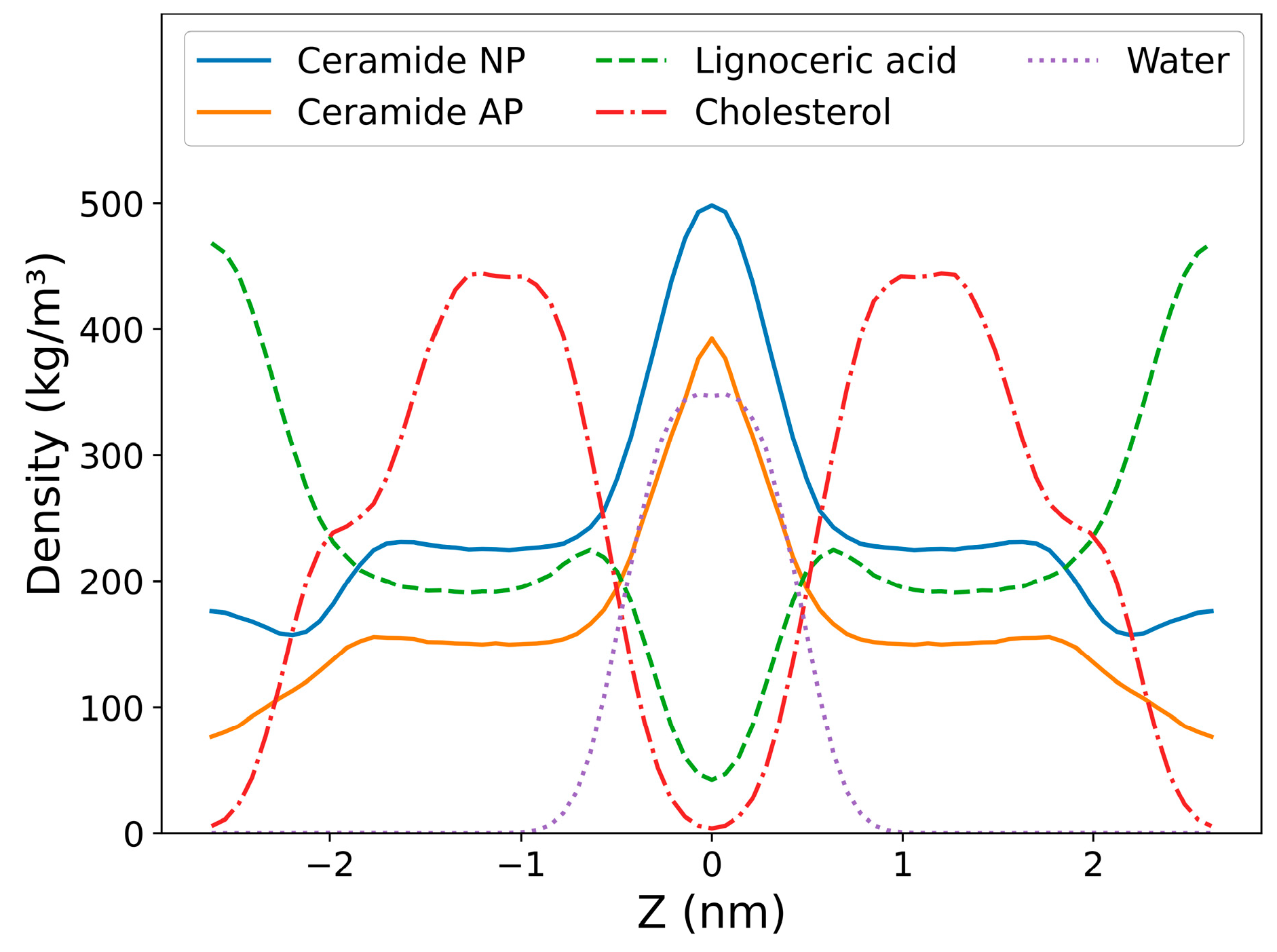
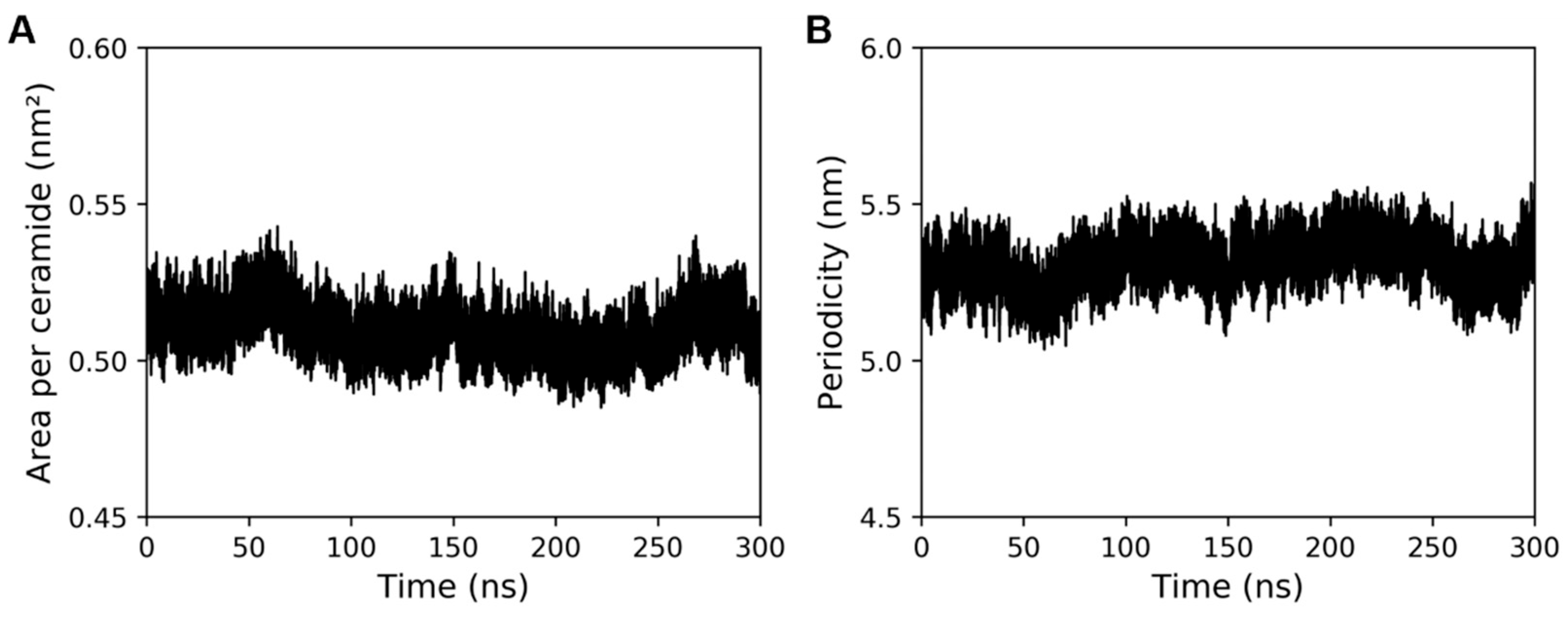
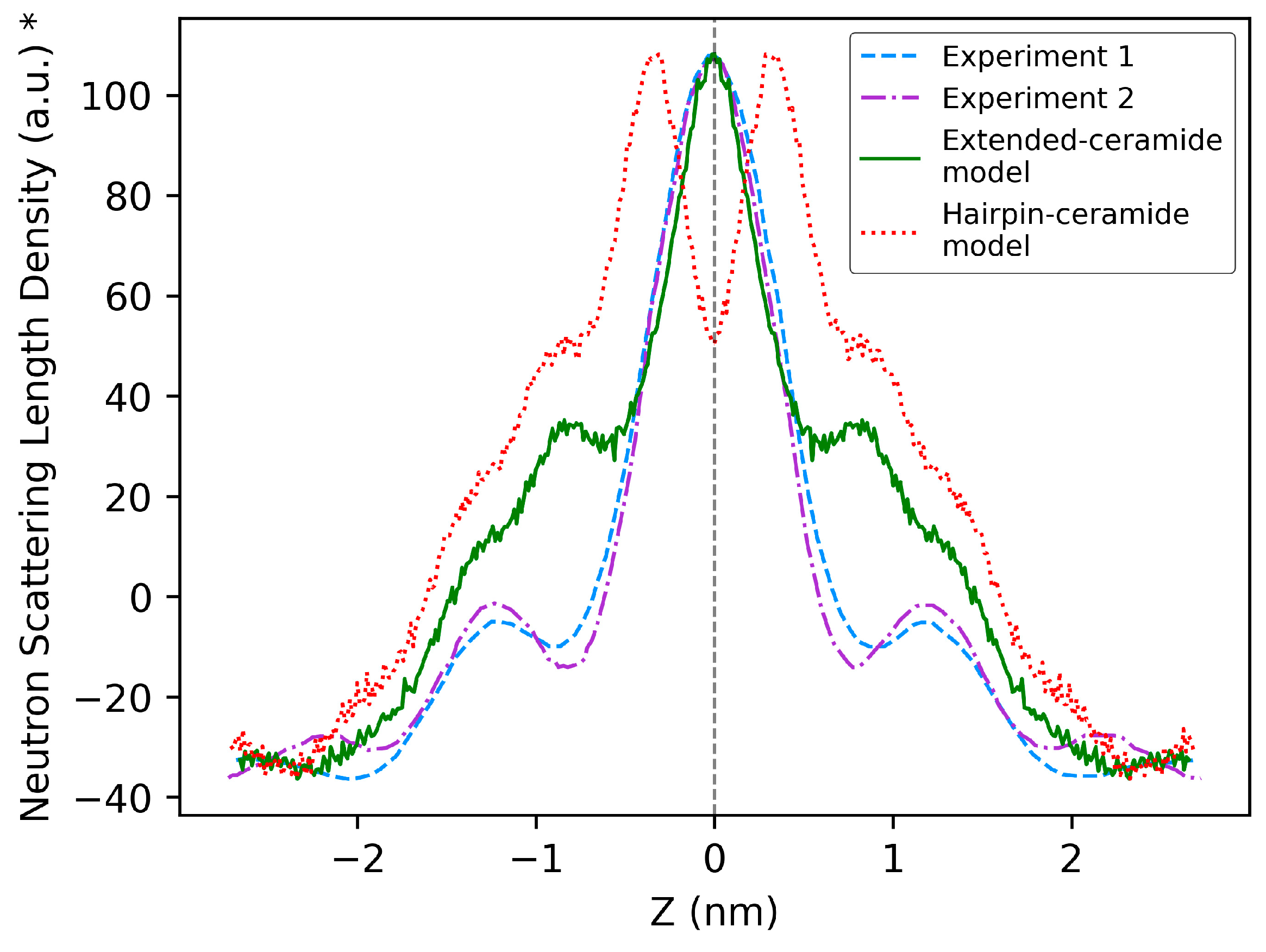
2.2. Comparison of Model Properties with Experimental Observations from the Literature
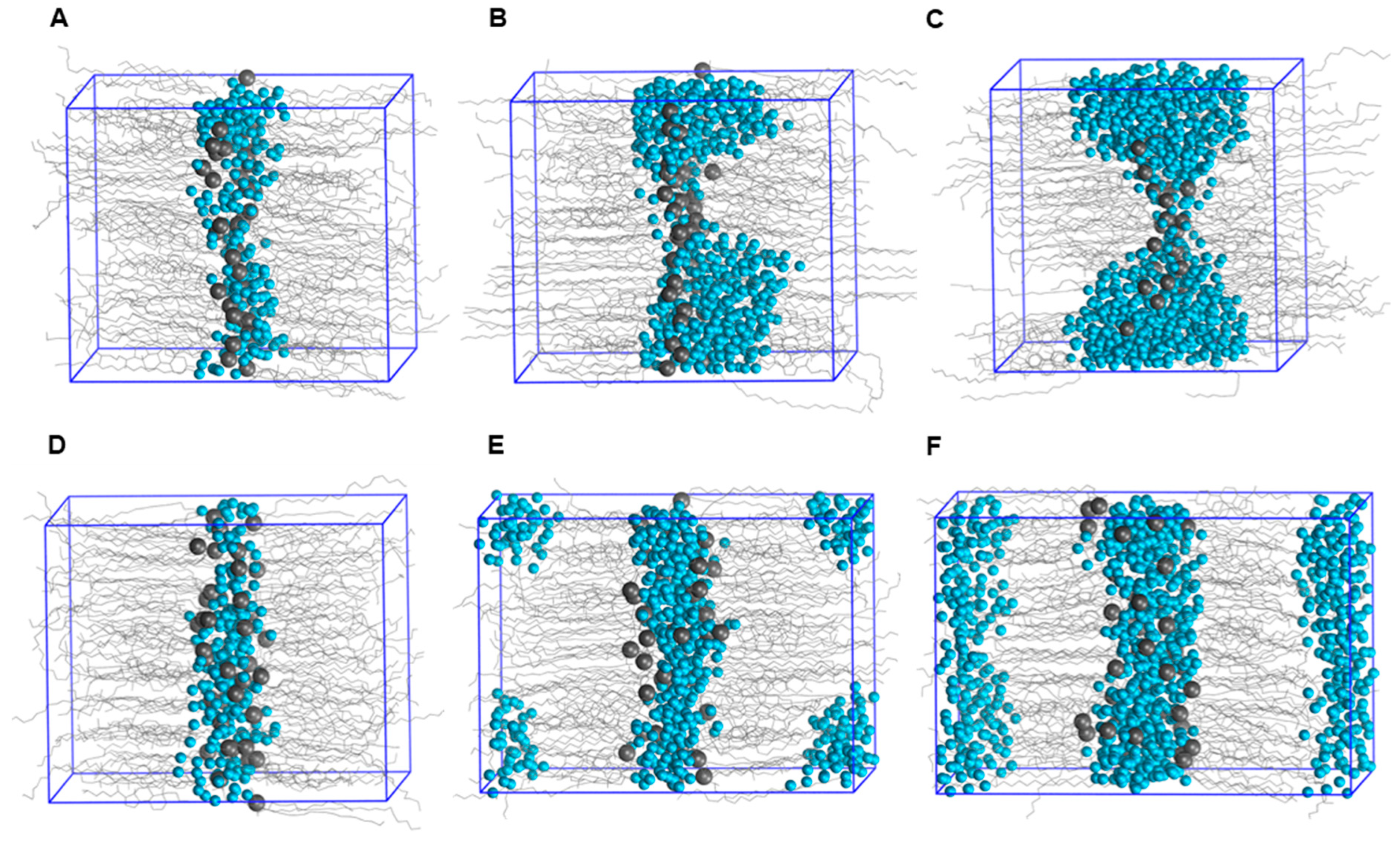
2.3. Permeation Studies of Small Molecules Using the Model
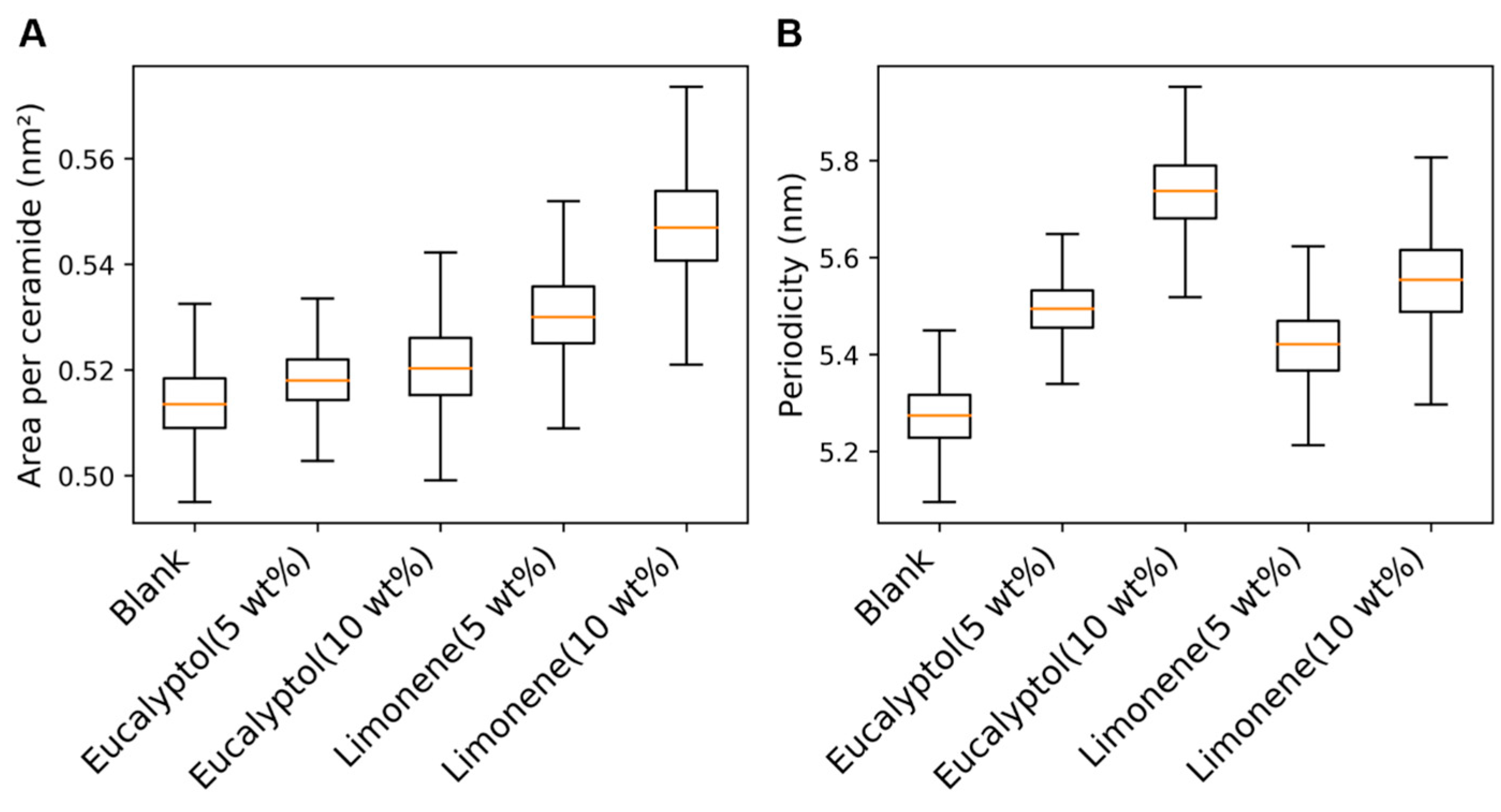
2.4. Mechanism of Action of Permeation Enhancers
3. Discussion
4. Materials and Methods
4.1. Building the Model
4.2. Equilibration of the Built Model
4.3. Calculation of System Properties
4.4. Permeability Assessment of Small Molecules Using the Built Model
4.5. Studying the Mechanism of Action of Permeation Enhancers
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neupane, R.; Boddu, S.H.S.; Abou-Dahech, M.S.; Bachu, R.D.; Terrero, D.; Babu, R.J.; Tiwari, A.K. Transdermal Delivery of Chemotherapeutics: Strategies, Requirements, and Opportunities. Pharmaceutics 2021, 13, 960. [Google Scholar] [CrossRef] [PubMed]
- Elias, P.M. Epidermal lipids, barrier function, and desquamation. J. Investig. Dermatol. 1983, 80, 44s–49s. [Google Scholar] [CrossRef] [PubMed]
- Menton, D.N.; Eisen, A.Z. Structure and organization of mammalian stratum corneum. J. Ultrastruct. Res. 1971, 35, 247–264. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.B.; Traynor, M.J.; Martin, G.P.; Akomeah, F.K. Transdermal drug delivery systems: Skin perturbation devices. Methods Mol. Biol. 2008, 437, 119–139. [Google Scholar] [CrossRef]
- Bolzinger, M.A.; Briançon, S.; Pelletier, J.; Chevalier, Y. Penetration of drugs through skin, a complex rate-controlling membrane. Curr. Opin. Colloid Interface Sci. 2012, 17, 156–165. [Google Scholar] [CrossRef]
- Weerheim, A.; Ponec, M. Determination of stratum corneum lipid profile by tape stripping in combination with high-performance thin-layer chromatography. Arch. Dermatol. Res. 2001, 293, 191–199. [Google Scholar] [CrossRef]
- Masukawa, Y.; Narita, H.; Sato, H.; Naoe, A.; Kondo, N.; Sugai, Y.; Oba, T.; Homma, R.; Ishikawa, J.; Takagi, Y. Comprehensive quantification of ceramide species in human stratum corneum. J. Lipid Res. 2009, 50, 1708–1719. [Google Scholar] [CrossRef]
- t’Kindt, R.; Jorge, L.; Dumont, E.; Couturon, P.; David, F.; Sandra, P.; Sandra, K. Profiling and characterizing skin ceramides using reversed-phase liquid chromatography–quadrupole time-of-flight mass spectrometry. Anal. Chem. 2012, 84, 403–411. [Google Scholar] [CrossRef]
- van Smeden, J.; Boiten, W.A.; Hankemeier, T.; Rissmann, R.; Bouwstra, J.A.; Vreeken, R.J. Combined LC/MS-platform for analysis of all major stratum corneum lipids, and the profiling of skin substitutes. Biochim. Biophys. Acta Mol. Cell Biol. Lipids 2014, 1841, 70–79. [Google Scholar] [CrossRef]
- Breathnach, A.S.; Goodman, T.; Stolinski, C.; Gross, M. Freeze-fracture replication of cells of stratum corneum of human epidermis. J. Anat. 1973, 114, 65–81. [Google Scholar]
- Elias, P.M.; Friend, D.S. The permeability barrier in mammalian epidermis. J. Cell Biol. 1975, 65, 180–191. [Google Scholar] [CrossRef]
- Swartzendruber, D.C.; Wertz, P.W.; Kitko, D.J.; Madison, K.C.; Downing, D.T. Molecular models of the intercellular lipid lamellae in mammalian stratum corneum. J. Investig. Dermatol. 1989, 92, 251–257. [Google Scholar] [CrossRef]
- Hill, J.R.; Wertz, P.W. Molecular models of the intercellular lipid lamellae from epidermal stratum corneum. Biochim. Biophys. Acta 2003, 1616, 121–126. [Google Scholar] [CrossRef]
- Bouwstra, J.; Dubbelaar, F.; Gooris, G.; Ponec, M. The lipid organisation in the skin barrier. Acta Derm. Venereol. Suppl. 2000, 80, 23–30. [Google Scholar]
- Norlén, L. Skin barrier structure and function: The single gel phase model. J. Investig. Dermatol. 2001, 117, 830–836. [Google Scholar] [CrossRef]
- Lundborg, M.; Narangifard, A.; Wennberg, C.L.; Lindahl, E.; Daneholt, B.; Norlen, L. Human skin barrier structure and function analyzed by cryo-EM and molecular dynamics simulation. J. Struct. Biol. 2018, 203, 149–161. [Google Scholar] [CrossRef]
- Bouwstra, J.A.; Nădăban, A.; Bras, W.; McCabe, C.; Bunge, A.; Gooris, G.S. The skin barrier: An extraordinary interface with an exceptional lipid organization. Prog. Lipid Res. 2023, 92, 101252. [Google Scholar] [CrossRef]
- Naik, A.; Kalia, Y.N.; Guy, R.H. Transdermal drug delivery: Overcoming the skin's barrier function. Pharm. Sci. Technol. Today 2000, 3, 318–326. [Google Scholar] [CrossRef]
- Souto, E.B.; Fangueiro, J.F.; Fernandes, A.R.; Cano, A.; Sanchez-Lopez, E.; Garcia, M.L.; Severino, P.; Paganelli, M.O.; Chaud, M.V.; Silva, A.M. Physicochemical and biopharmaceutical aspects influencing skin permeation and role of SLN and NLC for skin drug delivery. Heliyon 2022, 8, e08938. [Google Scholar] [CrossRef]
- Patil, U.K.; Saraogi, R. Natural products as potential drug permeation enhancer in transdermal drug delivery system. Arch. Dermatol. Res. 2014, 306, 419–426. [Google Scholar] [CrossRef]
- Marwah, H.; Garg, T.; Goyal, A.K.; Rath, G. Permeation enhancer strategies in transdermal drug delivery. Drug Deliv. 2016, 23, 564–578. [Google Scholar] [CrossRef]
- Williams, A.C.; Barry, B.W. Penetration enhancers. Adv. Drug Deliv. Rev. 2004, 56, 603–618. [Google Scholar] [CrossRef]
- Lian, G.; Chen, L.; Han, L. An evaluation of mathematical models for predicting skin permeability. J. Pharm. Sci. 2008, 97, 584–598. [Google Scholar] [CrossRef]
- Mitragotri, S.; Anissimov, Y.G.; Bunge, A.L.; Frasch, H.F.; Guy, R.H.; Hadgraft, J.; Kasting, G.B.; Lane, M.E.; Roberts, M.S. Mathematical models of skin permeability: An overview. Int. J. Pharm. 2011, 418, 115–129. [Google Scholar] [CrossRef]
- Lee, C.T.; Comer, J.; Herndon, C.; Leung, N.; Pavlova, A.; Swift, R.V.; Tung, C.; Rowley, C.N.; Amaro, R.E.; Chipot, C.; et al. Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds. J. Chem. Inf. Model. 2016, 56, 721–733. [Google Scholar] [CrossRef]
- Marrink, S.J.; Berendsen, H.J.C. Permeation Process of Small Molecules across Lipid Membranes Studied by Molecular Dynamics Simulations. J. Phys. Chem. 1996, 100, 16729–16738. [Google Scholar] [CrossRef]
- Das, C.; Olmsted, P.D.; Noro, M.G. Water permeation through stratum corneum lipid bilayers from atomistic simulations. Soft Matter 2009, 5, 4549–4555. [Google Scholar] [CrossRef]
- Shamaprasad, P.; Frame, C.O.; Moore, T.C.; Yang, A.; Iacovella, C.R.; Bouwstra, J.A.; Bunge, A.L.; McCabe, C. Using molecular simulation to understand the skin barrier. Prog. Lipid Res. 2022, 88, 101184. [Google Scholar] [CrossRef]
- Gupta, R.; Sridhar, D.; Rai, B. Molecular dynamics simulation study of permeation of molecules through skin lipid bilayer. J. Phys. Chem. B 2016, 120, 8987–8996. [Google Scholar] [CrossRef]
- Gupta, R.; Badhe, Y.; Rai, B.; Mitragotri, S. Molecular mechanism of the skin permeation enhancing effect of ethanol: A molecular dynamics study. RSC Adv. 2020, 10, 12234–12248. [Google Scholar] [CrossRef]
- Gupta, R.; Dwadasi, B.S.; Rai, B.; Mitragotri, S. Effect of Chemical Permeation Enhancers on Skin Permeability: In silico screening using Molecular Dynamics simulations. Sci. Rep. 2019, 9, 1456. [Google Scholar] [CrossRef]
- Corkery, R.W.; Hyde, S.T. On the Swelling of Amphiphiles in Water. Langmuir ACS J. Surf. Colloids 1996, 12, 5528–5529. [Google Scholar] [CrossRef]
- Gruzinov, A.Y.; Zabelin, A.V.; Kiselev, M.A. Short periodicity phase based on ceramide [AP] in the model lipid membranes of stratum corneum does not change during hydration. Chem. Phys. Lipids 2017, 202, 1–5. [Google Scholar] [CrossRef]
- Kiselev, M.A.; Ryabova, N.Y.; Balagurov, A.M.; Dante, S.; Hauss, T.; Zbytovska, J.; Wartewig, S.; Neubert, R.H. New insights into the structure and hydration of a stratum corneum lipid model membrane by neutron diffraction. Eur. Biophys. J. EBJ 2005, 34, 1030–1040. [Google Scholar] [CrossRef]
- Bouwstra, J.A.; de Graaff, A.; Gooris, G.S.; Nijsse, J.; Wiechers, J.W.; van Aelst, A.C. Water distribution and related morphology in human stratum corneum at different hydration levels. J. Investig. Dermatol. 2003, 120, 750–758. [Google Scholar] [CrossRef]
- Schmitt, T.; Lange, S.; Dobner, B.; Sonnenberger, S.; Hauss, T.; Neubert, R.H.H. Investigation of a CER[NP]- and [AP]-Based Stratum Corneum Modeling Membrane System: Using Specifically Deuterated CER Together with a Neutron Diffraction Approach. Langmuir ACS J. Surf. Colloids 2018, 34, 1742–1749. [Google Scholar] [CrossRef]
- Bouwstra, J.A.; Gooris, G.S.; van der Spek, J.A.; Bras, W. Structural investigations of human stratum corneum by small-angle X-ray scattering. J. Investig. Dermatol. 1991, 97, 1005–1012. [Google Scholar] [CrossRef]
- Groen, D.; Gooris, G.S.; Barlow, D.J.; Lawrence, M.J.; van Mechelen, J.B.; Deme, B.; Bouwstra, J.A. Disposition of ceramide in model lipid membranes determined by neutron diffraction. Biophys. J. 2011, 100, 1481–1489. [Google Scholar] [CrossRef]
- Schmitt, T.; Neubert, R.H.H. State of the Art in Stratum Corneum Research. Part II: Hypothetical Stratum Corneum Lipid Matrix Models. Ski. Pharmacol. Physiol. 2020, 33, 213–230. [Google Scholar] [CrossRef]
- Lundborg, M.; Wennberg, C.L.; Narangifard, A.; Lindahl, E.; Norlén, L. Predicting drug permeability through skin using molecular dynamics simulation. J. Control Release 2018, 283, 269–279. [Google Scholar] [CrossRef]
- Bouwstra, J.A.; Gooris, G.S.; Dubbelaar, F.; Ponec, M. Phase behavior of lipid mixtures based on human ceramides: Coexistence of crystalline and liquid phases. J. Lipid Res. 2001, 42, 1759–1770. [Google Scholar] [CrossRef]
- Wang, E.; Klauda, J.B. Simulations of Pure Ceramide and Ternary Lipid Mixtures as Simple Interior Stratum Corneum Models. J. Phys. Chem. B 2018, 122, 2757–2768. [Google Scholar] [CrossRef]
- Awoonor-Williams, E.; Rowley, C.N. Molecular simulation of nonfacilitated membrane permeation. Biochim. Biophys. Acta Biomembr. 2016, 1858, 1672–1687. [Google Scholar] [CrossRef]
- Cheng, T.; Zhao, Y.; Li, X.; Lin, F.; Xu, Y.; Zhang, X.; Li, Y.; Wang, R.; Lai, L. Computation of octanol− water partition coefficients by guiding an additive model with knowledge. J. Chem. Inf. Model. 2007, 47, 2140–2148. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem in 2021: New data content and improved web interfaces. Nucleic Acids Res. 2021, 49, D1388–D1395. [Google Scholar] [CrossRef]
- Astley, J.P.; Levine, M. Effect of dimethyl sulfoxide on permeability of human skin in vitro. J. Pharm. Sci. 1976, 65, 210–215. [Google Scholar] [CrossRef]
- Barber, E.D.; Teetsel, N.M.; Kolberg, K.F.; Guest, D. A comparative study of the rates of in vitro percutaneous absorption of eight chemicals using rat and human skin. Fundam. Appl. Toxicol. 1992, 19, 493–497. [Google Scholar] [CrossRef]
- Mitragotri, S.; Blankschtein, D.; Langer, R. Transdermal drug delivery using low-frequency sonophoresis. Pharm. Res. 1996, 13, 411–420. [Google Scholar] [CrossRef]
- Bond, J.R.; Barry, B.W. Limitations of hairless mouse skin as a model for in vitro permeation studies through human skin: Hydration damage. J. Investig. Dermatol. 1988, 90, 486–489. [Google Scholar] [CrossRef]
- Clowes, H.M.; Scott, R.C.; Heylings, J.R. Skin absorption: Flow-through or static diffusion cells. Toxicol. Vitr. 1994, 8, 827–830. [Google Scholar] [CrossRef]
- Rigg, P.C.; Barry, B.W. Shed snake skin and hairless mouse skin as model membranes for human skin during permeation studies. J. Investig. Dermatol. 1990, 94, 235–240. [Google Scholar] [CrossRef]
- Scott, R.C.; Corrigan, M.A.; Smith, F.; Mason, H. The influence of skin structure on permeability: An intersite and interspecies comparison with hydrophilic penetrants. J. Investig. Dermatol. 1991, 96, 921–925. [Google Scholar] [CrossRef]
- Barber, E.D.; Hill, T.; Schum, D.B. The percutaneous absorption of hydroquinone (HQ) through rat and human skin in vitro. Toxicol. Lett. 1995, 80, 167–172. [Google Scholar] [CrossRef]
- Blank, I.H.; McAuliffe, D.J. Penetration of benzene through human skin. J. Investig. Dermatol. 1985, 85, 522–526. [Google Scholar] [CrossRef]
- Mitragotri, S.; Edwards, D.A.; Blankschtein, D.; Langer, R. A mechanistic study of ultrasonically-enhanced transdermal drug delivery. J. Pharm. Sci. 1995, 84, 697–706. [Google Scholar] [CrossRef]
- Galey, W.R.; Lonsdale, H.K.; Nacht, S. The in vitro permeability of skin and buccal mucosa to selected drugs and tritiated water. J. Investig. Dermatol. 1976, 67, 713–717. [Google Scholar] [CrossRef]
- Goodman, M.; Barry, B.W. Action of penetration enhancers on human skin as assessed by the permeation of model drugs 5-fluorouracil and estradiol. I. Infinite dose technique. J. Investig. Dermatol. 1988, 91, 323–327. [Google Scholar] [CrossRef]
- Johnson, M.E.; Blankschtein, D.; Langer, R. Permeation of steroids through human skin. J. Pharm. Sci. 1995, 84, 1144–1146. [Google Scholar] [CrossRef]
- Johnson, M.E.; Mitragotri, S.; Patel, A.; Blankschtein, D.; Langer, R. Synergistic effects of chemical enhancers and therapeutic ultrasound on transdermal drug delivery. J. Pharm. Sci. 1996, 85, 670–679. [Google Scholar] [CrossRef]
- Knutson, K.; Harrison, D.; Pershing, L.; Goates, C. Transdermal absorption of steroids. J. Control Release 1993, 24, 95–108. [Google Scholar] [CrossRef]
- Michaels, A.S.; Chandrasekaran, S.K.; Shaw, J.E. Drug permeation through human skin: Theory and invitro experimental measurement. AIChE J. 1975, 21, 985–996. [Google Scholar] [CrossRef]
- Stepanov, D.; Canipa, S.; Wolber, G. HuskinDB, a database for skin permeation of xenobiotics. Sci. Data 2020, 7, 426. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, Q.D.; Chai, Y.P.; Zhang, H.; Peng, P.; Yang, X.X. Natural Terpenes as Penetration Enhancers for Transdermal Drug Delivery. Molecules 2016, 21, 1709. [Google Scholar] [CrossRef]
- Hmingthansanga, V.; Singh, N.; Banerjee, S.; Manickam, S.; Velayutham, R.; Natesan, S. Improved Topical Drug Delivery: Role of Permeation Enhancers and Advanced Approaches. Pharmaceutics 2022, 14, 2818. [Google Scholar] [CrossRef]
- Herman, A.; Herman, A.P. Essential oils and their constituents as skin penetration enhancer for transdermal drug delivery: A review. J. Pharm. Pharmacol. 2015, 67, 473–485. [Google Scholar] [CrossRef]
- El-Kattan, A.F.; Asbill, C.S.; Michniak, B.B. The effect of terpene enhancer lipophilicity on the percutaneous permeation of hydrocortisone formulated in HPMC gel systems. Int. J. Pharm. 2000, 198, 179–189. [Google Scholar] [CrossRef]
- Schrödinger Release 2022-3; Maestro, Schrödinger LLC: New York, NY, USA, 2021.
- Martinez, L.; Andrade, R.; Birgin, E.G.; Martinez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Berendsen, H.J.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅ log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Wu, E.L.; Cheng, X.; Jo, S.; Rui, H.; Song, K.C.; Dávila-Contreras, E.M.; Qi, Y.; Lee, J.; Monje-Galvan, V.; Venable, R.M.; et al. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J. Comput. Chem. 2014, 35, 1997–2004. [Google Scholar] [CrossRef]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef]
- Kucerka, N.; Katsaras, J.; Nagle, J.F. Comparing membrane simulations to scattering experiments: Introducing the SIMtoEXP software. J. Membr. Biol. 2010, 235, 43–50. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Diamond, J.M.; Katz, Y. Interpretation of nonelectrolyte partition coefficients between dimyristoyl lecithin and water. J. Membr. Biol. 1974, 17, 121–154. [Google Scholar] [CrossRef]
- Marrink, S.-J.; Berendsen, H.J.C. Simulation of water transport through a lipid membrane. J. Phys. Chem. 1994, 98, 4155–4168. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Hub, J.S.; de Groot, B.L.; van der Spoel, D. g_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput. 2010, 6, 3713–3720. [Google Scholar] [CrossRef]
- Hummer, G. Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations. New J. Phys. 2005, 7, 34. [Google Scholar] [CrossRef]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]


| Permeability Coefficients Calculated Using the Built Model log P (cm/s) | Range of Permeability Coefficients Reported in Experimental Studies log P (cm/s) | log KOW | Permeability Coefficients Reported in Previous MD Simulation Studies log P (cm/s) | ||
|---|---|---|---|---|---|
| Study 1 ′ | Study 2 ″ | ||||
| Water | −6.45 | −5.34–−7.08 a,b,c,d,e,f,g,h | −0.5 | −4.15 | −8.26 |
| Benzene | −0.11 | −4.35–−4.51 i,j | 2.1 | 0.28 | −4.56 |
| Estradiol | 1.16 | −4.81–−6.68 c,k,l,m,n,o,p,j | 4 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radhakrishnan, N.; Kaul, S.C.; Wadhwa, R.; Yang, L.-W.; Sundar, D. Establishing a General Atomistic Model for the Stratum Corneum Lipid Matrix Based on Experimental Data for Skin Permeation Studies. Int. J. Mol. Sci. 2025, 26, 674. https://doi.org/10.3390/ijms26020674
Radhakrishnan N, Kaul SC, Wadhwa R, Yang L-W, Sundar D. Establishing a General Atomistic Model for the Stratum Corneum Lipid Matrix Based on Experimental Data for Skin Permeation Studies. International Journal of Molecular Sciences. 2025; 26(2):674. https://doi.org/10.3390/ijms26020674
Chicago/Turabian StyleRadhakrishnan, Navaneethan, Sunil C. Kaul, Renu Wadhwa, Lee-Wei Yang, and Durai Sundar. 2025. "Establishing a General Atomistic Model for the Stratum Corneum Lipid Matrix Based on Experimental Data for Skin Permeation Studies" International Journal of Molecular Sciences 26, no. 2: 674. https://doi.org/10.3390/ijms26020674
APA StyleRadhakrishnan, N., Kaul, S. C., Wadhwa, R., Yang, L.-W., & Sundar, D. (2025). Establishing a General Atomistic Model for the Stratum Corneum Lipid Matrix Based on Experimental Data for Skin Permeation Studies. International Journal of Molecular Sciences, 26(2), 674. https://doi.org/10.3390/ijms26020674







