CG-Based Stratification of 8-mers Highlights Functional Roles and Phylogenetic Divergence Markers
Abstract
1. Introduction
2. Results
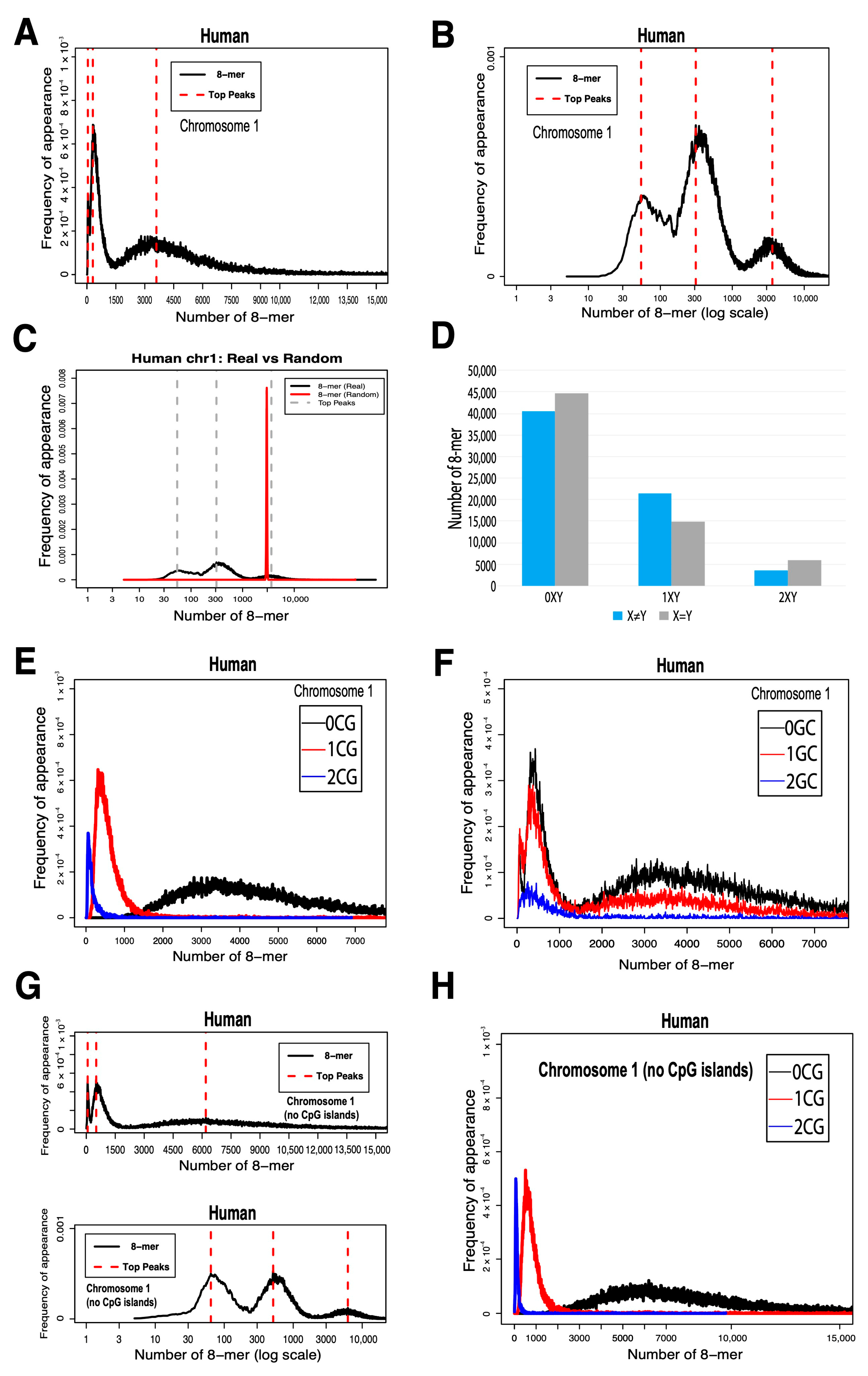
2.1. 8-mer Distribution in Human Chromosome 1
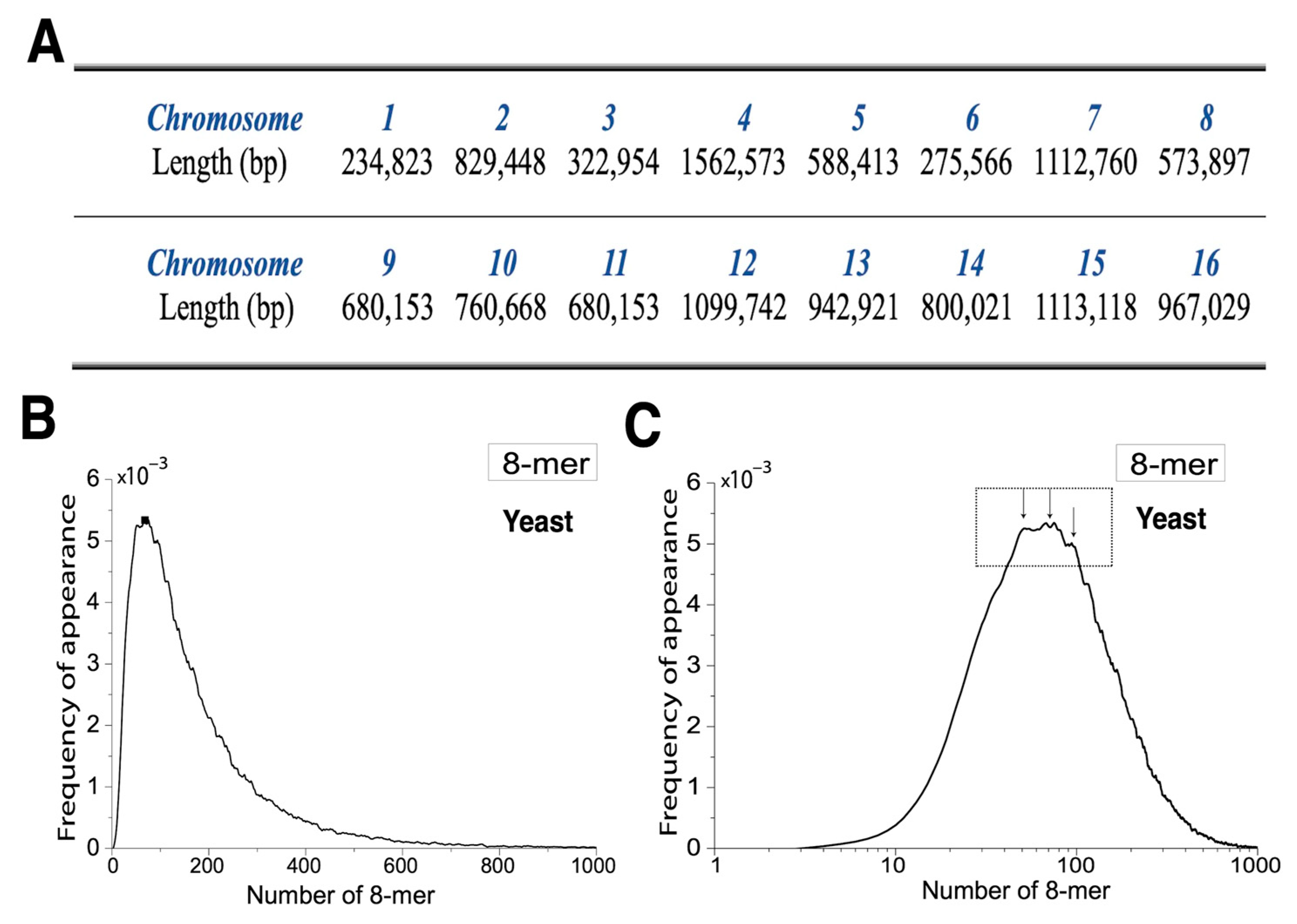
2.2. Distribution of 8-mer Frequency of Appearance in Yeast
2.3. The 8-mer Distribution of Yeast Based on the XY Dinucleotide Classification
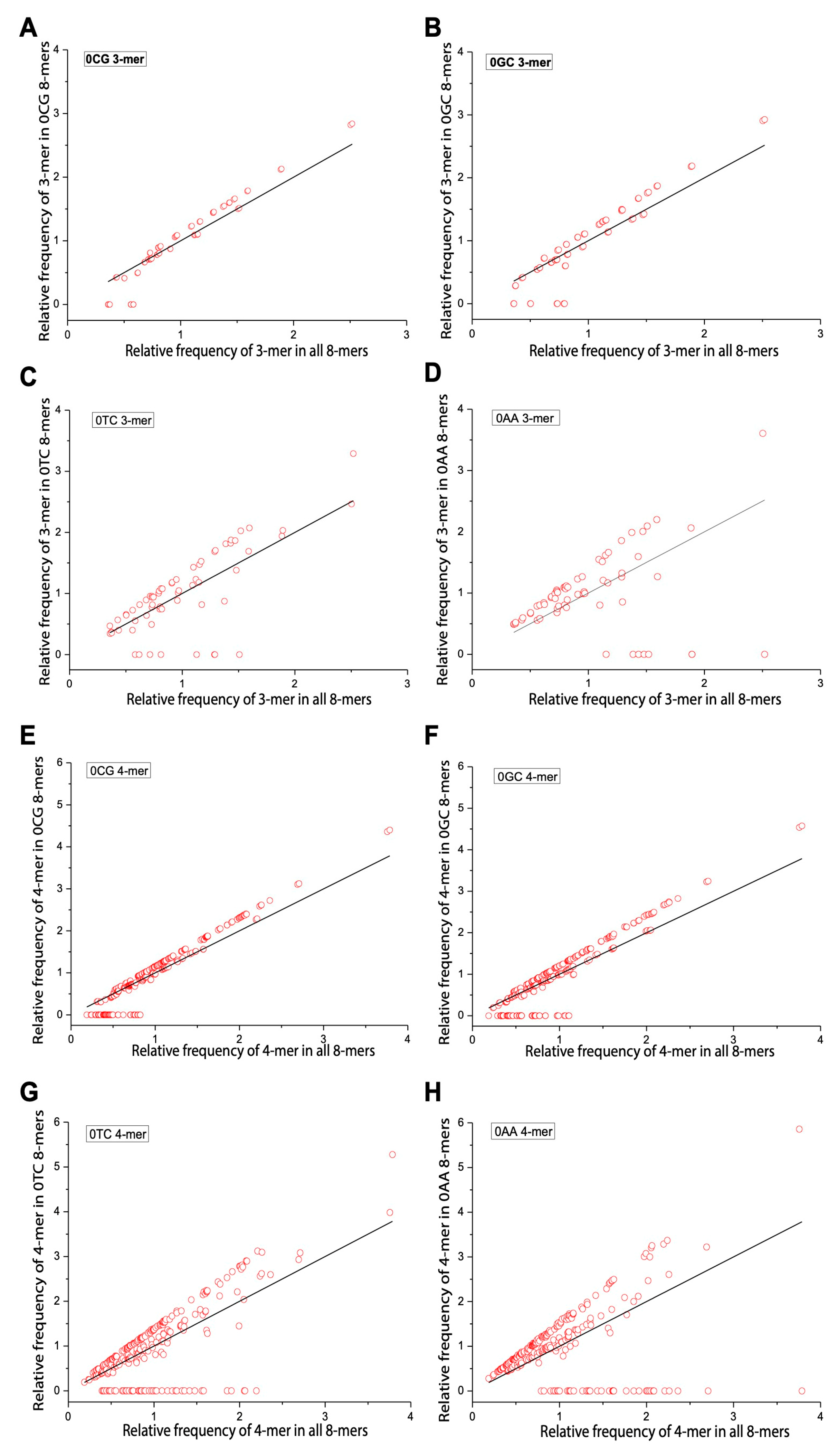
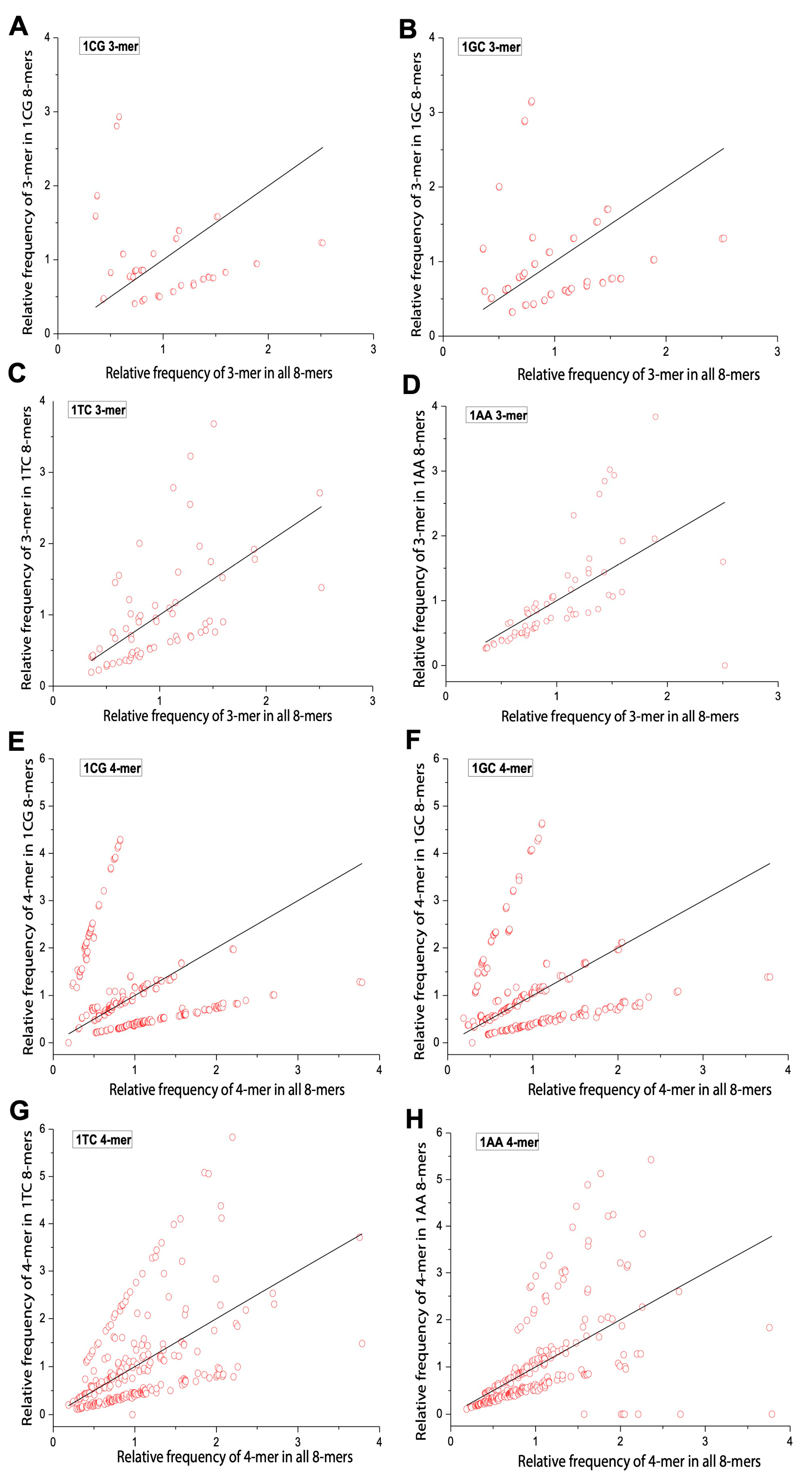
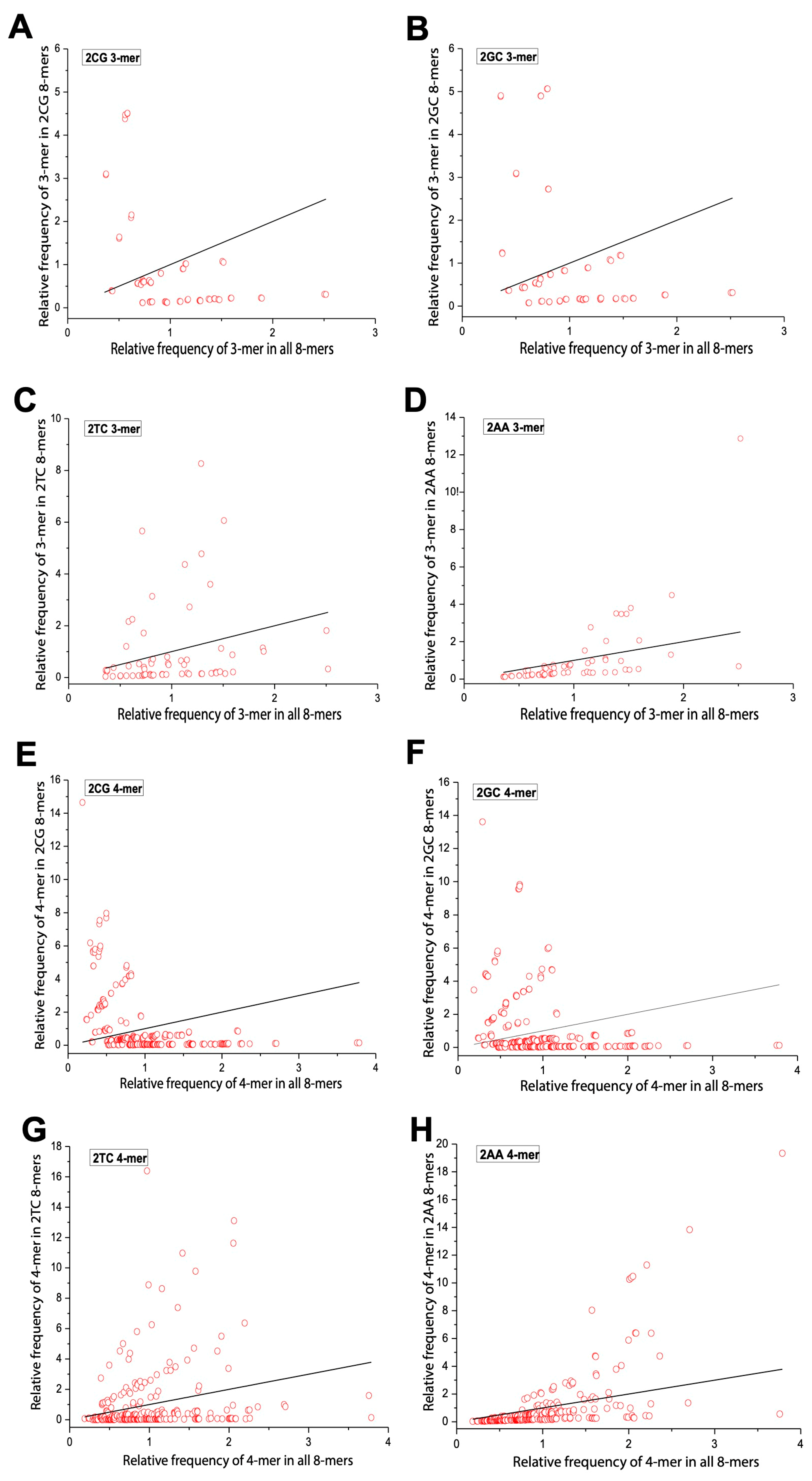
2.4. Comparison of m-mer Usage in 8-mers Classified by 0XY, 1XY, 2XY
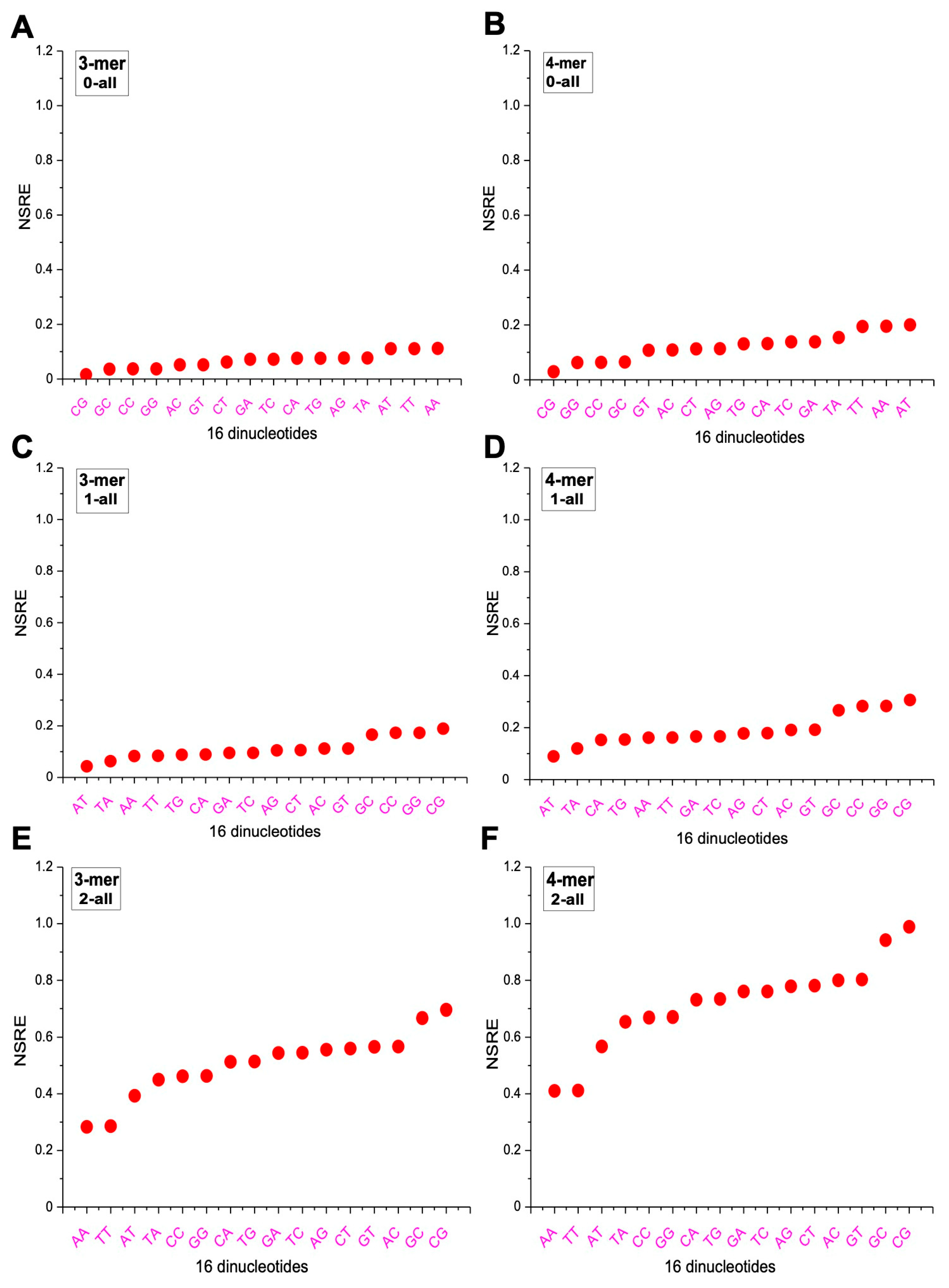
2.5. Differences in m-mer Usage Based on NSRE
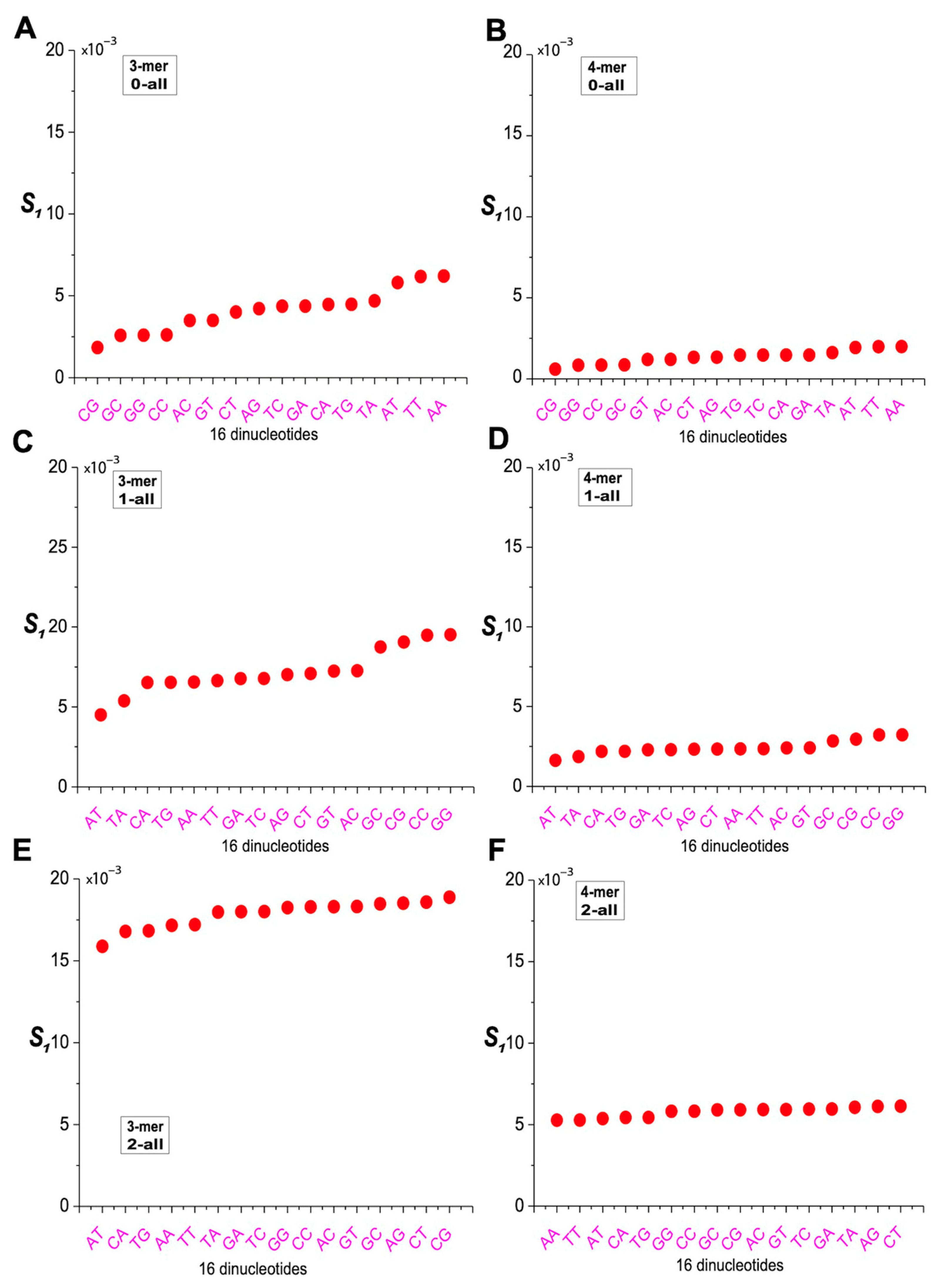
2.6. Characterization of m-mer Usage Bias Based on Distance Differences
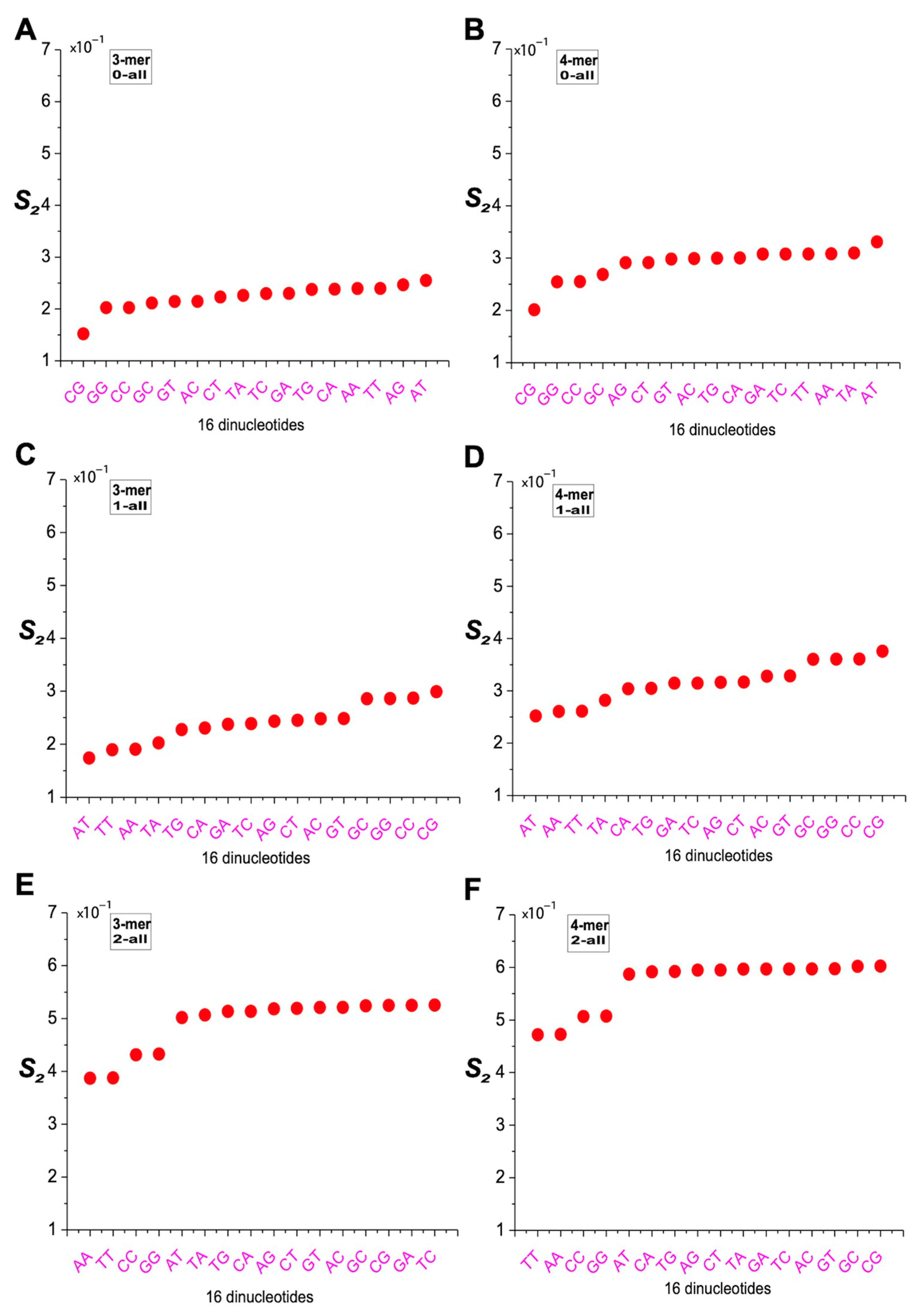
2.7. Characterization of m-mer Usage Bias Based on Angular Deviation
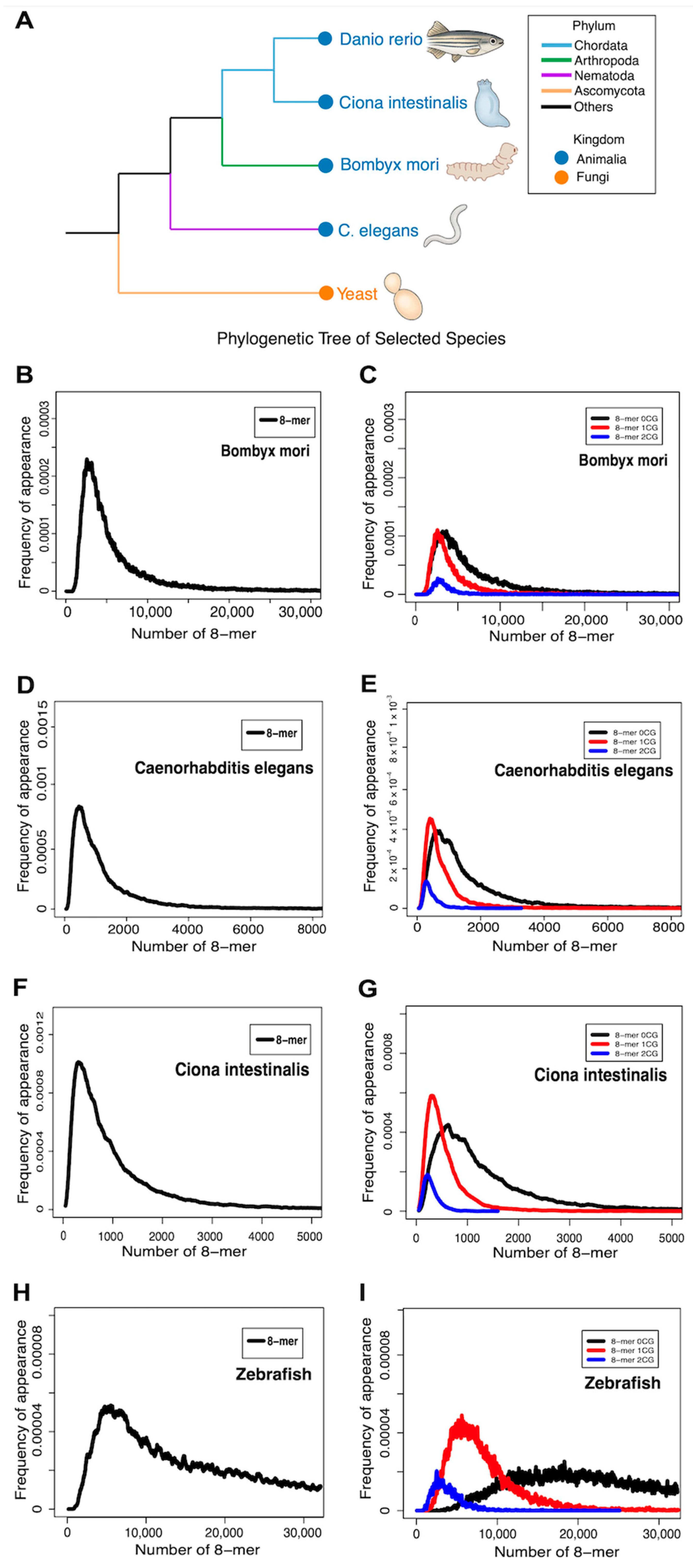
2.8. Comparative Analysis of CG-Classified 8-mers Reveals Evolutionary Trends
3. Discussion
4. Materials and Methods
4.1. Acquisition and Assembly of Whole Genome Sequences
4.2. Definition of k-mer Frequency of Appearance (FA)
4.3. Definition of the Relative Frequency of m-mers Within 8-mers
4.4. Definition of New Symmetric Relative Entropy
4.5. Definitions of Distance Difference and Angular Deviation
4.6. Definition of Peak Distance Difference
4.7. Definition of Nonparametric Permutation Test
5. Conclusions
- Human chromosome 1 exhibits a trimodal distribution of 8-mers classified by CG dinucleotide content, where 0CG motifs align with random distributions, while 1CG and 2CG motifs show significant deviations, indicating possible functional constraints.
- The unimodal distribution of 8-mers may arise from the close clustering of the distribution centers of 0CG, 1CG, and 2CG motifs.
- Comparative studies across species show that differences in CG-classified 8-mer distributions correlate with evolutionary complexity.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Choi, J.K.; Kim, Y.J. Epigenetic regulation and the variability of gene expression. Nat. Genet. 2008, 40, 141–147. [Google Scholar] [CrossRef]
- Choi, J.K.; Kim, Y.J. Intrinsic variability of gene expression encoded in nucleosome positioning sequences. Nat. Genet. 2009, 41, 498–503. [Google Scholar] [CrossRef]
- Stunkel, W.; Kober, I.; Seifart, K.H. A nucleosome positioned in the Distal promoter region activates transcription of the human U6 gene. Mol. Cell. Biol. 1997, 17, 4397–4405. [Google Scholar] [CrossRef]
- Kornberg, R.D.; Lorch, Y. Twenty-five years of the nucleosome: Fundamental particle of the eukaiyote chromosome. Cell 1999, 98, 285–294. [Google Scholar] [CrossRef]
- Jiang, C.; Pugh, B.F. Nucleosome positioning and gene regulation: Anvances through genomics. Nat. Rev. Genet. 2009, 10, 161–172. [Google Scholar] [CrossRef]
- Segal, E.; Widom, J. What controls nucleosome positions? Trends Genet. 2009, 25, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Panyukov, V.V.; Kiselev, S.S.; Ozoline, O.N. Unique k-mers as Strain-Specific Barcodes for Phylogenetic Analysis and Natural Microbiome Profiling. Int. J. Mol. Sci. 2020, 21, 944. [Google Scholar] [CrossRef] [PubMed]
- Nilamyani, A.N.; Auliah, F.N.; Moni, M.A.; Shoombuatong, W.; Hasan, M.M.; Kurata, H. PredNTS: Improved and Robust Prediction of Nitrotyrosine Sites by Integrating Multiple Sequence Features. Int. J. Mol. Sci. 2021, 22, 2704. [Google Scholar] [CrossRef]
- Francino, M.P.; Ochman, H. Strand symmetry around the beta-globin origin of replication inprimates. Mol. Biol. Evol. 2000, 17, 416–422. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Hughes, T.R.; Morris, Q. RankMotif++: A motif-search algorithm that accounts for relative ranks of K-mers in binding transcription factors. Bioinformatics 2007, 23, i72–i79. [Google Scholar] [CrossRef]
- Bultrini, E.; Pizzi, E.; Del Giudice, P.; Frontali, C. Pentamer vocabularies characterizing introns and intron-like intergenic tracts from Caenorhabditis elegans and Drosophila melanogaster. Gene 2003, 304, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Han, S.; Zhang, H.; Li, Y. RPITER: A Hierarchical Deep Learning Framework for ncRNA−Protein Interaction Prediction. Int. J. Mol. Sci. 2019, 20, 1070. [Google Scholar] [CrossRef]
- Kaplan, N.; Moore, I.K.; Fondufe-Mittendorf, Y.; Gossett, A.J.; Tillo, D.; Field, Y.; LeProust, E.M.; Hughes, T.R.; Lieb, J.D.; Widom, J.; et al. The DNA-encoded nucleosome organization of a eukaryotic genome. Nature 2009, 458, 362–366. [Google Scholar] [CrossRef]
- Ogawa, R.; Kitagawa, N.; Ashida, H.; Saito, R.; Tomita, M. Computational prediction of nucleosome positioning by calculating the relative fragment frequency index of nucleosomal sequences. FEBS Lett. 2010, 584, 1498–1502. [Google Scholar] [CrossRef]
- Ruan, H.; Wang, Y.H. Friedreich’s ataxia GAA TTC duplex and GAA GAA TTC triplex structures exclude nucleosome assembly. J. Mol. Biol. 2008, 383, 292–300. [Google Scholar] [CrossRef]
- Wang, Y.H.; Griffith, J. Expanded CTG triplet blocks from the myotonic dystrophy gene createthe strongest known natural nucleosome positioning elements. Genomics 1995, 25, 570–573. [Google Scholar] [CrossRef]
- Marchet, C.; Boucher, C.; Puglisi, S.J.; Medvedev, P.; Salson, M.; Chikhi, R. Data structures based on k-mers for querying large collections of sequencing data sets. Genome Res. 2021, 31, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Schones, D.E.; Cui, K.; Cuddapah, S.; Roh, T.Y.; Barski, A.; Wang, Z.; Wei, G.; Zhao, K. Dynamic regulation of nucleosome positioning in the human genome. Cell 2008, 132, 887–898. [Google Scholar] [CrossRef]
- Hesse, U. K-Mer-Based Genome Size Estimation in Theory and Practice. Methods Mol. Biol. 2023, 2672, 79–113. [Google Scholar]
- Hughes, A.L.; Jin, Y.; Rando, O.J.; Struhl, K. A functional evolutionary approach to identify determinants of nucleosome positioning: A unifying model for establishing the genome-wide pattern. Cell 2012, 48, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Karikari, B.; Lemay, M.A.; Belzile, F. k-mer-Based Genome-Wide Association Studies in Plants: Advances, Challenges, and Perspectives. Genes 2023, 14, 1439. [Google Scholar] [CrossRef]
- Fofanov, Y.; Luo, Y.; Katili, C.; Wang, J.; Belosludtsev, Y.; Powdrill, T.; Belapurkar, C.; Fofanov, V.; Li, T.B.; Chumakov, S.; et al. How independent are the appearances of n-mers in different genomes? Bioinformatics 2004, 20, 2421–2428. [Google Scholar] [CrossRef] [PubMed]
- Reinert, G.; Schbath, S.; Waterman, M.S. Probabilistic and statistical properties of words: An overview. J. Comput. Biol. 2000, 7, 1–46. [Google Scholar] [CrossRef] [PubMed]
- Chor, B.; Horn, D.; Goldman, N.; Levy, Y.; Massingham, T. Genomic DNA k-mer spectra. models and modalities. Genome Biol. 2009, 10, R108. [Google Scholar] [CrossRef]
- Xie, H.; Hao, B. Visualization of K-tuple distribution in procaryote complete genomes and their randomized counterparts. Proc. IEEE Comput. Soc. Bioinform. Conf. 2002, 1, 31–42. [Google Scholar]
- Hsieh, L.C.; Luo, L.F.; Lee, H.C. Short segmental duplication: Parsimony in growth of microbial genomes. Genome Biol. 2003, 4, 7. [Google Scholar] [CrossRef]
- Stacey, K.J.; Young, G.R.; Clark, F.; Sester, D.P.; Roberts, T.L.; Naik, S.; Sweet, M.J.; Hume, D.A. The molecular basis for the lack of immunostimulatory activity of verterbrate DNA. J. Immunol. 2003, 170, 3614–3620. [Google Scholar] [CrossRef]
- Chen, Y.H.; Nyeo, S.L.; Yeh, C.Y. Model for the distributions of k-mers in DNA sequences. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005, 72, 011908. [Google Scholar] [CrossRef]
- Choi, J.K. Contrasting chromatin organization of CpG islands and exons in the human genome. Genome Biol. 2010, 11, R70. [Google Scholar] [CrossRef]
- Brown, W.R.; Bird, A.P. Long-range restriction site mapping of mammalian genomic DNA. Nature 1986, 322, 477–481. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, H.; Li, X. Effect of the Nucleosome-Depleted Region in the Transcribed Regions of Saccharomyces cerevisiae Genes on Exogenous Gene Expression. Appl. Sci. 2024, 14, 11339. [Google Scholar] [CrossRef]
- Jia, Y.; Li, H.; Wang, J.; Meng, H.; Yang, Z. Spectrum structures and biological functions of 8-mers in the human genome. Genomics 2019, 111, 483–491. [Google Scholar] [CrossRef]
- Meng, H.; Li, H.; Yang, Z.; Si, Y. Nucleosome sliding mechanism based on the potential energy of sequence. Gen. Physiol. Biophys. 2020, 39, 269–276. [Google Scholar] [CrossRef]
- Mohamed Hashim, E.K.; Abdullah, R. Rare k-mer DNA: Identification of sequence motifs and prediction of CpG island and promoter. J. Theor. Biol. 2015, 387, 88–100. [Google Scholar] [CrossRef]
- Kogan, S.B.; Kato, M.; Kiyama, R.; Trifonov, E.N. Sequence structure of human nucleosome DNA. J. Biomol. Struct. Dyn. 2006, 24, 43–48. [Google Scholar] [CrossRef]
- Gupta, S.; Dennis, J.; Thurman, R.E.; Kingston, R.; Stamatoyannopoulos, J.A.; Noble, W.S. Predicting human nucleosome occupancy from primary sequence. PLoS Comput. Biol. 2008, 4, e1000134. [Google Scholar] [CrossRef]
- Peckham, H.E.; Thurman, R.E.; Fu, Y.; Stamatoyannopoulos, J.A.; Noble, W.S.; Struhl, K.; Weng, Z. Nucleosome positioning signals in genomic DNA. Genome Res. 2007, 17, 1170–1177. [Google Scholar] [CrossRef]
- Johnson, S.M.; Tan, F.J.; McCullough, H.L.; Riordan, D.P.; Fire, A.Z. Flexibility and constraint in the nucleosome core landscape of Caenorhabditis elegans chromatin. Genome Res. 2006, 16, 1505–1516. [Google Scholar] [CrossRef] [PubMed]
- Nyamdavaa; Li, H.; Zhou, D.L.; Yang, Y.X. Theoretical prediction and verification of the nucleosome bounding motifs. J. Inn. Mong. Univ. 2015, 46, 488–499. [Google Scholar]
- Song, H.D.; Sun, X.J.; Deng, M.; Zhang, G.W.; Zhou, Y.; Wu, X.Y.; Sheng, Y.; Chen, Y.; Ruan, Z.; Jiang, C.L.; et al. Hematopoietic gene expression profile in zebrafish kidney marrow. Proc. Natl. Acad. Sci. USA 2004, 101, 16240–16245. [Google Scholar] [CrossRef] [PubMed]
- Choi, T.Y.; Choi, T.I.; Lee, Y.R.; Choe, S.K.; Kim, C.H. Zebrafish as an animal model for biomedical research. Exp. Mol. Med. 2021, 53, 310–317. [Google Scholar] [CrossRef] [PubMed]
- FitzGerald, P.C.; Shlyakhtenko, A.; Mir, A.A.; Vinson, C. Clustering of DNA sequences in human promoters. Genome Res. 2004, 14, 1562–1574. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, M.; Mohammad-Rafiee, R. Geometrical correlations in the nucleosoma DNA conformation and the role of the covalent bonds rigidity. Nucleic Acids Res. 2011, 39, 1220–1230. [Google Scholar] [CrossRef] [PubMed]
- Travers, A.; Hiriart, E.; Churcher, M.; Caserta, M.; Di Mauro, E. The DNA sequence-dependence of nucleosome positioning in vivo and in vitro. J. Biomol. Struct. Dyn. 2010, 27, 713–724. [Google Scholar] [CrossRef] [PubMed]
- Tsankov, A.; Yanagisawa, Y.; Rhind, N.; Regev, A.; Rando, O.J. Evolutionary divergence of intrinsic and trans-regulated nucleosome positioning sequences reveals plastic rules for chromatin organization. Genome Res. 2011, 21, 1851–1862. [Google Scholar] [CrossRef]
- Goh, W.S.; Orlov, Y.; Li, J.; Clarke, N.D. Blurring of high-Resolution data shows that the effect of intrinsic nucleosome occupancy on transcription factor binding is mostly regional, not local. PLoS Comput. Biol. 2010, 6, e1000649. [Google Scholar] [CrossRef]
- Hodges, C.; Bintu, L.; Lubkowska, L.; Kashlev, M.; Bustamante, C. Nucleosomal fluctuations govern the transcription dynamics of RNA polymerase II. Science 2009, 235, 626–628. [Google Scholar] [CrossRef]
- Frith, M.C.; Valen, E.; Krogh, A.; Hayashizaki, Y.; Carninci, P.; Sandelin, A. A code for transcription initiation in mammalian genomes. Genome Res. 2008, 18, 1–12. [Google Scholar] [CrossRef]
- Yang, Z.; Li, H.; Jia, Y.; Zheng, Y.; Meng, H.; Bao, T.; Li, X.; Luo, L. Intrinsic laws of k-mer spectra of genome sequences and evolution mechanism of genomes. BMC Evol. Biol. 2020, 20, 157. [Google Scholar] [CrossRef]
- Diffley, J.F. Once and only once upon a time: Specifying and regulating origins of DNA replication in eukaryotic cells. Genes Dev. 1996, 10, 2819–2830. [Google Scholar] [CrossRef]
- Prendergast, J.G.; Semple, C.A. Widespread signatures of recent selection linked to nucleosome positioning in the human lineage. Genome Res. 2011, 21, 1777–1787. [Google Scholar] [CrossRef] [PubMed]
- Collings, C.K.; Fernandez, A.G.; Pitschka, C.G.; Hawkins, T.B.; Anderson, J.N. Oligonucleotide sequence motifs as nucleosome positioning signals. PLoS ONE 2010, 5, 1235–1244. [Google Scholar] [CrossRef]
- Fraser, R.M.; Keszenman-Pereyra, D.; Simmen, M.W.; Allan, J. High-resolution mapping of sequence-directed nucleosome positioning on genomic DNA. J. Mol. Biol. 2009, 390, 292–305. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Yang, Z.; Wu, Y.; Zhang, M. Exploring objective feature sets in constructing the evolution relationship of animal genome sequences. BMC Genom. 2023, 24, 634. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Yang, Z.; Wang, L. Distribution rules of 8-mer spectra and characterization of evolution state in animal genome sequences. BMC Genom. 2024, 25, 855. [Google Scholar] [CrossRef]
- Meng, H.; Li, H.; Zheng, Y.; Yang, Z.; Jia, Y.; Bo, S. Evolutionary analysis of nucleosome positioning sequences based on New Symmetric Relative Entropy. Genomics 2018, 110, 154–161. [Google Scholar] [CrossRef]
- Goffeau, A.; Barrell, B.G.; Bussey, H.; Davis, R.W.; Dujon, B.; Feldmann, H.; Galibert, F.; Hoheisel, J.D.; Jacq, C.; Johnston, M.; et al. Life with 6000 genes. Science 1996, 274, 546–567. [Google Scholar] [CrossRef]
- Sulston, J.E.; Schierenberg, E.; White, J.G.; Thomson, J.N. The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev. Biol. 1983, 100, 64–119. [Google Scholar] [CrossRef]
- Satoh, N. The ascidian tadpole larva: Comparative molecular development and genomics. Nat. Rev. Genet. 2003, 4, 285–295. [Google Scholar] [CrossRef] [PubMed]
- Xia, Q.; Zhou, Z.; Lu, C.; Cheng, D.; Dai, F.; Li, B.; Zhao, P.; Zha, X.; Cheng, T.; Chai, C. A draft sequence for the genome of the domesticated silkworm (Bombyx mori). Science 2004, 306, 1937–1940. [Google Scholar] [CrossRef] [PubMed]
- Howe, K.; Clark, M.D.; Torroja, C.F.; Torrance, J.; Berthelot, C.; Muffato, M.; Collins, J.E.; Humphray, S.; McLaren, K.; Matthews, L.; et al. The zebrafish reference genome sequence and its relationship to the human genome. Nature 2013, 496, 498–503. [Google Scholar] [CrossRef] [PubMed]
- Trede, N.S.; Langenau, D.M.; Traver, D.; Look, A.T.; Zon, L.I. The use of zebrafish to understand immunity. Immunity 2004, 20, 367–379. [Google Scholar] [CrossRef]
- Norton, W.H.J.; Bally-Cuif, L. Adult zebrafish as a model organism for behavioural genetics. BMC Neurosci. 2010, 11, 90. [Google Scholar] [CrossRef]
- Frontali, C.; Pizzi, E. Similarity in oligonucleotide usage in introns and intergenic regions contributes to long-range correlation in the Caenorhabditis elegans genome. Gene 1999, 232, 87–95. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, H.; Wang, Y.; Meng, H.; Zhang, Q.; Zhao, X. Evolutionary mechanism and biological functions of 8-mers containing CG dinucleotide in yeast. Chromosome Res. 2017, 25, 173–189. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Phipson, B.; Smyth, G.K. Permutation p-values should never be zero: Calculating exact p-values when permutations are randomly drawn. Stat. Appl. Genet. Mol. Biol. 2010, 9, 39. [Google Scholar] [CrossRef] [PubMed]

| Species | Version | Sequence Length | Number of Chromosomes | Source |
|---|---|---|---|---|
| Homo sapiens | GCA_000001405.15 (GRCh38) | 230,481,012 bp | 1 | UCSC |
| Saccharomyces cerevisiae (Yeast) | GCA_000146055.2 (SacCer3) | 12,312,773 bp | 16 | UCSC |
| Caenorhabditis elegans | GCF_000002985.6 (WBcel235) | 100,272,607 bp | 6 | NCBI |
| Danio rerio (Zebrafish) | GCF_000002035.6 (GRCz11) | 1,345,101,833 bp | 25 | NCBI |
| Ciona intestinalis (Sea squirt) | GCF_000224145.3 (KH) | 78,296,155 bp | 14 | NCBI |
| Bombyx mori (Silkworm) | GCF_030269925.1 (ASM3026992v2) | 461,688,958 bp | 29 | NCBI |
| 3-mer | RF | 3-mer | RF |
|---|---|---|---|
| GCG | 0.358 | TAC | 0.908 |
| CGC | 0.36 | GTA | 0.91 |
| CGG | 0.372 | TGG | 0.948 |
| CCG | 0.374 | CCA | 0.957 |
| GGG | 0.428 | ACT | 0.964 |
| CCC | 0.436 | AGT | 0.97 |
| GGC | 0.502 | TGT | 1.092 |
| GCC | 0.503 | ACA | 1.1 |
| CGT | 0.559 | GAT | 1.121 |
| ACG | 0.56 | ATC | 1.128 |
| TCG | 0.582 | GTT | 1.148 |
| CGA | 0.583 | AAC | 1.154 |
| GTC | 0.618 | ATG | 1.168 |
| GAC | 0.622 | CAT | 1.174 |
| GTG | 0.68 | TCT | 1.286 |
| CAC | 0.684 | TGA | 1.288 |
| CTC | 0.714 | TCA | 1.29 |
| GAG | 0.715 | AGA | 1.295 |
| CCT | 0.728 | CTT | 1.375 |
| AGG | 0.731 | AAG | 1.386 |
| GCT | 0.731 | TTA | 1.43 |
| AGC | 0.734 | TAA | 1.433 |
| GGT | 0.736 | TTG | 1.47 |
| ACC | 0.745 | CAA | 1.48 |
| TGC | 0.791 | TTC | 1.508 |
| GCA | 0.795 | GAA | 1.52 |
| CTG | 0.801 | TAT | 1.59 |
| CAG | 0.804 | ATA | 1.596 |
| TCC | 0.811 | ATT | 1.885 |
| GGA | 0.812 | AAT | 1.893 |
| CTA | 0.819 | TTT | 2.503 |
| TAG | 0.824 | AAA | 2.519 |
| 4-mer Rare | RF | 4-mer Optimal | RF |
|---|---|---|---|
| CGCG | 0.187 | CAAA | 2.05 |
| CGGG | 0.237 | TTCT | 2.055 |
| CCCG | 0.245 | TCTT | 2.063 |
| GCGC | 0.288 | AGAA | 2.077 |
| CCGG | 0.298 | AAGA | 2.086 |
| GGGG | 0.308 | TTTC | 2.197 |
| CCCC | 0.318 | GAAA | 2.21 |
| GCCG | 0.324 | TATT | 2.239 |
| CGGC | 0.325 | ATAT | 2.258 |
| CCGC | 0.329 | AATA | 2.262 |
| GCGG | 0.331 | AATT | 2.361 |
| GGCG | 0.348 | ATTT | 2.691 |
| GGGC | 0.351 | AAAT | 2.708 |
| CGCC | 0.353 | TTTT | 3.756 |
| GCCC | 0.356 | AAAA | 3.786 |
| Species | Observed Distance (0CG vs. 1CG) | Observed Distance (0CG vs. 2CG) | Observed Distance (1CG vs. 2CG) | Permutation p-value (0CG vs. 1CG) | Permutation p-Value (0CG vs. 2CG) | Permutation p-Value (1CG vs. 2CG) |
|---|---|---|---|---|---|---|
| Yeast | 71 | 95 | 24 | 0.3098 | 0 | 0.0015 |
| Bombyx mori | 1074 | 1037 | 37 | 0.0575 | 0 | 0.4764 |
| Caenorhabditis elegans | 211 | 318 | 107 | 0.4357 | 0 | 0 |
| Ciona intestinalis | 317 | 403 | 86 | 0.0259 | 0 | 0 |
| Zebrafish | 12,675 | 15,784 | 3109 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Meng, H.; Yang, Z.; Liu, G.; Xing, Y.; Xiao, N. CG-Based Stratification of 8-mers Highlights Functional Roles and Phylogenetic Divergence Markers. Int. J. Mol. Sci. 2025, 26, 9477. https://doi.org/10.3390/ijms26199477
Liu G, Meng H, Yang Z, Liu G, Xing Y, Xiao N. CG-Based Stratification of 8-mers Highlights Functional Roles and Phylogenetic Divergence Markers. International Journal of Molecular Sciences. 2025; 26(19):9477. https://doi.org/10.3390/ijms26199477
Chicago/Turabian StyleLiu, Guojun, Hu Meng, Zhenhua Yang, Guoqing Liu, Yongqiang Xing, and Ningkun Xiao. 2025. "CG-Based Stratification of 8-mers Highlights Functional Roles and Phylogenetic Divergence Markers" International Journal of Molecular Sciences 26, no. 19: 9477. https://doi.org/10.3390/ijms26199477
APA StyleLiu, G., Meng, H., Yang, Z., Liu, G., Xing, Y., & Xiao, N. (2025). CG-Based Stratification of 8-mers Highlights Functional Roles and Phylogenetic Divergence Markers. International Journal of Molecular Sciences, 26(19), 9477. https://doi.org/10.3390/ijms26199477




