Simulation of Fish Acute Toxicity of Pharmaceuticals Using Simplified Molecular Input Line Entry System (SMILES) Notation as a Representation of Molecular Structure
Abstract
1. Introduction
2. Results
2.1. Search for Outliers
2.2. Mechanistic Interpretation
2.3. Comparison of the Results with Other QSAR Models
3. Discussion
4. Materials and Methods
4.1. Database
- (1)
- Data provided by PREMIER were maintained;
- (2)
- The second choice was data provided by EFPIA;
- (3)
- (4)
- In case of duplicates in PREMIER data, we considered the more generic stereochemistry structure because our in silico model cannot deal with this chemical information.
- (i)
- The active training set is the set used to initially build the model, i.e., compounds of this set are used to build the predictive model.
- (ii)
- The passive training set is the inspector of the model, i.e., compounds of this set are used to assess whether the model is satisfactory for substances that are absent in the active training set.
- (iii)
- The task of the calibration set is to detect the start of the overtraining using an increased number of epochs.
- (iv)
- The validation set is used for the final validation of the predictive potential of the model.
4.2. Simulation
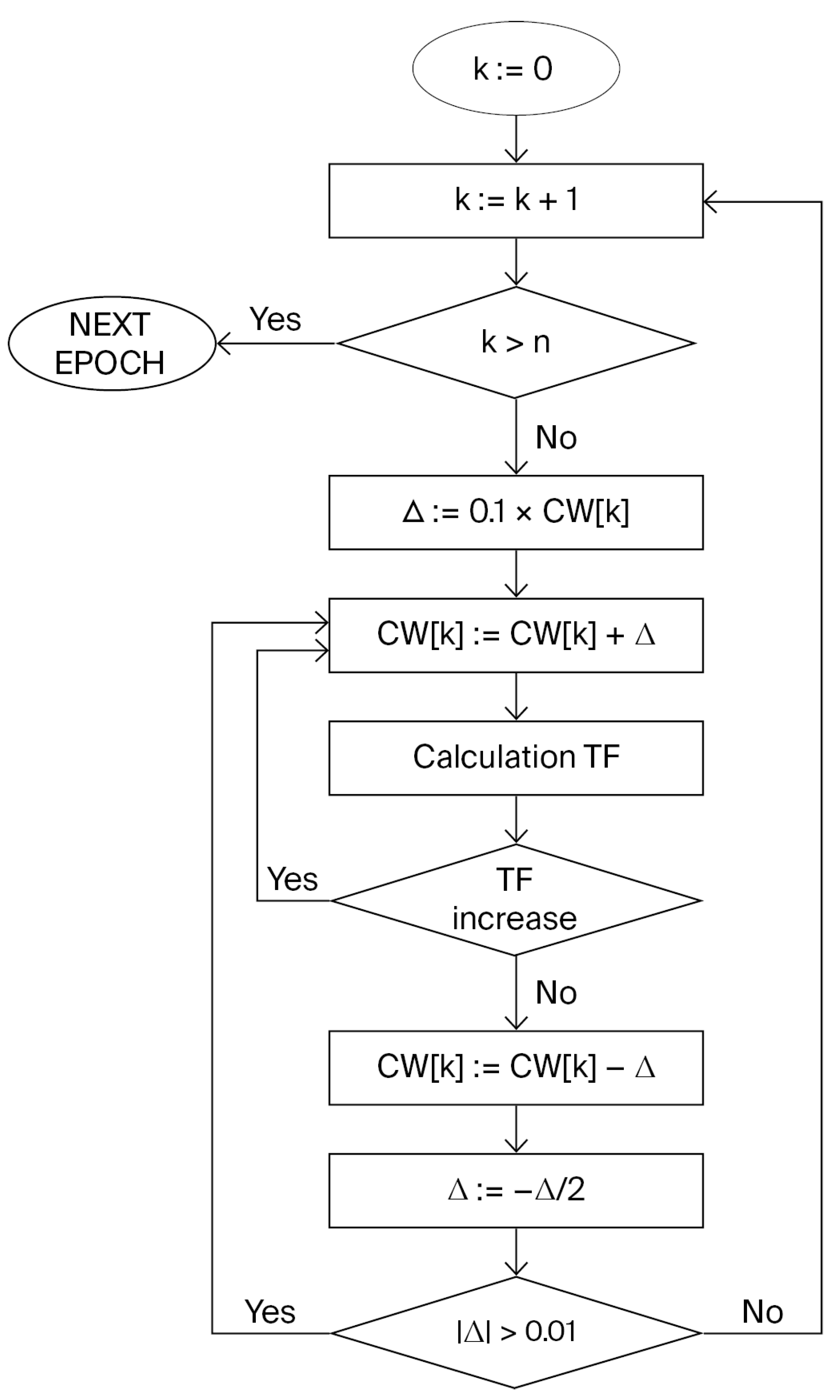
4.3. Monte Carlo Optimization
4.4. Descriptor
4.5. The Monte Carlo Optimization
4.6. Applicability Domain
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QSAR | Quantitative structure–activity relationships |
| DCW | Descriptor of correlation weights |
| SMILES | Simplified Molecular Input Line Entry System |
| CCC | Concordance correlation coefficient |
| R2 | Correlation coefficient |
| Q2 | Leave-one-out cross-validated R2 |
| RMSE | Root means squared error |
| MAE | Mean absolute error |
| F | Fischer F-ratio |
| TF | Target function |
| IIC | Index of ideality of correlation |
References
- Toropov, A.A.; Toropova, A.P.; Benfenati, E. Additive SMILES-based carcinogenicity models: Probabilistic principles in the search for robust predictions. Int. J. Mol. Sci. 2009, 10, 3106–3127. [Google Scholar] [CrossRef]
- Selvestrel, G.; Lavado, G.J.; Toropova, A.P.; Toropov, A.A.; Gadaleta, D.; Marzo, M.; Baderna, D.; Benfenati, E. Monte Carlo models for sub-chronic repeated-dose toxicity: Systemic and organ-specific toxicity. Int. J. Mol. Sci. 2022, 23, 6615. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A.; Fjodorova, N. In silico simulation of impacts of metal nano-oxides on cell viability in THP-1 cells based on the correlation weights of the fragments of molecular structures and codes of experimental conditions represented by means of quasi-SMILES. Int. J. Mol. Sci. 2023, 24, 2058. [Google Scholar] [CrossRef] [PubMed]
- Jung, U.; Lee, B.; Kim, G.; Shin, H.K.; Kim, K.-T. Nano-QTTR development for interspecies aquatic toxicity of silver nanoparticles between daphnia and fish. Chemosphere 2021, 283, 131164. [Google Scholar] [CrossRef]
- Li, Z.; Lu, T.; Li, M.; Mortimer, M.; Guo, L.-H. Direct and gut microbiota-mediated toxicities of environmental antibiotics to fish and aquatic invertebrates. Chemosphere 2023, 329, 138692. [Google Scholar] [CrossRef]
- Mlnaříková, M.; Pípal, M.; Bláhová, L.; Bláha, L. Is environmental risk assessment possible with the alternatives to acute fish toxicity test? Case study with pharmaceuticals. Environ. Sci. Eur. 2024, 36, 192. [Google Scholar] [CrossRef]
- Pandey, S.K.; Ojha, P.K.; Roy, K. Exploring QSAR models for assessment of acute fish toxicity of environmental transformation products of pesticides (ETPPs). Chemosphere 2020, 252, 126508. [Google Scholar] [CrossRef]
- Wang, S.; Yan, L.C.; Zheng, S.S.; Li, T.T.; Fan, L.Y.; Huang, T.; Li, C.; Zhao, Y.H. Toxicity of some prevalent organic chemicals to tadpoles and comparison with toxicity to fish based on mode of toxic action. Ecotoxicol. Environ. Saf. 2019, 167, 138–145. [Google Scholar] [CrossRef]
- Furuhama, A.; Hayashi, T.I.; Yamamoto, H. Development of QSAAR and QAAR models for predicting fish early-life stage toxicity with a focus on industrial chemicals. SAR QSAR Environ. Res. 2019, 30, 825–846. [Google Scholar] [CrossRef]
- Sheffield, T.Y.; Judson, R.S. Ensemble QSAR modeling to predict multispecies fish toxicity lethal concentrations and points of departure. Environ. Sci. Technol. 2019, 53, 12793–12802. [Google Scholar] [CrossRef]
- Teixidó, E.; Leuthold, D.; de Crozé, N.; Léonard, M.; Scholz, S. Comparative assessment of the sensitivity of fish early-life stage, Daphnia, and algae tests to the chronic ecotoxicity of xenobiotics: Perspectives for alternatives to animal testing. Environ. Toxicol. Chem. 2020, 39, 30–41. [Google Scholar] [CrossRef]
- Lunghini, F.; Marcou, G.; Azam, P.; Enrici, M.H.; Van Miert, E.; Varnek, A. Consensus QSAR models estimating acute toxicity to aquatic organisms from different trophic levels: Algae, Daphnia and fish. SAR QSAR Environ. Res. 2020, 31, 655–675. [Google Scholar] [CrossRef]
- Yu, X.; Zeng, Q. Random forest algorithm-based classification model of pesticide aquatic toxicity to fishes. Aquat. Toxicol. 2022, 251, 106265. [Google Scholar] [CrossRef]
- Drgan, V.; Vračko, M. Counter-propagation neural networks for modeling and read across in aquatic (fish) toxicity. In Chemometrics and Cheminformatics in Aquatic Toxicology; Roy, K., Ed.; Wiley: Hoboken, NJ, USA, 2021; pp. 157–165. [Google Scholar] [CrossRef]
- Yu, X. Support vector machine-based model for toxicity of organic compounds against fish. Regul. Toxicol. Pharmacol. 2021, 123, 104942. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Fan, D.; Yin, W.; Gu, W.; Wang, Z.; Liu, J.; Xu, Y.; Shi, L.; Liu, M.; Ji, G. Comparison of seven in silico tools for evaluating of daphnia and fish acute toxicity: Case study on Chinese Priority Controlled Chemicals and new chemicals. BMC Bioinform. 2021, 22, 151. [Google Scholar] [CrossRef] [PubMed]
- Meador, J.P. The fish early-life stage sublethal toxicity syndrome—A high-dose baseline toxicity response. Environ. Pollut. 2021, 291, 118201. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Li, X.; Du, M.; Ren, Z.; Li, Q.; Li, Y. Identification and regulation of ecotoxicity of polychlorinated naphthalenes to aquatic food Chain (green algae-Daphnia magna-fish). Aquat. Toxicol. 2021, 233, 105774. [Google Scholar] [CrossRef]
- Pulido-Reyes, G.; Moreno-Martín, G.; Gómez-Gómez, B.; Navas, J.M.; Madrid, Y.; Fernández-Cruz, M.L. Fish acute toxicity of nine nanomaterials: Need of pre-tests to ensure comparability and reuse of data. Environ. Res. 2024, 245, 118072. [Google Scholar] [CrossRef]
- Klüver, N.; Vogs, C.; Altenburger, R.; Escher, B.I.; Scholz, S. Development of a general baseline toxicity QSAR model for the fish embryo acute toxicity test. Chemosphere 2016, 164, 164–173. [Google Scholar] [CrossRef]
- Austin, T.; Denoyelle, M.; Chaudry, A.; Stradling, S.; Eadsforth, C. European chemicals agency dossier submissions as an experimental data source: Refinement of a fish toxicity model for predicting acute LC50 values. Environ. Toxicol. Chem. 2015, 34, 369–378. [Google Scholar] [CrossRef]
- Roy, K.; Kar, S. In silico models for ecotoxicity of pharmaceuticals. Methods Mol. Biol. 2016, 1425, 237–304. [Google Scholar] [CrossRef]
- Kidd, K.A.; Blanchfield, P.J.; Mills, K.H.; Palace, V.P.; Evans, R.E.; Lazorchak, J.M.; Flick, R.W. Collapse of a fish population after exposure to a synthetic estrogen. Proc. Natl. Acad. Sci. USA 2007, 104, 8897–8901. [Google Scholar] [CrossRef]
- Tang, J.; Liu, A.; Chen, K.; Shi, Y.; Qiu, X. Exposure to amitriptyline disturbs behaviors in adult zebrafish and their offspring via altering neurotransmitter levels. Comp. Biochem. Physiol. C Pharmacol. 2025, 288, 110079. [Google Scholar] [CrossRef]
- McCallum, E.S.; Krutzelmann, E.; Brodin, T.; Fick, J.; Sundelin, A.; Balshine, S. Exposure to wastewater effluent affects fish behaviour and tissue-specific uptake of pharmaceuticals. Sci. Total Environ. 2017, 605–606, 578–588. [Google Scholar] [CrossRef]
- European Medicines Agency (EMEA). Guideline on the Environmental Risk Assessment of Medicinal Products for Human Use—Revision 1; European Medicines Agency: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Sangion, A.; Gramatica, P. Hazard of pharmaceuticals for aquatic environment: Prioritization by structural approaches and prediction of ecotoxicity. Environ. Int. 2016, 95, 131–143. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a Chemical Language and Information System: 1: Introduction to Methodology and Encoding Rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Toropov, A.A.; Benfenati, E. Optimisation of correlation weights of SMILES invariants for modelling oral quail toxicity. Eur. J. Med. Chem. 2007, 42, 606–613. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Toropova, A.P.; Martyanov, S.E.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. CORAL: Predictions of rate constants of hydroxyl radical reaction using representation of the molecular structure obtained by combination of SMILES and Graph approaches. Chemometr. Intell. Lab. Syst. 2012, 112, 65–70. [Google Scholar] [CrossRef]
- Fatemi, M.H.; Malekzadeh, H. CORAL: Predictions of retention indices of volatiles in cooking rice using representation of the molecular structure obtained by combination of SMILES and graph approaches. J. Iran. Chem. Soc. 2015, 12, 405–412. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, A. CORAL: QSAR models of CB1 cannabinoid receptor inhibitors based on local and global SMILES attributes with the index of ideality of correlation and the correlation contradiction index. Chemometr. Intell. Lab. Syst. 2020, 200, 103982. [Google Scholar] [CrossRef]
- Chopdar, K.S.; Dash, G.C.; Mohapatra, P.K.; Nayak, B.; Raval, M.K. Monte-Carlo method-based QSAR model to discover phytochemical urease inhibitors using SMILES and GRAPH descriptors. J. Biomol. Struct. Dyn. 2022, 40, 5090–5099. [Google Scholar] [CrossRef]
- Tabti, K.; Elmchichi, L.; Sbai, A.; Maghat, H.; Bouachrine, M.; Lakhlifi, T. Molecular modelling of antiproliferative inhibitors based on SMILES descriptors using Monte-Carlo method, docking, MD simulations and ADME/Tox studies. Mol. Simul. 2022, 48, 1575–1591. [Google Scholar] [CrossRef]
- Rezaie-keikhaie, N.; Shiri, F.; Ahmadi, S.; Salahinejad, M. QSTR based on Monte Carlo approach using SMILES and graph features for toxicity toward Tetrahymena pyriformis. J. Iran. Chem. Soc. 2023, 20, 2609–2620. [Google Scholar] [CrossRef]
- Ouabane, M.; Zaki, K.; Tabti, K.; Alaqarbeh, M.; Sbai, A.; Sekkate, C.; Bouachrine, M.; Lakhlifi, T. Molecular toxicity of nitrobenzene derivatives to tetrahymena pyriformis based on SMILES descriptors using Monte Carlo, docking, and MD simulations. Comput. Biol. Med. 2024, 169, 107880. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A. The index of ideality of correlation: A criterion of predictability of QSAR models for skin permeability? Sci. Total Environ. 2017, 586, 466–472. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A.; Viganò, E.L.; Colombo, E.; Roncaglioni, A.; Benfenati, E. Carcinogenicity prediction using the index of ideality of correlation. SAR QSAR Environ. Res. 2022, 33, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Toropova, A.P.; Roncaglioni, A.; Benfenati, E. In silico prediction of the mutagenicity of nitroaromatic compounds using correlation weights of fragments of local symmetry. Mutat. Res. Genet. Toxicol. Environ. Mutagen. 2023, 891, 503684. [Google Scholar] [CrossRef]
- Javidfar, M.; Ahmadi, S. QSAR modelling of larvicidal phytocompounds against Aedes aegypti using index of ideality of correlation. SAR QSAR Environ. Res. 2020, 31, 717–739. [Google Scholar] [CrossRef]
- Ghiasi, T.; Ahmadi, S.; Ahmadi, E.; Talei Bavil Olyai, M.R.; Khodadadi, Z. The index of ideality of correlation: QSAR studies of hepatitis C virus NS3/4A protease inhibitors using SMILES descriptors. SAR QSAR Environ. Res. 2021, 32, 495–520. [Google Scholar] [CrossRef]
- Ahmadi, S.; Lotfi, S.; Kumar, P. Quantitative structure–toxicity relationship models for predication of toxicity of ionic liquids toward leukemia rat cell line IPC-81 based on index of ideality of correlation. Toxicol. Mech. Methods 2022, 32, 302–312. [Google Scholar] [CrossRef]
- Duhan, M.; Sindhu, J.; Kumar, P.; Devi, M.; Singh, R.; Kumar, R.; Lal, S.; Kumar, A.; Kumar, S.; Hussain, K. Quantitative structure activity relationship studies of novel hydrazone derivatives as α-amylase inhibitors with index of ideality of correlation. J. Biomol. Struct. Dyn. 2022, 40, 4933–4953. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Kumar, P.; Singh, D. QSRR modelling for the investigation of gas chromatography retention indices of flavour and fragrance compounds on Carbowax 20 M glass capillary column with the index of ideality of correlation and the consensus modelling. Chemometr. Intell. Lab. Syst. 2022, 224, 104552. [Google Scholar] [CrossRef]
- Goyal, S.; Rani, P.; Chahar, M.; Hussain, K.; Kumar, P.; Sindhu, J. Quantitative structure activity relationship studies of androgen receptor binding affinity of endocrine disruptor chemicals with index of ideality of correlation, their molecular docking, molecular dynamics and ADME studies. J. Biomol. Struct. Dyn. 2023, 41, 13616–13631. [Google Scholar] [CrossRef]
- Bhawna; Kumar, S.; Kumar, P.; Kumar, A. Correlation intensity index-index of ideality of correlation: A hyphenated target function for furtherance of MAO-B inhibitory activity assessment. Comput. Biol. Chem. 2024, 108, 107975. [Google Scholar] [CrossRef]
- Khan, K.; Baderna, D.; Cappelli, C.; Toma, C.; Lombardo, A.; Roy, K.; Benfenati, E. Ecotoxicological QSAR modeling of organic compounds against fish: Application of fragment based descriptors in feature analysis. Aquat. Toxicol. 2019, 212, 162–174. [Google Scholar] [CrossRef]
- Petoumenou, M.I.; Pizzo, F.; Cester, J.; Fernández, A.; Benfenati, E. Comparison between bioconcentration factor (BCF) data provided by industry to the European Chemicals Agency (ECHA) and data derived from QSAR models. Environ. Res. 2015, 142, 529–534. [Google Scholar] [CrossRef]
- de Morais E Silva, L.; Alves, M.F.; Scotti, L.; Lopes, W.S.; Scotti, M.T. Predictive ecotoxicity of MoA 1 of organic chemicals using in silico approaches. Ecotoxicol. Environ. Saf. 2018, 153, 151–159. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Benfenati, E.; Gini, G. Co-evolutions of correlations for QSAR of toxicity of organometallic and inorganic substances: An unexpected good prediction based on a model that seems untrustworthy. Chemometr. Intell. Lab. Syst. 2011, 105, 215–219. [Google Scholar] [CrossRef]
- Vukomanović, P.; Stefanović, M.; Stevanović, J.M.; Petrić, A.; Trenkić, M.; Andrejević, L.; Lazarević, M.; Sokolović, D.; Veselinović, A.M. Monte Carlo optimization method based QSAR modeling of placental barrier permeability. Pharm. Res. 2024, 41, 493–500. [Google Scholar] [CrossRef] [PubMed]
- Šarić, S.; Kostić, T.; Lović, M.; Aleksić, I.; Hristov, D.; Šarac, M.; Veselinović, A.M. In silico development of novel angiotensin-converting-enzyme-I inhibitors by Monte Carlo optimization based QSAR modeling, molecular docking studies and ADMET predictions. Comput. Biol. Chem. 2024, 112, 108167. [Google Scholar] [CrossRef]
- Nikolić, N.; Kostić, T.; Golubović, M.; Nikolić, T.; Marinković, M.; Perić, V.; Mladenović, S.; Veselinovic, A. Monte Carlo optimization based QSAR modeling of angiotensin II receptor antagonists. Acta Chim. Slov. 2023, 70, 318–326. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Raškova, M.; Raška, I., Jr.; Toropov, A.A. The sequence of amino acids as the basis for the model of biological activity of peptides. Theor. Chem. Acc. 2021, 140, 15. [Google Scholar] [CrossRef] [PubMed]
- Ciemny, M.P.; Badaczewska-Dawid, A.E.; Pikuzinska, M.; Kolinski, A.; Kmiecik, S. Modeling of disordered protein structures using Monte Carlo simulations and knowledge-based statistical force fields. Int. J. Mol. Sci. 2019, 20, 606. [Google Scholar] [CrossRef]
- Especial, J.N.C.; Rey, A.; Faísca, P.F.N. A note on the effects of linear topology preservation in Monte Carlo simulations of knotted proteins. Int. J. Mol. Sci. 2022, 23, 13871. [Google Scholar] [CrossRef]
- Penabeï, S.; Meesungnoen, J.; Jay-Gerin, J.-P. Comparative analysis of cystamine and cysteamine as radioprotectors and antioxidants: Insights from Monte Carlo chemical modeling under high linear energy transfer radiation and high dose rates. Int. J. Mol. Sci. 2024, 25, 10490. [Google Scholar] [CrossRef]
- Wüstner, D.; Sklenar, H. Atomistic Monte Carlo simulation of lipid membranes. Int. J. Mol. Sci. 2014, 15, 1767–1803. [Google Scholar] [CrossRef] [PubMed]
- Peukert, D.; Kempson, I.; Douglass, M.; Bezak, E. Gold nanoparticle enhanced proton therapy: Monte Carlo modeling of reactive species’ distributions around a gold nanoparticle and the effects of nanoparticle proximity and clustering. Int. J. Mol. Sci. 2019, 20, 4280. [Google Scholar] [CrossRef]
- Li, S.W.; Lin, A.Y.C. Increased acute toxicity to fish caused by pharmaceuticals in hospital effluents in a pharmaceutical mixture and after solar irradiation. Chemosphere 2015, 139, 190–196. [Google Scholar] [CrossRef]
- Yang, J.-S.; Panchangam, S.C.; Lin, A.Y.C. Exploring simulated sunlight sulfite process for enhanced removal of mixed pharmaceutical and personal care products from aqueous solution. J. Water Process Eng. 2025, 72, 107461. [Google Scholar] [CrossRef]
- Coors, A.; Ross Brown, A.; Maynard, S.K.; Nimrod Perkins, A.; Owen, S.; Tyler, C.R. Minimizing Experimental Testing on Fish for Legacy Pharmaceuticals. Environ. Sci. Technol. 2023, 57, 1721–1730. [Google Scholar] [CrossRef]
- Khan, K.; Benfenati, E.; Roy, K. Consensus QSAR modeling of toxicity of pharmaceuticals to different aquatic organisms: Ranking and prioritization of the DrugBank database compounds. Ecotoxicol. Environ. Saf. 2019, 168, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.; Khan, P.M.; Lavado, G.; Valsecchi, C.; Pasqualini, J.; Baderna, D.; Marzo, M.; Lombardo, A.; Roy, K.; Benfenati, E. QSAR modeling of Daphnia magna and fish toxicities of biocides using 2D descriptors. Chemosphere 2019, 229, 8–17, Erratum in Chemosphere 2019, 237, 124397. https://doi.org/10.1016/j.chemosphere.2019.124397. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Roy, K. First report on interspecies quantitative correlation of ecotoxicity of pharmaceuticals. Chemosphere 2010, 81, 738–747. [Google Scholar] [CrossRef] [PubMed]
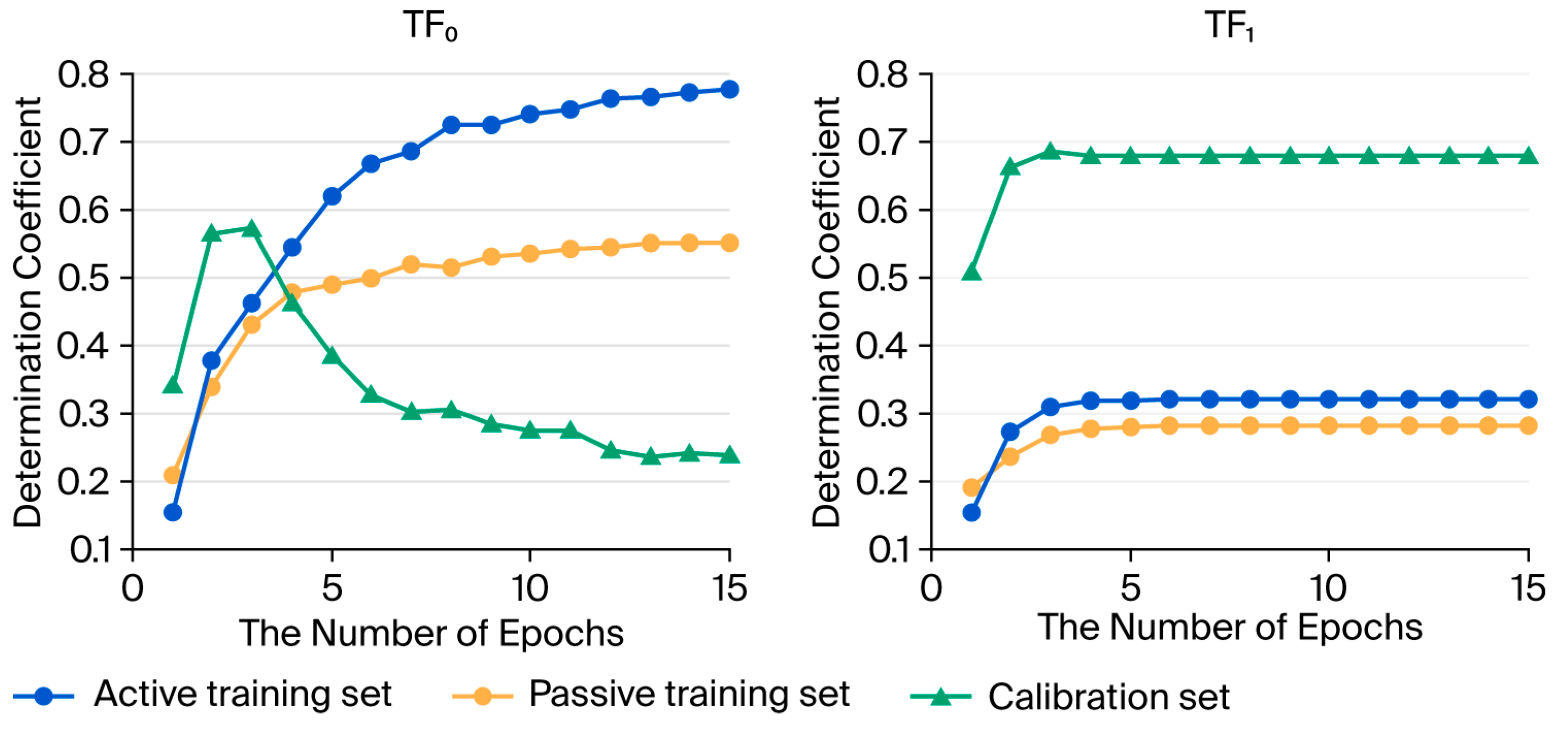
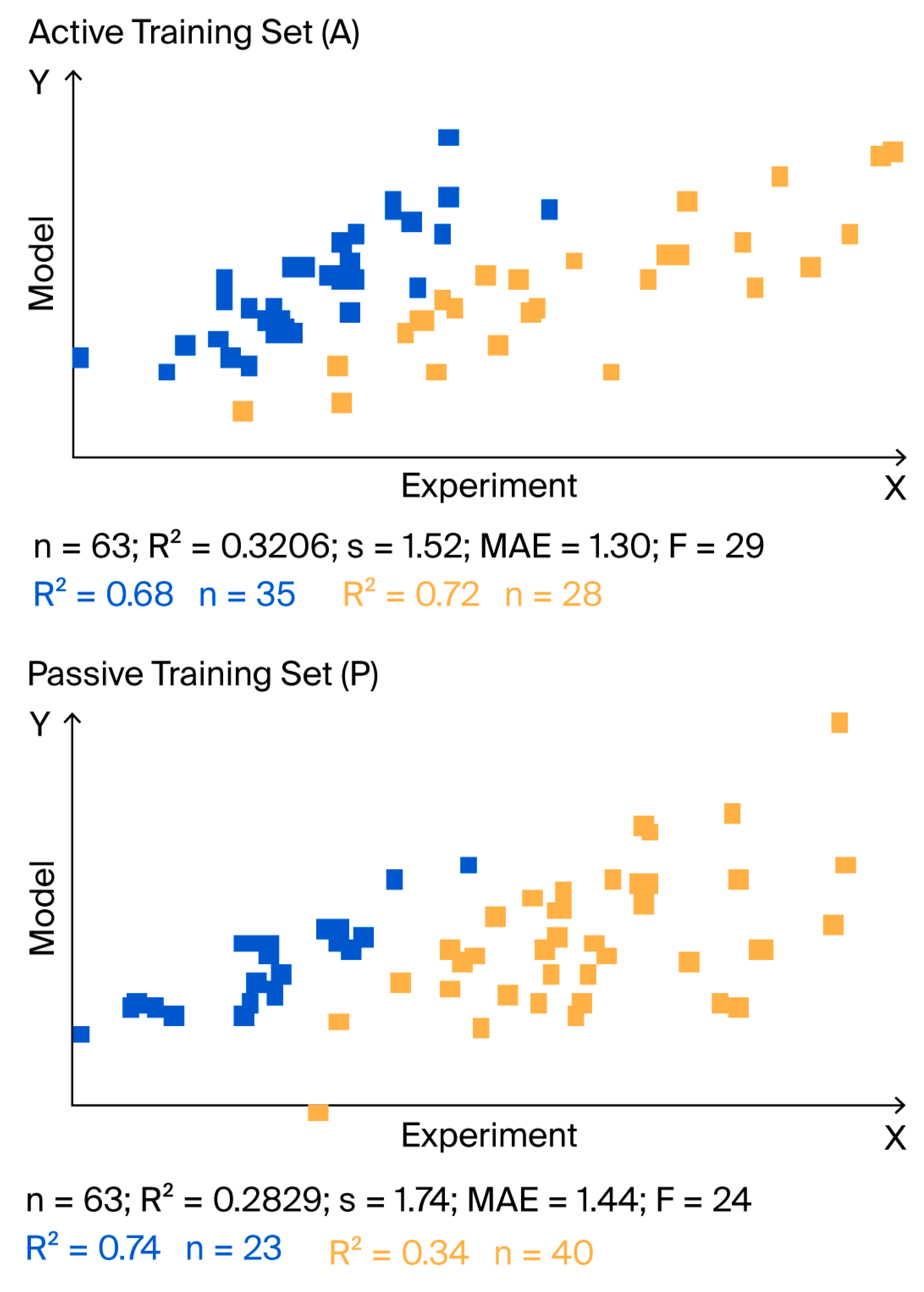
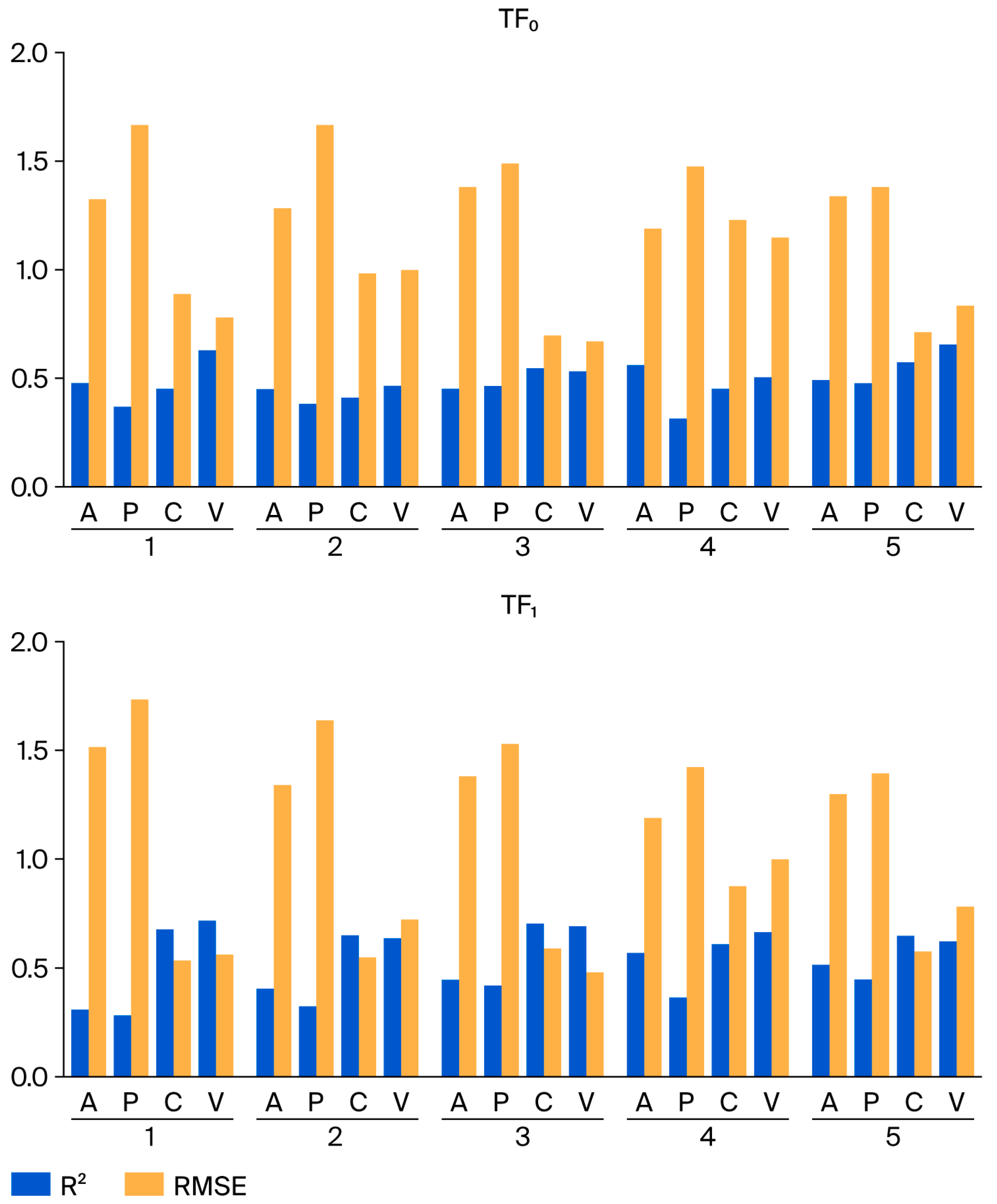
| Target Function | Split | Set * | n | R2 | CCC | IIC | Q2 | RMSE | MAE | F |
|---|---|---|---|---|---|---|---|---|---|---|
| TF0 | 1 | A | 63 | 0.4791 | 0.6479 | 0.5904 | 0.4405 | 1.33 | 1.13 | 56 |
| P | 63 | 0.3648 | 0.5118 | 0.3703 | 0.3295 | 1.67 | 1.35 | 35 | ||
| C | 65 | 0.4507 | 0.6380 | 0.5642 | 0.3651 | 0.889 | 0.611 | 52 | ||
| V | 60 | 0.6360 | - | - | - | 0.78 | 0.61 | - | ||
| 2 | A | 62 | 0.4473 | 0.6182 | 0.5878 | 0.4126 | 1.29 | 1.10 | 49 | |
| P | 59 | 0.3894 | 0.5497 | 0.2845 | 0.3546 | 1.67 | 1.33 | 36 | ||
| C | 63 | 0.4161 | 0.5352 | 0.4373 | 0.3736 | 0.996 | 0.779 | 43 | ||
| V | 67 | 0.4696 | - | - | - | 1.01 | 0.73 | - | ||
| 3 | A | 66 | 0.4589 | 0.6291 | 0.5310 | 0.4243 | 1.39 | 1.18 | 54 | |
| P | 60 | 0.4700 | 0.4753 | 0.3848 | 0.4389 | 1.50 | 1.26 | 51 | ||
| C | 59 | 0.5530 | 0.7404 | 0.7424 | 0.5196 | 0.699 | 0.530 | 71 | ||
| V | 66 | 0.5378 | - | - | - | 0.68 | 0.52 | - | ||
| 4 | A | 66 | 0.5687 | 0.7251 | 0.6285 | 0.5453 | 1.20 | 0.968 | 84 | |
| P | 64 | 0.3214 | 0.5503 | 0.4334 | 0.2719 | 1.48 | 1.19 | 29 | ||
| C | 62 | 0.4549 | 0.6063 | 0.5552 | 0.4100 | 1.23 | 0.922 | 50 | ||
| V | 59 | 0.5075 | - | - | - | 1.15 | 0.88 | - | ||
| 5 | A | 60 | 0.4992 | 0.6659 | 0.6182 | 0.4708 | 1.34 | 1.11 | 58 | |
| P | 66 | 0.4753 | 0.6076 | 0.5263 | 0.4412 | 1.38 | 1.17 | 58 | ||
| C | 61 | 0.5726 | 0.7344 | 0.6651 | 0.5377 | 0.716 | 0.527 | 79 | ||
| V | 64 | 0.6604 | - | - | - | 0.84 | 0.64 | - | ||
| TF1 | 1 | A ** | 63 | 0.3206 | 0.4856 | 0.4530 | 0.2680 | 1.52 | 1.30 | 29 |
| P | 63 | 0.2829 | 0.4209 | 0.3449 | 0.2438 | 1.74 | 1.44 | 24 | ||
| C | 65 | 0.6803 | 0.8225 | 0.8248 | 0.6608 | 0.541 | 0.418 | 134 | ||
| V | 60 | 0.7189 | - | - | - | 0.57 | 0.43 | - | ||
| 2 | A | 62 | 0.4053 | 0.5768 | 0.5968 | 0.3562 | 1.34 | 1.16 | 41 | |
| P | 59 | 0.3246 | 0.4869 | 0.3736 | 0.2807 | 1.65 | 1.37 | 27 | ||
| C | 63 | 0.6543 | 0.8026 | 0.8089 | 0.6251 | 0.557 | 0.456 | 115 | ||
| V | 67 | 0.6404 | - | - | - | 0.73 | 0.52 | - | ||
| 3 | A | 66 | 0.4588 | 0.6290 | 0.5999 | 0.4209 | 1.39 | 1.24 | 54 | |
| P | 60 | 0.4267 | 0.4518 | 0.3712 | 0.3911 | 1.53 | 1.29 | 43 | ||
| C | 59 | 0.7075 | 0.8304 | 0.8410 | 0.6850 | 0.596 | 0.470 | 138 | ||
| V | 66 | 0.7027 | - | - | - | 0.49 | 0.41 | - | ||
| 4 | A | 66 | 0.5773 | 0.7320 | 0.7151 | 0.5509 | 1.19 | 0.980 | 87 | |
| P | 64 | 0.3646 | 0.5932 | 0.4799 | 0.3198 | 1.43 | 1.13 | 36 | ||
| C | 62 | 0.6193 | 0.7593 | 0.7856 | 0.5905 | 0.886 | 0.670 | 98 | ||
| V | 59 | 0.6744 | - | - | - | 1.00 | 0.77 | - | ||
| 5 | A | 60 | 0.5218 | 0.6858 | 0.5524 | 0.4953 | 1.31 | 1.05 | 63 | |
| P | 66 | 0.4557 | 0.5894 | 0.5492 | 0.4178 | 1.40 | 1.22 | 54 | ||
| C | 61 | 0.6524 | 0.8032 | 0.8077 | 0.6140 | 0.577 | 0.427 | 111 | ||
| V | 64 | 0.6276 | - | - | - | 0.78 | 0.60 | - |
| Sk and SSk | CWs Probe 1 | CWs Probe 2 | CWs Probe 3 | NA * | NP | NC | Statistical Results |
|---|---|---|---|---|---|---|---|
| CC | 0.5820 | 0.8181 | 0.4444 | 41 | 43 | 39 | 0.0013 |
| cc | 0.3720 | 1.1446 | 0.7268 | 37 | 34 | 38 | 0.0009 |
| c1 | 0.8266 | 0.8609 | 0.2485 | 31 | 30 | 40 | 0.0028 |
| 2( | 0.3638 | 0.9570 | 0.4046 | 20 | 8 | 4 | 0.0160 |
| C= | 0.2293 | 1.1986 | 0.6943 | 20 | 18 | 20 | 0.0011 |
| Cl | 1.0875 | 1.2502 | 1.0198 | 12 | 8 | 9 | 0.0044 |
| Cl( | 0.9531 | 0.9448 | 1.2444 | 11 | 6 | 8 | 0.0063 |
| cC | 0.9585 | 1.2576 | 1.3355 | 11 | 7 | 18 | 0.0092 |
| C3 | 0.5438 | 0.0123 | 0.3713 | 8 | 3 | 5 | 0.0099 |
| cO | 0.7980 | 0.2225 | 0.4021 | 8 | 9 | 9 | 0.0012 |
| S | 1.8502 | 2.1259 | 2.9819 | 6 | 9 | 2 | 0.0132 |
| 3( | 0.3044 | 1.0361 | 0.8304 | 5 | 4 | 2 | 0.0088 |
| O1 | 0.0996 | 0.5437 | 0.1507 | 5 | 4 | 12 | 0.0115 |
| c3 | 0.9363 | 1.2044 | 0.3981 | 5 | 5 | 2 | 0.0081 |
| =1 | 2.8638 | 3.3565 | 1.4123 | 4 | 2 | 4 | 0.0063 |
| O | −0.3447 | −0.4275 | −0.0051 | 53 | 48 | 56 | 0.0013 |
| 1 | −0.2970 | −0.5514 | −0.1329 | 47 | 42 | 50 | 0.0015 |
| c( | −0.4694 | −0.2529 | −0.0718 | 34 | 31 | 34 | 0.0010 |
| 2 | −0.4471 | −0.2852 | −0.4106 | 31 | 20 | 18 | 0.0062 |
| N | −0.1206 | −0.3566 | −0.7018 | 31 | 22 | 28 | 0.0035 |
| NC | −0.5968 | −0.8148 | −0.6733 | 19 | 13 | 21 | 0.0044 |
| C2 | −0.1557 | −0.3257 | −0.2129 | 16 | 7 | 6 | 0.0111 |
| N( | −0.3278 | −0.0950 | −0.4204 | 16 | 15 | 20 | 0.0027 |
| N= | −0.7064 | −1.2648 | −0.2549 | 8 | 7 | 6 | 0.0033 |
| N1 | −1.7236 | −1.9358 | −0.7488 | 7 | 3 | 6 | 0.0079 |
| cN | −0.1443 | −1.5157 | −1.8619 | 6 | 2 | 5 | 0.0098 |
| 4 | −0.6547 | −0.5008 | −0.2820 | 4 | 4 | 1 | 0.0107 |
| 5( | −0.3569 | −0.1286 | −0.9625 | 2 | 1 | 0 | 1.0000 |
| N2 | −0.5617 | −0.9860 | −0.3725 | 2 | 1 | 0 | 1.0000 |
| Models of Fish Acute Toxicity from the Literature | Models of Fish Toxicity Obtained by CORAL Software | |||||||
|---|---|---|---|---|---|---|---|---|
| Ntrain * | Dtrain | Nvalid | Dvalid | Method | Ntrain | Dtrain | Nvalid | Dvalid |
| 211 | - | 14 | 0.97 | LR [20] | 158 ± 1 | 0.577 ± 0.10 | 53 ± 1 | 0.815 ± 0.07 |
| 86 | 0.67 | 25 | 0.83 | PLS [49] | 84 ± 3 | 0.711 ± 0.06 | 28 ± 1 | 0.947 ± 0.02 |
| 39 | 0.80 | 16 | 0.84 | PCA [27] | 42 ± 1 | 0.650 ± 0.09 | 14 ± 1 | 0.749 ± 0.05 |
| 188 ± 2 | 0.457 ± 009 | 60 ± 2 | 0.673 ± 0.03 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toropova, A.P.; Toropov, A.A.; Colombo, E.; Viganò, E.L.; Lombardo, A.; Roncaglioni, A.; Benfenati, E. Simulation of Fish Acute Toxicity of Pharmaceuticals Using Simplified Molecular Input Line Entry System (SMILES) Notation as a Representation of Molecular Structure. Int. J. Mol. Sci. 2025, 26, 9348. https://doi.org/10.3390/ijms26199348
Toropova AP, Toropov AA, Colombo E, Viganò EL, Lombardo A, Roncaglioni A, Benfenati E. Simulation of Fish Acute Toxicity of Pharmaceuticals Using Simplified Molecular Input Line Entry System (SMILES) Notation as a Representation of Molecular Structure. International Journal of Molecular Sciences. 2025; 26(19):9348. https://doi.org/10.3390/ijms26199348
Chicago/Turabian StyleToropova, Alla P., Andrey A. Toropov, Erika Colombo, Edoardo Luca Viganò, Anna Lombardo, Alessandra Roncaglioni, and Emilio Benfenati. 2025. "Simulation of Fish Acute Toxicity of Pharmaceuticals Using Simplified Molecular Input Line Entry System (SMILES) Notation as a Representation of Molecular Structure" International Journal of Molecular Sciences 26, no. 19: 9348. https://doi.org/10.3390/ijms26199348
APA StyleToropova, A. P., Toropov, A. A., Colombo, E., Viganò, E. L., Lombardo, A., Roncaglioni, A., & Benfenati, E. (2025). Simulation of Fish Acute Toxicity of Pharmaceuticals Using Simplified Molecular Input Line Entry System (SMILES) Notation as a Representation of Molecular Structure. International Journal of Molecular Sciences, 26(19), 9348. https://doi.org/10.3390/ijms26199348









