Stacking in Layered Covalent Organic Frameworks: A Computational Approach and PXRD Reference Guide
Abstract
1. Introduction
2. Results
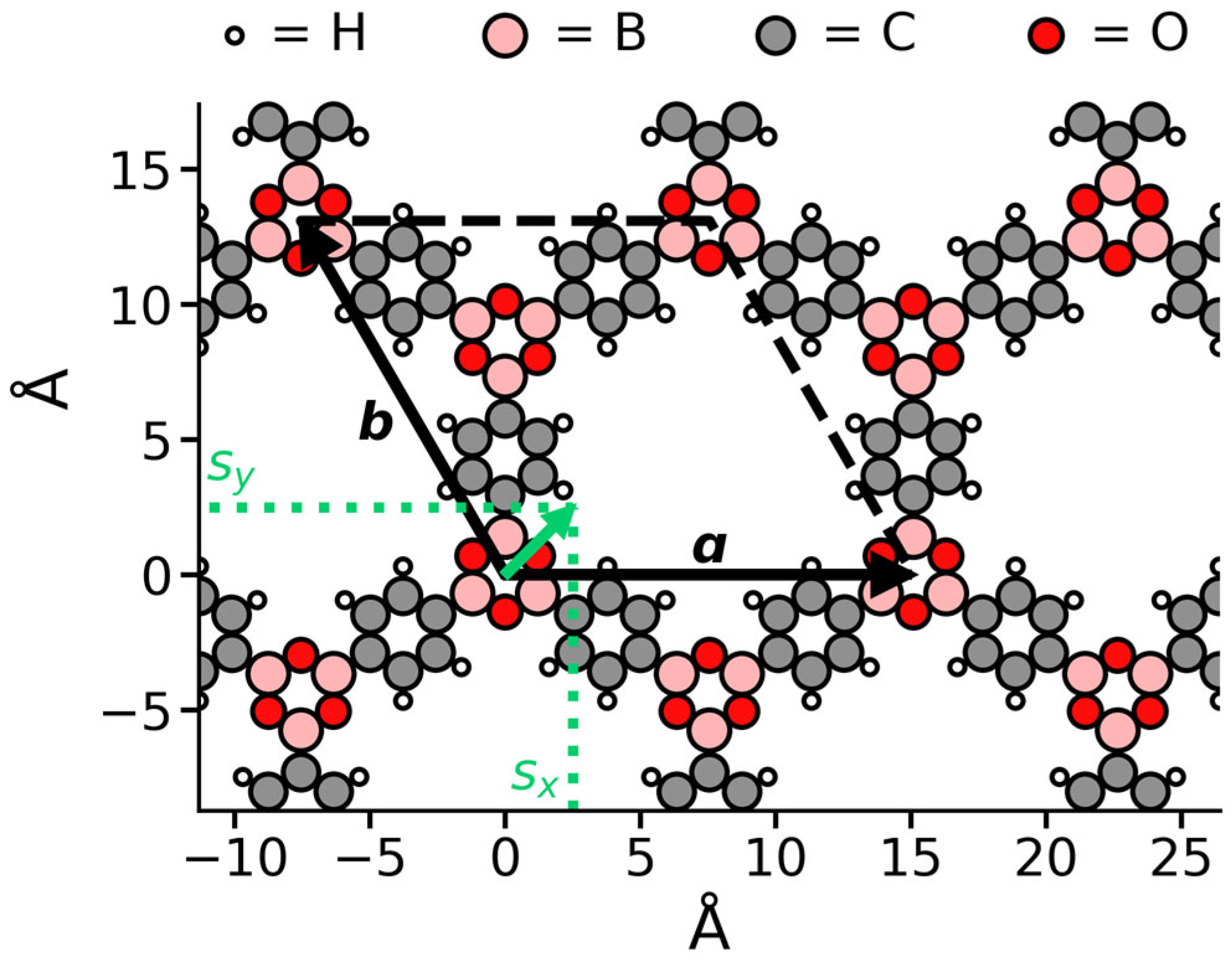
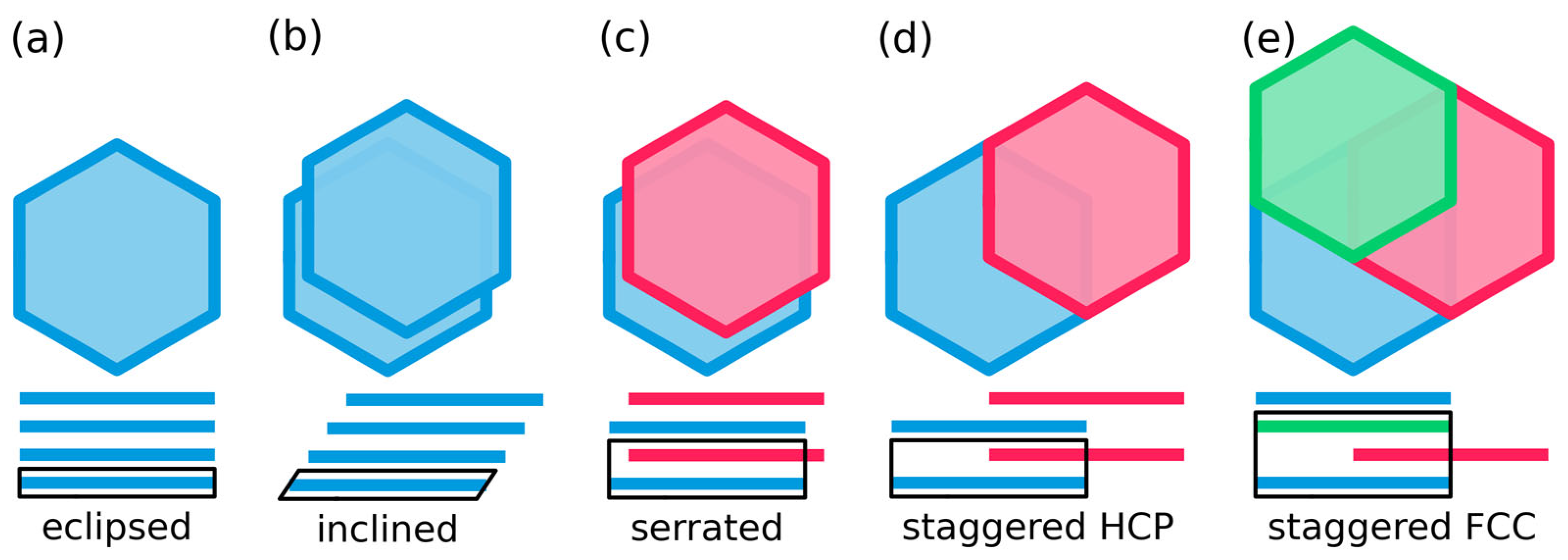
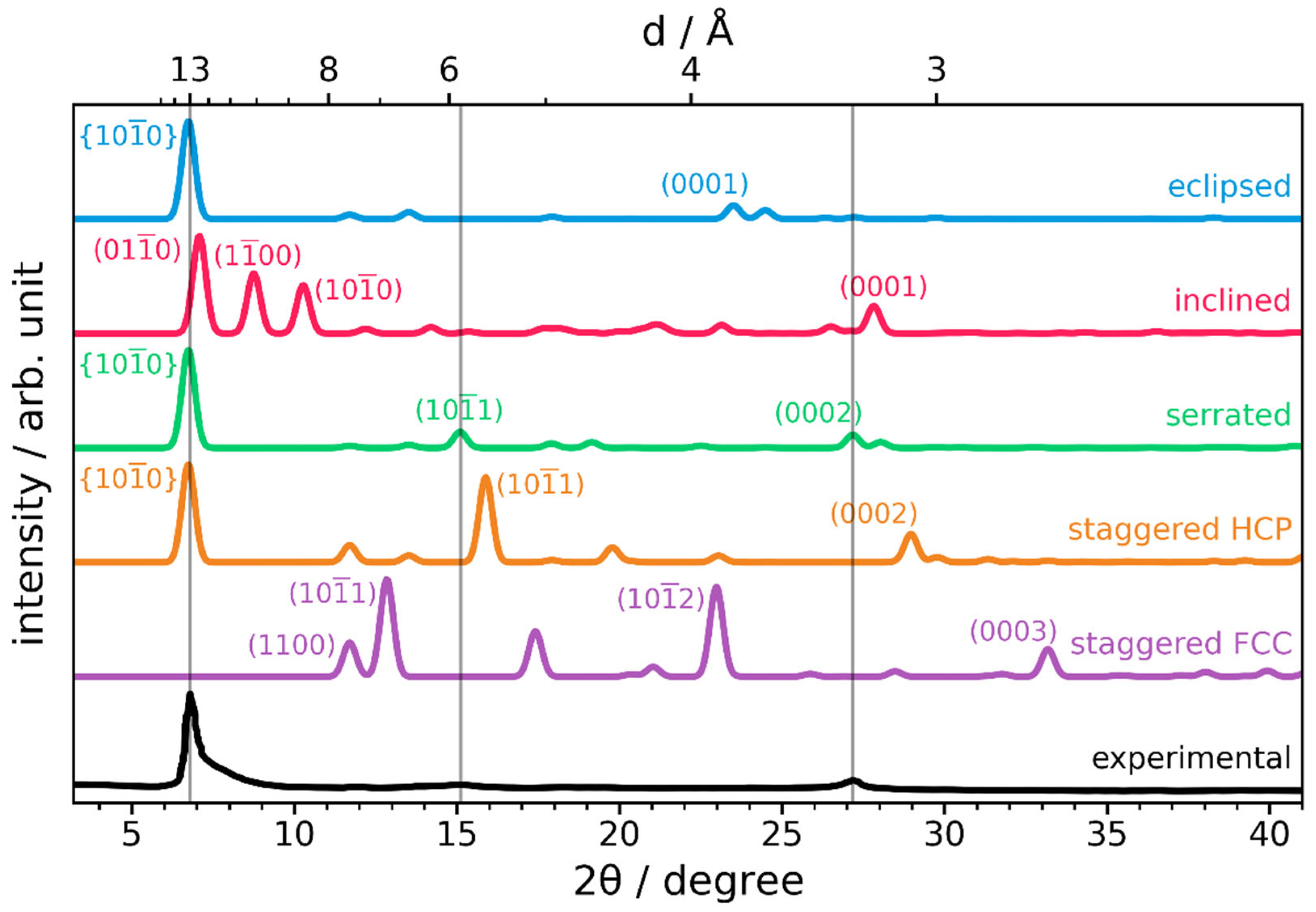
2.1. Inconsistency of Idealized Stacking Modes with Experimental Observations
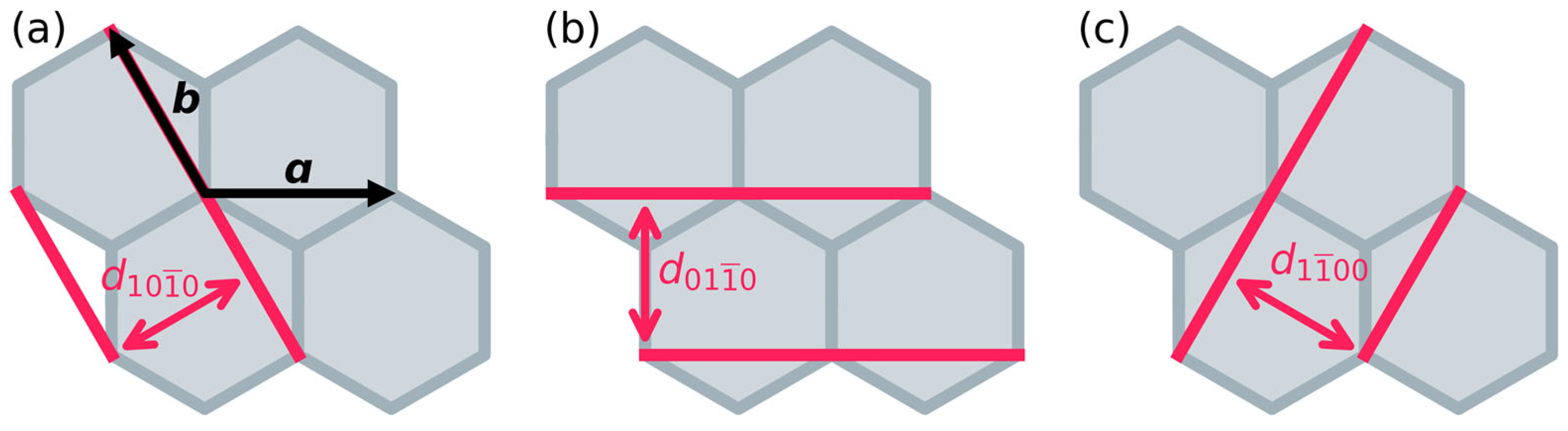
2.2. A PXRD Reference Guide for Slipped LCOFs
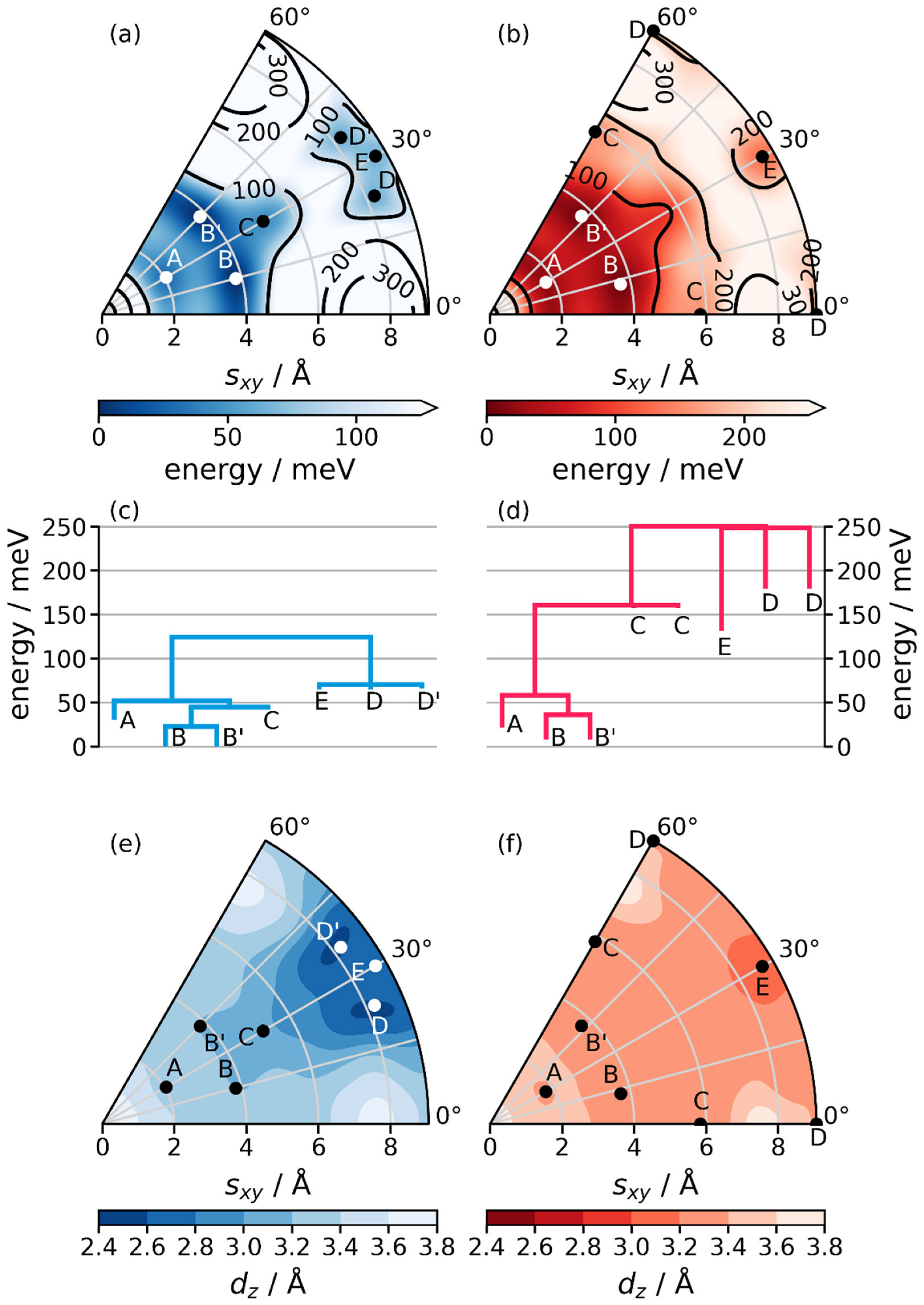
2.3. The Stacking Energy Landscape of COF-1
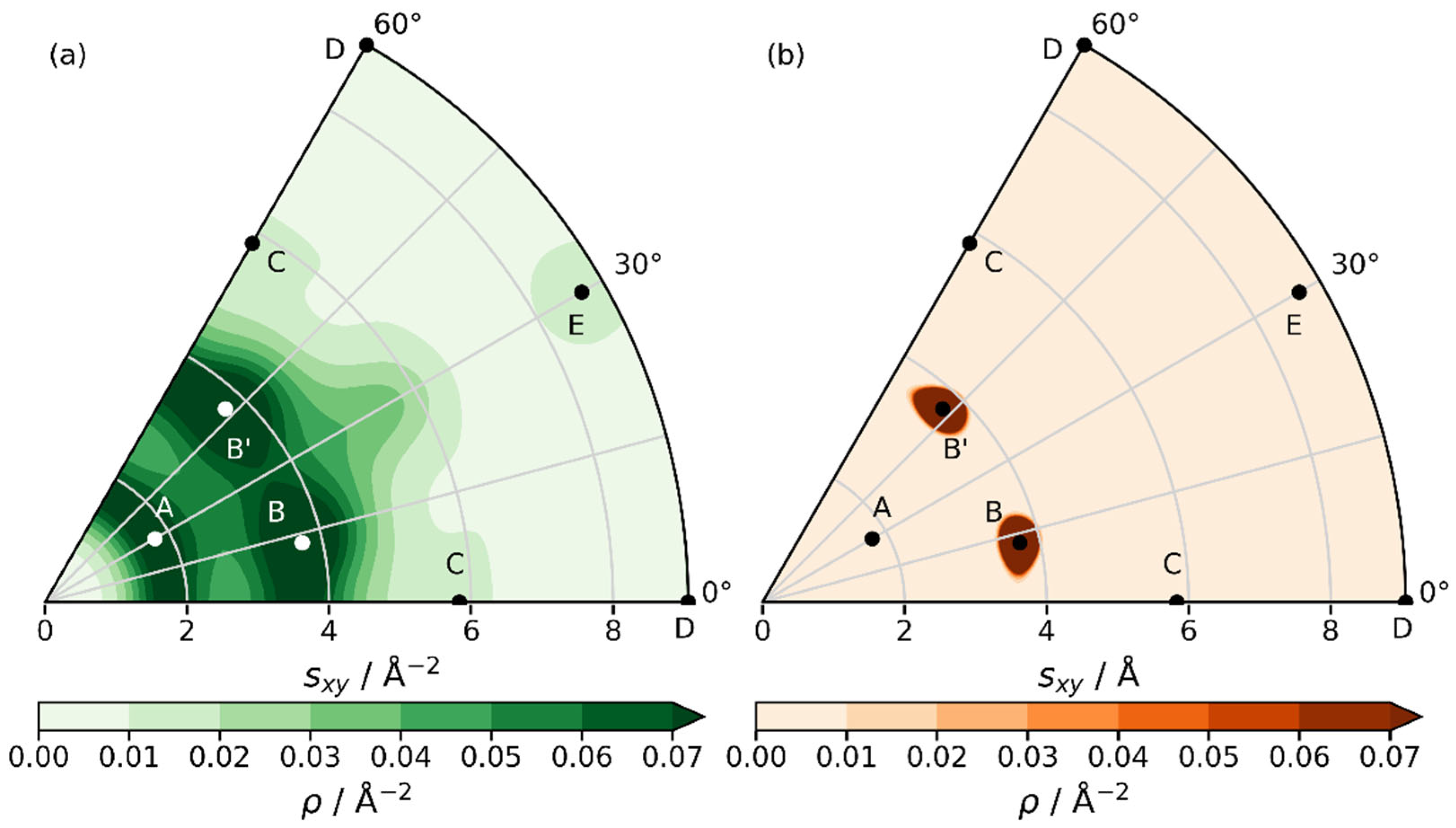
2.4. Structural Models Including Disorder
3. Methods
3.1. DFT Simulations
3.2. Generating Potential Energy Surfaces Using Gaussian Process Regression
3.3. Idealized Geometries
3.4. PXRD Reference Guide Geometries
3.5. Boltzmann Distribution
3.6. Disordered Geometries
3.7. PXRD Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cote, A.P.; Benin, A.I.; Ockwig, N.W.; O’Keeffe, M.; Matzger, A.J.; Yaghi, O.M. Porous, Crystalline, Covalent Organic Frameworks. Science 2005, 310, 1166–1170. [Google Scholar] [CrossRef]
- Côté, A.P.; El-Kaderi, H.M.; Furukawa, H.; Hunt, J.R.; Yaghi, O.M. Reticular Synthesis of Microporous and Mesoporous 2D Covalent Organic Frameworks. J. Am. Chem. Soc. 2007, 129, 12914–12915. [Google Scholar] [CrossRef]
- Kuhn, P.; Forget, A.; Su, D.; Thomas, A.; Antonietti, M. From Microporous Regular Frameworks to Mesoporous Materials with Ultrahigh Surface Area: Dynamic Reorganization of Porous Polymer Networks. J. Am. Chem. Soc. 2008, 130, 13333–13337. [Google Scholar] [CrossRef]
- Mu, Z.; Zhu, Y.; Li, B.; Dong, A.; Wang, B.; Feng, X. Covalent Organic Frameworks with Record Pore Apertures. J. Am. Chem. Soc. 2022, 144, 5145–5154. [Google Scholar] [CrossRef]
- Wu, M.-X.; Yang, Y.-W. Applications of Covalent Organic Frameworks (COFs): From Gas Storage and Separation to Drug Delivery. Chin. Chem. Lett. 2017, 28, 1135–1143. [Google Scholar] [CrossRef]
- Huang, N.; Chen, X.; Krishna, R.; Jiang, D. Two-Dimensional Covalent Organic Frameworks for Carbon Dioxide Capture through Channel-Wall Functionalization. Angew. Chem. Int. Ed. 2015, 54, 2986–2990. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, Y.-B. Crystallization of Covalent Organic Frameworks for Gas Storage Applications. Molecules 2017, 22, 1149. [Google Scholar] [CrossRef] [PubMed]
- Tylianakis, E.; Klontzas, E.; Froudakis, G.E. Multi-Scale Theoretical Investigation of Hydrogen Storage in Covalent Organic Frameworks. Nanoscale 2011, 3, 856. [Google Scholar] [CrossRef] [PubMed]
- Bian, G.; Yin, J.; Zhu, J. Recent Advances on Conductive 2D Covalent Organic Frameworks. Small 2021, 17, 2006043. [Google Scholar] [CrossRef]
- Babu, H.V.; Bai, M.G.M.; Rajeswara Rao, M. Functional π-Conjugated Two-Dimensional Covalent Organic Frameworks. ACS Appl. Mater. Interfaces 2019, 11, 11029–11060. [Google Scholar] [CrossRef]
- Haase, F.; Gottschling, K.; Stegbauer, L.; Germann, L.S.; Gutzler, R.; Duppel, V.; Vyas, V.S.; Kern, K.; Dinnebier, R.E.; Lotsch, B.V. Tuning the Stacking Behaviour of a 2D Covalent Organic Framework through Non-Covalent Interactions. Mater. Chem. Front. 2017, 1, 1354–1361. [Google Scholar] [CrossRef]
- Alahakoon, S.B.; Diwakara, S.D.; Thompson, C.M.; Smaldone, R.A. Supramolecular Design in 2D Covalent Organic Frameworks. Chem. Soc. Rev. 2020, 49, 1344–1356. [Google Scholar] [CrossRef]
- Emmerling, S.T.; Schuldt, R.; Bette, S.; Yao, L.; Dinnebier, R.E.; Kästner, J.; Lotsch, B.V. Interlayer Interactions as Design Tool for Large-Pore COFs. J. Am. Chem. Soc. 2021, 143, 15711–15722. [Google Scholar] [CrossRef]
- Duong, P.H.H.; Shin, Y.K.; Kuehl, V.A.; Afroz, M.M.; Hoberg, J.O.; Parkinson, B.; Van Duin, A.C.T.; Li-Oakey, K.D. Molecular Interactions and Layer Stacking Dictate Covalent Organic Framework Effective Pore Size. ACS Appl. Mater. Interfaces 2021, 13, 42164–42175. [Google Scholar] [CrossRef]
- Kuc, A.; Springer, M.A.; Batra, K.; Juarez-Mosqueda, R.; Wöll, C.; Heine, T. Proximity Effect in Crystalline Framework Materials: Stacking-Induced Functionality in MOFs and COFs. Adv. Funct. Mater. 2020, 30, 1908004. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley: Hoboken, NJ, USA, 2004; ISBN 978-0-471-41526-8. [Google Scholar]
- Ma, T.; Kapustin, E.A.; Yin, S.X.; Liang, L.; Zhou, Z.; Niu, J.; Li, L.-H.; Wang, Y.; Su, J.; Li, J.; et al. Single-Crystal X-Ray Diffraction Structures of Covalent Organic Frameworks. Science 2018, 361, 48–52. [Google Scholar] [CrossRef]
- Fratschko, M.; Strasser, N.; Taghizade, N.; Linares-Moreau, M.; Fischer, J.C.; Zhao, T.; Howard, I.A.; Falcaro, P.; Zojer, E.; Resel, R. Identifying Structure and Texture of Metal–Organic Framework Cu2 (Bdc)2 (Dabco) Thin Films by Combining X-Ray Diffraction and Quantum Mechanical Modeling. Cryst. Growth Des. 2025, 25, 3665–3679. [Google Scholar] [CrossRef] [PubMed]
- Haase, F.; Lotsch, B.V. Solving the COF Trilemma: Towards Crystalline, Stable and Functional Covalent Organic Frameworks. Chem. Soc. Rev. 2020, 49, 8469–8500. [Google Scholar] [CrossRef] [PubMed]
- Lukose, B.; Kuc, A.; Heine, T. The Structure of Layered Covalent-Organic Frameworks. Chem. A Eur. J. 2011, 17, 2388–2392. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.; Zhang, Z.; Wee, V.; Usadi, A.K.; Calabro, D.C.; Baugh, L.S.; Wang, S.; Wang, Y.; Zhao, D. Interlayer Shifting in Two-Dimensional Covalent Organic Frameworks. J. Am. Chem. Soc. 2020, 142, 12995–13002. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, X.; Cui, J.; Liang, S. Identification of the Miller Indices of a Crystallographic Plane: A Tutorial and a Comprehensive Review on Fundamental Theory, Universal Methods Based on Different Case Studies and Matters Needing Attention. Nanoscale 2020, 12, 16657–16677. [Google Scholar] [CrossRef]
- Pütz, A.M.; Terban, M.W.; Bette, S.; Haase, F.; Dinnebier, R.E.; Lotsch, B.V. Total Scattering Reveals the Hidden Stacking Disorder in a 2D Covalent Organic Framework. Chem. Sci. 2020, 11, 12647–12654. [Google Scholar] [CrossRef]
- Zhang, Y.; Položij, M.; Heine, T. Statistical Representation of Stacking Disorder in Layered Covalent Organic Frameworks. Chem. Mater. 2022, 34, 2376–2381. [Google Scholar] [CrossRef]
- Spitler, E.L.; Dichtel, W.R. Lewis Acid-Catalysed Formation of Two-Dimensional Phthalocyanine Covalent Organic Frameworks. Nat. Chem. 2010, 2, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Hahn, T. (Ed.) International Tables for Crystallography: Space-Group Symmetry. In International Tables for Crystallography, 1st ed.; International Union of Crystallography: Chester, UK, 2006; Volume A, ISBN 978-0-7923-6590-7. [Google Scholar]
- Winkler, C.; Kamencek, T.; Zojer, E. Understanding the Origin of Serrated Stacking Motifs in Planar Two-Dimensional Covalent Organic Frameworks. Nanoscale 2021, 13, 9339–9353. [Google Scholar] [CrossRef] [PubMed]
- Van Gele, S.; Bette, S.; Lotsch, B.V. The Devil Is in the Details: Pitfalls and Ambiguities in the Analysis of X-Ray Powder Diffraction Data of 2D Covalent Organic Frameworks. JACS Au 2025, 5, 388–398. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Han, X.; Liu, Y.; Liu, Y.; Cui, Y. Control Interlayer Stacking and Chemical Stability of Two-Dimensional Covalent Organic Frameworks via Steric Tuning. J. Am. Chem. Soc. 2018, 140, 16124–16133. [Google Scholar] [CrossRef]
- Zojer, E. Tuning the Electrostatic Energy Landscape within the Pores of Covalent Organic Frameworks: Post-Synthetic Modification Reactions and Structural Imperfections. J. Mater. Chem. A 2024, 12, 10166–10184. [Google Scholar] [CrossRef]
- Deringer, V.L.; Bartók, A.P.; Bernstein, N.; Wilkins, D.M.; Ceriotti, M.; Csányi, G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021, 121, 10073–10141. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006; ISBN 978-0-262-18253-9. [Google Scholar]
- Gray, M.; Herbert, J.M. Origins of Offset-Stacking in Porous Frameworks. J. Phys. Chem. C 2023, 127, 2675–2686. [Google Scholar] [CrossRef]
- Heenen, H.H.; Reuter, K. On Boltzmann Averaging in Ab Initio Thermodynamics. J. Chem. Phys. 2025, 163, 114107. [Google Scholar] [CrossRef] [PubMed]
- Steentjes, R.; Zojer, E. The dynamics of stacking in layered covalent organic frameworks. In Monatsh. Chem. (Chem. Mon.); 2025; submitted (under review). [Google Scholar]
- Jinnouchi, R.; Lahnsteiner, J.; Karsai, F.; Kresse, G.; Bokdam, M. Phase Transitions of Hybrid Perovskites Simulated by Machine-Learning Force Fields Trained on the Fly with Bayesian Inference. Phys. Rev. Lett. 2019, 122, 225701. [Google Scholar] [CrossRef]
- Jinnouchi, R.; Karsai, F.; Kresse, G. On-the-Fly Machine Learning Force Field Generation: Application to Melting Points. Phys. Rev. B 2019, 100, 014105. [Google Scholar] [CrossRef]
- Jinnouchi, R.; Karsai, F.; Verdi, C.; Asahi, R.; Kresse, G. Descriptors Representing Two- and Three-Body Atomic Distributions and Their Effects on the Accuracy of Machine-Learned Inter-Atomic Potentials. J. Chem. Phys. 2020, 152, 234102. [Google Scholar] [CrossRef] [PubMed]
- Sherrill, C.D. Energy Component Analysis of π Interactions. Acc. Chem. Res. 2013, 46, 1020–1028. [Google Scholar] [CrossRef]
- Thomas, S.; Li, H.; Dasari, R.R.; Evans, A.M.; Castano, I.; Allen, T.G.; Reid, O.G.; Rumbles, G.; Dichtel, W.R.; Gianneschi, N.C.; et al. Design and Synthesis of Two-Dimensional Covalent Organic Frameworks with Four-Arm Cores: Prediction of Remarkable Ambipolar Charge-Transport Properties. Mater. Horiz. 2019, 6, 1868–1876. [Google Scholar] [CrossRef]
- Dalapati, S.; Addicoat, M.; Jin, S.; Sakurai, T.; Gao, J.; Xu, H.; Irle, S.; Seki, S.; Jiang, D. Rational Design of Crystalline Supermicroporous Covalent Organic Frameworks with Triangular Topologies. Nat. Commun. 2015, 6, 7786. [Google Scholar] [CrossRef]
- Haldar, S.; Wang, M.; Bhauriyal, P.; Hazra, A.; Khan, A.H.; Bon, V.; Isaacs, M.A.; De, A.; Shupletsov, L.; Boenke, T.; et al. Porous Dithiine-Linked Covalent Organic Framework as a Dynamic Platform for Covalent Polysulfide Anchoring in Lithium–Sulfur Battery Cathodes. J. Am. Chem. Soc. 2022, 144, 9101–9112. [Google Scholar] [CrossRef]
- August, D.P.; Dryfe, R.A.W.; Haigh, S.J.; Kent, P.R.C.; Leigh, D.A.; Lemonnier, J.-F.; Li, Z.; Muryn, C.A.; Palmer, L.I.; Song, Y.; et al. Self-Assembly of a Layered Two-Dimensional Molecularly Woven Fabric. Nature 2020, 588, 429–435. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab Initio Molecular Simulations with Numeric Atom-Centered Orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef]
- Knuth, F.; Carbogno, C.; Atalla, V.; Blum, V.; Scheffler, M. All-Electron Formalism for Total Energy Strain Derivatives and Stress Tensor Components for Numeric Atom-Centered Orbitals. Comput. Phys. Commun. 2015, 190, 33–50. [Google Scholar] [CrossRef]
- Havu, V.; Blum, V.; Havu, P.; Scheffler, M. Efficient Integration for All-Electron Electronic Structure Calculation Using Numeric Basis Functions. J. Comput. Phys. 2009, 228, 8367–8379. [Google Scholar] [CrossRef]
- Yu, V.W.; Corsetti, F.; García, A.; Huhn, W.P.; Jacquelin, M.; Jia, W.; Lange, B.; Lin, L.; Lu, J.; Mi, W.; et al. ELSI: A Unified Software Interface for Kohn–Sham Electronic Structure Solvers. Comput. Phys. Commun. 2018, 222, 267–285. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Hermann, J.; Tkatchenko, A. Density Functional Model for van Der Waals Interactions: Unifying Many-Body Atomic Approaches with Nonlocal Functionals. Phys. Rev. Lett. 2020, 124, 146401. [Google Scholar] [CrossRef] [PubMed]
- Lenthe, E.V.; Baerends, E.J.; Snijders, J.G. Relativistic Regular Two-Component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006; ISBN 978-0-387-40065-5. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Cullity, B.D.; Stock, S.R. Elements of X-Ray Diffraction, 3rd ed.; New Internat. ed. Pearson Education: Harlow, UK, 2014; ISBN 978-1-292-04054-7. [Google Scholar]
- Warren, B.E. X-Ray Diffraction, Dover ed.; Dover Publications: New York, NY, USA, 1990; ISBN 978-0-486-66317-3. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steentjes, R.; Zojer, E. Stacking in Layered Covalent Organic Frameworks: A Computational Approach and PXRD Reference Guide. Int. J. Mol. Sci. 2025, 26, 9222. https://doi.org/10.3390/ijms26189222
Steentjes R, Zojer E. Stacking in Layered Covalent Organic Frameworks: A Computational Approach and PXRD Reference Guide. International Journal of Molecular Sciences. 2025; 26(18):9222. https://doi.org/10.3390/ijms26189222
Chicago/Turabian StyleSteentjes, Robbin, and Egbert Zojer. 2025. "Stacking in Layered Covalent Organic Frameworks: A Computational Approach and PXRD Reference Guide" International Journal of Molecular Sciences 26, no. 18: 9222. https://doi.org/10.3390/ijms26189222
APA StyleSteentjes, R., & Zojer, E. (2025). Stacking in Layered Covalent Organic Frameworks: A Computational Approach and PXRD Reference Guide. International Journal of Molecular Sciences, 26(18), 9222. https://doi.org/10.3390/ijms26189222





