Automated Segmentation and Morphometric Analysis of Thioflavin-S-Stained Amyloid Deposits in Alzheimer’s Disease Brains and Age-Matched Controls Using Weakly Supervised Deep Learning
Abstract
1. Introduction
2. Results
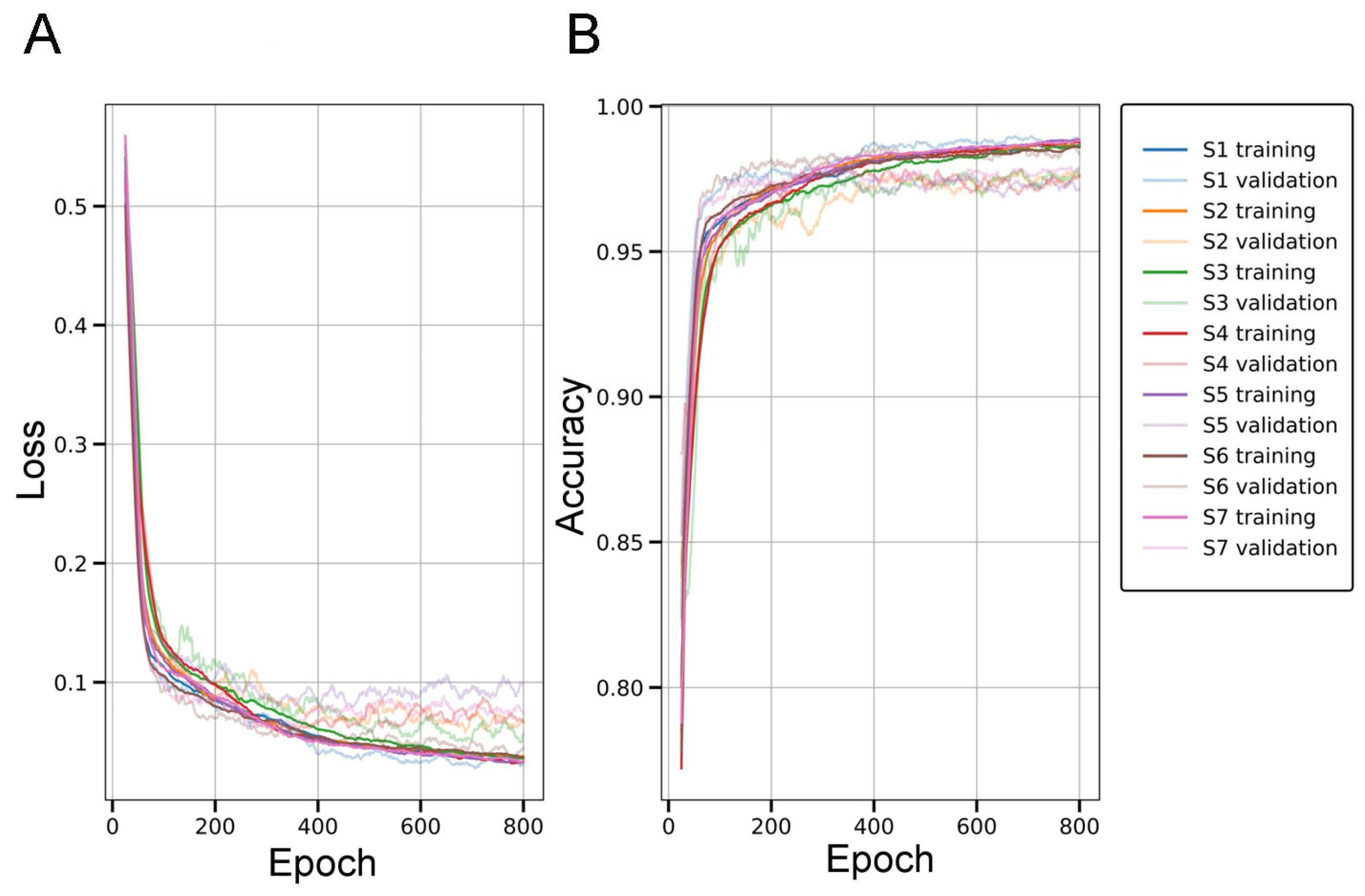
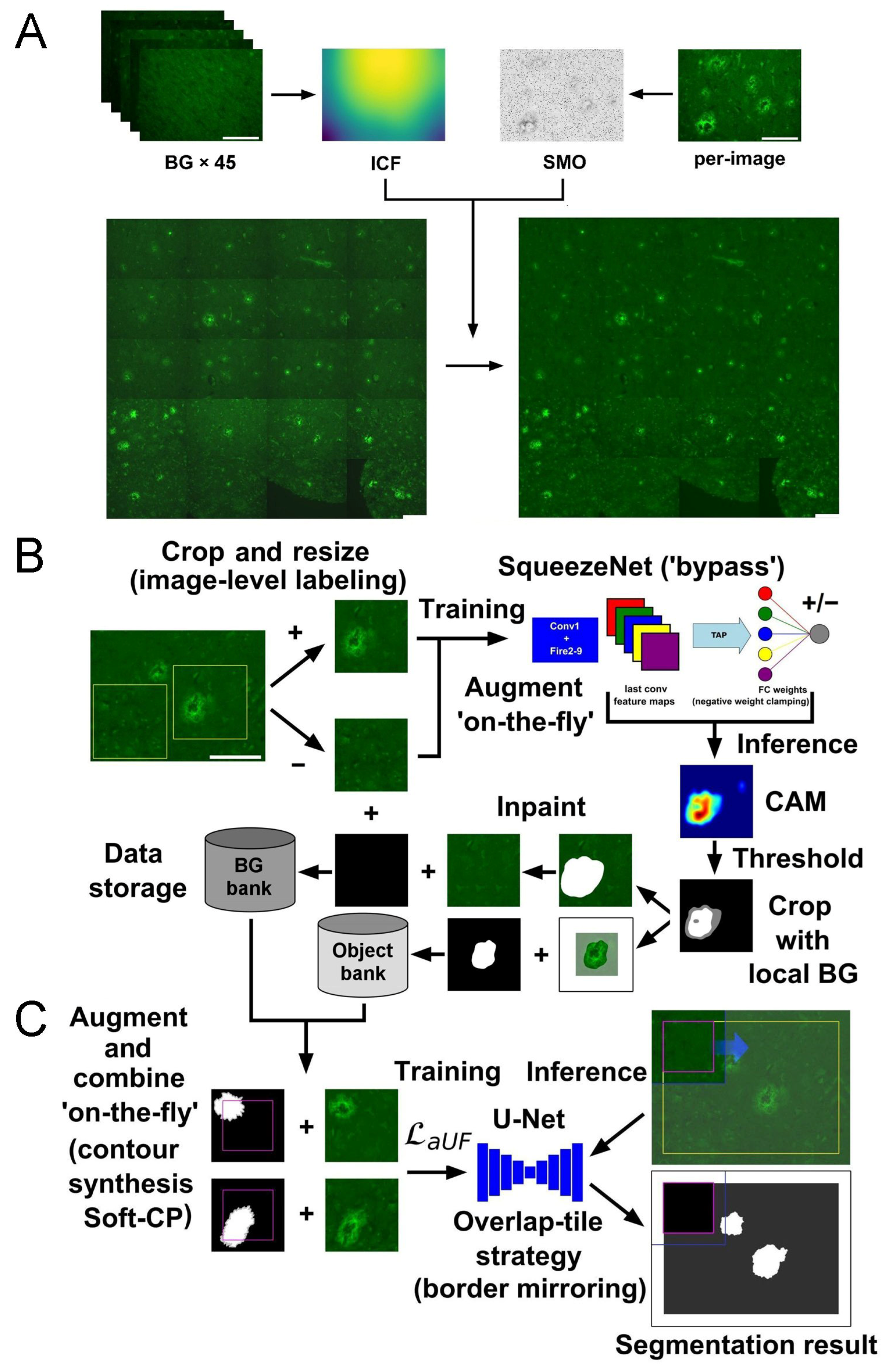
2.1. Evaluation of the SqueezeNet Classifier for Parenchymal Amyloid Detection
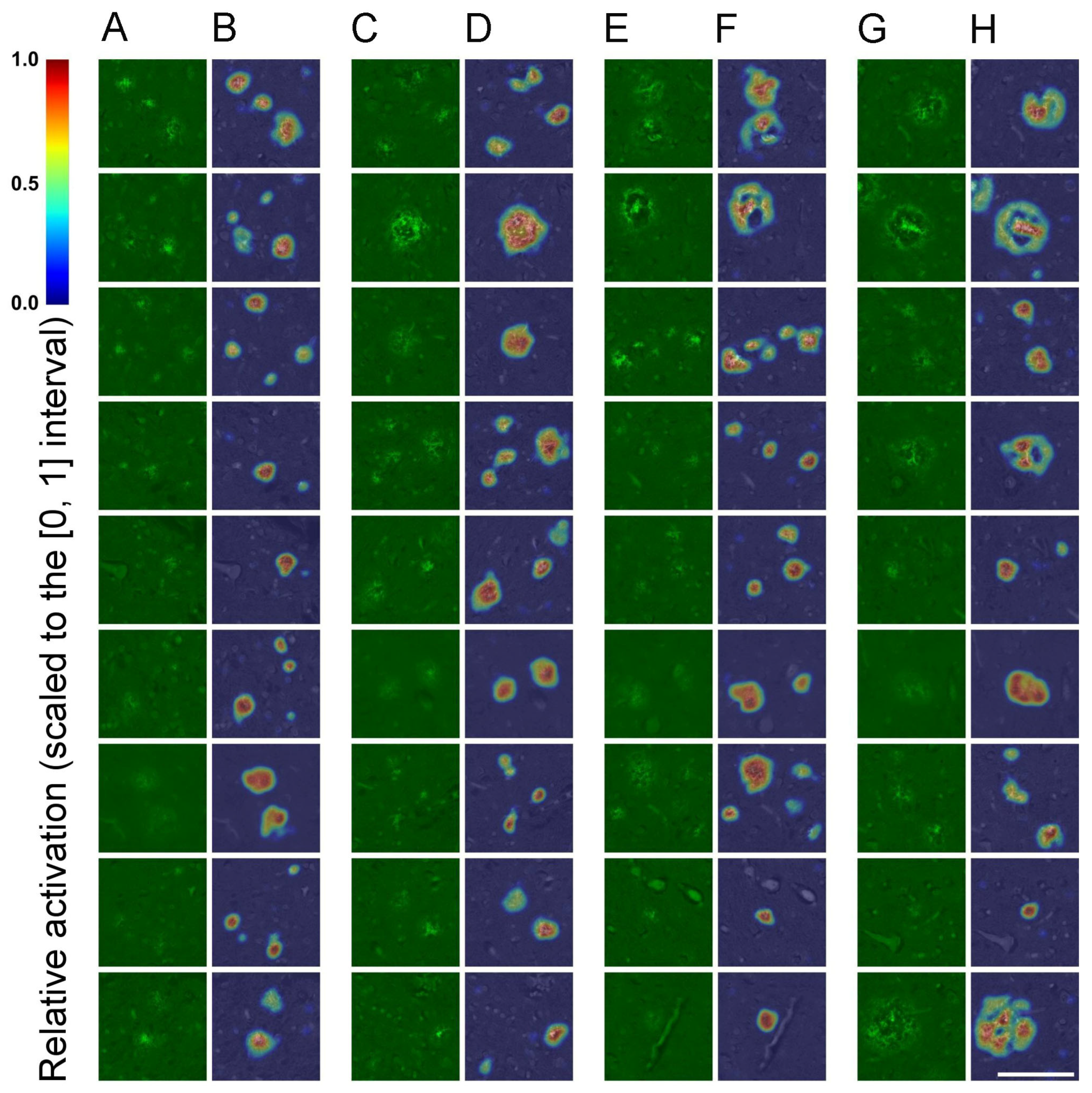
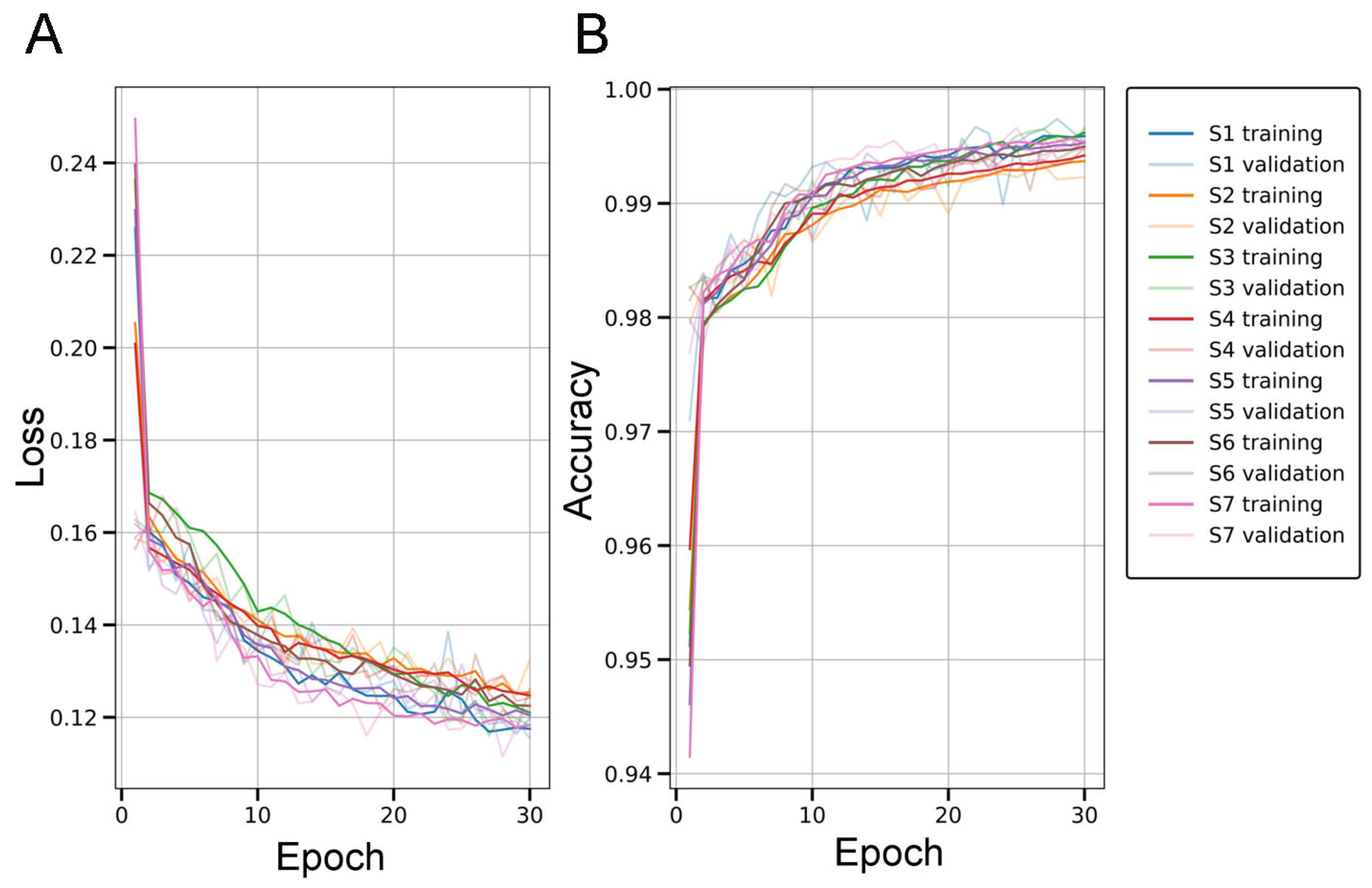
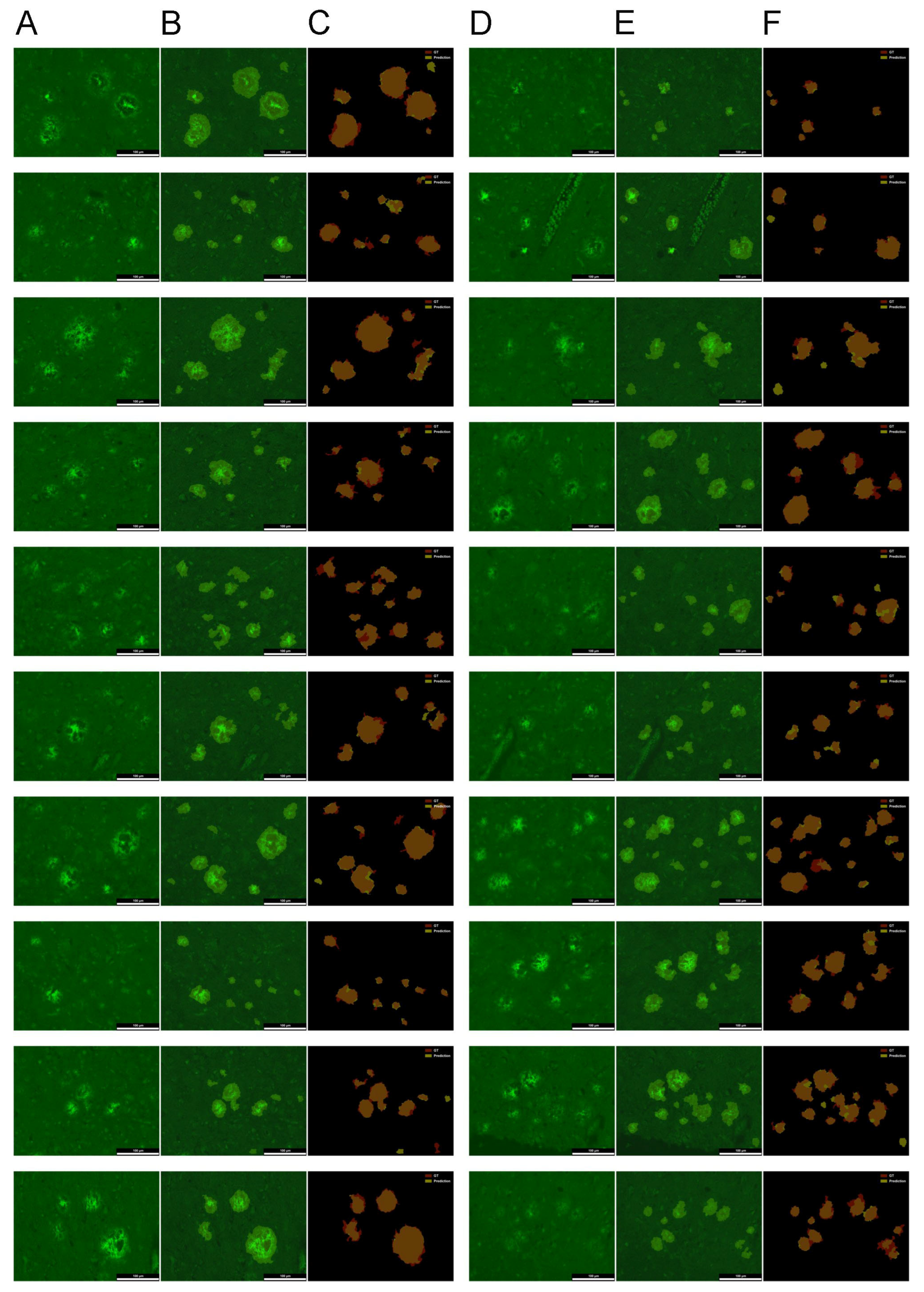
2.2. Evaluation of the U-Net for Parenchymal Amyloid Segmentation
2.3. Morphometric Profiling of Amyloid Plaques via Particle Analysis
3. Discussion
3.1. SqueezeNet-Based CAM for Weakly Supervised Localization
3.2. U-Net Segmentation with Advanced Object-Level Augmentation
3.3. Morphometric Profiling of Amyloid Plaques via Particle Analysis
4. Materials and Methods
4.1. Brain Sections
4.2. ThioS Staining and Epifluorescence Microscopy for Amyloid Detection
4.3. Preprocessing Fluorescent Micrographs: Uneven Illumination, Background Estimation, and Annotation Preparation
4.4. Implementation of SqueezeNet-Based CAM for Weakly Supervised Localization
- Accuracy, defined as TPcls/(TPcls + TNcls + FPcls + FNcls), measures the overall proportion of correctly classified image patches, regardless of class. It provides a general indication of the model’s reliability in distinguishing between positive and negative instances.
- Precision, defined as TPcls/(TPcls + FPcls), quantifies the proportion of true positive predictions among all patches predicted as positive, indicating how many of the identified amyloid-positive regions were correctly detected.
- Recall, calculated as TPcls/(TPcls + FNcls), measures the capacity of the model to correctly identify all truly positive instances; i.e., the proportion of actual amyloid-containing patches that were successfully detected.
- F1-score expresses the trade-off between precision and recall through their harmonic mean, computed as 2TPcls/(2TPcls + FPcls + FNcls), and proves especially informative in imbalanced classification contexts.
4.5. Implementation of U-Net Segmentation with Advanced Object-Level Augmentation
- Dice coefficient, defined as 2TPseg/(2TPseg + FPseg +FNseg), quantifies the spatial overlap between predicted and GT segmentation masks. It reflects both precision and recall and is widely used in biomedical image segmentation to assess agreement.
- Jaccard index (also known as Intersection over Union), given by TPseg/(TPseg + FPseg + FNseg), provides a stricter measure of overlap than the Dice coefficient. It evaluates the proportion of shared positive predictions relative to the union of predicted and actual positives.
- Recall, calculated as TPseg/(TPseg + FNseg), measures the ability of the model to correctly detect all amyloid-positive pixels.
- Pixel-level accuracy (PA), computed as (TPseg + TNseg)/(TPseg + TNseg + FPseg + FNseg), assesses the overall correctness of predictions across all pixels, including both FG and BG. However, in cases of strong class imbalance, where BG pixels vastly outnumber FG pixels, accuracy may be inflated and fail to reflect true segmentation performance.
- Specificity, calculated as TNseg/(TNseg + FPseg), reflects the model’s ability to correctly identify BG (non-deposit) pixels, reducing the likelihood of over-segmentation.
- Precision, defined as TPseg/(TPseg + FPseg), indicates the fraction of true deposit pixels among all those classified as deposits.
- Negative Predictive Value (NPV), calculated as TNseg/(TNseg + FNseg), indicates the proportion of correctly classified BG pixels among all BG predictions.
- False Positive Rate (FPR), given by FPseg/(FPseg + TNseg), quantifies the proportion of BG pixels incorrectly labeled as deposits.
- False Discovery Rate (FDR), calculated as FPseg/(FPseg + TPseg), indicates the proportion of incorrect deposit predictions among all positive predictions.
- False Negative Rate (FNR), defined as FNseg/(FNseg + TPseg), represents the fraction of actual deposit pixels that were missed by the model.
- False Omission Rate (FOR), defined as FNseg/(FNseg + TNseg), measures the proportion of missed FG pixels among all predicted BG pixels.
4.6. Implementation of Morphometric Profiling of Amyloid Plaques via Particle Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Alzheimer’s disease |
| Adam | adaptive moment estimation |
| ANOVA | analysis of variance |
| Aβ | amyloid-β |
| BG | background |
| CAM | class activation maps/mapping |
| CNNs | convolutional neural networks |
| FDR | false discovery rate |
| FG | foreground |
| FNcls/seg | false negatives for classification/segmentation tasks |
| FNR | false negative rate |
| FOR | false omission rate |
| FPcls/seg | false positives for classification/segmentation tasks |
| FPR | false positive rate |
| GAP | global average pooling |
| GMP | global max pooling |
| GT | ground truth |
| ICF | illumination correction function |
| mTI | modified Tversky index |
| NPV | negative predictive value |
| PA | pixel-level accuracy |
| PCA | principal component analysis |
| PCs | principal components |
| RMSprop | root mean square propagation |
| ROI | region of interest |
| SMO | Silver Mountain Operator |
| Soft-CP | soft-copy and soft-paste |
| TAP | thresholded average pooling |
| ThioS | thioflavin-S |
| TNcls/seg | true negatives for classification/segmentation tasks |
| TPcls/seg | true positives for classification/segmentation tasks |
| WSOL | weakly supervised object localization |
| WSSS | weakly supervised semantic segmentation |
| aUF | asymmetric unified focal loss |
| BC | binary cross-entropy loss |
| maF | modified asymmetric focal loss |
| maFT | modified asymmetric focal Tversky loss |
References
- Braak, H.; Braak, E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol. 1991, 82, 239–259. [Google Scholar] [CrossRef] [PubMed]
- Arendt, T.; Stieler, J.; Ueberham, U. Is sporadic Alzheimer’s disease a developmental disorder? J. Neurosci. 2017, 143, 396–408. [Google Scholar] [CrossRef] [PubMed]
- DeTure, M.A.; Dickson, D.W. The neuropathological diagnosis of Alzheimer’s disease. Mol. Neurodegener. 2019, 14, 32. [Google Scholar] [CrossRef] [PubMed]
- Walker, L.C. Aβ Plaques. Free neuropathol. 2020, 1, 31. [Google Scholar] [CrossRef] [PubMed]
- Cole, S.L.; Vassar, R. The Alzheimer’s disease beta-secretase enzyme, BACE1. Mol. Neurodegener. 2007, 2, 22. [Google Scholar] [CrossRef] [PubMed]
- Jankovska, N.; Olejar, T.; Matej, R. Extracellular protein aggregates colocalization and neuronal dystrophy in comorbid Alzheimer’s and Creutzfeldt-Jakob disease: A micromorphological pilot study on 20 brains. Int. J. Mol. Sci. 2021, 22, 2099. [Google Scholar] [CrossRef] [PubMed]
- Lauritzen, I.; Pardossi-Piquard, R.; Bauer, C.; Brigham, E.; Abraham, J.D.; Ranaldi, S.; Fraser, P.; St-George-Hyslop, P.; Le Thuc, O.; Espin, V.; et al. The β-secretase-derived C-terminal fragment of βAPP, C99, but not Aβ, is a key contributor to early intraneuronal lesions in triple-transgenic mouse hippocampus. J. Neurosci. 2012, 32, 16243–16255. [Google Scholar] [CrossRef] [PubMed]
- Serrano-Pozo, A.; Frosch, M.P.; Masliah, E.; Hyman, B.T. Neuropathological alterations in Alzheimer disease. Cold Spring Harb. Perspect. Med. 2011, 1, a006189. [Google Scholar] [CrossRef] [PubMed]
- Hardy, J.; Selkoe, D.J. The amyloid hypothesis of Alzheimer’s disease: Progress and problems on the road to therapeutics. Science 2002, 297, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Thal, D.R.; Rüb, U.; Orantes, M.; Braak, H. Phases of A beta-deposition in the human brain and its relevance for the development of AD. Neurology 2002, 58, 1791–1800. [Google Scholar] [CrossRef] [PubMed]
- Pirici, D.; Van Cauwenberghe, C.; Van Broeckhoven, C.; Kumar-Singh, S. Fractal analysis of amyloid plaques in Alzheimer’s disease patients and mouse models. Neurobiol. Aging 2011, 32, 1579–1587. [Google Scholar] [CrossRef] [PubMed]
- Thal, D.R.; Capetillo-Zarate, E.; Del Tredici, K.; Braak, H. The development of amyloid beta protein deposits in the aged brain. Sci. Aging Knowl. Environ. 2006, 6, re1. [Google Scholar] [CrossRef]
- Bussière, T.; Bard, F.; Barbour, R.; Grajeda, H.; Guido, T.; Khan, K.; Schenk, D.; Games, D.; Seubert, P.; Buttini, M. Morphological characterization of Thioflavin-S-positive amyloid plaques in transgenic Alzheimer mice and effect of passive Abeta immunotherapy on their clearance. Am. J. Pathol. 2004, 165, 987–995. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, R.A. Beta-amyloid plaques: Stages in life history or independent origin? Dement. Geriatr. Cogn. Dis. 1998, 9, 227–238. [Google Scholar] [CrossRef] [PubMed]
- Röhr, D.; Boon, B.; Schuler, M.; Kremer, K.; Hoozemans, J.; Bouwman, F.H.; El-Mashtoly, S.F.; Nabers, A.; Großerueschkamp, F.; Rozemuller, A.; et al. Label-free vibrational imaging of different Aβ plaque types in Alzheimer’s disease reveals sequential events in plaque development. Acta Neuropathol. Comm. 2020, 8, 222. [Google Scholar] [CrossRef] [PubMed]
- MacKeigan, T.P.; Morgan, M.L.; Stys, P.K. Quantitation of tissue amyloid via fluorescence spectroscopy using controlled concentrations of thioflavin-S. Molecules 2023, 28, 4483. [Google Scholar] [CrossRef] [PubMed]
- Sun, A.; Nguyen, X.V.; Bing, G. Comparative Analysis of an Improved Thioflavin-S Stain, Gallyas Silver Stain, and Immunohistochemistry for Neurofibrillary Tangle Demonstration on the Same Sections. J. Histochem. Cytochem. 2002, 50, 463–472. [Google Scholar] [CrossRef] [PubMed]
- Rajamohamedsait, H.B.; Sigurdsson, E.M. Histological staining of amyloid and pre-amyloid peptides and proteins in mouse tissue. Methods Mol. Biol. 2012, 849, 411–424. [Google Scholar] [CrossRef] [PubMed]
- Wilcock, D.M.; Gordon, M.N.; Morgan, D. Quantification of cerebral amyloid angiopathy and parenchymal amyloid plaques with Congo red histochemical stain. Nat. Protoc. 2006, 1, 1591–1595. [Google Scholar] [CrossRef] [PubMed]
- Barton, S.M.; To, E.; Rogers, B.P.; Whitmore, C.; Uppal, M.; Matsubara, J.A.; Pham, W. Inhalable thioflavin S for the detection of amyloid beta deposits in the retina. Molecules 2021, 26, 835. [Google Scholar] [CrossRef] [PubMed]
- Piccinini, F.; Lucarelli, E.; Gherardi, A.; Bevilacqua, A. Multi-image based method to correct vignetting effect in light microscopy images. J. Microsc. 2012, 248, 6–22. [Google Scholar] [CrossRef] [PubMed]
- Silberberg, M.; Grecco, H.E. Robust and unbiased estimation of the background distribution for automated quantitative imaging. J. Opt. Soc. Am. A 2023, 40, C8–C15. [Google Scholar] [CrossRef] [PubMed]
- Krutsay, M. Patológiai Technika; Medicina: Budapest, Hungary, 1999; ISBN 963 242 434 4. [Google Scholar]
- Yang, R.; Yu, Y. Artificial convolutional neural network in object detection and semantic segmentation for medical imaging analysis. Front. Oncol. 2021, 11, 638182. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Jiang, Y.; Peng, Y.; Yuan, F.; Zhang, X.; Wang, J. Medical image segmentation: A comprehensive review of deep learning-based methods. Tomography 2025, 11, 52. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative jocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar] [CrossRef]
- Han, C.; Lin, J.; Mai, J.; Wang, Y.; Zhang, Q.; Zhao, B.; Chen, X.; Pan, X.; Shi, Z.; Xu, Z.; et al. Multi-layer pseudo-supervision for histopathology tissue semantic segmentation using patch-level classification labels. Med. Image Anal. 2022, 80, 102487. [Google Scholar] [CrossRef] [PubMed]
- Din, N.U.; Yu, J. Training a deep learning model for single-cell segmentation without manual annotation. Sci. Rep. 2021, 11, 23995. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, K.; Ker, E.; Bise, R. Weakly supervised cell instance segmentation by propagating from detection response. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2019; Shen, D., Ed.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 2019, p. 11764. [Google Scholar] [CrossRef]
- Ramananda, S.H.; Sundaresan, V. Class activation map-based weakly supervised hemorrhage segmentation using Resnet-LSTM in non-contrast computed tomography images. arXiv 2023, arXiv:2309.16627. [Google Scholar] [CrossRef]
- Li, Z.; Xia, Y. Deep reinforcement learning for weakly-supervised lymph node segmentation in CT images. IEEE J. Biomed. Health Inform. 2021, 25, 774–783. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Lu, T.; Zhang, S.; Wang, G. UM-CAM: Uncertainty-weighted multi-resolution class activation maps for weakly-supervised fetal brain segmentation. Pattern Recognit. 2023, 160, 111204. [Google Scholar] [CrossRef]
- Liu, Y.; Lian, L.; Zhang, E.; Xu, L.; Xiao, C.; Zhong, X.; Li, F.; Jiang, B.; Dong, Y.; Ma, L.; et al. Mixed-UNet: Refined class activation mapping for weakly-supervised semantic segmentation with multi-scale inference. Front. Comput. Sci. 2022, 4, 1036934. [Google Scholar] [CrossRef]
- Sampaio, V.; Cordeiro, F. Improving mass detection in mammography images: A study of weakly supervised learning and class activation map methods. In Proceedings of the 36th SIBGRAPI Conference on Graphics, Patterns and Images, Rio de Janeiro, Brazil, 17–20 October 2023; pp. 139–144. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Y.; Zou, Y.; Xiang, T.; Li, X. Online easy example mining for weakly-supervised gland segmentation from histology images. arXiv 2022, arXiv:2206.06665v3. [Google Scholar] [CrossRef]
- SukeshAdiga, V.; Dolz, J.; Lombaert, H. Manifold-driven attention maps for weakly supervised segmentation. arXiv 2020, arXiv:2004.03046v1. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.J.; Kim, C.; Lee, J.H.; Kim, K.W.; Park, Y.M.; Kim, H.W.; Ki, S.Y.; Kim, Y.M.; Kim, W.H. Weakly-supervised deep learning for ultrasound diagnosis of breast cancer. Sci. Rep. 2021, 11, 24382. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, A.; Gupta, S.; Bhanushali, A.; Rai Dastidar, T. Rapid training data creation by synthesizing medical images for classification and localization. arXiv 2023, arXiv:2308.04687. [Google Scholar] [CrossRef]
- Zhang, A.; Shailja, S.; Borba, C.; Miao, Y.; Goebel, M.; Ruschel, R.; Ryan, K.; Smith, W.; Manjunath, B.S. Automatic classification and neurotransmitter prediction of synapses in electron microscopy. Biol. Imaging 2022, 2, e6. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhang, D.; Song, Y.; Zhang, F.; ODonnell, L.; Huang, H.; Chen, M.; Cai, W. Unsupervised instance segmentation in microscopy images via panoptic domain adaptation and task Re-Weighting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Curti, N.; Merli, Y.; Zengarini, C.; Giampieri, E.; Merlotti, A.; Dall’Olio, D.; Marcelli, E.; Bianchi, T.; Castellani, G. Effectiveness of Semi-Supervised Active Learning in Automated Wound Image Segmentation. Int. J. Mol. Sci. 2023, 24, 706. [Google Scholar] [CrossRef] [PubMed]
- Arvaniti, E.; Fricker, K.; Moret, M.; Rupp, N.; Hermanns, T.; Fankhauser, C.; Wey, N.; Wild, P.; Rüschoff, J.; Claassen, M. Automated Gleason grading of prostate cancer tissue microarrays via deep learning. Sci. Rep. 2018, 8, 12054. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Wang, L.; Nan, Y.; Jin, F.; Wang, Q.; Pu, J. SDFN: Segmentation-based deep fusion network for thoracic disease classification in chest X-ray images. Comput. Med. Imaging Graph. 2019, 75, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Meng, M.; Zhang, M.; Shen, D.; He, G. Differentiation of breast lesions on dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) using deep transfer learning based on DenseNet201. Medicine 2022, 101, e31214. [Google Scholar] [CrossRef] [PubMed]
- Sulaiman, A.; Anand, V.; Gupta, S.; Rajab, A.; Alshahrani, H.; Al Reshan, M.; Shaikh, A.; Hamdi, M. Attention based UNet model for breast cancer segmentation using BUSI dataset. Sci. Rep. 2024, 14, 22422. [Google Scholar] [CrossRef] [PubMed]
- Dornadula, B.; Geetha, S.; Anbarasi, L.; Kadry, S. A Survey of COVID-19 detection from chest X-rays using deep learning methods. Inter. J. Data Warehous. Min. 2022, 18, 1–16. [Google Scholar] [CrossRef]
- Ullah, I.; Ali, F.; Shah, B.; El-Sappagh, S.; Abuhmed, T.; Park, S. A deep learning based dual encoder-decoder framework for anatomical structure segmentation in chest X-ray images. Sci. Rep. 2023, 13, 791. [Google Scholar] [CrossRef]
- Wei, J.W.; Wei, J.W.; Jackson, C.R.; Ren, B.; Suriawinata, A.A.; Hassanpour, S. Automated detection of celiac disease on duodenal biopsy slides: A deep learning approach. J. Pathol. Inform. 2019, 10, 7. [Google Scholar] [CrossRef] [PubMed]
- Nguyen Thi Phuong, H.; Shin, C.-S.; Jeong, H.-Y. Finding the differences in capillaries of taste buds between smokers and non-smokers using the convolutional neural networks. Appl. Sci. 2021, 11, 3460. [Google Scholar] [CrossRef]
- Richmond, D.; Jost, A.P.; Lambert, T.J.; Waters, J.C.; Elliott, H. DeadNet: Identifying phototoxicity from label-free microscopy images of cells using deep ConvNets. arXiv 2017, arXiv:1701.06109v1. [Google Scholar] [CrossRef]
- Irmak, E. A novel implementation of deep-learning approach on malaria parasite detection from thin blood cell images. Electrica 2021, 21, 216–224. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, W.; Pang, K.; Xia, D.; Guo, L.; Chen, X.; Wu, F.; Wang, H. Weakly supervised learning analysis of Aβ plaque distribution in the whole rat brain. Front. Neurosci. 2023, 16, 1097019. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Chuang, K.V.; DeCarli, C.; Jin, L.W.; Beckett, L.; Keiser, M.J.; Dugger, B.N. Interpretable classification of Alzheimer’s disease pathologies with a convolutional neural network pipeline. Nat. Commun. 2019, 10, 2173. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.; Röhr, D.; Boon, B.D.C.; Wulf, M.; Arto, T.; Hoozemans, J.J.M.; Marcus, K.; Rozemuller, A.J.M.; Großerueschkamp, F.; Mosig, A.; et al. Label-free Aβ plaque detection in Alzheimer’s disease brain tissue using infrared microscopy and neural networks. Heliyon 2025, 11, e42111. [Google Scholar] [CrossRef] [PubMed]
- Chabrun, F.; Dieu, X.; Doudeau, N.; Gautier, J.; Luque-Paz, D.; Geneviève, F.; Ferré, M.; Mirebeau-Prunier, D.; Annweiler, C.; Reynier, P. Deep learning shows no morphological abnormalities in neutrophils in Alzheimer’s disease. Alzheimer’s Dement. 2021, 13, e12146. [Google Scholar] [CrossRef] [PubMed]
- Iandola, F.N.; Moskewicz, M.W.; Ashraf, K.; Han, S.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <1MB model size. arXiv 2016, arXiv:1602.07360v4. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2014, arXiv:1312.4400v3. [Google Scholar] [CrossRef] [PubMed]
- Selvaraju, R.R.; Das, A.; Vedantam, R.; Cogswell, M.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
- Bae, W.; Noh, J.; Kim, G. Rethinking class activation mapping for weakly supervised object localization. In Computer Vision–ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12360, pp. 618–634. [Google Scholar] [CrossRef]
- Oquab, M.; Bottou, L.; Laptev, I.; Sivic, J. Is object localization for free?–Weakly-supervised learning with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 685–694. [Google Scholar] [CrossRef]
- Pinheiro, P.H.O.; Collobert, R. From image-level to pixel-level labeling with convolutional networks. arXiv 2015, arXiv:1411.6228v3. [Google Scholar] [CrossRef]
- Dogan, Y. A new global pooling method for deep neural networks: Global average of top-k max-pooling. Trait. Du Signal 2023, 40, 577–587. [Google Scholar] [CrossRef]
- Nieradzik, L.; Stephani, H.; Keuper, J. Top-GAP: Integrating size priors in CNNs for more interpretability, robustness, and bias mitigation. arXiv 2024, arXiv:2409.04819v1. [Google Scholar] [CrossRef]
- Christlein, V.; Spranger, L.; Seuret, M.; Nicolaou, A.; Král, P.; Maier, A.K. Deep generalized max pooling. In Proceedings of the International Conference on Document Analysis and Recognition, Sydney, NSW, Australia, 22–26 September 2019; pp. 1090–1096. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized gradient-based visual explanations for deep convolutional networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Lake Tahoe, NV, USA, 12–15 March 2018; pp. 839–847. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Du, M.; Yang, F.; Zhang, Z.; Ding, S.; Mardziel, P.; Hu, X. Score-CAM: Score-weighted visual explanations for convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020. [Google Scholar] [CrossRef]
- Englebert, A.; Cornu, O.; Vleeschouwer, C.D. Poly-CAM: High resolution class activation map for convolutional neural networks. Mach. Vis. Appl. 2022, 35, 89. [Google Scholar] [CrossRef]
- Shinde, S.; Chougule, T.; Saini, J.; Ingalhalikar, M. HR-CAM: Precise localization of pathology using multi-level learning in CNNs. arXiv 2019, arXiv:1909.12919v1. [Google Scholar] [CrossRef]
- Shen, W.; Peng, Z.; Wang, X.; Wang, H.; Cen, J.; Jiang, D.; Xie, L.; Yang, X.; Tian, Q. A survey on label-efficient deep image segmentation: Bridging the gap between weak supervision and dense prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9284–9305. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Li, G.; Wunderlich, T.; Wang, L. A survey on deep learning-based precise boundary recovery of semantic segmentation for images and point clouds. Int. J. Appl. Earth Observ. Geoinform. 2021, 102, 102411. [Google Scholar] [CrossRef]
- Kwak, S.; Hong, S.; Han, B. Weakly supervised semantic segmentation using superpixel pooling network. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar] [CrossRef]
- Zheng, S.; Jayasumana, S.; Romera-Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P.H. Conditional random fields as recurrent neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1529–1537. [Google Scholar] [CrossRef]
- Bressan, P.O.; Junior, J.M.; Martins, J.A.C.; De Melo, M.J.; Gonçalves, D.N.; Freitas, D.M.; Ramos, A.P.M.; Furuya, M.T.G.; Osco, L.P.; De Andrade Silva, J.; et al. Semantic segmentation with labeling uncertainty and class imbalance applied to vegetation mapping. Int. J. Applied Earth Observ. Geoinform. 2022, 108, 102690. [Google Scholar] [CrossRef]
- Kervadec, H.; Bouchtiba, J.; Desrosiers, C.; Granger, E.; Dolz, J.; Ayed, I.B. Boundary loss for highly unbalanced segmentation. Med. Image Anal. 2021, 67, 101851. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-NET: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Lecture notes in computer science; Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Guo, R.; Sun, X.; Chen, K.; Zhou, X.; Yan, Z.; Diao, W.; Yan, M. JMLNet: Joint multi-label learning network for weakly supervised semantic segmentation in aerial images. Remote Sens. 2020, 12, 3169. [Google Scholar] [CrossRef]
- Islam, M.; Glocker, B. Spatially Varying Label Smoothing: Capturing Uncertainty from Expert Annotations. In Information Processing in Medical Imaging. IPMI 2021; Feragen, A., Sommer, S., Schnabel, J., Nielsen, M., Eds.; Lecture notes in computer science; Springer: Cham, Switzerland, 2021; Volume 12729, pp. 677–688. [Google Scholar] [CrossRef]
- Kats, E.; Goldberger, J.; Greenspan, H. Soft labeling by distilling anatomical knowledge for improved MS lesion segmentation. In Proceedings of the IEEE 16th International Symposium on Biomedical Imaging (ISBI), Venice, Italy, 8–11 April 2019; pp. 1563–1566. [Google Scholar] [CrossRef]
- Vasudeva, S.A.; Dolz, J.; Lombaert, H. GeoLS: An intensity-based, geodesic soft labeling for image segmentation. J. Mach. Learn. Biomed. Imaging 2025, 2, 120–134. [Google Scholar] [CrossRef]
- Dang, T.; Nguyen, H.; Tiulpin, A. SiNGR: Brain tumor segmentation via signed normalized geodesic transform regression. arXiv 2024, arXiv:2405.16813v4. [Google Scholar] [CrossRef]
- Jiangtao, W.; Ruhaiyem, N.I.R.; Panpan, F. A comprehensive review of U-Net and its variants: Advances and applications in medical image segmentation. IET Image Process. 2025, 19, e70019. [Google Scholar] [CrossRef]
- Solopov, M.; Chechekhina, E.; Kavelina, A.; Akopian, G.; Turchin, V.; Popandopulo, A.; Filimonov, D.; Ishchenko, R. Comparative study of deep transfer learning models for semantic segmentation of human mesenchymal stem cell micrographs. Int. J. Mol. Sci. 2025, 26, 2338. [Google Scholar] [CrossRef] [PubMed]
- Ibragimov, A.; Senotrusova, S.; Markova, K.; Karpulevich, E.; Ivanov, A.; Tyshchuk, E.; Grebenkina, P.; Stepanova, O.; Sirotskaya, A.; Kovaleva, A.; et al. Deep semantic segmentation of angiogenesis images. Int. J. Mol. Sci. 2023, 24, 1102. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Zhou, W.; Wang, Z. A survey of data augmentation in domain generalization. Neural Process. Lett. 2025, 57, 34. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, P.; Liu, K.; Wang, P.; Fu, Y.; Lu, C.; Aggarwal, C.C.; Pei, J.; Zhou, Y. A comprehensive survey on data augmentation. arXiv 2025, arXiv:2405.09591v3. [Google Scholar] [CrossRef]
- Kumar, T.; Brennan, R.; Mileo, A.; Bendechache, M. Image data augmentation approaches: A comprehensive survey and future directions. IEEE Access 2024, 12, 187536–187571. [Google Scholar] [CrossRef]
- Ma, J.; Hu, C.; Zhou, P.; Jin, F.; Wang, X.; Huang, H. Review of image augmentation used in deep learning-based material microscopic image segmentation. Appl. Sci. 2023, 13, 6478. [Google Scholar] [CrossRef]
- Lewy, D.; Mańdziuk, J. An overview of mixing augmentation methods and augmentation strategies. Artif. Intell. Rev. 2022, 56, 2111–2169. [Google Scholar] [CrossRef]
- Zhang, H.; Cissé, M.; Dauphin, Y.; Lopez-Paz, D. Mixup: Beyond empirical risk minimization. arXiv 2018, arXiv:1710.09412v2. [Google Scholar] [CrossRef]
- Verma, V.; Lamb, A.; Beckham, C.; Najafi, A.; Courville, A.C.; Mitliagkas, I.; Bengio, Y. Manifold mixup: Learning better representations by interpolating hidden states. arXiv 2019, arXiv:1806.05236v7. [Google Scholar] [CrossRef]
- Yun, S.; Han, D.; Chun, S.; Oh, S.J.; Yoo, Y.; Choe, J. CutMix: Regularization strategy to train strong classifiers with localizable features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6022–6031. [Google Scholar] [CrossRef]
- Olsson, V.; Tranheden, W.; Pinto, J.; Svensson, L. ClassMix: Segmentation-based data augmentation for semi-supervised learning. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 1368–1377. [Google Scholar] [CrossRef]
- Su, Y.; Sun, R.; Lin, G.; Wu, Q. Context decoupling augmentation for weakly supervised semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 6984–6994. [Google Scholar] [CrossRef]
- Sun, D.; Dornaika, F.; Charafeddine, J. LCAMix: Local-and-contour aware grid mixing based data augmentation for medical image segmentation. Inf. Fusion 2024, 110, 102484. [Google Scholar] [CrossRef]
- Sun, D.; Dornaika, F.; Barrena, N. HSMix: Hard and soft mixing data augmentation for medical image segmentation. Inf. Fusion 2025, 115, 102741. [Google Scholar] [CrossRef]
- Dwibedi, D.; Misra, I.; Hebert, M. Cut, paste and learn: Surprisingly easy synthesis for instance detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1310–1319. [Google Scholar] [CrossRef]
- Ghiasi, G.; Cui, Y.; Srinivas, A.; Qian, R.; Lin, T.; Cubuk, E.D.; Le, Q.V.; Zoph, B. Simple copy-paste is a strong data augmentation method for instance segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2917–2927. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Xu, X. ObjectAUG: Object-level data augmentation for semantic image segmentation. In Proceedings of the International Joint Conference on Neural Networks, Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, X.; Ono, K.; Bise, R. A data augmentation approach that ensures the reliability of foregrounds in medical image segmentation. Image Vis. Comput. 2024, 147, 105056. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Liang, Y.; Zhang, Y.; He, L.; He, Z. TumorCP: A simple but effective object-level data augmentation for tumor segmentation. arXiv 2021, arXiv:2107.09843v1. [Google Scholar] [CrossRef]
- Dai, P.; Dong, L.; Zhang, R.; Zhu, H.; Wu, J.; Yuan, K. Soft-CP: A credible and effective data augmentation for semantic segmentation of medical lesions. arXiv 2022, arXiv:2203.10507v1. [Google Scholar] [CrossRef]
- Zwanenburg, A.; Leger, S.; Agolli, L.; Pilz, K.; Troost, E.G.C.; Richter, C.; Löck, S. Assessing robustness of radiomic features by image perturbation. Sci. Rep. 2019, 9, 614. [Google Scholar] [CrossRef] [PubMed]
- Lo Iacono, F.; Maragna, R.; Pontone, G.; Corino, V. A novel data augmentation method for radiomics analysis using image perturbations. J. Imaging Inform. Med. 2024, 37, 2401–2414. [Google Scholar] [CrossRef]
- Soares, L.D.A.; Côco, K.F.; Ciarelli, P.M.; Salles, E.O.T. A class-independent texture-separation method based on a pixel-wise binary classification. Sensors 2020, 20, 5432. [Google Scholar] [CrossRef] [PubMed]
- Hyman, B.T.; West, H.L.; Rebeck, G.W.; Buldyrev, S.V.; Mantegna, R.N.; Ukleja, M.; Havlin, S.; Stanley, H.E. Quantitative analysis of senile plaques in Alzheimer disease: Observation of log-normal size distribution and molecular epidemiology of differences associated with apolipoprotein E genotype and trisomy 21 (Down syndrome). Proc. Natl. Acad. Sci. USA 1995, 92, 3586–3590. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, L.N.; Bales, K.R.; DiCarlo, G.; Gordon, M.N.; Morgan, D.; Paul, S.M.; Potter, H. Alpha-1-antichymotrypsin promotes beta-sheet amyloid plaque deposition in a transgenic mouse model of Alzheimer’s disease. J. Neurosci. 2001, 21, 1444–1451. [Google Scholar] [CrossRef] [PubMed]
- Karperien, A.L.; Jelinek, H.F.; Buchan, A.M. Box-counting analysis of microglia form in schizophrenia. Alzheimer’s disease and affective disorder. Fractals 2008, 16, 103–107. [Google Scholar] [CrossRef]
- Karperien, A.; Jelinek, H.F.; Milosevic, N.T. Lacunarity analysis and classification of microglia in neuroscience. In Proceedings of the 8th European Conference on Mathematical and Theoretical Biology, European Society for Mathematical and Theoretical Biology, London, UK, 11–15 July 2011. MS#88. [Google Scholar] [CrossRef]
- Fernández-Arjona, M.; Grondona, J.M.; Granados-Durán, P.; Fernández-Llebrez, P.; López-Ávalos, M.D. Microglia morphological categorization in a rat model of neuroinflammation by hierarchical cluster and principal components analysis. Front. Cell. Neurosci. 2017, 11, 235. [Google Scholar] [CrossRef] [PubMed]
- Stojić, D.; Radošević, D.; Rajković, N.; Milošević, N.T. 2D images of astrocytes in the human principal olivary nucleus: Monofractal analysis of the morphology. J. Biosci. Med. 2021, 9, 38–48. [Google Scholar] [CrossRef]
- Amin, E.; Elgammal, Y.M.; Zahran, M.A.; Abdelsalam, M.M. Alzheimer’s disease: New insight in assessing of amyloid plaques morphologies using multifractal geometry based on Naive Bayes optimized by random forest algorithm. Sci. Rep. 2023, 13, 18568. [Google Scholar] [CrossRef] [PubMed]
- Puntambekar, S.S.; Moutinho, M.; Lin, P.B.; Jadhav, V.; Tumbleson-Brink, D.; Balaji, A.; Benito, M.A.; Xu, G.; Oblak, A.; Lasagna-Reeves, C.A.; et al. CX3CR1 deficiency aggravates amyloid driven neuronal pathology and cognitive decline in Alzheimer’s disease. Mol. Neurodegener. 2022, 17, 47. [Google Scholar] [CrossRef] [PubMed]
- Meilandt, W.J.; Ngu, H.; Gogineni, A.; Lalehzadeh, G.; Lee, S.H.; Srinivasan, K.; Imperio, J.; Wu, T.; Weber, M.; Kruse, A.J.; et al. Trem2 deletion reduces late-stage amyloid plaque accumulation, elevates the Aβ42:Aβ40 ratio, and exacerbates axonal dystrophy and dendritic spine loss in the PS2APP Alzheimer’s mouse model. J. Neurosci. 2020, 40, 1956–1974. [Google Scholar] [CrossRef] [PubMed]
- Gulyas, B.; Sovago, J.; Gomez-Mancilla, B.; Jia, Z.; Szigeti, C.; Gulya, K.; Schumacher, M.; Maguire, R.P.; Gasparini, F.; Halldin, C. Decrease of mGluR5 receptor density goes parallel with changes in enkephalin and substance P immunoreactivity in Huntington’s disease: A preliminary investigation in the postmortem human brain. Brain Struct. Funct. 2015, 220, 3043–3051. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Bray, M.A.; Jones, T.R.; Carpenter, A.E. Pipeline for illumination correction of images for high-throughput microscopy. J. Microsc. 2014, 256, 231–236. [Google Scholar] [CrossRef] [PubMed]
- Waters, J.C.; Wittmann, T. Concepts in quantitative fluorescence microscopy. Methods Cell Biol. 2014, 123, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Likar, B.; Maintz, J.B.; Viergever, M.A.; Pernus, F. Retrospective shading correction based on entropy minimization. J. Microsc. 2000, 197, 285–295. [Google Scholar] [CrossRef] [PubMed]
- Leong, F.J.; Brady, M.; McGee, J.O. Correction of uneven illumination (vignetting) in digital microscopy images. J. Clin. Pathol. 2003, 56, 619–621. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.C.; Bajcsy, P. Intensity correction of fluorescent confocal laser scanning microscope images by mean-weight filtering. J. Microsc. 2006, 221, 122–136. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Sternberg, S.R. Biomedical image processing. Computer 1983, 16, 22–34. [Google Scholar] [CrossRef]
- van Rossum, G. Python reference manual. In Department of Computer Science; Centrum Wiskunde & Informatica: Amsterdam, The Netherlands, 1995; ISSN 0169-118X. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools 2000, 25/11, 122–125. [Google Scholar]
- Bisong, E. Google colaboratory. In Building Machine Learning and Deep Learning Models on Google Cloud Platform; Apress: Berkeley, CA, USA, 2019. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467v2. [Google Scholar] [CrossRef]
- He, K.; Sun, J. Statistics of patch offsets for image completion. In Computer Vision–ECCV 2012. Lecture Notes in Computer Science; Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7573. [Google Scholar] [CrossRef]
- Park, S.; Choi, Y.; Hwang, H. SACuP: Sonar Image Augmentation with Cut and Paste based DataBank for semantic segmentation. Remote Sens. 2023, 15, 5185. [Google Scholar] [CrossRef]
- Brorsson, E.; Åkesson, K.; Svensson, L.; Bengtsson, K. ECAP: Extensive cut-and-paste augmentation for unsupervised domain adaptive semantic segmentation. In Proceedings of the IEEE International Conference on Image Processing, Abu Dhabi, UAE, 27–30 October 2024; pp. 610–616. [Google Scholar] [CrossRef]
- Guan, S.; Samala, R.K.; Kahaki, S.M.M.; Chen, W. Restorable synthesis: Average synthetic segmentation converges to a polygon approximation of an object contour in medical images. In Proceedings of the IEEE Southwest Symposium on Image Analysis and Interpretation, Santa Fe, NM, USA, 17–19 March 2024; pp. 77–80. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2017, arXiv:1412.6980v9. [Google Scholar] [CrossRef]
- Yeung, M.; Sala, E.; Schönlieb, C.-B.; Rundo, L. Unified focal loss: Generalising Dice and cross entropy-based losses to handle class imbalanced medical image segmentation. Comput. Med. Imaging Graph. 2022, 95, 102026. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. SciKit-Learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- West, R.M. Best practice in statistics: The use of log transformation. Ann. Clin. Biochem. 2022, 59, 162–165. [Google Scholar] [CrossRef] [PubMed]
- Pither, J. Tutorials for BIOL202: Introduction to Biostatistics. Available online: https://ubco-biology.github.io/BIOL202/index.html (accessed on 15 February 2025).
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; van der Walt, S., Millman, J., Eds.; SciPy.org: Austin, TX, USA, 2010; Volume 445, pp. 56–61. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272, Erratum in Nat. Methods 2020, 17, 352. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.D. MatPlotLib: A 2D Graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012; ISBN 3-900051-07-0. Available online: https://www.R-pr-oject.org/ (accessed on 15 February 2025).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barczánfalvi, G.; Nyári, T.; Tolnai, J.; Tiszlavicz, L.; Gulyás, B.; Gulya, K. Automated Segmentation and Morphometric Analysis of Thioflavin-S-Stained Amyloid Deposits in Alzheimer’s Disease Brains and Age-Matched Controls Using Weakly Supervised Deep Learning. Int. J. Mol. Sci. 2025, 26, 7134. https://doi.org/10.3390/ijms26157134
Barczánfalvi G, Nyári T, Tolnai J, Tiszlavicz L, Gulyás B, Gulya K. Automated Segmentation and Morphometric Analysis of Thioflavin-S-Stained Amyloid Deposits in Alzheimer’s Disease Brains and Age-Matched Controls Using Weakly Supervised Deep Learning. International Journal of Molecular Sciences. 2025; 26(15):7134. https://doi.org/10.3390/ijms26157134
Chicago/Turabian StyleBarczánfalvi, Gábor, Tibor Nyári, József Tolnai, László Tiszlavicz, Balázs Gulyás, and Karoly Gulya. 2025. "Automated Segmentation and Morphometric Analysis of Thioflavin-S-Stained Amyloid Deposits in Alzheimer’s Disease Brains and Age-Matched Controls Using Weakly Supervised Deep Learning" International Journal of Molecular Sciences 26, no. 15: 7134. https://doi.org/10.3390/ijms26157134
APA StyleBarczánfalvi, G., Nyári, T., Tolnai, J., Tiszlavicz, L., Gulyás, B., & Gulya, K. (2025). Automated Segmentation and Morphometric Analysis of Thioflavin-S-Stained Amyloid Deposits in Alzheimer’s Disease Brains and Age-Matched Controls Using Weakly Supervised Deep Learning. International Journal of Molecular Sciences, 26(15), 7134. https://doi.org/10.3390/ijms26157134





