Physically Consistent Self-Diffusion Coefficient Calculation with Molecular Dynamics and Symbolic Regression
Abstract
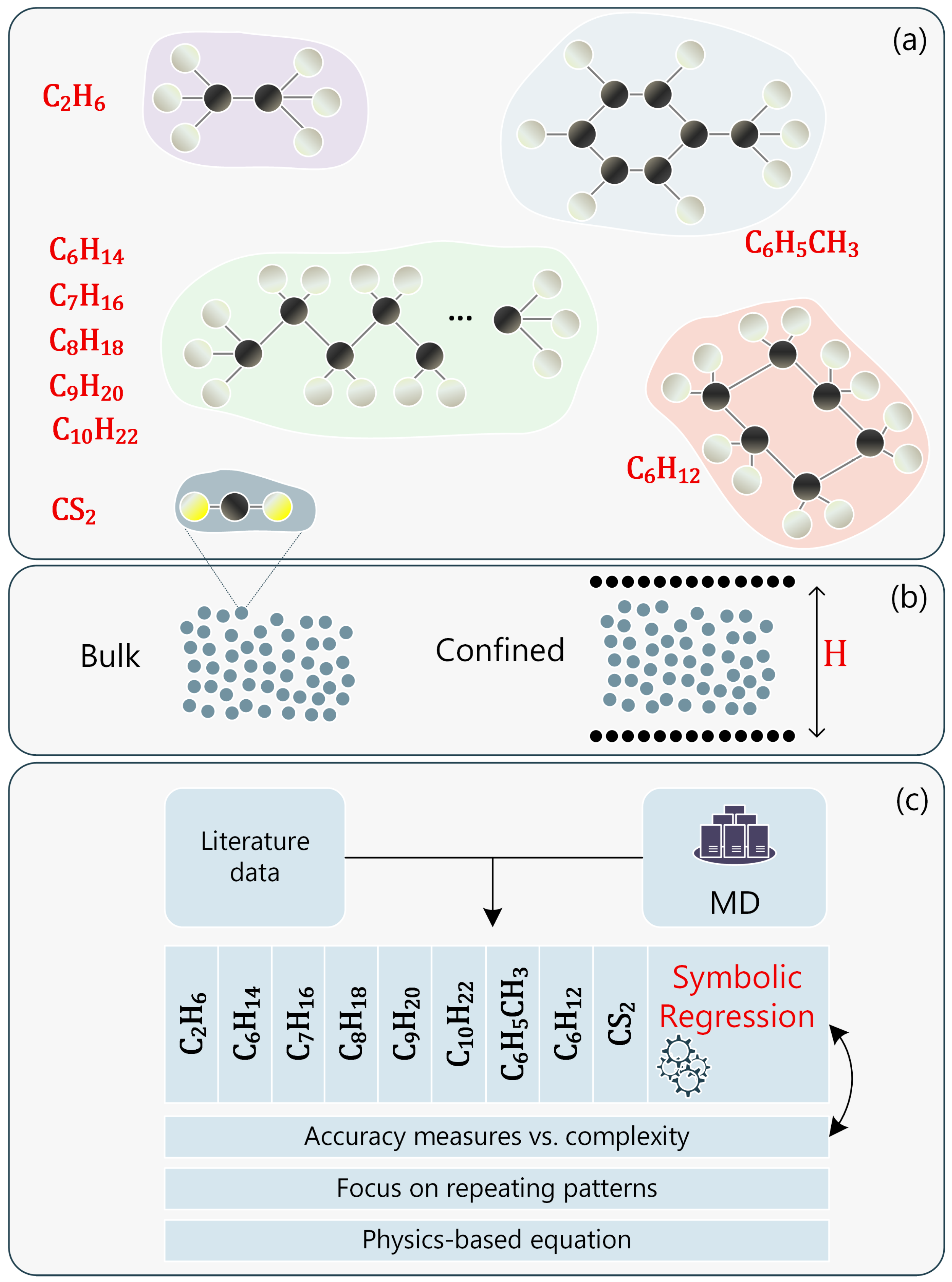
1. Introduction
- Accuracy: Evaluation with the appropriate statistical measures.
- Complexity: Avoid complex mathematical expressions.
- Equation recurrence: Focus on repeating patterns.
- Data analysis: Focus on the physical interpretation of the result, taking into account the correlation of the system variables.
2. Results and Discussion
2.1. Expression Selection Methodology
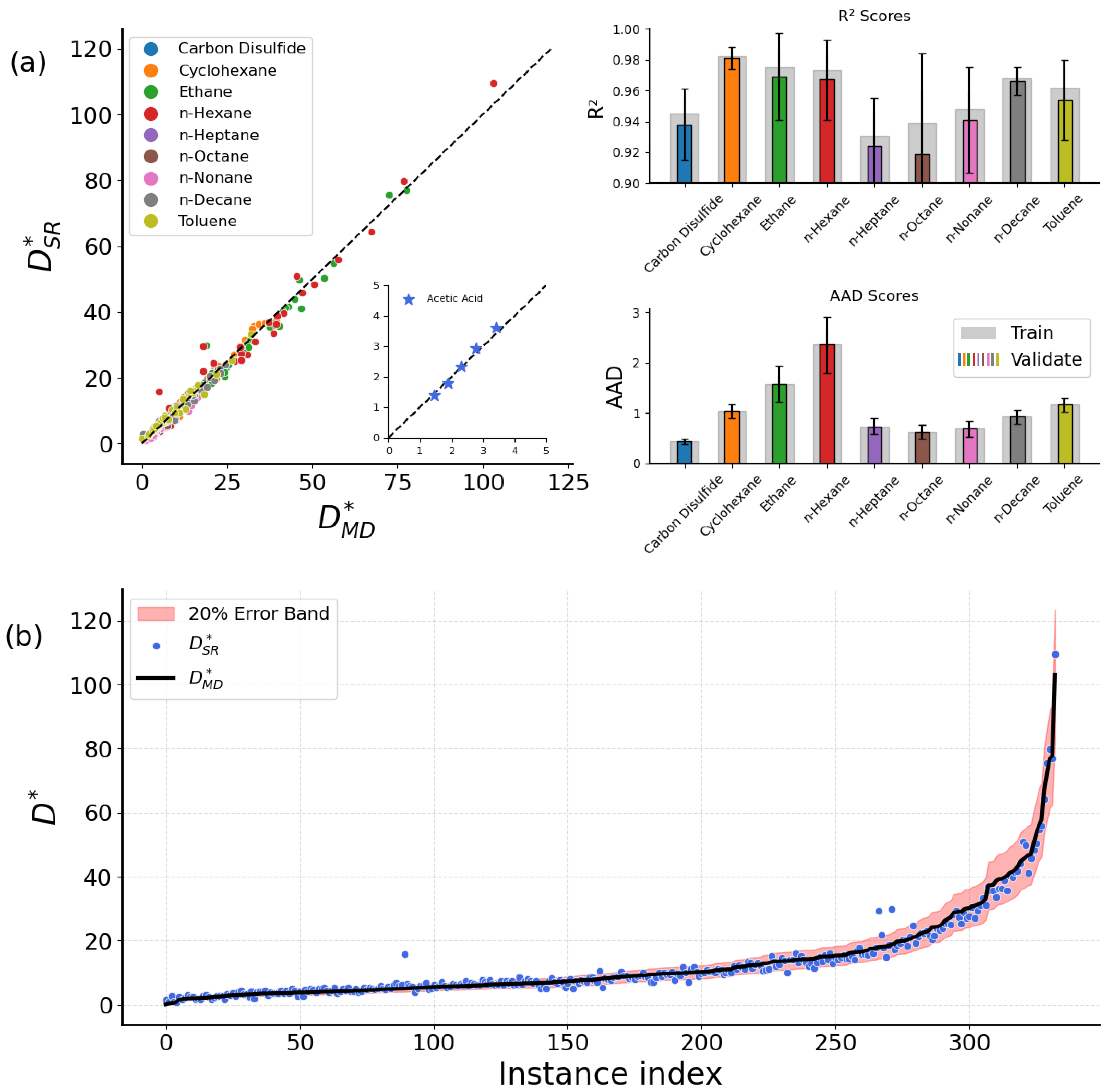
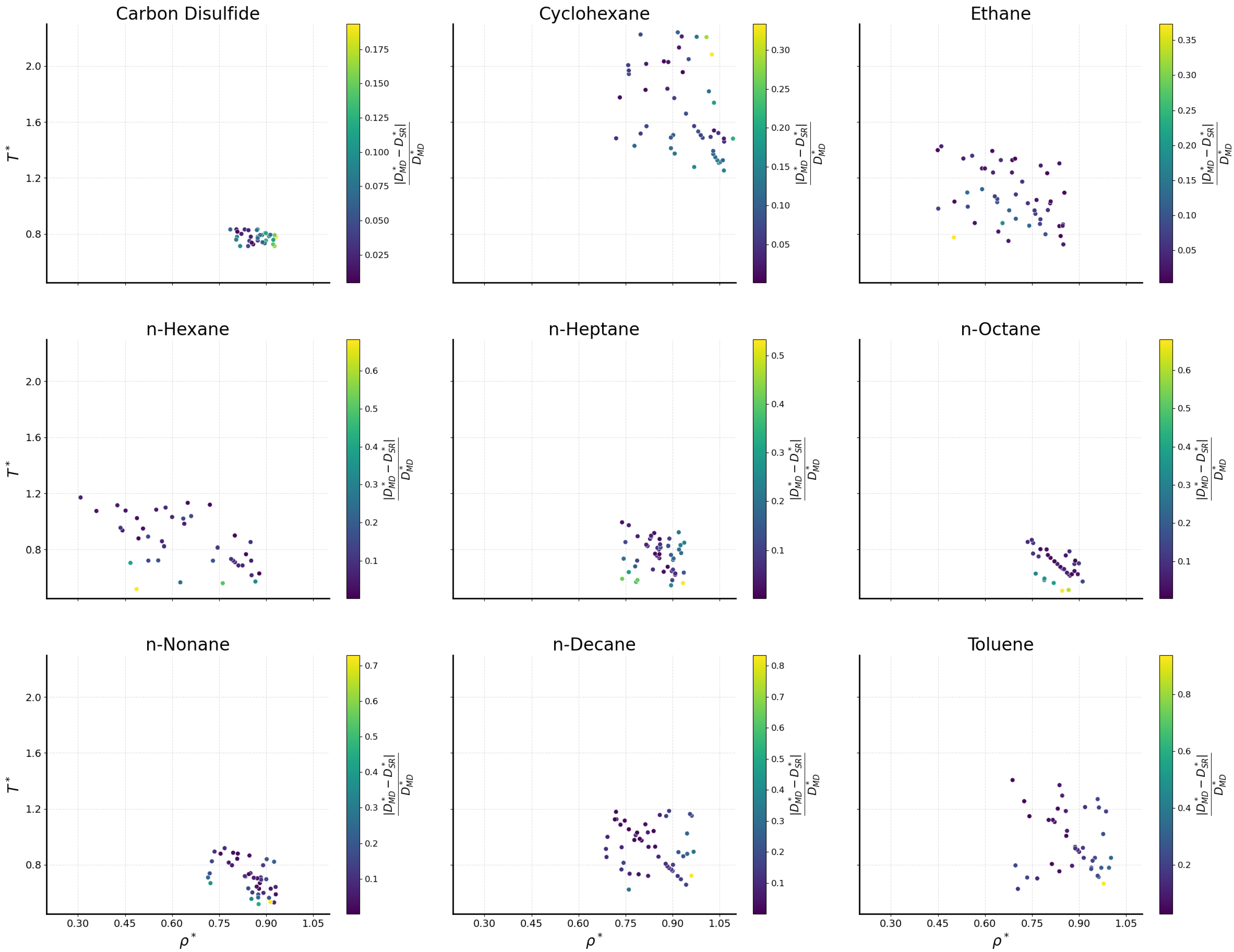
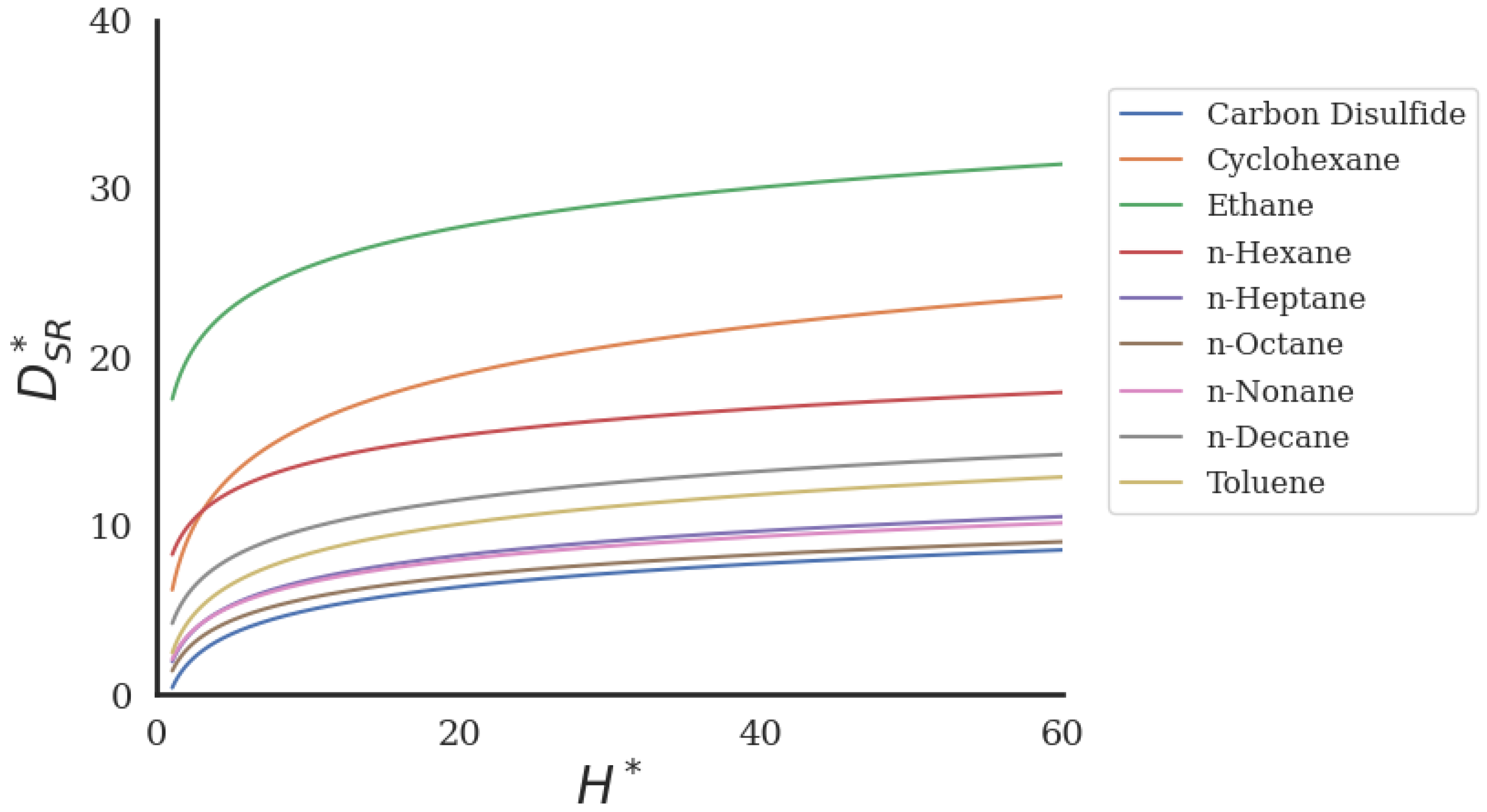
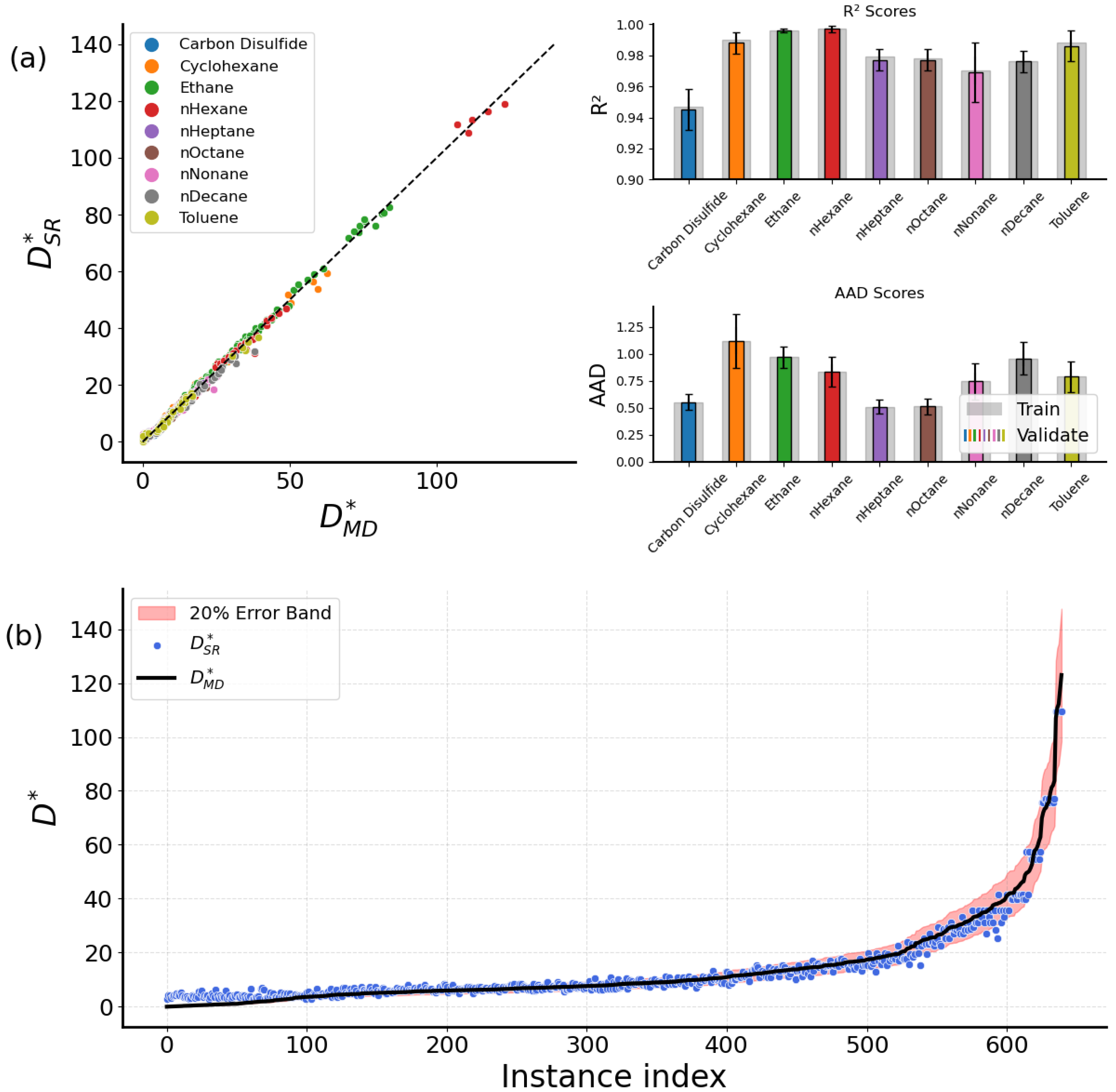
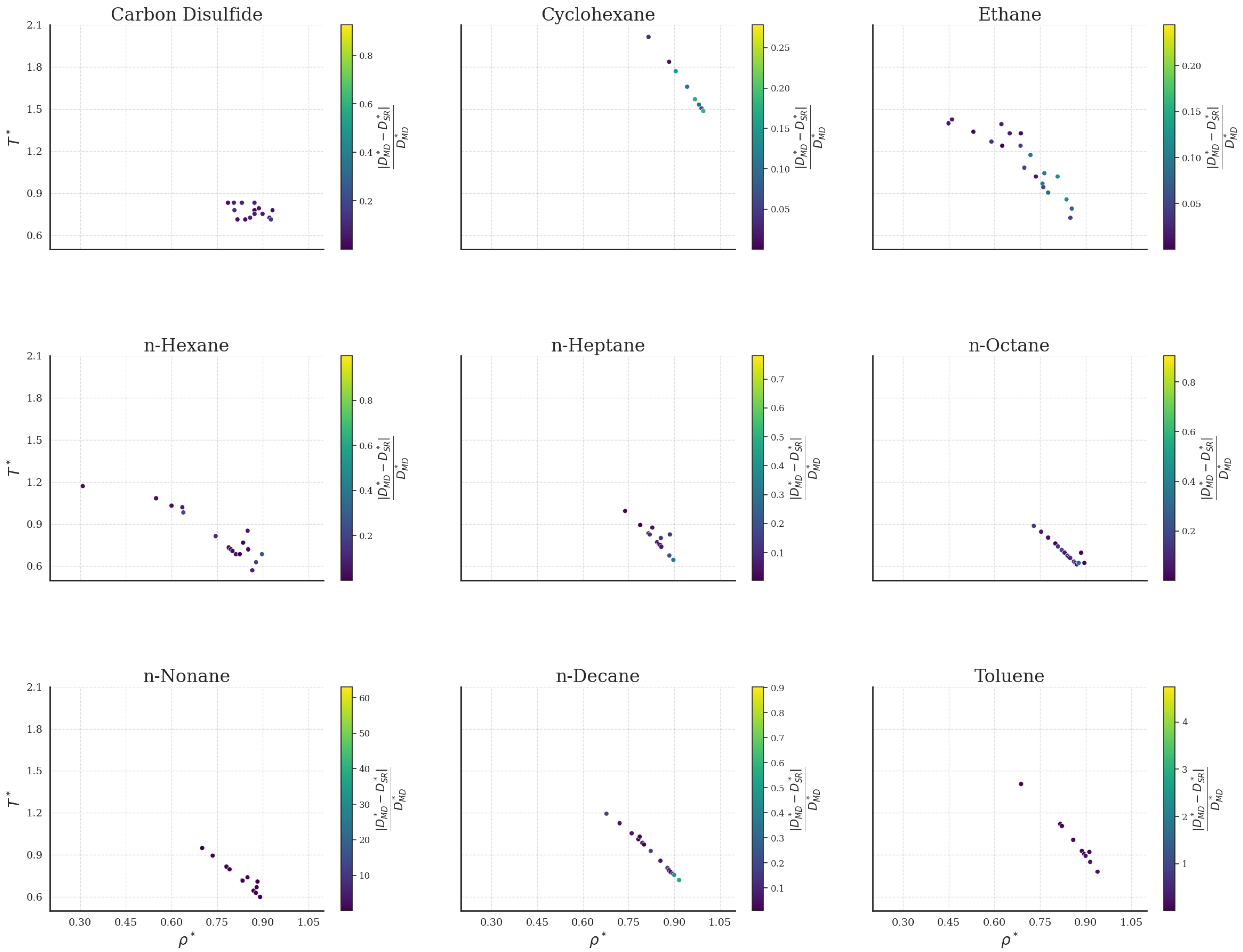
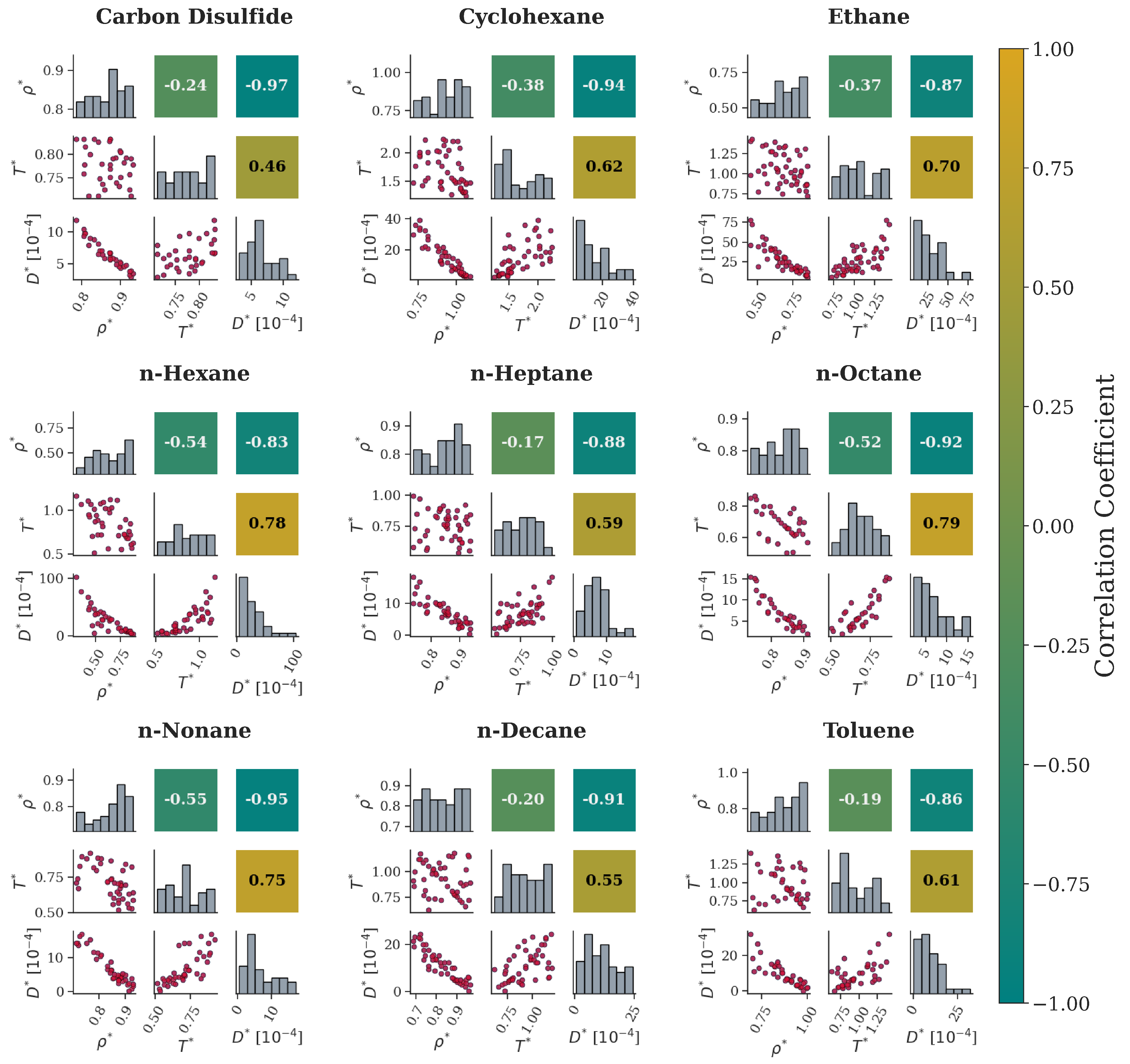
2.2. Comparison with Simulation Data
2.2.1. Bulk Fluids
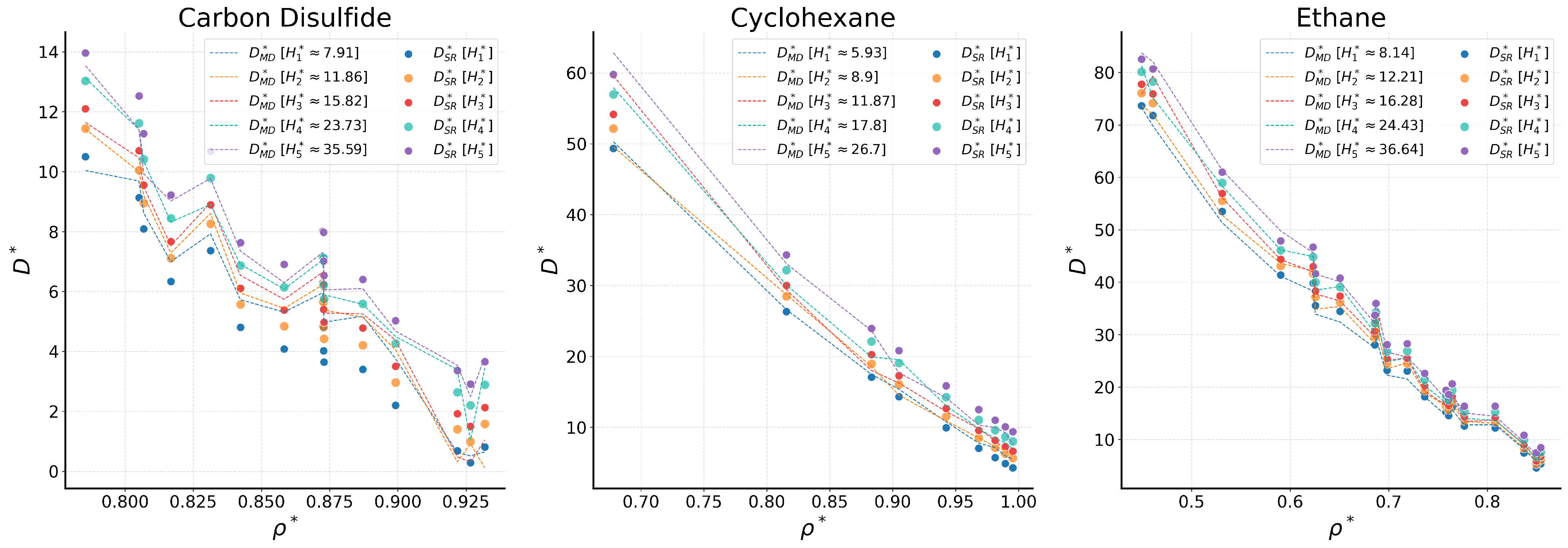
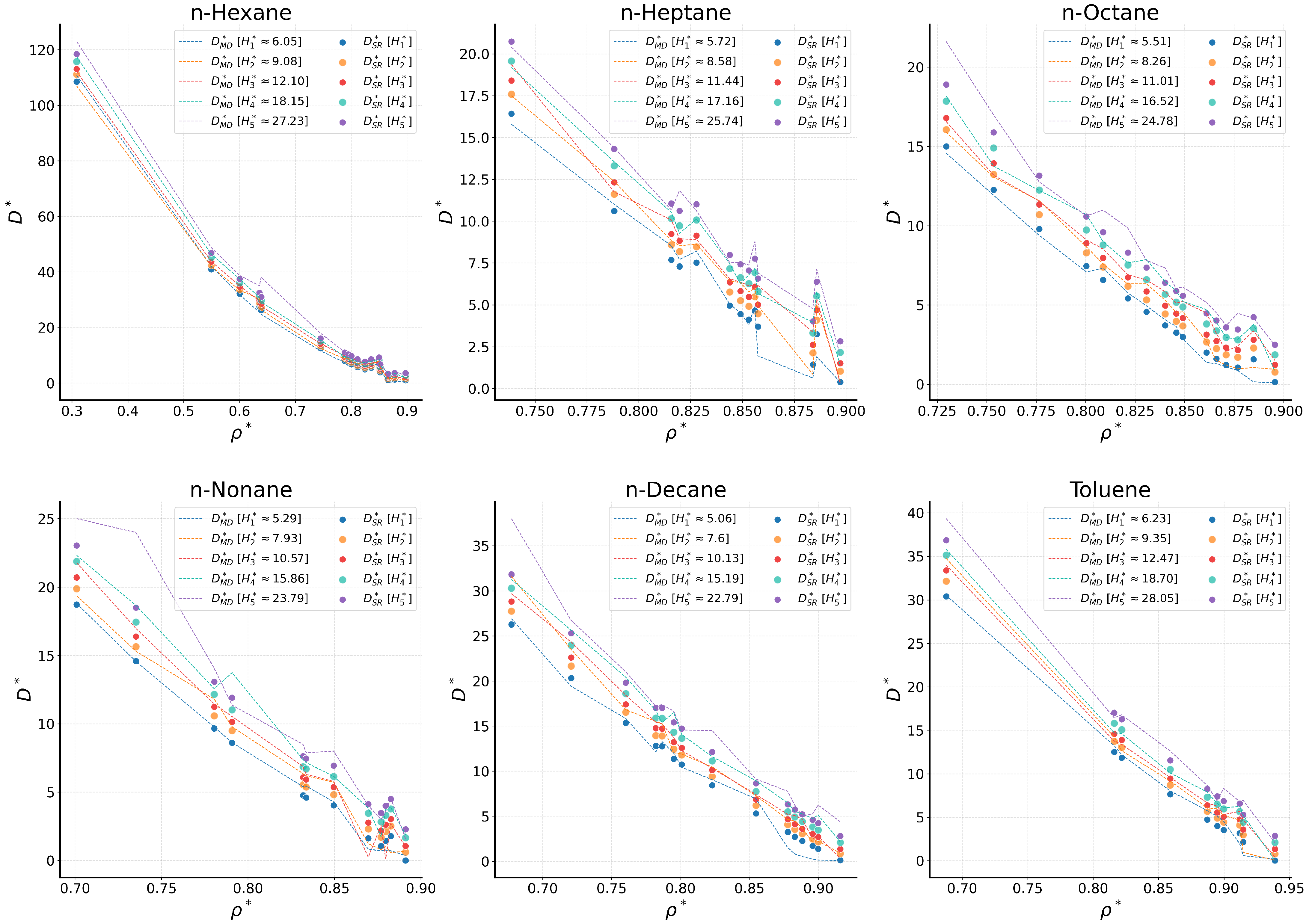
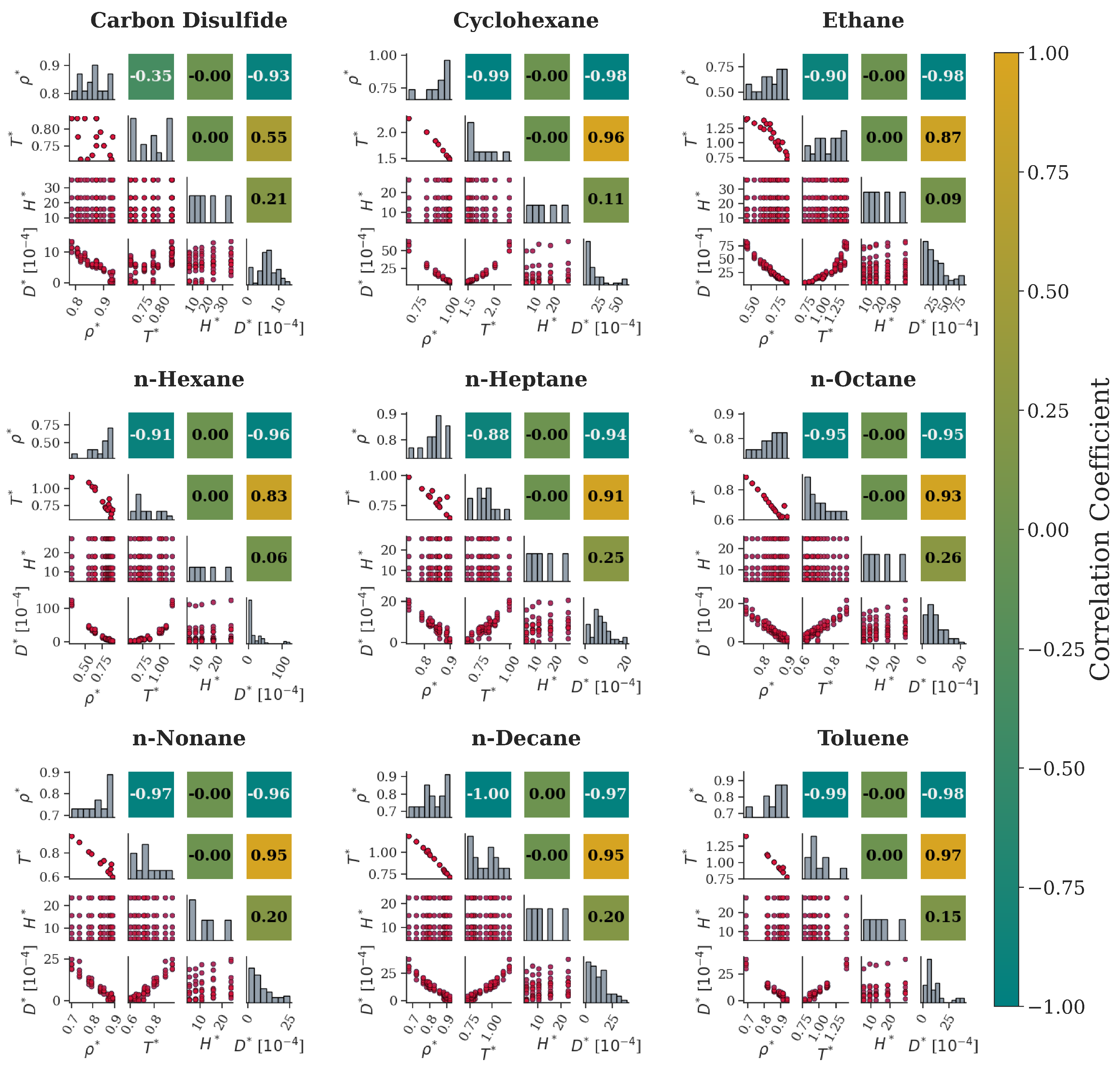
2.2.2. Fluids in Nanochannels
3. Materials and Methods
3.1. Diffusion Coefficient Calculation
3.2. Molecular Dynamics
3.3. Data Analysis and Preprocessing
3.4. Symbolic Regression
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef][Green Version]
- Binder, K.; Horbach, J.; Kob, W.; Paul, W.; Varnik, F. Molecular dynamics simulations. J. Phys. Condens. Matter 2004, 16, S429. [Google Scholar] [CrossRef]
- Mavrantzas, V.G. Using Monte Carlo to Simulate Complex Polymer Systems: Recent Progress and Outlook. Front. Phys. 2021, 9, 661367. [Google Scholar] [CrossRef]
- Argaman, N.; Makov, G. Density functional theory: An introduction. Am. J. Phys. 2000, 68, 69–79. [Google Scholar] [CrossRef]
- Ollitrault, P.J.; Miessen, A.; Tavernelli, I. Molecular Quantum Dynamics: A Quantum Computing Perspective. Accounts Chem. Res. 2021, 54, 4229–4238. [Google Scholar] [CrossRef]
- Smith, E.R.; Theodorakis, P.E. Multiscale simulation of fluids: Coupling molecular and continuum. Phys. Chem. Chem. Phys. 2024, 26, 724–744. [Google Scholar] [CrossRef]
- Schneider, R.; Sharma, A.R.; Rai, A. Introduction to molecular dynamics. In Computational Many-Particle Physics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–40. [Google Scholar] [CrossRef]
- Allers, J.P.; Harvey, J.A.; Garzon, F.H.; Alam, T.M. Machine learning prediction of self-diffusion in Lennard-Jones fluids. J. Chem. Phys. 2020, 153, 034102. [Google Scholar] [CrossRef]
- Angelis, D.; Sofos, F.; Papastamatiou, K.; Karakasidis, T.E. Fluid properties extraction in confined nanochannels with molecular dynamics and symbolic regression methods. Micromachines 2023, 14, 1446. [Google Scholar] [CrossRef]
- Papastamatiou, K.; Sofos, F.; Karakasidis, T.E. Machine learning symbolic equations for diffusion with physics-based descriptions. AIP Adv. 2022, 12, 025004. [Google Scholar] [CrossRef]
- Li, Y.; Xu, J.; Li, D. Molecular dynamics simulation of nanoscale liquid flows. Microfluid. Nanofluidics 2010, 9, 1011–1031. [Google Scholar] [CrossRef]
- Stavrogiannis, C.; Sofos, F.; Sagri, M.; Vavougios, D.; Karakasidis, T.E. Twofold Machine-Learning and Molecular Dynamics: A Computational Framework. Computers 2024, 13, 2. [Google Scholar] [CrossRef]
- Mehta, P.; Bukov, M.; Wang, C.H.; Day, A.G.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to machine learning for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef] [PubMed]
- Westermayr, J.; Gastegger, M.; Schütt, K.T.; Maurer, R.J. Perspective on integrating machine learning into computational chemistry and materials science. J. Chem. Phys. 2021, 154, 230903. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 2–6. [Google Scholar] [CrossRef]
- Rodrigues, F.A. Machine learning in physics: A short guide. Europhys. Lett. 2023, 144, 22001. [Google Scholar] [CrossRef]
- Kronberger, G.; Burlacu, B.; Kommenda, M.; Winkler, S.M.; Affenzeller, M. Symbolic Regression; ImprintChapman and Hall/CRC: New York, NY, USA, 2024. [Google Scholar] [CrossRef]
- Neumann, P.; Cao, L.; Russo, D.; Vassiliadis, V.S.; Lapkin, A.A. A new formulation for symbolic regression to identify physico-chemical laws from experimental data. Chem. Eng. J. 2020, 387, 123412. [Google Scholar] [CrossRef]
- Wang, G.; Wang, E.; Li, Z.; Zhou, J.; Sun, Z. Exploring the mathematic equations behind the materials science data using interpretable symbolic regression. Interdiscip. Mater. 2024, 3, 637–657. [Google Scholar] [CrossRef]
- Angelis, D.; Sofos, F.; Karakasidis, T.E. Artificial Intelligence in Physical Sciences: Symbolic Regression Trends and Perspectives. Arch. Comput. Methods Eng. 2023, 30, 3845–3865. [Google Scholar] [CrossRef]
- Mueller, T.; Hernandez, A.; Wang, C. Machine learning for interatomic potential models. J. Chem. Phys. 2020, 152, 050902. [Google Scholar] [CrossRef]
- Ma, L.; Guo, Q.; Li, X.; Xu, S.; Zhou, J.; Ye, M.; Liu, Z. Drag correlations for flow past monodisperse arrays of spheres and porous spheres based on symbolic regression: Effects of permeability. Chem. Eng. J. 2022, 445, 136653. [Google Scholar] [CrossRef]
- Wang, D.; Chen, Y.; Chen, S. Discovering an interpretable mathematical expression for a full wind-turbine wake with artificial intelligence enhanced symbolic regression. Phys. Fluids 2024, 36, 105110. [Google Scholar] [CrossRef]
- Anj̣elić, N.; Lorencin, I.; Mrzljak, V.; Car, Z. On the application of symbolic regression in the energy sector: Estimation of combined cycle power plant electrical power output using genetic programming algorithm. Eng. Appl. Artif. Intell. 2024, 133, 108213. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Wei, Z.; Jin, X.; Shangguan, W.; Yuan, H.; Zhu, J.; Li, L.; Liu, P.; Chen, X.; et al. Advancing symbolic regression for earth science with a focus on evapotranspiration modeling. NPJ Clim. Atmos. Sci. 2024, 7, 321. [Google Scholar] [CrossRef]
- Tsimpanogiannis, I.N.; Moultos, O.A.; Franco, L.F.; Spera, M.B.d.M.; Erdos, M.; Economou, I.G. Self-diffusion coefficient of bulk and confined water: A critical review of classical molecular simulation studies. Mol. Simul. 2019, 45, 425–453. [Google Scholar] [CrossRef]
- Wang, J.; Hou, T. Application of molecular dynamics simulations in molecular property prediction II: Diffusion coefficient. J. Comput. Chem. 2011, 32, 3505–3519. [Google Scholar] [CrossRef] [PubMed]
- Higgoda, U.A.; Hellmann, R.; Koller, T.M.; Fröba, A.P. Self-diffusion coefficient and viscosity of methane and carbon dioxide via molecular dynamics simulations based on new ab initio-derived force fields. Fluid Phase Equilibria 2019, 481, 15–27. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, X.; Zhou, J.; Wang, Y.; Shi, J. Prediction of diffusion coefficients for gas, liquid and supercritical fluid: Application to pure real fluids and infinite dilute binary solutions based on the simulation of Lennard–Jones fluid. Fluid Phase Equilibria 2002, 194, 1141–1159. [Google Scholar] [CrossRef]
- Alam, T.M.; Allers, J.P.; Leverant, C.J.; Harvey, J.A. Symbolic regression development of empirical equations for diffusion in Lennard-Jones fluids. J. Chem. Phys. 2022, 157, 014503. [Google Scholar] [CrossRef]
- Kharlamov, G.; Zhilkin, S. The molecular dynamics simulation of self-diffusion in gases and liquids. Proc. J. Phys. Conf. Ser. 2017, 899, 052009. [Google Scholar] [CrossRef]
- Sofos, F.; Charakopoulos, A.; Papastamatiou, K.; Karakasidis, T.E. A combined clustering/symbolic regression framework for fluid property prediction. Phys. Fluids 2022, 34, 062004. [Google Scholar] [CrossRef]
- Papastamatiou, K.; Sofos, F.; Karakasidis, T.E. Calculating material properties with purely data-driven methods: From clusters to symbolic expressions. In Proceedings of the 12th Hellenic Conference on Artificial Intelligence, Corfu, Greece, 7–9 September 2022; pp. 1–9. [Google Scholar] [CrossRef]
- Leverant, C.J.; Greathouse, J.A.; Harvey, J.A.; Alam, T.M. Machine Learning Predictions of Simulated Self-Diffusion Coefficients for Bulk and Confined Pure Liquids. J. Chem. Theory Comput. 2023, 19, 3054–3062. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E. Machine Learning techniques for fluid flows at the nanoscale. Fluids 2021, 6, 96. [Google Scholar] [CrossRef]
- Giannakopoulos, A.; Sofos, F.; Karakasidis, T.; Liakopoulos, A. Unified description of size effects of transport properties of liquids flowing in nanochannels. Int. J. Heat Mass Transf. 2012, 55, 5087–5092. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.; Liakopoulos, A. Transport properties of liquid argon in krypton nanochannels: Anisotropy and non-homogeneity introduced by the solid walls. Int. J. Heat Mass Transf. 2009, 52, 735–743. [Google Scholar] [CrossRef]
- Leverant, C.J.; Harvey, J.A.; Alam, T.M.; Greathouse, J.A. Machine learning self-diffusion prediction for Lennard-Jones fluids in pores. J. Phys. Chem. C 2021, 125, 25898–25906. [Google Scholar] [CrossRef]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Silva, S.; Vanneschi, L.; Cabral, A.I.; Vasconcelos, M.J. A semi-supervised Genetic Programming method for dealing with noisy labels and hidden overfitting. Swarm Evol. Comput. 2018, 39, 323–338. [Google Scholar] [CrossRef]
- O’Neill, M.; Vanneschi, L.; Gustafson, S.; Banzhaf, W. Open Issues in Genetic Programming. Genet. Program. Evolvable Mach. 2010, 11, 339–363. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Karakasidis, T.; Liakopoulos, A. Two-regime dynamical behaviour in Lennard–Jones systems: Spectral and rescaled range analysis. Phys. A Stat. Mech. Appl. 2004, 333, 225–240. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases: An Account of The Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Speedy, R.; Prielmeier, F.; Vardag, T.; Lang, E.; Lüdemann, H.D. Diffusion in simple fluids. Mol. Phys. 1989, 66, 577–590. [Google Scholar] [CrossRef]
- Smith, I.W. Kinetics and Dynamics of Elementary Gas Reactions: Butterworths Monographs in Chemistry and Chemical Engineering; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Rutkai, G.; Thol, M.; Span, R.; Vrabec, J. How well does the Lennard-Jones potential represent the thermodynamic properties of noble gases? Mol. Phys. 2017, 115, 1104–1121. [Google Scholar] [CrossRef]
- Angelis, D.; Sofos, F.; Karakasidis, T.E. Reassessing the transport properties of fluids: A symbolic regression approach. Phys. Rev. E 2024, 109, 015105. [Google Scholar] [CrossRef] [PubMed]
- Meier, K.; Laesecke, A.; Kabelac, S. Transport coefficients of the Lennard-Jones model fluid. II Self-diffusion. J. Chem. Phys. 2004, 121, 9526–9535. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Zhou, Z.; Ling, F.; Alexiadis, A.; Van den Bergh, W.; Cannone Falchetto, A.; Balieu, R.; Zhu, J.; Valentin, J.; Kowalski, K.J.; et al. A Coarse-Grained Molecular Model for Simulating Self-Healing of Bitumen. Appl. Sci. 2022, 12, 10360. [Google Scholar] [CrossRef]
- Vaddireddy, H.; Rasheed, A.; Staples, A.E.; San, O. Feature engineering and symbolic regression methods for detecting hidden physics from sparse sensor observation data. Phys. Fluids 2020, 32, 015113. [Google Scholar] [CrossRef]
- Gilpin, W. Chaos as an interpretable benchmark for forecasting and data-driven modelling. arXiv 2023, arXiv:2110.05266. [Google Scholar]
- Makke, N.; Chawla, S. Interpretable Scientific Discovery with Symbolic Regression: A Review. Artif. Intell. Rev. 2024, 57, 2. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming as a Means for Programming Computers by Natural Selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Jin, Y.; Sendhoff, B. Pareto-Based Multiobjective Machine Learning: An Overview and Case Studies. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 397–415. [Google Scholar] [CrossRef]
- Wagner, S.; Kronberger, G.; Beham, A.; Kommenda, M.; Scheibenpflug, A.; Pitzer, E.; Vonolfen, S.; Kofler, M.; Winkler, S.; Dorfer, V.; et al. Architecture and Design of the HeuristicLab Optimization Environment. In Advanced Methods and Applications in Computational Intelligence; Topics in Intelligent Engineering and Informatics; Springer: Heidelberg, Germany, 2014; Volume 6. [Google Scholar] [CrossRef]
- Cranmer, M. Interpretable Machine Learning for Science with PySR and SymbolicRegression.jl. arXiv 2023, arXiv:2305.01582. [Google Scholar]

| Molecular Fluid | Type | ||||
|---|---|---|---|---|---|
| Carbon Disulfide | 12.83 | 0.63 | 2.58 | 9.507 | |
| Cyclohexane | 13.05 | 0.82 | 2.59 | 10.91 | |
| Ethane | 22.59 | 0.91 | 1.38 | 15.605 | |
| n-Hexane | 23.81 | 1.26 | 1.19 | 12.14 | |
| n-Heptane | 12.63 | 0.68 | 2.62 | 9.32 | |
| n-Octane | 9.34 | 0.78 | 3.17 | 6.05 | |
| n-Nonane | 11.11 | 0.74 | 2.84 | 7.72 | |
| n-Decane | 18.84 | 0.55 | 1.95 | 15.605 | |
| Toluene | 12.37 | 0.79 | 2.55 | 8.731 |
| Molecular Fluid | Type | N | |||
|---|---|---|---|---|---|
| Carbon Disulfide | 34 | 0.785–0.932 | 0.712–0.832 | 3.015–11.888 | |
| Cyclohexane | 49 | 0.720–1.092 | 1.253–2.241 | 2.763–39.433 | |
| Ethane | 49 | 0.449–0.853 | 0.724–1.426 | 6.475–77.694 | |
| n-Hexane | 40 | 0.308–0.878 | 0.516–1.170 | 3.621–102.942 | |
| n-Heptane | 48 | 0.739–0.937 | 0.544–0.992 | 0.551–18.144 | |
| n-Octane | 33 | 0.736–0.911 | 0.505–0.866 | 2.107–15.479 | |
| n-Nonane | 42 | 0.715–0.930 | 0.519–0.919 | 0.317–17.013 | |
| n-Decane | 47 | 0.687–0.967 | 0.623–1.186 | 0.463–24.382 | |
| Toluene | 40 | 0.688–1.001 | 0.628–1.406 | 0.102–32.018 |
| Molecular Fluid | Type | N | ||||
|---|---|---|---|---|---|---|
| Carbon Disulfide | 80 | 0.785–0.932 | 0.712–0.832 | 7.909–35.590 | 0.120–13.540 | |
| Cyclohexane | 45 | 0.678–0.995 | 1.486–2.282 | 5.933–26.698 | 5.484–62.824 | |
| Ethane | 100 | 0.449–0.854 | 0.724–1.426 | 8.142–36.639 | 5.747–83.731 | |
| n-Hexane | 85 | 0.308–0.897 | 0.571–1.170 | 6.052–27.232 | 0.002–122.979 | |
| n-Heptane | 65 | 0.739–0.897 | 0.645–0.992 | 5.720–25.742 | 0.331–20.399 | |
| n-Octane | 80 | 0.730–0.896 | 0.613–0.886 | 5.508–24.784 | 0.077–21.614 | |
| n-Nonane | 60 | 0.701–0.891 | 0.599–0.949 | 5.287–23.793 | 0.110–25.000 | |
| n-Decane | 75 | 0.677–0.916 | 0.720–1.194 | 5.064–22.788 | 0.095–37.997 | |
| Toluene | 50 | 0.688–0.939 | 0.780–1.406 | 6.233–28.050 | 0.035–39.326 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelis, D.; Georgakopoulos, C.; Sofos, F.; Karakasidis, T.E. Physically Consistent Self-Diffusion Coefficient Calculation with Molecular Dynamics and Symbolic Regression. Int. J. Mol. Sci. 2025, 26, 6748. https://doi.org/10.3390/ijms26146748
Angelis D, Georgakopoulos C, Sofos F, Karakasidis TE. Physically Consistent Self-Diffusion Coefficient Calculation with Molecular Dynamics and Symbolic Regression. International Journal of Molecular Sciences. 2025; 26(14):6748. https://doi.org/10.3390/ijms26146748
Chicago/Turabian StyleAngelis, Dimitrios, Chrysostomos Georgakopoulos, Filippos Sofos, and Theodoros E. Karakasidis. 2025. "Physically Consistent Self-Diffusion Coefficient Calculation with Molecular Dynamics and Symbolic Regression" International Journal of Molecular Sciences 26, no. 14: 6748. https://doi.org/10.3390/ijms26146748
APA StyleAngelis, D., Georgakopoulos, C., Sofos, F., & Karakasidis, T. E. (2025). Physically Consistent Self-Diffusion Coefficient Calculation with Molecular Dynamics and Symbolic Regression. International Journal of Molecular Sciences, 26(14), 6748. https://doi.org/10.3390/ijms26146748








