Turnover Rates and Numbers of Exchangeable Hydrogens in Deuterated Water Labeled Samples
Abstract
1. Introduction
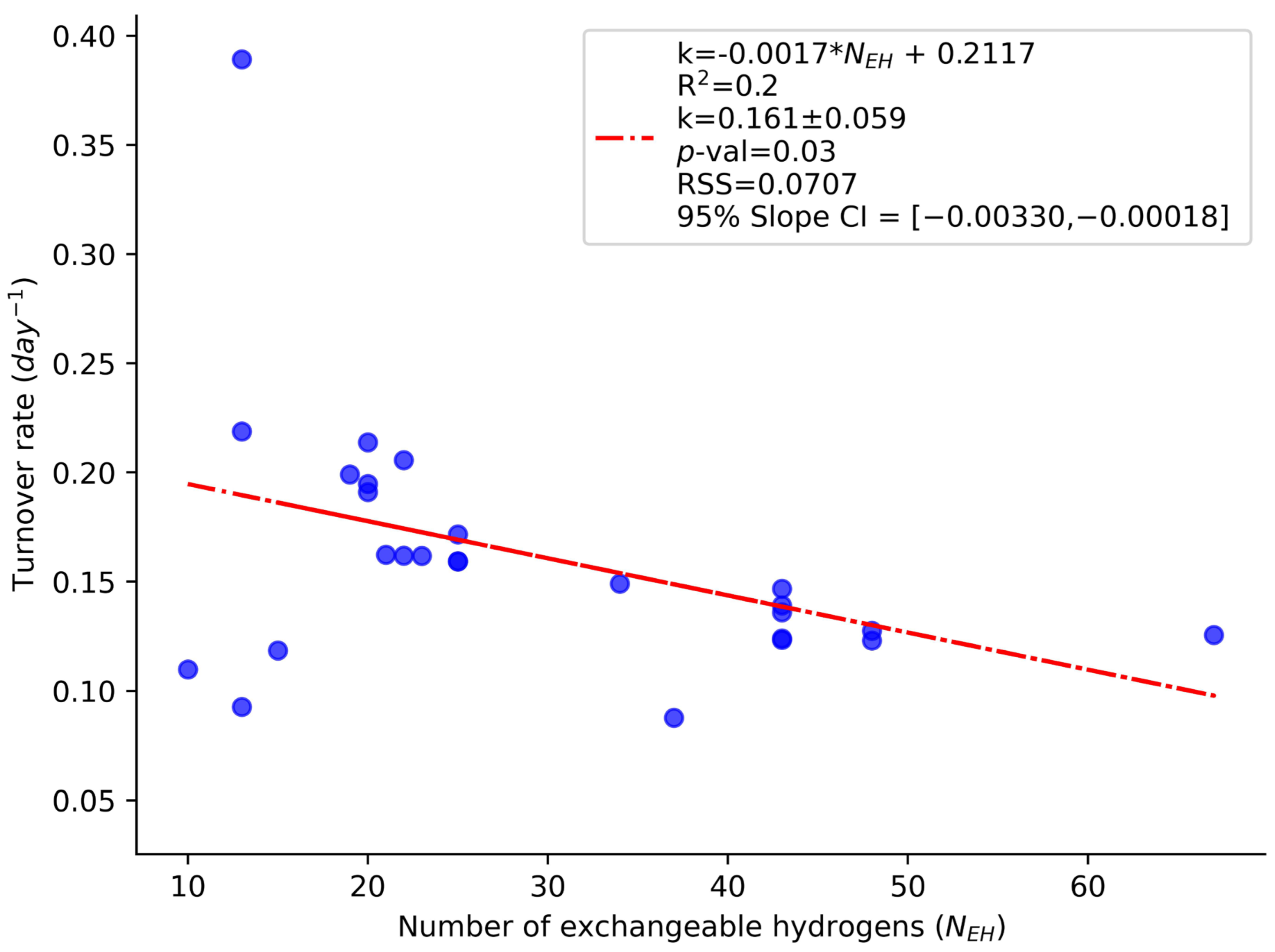
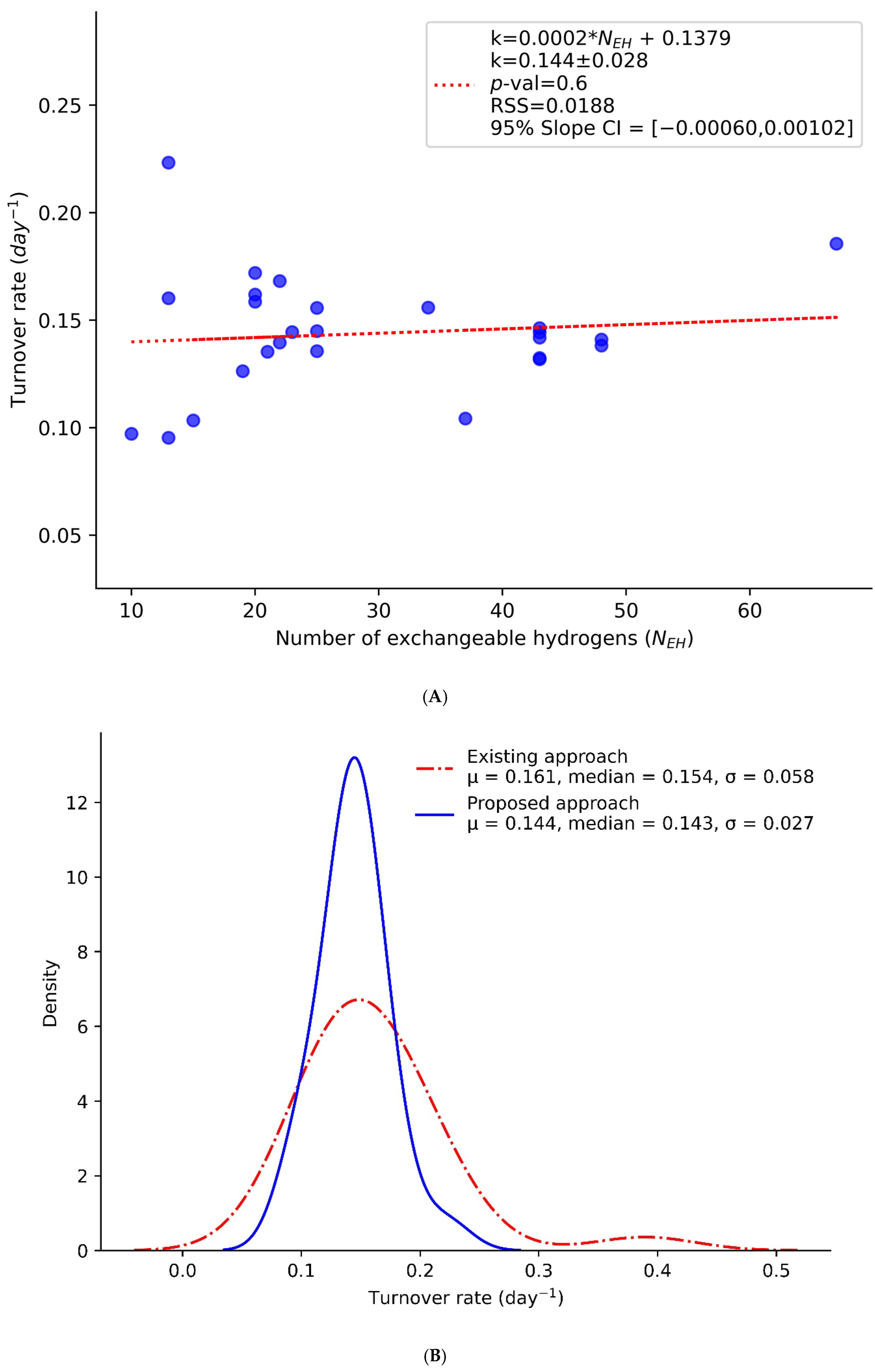
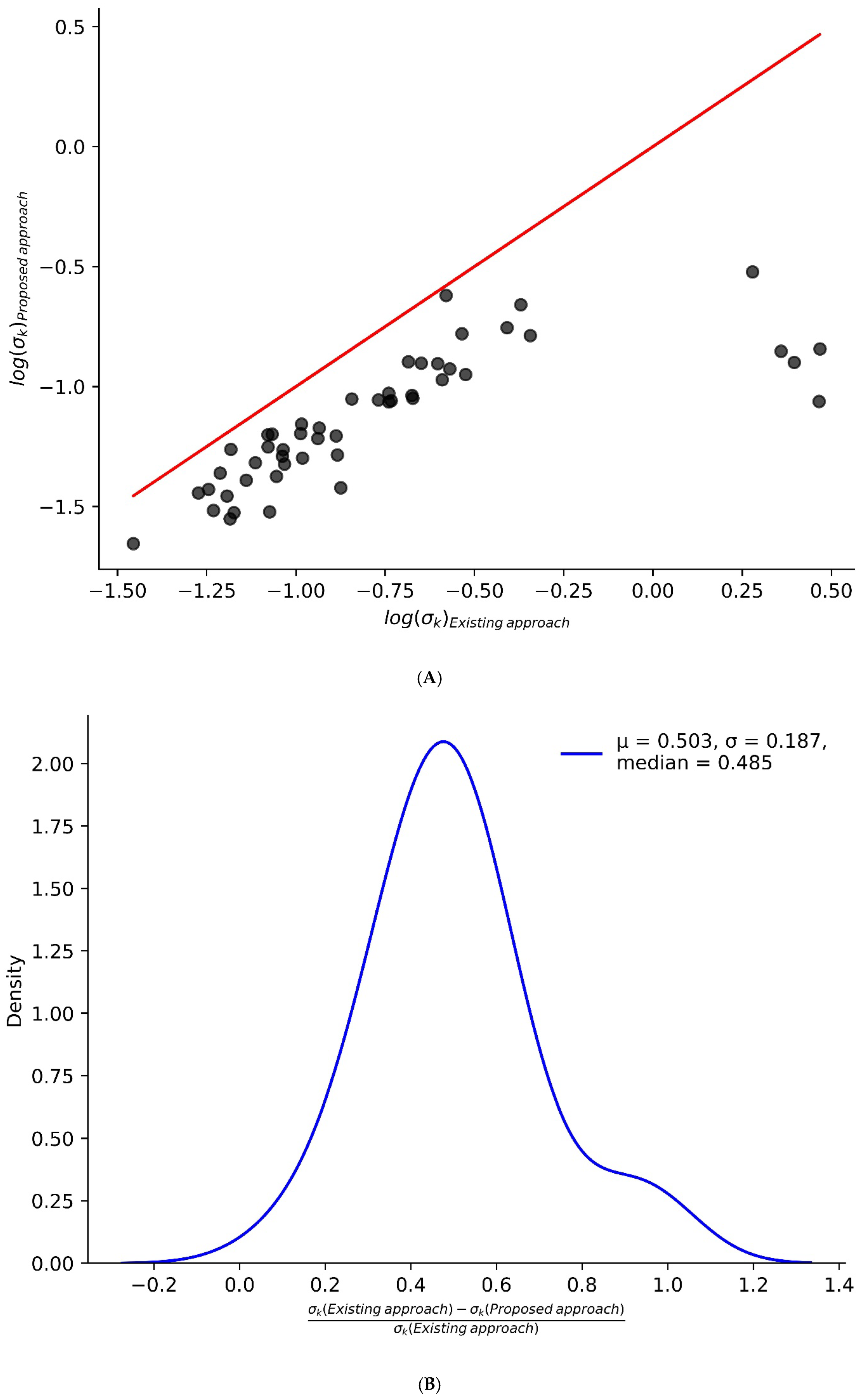
2. Results and Discussion
3. Materials and Methods
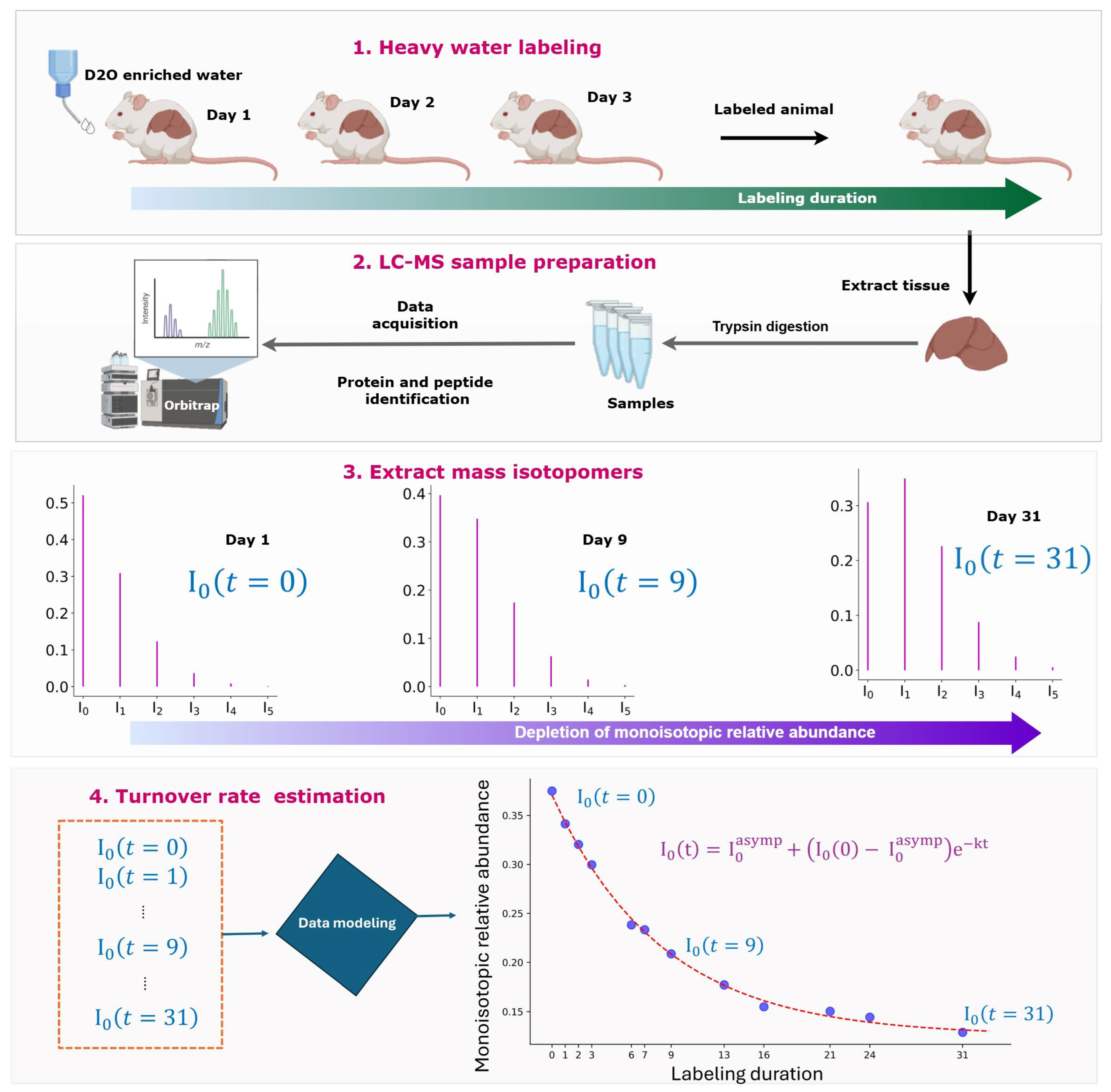
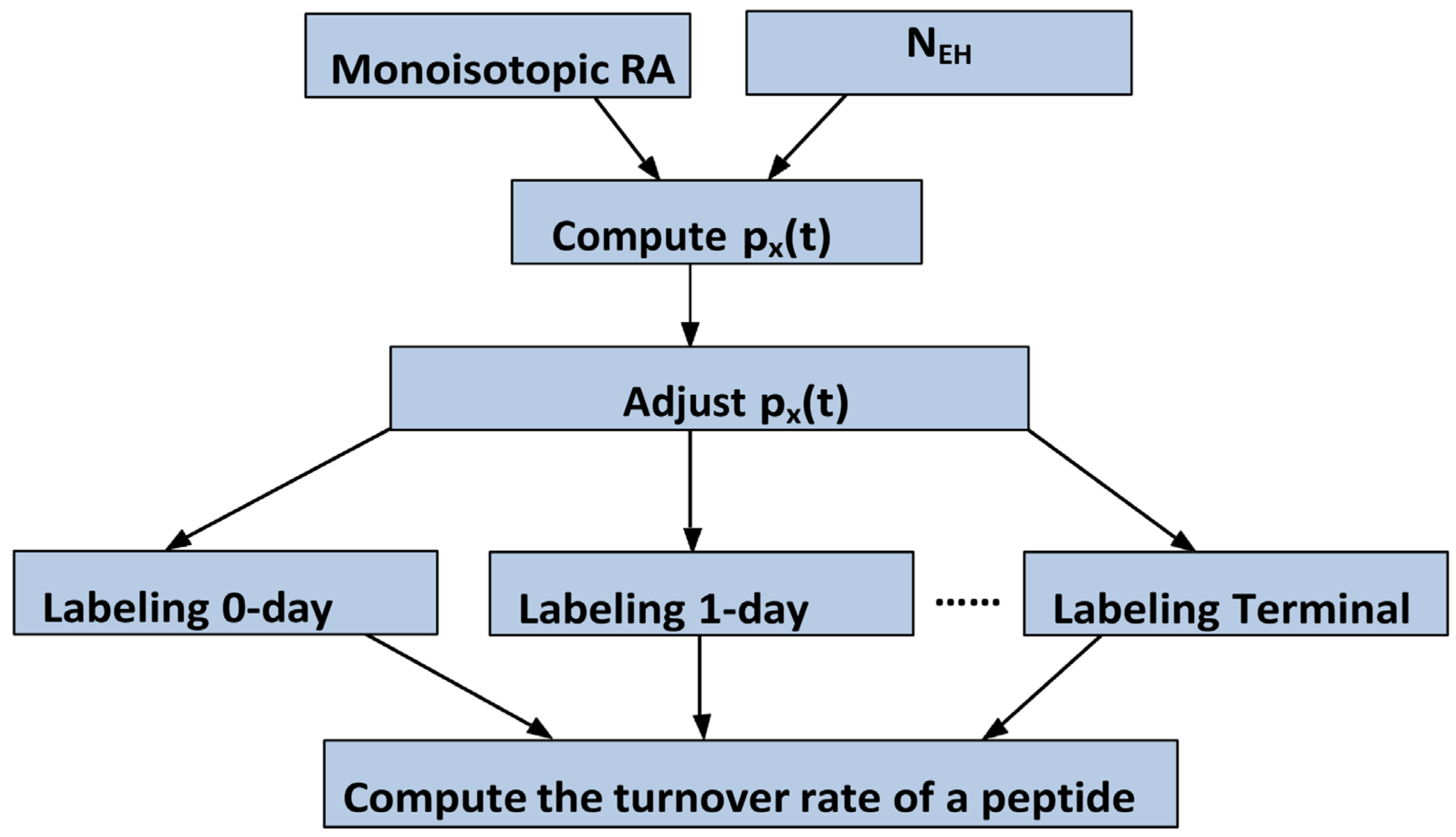
3.1. Turnover Rates Are Determined from the Time Course of Monoisotopic RA
3.2. Mass Spectral Datasets
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balch, W.E.; Morimoto, R.I.; Dillin, A.; Kelly, J.W. Adapting proteostasis for disease intervention. Science 2008, 319, 916–919. [Google Scholar] [CrossRef] [PubMed]
- Chondrogianni, N.; Petropoulos, I.; Grimm, S.; Georgila, K.; Catalgol, B.; Friguet, B.; Grune, T.; Gonos, E.S. Protein damage, repair and proteolysis. Mol. Aspects Med. 2014, 35, 1–71. [Google Scholar] [CrossRef] [PubMed]
- Porter, C.; Hurren, N.M.; Herndon, D.N.; Borsheim, E. Whole body and skeletal muscle protein turnover in recovery from burns. Int. J. Burns Trauma. 2013, 3, 9–17. [Google Scholar]
- Basisty, N.; Meyer, J.G.; Schilling, B. Protein Turnover in Aging and Longevity. Proteomics 2018, 18, e1700108. [Google Scholar] [CrossRef] [PubMed]
- Ryazanov, A.G.; Nefsky, B.S. Protein turnover plays a key role in aging. Mech. Ageing Dev. 2002, 123, 207–213. [Google Scholar] [CrossRef]
- Doherty, M.K.; Hammond, D.E.; Clague, M.J.; Gaskell, S.J.; Beynon, R.J. Turnover of the human proteome: Determination of protein intracellular stability by dynamic SILAC. J. Proteome Res. 2009, 8, 104–112. [Google Scholar] [CrossRef]
- Cambridge, S.B.; Gnad, F.; Nguyen, C.; Bermejo, J.L.; Kruger, M.; Mann, M. Systems-wide proteomic analysis in mammalian cells reveals conserved, functional protein turnover. J. Proteome Res. 2011, 10, 5275–5284. [Google Scholar] [CrossRef]
- Alber, A.B.; Suter, D.M. Dynamics of protein synthesis and degradation through the cell cycle. Cell Cycle 2019, 18, 784–794. [Google Scholar] [CrossRef]
- Holmes, W.E.; Angel, T.E.; Li, K.W.; Hellerstein, M.K. Dynamic Proteomics: In Vivo Proteome-Wide Measurement of Protein Kinetics Using Metabolic Labeling. Methods Enzymol. 2015, 561, 219–276. [Google Scholar] [CrossRef]
- Miller, B.F.; Reid, J.J.; Price, J.C.; Lin, H.L.; Atherton, P.J.; Smith, K. CORP: The use of deuterated water for the measurement of protein synthesis. J. Appl. Physiol. 2020, 128, 1163–1176. [Google Scholar] [CrossRef]
- Meadow, M.E.; Broas, S.; Hoare, M.; Alimohammadi, F.; Welle, K.A.; Swovick, K.; Hryhorenko, J.R.; Martinez, J.C.; Biashad, S.A.; Seluanov, A.; et al. Proteome Birthdating Reveals Age-Selectivity of Protein Ubiquitination. Mol. Cell Proteomics 2024, 23, 100791. [Google Scholar] [CrossRef] [PubMed]
- Guan, S.; Price, J.C.; Ghaemmaghami, S.; Prusiner, S.B.; Burlingame, A.L. Compartment modeling for mammalian protein turnover studies by stable isotope metabolic labeling. Anal. Chem. 2012, 84, 4014–4021. [Google Scholar] [CrossRef]
- MacCoss, M.J.; Wu, C.C.; Matthews, D.E.; Yates, J.R., III. Measurement of the isotope enrichment of stable isotope-labeled proteins using high-resolution mass spectra of peptides. Anal. Chem. 2005, 77, 7646–7653. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Dasgupta, A.; Yang, K.; Wang, S.; Hemandhar-Kumar, N.; Chepyala, S.R.; Yarbro, J.M.; Hu, Z.; Salovska, B.; Fornasiero, E.F.; et al. Turnover atlas of proteome and phosphoproteome across mouse tissues and brain regions. Cell 2025, 188, 2267–2287.e21. [Google Scholar] [CrossRef]
- Rauniyar, N.; McClatchy, D.B.; Yates, J.R., 3rd. Stable isotope labeling of mammals (SILAM) for in vivo quantitative proteomic analysis. Methods 2013, 61, 260–268. [Google Scholar] [CrossRef] [PubMed]
- Basisty, N.; Shulman, N.; Wehrfritz, C.; Marsh, A.N.; Shah, S.; Rose, J.; Ebert, S.; Miller, M.; Dai, D.F.; Rabinovitch, P.S.; et al. TurnoveR: A Skyline External Tool for Analysis of Protein Turnover in Metabolic Labeling Studies. J. Proteome Res. 2022, 22, 311–322. [Google Scholar] [CrossRef]
- Kim, J.; Seo, S.; Kim, T.Y. Metabolic deuterium oxide (D(2)O) labeling in quantitative omics studies: A tutorial review. Anal. Chim. Acta 2023, 1242, 340722. [Google Scholar] [CrossRef]
- Ross, A.B.; Langer, J.D.; Jovanovic, M. Proteome Turnover in the Spotlight: Approaches, Applications, and Perspectives. Mol. Cell Proteomics 2020, 20, 100016. [Google Scholar] [CrossRef]
- Fornasiero, E.F.; Savas, J.N. Determining and interpreting protein lifetimes in mammalian tissues. Trends Biochem. Sci. 2022, 48, 106–118. [Google Scholar] [CrossRef]
- Hammond, D.E.; Simpson, D.M.; Franco, C.; Wright Muelas, M.; Waters, J.; Ludwig, R.W.; Prescott, M.C.; Hurst, J.L.; Beynon, R.J.; Lau, E. Harmonizing Labeling and Analytical Strategies to Obtain Protein Turnover Rates in Intact Adult Animals. Mol. Cell Proteomics 2022, 21, 100252. [Google Scholar] [CrossRef]
- De Riva, A.; Deery, M.J.; McDonald, S.; Lund, T.; Busch, R. Measurement of protein synthesis using heavy water labeling and peptide mass spectrometry: Discrimination between major histocompatibility complex allotypes. Anal. Biochem. 2010, 403, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Busch, R.; Kim, Y.K.; Neese, R.A.; Schade-Serin, V.; Collins, M.; Awada, M.; Gardner, J.L.; Beysen, C.; Marino, M.E.; Misell, L.M.; et al. Measurement of protein turnover rates by heavy water labeling of nonessential amino acids. Biochim. Biophys. Acta 2006, 1760, 730–744. [Google Scholar] [CrossRef]
- Kim, T.Y.; Wang, D.; Kim, A.K.; Lau, E.; Lin, A.J.; Liem, D.A.; Zhang, J.; Zong, N.C.; Lam, M.P.; Ping, P. Metabolic labeling reveals proteome dynamics of mouse mitochondria. Mol. Cell Proteomics 2012, 11, 1586–1594. [Google Scholar] [CrossRef] [PubMed]
- Lau, E.; Cao, Q.; Ng, D.C.; Bleakley, B.J.; Dincer, T.U.; Bot, B.M.; Wang, D.; Liem, D.A.; Lam, M.P.; Ge, J.; et al. A large dataset of protein dynamics in the mammalian heart proteome. Sci. Data 2016, 3, 160015. [Google Scholar] [CrossRef]
- Currie, J.; Ng, D.C.M.; Pandi, B.; Black, A.; Manda, V.; Pavelka, J.; Lam, M.P.Y.; Lau, E. Improved determination of protein turnover rate with heavy water labeling by mass isotopomer ratio selection. bioRxiv 2024. [Google Scholar] [CrossRef]
- Shi, Y.; Del Rosario, A.; Wang, S.P.; Kang, L.; Liu, H.; Rady, B.; Jian, W. Measuring HSD17beta13 protein turnover in mouse liver with D(2)O metabolic labeling and hybrid LC-MS. Bioanalysis 2025, 17, 151–159. [Google Scholar] [CrossRef]
- Zecha, J.; Meng, C.; Zolg, D.P.; Samaras, P.; Wilhelm, M.; Kuster, B. Peptide Level Turnover Measurements Enable the Study of Proteoform Dynamics. Mol. Cell Proteomics 2018, 17, 974–992. [Google Scholar] [CrossRef]
- Deberneh, H.M.; Taylor, M.E.; Borowik, A.K.; Miyagi, M.; Miller, B.F.; Sadygov, R.G. Numbers of Exchangeable Hydrogens from LC-MS Data of Heavy Water Metabolically Labeled Samples. J. Am. Soc. Mass. Spectrom. 2024, 35, 1826–1837. [Google Scholar] [CrossRef]
- Deberneh, H.M.; Sadygov, R.G. Software Tool for Visualization and Validation of Protein Turnover Rates Using Heavy Water Metabolic Labeling and LC-MS. Int. J. Mol. Sci. 2022, 23, 4620. [Google Scholar] [CrossRef]
- Deberneh, H.M.; Sadygov, R.G. Flexible Quality Control for Protein Turnover Rates Using d2ome. Int. J. Mol. Sci. 2023, 24, 15553. [Google Scholar] [CrossRef]
- Lau, E.; Cao, Q.; Lam, M.P.Y.; Wang, J.; Ng, D.C.M.; Bleakley, B.J.; Lee, J.M.; Liem, D.A.; Wang, D.; Hermjakob, H.; et al. Integrated omics dissection of proteome dynamics during cardiac remodeling. Nat. Commun. 2018, 9, 120. [Google Scholar] [CrossRef] [PubMed]
- Deberneh, H.M.; Abdelrahman, D.R.; Verma, S.K.; Linares, J.J.; Murton, A.J.; Russell, W.K.; Kuyumcu-Martinez, M.N.; Miller, B.F.; Sadygov, R.G. A large-scale LC-MS dataset of murine liver proteome from time course of heavy water metabolic labeling. Sci. Data 2023, 10, 635. [Google Scholar] [CrossRef]
- Sadygov, R.G.; Hao, Z.; Huhmer, A.F. Charger: Combination of signal processing and statistical learning algorithms for precursor charge-state determination from electron-transfer dissociation spectra. Anal. Chem. 2008, 80, 376–386. [Google Scholar] [CrossRef]
- Ziari, N.; Hellerstein, M.K. PyMIDA: A Graphical User Interface for Mass Isotopomer Distribution Analysis. Anal. Chem. 2024, 96, 2303–2308. [Google Scholar] [CrossRef] [PubMed]
- Kincaid, D.; Cheney, E.W. Numerical Analysis: Mathematics of Scientific Computing, 3rd ed.; Brooks/Cole: Pacific Grove, CA, USA, 2002; 788p. [Google Scholar]
- Martens, L.; Chambers, M.; Sturm, M.; Kessner, D.; Levander, F.; Shofstahl, J.; Tang, W.H.; Rompp, A.; Neumann, S.; Pizarro, A.D.; et al. mzML—A community standard for mass spectrometry data. Mol. Cell Proteomics 2011, 10, R110.000133. [Google Scholar] [CrossRef]
- Chambers, M.C.; Maclean, B.; Burke, R.; Amodei, D.; Ruderman, D.L.; Neumann, S.; Gatto, L.; Fischer, B.; Pratt, B.; Egertson, J.; et al. A cross-platform toolkit for mass spectrometry and proteomics. Nat. Biotechnol. 2012, 30, 918–920. [Google Scholar] [CrossRef] [PubMed]
- Kessner, D.; Chambers, M.; Burke, R.; Agus, D.; Mallick, P. ProteoWizard: Open source software for rapid proteomics tools development. Bioinformatics 2008, 24, 2534–2536. [Google Scholar] [CrossRef]
- Perkins, D.N.; Pappin, D.J.; Creasy, D.M.; Cottrell, J.S. Probability-based protein identification by searching sequence databases using mass spectrometry data. Electrophoresis 1999, 20, 3551–3567. [Google Scholar] [CrossRef]
- UniProt, C. UniProt: The universal protein knowledgebase in 2021. Nucleic Acids Res. 2021, 49, D480–D489. [Google Scholar] [CrossRef]
- Sadygov, R.G.; Zhu, J.X.; Deberneh, H.M. Exact Integral Formulas for False Discovery Rate and the Variance of False Discovery Proportion. J. Proteome Res. 2024, 23, 2298–2305. [Google Scholar] [CrossRef]
- Jones, A.R.; Eisenacher, M.; Mayer, G.; Kohlbacher, O.; Siepen, J.; Hubbard, S.J.; Selley, J.N.; Searle, B.C.; Shofstahl, J.; Seymour, S.L.; et al. The mzIdentML data standard for mass spectrometry-based proteomics results. Mol. Cell Proteomics 2012, 11, M111 014381. [Google Scholar] [CrossRef]
- Deutsch, E.W.; Csordas, A.; Sun, Z.; Jarnuczak, A.; Perez-Riverol, Y.; Ternent, T.; Campbell, D.S.; Bernal-Llinares, M.; Okuda, S.; Kawano, S.; et al. The ProteomeXchange consortium in 2017: Supporting the cultural change in proteomics public data deposition. Nucleic Acids Res. 2017, 45, D1100–D1106. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deberneh, H.M.; Bagherinia, A.; Sadygov, R.G. Turnover Rates and Numbers of Exchangeable Hydrogens in Deuterated Water Labeled Samples. Int. J. Mol. Sci. 2025, 26, 6398. https://doi.org/10.3390/ijms26136398
Deberneh HM, Bagherinia A, Sadygov RG. Turnover Rates and Numbers of Exchangeable Hydrogens in Deuterated Water Labeled Samples. International Journal of Molecular Sciences. 2025; 26(13):6398. https://doi.org/10.3390/ijms26136398
Chicago/Turabian StyleDeberneh, Henock M., Ali Bagherinia, and Rovshan G. Sadygov. 2025. "Turnover Rates and Numbers of Exchangeable Hydrogens in Deuterated Water Labeled Samples" International Journal of Molecular Sciences 26, no. 13: 6398. https://doi.org/10.3390/ijms26136398
APA StyleDeberneh, H. M., Bagherinia, A., & Sadygov, R. G. (2025). Turnover Rates and Numbers of Exchangeable Hydrogens in Deuterated Water Labeled Samples. International Journal of Molecular Sciences, 26(13), 6398. https://doi.org/10.3390/ijms26136398






