Investigating Endogenous Opioids Unravels the Mechanisms Behind Opioid-Induced Constipation, a Mathematical Modeling Approach
Abstract
1. Introduction
2. Results
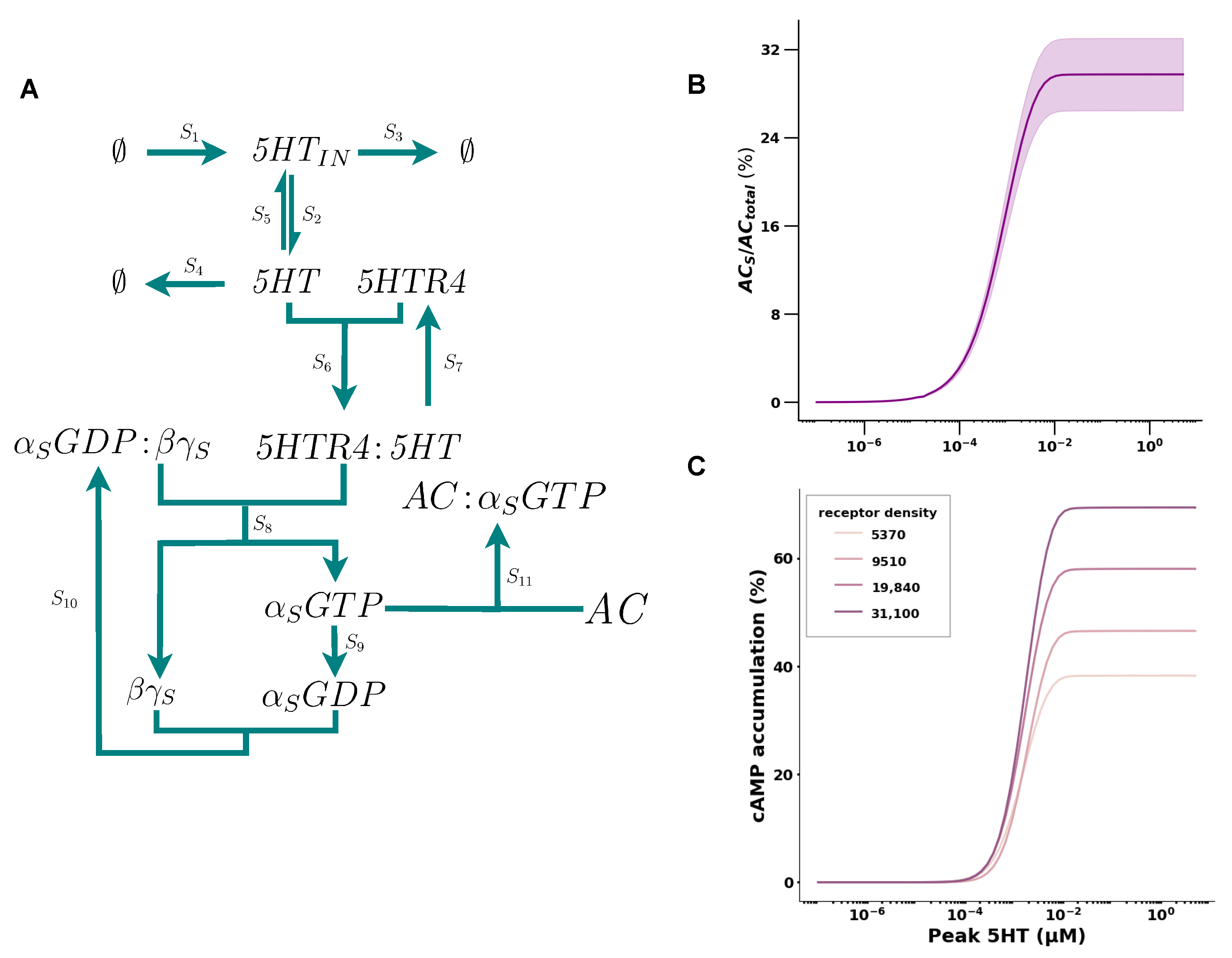
2.1. 5HT Has a Positive Cooperative Effect on cAMP Accumulation
| Species (Reaction Network) | Species (COPASI) | Initial Concentration in μM | Source |
|---|---|---|---|
| 5HT | 5HT | Model Calibration Appendix A.2 | |
| 5HTIN | 5HT_IN | Model Calibration Appendix A.2 | |
| 5HTR4 | 5HTR4 | [31] | |
| AC | AC | Model Calibration Appendix A.2 | |
| 5HTR4:5HT | 0 | ||
| AC:ALPHA_S_GTP | 0 | ||
| AC:ALPHA_I_GTP | 0 | ||
| ALPHA_S_GDP | 0 | ||
| ALPHA_I_GDP | 0 | ||
| ALPHA_S_GDP_BG_S | 0.05 | Model Calibration Appendix A.2 | |
| ALPHA_I_GDP_BG_I | 0.05 | Model Calibration Appendix A.2 | |
| ALPHA_S_GTP | 0 | ||
| ALPHA_I_GTP | 0 | ||
| BG_S | 0 | ||
| BG_I | 0 | ||
| MOR | MOR | [31] | |
| MOR:OL | 0 | ||
| OL | OL | 0 | |
| OL_Blood | 0 |
| Parameter | Description | Value | Source |
|---|---|---|---|
| Endogenous serotonin (in EC cell) synthesis rate constant | ms−1 | Model calibration Appendix A.3 | |
| Endogenous serotonin (in EC cell) release rate constant | 0.001 ms−1 | Calculated from [14] | |
| Endogenous serotonin (in EC cell) degradation rate constant | 0.01 ms−1 | Model calibration Appendix A.3 | |
| Cellular serotonin degradation rate constant | 0.01 ms−1 | Model calibration Appendix A.3 | |
| Reuptake of intracellular serotonin into EC cell rate constant | ms−1 | Model calibration Appendix A.3 | |
| Endogenous 5HT binding to 5HTR4 | M−1·ms−1 | Model calibration Appendix A.3 | |
| Endogenous 5HT unbinding from 5HTR4 | ms−1 | Model calibration Appendix A.3 | |
| Rate at which administered opioid reaches the desired tissue via the blood | ms−1 | Estimated from [32] | |
| rate at which opioid in the desired tissue is metabolized | ms−1 | Estimated from [32] | |
| Rate at which opioid in the blood stream is eliminated | ms−1 | Estimated from [32] | |
| Rate at which opioid binds to MOR | varying for opioids | Calculated from different sources Appendix A.3 | |
| Rate at which opioid unbinds from MOR | varying for opioids | Calculated from different sources Appendix A.3 | |
| Rate at which subunint is activated | 0.2 M−1·ms−1 | Calculated from [33] | |
| Rate at which and reform into G protein complex | 0.033 M−1·ms−1 | Calculated from [33] | |
| Rate at which the GTP is hydrolyzed into a GDP | ms−1 | Calculated from [34] | |
| Rate at which AC and form a complex | M−1·ms−1 | [35] | |
| Rate at which AC and form a complex | M−1·ms−1 | [35] | |
| rate at which dissociates from AC | ms−1 | Model calibration Appendix A.3 | |
| rate at which dissociates from AC | ms−1 | Model calibration Appendix A.3 |
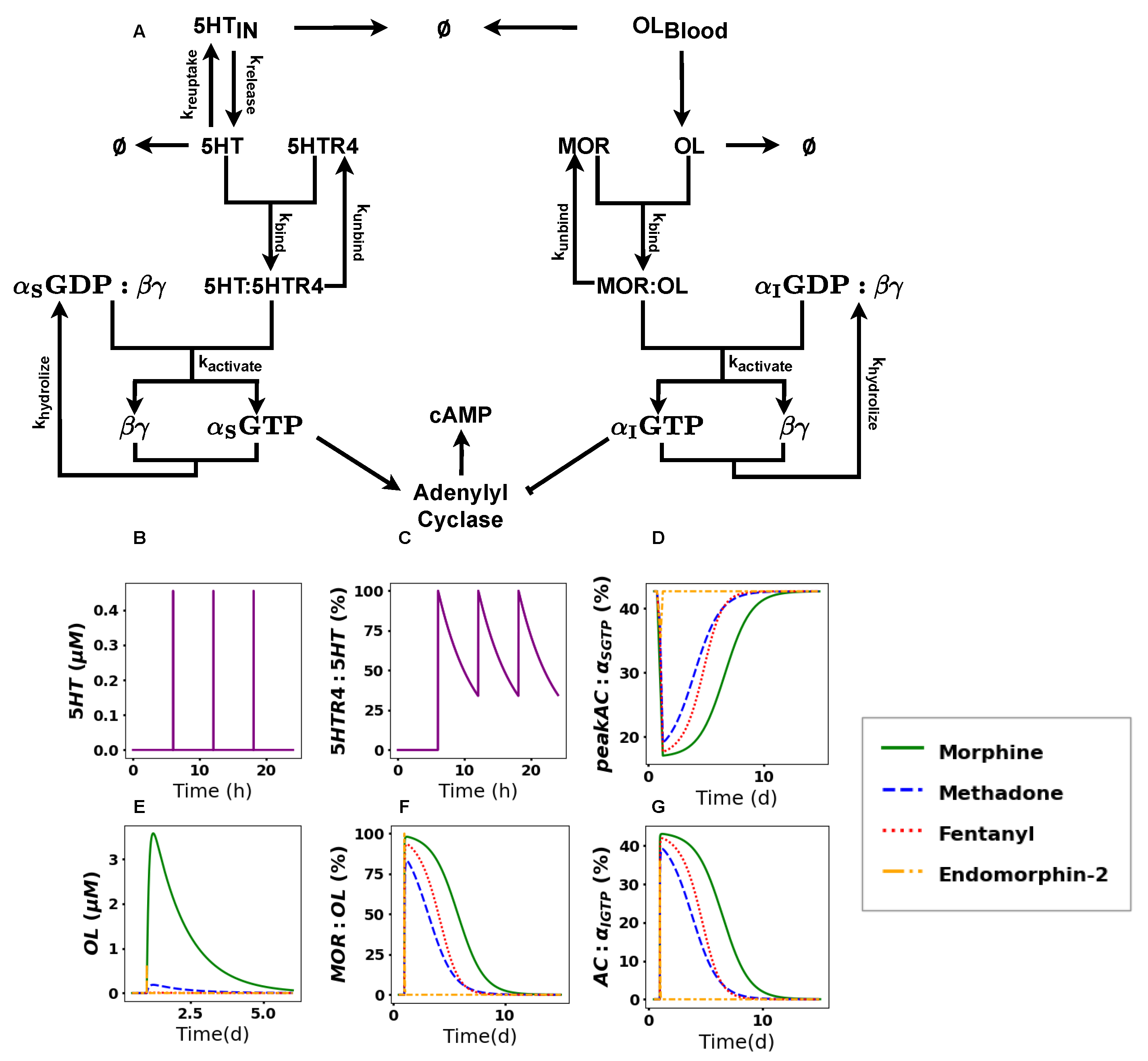
2.2. The Activation of the Opioid Pathway Inhibits cAMP Accumulation
2.3. cAMP Accumulation Drastically Decreases upon Acute Treatment with Opioids
2.4. cAMP Shows Differences in Recovery Times
2.5. Modulating Opioid Degradation Is an Alternative Approach to Improving the cAMP Recovery
3. Discussion
4. Methods and Materials
4.1. Reaction Network
4.2. Software and Model Implementation
4.3. Mapping AC Activity to cAMP Production
4.4. In Silico Protonation of Endomorphin-2
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Reaction Parameters
| Receptor Density | Fitted (k1, k2, , n) | (nM) | (%) |
|---|---|---|---|
| 5730 | (0.1, 1.0, 2.1, 1.96) | 1.37 | 38 |
| 9510 | (0.0065, 14.14, 13.5, 2.44) | 1.7 | 46 |
| 19,840 | (0.018, 2.97, 6.2, 2.09) | 1.49 | 58 |
| 31,100 | (0.007, 50.25, 25.99, 2.24) | 1.59 | 69 |
Appendix A.2. Initial Conditions
- We calibrated the initial concentration of AC, such that the AC activity is around 40%. It was shown by Das et al. that the baseline muscle contraction is in the human colon is around 40% [12].
- We calibrated the initial concentrations of 5HT and 5HTIN such that 5HTIN is smaller than 5HT as estimated in [29].
- We calibrated the initial concentration of the receptor species MOR and 5HTR4 to that given in [31]. We calibrated the initial concentration of both and to ensure an approximate maximum AC activity of 40%.
Appendix A.3. Parameter Settings
- Synthesis of 5HTIN was calibrated using the COPASI sliders to ensure that the concentration ratio of 5HTIN and 5HT was greater than 1 as estimated in [29].
- We calibrated and to ensure a ratio greater than 1 for 5HTIN and 5HT.
- We calibrated to ensure a particular clearance time.
- We calibrated the binding and unbinding rate for 5HT to ensure an of around 0.05 M, as implemented in Das et al.
- We calculated the binding and unbinding rates using values from available resources (see Table 4).
- We calibrated the reaction rates for , , and , such that the maximum amplitude of AC was capped at 40%, as suggested in Das et al.
Appendix A.4. Stoichiometric Matrix
Appendix A.5. Choice of Recovery Treshold
| Treshold | Morphine (d) | Methadone (d) | Fentanyl (d) | Endomorphin-2 (h) |
|---|---|---|---|---|
| 50% | 6.162 | 4.446 | 4.177 | 6.191 |
| 57.5% | 6.539 | 4.781 | 4.454 | 6.191 |
| 65% | 6.891 | 5.117 | 4.705 | 6.191 |
| 72.5% | 7.318 | 5.563 | 4.957 | 6.191 |
| 80% | 7.796 | 5.982 | 5.259 | 6.191 |
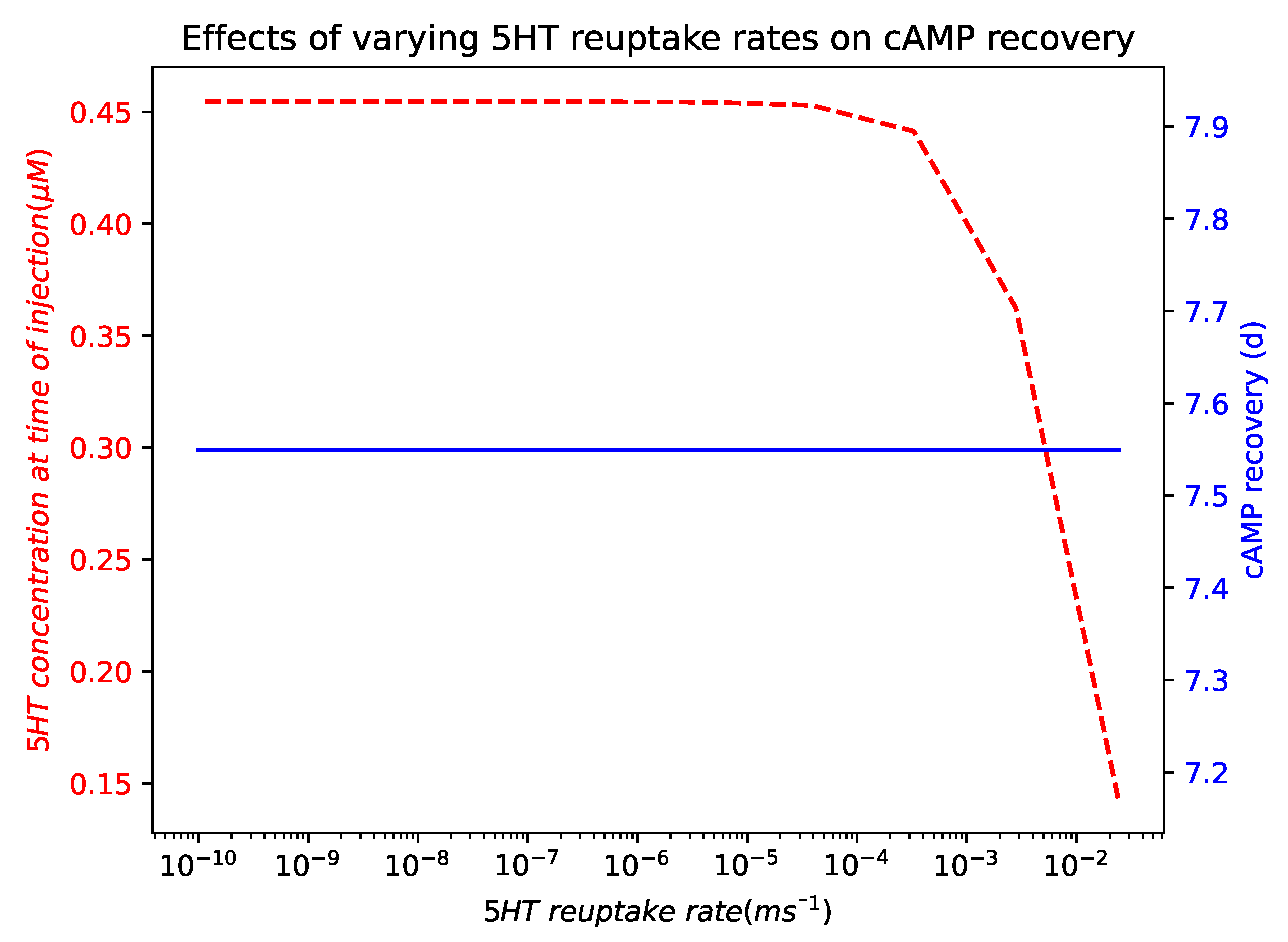
Appendix A.6. Effects of Varying 5HT Reuptake Rates on cAMP Recovery
References
- Kamato, D.; Thach, L.; Bernard, R.; Chan, V.; Zheng, W.; Kaur, H.; Brimble, M.; Osman, N.; Little, P.J. Structure, Function, Pharmacology, and Therapeutic Potential of the G Protein, Gα q,11. Front. Cardiovasc. Med. 2015, 2, 14. [Google Scholar] [CrossRef]
- Thies, A.; Sunkara, V.; Ray, S.; Wulkow, H.; Celik, M.Ö.; Yergöz, F.; Schütte, C.; Stein, C.; Weber, M.; Winkelmann, S. Modelling altered signalling of G-protein coupled receptors in inflamed environment to advance drug design. Sci. Rep. 2023, 13, 607. [Google Scholar] [CrossRef] [PubMed]
- Benyamin, R.; Trescot, A.M.; Datta, S.; Buenaventura, R.M.; Adlaka, R.; Sehgal, N.; Glaser, S.E.; Vallejo, R. Opioid complications and side effects. Pain Phys. 2008, 11, S105. [Google Scholar] [CrossRef]
- Paul, A.K.; Smith, C.M.; Rahmatullah, M.; Nissapatorn, V.; Wilairatana, P.; Spetea, M.; Gueven, N.; Dietis, N. Opioid Analgesia and Opioid-Induced Adverse Effects: A Review. Pharmaceuticals 2021, 14, 1091. [Google Scholar] [CrossRef] [PubMed]
- Cruz, S.L. Opioids: Pharmacology, Abuse, and Addiction; Springer International Publishing AG: Cham, Switzerland, 2022. [Google Scholar]
- Rosow, C.E.; Dershwitz, M. Clinical pharmacology of opioids. In Anesthetic Pharmacology: Basic Principles and Clinical Practice; Evers, A.S., Maze, M., Kharasch, E.D., Eds.; Cambridge University Press: Cambridge, UK, 2011; pp. 531–547. [Google Scholar]
- Kumar, L.; Barker, C.; Emmanuel, A. Opioid-Induced Constipation: Pathophysiology, Clinical Consequences, and Management. Gastroenterol. Res. Pract. 2014, 2014, 141737. [Google Scholar] [CrossRef]
- Nelson, A.D.; Camilleri, M. Chronic opioid induced constipation in patients with nonmalignant pain: Challenges and opportunities. Ther. Adv. Gastroenterol. 2015, 8, 206–220. [Google Scholar] [CrossRef]
- Sobczak, M.; Sałaga, M.; Storr, M.A.; Fichna, J. Physiology, signaling, and pharmacology of opioid receptors and their ligands in the gastrointestinal tract: Current concepts and future perspectives. J. Gastroenterol. 2013, 49, 24–45. [Google Scholar] [CrossRef]
- McLean, P.G.; Borman, R.A.; Lee, K. 5-HT in the enteric nervous system: Gut function and neuropharmacology. Trends Neurosci. 2007, 30, 9–13. [Google Scholar] [CrossRef]
- Fleming, M.A.; Ehsan, L.; Moore, S.R.; Levin, D.E. The Enteric Nervous System and Its Emerging Role as a Therapeutic Target. Gastroenterol. Res. Pract. 2020, 2020, 8024171. [Google Scholar] [CrossRef]
- Das, R.; Wille, L.; Zhang, L.; Chen, C.; Winchester, W.; Selimkhanov, J.; Wykosky, J.; Apgar, J.F.; Burke, J.M.; Rogge, M.; et al. A quantitative systems pharmacology model of colonic motility with applications in drug development. J. Pharmacokinet. Pharmacodyn. 2019, 46, 485–498. [Google Scholar] [CrossRef]
- Spencer, N.J.; Hu, H. Enteric nervous system: Sensory transduction, neural circuits and gastrointestinal motility. Nat. Rev. Gastroenterol. Hepatol. 2020, 17, 338–351. [Google Scholar] [CrossRef] [PubMed]
- Bertrand, P.P.; Hu, X.; Mach, J.; Bertrand, R.L. Serotonin (5-HT) release and uptake measured by real-time electrochemical techniques in the rat ileum. Am. J. Physiol.-Gastrointest. Liver Physiol. 2008, 295, G1228–G1236. [Google Scholar] [CrossRef]
- Guzel, T.; Mirowska-Guzel, D. The Role of Serotonin Neurotransmission in Gastrointestinal Tract and Pharmacotherapy. Molecules 2022, 27, 1680. [Google Scholar] [CrossRef]
- Sabbatini, M.E.; Gorelick, F.; Glaser, S. Adenylyl cyclases in the digestive system. Cell. Signal. 2014, 26, 1173–1181. [Google Scholar] [CrossRef] [PubMed]
- Sudlow, L.C.; Gillette, R. Cyclic AMP Levels, Adenylyl Cyclase Activity, and Their Stimulation by Serotonin Quantified in Intact Neurons. J. Gen. Physiol. 1997, 110, 243–255. [Google Scholar] [CrossRef]
- Khansari, M.; Sohrabi, M.; Zamani, F. The useage of opioids and their adverse effects in gastrointestinal practice: A review. Middle East J. Dig. Dis. 2013, 5, 5–16. [Google Scholar] [PubMed]
- Gao, H.; Zhang, Y.; Li, Y.; Chang, H.; Cheng, B.; Li, N.; Yuan, W.; Li, S.; Wang, Q. μ-Opioid Receptor–Mediated Enteric Glial Activation Is Involved in Morphine-Induced Constipation. Mol. Neurobiol. 2021, 58, 3061–3070. [Google Scholar] [CrossRef]
- Monory, K.; Bourin, M.C.; Spetea, M.; Tömböly, C.; Tóth, G.; Matthes, H.W.; Kieffer, B.L.; Hanoune, J.; Borsodi, A. Specific activation of the μ opioid receptor (MOR) by endomorphin 1 and endomorphin 2. Eur. J. Neurosci. 2000, 12, 577–584. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1046/j.1460-9568.2000.00936.x (accessed on 20 June 2025). [CrossRef]
- Kerr, P.; Sirbu, C.; Gregg, J. Endogenous Opioids: From Basic Science to Biopsychosocial Applications; Advances in Neurobiology; Springer International Publishing: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Tömböly, C.; Péter, A.; Tóth, G. In vitro quantitative study of the degradation of endomorphins. Peptides 2002, 23, 1573–1580. [Google Scholar] [CrossRef]
- LaVigne, J.; Keresztes, A.; Chiem, D.; Streicher, J.M. The endomorphin-1/2 and dynorphin-B peptides display biased agonism at the mu opioid receptor. Pharmacol. Rep. 2020, 72, 465–471. [Google Scholar] [CrossRef]
- Fichna, J.; Perlikowska, R.; Gach, K.; Do-Rego, J.C.; Cravezic, A.; Janecka, A.; Storr, M.A. The Novel Endomorphin Degradation Blockers Tyr-Pro-DClPhe-Phe-NH2 (EMDB-1) and Tyr-Pro-Ala-NH2 (EMDB-2) Prolong Endomorphin-2 Action in Rat Ileum In Vitro. Chem. Biol. Drug Des. 2010, 76, 77–81. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1747-0285.2010.00977.x (accessed on 20 June 2025). [CrossRef] [PubMed]
- Lee, C.W.S.; Yan, J.Y.; Chiang, Y.C.; Hung, T.W.; Wang, H.L.; Chiou, L.C.; Ho, I.K. Differential Pharmacological Actions of Methadone and Buprenorphine in Human Embryonic Kidney 293 Cells Coexpressing Human μ-Opioid and Opioid Receptor-Like 1 Receptors. Neurochem. Res. 2011, 36, 2008–2021. [Google Scholar] [CrossRef]
- Taguchi, A.; Sharma, N.; Saleem, R.M.; Sessler, D.I.; Carpenter, R.L.; Seyedsadr, M.; Kurz, A. Selective Postoperative Inhibition of Gastrointestinal Opioid Receptors. N. Engl. J. Med. 2001, 345, 935–940. [Google Scholar] [CrossRef]
- Schmidt, W.K. Alvimopan*(ADL 8-2698) Is a Novel Peripheral Opioid Antagonist. Am. J. Surg. 2001, 182, S27–S38. [Google Scholar] [CrossRef] [PubMed]
- Kuo, A.; Wyse, B.; Meutermans, W.; Smith, M. In vivo profiling of seven common opioids for antinociception, constipation and respiratory depression: No two opioids have the same profile. Br. J. Pharmacol. 2015, 172, 532–548. [Google Scholar] [CrossRef]
- Best, J.; Nijhout, H.F.; Reed, M. Serotonin synthesis, release and reuptake in terminals: A mathematical model. Theor. Biol. Med. Model. 2010, 7, 34. [Google Scholar] [CrossRef]
- Pellissier, L.P.; Sallander, J.; Campillo, M.; Gaven, F.; Queffeulou, E.; Pillot, M.; Dumuis, A.; Claeysen, S.; Bockaert, J.; Pardo, L. Conformational Toggle Switches Implicated in Basal Constitutive and Agonist-Induced Activated States of 5-Hydroxytryptamine-4 Receptors. Mol. Pharmacol. 2009, 75, 982–990. [Google Scholar] [CrossRef]
- Ray, S.; Sunkara, V.; Schütte, C.; Weber, M. How to calculate pH-dependent binding rates for receptor–ligand systems based on thermodynamic simulations with different binding motifs. Mol. Simul. 2020, 46, 1443–1452. [Google Scholar] [CrossRef]
- Khanday, M.; Rafiq, A.; Nazir, K. Mathematical models for drug diffusion through the compartments of blood and tissue medium. Alex. J. Med. 2017, 53, 245–249. [Google Scholar] [CrossRef]
- Hein, P.; Rochais, F.; Hoffmann, C.; Dorsch, S.; Nikolaev, V.O.; Engelhardt, S.; Berlot, C.H.; Lohse, M.J.; Bünemann, M. GS Activation Is Time-limiting in Initiating Receptor-mediated Signaling. J. Biol. Chem. 2006, 281, 33345–33351. [Google Scholar] [CrossRef]
- Lan, K.L.; Zhong, H.; Nanamori, M.; Neubig, R.R. Rapid Kinetics of Regulator of G-protein Signaling (RGS)-mediated Gαi and Gαo Deactivation. J. Biol. Chem. 2000, 275, 33497–33503. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, G. Protein–Protein Interactions: Kinetics. In Encyclopedia of Biophysics; Roberts, G.C.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 2098–2101. [Google Scholar] [CrossRef]
- Olson, K.M.; Duron, D.I.; Womer, D.; Fell, R.; Streicher, J.M. Comprehensive molecular pharmacology screening reveals potential new receptor interactions for clinically relevant opioids. PLoS ONE 2019, 14, e0217371. [Google Scholar] [CrossRef]
- Livingston, K.E.; Mahoney, J.P.; Manglik, A.; Sunahara, R.K.; Traynor, J.R. Measuring ligand efficacy at the mu-opioid receptor using a conformational biosensor. eLife 2018, 7, e32499. [Google Scholar] [CrossRef]
- Volpe, D.A.; Tobin, G.A.M.; Mellon, R.D.; Katki, A.G.; Parker, R.J.; Colatsky, T.; Kropp, T.J.; Verbois, S.L. Uniform assessment and ranking of opioid μ receptor binding constants for selected opioid drugs. Regul. Toxicol. Pharmacol. RTP 2011, 59, 385–390. [Google Scholar] [CrossRef] [PubMed]
- Bot, G.; Blake, A.D.; Li, S.X.; Reisine, T.D. Fentanyl and its analogs desensitize the cloned mu opioid receptor. J. Pharmacol. Exp. Ther. 1998, 285 3, 1207–1218. [Google Scholar] [CrossRef]
- Meyer, J.; Del Vecchio, G.; Seitz, V.; Massaly, N.; Stein, C. Modulation of μ-opioid receptor activation by acidic pH is dependent on ligand structure and an ionizable amino acid residue. Br. J. Pharmacol. 2019, 176, 4510–4520. [Google Scholar] [CrossRef] [PubMed]
- Janecka, A.; Staniszewska, R.; Gach, K.; Fichna, J. Enzymatic degradation of endomorphins. Peptides 2008, 29, 2066–2073. [Google Scholar] [CrossRef]
- Baldo, B.A.; Rose, M.A. The anaesthetist, opioid analgesic drugs, and serotonin toxicity: A mechanistic and clinical review. Br. J. Anaesth. 2020, 124, 44–62. [Google Scholar] [CrossRef] [PubMed]
- Spahn, V.; Vecchio, G.D.; Labuz, D.; Rodriguez-Gaztelumendi, A.; Massaly, N.; Temp, J.; Durmaz, V.; Sabri, P.; Reidelbach, M.; Machelska, H.; et al. A nontoxic pain killer designed by modeling of pathological receptor conformations. Science 2017, 355, 966–969. Available online: https://www.science.org/doi/pdf/10.1126/science.aai8636 (accessed on 20 June 2025). [CrossRef]
- Mawe, G.; Hoffman, J. Serotonin signalling in the gut–functions, dysfunctions and therapeutic targets. Nat. Rev. Gastroenterol. Hepatol. 2013, 10, 473–486. [Google Scholar] [CrossRef]
- Meng, J.; Sindberg, G.M.; Roy, S. Disruption of gut homeostasis by opioids accelerates HIV disease progression. Front. Microbiol. 2015, 6, 643. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, S.; Schütte, C. Stochastic Dynamics in Computational Biology; Springer: Berlin/Heidelberg, Germany, 2020; Volume 645. [Google Scholar]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI–a COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- Petzold, L. Automatic Selection of Methods for Solving Stiff and Nonstiff Systems of Ordinary Differential Equations. SIAM J. Sci. Stat. Comput. 1983, 4, 136–148. [Google Scholar] [CrossRef]
- Bergmann, F.T. BASICO: A simplified Python interface to COPASI. J. Open Source Softw. 2023, 8, 5553. [Google Scholar] [CrossRef]
- Python Package Index-PyPI. Available online: https://pypi.org/ (accessed on 28 March 2021).
- PlotDigitizer: Version 3.1.5. 2024. Available online: https://plotdigitizer.com (accessed on 20 June 2025).
- Abarbanel, O.D.; Hutchison, G.R. QupKake: Integrating Machine Learning and Quantum Chemistry for Micro-pKa Predictions. J. Chem. Theory Comput. 2024, 20, 6946–6956. [Google Scholar] [CrossRef] [PubMed]
- Johnston, R.C.; Yao, K.; Kaplan, Z.; Chelliah, M.; Leswing, K.; Seekins, S.; Watts, S.; Calkins, D.; Chief Elk, J.; Jerome, S.V.; et al. Epik: pKa and protonation state prediction through machine learning. ChemRxiv 2023. [Google Scholar] [CrossRef]
- Misiolek, H.; Zajączkowska, R.; Daszkiewicz, A.; Woroń, J.; Dobrogowski, J.; Wordliczek, J.; Owczuk, R. Postoperative pain management-2018 consensus statement of the section of regional anaesthesia and pain therapy of the polish society of anaesthesiology and intensive therapy, the polish society of regional anaesthesia and pain therapy, the polish association for the study of pain and the national consultant in anaesthesiology and intensive therapy. Anaesthesiol. Intensive Ther. 2018, 50, 173–199. [Google Scholar]


| Compartment | i | |
|---|---|---|
| Serotonin Pathway () | 1 | * |
| 2 | IN | |
| 3 | IN | |
| 4 | ||
| 5 | IN | |
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| Opioid Pathway () | 1 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| Competing Pathway () | 1 | see Equation (2) |
| 2 | ||
| 3 |
| Drug | (nM) | Simulations | Reference |
|---|---|---|---|
| Morphine | 76.08 ± 9.19 [36] | 6.7 [37] | |
| Methadone | 41.92 ± 28.31 [38] | 8.7 ± 0.13 | 7.5 [37] |
| Fentanyl | 0.57± 0.12 [39] | 10.04 ± 0.03 | 8.9 [40] |
| Endomorphin-2 | 2.33 ± 0.19 [20] | 9.43 ± 0.01 | 8.42 [23] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coomber, C.; Chewle, S.; Secker, C.; Fackeldey, K.; Weber, M.; Winkelmann, S.; Schütte, C.; Sunkara, V. Investigating Endogenous Opioids Unravels the Mechanisms Behind Opioid-Induced Constipation, a Mathematical Modeling Approach. Int. J. Mol. Sci. 2025, 26, 6207. https://doi.org/10.3390/ijms26136207
Coomber C, Chewle S, Secker C, Fackeldey K, Weber M, Winkelmann S, Schütte C, Sunkara V. Investigating Endogenous Opioids Unravels the Mechanisms Behind Opioid-Induced Constipation, a Mathematical Modeling Approach. International Journal of Molecular Sciences. 2025; 26(13):6207. https://doi.org/10.3390/ijms26136207
Chicago/Turabian StyleCoomber, Celvic, Surahit Chewle, Christopher Secker, Konstantin Fackeldey, Marcus Weber, Stefanie Winkelmann, Christof Schütte, and Vikram Sunkara. 2025. "Investigating Endogenous Opioids Unravels the Mechanisms Behind Opioid-Induced Constipation, a Mathematical Modeling Approach" International Journal of Molecular Sciences 26, no. 13: 6207. https://doi.org/10.3390/ijms26136207
APA StyleCoomber, C., Chewle, S., Secker, C., Fackeldey, K., Weber, M., Winkelmann, S., Schütte, C., & Sunkara, V. (2025). Investigating Endogenous Opioids Unravels the Mechanisms Behind Opioid-Induced Constipation, a Mathematical Modeling Approach. International Journal of Molecular Sciences, 26(13), 6207. https://doi.org/10.3390/ijms26136207







