Diversity of Effects of Mechanical Influences on Living Systems and Aqueous Solutions

Abstract

Water is the basis of life. Any factors acting on water will also affect the functioning of living organisms, including humans. Mechanical effects are as ubiquitous as temperature or magnetic fields. Numerous works have been devoted to the action of mechanical impacts on living systems, aqueous solutions, and water. However, no unified theory that would allow predicting the consequences of mechanical effects on living organisms based on their characteristics. In this review, we have attempted to systematize the available quantitative data on the effects of mechanical impacts on living organisms, cells, aqueous solutions, and purified water. In addition, in this review, we provide a basic overview of the variety of mechanical effects and the mechanisms of their realization. The responses of living systems and aqueous solutions depend quantitatively on different sets of characteristics of the vibration action. The magnitude of responses of living systems (cells and organisms) to mechanical action correlates with frequency, acceleration, and force. Mechanical action changes the characteristics of water and aqueous solutions as a function of frequency, acceleration, and duration. The data obtained may find application in a wide range of fields: from analytical chemistry and pharmacology to environmental protection.

1. Introduction

Water and aqueous solutions are subjected to mechanical action on a daily basis: from bars to pharmaceutical production, from water purification systems to the propellers of supertankers, from air humidifiers to watering plants in agriculture [1,2,3,4]. Mechanical action on aqueous solutions is used for various tasks in human activities. The most common application of mechanical action to aqueous solutions is to dissolve and/or mix and/or change temperature and/or transfer torque/force and/or wet something [5]. Mechanical effects are even used in nanotechnology, e.g., to concentrate particle separation molecules from the solvent by flotation [6] or to control nanoparticle aggregation [7]. More than a hundred years ago, it was found that mechanical impacts of high intensities are observed to alter/damage organic molecules in water. For example, denaturation of proteins in aqueous colloids is observed when they are mechanically impacted [8]. This discovery was later proposed to be used as a stress test to check the quality of antibodies [9]. Today, a whole section of chemistry (mechanochemistry) studies changes in the properties of substances and their mixtures, as well as physicochemical transformations under mechanical effects [10]. The negative effects of prolonged mechanical impact on the level of living tissues and organisms have been well described. There is a separate group of so-called vibration diseases, which belong to occupational diseases and affect various body systems. The complex of vibration diseases affects both pathologies of the nervous system (peripheral neuropathy) and musculoskeletal system (aseptic necrosis, fatigue fractures, degenerative joint disease, carpal tunnel syndrome), as well as the cardiovascular system (Raynaud’s syndrome) [11]. Even though modern working conditions are designed to provide a high level of safety in chronic vibration exposure due to modernization of impact tools and new technological elements of vibration protection [12], the incidence of vibration diseases in workers of construction, mining, metalworking industries and operators of heavy machinery is still about 10–40%, depending on the length of service and occupation [13]. It is known that the highest frequency of vibration disease is observed among workers in the mining industry and construction workers. The risk of vibration diseases increases significantly after 5–7 years of work in these industries. Unfortunately, there are no unified working recommendations on the prevention and ideal treatment of vibration diseases. Unfortunately, there are no unified working recommendations on prevention and ideal therapy of vibration diseases today [14].

In order to create more effective ways to treat aqueous solutions, to create new biotechnological approaches, to improve the quality and safety of life, it is necessary to understand in detail the regularities of mechanical (especially weak) effects on water, aqueous solutions and living organisms, which are 70–90% composed of water [15].

Almost 300,000 works have been published on the mechanobiology issues (https://pubmed.ncbi.nlm.nih.gov/?term=mechanobiology accessed on 26 March 2025). However, there is no common unified theory linking the characteristics of heterogeneous mechanical effects (vibration, shear stress, pressure, and sound action) to date. In this review, we have attempted to find general regularities that determine the magnitude of the effect of mechanical action on aqueous solutions and biological objects depending on the characteristics of mechanical action (duration, frequency, acceleration, force, and other features).

In addition, this review will describe the main effects of mechanical action on purified water, aqueous solutions of organic compounds, cell cultures, and whole organisms. The main mechanisms of the realization of mechanical impact effects will be discussed.

2. Diversity of Effects of Mechanical Influences on Living Systems and Aqueous Solutions

2.1. Impact Types

Mechanical effects on aqueous solutions are ubiquitous around us in all spheres of life: household, technology, agriculture, and the pharmacological industry [16,17,18,19]. However, the exact dependence of the effects of mechanical actions on water and aqueous solutions on their characteristics has not yet been determined. The mechanical effects that can be exerted on water, aqueous solutions, and living organisms are quite diverse. They include the following: sinusoidal vibrations [20,21], different mixing modes (turbulent, laminar, etc.) [22,23,24], centrifugation [25], shear stress in constant flow [26], dropping from a height in the form of drops or vials [24,27,28], formation of nanobubbles under pressure, and others [29]. Separately, ultrasound exposure is the subject of research as a potential therapeutic agent [30,31]. In addition, mechanical effects are often used simultaneously with other weak effects, such as weak permanent and alternating magnetic fields, electric fields, and others [32,33,34,35]. Vibration effects have an impact on the physicochemical properties of solutions. Their effects have already found application in practice, in particular, it is used in the technology of preparing vibratory iterations [16,36] and the technology of preparing highly dilute solutions [37,38].

In the present work, we attempted to systematize the available literature data and to identify the general regularities that determine the magnitude of mechanical effects on water, aqueous solutions, and living organisms based on the characteristics of these effects.

Analyzed works can be conditionally divided into works on the study of mechanical effects such as shaking, impact, ultrasonic effects, etc. (Appendix A). In order to evaluate quantitative dependencies of the magnitude of the effects of impacts, we further divided them into two groups: mechanical (vibration) and ultrasonic.

2.2. Effects of Mechanical Influences

According to the objects of study, the analyzed works can be divided into three large groups:

• The whole organism in vivo;
• Cell cultures;
• Aqueous solutions or deionized water.

For this reason, we will use this classification when describing the effects.

2.2.1. Mechanical Impact on Living Systems

Most of the work on in vivo mechanical effects focuses on the cardiovascular, immune, and musculoskeletal systems. The circulatory system can be a target of weak mechanical effects. At the systemic level, whole-body vibration causes an increase in HR and blood pressure [39]. In rodents, it was shown that sinusoidal mechanical vibration reduced the number of capillaries (lectin-positive vessels), venules, and arterioles (α-actin-positive blood vessels) in muscle fibers compared to controls [20]. Another work showed a decrease in vascular lumen under the effect of vibration by increasing the smooth muscle work of microvessels [40]. Micro-damage of endothelial cells (increase in the number of vacuoles, membrane ruptures), as well as damage to the integrity of the inner walls of blood vessels, were found at the cellular-tissue level [41]. Intermittent mechanical impacts, even on isolated body parts, can induce a proinflammatory response in the body, expressed in the activation of NFAT-dependent signaling pathways, increased IL-6 synthesis, and oxidative stress [40,41]. Intermittent jade vibration of isolated limbs increases the activity of total plasma creatine phosphokinase (t-CPK), the excess of which is a marker of tissue damage [42,43]. However, more moderate loads with low acceleration and high total duration can have a positive effect on bone mineralization in humans by reducing TRAP-dependent osteoclast activity [44,45].

In humans, whole-body vibration after 8 days increased plasma concentrations of the osteoporosis markers P1NP and CTx [46,47]. An increase in leg skin temperature has also been reported after vibration impact [46]. In another study on rats with hip implants, an improvement in bone-implant contact was shown [48]. In a rat osteoporosis model, whole-body vibration promoted protection against obesity and increased bone mineralization, and worsened their mechanical characteristics (stiffness, maximum load in vertebra compression test) [28]. The mechanism of the vibration effect involves a decrease in the viability of osteoblasts, a reduction in alkaline phosphatase (ALP) activity, and a decrease in the expression of osteogenesis regulators, including MMP-2 and OSX [28,49,50]. A positive effect of intermittent vibration on muscle strength assessed by apparent mass and mechanical resistance was observed in studies on volunteers [51].

A positive effect of mechanical vibration on human respiratory system functions (peak inspiratory flow rate, inspired volume, and expired volume) has been described [52].

Weak mechanical vibration can also act on the nervous system, in particular, it increases the diameter of myelin fibers in muscles in rabbits [53]. Similar results were obtained in rats, demonstrating an acceleration of regeneration of the injured nerve due to an increase in IGF-I expression [54]. In part of the in vivo studies, the quantitative acceleration-effect or frequency-effect relationship was bell-shaped or reached a plateau after certain values [48].

Shaking can also act on plants in addition to animals. In particular, it has been shown that shaking at an angle of 45° slows seed germination by reducing seedling stem length, number of leaves, basal diameter, and total shoot biomass [55].

The effects of mechanical action (centrifugation, shear stress, vibration) depend largely on the cell lineage and may be opposite for different cell types. Periodic application of centrifugal force (100–200 g centrifugation) to culture stem cells from human exfoliated deciduous teeth inhibited their proliferation [25]. Vibrations altered the proliferation rate of Chinese hamster ovary cells and T cells [56]. The direction of the effect depended on the frequency: at 30 Hz, an increase in proliferation was observed, and at >50 Hz, an inhibition was observed [56]. Sinusoidal vibration causes a dramatic decrease in the viability of fibroblasts [55]. Erythrocytes become more susceptible to lysis under shock shaking [57]. Vibration caused an acceleration of proliferation and differentiation in MC3T3-E1 osteoblast culture [26]. The degree of differentiation was assessed by alkaline phosphatase activity, osteocalcin levels, Runx2, and Osx gene expression [26,58]. Notably, the application of constant shear stress (ductal culturing) did not produce similar results as vibration [26]. Cyclic shear stress (agitation of the medium) also enhanced the differentiation of primary fibrochondrocytes: a number of BrdU-positive cells, ACAN, and SOX9 expression [59]. Vibration increased the proliferation of embryonic cell line GD25 cells and human osteoblast-like cells [60,61]. Vibration also decreased alkaline phosphatase activity in the primary culture of human osteoblast-like cells [60]. Shear stress increases the metabolism of human periodontal ligament cells (hPDLSC), increases the expression and activity of indoleamine 2,3-dioxygenase, cyclooxygenase-2, kynurenine synthesis, TGF-β1 growth factor expression, and decreases the synthesis of the pro-inflammatory cytokine IFN-β [62]. The combination of these latter effects suggests an anti-inflammatory effect of the applied exposure [63]. Vibration stimulated the synthesis of osteoarthritis markers collagen II and aggrecan in pig chondrocytes [64,65]. On the other hand, vibration increased proliferation and protected the MLO-Y4 osteocyte lineage from apoptosis [66]. The molecular mechanisms of the observed effects are decreased expression of RANKL and TNF-α [66].

However, constant shear exposure causes an increase in collagen content in mesenchymal stem cells MSCs [67]. The attenuation of differentiation in pluripotent iPSC stem cells under the influence of vibration has been described [68]. For another type of stem cell (human adipose-derived stem cells, hASCs), an increase in A cytochrome P450 monooxygenase CYP1B1 expression and metabolic activity has been described [69]. The combination of mechanical shaking and weak alternating magnetic fields causes an enhancement of fMLF- and PMA-induced ROS production by mouse granulocytes or ‘neutrophil respiratory burst’ [32,33]. Continuous shear stress can affect the calcium homeostasis of endotheliocytes and induce periodical changes in resting calcium concentration, and alter the characteristics of calcium oscillations on the background of AChR ligand application [70,71].

The application of constant pressure can be considered as a special case of mechanical action [72]. For example, ultrasonic influence can be expressed not only in intensity and frequency but also in the pressure exerted by the ultrasonic wave on the sample [73]. The application of constant pressure of different magnitudes, in the case of cells, can be modeled using substrates with different densities. Growing differentiated dendritic cells on substrates of different densities can alter cell metabolism by reducing the efficiency of glycolysis, lactase activity, and oxygen consumption [72]. In addition, a softer substrate (calculated pressure of 2000 Pa) increased oxygen consumption and gene expression of glycolysis enzymes Hexokinase II (Hk2) and glucose transporter GLUT1 (Slc2a1) compared to the harder standard substrate (calculated pressure of 50,000 Pa) [72]. In addition, cells grown on the harder substrate showed more pronounced immune activity: their immune memory and antitumor activity were improved when injected in vivo into mice with solid tumors [72]. Thus, it can be concluded that the density of the extracellular matrix is one of the potential mechanisms of regulation of immune cell functioning. Water-swelling polymers such as poly(ethylene glycol) (PEG), poly(vinyl alcohol) (PVS), poly(2-hydroxyethyl methacrylate) (PHEMA), and poly(acrylamide) (PAAM) can form elastic hydrogels that can reproduce the basic mechanical characteristics of soft tissues and be used for mechano-mediated regulation of cell function in culture [74,75,76].

The wastewater treatment problem has been relevant since ancient times and is still unsolved. The search for new, cheaper, faster, and more effective methods of wastewater treatment continues [77,78]. Vibration can be applied to increase the efficiency of bioelectrolytic wastewater treatment systems. In particular, constant agitation with nitrogen purging of water has been shown to increase nitrate uptake and sodium removal from wastewater by T. denitrificans bacteria immobilized on the electrode. At the same time, the voltage on the electrodes increased almost 2-fold compared to non-stirred water [79].

A summary of the mechanical impact effects is shown in

Table 1. Effect of mechanical impacts on different levels of living systems.

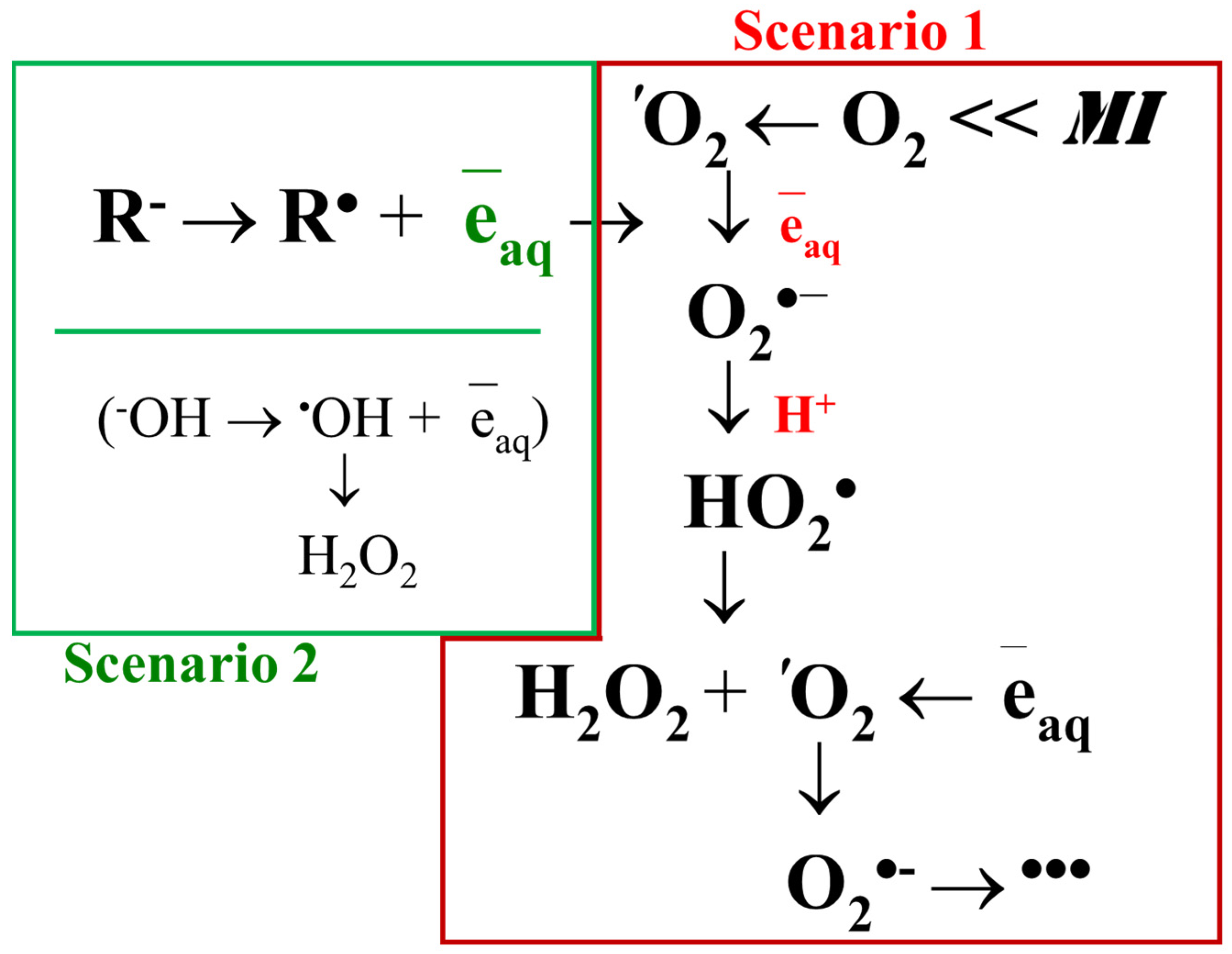
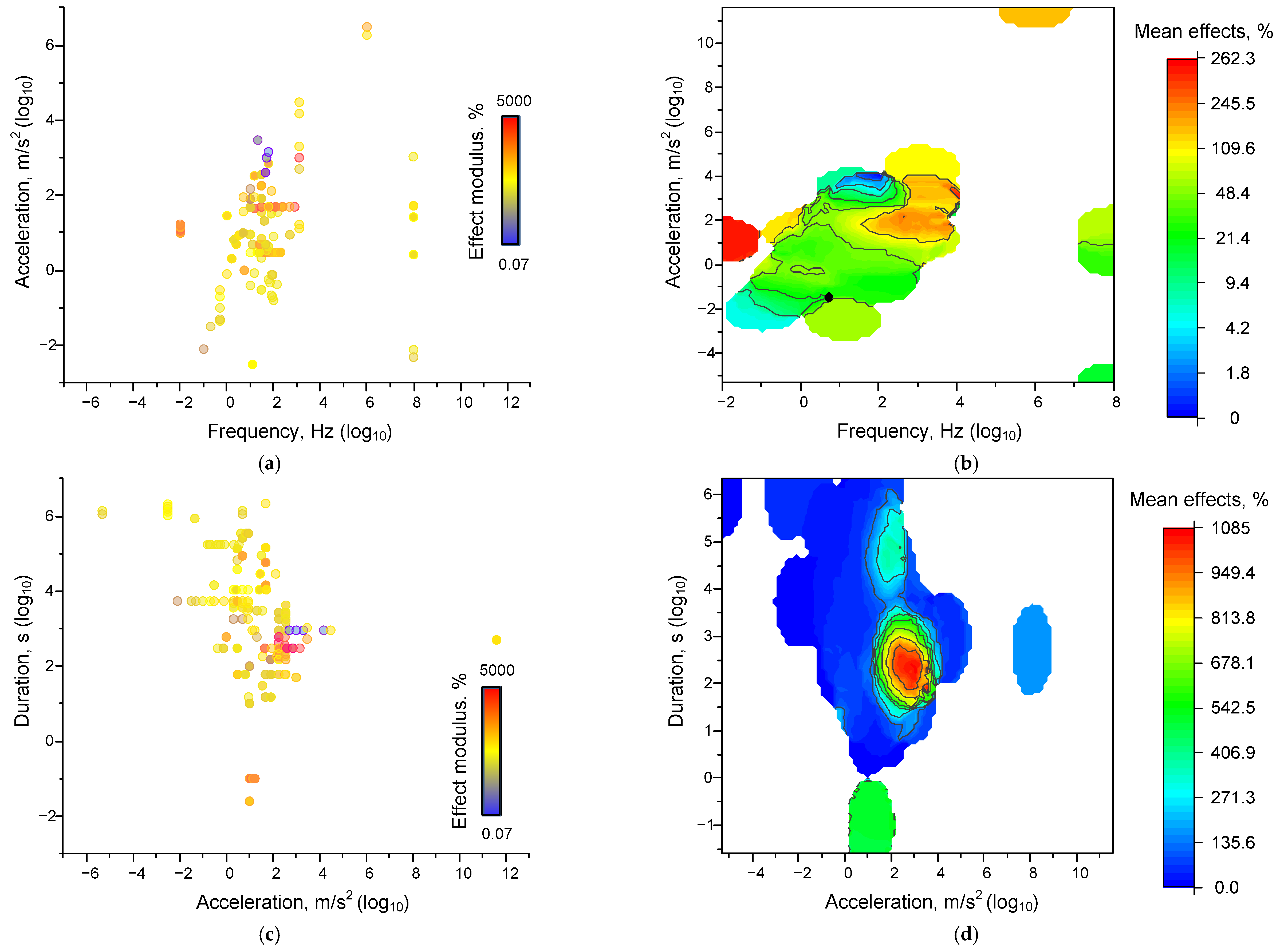
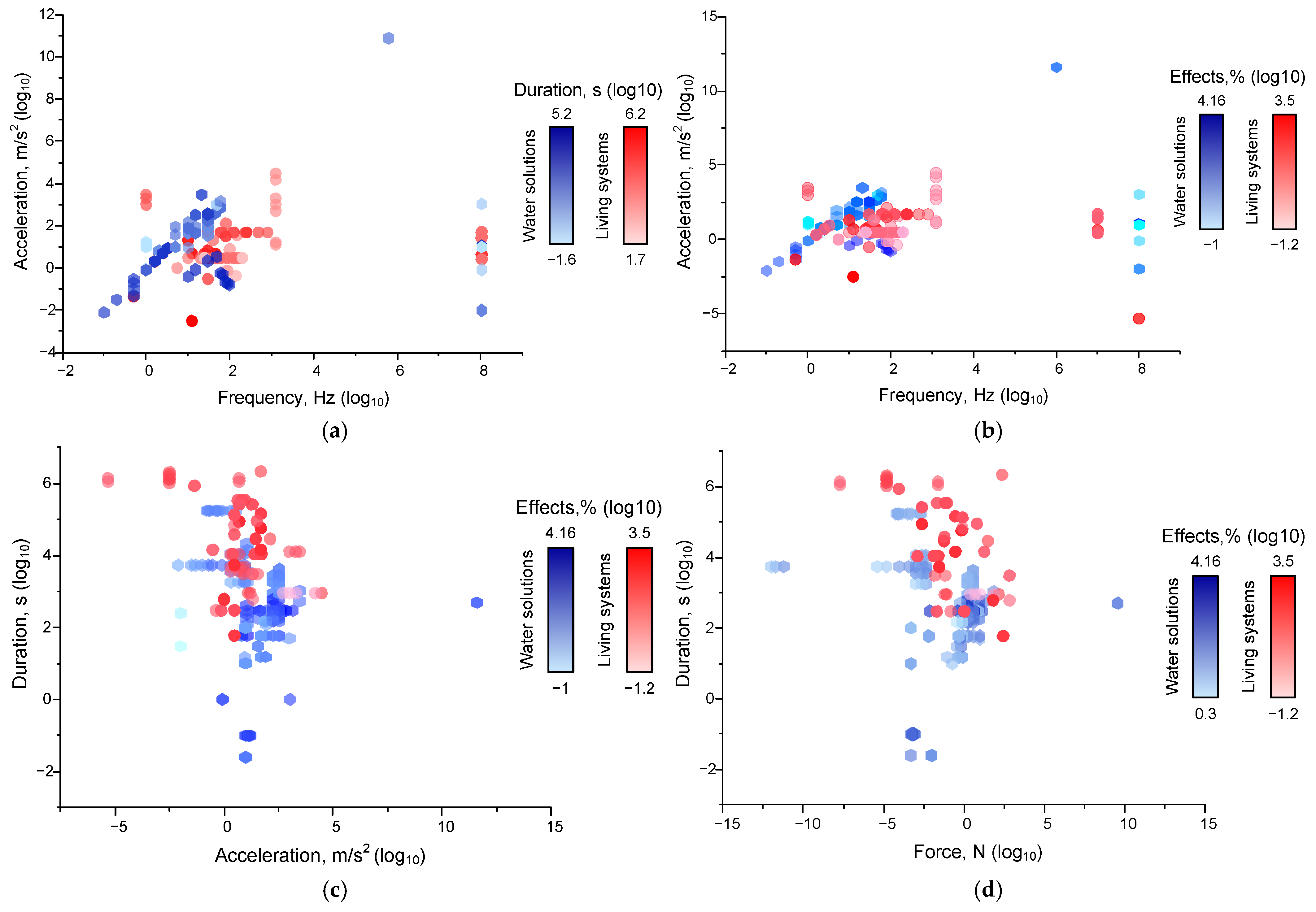
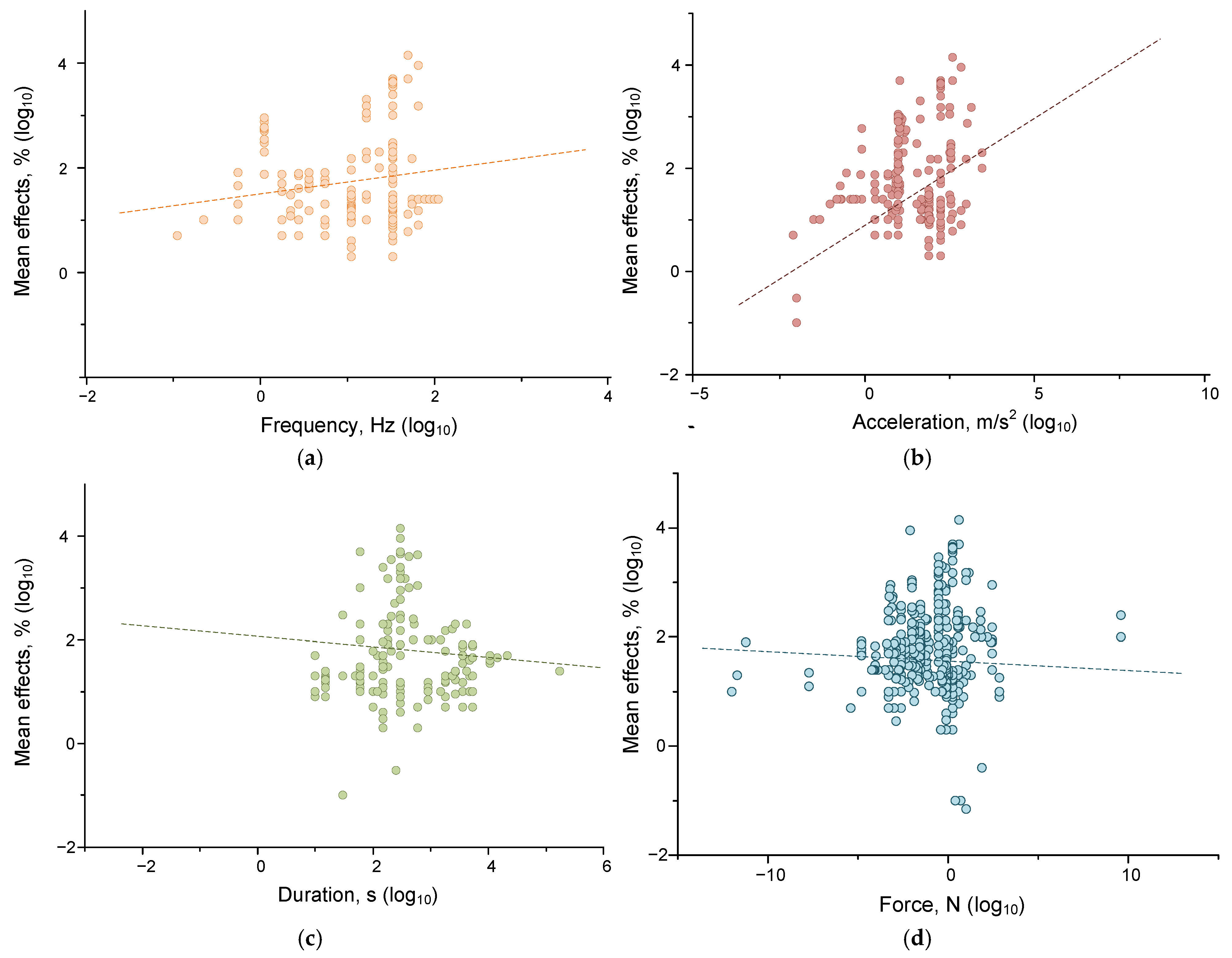
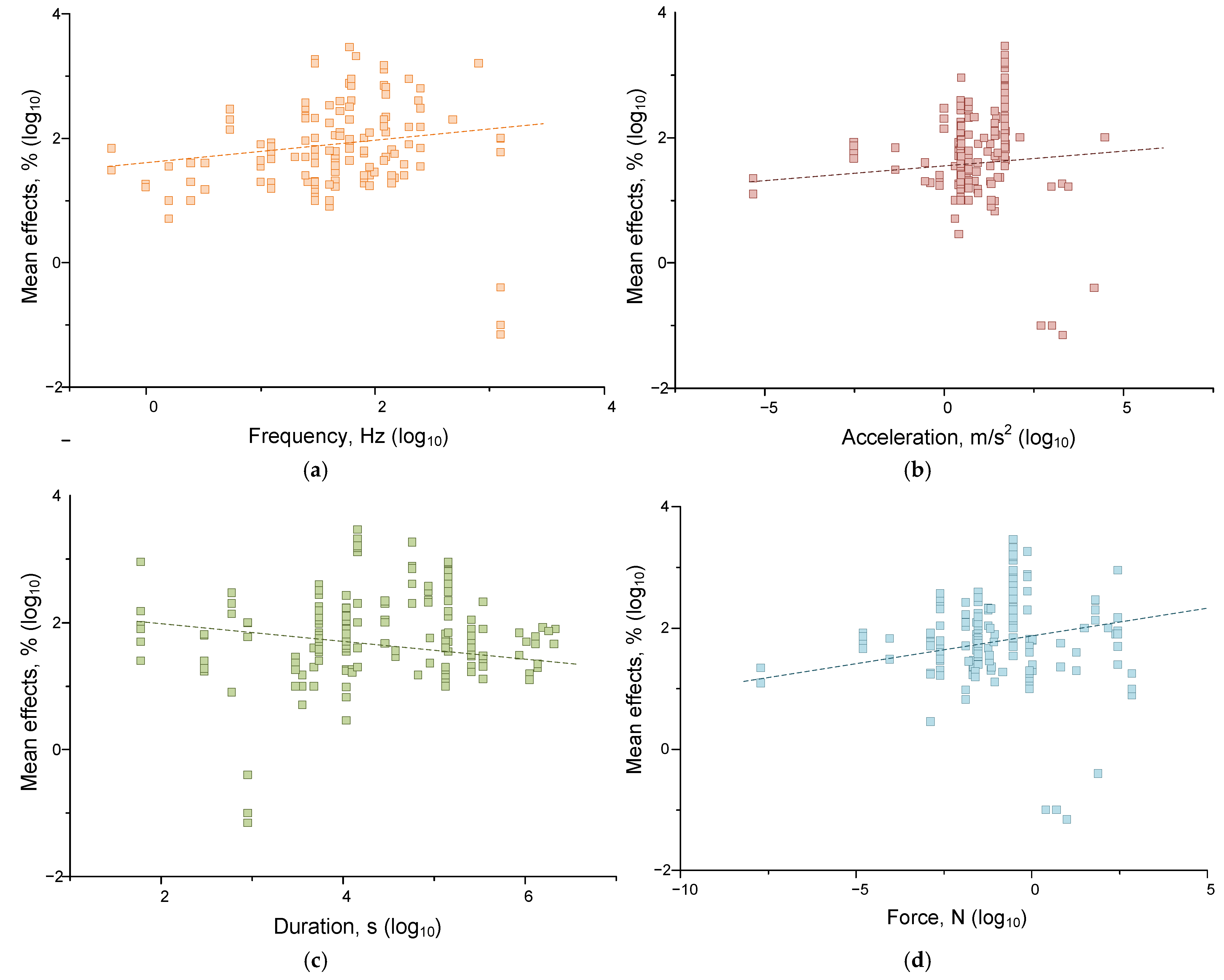
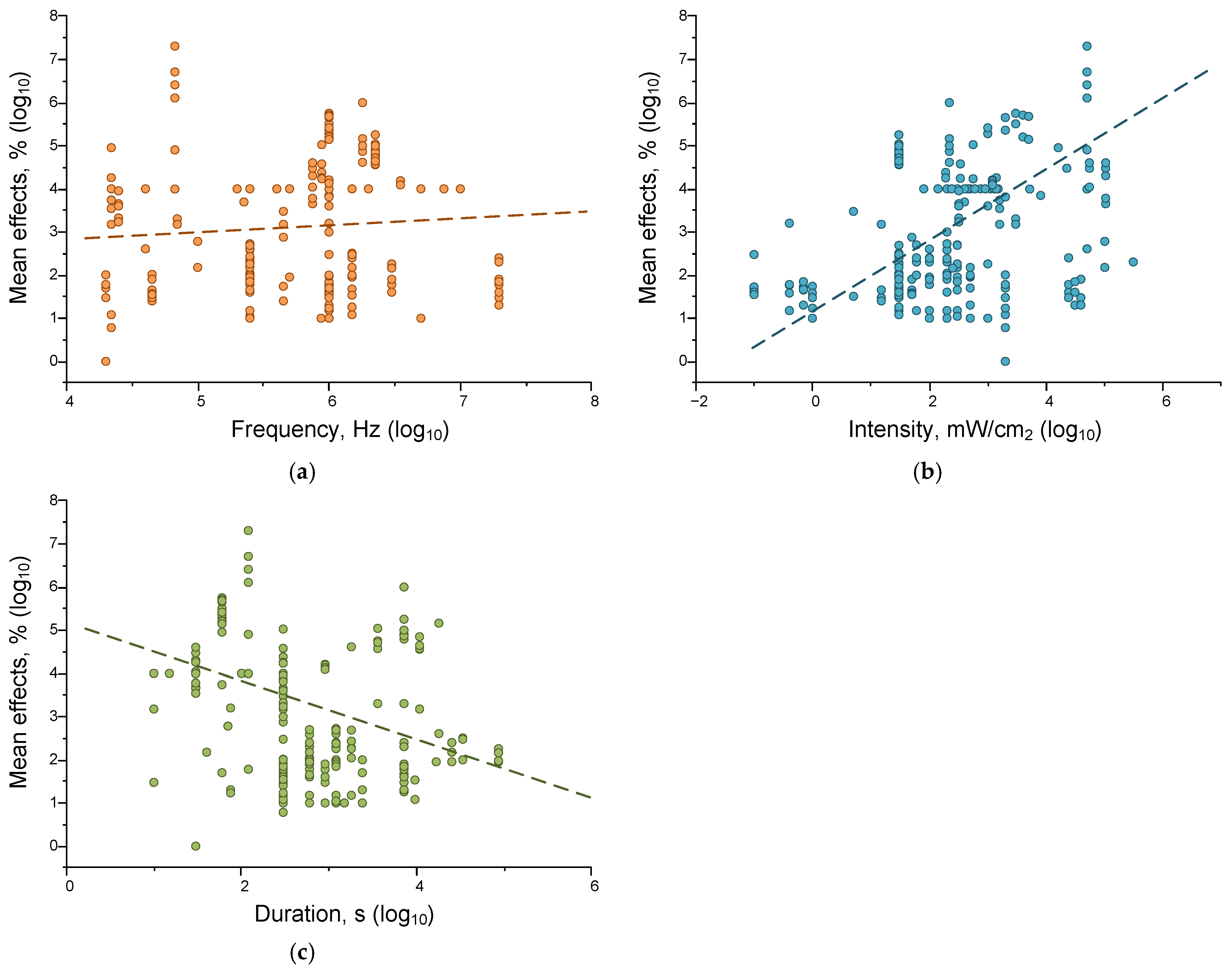
System	Level	Reaction	Benefit	References
Cardiovascular	Molecular	Change Ca2+ responses to AChR ligands	↓ or ↑ depend on conditions	[70,71]
	Cells	Micro-damage of endothelial cells damage	↓	[41]
		Calcium homeostasis of endotheliocytes changes	↑	[70,71]
	Tissues	Number of capillaries, venules, and arterioles reduction	↓	[20]
		Smooth muscle work of microvessels	↑	[40]
	Organisms	HR and blood pressure, Raynaud’s syndrome, etc.	↓	[11,39]
Immune and blood cells	Molecular	NFAT activity, IL-6 synthesis, ROS production, and t-CPK activity increasing	↓	[40,41,42,43]
		Decreasing the synthesis of pro-inflammatory IFN-β, RANKL, and TNF-α, increased oxygen consumption, and gene expression of glycolysis enzymes and transporters (Hk2, GLUT1)	↑	[62,66,72]
	Cells	Erythrocytes hemolysis rate increasing	↓	[57]
		T-cell proliferation altered, ‘neutrophil respiratory burst’ (ROS productions), reduction of differentiated dendritic cell proliferation	↓ or ↑ depend on frequency and conditions	[32,33,56,72]
	Tissues	Immune memory and antitumor activity of dendric cells	↑	[72]
	Organisms	Anti-inflammatory effect	↑	[63]
		Proinflammatory effect	↓ or ↑ depend on conditions	[32,33]
Musculoskeletal	Molecular	TRAP-dependent pathway activation, increasing of ACAN and SOX9 expression, increasing of collagen content	↑	[44,45,59,67]
		P1NP and CTx concentration increase, osteogenesis regulators MMP 2 and OSX expression decreasing. Decreasing of osteocalcin levels, Runx2 and Osx gene expression, synthesis of osteoarthritis markers collagen II and aggrecan	↓	[26,28,46,47,49,50,58,64,65]
	Cells	Osteoclast proliferation, differentiations and activity increasing, increasing of differentiation of primary fibro chondrocytes	↑	[26,44,45,59,60,61]
		The viability of osteoblasts decreases; decrease of osteoblast differentiation	↓	[26,58]
	Tissues	Improving bone mechanical characteristics and bone structure	↑	[28,44,45]
		Bone tissue damage	↓	[42,43]
	Organisms	Osteoporosis markers P1NP and CTx levels	↓	[46,47]
		Improvement bone-implant contact, obesity decreasing, and muscle strength increasing	↑	[28,48,51]
Respiratory	Organisms	Inspiratory flow rate, inspired volume, and expired volume	↑	[52]
Nervous	Molecular	Increasing the expression of the IGF-I factor	↑	[54]
	Cells	Improve of myelinization	↑	[53]
Other	Molecular	Increasing in A cytochrome P450 monooxygenase CYP1B1 expression and metabolic activity changes	↑	[69]
	Cells	Stem cell proliferation inhibition	↓	[25]

↑ and ↓ indicate possible positive or negative effects on organisms, respectively.

.

2.2.2. Mechanical Impact on Water Solution

Mechanical effects on aqueous solutions include shaking, tumbling, and high-pressure blowing (formation of microbubbles). Mechanical shaking of pure water at 30 Hz also changed the pH to 0.6 pH units [80]. The effect may seem small, but it must be recalled that physiological pH in a living organism is actively maintained within narrow limits. For example, a deviation of blood pH by a fraction of a unit from the normal range of 7.35–7.45 can lead to dangerous conditions such as acidosis or alkalosis [81].

Water stirring also enhances the absorption of water in the terahertz region 140–230 cm⁻¹ [82] and changes the characteristics of water fluorescence in the UV region: the absorption maximum shifts from 250 nm to 340 nm and the emission maximum from 270 to 330 nm [83]. The fluorescence intensity increases ~5 times [83]. Prolonged (several hours) shaking changes the spectral parameters of water in the UV region. Fluorescence increases at a wavelength of 255 nm, and light scattering increases at a wavelength of 355 nm [83].

Vertical mechanical shaking or agitation causes the generation of hydrogen peroxide H₂O₂, singlet oxygen, and OH-radicals in pure water [80,84,85]. It is noteworthy that the amount of ROS generated is positively dependent on the frequency, amplitude, and duration of vibration impact [86]. The type of agitation affects the efficiency of ROS generation: turbulent agitation causes the generation of ~10 times more ROS than laminar agitation [85]. However, it is worth noting that under the conditions studied by the authors (frequency 10–30 Hz, amplitude 1 cm), the concentration of ROS is very small (tens of nM), which is less than the described concentrations exerting biological effects [87,88]. The falling of deionized water drops on a solid surface also causes the generation of H₂O₂, and OH-radicals in water, the concentration of which grows in proportion to the height from which the drop fell [27]. High-frequency mechanical vibration of water coated with a layer of oil increased its redox potential by 2.5 times compared to untreated samples [89].

Mechanical impact changes not only the properties of water, but aqueous solutions too (both one-substance solutions and complex mixtures). Circular agitation of an aqueous solution of interferon-gamma (IFNγ) increases its electrical conductivity compared to an unagitated solution [34]. Vertical shaking at frequencies of 10–50 Hz of deionized water causes an increase in its spontaneous chemiluminescence for at least the next 15 min [21]. The addition of 1 mg/mL of BSA protein to the water cancels the effects of mechanical action on the water [21]. Circular agitation of an aqueous solution of polyclonal antibody to IFNγ enhances the luminescence of the solution [16]. A series of impacts also causes luminescence enhancement of aqueous solutions of carbohydrates, using lactose as an example [17]. Vertical shaking of an aqueous solution of human immunoglobulin causes the generation of ~200 nm nanobubbles [23,90]. At the same time, the concentration of molecular oxygen in water and water temperature (by a fraction of a percent) increased [80]. The magnitudes of the effects were proportional to the frequency of shaking.

Dropping of vials with aqueous buffer solutions of anti-antistreptavidin IgG1 enhances protein aggregation as assessed by the number of suspended particles and separation of proteins from the walls after treatment with urea and guanidine hydrochloride [24,91]. Shaking even with small amplitudes (less than 0.1 mm) and frequencies (10 Hz) retarded protein crystallization using chicken egg lysozyme in a buffer solution, for example [92]. The change in flow rate affects the precipitation of lysozyme after treatment with a high concentration of NaCl [93], indicating possible conformational changes of the protein molecule, and could potentially be applied in protein production technology.

The method of solution stirring can change the geometric characteristics of crystals formed during the evaporation of aqueous extracts of medicinal plants [22]. Turbulent mixing produces less ordered and more heterogeneous crystals, while circular mixing produces more ordered structures (having less lacunarity and entropy) with more pronounced fractal properties [22]. Serial impacts alter the shape of crystals formed from plant and inorganic components during the evaporation of aqueous extracts of echinacea, baptisia, and luffa [23].

Microfluidic agitation can also be considered a variant of mechanical action. It has been shown that microfluidic mixing of a solution of acetate of europium (AcEu) causes a change in its Raman spectra in the region of 1360–1770 cm⁻¹, in particular increasing the intensity of the OH groups’ stretching vibrations peak [94]. The stretching of a column of an aqueous solution of hydrogel precursors between two sites affects the spatial structure of the synthesized hydrogel. By varying the tension alone, a controlled (including mathematically predicted) change in the net structure of the final polymer can be achieved [95].

Passing deionized water through a nozzle at high speed causes the creation of water nanodroplets that contain hydrogen peroxide. The size of the microdroplets determined the concentration of hydrogen peroxide that was generated in them. The smaller the microdroplet, the greater the concentration of hydrogen peroxide. It is noteworthy that degassing water by nitrogen purging did not cause a significant decrease in hydrogen peroxide generation in the microdroplets compared to the control. Hence, the process may occur without the involvement of oxygen [90]. The creation of microdroplets can be one of the ways to catalyze chemical reactions. In particular, when microdroplets of aqueous solution of substrates of the Pomeranz-Fritsch reaction are squeezed together under accelerated nitrogen purging, the reaction rate can be increased by 5–7 times compared to the reaction rate in the control solution [29]. The combination of mechanical and electrical effects can weakly change the volt-ampere characteristics of solutions of organic and inorganic mercury compounds [35]. Stirring of the solution can also be attributed to mechanical effects. Stirring of water creates nanobubbles in it, the number of which is proportional to the duration of stirring [96].

2.3. Ultrasound Impact

Works on the ultrasound (US) impact on living systems are usually represented by studies on cell lines and aqueous solutions [95]. The influence of ultrasound on living organisms is investigated by the new field of sonobiology [96]. We will combine in vivo and in vitro results in one section when discussing the effects.

2.3.1. US Impact on Living Systems

Periodic US exposure promoted more effective tissue regeneration in rats with a model of muscle injury (transection), which was estimated by total protein mass and muscle fiber diameter due to increased myocyte proliferation [97,98]. The US may also accelerate drug delivery in eye tissues [99]. It was demonstrated that exposure to ultrasound at a frequency of 1 MHz and an intensity greater than 8 W/cm² disrupted the ER structure. Immediately after exposure, disruption to the ER microstructure was observed in all the cells studied, and after three and 24 h, recovery of the ER was observed in 16% and 26% of cells, respectively [100]. The effect of ultrasound depends on the organism’s taxonomic classification. For example, ultrasound did not affect Vicia faba root meristem cells at a frequency of 1.1 MHz and 8 mW/cm² [101], whereas animal cells showed effects at lower frequencies and intensities.

The works on the influence of the US on cell proliferation and differentiation are quite numerous. There are data on the effect on the primary culture of human fibroblasts, human amnion-derived mesenchymal stem cells (hAD-MSC), and murine myoblasts C2C12 [102,103,104]. Ultrasound causes the acceleration of human fibroblasts’ proliferation, increased expression of collagen, and secretion of proinflammatory cytokines IL-1β and IL-8 [102]. The regulation of proliferation occurs with the participation of EGFb regulatory factors [102,105]. Ultrasound enhances the secretion of angiogenesis stimulator VEGF by fibroblasts, which may indicate the ability of the US to enhance angiogenesis in tissues [102,106]. The effect is slightly dependent on the intensity and, to a lesser extent, on the US frequency [102]. Ultrasound enhances the differentiation and division rate of hAD-MSC stem cells by increasing protein synthesis of the cell cycle regulators Cyclin D1/β, Cyclin B1/β, Cyclin E1/β, and Cyclin A1/β [103]. Since the concentrations of all four forms of Cyclins were increased, it can be concluded that US affects beyond the G1, G2, and M stages of the cell cycle [107]. In terms of blood cells, the following were recorded in the US: induction of Ca²⁺ influx and platelet aggregation; induction of apoptosis in the HL-60 and U937 leukocyte cell lines; hemolysis of erythrocytes; and an increase in the number of chromosomal aberrations in whole blood cells [108,109,110,111]. Ultrasound with a frequency of over 5 MHz can alter the spatial orientation of platelets [112].

Ultrasound almost doubled the rate of division of mouse myoblast culture and bovine aortic endothelial cells, and promoted differentiation, expressed as an increase in the length of myotubes and the number of cells fused into one myotube, and regeneration of myofibrils [104,113,114]. At the molecular level, the expression of myogenin, Pax7, COX2, and the inhibition of pro-inflammatory reactions were observed [113,115]. The action of the US on neuronal cells accelerates the differentiation, assessed by the expression of markers Alk, Cenpf, and Pcdh17, as well as the expression of actin involved in the formation of outgrowths [116].

The US destroys bacterial spores and cells, and induces DNA release from them [117,118]. The US also accelerates DNA plasmid transfer in bacterial cultures [119]. The US inhibits plant photosynthesis [120]. A summary of US impacts on living systems is shown in

Table 2. Effect of US impacts on different levels of living systems.

System	Level	Reaction	Benefit	References
Cardiovascular	Molecular	Enhancing VEGF secretion	↑	[102]
	Tissues	Enhance angiogenesis		[102,106]
Immune and blood cells	Molecular	Secretion of proinflammatory cytokines IL-1β, IL-8	↑	[102]
		Increasing the number of chromosomal aberrations	↓	[111]
	Cells	Induction of Ca2+ influx and platelet aggregation; induction of apoptosis of leucocyte cells	↓	[108,109,110,111,112]
	Organisms	inhibition of pro-inflammatory reactions	↑ or ↓ depend on situation	[113,115]
Musculoskeletal	Molecular	Increased expression of collagen, expression of myogenin, Pax7, COX2	↑	[102,113,115]
	Cells	Increasing of myocyte proliferation, myoblast differentiation	↑	[97,98,104]
	Tissues	Increasing of length of myotubes and the number of cells fused into one myotube, and regeneration of myofibrils	↑	[97,98,104,113,114]
Nervous	Molecular	Enhanced expression of markers Alk, Cenpf, Pcdh17 and actin	↑	[116]
	Cells	Promotions of proliferation and differentiation of neurons, formation of outgrowths	↑	[116]
Other	Molecular	Acceleration of drug delivery, EGFb regulatory factor expression increasing, change Cyclin D1/β, Cyclin B1/β, Cyclin E1/β, and Cyclin A1/β levels	↑	[99,102,103,105]
		Accelerate DNA plasmid transfer in bacterial cells	↑	[119]
		Plants photosynthesis inhibition	↓	[120]
	Cells	ER microstructure damage	↓	[100]
		Stem cell differentiation and proliferation increasing	↑	[102,103,104,107]
		Destruction of bacterial spores and cells	↓	[117,118]

↑ and ↓ indicate possible positive or negative effects on organisms, respectively.

.

2.3.2. US Impact on Water Solutions

The ultrasonic treatment of deionized and artesian water changes its pH by 0.3–0.6 and 0.5–1.05 pH units, respectively [121]. At the same time, the US treatment causes acidification of deionized water and alkalization of artesian water, indicating the role of dissolved salts in the effect of ultrasonic treatment on water pH [121]. US treatment promotes accelerated crystallization of HEWL in acetate buffer [93]. Currently, approaches are being developed for the practical application of the US in accelerating the precipitation of soya proteins in biotechnological processes [122,123]. In addition to proteins, ultrasonics accelerate the precipitation of clay particles in aqueous colloids [124]. Increasing the duration of the US treatment favors faster precipitation. Methods for accelerating precipitation using ultrasonics have also found applications in other fields, such as nanoparticle synthesis [4,125]. The US can catalyze H₂O₂ generation reactions in water in the presence of solid catalysts (Bi₃TiNbO₉) [126]. Currently, there is a problem of finding a cheaper and safer method of hydrogen peroxide synthesis than the currently used anthraquinone process [127], so the use of US and solid catalysts for this purpose seems reasonable.

3. Mechanisms of the Mechanical Impact Effects

3.1. Receptor Response of Living Systems. Mechanotransduction

Mechanotransduction is a group of processes of signal conversion from receptor structures of cells into molecular and biochemical responses of cells [128,129,130]. Mechanotransduction involves millisecond processes of the response of sensitive molecules and structures (usually receptors) and triggering of signaling pathways (changes in transcriptional activity, auto- and paracrine regulation), which further determine the fate of cells and the organism as a whole [31]. Mechanotransduction events can be conditionally divided into three main stages: mechanosensing, mechanotransmission, and mechanoresponse. Classically, these processes appear to be sequential; however, parallel and cyclic processes are possible [131,132,133].

The first stage includes receptor perception of a mechanical stimulus due to changes in the conformation of receptor proteins. Mechanosensing can occur passively in either an outside-in or an inside-out way. Outside-in scheme realized through events: “external force → change of protein structure → signal transduction”.

When implementing the inside-out mechanism, two modes are possible:

• “elements of cytoskeleton → creation of internal force on the mechanoreceptor from the intracellular matrix → activation of mechanoreceptor → detection of changes in the extracellular matrix under external mechanical stimulation” (inside out).
• “absence of internal force on the mechanoreceptor from the intracellular matrix → inhibition of mechanoreceptor → inhibition of detection of changes in the extracellular matrix under external mechanical stimulation”

The advantage of the first pathway is the ability of the cell to respond to mechanical stimuli at any time (excluding refractoriness). The advantage of the second method is the possibility for selective “on/off” mechanosensitivity by the cell [128].

Examples of outside-in receptors are TRP receptors (TRPV1, TRPV2, TRPV4, etc.), which can open directly upon mechanical membrane deformation or open indirectly via a phospholipase A2 (PLA2)-dependent pathway [134,135]. Nuclear proteins associated with cytoskeleton proteins transmit mechanical stress to the nuclear apparatus and alter the transcriptional activity of the cell. For example, LINC (Linker of Nucleoskeleton and Cytoskeleton) complexes include a group of protein INM on the inner nuclear membrane, SUN1 and SUN2 proteins in the nuclear envelope lumen and outer nuclear membrane, and KASH proteins on the outer side of the outer nuclear membrane [136]. KASH protein mediates interactions with actin cables through Nesprin 2. A-type and B-type lamins are also involved in mechanoreception through the spatial reorganization of chromosomes [137,138,139]. Some subtypes of K⁺ channels, K2P and ASIC families, can also respond to mechanical stress [140,141,142,143]. Different ASIC subtypes can act as primary mechanosensing receptors (ASIC1a, ASIC1b) or modulate and regulate the pain pathway and nociception as a special case of mechanoreception (ASIC2 and ASIC3) [14,144,145,146].

The inside-out system consists of actin, talin, myosin II, vinculin, and integrin proteins bound in the extracellular matrix from the fibrillar proteins surrounding the cell [147,148].

It is worth noting that many receptor structures and ensembles are capable of operating in both modes. In particular, FA (focal adhesions)-proteins, membrane G-protein coupled receptors (GPCRs), dense intercellular AJs contacts (adherens junctions), and most of the stress-activated channels (SACs) [21,74,75,76,128,131,132,133,134,135,137,138,139,147,148,149,150,151,152,153,154,155,156,157,158]. Therefore, the division into inside-out and outside-in is more valid for how a particular response of the same structure is regulated than for a specific structure.

SACs include numerous ion channels of varying degrees of specificity belonging to the K2P potassium channel (TREK-1, TREK-2), DEG-ENa-ASIC, TRP, and piezo channel families [142,143,159,160,161]. There are two models of regulation of ion channel opening under the action of mechanical load: “force-from-lipid” and “force-from-filament”. According to the first “force-from-lipid” model, the response to mechanical stimulation follows the scheme: external force → reorganization of the lipid environment of receptors → conformational changes of the receptor → opening/closing of the channel or another way of signal transduction [149,154,157]. According to the second model, ion channels, such as part of SACs, are physically bound to proteins of the cytoskeleton and/or extracellular matrix. In this case, the channel opening scheme would be as follows: external force → tension changes of the extracellular or intracellular matrix → conformational change of the channel. It is assumed that changes in the tension of the cell matrix cause reorganization of membrane lipids. The latter further facilitates signal transmission from an open channel to a still closed channel [151,152]. Thus, signal transduction from an open mechanosensitive channel to long distances along the membrane can be achieved.

Further signal transduction (mechanotransmission and mechanoresponse steps) can occur through several signaling pathways. It is noteworthy that the type of receptors involved and the further signal transduction pathway are determined by the type of acting mechanical action [31]. The whole variety of mechanical impacts on the cellular level is finally reduced to compression, tension, shear, and their combinations.

Cell compression is perceived by receptors from the integrin families, piezo channels, and TRP- and FA-receptors that trigger Wnt/β- and YAP/TAZ-dependent signaling pathways [162,163,164,165]. Tension is perceived by a similar set of receptors (integrins, TRPs, FAs) with additional cytoskeletal involvement. However, the signaling pathways triggered are different and include Rho-ROCK, MAPK, and ERK kinase cascades [166,167]. Shift (shear stress) is recognized by a wider range of receptors than compression and tension. A shift-sensing system including GPCRs, tyrosine kinase receptors, lipid rafts, gap junctions, and cell contacts, triggering both Wnt/β-dependent and kinase signaling pathways (Rho-ROCK, MAPK ERK) [168,169,170,171,172,173,174,175,176].

Mechanotransduction during US treatment should be separately mentioned. The main acting factor in this case is the shock wave formed by the cavitation of microbubbles [168]. Acoustic stimulation activates TRPs, piezo channels, and cell contact areas. Signaling pathways include cascades involving Rho-ROCK, MAPK, ERK, Wnt, ESCRT, Epac-Rap, YAP, and PI3K/Akt [177]. The reader can learn more about each of these signaling pathways in the cited reviews. Another mechanism involves action on cell membrane lipids [178].

3.2. ROS Generation in Water Solutions

Water is subjected to mechanical action, not only by human will, but also by nature. For example, when water droplets fall on a solid surface during a rainstorm or when water falls from a waterfall. In this case, physicochemical parameters such as concentration of dissolved gases, hydrogen index, temperature, electrical conductivity [179], redox potential [89], and light scattering spectra in the near-ultraviolet region [83] change in water. Changes in some physicochemical properties of water after mechanical impact can persist for up to several days [180]. It has been found that mechanical impact leads to the formation of reactive oxygen species (ROS) [27]. ROS are extremely reactive compounds that, on the one hand, can damage biological macromolecules [181] and, on the other hand, play an important signaling and regulatory role in biological systems [182]. Of all ROSs, only hydrogen peroxide is a stable molecule. The other ROS species have short lifetimes [183]. This allows hydrogen peroxide to accumulate in the medium under prolonged exposure, which facilitates detection and allows us to work with large concentrations. In this connection, most of the works most often investigate the effect of a particular low-intensity physical factor on hydrogen peroxide generation. The generation of hydrogen peroxide under mechanical action seems to occur according to two main scenarios:

• Activation of oxygen molecules dissolved in water;
• Dissociation of water molecules and hydroxyl anions.

The first scenario is related to the activation of molecular oxygen (Figure 1). It has been shown that under mechanical action, a part of the molecules of dissolved oxygen in water change from a triplet to a singlet state [184]. It is assumed that the transition of oxygen molecules from the triplet state to the singlet state occurs due to the impacts of dipoles [185]; it is also assumed that a local magnetic field can be generated under mechanical action, affecting the triplet-singlet transition [186]. More detailed views on the processes occurring with oxygen molecules dissolved in water under mechanical action can be found in studies [86,187,188]. Experimental validation of scenario 1 and its detailed discussions in studies [80,179]. The mechanical-induced generation of singlet oxygen in water was proofed by inhibitory analysis with sodium azide, NaN₃ (singlet oxygen quencher). NaN₃ inhibits mechanically induced ROS production (measured by luminol-dependent chemiluminescence) by 30%. These data indicate that singlet oxygen is involved in the generation of hydrogen peroxide during mechanical stress (30 Hz, 5 mm amplitude, 5 min) [80].

Singlet oxygen is further reduced to superoxide anion radical, which is protonated to hydroperoxide radical. The dismutation of hydroperoxide radicals produces hydrogen peroxide and molecular oxygen, in some cases in the singlet state; the cycle is closed. A similar scenario is observed in the generation of hydrogen peroxide upon exposure to visible radiation [189], infrared radiation [190], and heat [191]. The chemical transformations of ROS characteristic of this scenario are described in detail [192].

The second scenario is related to the oxidation of hydroxyl anions and/or the dissociation of water molecules. The possibility of the existence of such a process was theoretically predicted almost half a century ago [193]. This prediction has been criticized in terms of the energetics of the process [194]. It is believed that a quantum with an energy of about 5 eV is required to break the O-H bond in a water molecule [195]. The formation of hydroxyl radicals from water molecules has been observed under the action of ionizing radiation [196], plasma [197], and other high-energy effects, for example, during the optical breakdown of water [198]. In general, the scientific community was rather skeptical about the information concerning the generation of hydroxyl radicals from hydroxyl anion or water molecules under ‘weak’ non-ionizing effects, including mechanical ones, until the publication of theoretical works by Prof. Nowakowka’s group [199] and others. Five years ago, the phenomenon of hydroxyl radical generation under mechanical action was brilliantly experimentally confirmed by the example of the generation of micron-sized water droplets [90]. Today, it is assumed that the oxidation of hydroxyl anions is based on the mechanism of asymmetric charge of water droplets. When water is atomized, charged microdroplets are formed carrying excessive amounts of their own OH⁻ or H⁺ ions, which repel each other towards the droplet surface. The formation of ROS is attributed to limited hydration at the water-air phase interface [200]. It is assumed that both of the described scenarios occur in parallel during mechanical action in water. The efficiency of ROS generation in the first or second scenario mainly depends on such parameters as the frequency and amplitude of impact, conditions for the generation of micron-sized droplets during impact, and the concentration of molecular oxygen dissolved in water.

4. Dependence of the Magnitude of the Effects of Mechanical Impacts on Their Characteristics

4.1. Mechanical Influence

4.1.1. Principal Conditions of Realisation of Effects

In the first stage, we evaluated the principal limits of the characteristics of the described mechanical effects. m/s²), and Characteristics we chose: frequency of vibration (Hz), acceleration that the sample acquires (sum duration of impact (s). Impact times, if expressed in hours or minutes, were converted to seconds. If periodic incubation was described (e.g., 5 times 100 s), the sum of the times was calculated and expressed in seconds (e.g., 500 s). Acceleration values were taken as initial values given in publications, or acceleration was calculated as the second derivative of the coordinates using the formula:

$$x(t)=A\sin (2\pi ft),$$

(1)

$$x^{″}(t)=-4A{\pi }^2{f}^2\sin (2\pi ft)$$

(2)

$${x^{″}}_{\max }=4A{\pi }^2{f}^2$$

(3)

where x(t) is the sample coordinate, f is the frequency, A is the oscillation amplitude, and x’’_max is the maximum acceleration.

Frequency in cases of expression in rpm, etc., was converted into Hz. In this case, to determine the specified limits, we constructed three-dimensional distributions. It can be seen that the boundaries of applied frequencies, accelerations, and durations are quite strictly localized (Figure 2). Most effects were registered at frequencies from 0.01 to 500 Hz and at accelerations from 0.01 to 1000 m/s². The duration of exposure required to achieve the effects increased as both frequency and acceleration decreased. Consequently, the effects of mechanical influence are realized when a certain “threshold” of transferred kinetic energy is overcome. This threshold is determined simultaneously by all three components: frequency, acceleration, and duration. At the same time, the values are partially interchangeable: low values of frequency and acceleration can be compensated by high duration and vice versa. Please note that Figure 2 shows not the magnitudes of the effects, but the threshold values of frequency, amplitude, and duration at which any effects were observed (taken as an “all-or-nothing” response). The quantitative values of the effects are already presented in the following figures.

4.1.2. Dependences of Mechanical Effects on the Combination of Factors

The articles analyzed assessed a wide variety of effects of mechanical exposure: from the concentration of ROS and inorganic ions to the fraction of differentiated cells and apparent human muscle strength [26,51,79,86,104]. All values are expected to have different units of measurement. Thus, it is not possible to directly compare the data obtained in different articles. For this reason, we have converted all data into dimensionless quantities: effects were expressed as a percentage of the control values. The effect of mechanical influence can be expressed both as an increase in the value of any arbitrarily chosen parameter (e.g., an increase in cell proliferation) and a decrease (a slowdown in cell proliferation). Since we are not interested in the direction but numerically in the magnitude of the treatment facilitation effect, we decided to take all calculated percentages modulo the magnitude. We will hereafter refer to the resulting values as “relative effect moduli” or simply “effects”.

To estimate quantitative dependencies, we applied the approach we used and described earlier [201]. To assess the influence of the combination of conditions, we constructed dot plots in 3 axes. Further, we will denote the axes under consideration in the following order: “ordinate axis—abscissa axis—z (colirbar) axis”.

We evaluated the dependence of the magnitude of the effects of mechanical influence. The magnitude of the moduli of the relative effects of mechanical influence was weakly dependent on the frequency, acceleration, and duration of the influence. The most obvious dependence was found for the “acceleration-duration-effect” dependence (Figure 3c,d). We can see a clear enough boundary of acceleration and duration values, below which the effects of mechanical influence cease to be realized, which confirms the observed “threshold” effect described above. For the set of “frequency-acceleration-effect” characteristics, the dependence takes an unobvious form (Figure 3a,b). The separation into regions of 0.001–1 Hz and above 1 Hz is visible. In the first region, the effects are registered relatively rarely. In the second region, most of the effects are registered. There is a general tendency for the magnitudes of mechanical effects to increase with increasing acceleration and/or frequency. However, the magnitudes of the effects depend on the values of acceleration and frequency, not monotonically. The region between frequencies of 10–100 Hz and accelerations of 10–50 m/s², at which the magnitudes of the effect moduli are the largest, can be seen. In the investigated works, there are often additional factors that are difficult to take into account (sample mass, laboratory temperature, and other microclimate features). In order to minimize the contribution of extraneous factors, we have attempted to calculate the force of the mechanical effect using the standard formula:

$$\mathit{F}=\mathit{m}\mathit{a},$$

(4)

where F is the force acting on the sample, m and a are the mass and the acceleration of the sample, respectively (taken from published papers or calculated from published data).

In the case of studies where the mass of the sample was clearly described, the values given by the authors were used. If the volumes of aqueous solutions studied were described, the assumption was made that m ≈ V, since the density of water under standard conditions is 0.99707 g/cm³. If “whole body mass” was specified in the in vivo experiments, the average mass of the animals or volunteer subjects specified in the paper was taken as mass. If the study was performed on an isolated limb or tail of the animal, the literature data on the mass of the indicated body parts were used [202,203].

We found that the shape of the dependence of the magnitude of the effect of mechanical impact on the combination of force and duration (Figure 3d,e) is similar to the shape of the acceleration-duration-effect relationship, but the point cloud is more widely distributed.

The increase in the “spread” of the dots indicates the dependence of the magnitude of the mechanical action on the mass of the sample, which determines the acceleration threshold required to achieve a certain value of acceleration. It is noteworthy that we found inhomogeneously distributed maxima of the effect moduli values within the force ranges from 0.0001 to 1000 N and from 1 s to several days. The presence of well-defined regions of frequency and acceleration values at which the effects are observed is consistent with the data of mathematical modeling and the theory of potential energy surfaces [204]. The form of the double force-duration or acceleration-duration dependence is similar to the previously described dependence obtained during the action of shear stress on non-neurons and myoblasts [153,155].

At the next stage, we attempted to answer the question: are there any fundamental differences between the magnitudes of the effects of mechanical influence from its characteristics, estimated earlier, for living and nonliving systems? For this purpose, we divided the data we analyzed into two groups. For the division, we used the classical paradigm of biology that the cell is the basic structural and functional unit of all life forms, and the manifestation of all the properties of living things begins at the level of the whole cell [205]. In the first group, we referred to the literature data on non-living systems: purified water, buffer solutions, isolated proteins in aqueous solutions, solutions of monomers in water, etc. The results on living systems included data obtained on cell lines, animals, and humans (Figure 4).

The threshold limits for non-living systems are broader than for living systems (Figure 4a) and are shifted to lower frequencies and accelerations. This is partly due to methodological limitations that are imposed on biological studies. However, this may explain the use of higher frequencies, accelerations, and durations. Reducing the above parameters should not cause methodological difficulties and/or confirmation of living subjects. In addition, mechanical action needs a much longer exposition to achieve an effect when acting on living systems than non-living systems. The difference in action time is on average 10–15 times. This phenomenon can be explained by fundamental differences in the way systems respond. “Response” of non-living systems to mechanical impact is provided exclusively by physical and chemical processes (energy dissipation, free radical reactions, etc.). Whereas, the responses of living systems are often mediated by specific receptors that trigger intracellular signaling cascades of events with some delay (see above). Receptor-mediated responses can take from fractions of seconds to minutes, hours, or even longer. Responses of living systems are also characterized by significant time delays due to the speed of the processes regulated by the cell or organism. Protein synthesis requires time delays of more than an hour, cell division—days, and tissue regeneration and remodeling—days or weeks.

Such a difference in “sensitivity” can be explained by the presence of homeostasis in living systems: up to a certain threshold, living systems can compensate for the effects of mechanical influence. According to our evaluation, the limits of metabolic compensation of mechanical impact lie in the areas of frequencies up to 10 Hz and accelerations up to 1 m/s² with durations not exceeding 100 s.

In the next step, we assessed the dependence of effect sizes on the combination of force and duration (Figure 4b). We also found a significant difference in the limits of force and duration values at which the effects are registered. For non-living systems, a force of 10⁻¹⁰ N or a duration of 0.01 s is sufficient for the development of effects. Whereas, for living systems, forces of at least 0.001 N and a duration of ~100 s are required. This difference can be explained by the ability of living systems to actively self-regulate and maintain homeostasis. With increasing force and/or duration, the effects of mechanical impact on nonliving systems grow relatively monotonically. The largest effect sizes (up to 2–4 orders of magnitude) for aqueous solutions are observed in the range of forces >10 N and durations of 100–1000 s. For living systems, the dependence of the magnitude of effects on force and duration is not obvious. We can detect a region of increased effect values between 0.001 and 10 N and 300 and 10,000 s, where the largest number of effects with the largest moduli are observed. However, the presence of this region may be due more to the convenience of studying cells and animals in the laboratory under these conditions. Thus, the effects of mechanical impact on non-living systems depend on a combination of factors, the leading ones being acceleration, force, and duration. In the case of non-living systems, there is an increase in the magnitude of the effect from the post force and/or duration. For living systems, a threshold mechanism of mechanical action close to the “all or nothing” principle and/or a complex character of dependence of the efficiency of mechanical action on its characteristics is most likely.

4.1.3. Correlations of Effects from Individual Parameters

At the next stage of the analysis, we tried to answer the question: which of the parameters of mechanical impact determines the magnitude of their effects to a greater extent? For this purpose, we evaluated the correlations between the magnitude of the effect of mechanical impact and its frequency, acceleration, force, and duration. Previously, we found that living and non-living systems respond differently to mechanical forcing, so in evaluating the correlations, we divided all evaluated responses into those of non-living (Figure 5) and living (Figure 6) systems. The strength, direction, and statistical significance of correlations were assessed using the Spearman criterion (

Table 3. Spearman correlation coefficients calculated for mechanical effects.

Coefficients	Mechanical Impact Parameters	Effect log10
		In Vivo	In Vitro
Spearman’s correlation	frequency, Hz (log10)	0.173	0.196
	acceleration, m/s2 (log10)	0.253	0.263
	duration, s (log10)	0.052	0.11407
	force, N (log10)	0.195	−0.06187
p-value	frequency, Hz (log10)	0.02344	0.01622
	acceleration, m/s2 (log10)	7.76 × 10−4	0.00113
	duration, s (log10)	0.49627	0.166
	force, N (log10)	0.01341	0.45196

The color scale in Spearman’s correlation corresponds to smaller negative (red) and larger positive (blue) values of Spearman’s Corr. The color scale in the p-value section shows significant (green, p < 0.05) and insignificant (orange, p ≥ 0.05) correlations.

).

We found that the magnitude of the effects of mechanical influence in the case of living systems depended on frequency, acceleration, and force. Significant correlations of the effect size with frequency (correlation strength 0.173 at p < 0.05), acceleration (correlation strength 0.253 at p < 0.001), and force (correlation 0.195, p < 0.05) were found. For non-living systems, the situation was somewhat different. Significant correlations were found between the magnitude of the effect size of mechanical impact and the frequency (p < 0.01), acceleration (p < 0.01), and duration (p < 0.001) of mechanical impact. However, the correlations found were of low strength: ~0.18 for the frequency-effect pair, ~0.22 for the acceleration-effect, and ~−0.26 for the duration-effect. Thus, mechanical effects with higher values of frequency and acceleration and the shortest durations should be most effective for water and aqueous solutions. It is noteworthy that living systems are more sensitive to acceleration and force than non-living systems. This can be explained by the ability of living systems to actively receive force (compression, stretching, shear stress) due to specialized receptor structures [128,129,130]. At the same time, nonliving systems are more sensitive to the duration of impact, which may indicate the contribution of mechanisms for maintaining homeostasis in living systems.

4.2. Dependence of the Magnitude of Ultrasound Effects on Its Characteristics

To assess the dependence of ultrasound (US) effects on its characteristics, we applied an approach similar to that described in Section 4.1.2 and Section 4.1.3. We chose the frequency, intensity, and duration of exposure as the main characteristics of US treatment (Figure 7).

The characteristics of ultrasound exposure used in most of the analysed works lie in the frequency ranges from 10⁴ to 10⁷ Hz, and intensity from 0.1 mW/cm² to 100 W/cm². The durations are from 10 s to several hours. The bulk of the effects with high values are concentrated in the frequency range from 0.1 to 1.0 MHz (Figure 7). Increasing both frequency and intensity enhances the effects of ultrasound (US) on living and non-living systems (Figure 7). The contribution of frequency appears to be more significant than that of power. Similarly, the contribution of duration appears to be more significant than that of intensity. A threshold duration of 1000 s is observed, after which the magnitude of the effects increases significantly, regardless of power.

Correlations of Ultrasound Effects on Individual Parameters

When assessing the correlations between the magnitudes of the effects of the US on living and non-living systems, we found no differences, so we calculated Spearman correlation coefficients for the whole sample of analyzed data (Figure 8 and

Table 4. Spearman correlation coefficients between effect size and KM characteristics.

Coefficients	US Impact Parameters	Effect log10
Spearman’s correlation	frequency, Hz (log10)	0.1086
	intensity, mW/cm2 (log10)_	0.38302
	duration, s (log10)	−0.27719
p-value	frequency, Hz (log10)	0.10657
	intensity, mW/cm2 (log10)_	3.60925 × 10−9
	duration, s (log10)	2.8004 × 10−5

The color scale in Spearman’s correlation corresponds to negative (red) and larger positive (blue) values of Spearman’s Corr. The color scale in the p-value section shows significant (green, p < 0.05) and insignificant (orange, p ≥ 0.05) correlations.

).

We found statistically significant correlations between the strength of the effect of ultrasound exposure and the intensity (correlation strength 0.38, p = 3.60925 × 10⁻⁹) and duration of exposure (correlation strength −0.27719, p = 2.8004 × 10⁻⁵). The positive correlation between the magnitude of US effects and its power seems more logical and does not require further explanation. The absence of a significant correlation between the magnitude of the effects of ultrasound (US) and its frequency indicates that frequency plays a less pronounced role in regulating the magnitude of US effects. Additionally, the frequency range used is narrower (3.5 orders of magnitude) than the duration and intensity ranges (5 and 7 orders of magnitude, respectively). The observed negative relationship between US exposure duration and effects can be explained by the fact that shorter exposure times were investigated at higher intensities, and vice versa (Figure 7a).

5. Limitations and Prospects

As can be seen from the Appendix A, there are more than a dozen (vibrations, shocks, stirring in different modes, falling, etc.) fundamentally different protocols of mechanical influence on aqueous solutions and living systems. For each of the effects, there may be critical conditions for the realization of effects that are not important for the other effects. For example, frequency is not applicable to falling, and height above the floor is not important in vibration. The difference in methods causes a difference in the information provided by the authors (see Appendix A), so the task of combining and comparing data becomes more difficult.

We have attempted to “arrive at a common denominator” when evaluating heterogeneous mechanical effects in the form of acceleration or force calculations. This approach allowed us to discover several interesting regularities, but it is not without disadvantages. In particular, when calculating the acceleration, we made the assumption that the oscillations are sinusoidal. However, we cannot guarantee that in all the analyzed articles the oscillations were sinusoidal. When calculating the force, we also used approximate mass values, since the authors’ exact mass values may simply not have been measured.

However, the approach we used was sufficient to find a number of generalizable acceleration-duration-effect and force-duration-effect patterns, and we also found differences between the responses to mechanical actions of living and non-living systems.

Two approaches can be suggested as future directions for research on this topic. The first is to deepen the analysis of already available data with the involvement of new methods of data analysis, for example, the principal component method, and the calculation of multiple correlation coefficients.

When planning future experiments, we would recommend limiting the number of measured effects in favor of expanding the number of exposure options. It is obligatory to perform adequate sham controls at all stages of the experiment [206]. In addition, when planning experiments (including those in other fields, not only mechanobiology) and interpreting the obtained data, it is necessary to take into account the possible effects of vibration and other influences on experimental samples, especially in vivo experiments.

The processes of cellular mechanotransduction are fundamentally different from those of solution mechanochemistry. In particular, actin-dependent transduction of mechanical signals in the cell is 40 to 50 times faster than diffusion of chemical reaction products [207,208]. However, as follows from the cited articles, mechanical action can affect the conformational states of proteins and enzymatic action in aqueous solution [91,92,209]. We proceed from the position that protein mechanochemistry, albeit altered, also occurs in the cytosol as in aqueous solutions, independent of signaling systems. Consequently, in a broad sense, the response of living systems to mechanical action will be the sum of aqueous solution mechanochemistry and mechanotransduction at the cellular level. Therefore, these processes are discussed together in this review.

We consider the use of mechanical effects for stem cell differentiation, more detailed in vivo studies, catalysis of chemical reactions in solutions, and nanobubbles as promising directions for future research.

6. Conclusions

Despite the diversity of mechanical effects, their characteristics can be summarised into a few key ones: frequency, acceleration, force, and duration. The magnitude of the effects of mechanical actions on living and non-living systems depends differently on the type of system affected. For non-living systems, there is a significant dependence of the response on the magnitude of acceleration, frequency, and duration of the impact. Responses of living systems depend on the magnitudes of acceleration, frequency, and force, but not duration. The magnitude of the effect changes insignificantly with the growth of these parameters of mechanical influence. Ultrasonic action depends on intensity and duration, both in aqueous solutions and in living organisms. Aqueous solutions require lower values of frequency and acceleration during mechanical action than living systems to initiate a ‘response’. This is due to the ability of living systems to maintain homeostasis. Notably, living systems are more sensitive to acceleration and force than non-living systems. This can be explained by the living system’s ability to actively receive force (compression, stretching, and shear stress) due to specialized receptor structures. At the same time, non-living systems are more sensitive to the duration of impact. These differences may indicate the contribution of mechanisms of homeostasis maintenance in living systems.